A Review on Recent Advances in Signal Processing in Interferometry
Abstract
1. Introduction
2. Patterns of Optical Interferometric Signals
2.1. Homodyne Signal
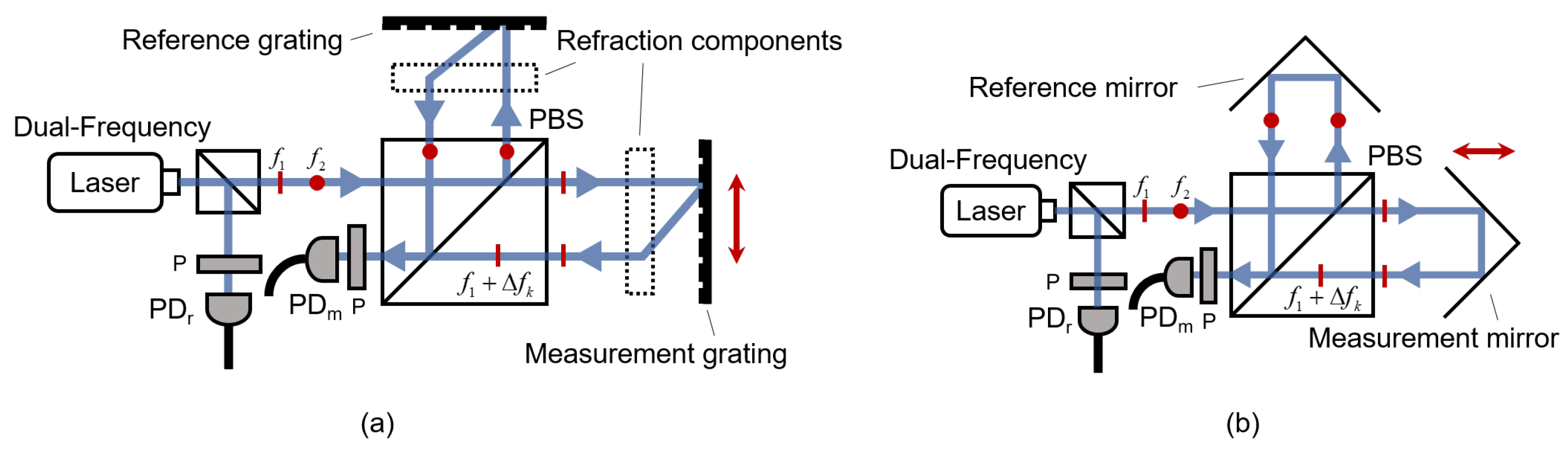
2.2. Heterodyne Signal
2.3. Comparison of Homodyne Signals and Heterodyne Signals
3. Optical Interferometric Signal Processing Techniques
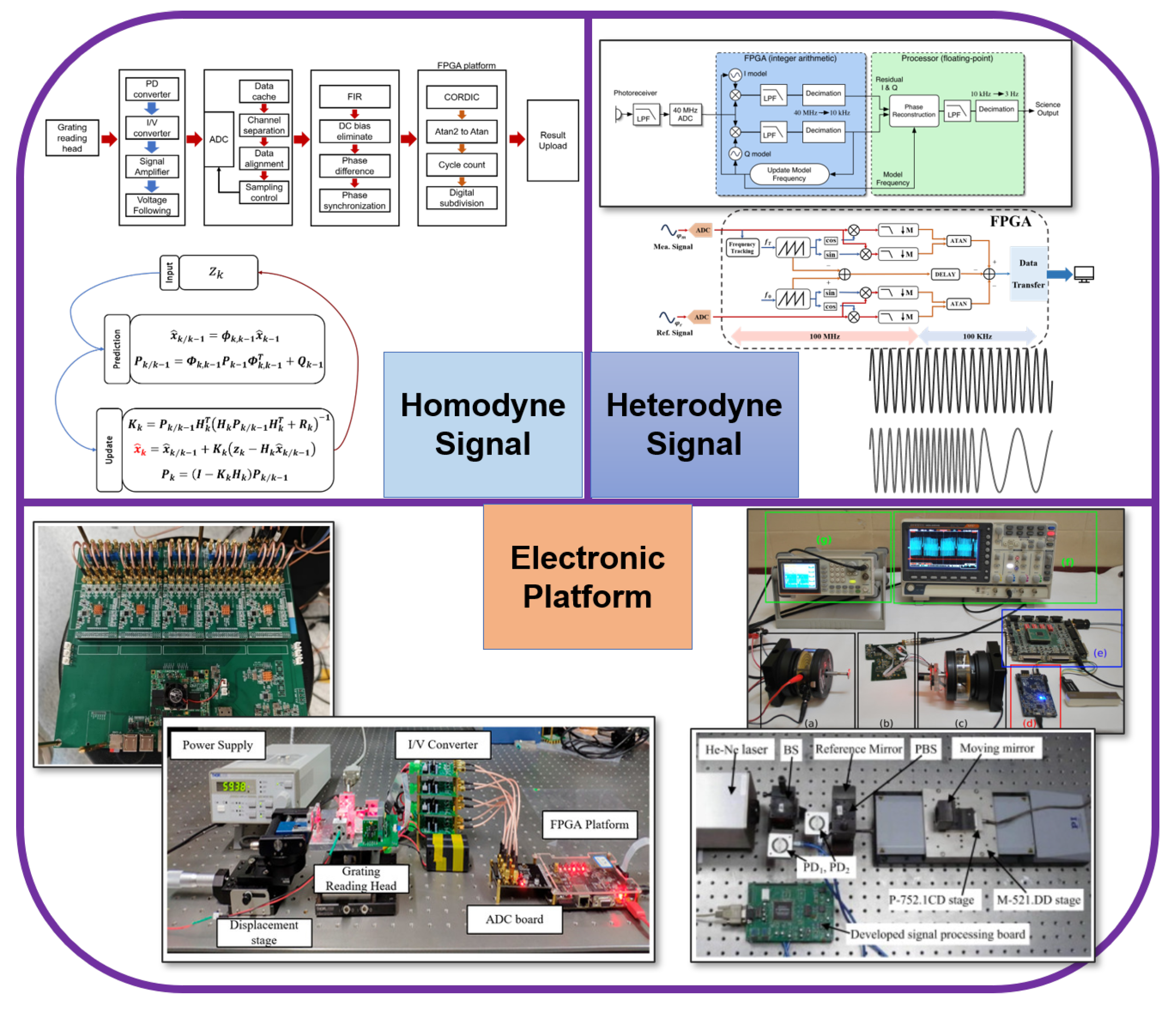
3.1. Phase Estimation Methods for Homodyne Signals
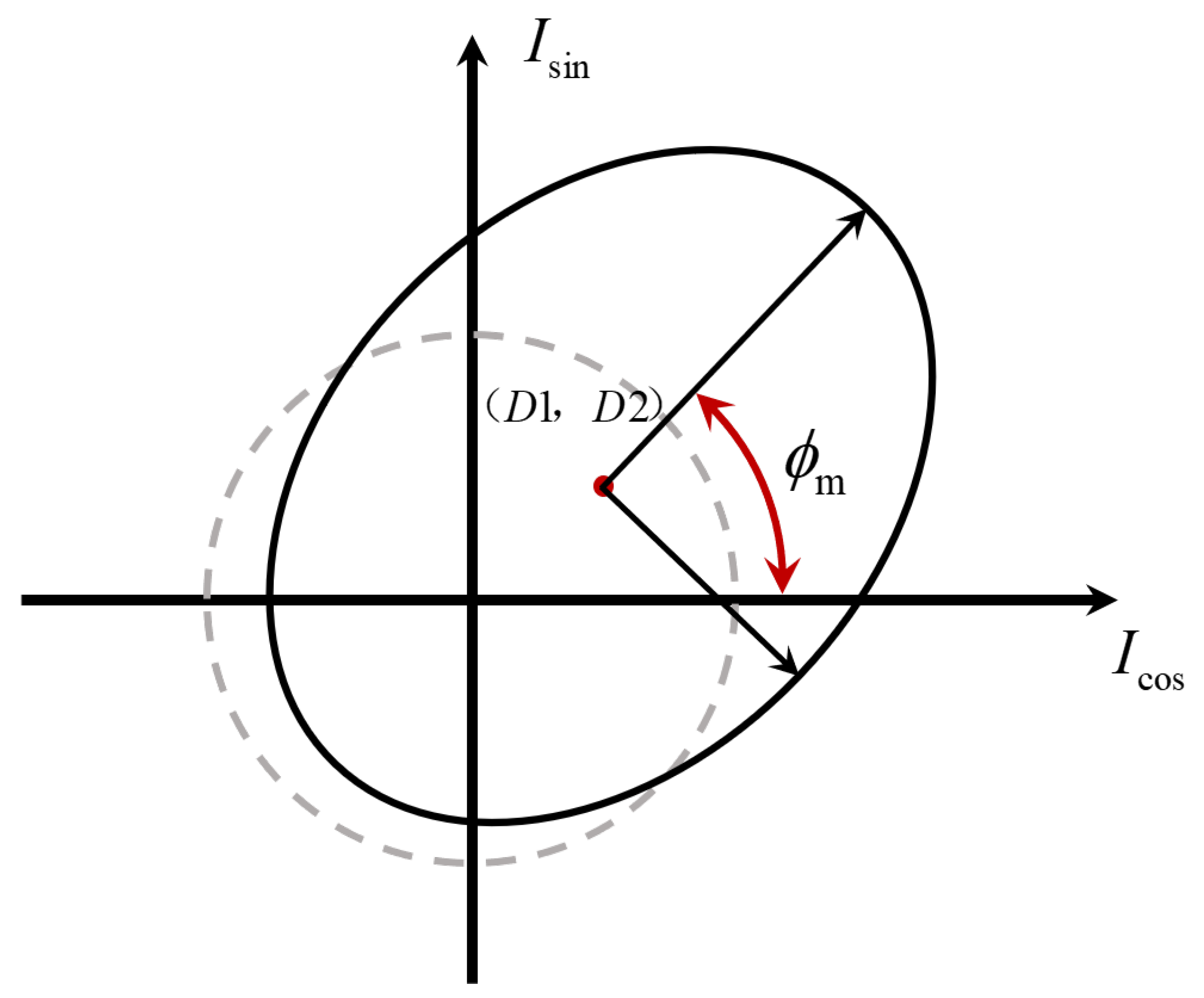
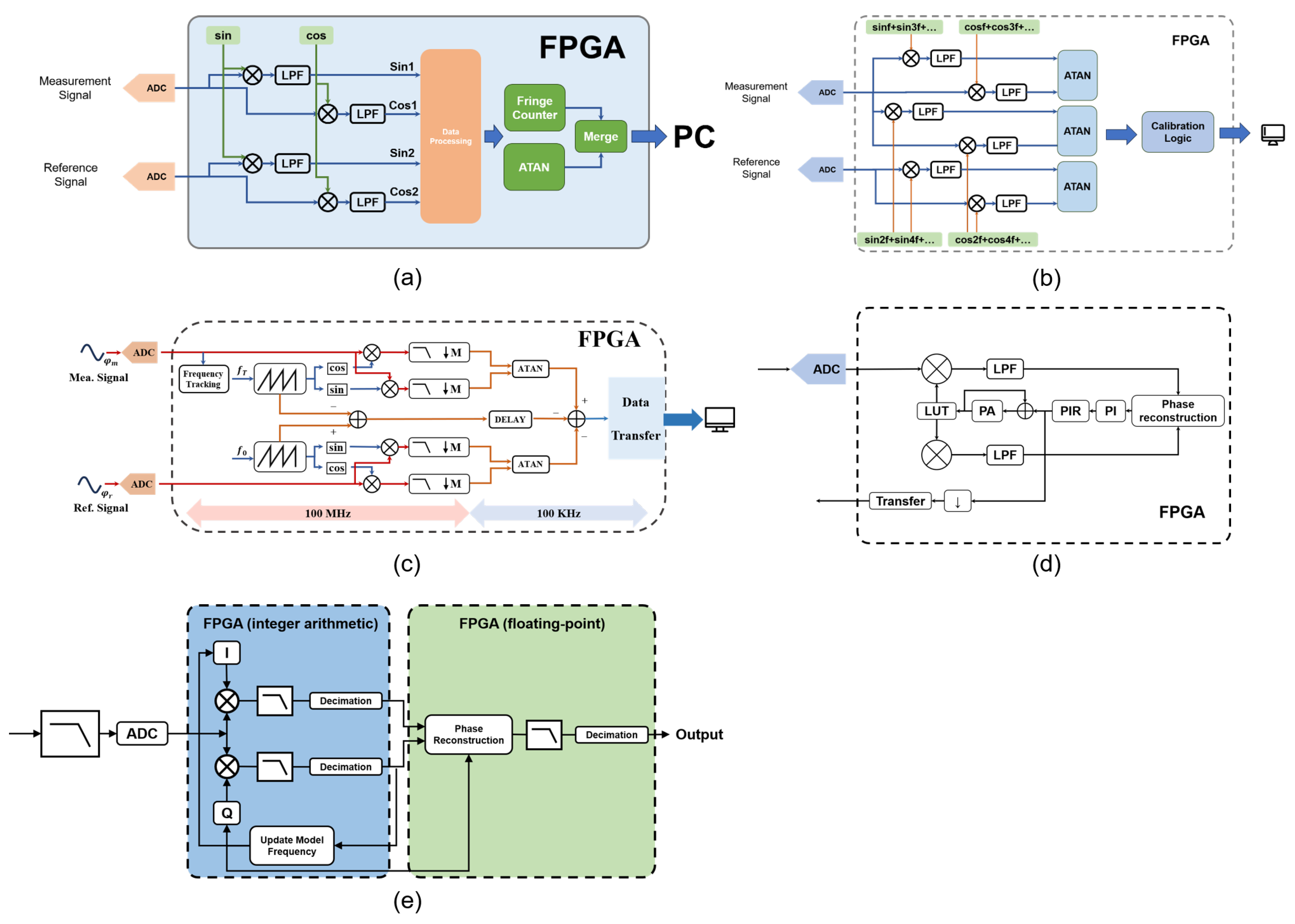
3.1.1. Error Calibration Methods
3.1.2. Ellipse Parameter Estimation Methods
3.2. Phase Estimation Methods for Heterodyne Signals
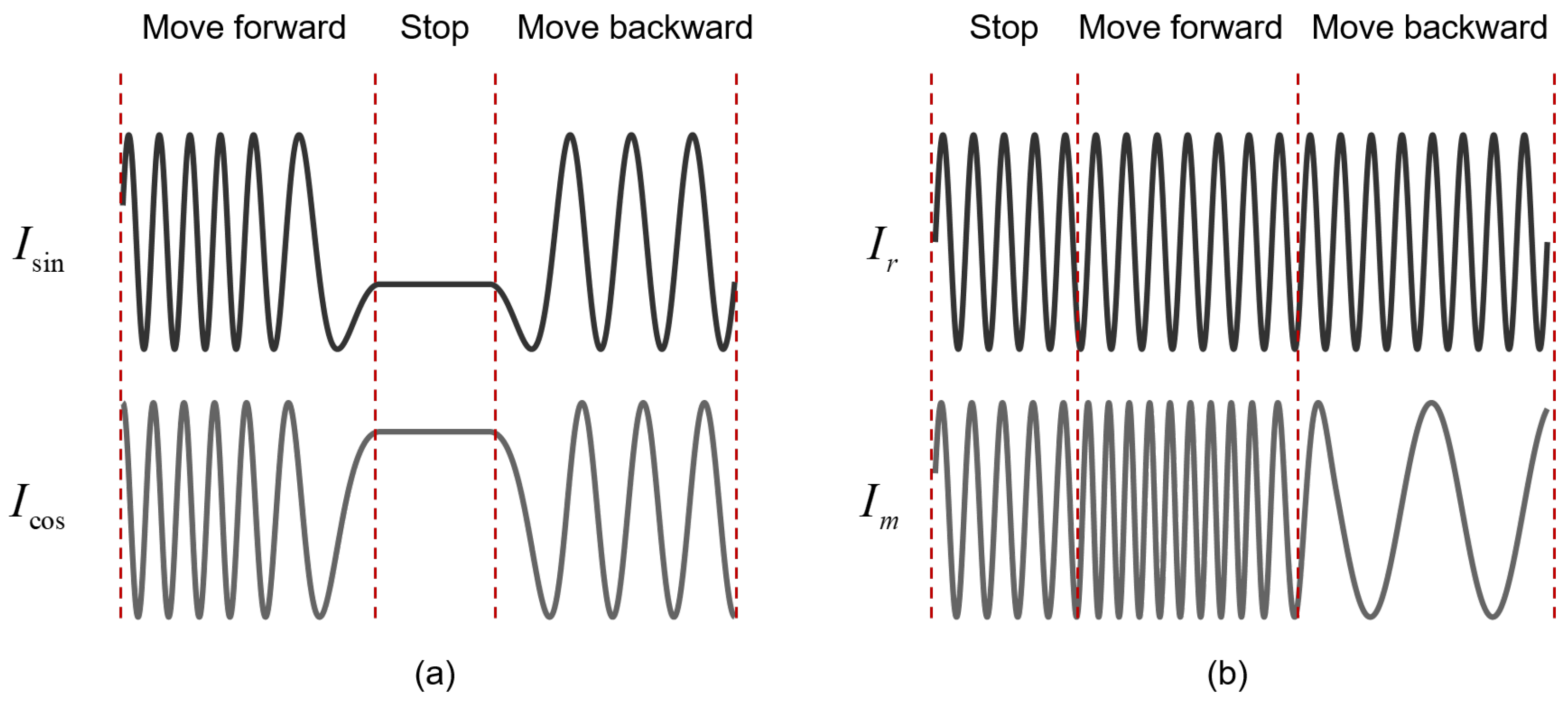
3.2.1. Pulse-Counting Methods
3.2.2. Quadrature Phase-Locked Methods
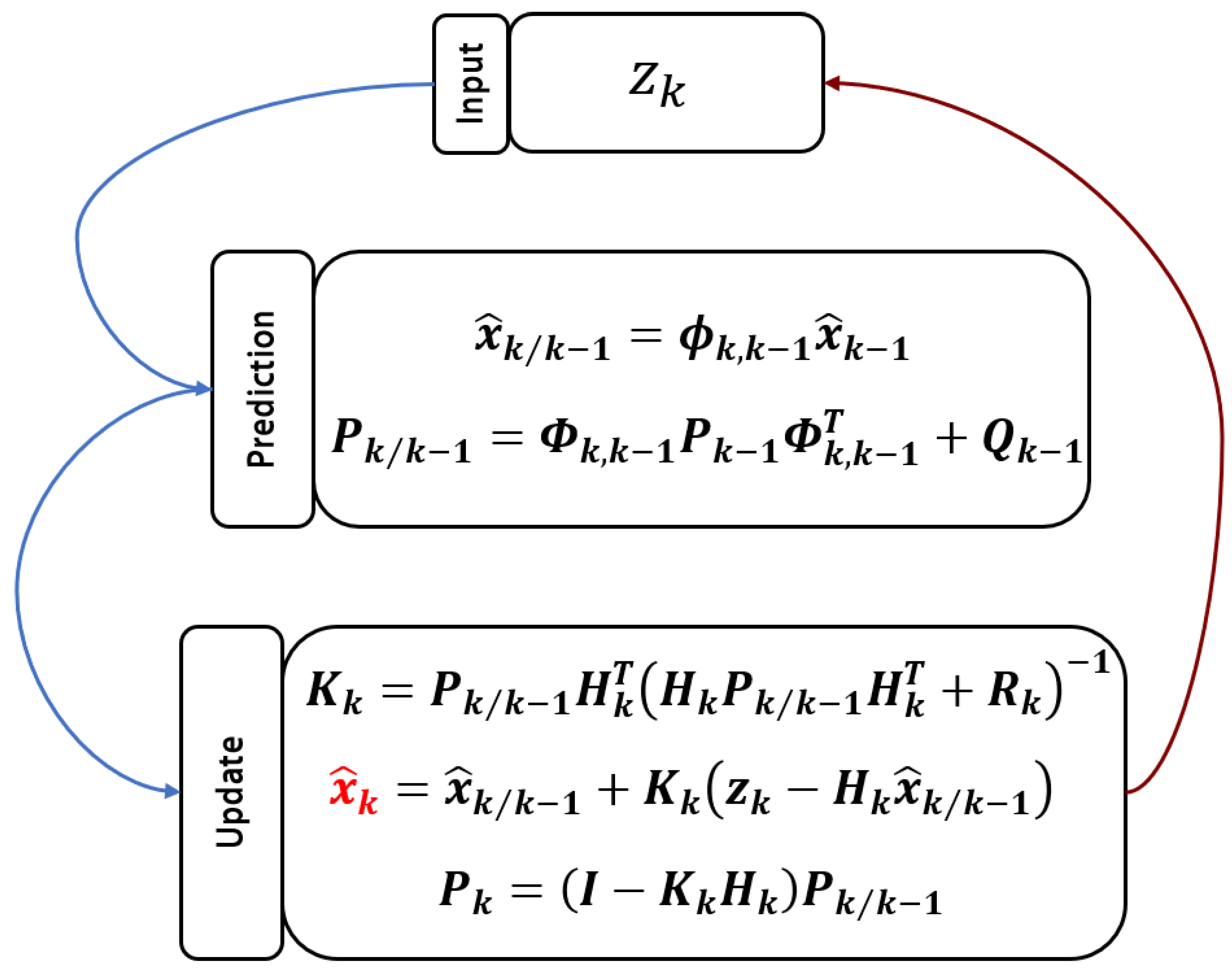
3.2.3. Kalman Filtering Method
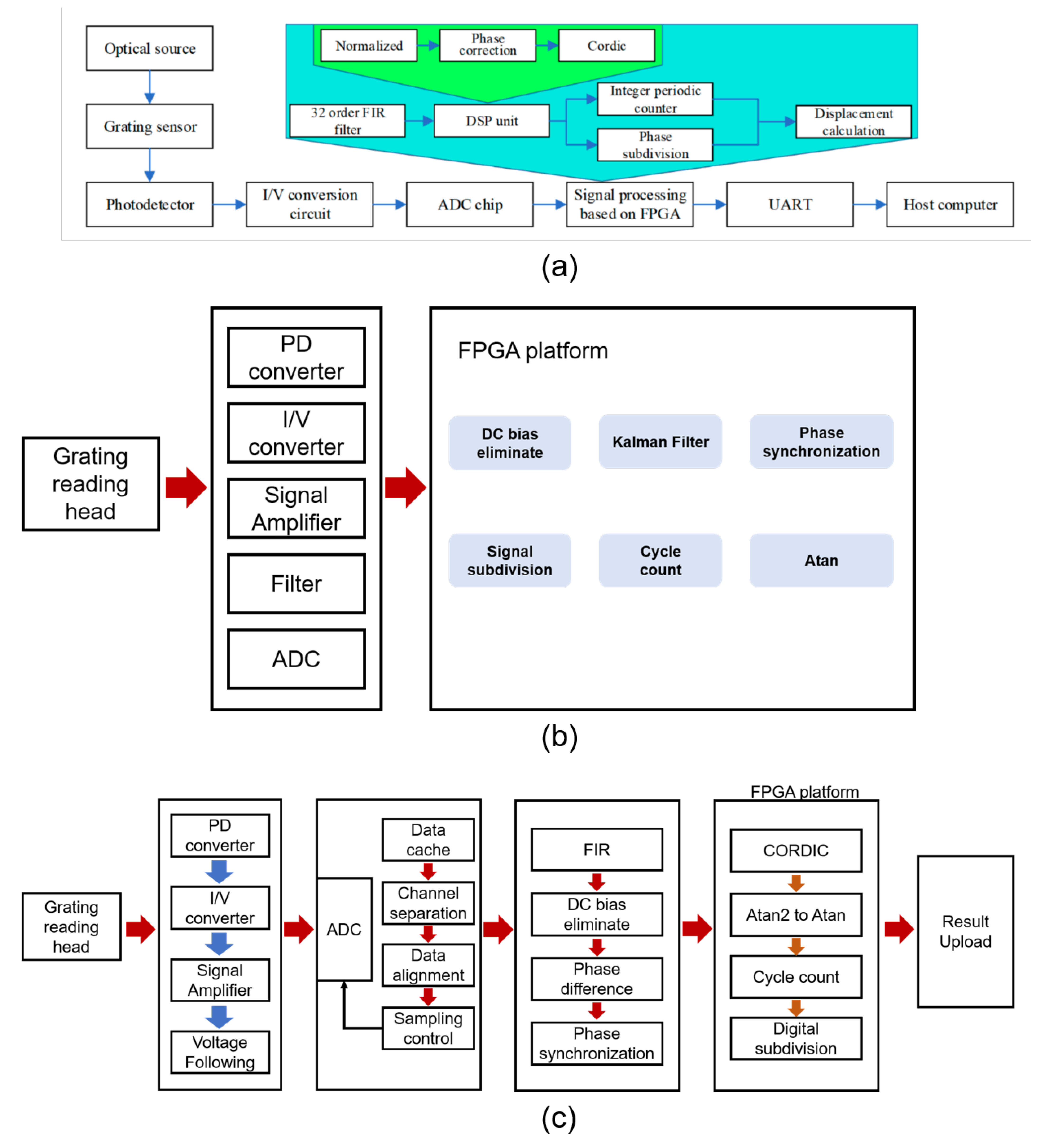
4. Electronic Platforms for Signal Processing
4.1. PCs
4.2. MCUs/DSPs
4.3. FPGAs
4.4. ASICs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Carr, J.; Desmulliez, M.; Weston, N.; McKendrick, D.; Cunningham, G.; McFarland, G.; Meredith, W.; McKee, A.; Langton, C. Miniaturised optical encoder for ultra precision metrology systems. Precis. Eng. 2009, 33, 263–267. [Google Scholar] [CrossRef]
- Han, M.; Lei, F.; Shi, W.; Lu, S.; Li, X. Uniaxial MEMS-based 3D reconstruction using pixel refinement. Opt. Express 2022, 31, 536–554. [Google Scholar] [CrossRef] [PubMed]
- Lei, F.; Han, M.; Jiang, H.; Wang, X.; Li, X. A phase-angle inspired calibration strategy based on MEMS projector for 3D reconstruction with markedly reduced calibration images and parameters. Opt. Lasers Eng. 2024, 176, 108078. [Google Scholar] [CrossRef]
- Zhou, Q.; Qiao, X.; Ni, K.; Li, X.; Wang, X. Depth detection in interactive projection system based on one-shot black-and-white stripe pattern. Opt. Express 2017, 25, 5341–5351. [Google Scholar] [CrossRef]
- Demarest, F.C. High-resolution, high-speed, low data age uncertainty, heterodyne displacement measuring interferometer electronics. Meas. Sci. Technol. 1998, 9, 1024. [Google Scholar] [CrossRef]
- Yuan, J.; Lyu, B.; Hang, W.; Deng, Q. Review on the progress of ultra-precision machining technologies. Front. Mech. Eng. 2017, 12, 158–180. [Google Scholar] [CrossRef]
- Gao, W. Precision Nanometrology: Sensors and Measuring Systems for Nanomanufacturing; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Catalucci, S.; Thompson, A.; Piano, S.; Branson III, D.T.; Leach, R. Optical metrology for digital manufacturing: A review. Int. J. Adv. Manuf. Technol. 2022, 120, 4271–4290. [Google Scholar] [CrossRef]
- Zhu, C.; Zhuang, Y.; Liu, B.; Huang, J. Review of fiber optic displacement sensors. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Sciammarella, C.A. A Review: Optical Methods That Evaluate Displacement. In Advancement of Optical Methods & Digital Image Correlation in Experimental Mechanics, Volume 3: Proceedings of the 2018 Annual Conference on Experimental and Applied Mechanics; Springer: Berlin/Heidelberg, Germany, 2018; pp. 23–52. [Google Scholar]
- Zvietcovich, F.; Larin, K.V. Wave-based optical coherence elastography: The 10-year perspective. Prog. Biomed. Eng. 2022, 4, 012007. [Google Scholar] [CrossRef]
- Han, Y.; Wu, G.; Feng, D. Vision-based displacement measurement using an unmanned aerial vehicle. Struct. Control Health Monit. 2022, 29, e3025. [Google Scholar] [CrossRef]
- Hosseinzadeh Sani, M.; Saghaei, H.; Mehranpour, M.A.; Asgariyan Tabrizi, A. A novel all-optical sensor design based on a tunable resonant nanocavity in photonic crystal microstructure applicable in MEMS accelerometers. Photonic Sens. 2021, 11, 457–471. [Google Scholar] [CrossRef]
- Armano, M.; Audley, H.; Baird, J.; Binetruy, P.; Born, M.; Bortoluzzi, D.; Brandt, N.; Castelli, E.; Cavalleri, A.; Cesarini, A.; et al. Sensor noise in LISA pathfinder: In-flight performance of the optical test mass readout. Phys. Rev. Lett. 2021, 126, 131103. [Google Scholar] [CrossRef]
- Zuo, C.; Qian, J.; Feng, S.; Yin, W.; Li, Y.; Fan, P.; Han, J.; Qian, K.; Chen, Q. Deep learning in optical metrology: A review. Light. Sci. Appl. 2022, 11, 1–54. [Google Scholar] [CrossRef] [PubMed]
- Brown, B.H.; Smallwood, R.H.; Barber, D.C.; Lawford, P.; Hose, D. Medical Physics and Biomedical Engineering; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Szelitzky, E.; Kuklyte, J.; Mândru, D.; O’Connor, N.E. Low cost angular displacement sensors for biomechanical applications—A review. J. Biomed. Eng. Technol. 2014, 2, 21–28. [Google Scholar]
- Masís Solano, M.; Richer, E.; Costantino, S.; Lesk, M.R. Optic nerve head pulsatile displacement in open-angle glaucoma after intraocular pressure reduction measured by optical coherence tomography: A pilot study. Bioengineering 2024, 11, 411. [Google Scholar] [CrossRef]
- Knobel, R.G.; Cleland, A.N. Nanometre-scale displacement sensing using a single electron transistor. Nature 2003, 424, 291–293. [Google Scholar] [CrossRef]
- Siebert, T.; Hack, E.; Lampeas, G.; Patterson, E.; Splitthof, K. Uncertainty quantification for DIC displacement measurements in industrial environments. Exp. Tech. 2021, 45, 685–694. [Google Scholar] [CrossRef]
- Xie, C.; Nguyen, H.; Bui, X.N.; Nguyen, V.T.; Zhou, J. Predicting roof displacement of roadways in underground coal mines using adaptive neuro-fuzzy inference system optimized by various physics-based optimization algorithms. J. Rock Mech. Geotech. Eng. 2021, 13, 1452–1465. [Google Scholar] [CrossRef]
- Gao, W.; Haitjema, H.; Fang, F.; Leach, R.; Cheung, C.; Savio, E.; Linares, J.M. On-machine and in-process surface metrology for precision manufacturing. Cirp Ann. 2019, 68, 843–866. [Google Scholar] [CrossRef]
- Li, D.; Wang, B.; Tong, Z.; Blunt, L.; Jiang, X. On-machine surface measurement and applications for ultra-precision machining: A state-of-the-art review. Int. J. Adv. Manuf. Technol. 2019, 104, 831–847. [Google Scholar] [CrossRef]
- Li, C.; Yan, H.; Qian, X.; Zhu, S.; Zhu, P.; Liao, C.; Tian, H.; Li, X.; Wang, X.; Li, X. A domain adaptation YOLOv5 model for industrial defect inspection. Measurement 2023, 213, 112725. [Google Scholar] [CrossRef]
- Sato, R.; Li, K.; Michihata, M.; Takahashi, S.; Gao, W. Advanced sensing and machine learning technologies for intelligent measurement in smart and precision manufacturing. Int. J. Autom. Technol. 2024, 18, 545–580. [Google Scholar] [CrossRef]
- Li, C.; Pan, X.; Zhu, P.; Zhu, S.; Liao, C.; Tian, H.; Qian, X.; Li, X.; Wang, X.; Li, X. Style Adaptation module: Enhancing detector robustness to inter-manufacturer variability in surface defect detection. Comput. Ind. 2024, 157, 104084. [Google Scholar] [CrossRef]
- Yao, T.F.; Duenner, A.; Cullinan, M. In-line metrology of nanoscale features in semiconductor manufacturing systems. Precis. Eng. 2017, 47, 147–157. [Google Scholar] [CrossRef]
- Maitra, V.; Su, Y.; Shi, J. Virtual metrology in semiconductor manufacturing: Current status and future prospects. Expert Syst. Appl. 2024, 249, 123559. [Google Scholar] [CrossRef]
- ASML. Twinscan NXE:3600D [EB/OL]. 2022. Available online: https://www.asml.com/en/products/euv-lithography-systems/twinscan-nxe-3600d (accessed on 6 March 2022).
- Banks-Sills, L.; Shklovsky, J.; Krylov, S.; Bruck, H.A.; Fourman, V.; Eliasi, R.; Ashkenazi, D. A Methodology for Accurately Measuring Mechanical Properties on the Micro-Scale. Strain 2011, 47, 288–300. [Google Scholar] [CrossRef]
- Anandan, N.; George, B. A wide-range capacitive sensor for linear and angular displacement measurement. IEEE Trans. Ind. Electron. 2017, 64, 5728–5737. [Google Scholar] [CrossRef]
- Kumar, A.A.; Anandan, N.; George, B.; Mukhopadhyay, S.C. Improved capacitive sensor for combined angular and linear displacement sensing. IEEE Sens. J. 2019, 19, 10253–10261. [Google Scholar] [CrossRef]
- Ye, Y.; Zhang, C.; He, C.; Wang, X.; Huang, J.; Deng, J. A review on applications of capacitive displacement sensing for capacitive proximity sensor. IEEE Access 2020, 8, 45325–45342. [Google Scholar] [CrossRef]
- Nabavi, M.R.; Nihtianov, S.N. Design strategies for eddy-current displacement sensor systems: Review and recommendations. IEEE Sens. J. 2012, 12, 3346–3355. [Google Scholar] [CrossRef]
- Tong, P.; Wu, L.; Yanchen, A.; Su, R.; Wu, Y. A novel eddy current sensor for displacement measurement with high accuracy and long range. IEEE Sens. J. 2023, 23, 12066–12075. [Google Scholar] [CrossRef]
- Borovik, S.; Kuteynikova, M.; Sekisov, Y. Reducing the Impact of Influence Factors on the Measurement Results from Single-Coil Eddy Current Sensors. Sensors 2022, 23, 351. [Google Scholar] [CrossRef]
- Zhu, H.M.; Wu, Y.Y.; Zheng, W.H.; Huang, Z.W. In-plane and out-of-plane displacement measurement by ultrasonic speckle correlation method (USCM). Arch. Appl. Mech. 2006, 75, 521–526. [Google Scholar] [CrossRef]
- Sumi, C. Displacement vector measurement using instantaneous ultrasound signal phase-multidimensional autocorrelation and Doppler methods. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 24–43. [Google Scholar] [CrossRef]
- Berkovic, G.; Shafir, E. Optical methods for distance and displacement measurements. Adv. Opt. Photonics 2012, 4, 441–471. [Google Scholar] [CrossRef]
- Fu, X.B.; Liu, B.; Zhang, Y.C. A displacement measurement system based on optical triangulation method. Optoelectron. Lett. 2011, 7, 380–383. [Google Scholar] [CrossRef]
- Chen, R.; Li, X.; Wang, X.; Li, J.; Xue, G.; Zhou, Q.; Ni, K. A planar pattern based calibration method for high precision structured laser triangulation measurement. In Proceedings of the Optical Metrology and Inspection for Industrial Applications VI, Hangzhou, China, 20–23 October 2019; SPIE: Cergy, France, 2019; Volume 11189, pp. 212–218. [Google Scholar]
- Bai, J.; Li, J.; Wang, X.; Li, X. Research progress of high precision chromatic confocal displacement measurement technology. Laser Optoelectron. Prog 2023, 60, 0312014. [Google Scholar] [CrossRef]
- Sato, R.; Li, X.; Fischer, A.; Chen, L.C.; Chen, C.; Shimomura, R.; Gao, W. Signal processing and artificial intelligence for dual-detection confocal probes. Int. J. Precis. Eng. Manuf. 2024, 25, 199–223. [Google Scholar] [CrossRef]
- Bai, J.; Li, X.; Wang, X.; Wang, J.; Ni, K.; Zhou, Q. Self-reference dispersion correction for chromatic confocal displacement measurement. Opt. Lasers Eng. 2021, 140, 106540. [Google Scholar] [CrossRef]
- Bai, J.; Li, X.; Wang, X.; Zhou, Q.; Ni, K. Chromatic confocal displacement sensor with optimized dispersion probe and modified centroid peak extraction algorithm. Sensors 2019, 19, 3592. [Google Scholar] [CrossRef]
- Kurtev, K.I.; Trujillo-Sevilla, J.M.; Rodríguez-Ramos, J.M. Long-Distance Measurements Using a Chromatic Confocal Sensor. Appl. Sci. 2024, 14, 9943. [Google Scholar] [CrossRef]
- Bai, J.; Li, X.; Zhou, Q.; Ni, K.; Wang, X. Improved chromatic confocal displacement-sensor based on a spatial-bandpass-filter and an X-shaped fiber-coupler. Opt. Express 2019, 27, 10961–10973. [Google Scholar] [CrossRef]
- Bai, J.; Wang, X.; Li, X.; Zhou, Q.; Ni, K. Design and testing of a chromatic dispersion system for displacement application by using a spatial-bandpass-filter. In Proceedings of the Tenth International Symposium on Precision Engineering Measurements and Instrumentation, Kunming, China, 8–10 August 2018; SPIE: Cergy, France, 2019; Volume 11053, pp. 905–911. [Google Scholar] [CrossRef]
- Badami, V.; de Groot, P. Displacement measuring interferometry. Handb. Opt. Dimens. Metrol. 2013, 4, 180–199. [Google Scholar]
- Haitjema, H. Calibration of displacement laser interferometer systems for industrial metrology. Sensors 2019, 19, 4100. [Google Scholar] [CrossRef]
- Požar, T.; Gregorčič, P.; Možina, J. A precise and wide-dynamic-range displacement-measuring homodyne quadrature laser interferometer. Appl. Phys. B 2011, 105, 575–582. [Google Scholar] [CrossRef]
- Yan, H.; Duan, H.Z.; Li, L.T.; Liang, Y.R.; Luo, J.; Yeh, H.C. A dual-heterodyne laser interferometer for simultaneous measurement of linear and angular displacements. Rev. Sci. Instruments 2015, 86, 123102. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.; Cui, C.; Lei, X.; Li, Q.; Yan, S.; Li, X.; Wang, G. A Review of Optical Interferometry for High-Precision Length Measurement. Micromachines 2024, 16, 6. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Wang, Y.; Du, H.; Zeng, Q.; Xiong, X. High-precision displacement measurement model for the grating interferometer system. Opt. Eng. 2020, 59, 045101. [Google Scholar] [CrossRef]
- Lee, J.Y.; Jiang, G.A. Displacement measurement using a wavelength-phase-shifting grating interferometer. Opt. Express 2013, 21, 25553–25564. [Google Scholar] [CrossRef]
- Lee, J.Y.; Chen, H.Y.; Hsu, C.C.; Wu, C.C. Optical heterodyne grating interferometry for displacement measurement with subnanometric resolution. Sens. Actuators A Phys. 2007, 137, 185–191. [Google Scholar] [CrossRef]
- Hsieh, H.L.; Pan, S.W. Development of a grating-based interferometer for six-degree-of-freedom displacement and angle measurements. Opt. Express 2015, 23, 2451–2465. [Google Scholar] [CrossRef] [PubMed]
- Guo, D.; Wang, M.; Hao, H. Displacement measurement using a laser feedback grating interferometer. Appl. Opt. 2015, 54, 9320–9325. [Google Scholar] [CrossRef]
- Fleming, A.J. A review of nanometer resolution position sensors: Operation and performance. Sens. Actuators A Phys. 2013, 190, 106–126. [Google Scholar] [CrossRef]
- Shimizu, Y.; Chen, L.C.; Kim, D.W.; Chen, X.; Li, X.; Matsukuma, H. An insight into optical metrology in manufacturing. Meas. Sci. Technol. 2021, 32, 042003. [Google Scholar] [CrossRef]
- Chen, S.; Xue, S.; Xiong, Y.; Peng, X.; Dai, Y. Research progress of ultra-precision measurement of optical surfaces for manufacturing. Laser Optoelectron. Prog. 2023, 60, 0312011. [Google Scholar]
- Teimel, A. Technology and applications of grating interferometers in high-precision measurement. Precis. Eng. 1992, 14, 147–154. [Google Scholar] [CrossRef]
- Fan, K.C.; Wang, H.Y.; Yang, H.W.; Chen, L.M. Techniques of multi-degree-of-freedom measurement on the linear motion errors of precision machines. Adv. Opt. Technol. 2014, 3, 375–386. [Google Scholar] [CrossRef]
- Xu, X.; Tan, Y.; Mu, H.; Li, Y.; Wang, J.; Jin, J. Laser interferometric multi-degree-of-freedom measurement technology in space gravitational-wave detection. Laser Optoelectron. Prog. 2023, 60, 0312006. [Google Scholar]
- Bai, Y.; Hu, P.; Lu, Y.; Li, Z.; Zhang, Z.; Tan, J. A six-axis heterodyne interferometer system for the joule balance. IEEE Trans. Instrum. Meas. 2016, 66, 1579–1585. [Google Scholar] [CrossRef]
- Cao, F.; Lu, S.; Luo, L.; Wang, S.; Li, X. In-plane and out-of-plane 4-DOF encoder based on grating. In Proceedings of the Second International Conference on Power Electronics and Artificial Intelligence (PEAI 2025), Guangzhou, China, 17–19 January 2025; SPIE: Cergy, France, 2025; Volume 13657, pp. 731–737. [Google Scholar]
- Matsukuma, H.; Ishizuka, R.; Furuta, M.; Li, X.; Shimizu, Y.; Gao, W. Reduction in cross-talk errors in a six-degree-of-freedom surface encoder. Nanomanuf. Metrol. 2019, 2, 111–123. [Google Scholar] [CrossRef]
- Hori, Y.; Gonda, S.; Bitou, Y.; Watanabe, A.; Nakamura, K. Periodic error evaluation system for linear encoders using a homodyne laser interferometer with 10 picometer uncertainty. Precis. Eng. 2018, 51, 388–392. [Google Scholar] [CrossRef]
- Wang, S.; Lu, S.; Cao, F.; Luo, L.; Wang, Y.; Li, X. Absolute grating encoder with high-precision and large measurement range. In Proceedings of the Holography, Diffractive Optics, and Applications XIV, Nantong, China, 12–15 October 2024; SPIE: Cergy, France, 2024; Volume 13240, pp. 182–187. [Google Scholar]
- Wang, S.; Zhu, J.; Shi, N.; Luo, L.; Wen, Y.; Li, X. Modeling and test of an absolute four-degree-of-freedom (DOF) grating encoder. In Proceedings of the Optical Metrology and Inspection for Industrial Applications IX, Online, 5–12 December 2022; SPIE: Cergy, France, 2022; Volume 12319, pp. 72–78. [Google Scholar]
- Wang, S.; Luo, L.; Li, X. Design and parameter optimization of zero position code considering diffraction based on deep learning generative adversarial networks. Nanomanuf. Metrol. 2024, 7, 2. [Google Scholar] [CrossRef]
- Wang, S.; Luo, L.; Zhu, J.; Shi, N.; Li, X. An ultra-precision absolute-type multi-degree-of-freedom grating encoder. Sensors 2022, 22, 9047. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Ni, K.; Zhou, Q.; Mao, X.; Zeng, L.; Wang, X.; Xiao, X. Two-probe optical encoder for absolute positioning of precision stages by using an improved scale grating. Opt. Express 2016, 24, 21378–21391. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Luo, L.; Cao, F.; Li, X. Nanoscale Absolute Grating Encoder with Wide Range Directional Discrimination Based on Asymmetric Code and Hybrid Positioning. In Proceedings of the CLEO: Fundamental Science, Charlotte, NC, USA, 5–10 May 2024; Optica Publishing Group: Washington, DC, USA, 2024; p. JTh2A-159. [Google Scholar]
- Goßler, S.; Bertolini, A.; Born, M.; Chen, Y.; Dahl, K.; Gering, D.; Gräf, C.; Heinzel, G.; Hild, S.; Kawazoe, F.; et al. The AEI 10 m prototype interferometer. Class. Quantum Gravity 2010, 27, 084023. [Google Scholar] [CrossRef]
- Jang, Y.S.; Kim, S.W. Compensation of the refractive index of air in laser interferometer for distance measurement: A review. Int. J. Precis. Eng. Manuf. 2017, 18, 1881–1890. [Google Scholar] [CrossRef]
- Ciddor, P.E. Refractive index of air: New equations for the visible and near infrared. Appl. Opt. 1996, 35, 1566–1573. [Google Scholar] [CrossRef]
- Wu, J.; Liu, W.; Lu, Y.; Zhang, Y.; Sun, S.; Li, J.; Zhou, Y. Calibration of the geometric error parameters of laser trackers in site environments. IEEE Sens. J. 2023, 23, 7077–7086. [Google Scholar] [CrossRef]
- Pengcheng, H.U.; Chang, D.; Tan, J.; Yang, R.; Yang, H.; Haijin, F.U. Displacement measuring grating interferometer: A review. Front. Inf. Technol. Electron. Eng. 2019, 20, 631–654. [Google Scholar] [CrossRef]
- Li, X.; Shi, Y.; Wang, P.; Ni, K.; Zhou, Q.; Wang, X. A compact design of optical scheme for a two-probe absolute surface encoders. In Proceedings of the Tenth International Symposium on Precision Engineering Measurements and Instrumentation, Kunming, China, 8–10 August 2018; SPIE: Cergy, France, 2019; Volume 11053, pp. 960–966. [Google Scholar]
- Wang, H.; Shi, Y.; Li, X.; Ni, K.; Zhou, Q.; Wang, X. Improvement of absolute positioning of precision stage based on cooperation the zero position pulse signal and incremental displacement signal. In Proceedings of the Journal of Physics: Conference Series, Dalian, China, 26–29 October 2017; IOP Publishing: Bristol, UK, 2018; Volume 986, p. 012002. [Google Scholar]
- Liao, B.; Wang, S.; Lin, J.; Dou, Y.; Wang, X.; Li, X. A research on compact short-distance grating interferometer based on ridge prism. In Proceedings of the 2021 International Conference on Optical Instruments and Technology: Optoelectronic Measurement Technology and Systems, Online, 8–10 April 2022; SPIE: Cergy, France, 2022; Volume 12282, pp. 411–418. [Google Scholar]
- Gao, W.; Kim, S.W.; Bosse, H.; Haitjema, H.; Chen, Y.; Lu, X.; Knapp, W.; Weckenmann, A.; Estler, W.; Kunzmann, H. Measurement technologies for precision positioning. CIRP Ann. 2015, 64, 773–796. [Google Scholar] [CrossRef]
- Li, X.; Yuan, W.; Ni, K.; Zhou, Q.; Wang, X. A two-probe linear encoder by using an arrayed scale grating stitched by multiple separate short gratings. In Proceedings of the Tenth International Symposium on Precision Engineering Measurements and Instrumentation, Kunming, China, 8–10 August 2018; SPIE: Cergy, France, 2019; Volume 11053, pp. 207–212. [Google Scholar]
- Ni, K.; Wang, H.; Li, X.; Wang, X.; Xiao, X.; Zhou, Q. Measurement uncertainty evaluation of the three degree of freedom surface encoder. In Proceedings of the Optical Metrology and Inspection for Industrial Applications IV, Beijing, China, 12–14 October 2016; SPIE: Cergy, France, 2016; Volume 10023, pp. 187–192. [Google Scholar]
- Luo, L.; Cao, F.; Wang, S.; Li, X. Design and demonstration of a large range precision grating sensor for simultaneous measurement of out-of-plane motions. Measurement 2025, 249, 116799. [Google Scholar] [CrossRef]
- Shi, Y.; Zhou, Q.; Li, X.; Ni, K.; Wang, X. Design and testing of a linear encoder capable of measuring absolute distance. Sens. Actuators A Phys. 2020, 308, 111935. [Google Scholar] [CrossRef]
- Shi, Y.; Ni, K.; Li, X.; Zhou, Q.; Wang, X. Highly accurate, absolute optical encoder using a hybrid-positioning method. Opt. Lett. 2019, 44, 5258–5261. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Q.; Zhu, X.; Lu, H.; Yang, L.; Ma, D.; Sun, J.; Ni, K.; Wang, X. Holographic fabrication of an arrayed one-axis scale grating for a two-probe optical linear encoder. Opt. Express 2017, 25, 16028–16039. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Lu, T.; Li, X. High dynamic wavefront stability control for high-uniformity periodic microstructure fabrication. Precis. Eng. 2025, 93, 216–223. [Google Scholar] [CrossRef]
- Shao, C.; Li, X. Technologies for Fabricating Large-Size Diffraction Gratings. Sensors 2025, 25, 1990. [Google Scholar] [CrossRef]
- Xue, G.; Lin, L.; Zhai, Q.; Zeng, C.; Wang, X.; Li, X. Development of dielectric-film-based polarization modulation scheme for patterning highly uniform 2d array structures with periodic tunability. Opt. Lasers Eng. 2023, 167, 107627. [Google Scholar] [CrossRef]
- Gao, X.; Li, J.; Zhong, Z.; Li, X. Global alignment reference strategy for laser interference lithography pattern arrays. Microsyst. Nanoeng. 2025, 11, 41. [Google Scholar] [CrossRef]
- Li, X.; Gao, W.; Shimizu, Y.; Ito, S. A two-axis Lloyd’s mirror interferometer for fabrication of two-dimensional diffraction gratings. CIRP Ann. 2014, 63, 461–464. [Google Scholar] [CrossRef]
- Li, X.; Lu, H.; Zhou, Q.; Wu, G.; Ni, K.; Wang, X. An orthogonal type two-axis Lloyd’s mirror for holographic fabrication of two-dimensional planar scale gratings with large area. Appl. Sci. 2018, 8, 2283. [Google Scholar] [CrossRef]
- Xue, G.; Lu, H.; Li, X.; Zhou, Q.; Wu, G.; Wang, X.; Zhai, Q.; Ni, K. Patterning nanoscale crossed grating with high uniformity by using two-axis Lloyd’s mirrors based interference lithography. Opt. Express 2020, 28, 2179–2191. [Google Scholar] [CrossRef]
- Xue, G.; Zhai, Q.; Lu, H.; Zhou, Q.; Ni, K.; Lin, L.; Wang, X.; Li, X. Polarized holographic lithography system for high-uniformity microscale patterning with periodic tunability. Microsyst. Nanoeng. 2021, 7, 31. [Google Scholar] [CrossRef]
- Wang, G.; Xue, G.; Zhai, Q.; Zhu, J.; Yu, K.; Huang, G.; Wang, M.; Zhong, A.; Zhu, L.; Yan, S.; et al. Planar diffractive grating for magneto-optical trap application: Fabrication and testing. Appl. Opt. 2021, 60, 9358–9364. [Google Scholar] [CrossRef]
- Kimura, A.; Gao, W.; Kim, W.; Hosono, K.; Shimizu, Y.; Shi, L.; Zeng, L. A sub-nanometric three-axis surface encoder with short-period planar gratings for stage motion measurement. Precis. Eng. 2012, 36, 576–585. [Google Scholar] [CrossRef]
- Wang, S.; Liao, B.; Shi, N.; Li, X. A compact and high-precision three-degree-of-freedom grating encoder based on a quadrangular frustum pyramid prism. Sensors 2023, 23, 4022. [Google Scholar] [CrossRef]
- Li, X.; Zhu, X.; Zhou, Q.; Wang, H.; Ni, K. Low-cost lithography for fabrication of one-dimensional diffraction gratings by using laser diodes. In Proceedings of the 2015 International Conference on Optical Instruments and Technology: Micro/Nano Photonics and Fabrication, Beijing, China, 17–19 May 2015; SPIE: Cergy, France, 2015; Volume 9624, pp. 51–56. [Google Scholar]
- Li, X.; Shimizu, Y.; Ito, S.; Gao, W. Fabrication of scale gratings for surface encoders by using laser interference lithography with 405 nm laser diodes. Int. J. Precis. Eng. Manuf. 2013, 14, 1979–1988. [Google Scholar] [CrossRef]
- Li, J.; Tan, S.H.; Li, X. Efficient fabrication and optimization of large-area metallic diffraction gratings. In Proceedings of the International Conference on Advanced Imaging, Detection, and Signal Processing (AIDSP 2024), Harbin, China, 27–29 December 2024; SPIE: Cergy, France, 2025; Volume 13693, pp. 14–19. [Google Scholar]
- Hu, H.; Qiu, X.; Wang, J.; Ju, A.; Zhang, Y. Subdivision and direction recognition of λ/16 of orthogonal fringes for nanometric measurement. Appl. Opt. 2009, 48, 6479–6484. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Li, J.; Zhao, P.; Li, X. Design of solving circuit for 6-DOF heterodyne grating interferometry system. In Proceedings of the Fourth International Conference on Mechatronics and Intelligent Control (MIC 2024), Nanchang, China, 27–29 December 2024; SPIE: Cergy, France, 2025; Volume 13643, pp. 472–478. [Google Scholar]
- Luo, L.; Cao, F.; Wang, S.; Li, X. Coupling error analysis and compensation algorithm for three-degree-of-freedom grating autocollimator. In Proceedings of the International Conference on Advanced Imaging, Detection, and Signal Processing (AIDSP 2024), Harbin, China, 27–29 December 2024; SPIE: Cergy, France, 2025; Volume 13693, pp. 231–238. [Google Scholar]
- Li, X.; Gao, W.; Muto, H.; Shimizu, Y.; Ito, S.; Dian, S. A six-degree-of-freedom surface encoder for precision positioning of a planar motion stage. Precis. Eng. 2013, 37, 771–781. [Google Scholar] [CrossRef]
- Yu, K.; Zhu, J.; Yuan, W.; Zhou, Q.; Xue, G.; Wu, G.; Wang, X.; Li, X. Two-channel six degrees of freedom grating-encoder for precision-positioning of sub-components in synthetic-aperture optics. Opt. Express 2021, 29, 21113–21128. [Google Scholar] [CrossRef]
- Li, X.; Shi, Y.; Xiao, X.; Zhou, Q.; Wu, G.; Lu, H.; Ni, K. Design and testing of a compact optical prism module for multi-degree-of-freedom grating interferometry application. Appl. Sci. 2018, 8, 2495. [Google Scholar] [CrossRef]
- Shimizu, Y.; Ito, T.; Li, X.; Kim, W.; Gao, W. Design and testing of a four-probe optical sensor head for three-axis surface encoder with a mosaic scale grating. Meas. Sci. Technol. 2014, 25, 094002. [Google Scholar] [CrossRef]
- Adany, P.; Allen, C.; Hui, R. Chirped lidar using simplified homodyne detection. J. Light. Technol. 2009, 27, 3351–3357. [Google Scholar] [CrossRef]
- Lin, X.; Su, X.; Wang, J.; Sun, Y.; Hu, P. Laser Interferometer Technology and Instruments for Sub-Nanometer and Picometer Displacement Measurements. Laser Optoelectron. Prog. 2023, 60, 312016. [Google Scholar]
- Watchi, J.; Cooper, S.; Ding, B.; Mow-Lowry, C.M.; Collette, C. Contributed Review: A review of compact interferometers. Rev. Sci. Instruments 2018, 89, 121501. [Google Scholar] [CrossRef]
- Köning, R.; Wimmer, G.; Witkovskỳ, V. The statistical uncertainty of the Heydemann correction: A practical limit of optical quadrature homodyne interferometry. Meas. Sci. Technol. 2015, 26, 084004. [Google Scholar] [CrossRef]
- Vishnyakov, G.; Minaev, V.; Shumsky, E. Homodyne quadrature displacement interferometer. Experimental results. Opt. Spectrosc. 2022, 130, 327–335. [Google Scholar] [CrossRef]
- Li, X.; Shimizu, Y.; Ito, T.; Cai, Y.; Ito, S.; Gao, W. Measurement of six-degree-of-freedom planar motions by using a multiprobe surface encoder. Opt. Eng. 2014, 53, 122405. [Google Scholar] [CrossRef]
- Xu, X.; Gu, D.; Gao, S.; Sun, L.; Lu, X.; Wang, K.; Bai, J. Back to Michelson interferometer: A precise inspection system for industrial intricate structures defect detection. Meas. Sci. Technol. 2023, 35, 035026. [Google Scholar] [CrossRef]
- Kim, J.A.; Kim, J.W.; Kang, C.S.; Eom, T.B.; Ahn, J. A digital signal processing module for real-time compensation of nonlinearity in a homodyne interferometer using a field-programmable gate array. Meas. Sci. Technol. 2008, 20, 017003. [Google Scholar] [CrossRef]
- Li, X.H.; Shimizu, Y.; Muto, H.; Ito, S.; Gao, W. Design of a three-axis surface encoder with a blue-ray laser diode. Key Eng. Mater. 2012, 523, 913–918. [Google Scholar] [CrossRef]
- Shaddock, D.A. Digitally enhanced heterodyne interferometry. Opt. Lett. 2007, 32, 3355–3357. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Wang, G.; Xue, G.; Zhou, Q.; Li, X. Heterodyne three-degree-of-freedom grating interferometer for ultra-precision positioning of lithography machine. In Proceedings of the 2021 International Conference on Optical Instruments and Technology: Optoelectronic Measurement Technology and Systems, Online, 8–10 April 2022; SPIE: Cergy, France, 2022; Volume 12282, pp. 21–32. [Google Scholar]
- Zhao, P.; Gao, L.; Cui, C.; Ma, Y.; Yang, M.; Liu, L.; Li, X. A grating interferometer for improving optical subdivision in Z-axis measurement. In Proceedings of the Optical Metrology and Inspection for Industrial Applications XI, Nantong, China, 12–15 October 2024; SPIE: Cergy, France, 2024; Volume 13241, pp. 238–246. [Google Scholar]
- Dong Nguyen, T.; Higuchi, M.; Tung Vu, T.; Wei, D.; Aketagawa, M. 10-pm-order mechanical displacement measurements using heterodyne interferometry. Appl. Opt. 2020, 59, 8478–8485. [Google Scholar] [CrossRef] [PubMed]
- Dong, N.T.; Tai, N.T.; Hoang, D.V.; Mai, N.T.P.; Tung, V.T.; Thang, V.T. Sub-nanometer displacement measurement using heterodyne interferometer and down-beat frequency technique. In Proceedings of the Regional Conference in Mechanical Manufacturing Engineering, Hanoi, Vietnam, 10–12 June 2022; Springer: Singapore, 2021; pp. 1170–1176. [Google Scholar]
- Cui, C.; Yang, M.; Liu, L.; Zhao, P.; Gao, L.; Li, X. A quasi-common-path heterodyne grating interferometer for six-degree-of-freedom measurement. In Proceedings of the Optical Metrology and Inspection for Industrial Applications XI, Nantong, China, 12–15 October 2024; SPIE: Cergy, France, 2024; Volume 13241, pp. 115–125. [Google Scholar]
- Liu, L.; Cui, C.; Yang, M.; Zhao, P.; Li, X. Blazed grating collimation strategy for a high-precision heterodyne grating interferometer. In Proceedings of the International Conference on Advanced Imaging, Detection, and Signal Processing (AIDSP 2024), Harbin, China, 27–29 December 2024; SPIE: Cergy, France, 2025; Volume 13693, pp. 81–87. [Google Scholar]
- Kunzmann, H.; Pfeifer, T.; Flügge, J. Scales vs. laser interferometers performance and comparison of two measuring systems. CIRP Ann. 1993, 42, 753–767. [Google Scholar] [CrossRef]
- Deng, J.; Yan, X.; Wei, C.; Lu, Y.; Li, M.; Xiang, X.; Jia, W.; Zhou, C. Eightfold optical encoder with high-density grating. Appl. Opt. 2018, 57, 2366–2375. [Google Scholar] [CrossRef] [PubMed]
- Eom, T.; Choi, T.; Lee, K.; Choi, H.; Lee, S. A simple method for thecompensation of the nonlinearity in the heterodyne interferometer. Meas. Sci. Technol. 2002, 13, 222. [Google Scholar] [CrossRef]
- Schmitz, T.; Chu, D.; Houck, L. First-order periodic error correction: Validation for constant and non-constant velocities with variable error magnitudes. Meas. Sci. Technol. 2006, 17, 3195. [Google Scholar] [CrossRef][Green Version]
- Zhu, J.; Yu, K.; Xue, G.; Shi, N.; Zhou, Q.; Wang, X.; Li, X. A simplified two-phase differential decoding algorithm for high precision grating encoder. In Proceedings of the Optical Metrology and Inspection for Industrial Applications VIII, Nantong, China, 10–20 October 2021; SPIE: Cergy, France, 2021; Volume 11899, pp. 49–58. [Google Scholar][Green Version]
- Zhu, J.; Yu, K.; Xue, G.; Zhou, Q.; Wang, X.; Li, X. An improved signal filtering strategy based on EMD algorithm for ultrahigh precision grating encoder. In Proceedings of the Real-time Photonic Measurements, Data Management, and Processing VI, Nantong, China, 10–20 October 2021; SPIE: Cergy, France, 2021; Volume 11902, pp. 140–149. [Google Scholar][Green Version]
- Han, Y.; Ni, K.; Li, X.; Wu, G.; Yu, K.; Zhou, Q.; Wang, X. An fpga platform for next-generation grating encoders. Sensors 2020, 20, 2266. [Google Scholar] [CrossRef]
- Shi, N.; Wang, S.; Xue, G.; Liu, M.; Han, Y.; Zhu, J.; Ni, K.; Wang, X.; Li, X. A real-time processing system for dual-channel six-degree-of-freedom grating ruler based on FPGA. In Proceedings of the Optical Design and Testing XI, Nantong, China, 10–20 October 2021; SPIE: Cergy, France, 2021; Volume 11895, pp. 250–260. [Google Scholar][Green Version]
- Wang, Y.; Shi, N.; Li, L.; Ni, K.; Li, X. Instantaneous grating signal subdivision system with non-linear Kalman filters. In Proceedings of the Optical Design and Testing XII, Online, 5–12 December 2022; SPIE: Cergy, France, 2022; Volume 12315, pp. 90–96. [Google Scholar][Green Version]
- Shi, N.; Zhu, J.; Wang, S.; Han, Y.; Yu, K.; Li, X.; Wang, X. FPGA displacement calculation platform and test of two-phase grating interference encoder. In Proceedings of the 2021 International Conference on Optical Instruments and Technology: Optoelectronic Measurement Technology and Systems, Online, 8–10 April 2022; SPIE: Cergy, France, 2022; Volume 12282, pp. 372–383. [Google Scholar][Green Version]
- Heydemann, P.L. Determination and correction of quadrature fringe measurement errors in interferometers. Appl. Opt. 1981, 20, 3382–3384. [Google Scholar] [CrossRef]
- Zhang, G.; Xu, L.; Ge, Q.; Wu, X.; Yu, B. Ameliorated PGC demodulation scheme using Taubin least squares fitting of ellipse in fiber optic interferometric sensors. Opt. Fiber Technol. 2023, 80, 103374. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Q. Normalized and orthogonal phase retrieval algorithm based on lissajous ellipse fitting. Opt. Lasers Eng. 2022, 151, 106917. [Google Scholar] [CrossRef]
- Wu, C.m.; Su, C.s.; Peng, G.S. Correction of nonlinearity in one-frequency optical interferometry. Meas. Sci. Technol. 1996, 7, 520. [Google Scholar] [CrossRef]
- Požar, T.; Možina, J. Enhanced ellipse fitting in a two-detector homodyne quadrature laser interferometer. Meas. Sci. Technol. 2011, 22, 085301. [Google Scholar] [CrossRef]
- Köning, R.; Wimmer, G.; Witkovskỳ, V. Ellipse fitting by nonlinear constraints to demodulate quadrature homodyne interferometer signals and to determine the statistical uncertainty of the interferometric phase. Meas. Sci. Technol. 2014, 25, 115001. [Google Scholar] [CrossRef]
- Fitzgibbon, A.; Pilu, M.; Fisher, R.B. Direct least square fitting of ellipses. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 21, 476–480. [Google Scholar] [CrossRef]
- Long, C.; Hu, Q.; Zhao, M.; Li, D.; Ouyang, Z.; Yan, D.M. A triple-stage robust ellipse fitting algorithm based on outlier removal. IEEE Trans. Instrum. Meas. 2023, 72, 1–14. [Google Scholar] [CrossRef]
- Yang, T.; Yan, L.; Chen, B.; Liu, Y.; Tian, Q. Signal processing method of phase correction for laser heterodyne interferometry. Opt. Lasers Eng. 2014, 57, 93–100. [Google Scholar] [CrossRef]
- Köchert, P.; Flügge, J.; Weichert, C.; Köning, R.; Manske, E. Phase measurement of various commercial heterodyne He–Ne-laser interferometers with stability in the picometer regime. Meas. Sci. Technol. 2012, 23, 074005. [Google Scholar] [CrossRef]
- Hu, P.; Wang, J.; Lin, X.; Xing, X.; Fu, H.; Tan, J. Phase measurement method based on digital dual frequency comb for high-precision high-speed heterodyne interferometry. IEEE Sens. J. 2023, 23, 9707–9715. [Google Scholar] [CrossRef]
- Lu, S.; Wang, Y.; Li, X. Robust phase measurement of high-speed signals using frequency tracking lock-in method. In Proceedings of the Holography, Diffractive Optics, and Applications XIV, Nantong, China, 12–15 October 2024; SPIE: Cergy, France, 2024; Volume 13240, pp. 188–197. [Google Scholar]
- Shaddock, D.; Ware, B.; Halverson, P.; Spero, R.; Klipstein, B. Overview of the LISA Phasemeter. In Proceedings of the AIP Conference Proceedings, Greenbelt, MD, USA, 19–23 June 2006; American Institute of Physics: College Park, MD, USA, 2006; Volume 873, pp. 654–660. [Google Scholar]
- Liu, H.; Luo, Z.; Jin, G. The development of phasemeter for Taiji space gravitational wave detection. Microgravity Sci. Technol. 2018, 30, 775–781. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, Y.; Lu, S.; Wang, S.; Li, X. High-accuracy and real-time phase solution algorithm based on extended Kalman filter for multi-degree-of-freedom grating interferometer. In Proceedings of the Optoelectronic Devices and Integration XIII, Nantong, China, 12–15 October 2024; SPIE: Cergy, France, 2024; Volume 13236, pp. 99–108. [Google Scholar]
- Wang, W.; Lin, J.; Jin, S.; Bai, Y.; Liu, L.; Liu, Z.; Sun, Y.; Li, W. A Real-time Determination Method for Homodyne Grating Interferometer Signal Nonlinear Error based on Duty Cycle Measurement of States. IEEE Trans. Instrum. Meas. 2024, 73, 7004208. [Google Scholar] [CrossRef]
- Yuan, B.; Yan, H.M.; Cao, X.Q. A new subdivision method for grating-based displacement sensor using imaging array. Opt. Lasers Eng. 2009, 47, 90–95. [Google Scholar] [CrossRef]
- Niu, R.; Chen, G.; Li, R.; Jia, Z.; Feng, Z. A high subdivision and light fluctuation-insensitive approach for grating displacement sensors. Opt. Lasers Eng. 2025, 184, 108545. [Google Scholar] [CrossRef]
- Hua-hui, Y.; Wei-li, F.; Fu, L. Subdivision Design of Grating Moire Fringes and Simulation by Simulink. J. Astronaut. Metrol. Meas. 2016, 36, 29. [Google Scholar]
- Ye, W.; Zhang, M.; Zhu, Y.; Wang, L.; Hu, J.; Li, X.; Hu, C. Ultraprecision real-time displacements calculation algorithm for the grating interferometer system. Sensors 2019, 19, 2409. [Google Scholar] [CrossRef]
- Jan, C.M.; Liu, C.S.; Lin, C.Y. Development of low-cost heterodyne interferometer with virtual electronic phasemeter. Meas. Control 2022, 55, 229–238. [Google Scholar] [CrossRef]
- Bo, L.; Jinyan, L. Research on signal subdivision of grating sensor. In Proceedings of the Proceedings of 2011 6th International Forum on Strategic Technology, Harbin, China, 22–24 August 2011; IEEE: New York, NY, USA, 2011; Volume 2, pp. 1235–1238. [Google Scholar]
- Yang, Z.; Zhang, Y. Grating subdivision based on single chip computer. In Proceedings of the Second International Conference on Optics and Communication Technology (ICOCT 2022), Hefei, China, 15–17 July 2022; SPIE: Cergy, France, 2022; Volume 12473, pp. 62–67. [Google Scholar]
- Tang, J.; Peng, H.; Yang, P.; Guo, S.; Sun, W.; Jin, L.; Xie, K.; Li, M. Design, Analysis, and Implementation of the Subdivision Interpolation Technique for the Grating Interferometric Micro-Displacement Sensor. Photonics 2025, 12, 64. [Google Scholar] [CrossRef]
- Chang, C.P.; Chang, S.C.; Wang, Y.C.; He, P.Y. A Novel Analog Interpolation Method for Heterodyne Laser Interferometer. Micromachines 2023, 14, 696. [Google Scholar] [CrossRef]
- Hussain, T.; Amin, S.; Zabit, U.; Bernal, O.D.; Bosch, T. A high performance real-time interferometry sensor system architecture. Microprocess. Microsystems 2019, 64, 23–33. [Google Scholar] [CrossRef]
- Straube, G.; Fischer Calderón, J.S.; Ortlepp, I.; Füßl, R.; Manske, E. A heterodyne interferometer with separated beam paths for high-precision displacement and angular measurements. Nanomanuf. Metrol. 2021, 4, 200–207. [Google Scholar] [CrossRef]
- Huang, Y.; Che, S.; Zheng, G.; Zhu, W.; Zhou, Y.; Xue, Z. An adaptive filter for subdivision of circular grating signal of angle measurement. IEEE Trans. Instrum. Meas. 2022, 71, 1–10. [Google Scholar] [CrossRef]
- Zhu, W.; Xu, Y.; Huang, Y.; Xue, Z.; Ye, S. Subdivision method for nonorthogonal Moiré signals. IEEE Trans. Instrum. Meas. 2020, 70, 1–10. [Google Scholar] [CrossRef]
- Hou, H.; Cao, G.; Ding, H.; Li, K.; Wang, A. Phase-locked subdivision method of digital signal based on FPGA. J. Phys. Conf. Ser. Iop Publ. 2022, 2181, 012016. [Google Scholar] [CrossRef]
- Li, X.; Xiao, S.; Zhou, Q.; Ni, K.; Wang, X. A real-time distance measurement data processing platform for multi-axis grating interferometry type optical encoders. In Proceedings of the Tenth International Symposium on Precision Engineering Measurements and Instrumentation, Kunming, China, 8–10 August 2018; SPIE: Cergy, France, 2019; Volume 11053, pp. 1028–1035. [Google Scholar]
- Deng, W.; Peng, X. A high precision phase extraction method in heterodyne interferometer based on FPGA. J. Phys. Conf. Ser. Iop Publ. 2022, 2387, 012002. [Google Scholar] [CrossRef]
- Vera-Salas, L.A.; Moreno-Tapia, S.V.; Garcia-Perez, A.; de Jesus Romero-Troncoso, R.; Osornio-Rios, R.A.; Serroukh, I.; Cabal-Yepez, E. FPGA-based smart sensor for online displacement measurements using a heterodyne interferometer. Sensors 2011, 11, 7710–7723. [Google Scholar] [CrossRef]
- Zhang, E.; Chen, B.; Yan, L.; Yang, T.; Hao, Q.; Dong, W.; Li, C. Laser heterodyne interferometric signal processing method based on rising edge locking with high frequency clock signal. Opt. Express 2013, 21, 4638–4652. [Google Scholar] [CrossRef]
- Zhou, J.; He, W.; Yu, Y. Fringe-to-pulse counting demodulation of a laser interferometer for primary vibration calibration. Measurement 2023, 221, 113490. [Google Scholar] [CrossRef]
- Tucker, D. The history of the homodyne and synchrodyne. J. Br. Inst. Radio Eng. 1954, 14, 143–154. [Google Scholar] [CrossRef]
- Schumaker, B.L. Noise in homodyne detection. Opt. Lett. 1984, 9, 189–191. [Google Scholar] [CrossRef] [PubMed]
- Jakeman, E.; Oliver, C.; Pike, E. Optical homodyne detection. Adv. Phys. 1975, 24, 349–405. [Google Scholar] [CrossRef]
- Kazovsky, L.G. Optical heterodyning versus optical homodyning: A comparison. J. Opt. Commun. 1985, 6, 18–24. [Google Scholar] [CrossRef]
- Braunstein, S.L. Homodyne statistics. Phys. Rev. A 1990, 42, 474. [Google Scholar] [CrossRef] [PubMed]
- Armen, M.A.; Au, J.K.; Stockton, J.K.; Doherty, A.C.; Mabuchi, H. Adaptive homodyne measurement of optical phase. Phys. Rev. Lett. 2002, 89, 133602. [Google Scholar] [CrossRef]
- Glance, B. Performance of homodyne detection of binary PSK optical signals. J. Light. Technol. 2003, 4, 228–235. [Google Scholar] [CrossRef]
- Seimetz, M. Phase diversity receivers for homodyne detection of optical DQPSK signals. J. Light. Technol. 2006, 24, 3384–3391. [Google Scholar] [CrossRef]
- Puttnam, B.J.; Luís, R.S.; Delgado Mendinueta, J.M.; Sakaguchi, J.; Klaus, W.; Kamio, Y.; Nakamura, M.; Wada, N.; Awaji, Y.; Kanno, A.; et al. Self-homodyne detection in optical communication systems. Photonics 2014, 1, 110–130. [Google Scholar] [CrossRef]
- Luo, L.; Gao, L.; Wang, S.; Deng, F.; Wu, Y.; Li, X. An ultra-precision error estimation for a multi-axes grating encoder using quadrant photodetectors. In Proceedings of the Optical Metrology and Inspection for Industrial Applications IX, Online, 5–12 December 2022; SPIE: Cergy, France, 2022; Volume 12319, pp. 57–65. [Google Scholar]
- Cao, F.; Wang, S.; Luo, L.; Li, X. Displacement compensation algorithm for high-precision absolute six-degree-of-freedom grating encoder. In Proceedings of the Optical Metrology and Inspection for Industrial Applications XI, Nantong, China, 12–15 October 2024; SPIE: Cergy, France, 2024; Volume 13241, pp. 73–81. [Google Scholar]
- He, Y.; Orr, B.J. Optical heterodyne signal generation and detection in cavity ringdown spectroscopy based on a rapidly swept cavity. Chem. Phys. Lett. 2001, 335, 215–220. [Google Scholar] [CrossRef]
- Takenaka, T.; Tanaka, K.; Fukumitsu, O. Signal-to-noise ratio in optical heterodyne detection for Gaussian fields. Appl. Opt. 1978, 17, 3466–3471. [Google Scholar] [CrossRef]
- Huang, C.C. Optical heterodyne profilometer. Opt. Eng. 1984, 23, 365–370. [Google Scholar] [CrossRef]
- Abbas, G.; Chan, V.; Yee, T. A dual-detector optical heterodyne receiver for local oscillator noise suppression. J. Light. Technol. 1985, 3, 1110–1122. [Google Scholar] [CrossRef]
- Maznev, A.; Nelson, K.; Rogers, J. Optical heterodyne detection of laser-induced gratings. Opt. Lett. 1998, 23, 1319–1321. [Google Scholar] [CrossRef]
- Fried, D.L. Optical heterodyne detection of an atmospherically distorted signal wave front. Proc. IEEE 2005, 55, 57–77. [Google Scholar] [CrossRef]
- Cui, C.; Gao, L.; Zhao, P.; Yang, M.; Liu, L.; Ma, Y.; Huang, G.; Wang, S.; Luo, L.; Li, X. Towards multi-dimensional atomic-level measurement: Integrated heterodyne grating interferometer with zero dead-zone. Light. Adv. Manuf. 2025, 6, 1–14. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, G.; Wang, S.; Li, X. A reflective-type heterodyne grating interferometer for three-degree-of-freedom subnanometer measurement. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]
- Yang, M.; Cui, C.; Liu, L.; Zhao, P.; Gao, L.; Li, X. An unfolding-based model for analysis of rotation and translation coupling in grating interferometers. In Proceedings of the Advanced Sensor Systems and Applications XIV, Nantong, China, 12–15 October 2024; SPIE: Cergy, France, 2024; Volume 13243, pp. 56–65. [Google Scholar]
- Liu, L.; Cui, C.; Yang, M.; Zhao, P.; Gao, L.; Li, X. An ultra-precision and real-time algorithm for 6-DOF displacements based on four grating interferometers. In Proceedings of the Advanced Sensor Systems and Applications XIV, Nantong, China, 12–15 October 2024; SPIE: Cergy, France, 2024; Volume 13243, pp. 71–81. [Google Scholar]
- Gao, L.; Zhu, J.; Huang, G.; Wang, G.; Wang, S.; Ni, K.; Wang, X.; Li, X. A polarization adjustment module for frequency aliasing of heterodyne grating interferometer. In Proceedings of the Optical Metrology and Inspection for Industrial Applications IX, Online, 5–12 December 2022; SPIE: Cergy, France, 2022; Volume 12319, pp. 362–369. [Google Scholar]
- Yang, Y.; Wang, G.; Zhu, J.; Wang, S.; Wu, Y.; Li, X. Method and system for phase measurement of the heterodyne interference system. In Proceedings of the 2021 International Conference on Optical Instruments and Technology: Optoelectronic Measurement Technology and Systems, Online, 8–10 April 2022; SPIE: Cergy, France, 2022; Volume 12282, pp. 431–442. [Google Scholar]
- Lu, Z.; Liu, B.; Zhang, K.; Lin, H.; Zhang, Y. A method for measuring the inclination of forgings based on an improved optimization algorithm for fitting ellipses. IEEE Trans. Instrum. Meas. 2022, 72, 1–11. [Google Scholar] [CrossRef]
- Wang, C.; Burnham-Fay, E.D.; Ellis, J.D. Real-time FPGA-based Kalman Filter for Constant and Non-constant Velocity Periodic Error Correction. Precis. Eng. 2016, 48, 133–143. [Google Scholar] [CrossRef]
- Kalisz, J. Review of methods for time interval measurements with picosecond resolution. Metrologia 2003, 41, 17–32. [Google Scholar] [CrossRef]
- Kim, M.S.; Kim, S.W. Two-way frequency-conversion phase measurement for high-speed and high-resolution heterodyne interferometry. Meas. Sci. Technol. 2004, 15, 2341. [Google Scholar] [CrossRef]
- Szplet, R.; Kalisz, J. Interpolating time counter with 100 ps resolution on a single FPGA device. Instrum. Meas. IEEE Trans. 2000, 49, 879–883. [Google Scholar] [CrossRef]
- Keranen, P.; Kostamovaara, J. A Wide Range, 4.2 ps(rms) Precision CMOS TDC With Cyclic Interpolators Based on Switched-Frequency Ring Oscillators. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 2795–2805. [Google Scholar] [CrossRef]
- Koscielnik, D.; Szyduczynski, J.; Rzepka, D.; Andrysiewicz, W.; Miskowicz, M. Optimized design of successive approximation time-to-digital converter with single set of delay lines. In Proceedings of the 2016 Second International Conference on Event-based Control, Communication, and Signal Processing (EBCCSP), Krakow, Poland, 13–15 June 2016. [Google Scholar]
- Takayama, M.; Dosho, S.; Takeda, N.; Miyahara, M.; Matsuzawa, A. A time-domain architecture and design method of high speed A-to-D converters with standard cells. IEICE Trans. Electron. 2013, 6, 813–819. [Google Scholar] [CrossRef]
- Mantyniemi, A.; Rahkonen, T.; Kostamovaara, J. A CMOS Time-to-Digital Converter (TDC) Based On a Cyclic Time Domain Successive Approximation Interpolation Method. IEEE J. Solid-State Circuits 2009, 44, 3067–3078. [Google Scholar] [CrossRef]
- Mantyniemi, A.; Kostamovaara, J. Time-to-digital converter (TDC) based on startable ring oscillators and successive approximation. In Proceedings of the 2014 NORCHIP, Tampere, Finland, 27–28 October 2014. [Google Scholar]
- Henzler, S.; Koeppe, S.; Kamp, W.; Mulatz, H.; Schmitt-Landsiedel, D. 90nm 4.7ps-Resolution 0.7-LSB Single-Shot Precision and 19pJ-per-Shot Local Passive Interpolation Time-to-Digital Converter with On-Chip Characterization. In Proceedings of the IEEE International Solid-state Circuits Conference, San Francisco, CA, USA, 3–7 February 2008; pp. 548–635. [Google Scholar]
- Wu, J.; Shi, Z. The 10-ps wave union TDC: Improving FPGA TDC resolution beyond its cell delay. In Proceedings of the IEEE Nuclear Science Symposium Conference Record, Dresden, Germany, 19–25 October 2008; pp. 3440–3446. [Google Scholar]
- Li, G.; Zhang, C.; Liu, N.; Liu, C. A Real-Time Data Processing Method Based on Orthogonal Phase-Locked Amplification and Its Application in Frequency Domain Semi-Airborne Electromagnetic Detection. IEEJ Trans. Electr. Electron. Eng. 2020, 15, 1160–1168. [Google Scholar] [CrossRef]
- Jarrett, J.W.; Liu, X.; Nealey, P.F.; Vaia, R.A.; Cerullo, G.; Knappenberger, K.L. Communication: SHG-detected circular dichroism imaging using orthogonal phase-locked laser pulses. J. Chem. Phys. 2015, 142, 151101. [Google Scholar] [CrossRef]
- Hu, P.; Tan, J.; Yang, H.; Fu, H.; Wang, Q. Recent developments in heterodyne laser interferometry at Harbin Institute of Technology. In Proceedings of the Eighth International Symposium on Precision Engineering Measurement and Instrumentation, Chengdu, China, 8–11 August 2012; SPIE: Cergy, France, 2013; Volume 8759, pp. 898–906. [Google Scholar]
- Yang, H.; Fu, H.; Hu, P.; Yang, R.; Xu, X.; Liang, Y.; Di, C.; Tan, J. Ultra-precision and high-speed laser interferometric displacement measurement technology and instrument. Laser Optoelectron. Prog 2022, 59, 0922018. [Google Scholar]
- Keysight Technologies. N1225A Four-Channel High-Resolution Laser Axis Board [EB/OL]. 2025. Available online: https://www.keysight.com.cn/cn/zh/product/N1225A/four-channel-high-resolution-laser-axis-board.html (accessed on 27 June 2025).
- Zygo Corporation. Measurement Electronics [EB/OL]. 2025. Available online: https://www.zygo.com/products/nano-position-sensors/displacement-measuring-interferometers/measurement-electronics (accessed on 27 June 2025).
- Losic, N.A. A quadrature-based phase-locked loop. In Proceedings of the IECON’03. 29th Annual Conference of the IEEE Industrial Electronics Society (IEEE Cat. No. 03CH37468), Roanoke, VA, USA, 2–6 November 2003; IEEE: New York, NY, USA, 2003; Volume 3, pp. 2957–2962. [Google Scholar]
- Golestan, S.; Guerrero, J.M.; Abusorrah, A.; Al-Hindawi, M.M.; Al-Turki, Y. An adaptive quadrature signal generation-based single-phase phase-locked loop for grid-connected applications. IEEE Trans. Ind. Electron. 2016, 64, 2848–2854. [Google Scholar] [CrossRef]
- Xu, C.; Tang, X.; Liu, G. A Novel Method for Frequency Estimation of AMB Rotor Based on Multiresonance Controller-Quadrature Phase-Locked Loop. IEEE Trans. Ind. Electron. 2024, 72, 1849–1859. [Google Scholar] [CrossRef]
- Hsieh, G.C.; Hung, J.C. Phase-locked loop techniques. A survey. IEEE Trans. Ind. Electron. 1996, 43, 609–615. [Google Scholar] [CrossRef]
- Pin, G.; Chen, B.; Fedele, G.; Parisini, T. Robust frequency-adaptive quadrature phase-locked-loops with Lyapunov-certified global stability. IEEE Trans. Control Syst. Technol. 2022, 31, 467–474. [Google Scholar] [CrossRef]
- Guo, Z.K.; Li, Y.G.; Yu, B.C.; Zhou, S.C.; Meng, Q.Y.; Lu, X.X.; Huang, Y.F.; Liu, G.P.; Lu, J. Research progress of lock-in amplifiers. Acta Phys. Sin. 2023, 72, 249901. [Google Scholar] [CrossRef]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter; University of North Carolina at Chapel Hill: Chapel Hill, NC, USA, 1995. [Google Scholar]
- Simon, D. Kalman filtering. Embed. Syst. Program. 2001, 14, 72–79. [Google Scholar]
- Khodarahmi, M.; Maihami, V. A review on Kalman filter models. Arch. Comput. Methods Eng. 2023, 30, 727–747. [Google Scholar] [CrossRef]
- Grewal, M.S. Kalman filtering. In International Encyclopedia of Statistical Science; Springer: Berlin/Heidelberg, Germany, 2011; pp. 705–708. [Google Scholar]
- Li, Q.; Li, R.; Ji, K.; Dai, W. Kalman filter and its application. In Proceedings of the 2015 8th International Conference on Intelligent Networks and Intelligent Systems (ICINIS), Tianjin, China, 1–3 November 2015; IEEE: New York, NY, USA, 2015; pp. 74–77. [Google Scholar]
- Mikrosensoranwendung Chemnitz GmbH. AM-IP4k Datasheet. 2020. Available online: https://amac-chemnitz.de/images/interpolation/AM-IP4k/50400-DB-1-3-E-IP4k_AMAC.pdf (accessed on 20 June 2025).
- Köning, R.; Wimmer, G.; Witkovský, V. EllipseFit4HC: A MATLAB algorithm for demodulation and uncertainty evaluation of the quadrature interferometer signals. In Advanced Mathematical And Computational Tools In Metrology And Testing X; World Scientific: London, UK, 2015; pp. 211–218. [Google Scholar]
- Yue, C.; Li, J.; Sun, J.; Zhu, R.; Hou, X.; Zhang, X.; Liu, L.; Chen, W. Homodyne coherent optical receiver for intersatellite communication. Appl. Opt. 2018, 57, 7915–7923. [Google Scholar] [CrossRef]
- Bartáková, Z.; Bálek, R. Use of the application of heterodyne laser interferometer in power ultrasonics. Ultrasonics 2006, 44, e1567–e1570. [Google Scholar] [CrossRef]
- Stöckling, C.A.; Pöschel, W.; Schulz, S. Optical Simulation and Design of Spatial Heterodyne Spectrometers for Remote Sensing Applications. In Proceedings of the EPJ Web of Conferences, Online, 20 August 2020; EDP Sciences: Les Ulis, France, 2020; Volume 238, p. 12018. [Google Scholar]
- Wang, R.; Zhang, Y.; Lu, M.; Wu, Y.; Wang, Y.; Li, W.; Zhang, H.; Li, D.; Wei, F. PyQt5 Coding and Optimization for Heterodyne Detected Vibrational Sum Frequency Generation Spectroscopy. Authorea Prepr. 2025, 139, 103827. [Google Scholar] [CrossRef]
- Sahoo, A.; Mathew, J.; Battisti, A.; Tucker, B. Compact Spatial Heterodyne Spectrographs for Future Space-Based Observations: Instrument Modeling and Applications. Sensors 2024, 24, 4709. [Google Scholar] [CrossRef] [PubMed]
- He, C.; Hang, L.; Wu, B. Application of homodyne demodulation system in fiber optic sensors using phase generated carrier based on LabVIEW in pipeline leakage detection. In Proceedings of the 2nd International Symposium on Advanced Optical Manufacturing and Testing Technologies: Optical Test and Measurement Technology and Equipment, Xi’an, China, 2–5 November 2005; SPIE: Cergy, France, 2006; Volume 6150, pp. 488–493. [Google Scholar]
- Holzer, M.; Mohr, F. Aspects of signal processing in laser vibrometry and their embedded-realisation on FPGA with NI-LabVIEW. In Proceedings of the 2007 17th International Conference Radioelektronika, Brno, Czech Republic, 24–25 April 2007; IEEE: New York, NY, USA, 2007; pp. 1–5. [Google Scholar]
- Carneiro, A.C.; Lopez-Barbero, A.P.; Silva, V.N.; Kitano, C.; Galeti, J.H.; dos Santos, A.B. High accuracy homodyne interferometric method for wide dynamic range applications. IEEE Sens. J. 2019, 20, 4221–4228. [Google Scholar] [CrossRef]
- Huang, J.B.; Li, Y.; Gu, H.C.; Li, R.Z.; Tan, B.; Yang, G. Homodyne coherent demodulation method for fiber laser hydrophone using a 3x3 coupler with gains adjusted real-time for symmetry. In Proceedings of the International Symposium on Photoelectronic Detection and Imaging 2011: Laser Sensing and Imaging; and Biological and Medical Applications of Photonics Sensing and Imaging, Beijing, China, 24–26 May 2011; SPIE: Cergy, France, 2011; Volume 8192, pp. 391–398. [Google Scholar]
- Patel, K.; Nagora, U.; Joshi, H.C.; Pathak, S.; Jadeja, K.A.; Patel, K.; Tanna, R.L. LabVIEW-FPGA-based real-time data acquisition system for ADITYA-U heterodyne interferometry. IEEE Trans. Plasma Sci. 2021, 49, 1891–1897. [Google Scholar] [CrossRef]
- Martinussen, H.; Aksnes, A.; Engan, H.E. Heterodyne interferometry for high sensitivity absolute amplitude vibrational measurements. In Proceedings of the Interferometry XIII: Techniques and Analysis, San Diego, CA, USA, 13–17 August 2006; SPIE: Cergy, France, 2006; Volume 6292, pp. 316–326. [Google Scholar]
- Wu, Y.; Qin, F.; Li, Y.; Ding, Z.; Xu, R. Designing an automatic frequency stabilization system for an external cavity diode laser using a data acquisition card in the LabVIEW platform. Appl. Sci. 2023, 14, 308. [Google Scholar] [CrossRef]
- Hue, J.; Moulin, V.; Oxaran, L.; Berg, V.; Rat, V.; Abdoul-Carime, K.; Dupont, B.; Martin, S.; Sermet, F.; Stanchina, S.; et al. Heterodyne detection for optical FMCW LiDAR: Tests, analysis, and experimental comparisons between photodetectors and configurations. In Proceedings of the Photonic Instrumentation Engineering XI, San Francisco, CA, USA, 27 January–1 February 2024; SPIE: Cergy, France, 2024; Volume 12893, pp. 36–51. [Google Scholar]
- Sun, C.; He, X.; Xu, R.; Lu, S.; Pan, X.; Bai, J. Optimization of signal-to-noise ratio of laser heterodyne radiometer. Microw. Opt. Technol. Lett. 2024, 66, e33857. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Dinh, G.N. Stability and Resolution of a Conventional Displacement Measuring Heterodyne Interferometer Using a Single Phase-Locked Loop. Exp. Mech. 2023, 63, 1015–1032. [Google Scholar] [CrossRef]
- Cavedo, F.; Pesatori, A.; Norgia, M.; di Milano, P.; Solari, G.E. Laser rangefinder for steel pipes characterization. In Proceedings of the 2015 IEEE International Instrumentation and Measurement Technology Conference (I2MTC) Proceedings, Pisa, Italy, 11–14 May 2015; IEEE: New York, NY, USA, 2015; pp. 1387–1390. [Google Scholar]
- Norgia, M.; Melchionni, D.; Magnani, A.; Pesatori, A. High-speed self-mixing laser distance sensor. In Proceedings of the AIP Conference Proceedings, Ancona, Italy, 25–27 June 2014; American Institute of Physics: College Park, MD, USA, 2014; Volume 1600, pp. 422–425. [Google Scholar]
- Ming, X.; Shuang, W.; Jie, H.; Ruicheng, Q.; Man, Z. Development of Agricultural Implement Visual Navigation Terminal Based on DSP and MCU. Nongye Jixie Xuebao/Transactions Chin. Soc. Agric. Mach. 2015, 46, 21–26. [Google Scholar]
- Jyrkkä, K.; Silven, O.; Ali-Yrkkö, O.; Heidari, R.; Berg, H. Component-based development of DSP software for mobile communication terminals. Microprocess. Microsyst. 2002, 26, 463–474. [Google Scholar] [CrossRef]
- Feng, Z.; Qiu, M. Design and Implementation of Self-Validating Pneumatic Actuator Hardware System Based on DSP and MCU. Int. J. Hybrid Inf. Technol. 2014, 7, 101–114. [Google Scholar] [CrossRef]
- Joost, R.; Salomon, R. Advantages of FPGA-based multiprocessor systems in industrial applications. In Proceedings of the 31st Annual Conference of IEEE Industrial Electronics Society, Raleigh, NC, USA, 6–10 November 2005; IEEE: New York, NY, USA, 2005; pp. 6–12. [Google Scholar]
- Rodríguez-Andina, J.J.; Valdes-Pena, M.D.; Moure, M.J. Advanced features and industrial applications of FPGAs—A review. IEEE Trans. Ind. Informatics 2015, 11, 853–864. [Google Scholar] [CrossRef]
- Farooq, U.; Marrakchi, Z.; Mehrez, H.; Farooq, U.; Marrakchi, Z.; Mehrez, H. FPGA architectures: An overview. In Tree-Based Heterogeneous FPGA Architectures: Application Specific Exploration and Optimization; Springer: Berlin/Heidelberg, Germany, 2012; pp. 7–48. [Google Scholar]
- Yang, H.; Zhang, J.; Sun, J.; Yu, L. Review of advanced FPGA architectures and technologies. J. Electron. 2014, 31, 371–393. [Google Scholar] [CrossRef]
- Gandhare, S.; Karthikeyan, B. Survey on FPGA architecture and recent applications. In Proceedings of the 2019 International Conference on Vision Towards Emerging Trends in Communication and Networking (ViTECoN), Vellore, India, 30–31 March 2019; IEEE: New York, NY, USA, 2019; pp. 1–4. [Google Scholar]




| Method | Resolution | Bandwidth | Cost | Application |
|---|---|---|---|---|
| Error Calibration Methods | High | High | High | Academia |
| Ellipse Parameter Estimation Methods | High | High | Low | Industry/Academia |
| Method | Resolution | Bandwidth | Cost | Application |
|---|---|---|---|---|
| Pulse-Counting Methods | Medium | High | Low | Industry/Academia |
| Quadrature Phase-Locked Methods | High | High | Medium | Industry/Academia |
| Kalman Filtering Method | High | Medium | Medium | Academia |
| Platform | Power | Volume | Dev. Cost | Dev. Time | Dep. Cost |
|---|---|---|---|---|---|
| PCs | High | High | Low | Short | Medium |
| MCUs/DSPs | Low | Low | Low | Short | Low |
| FPGAs | Medium | Low | Low | Medium | Medium |
| ASICs | Low | Low | High | Long | Low |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhao, F.; Luo, L.; Li, X. A Review on Recent Advances in Signal Processing in Interferometry. Sensors 2025, 25, 5013. https://doi.org/10.3390/s25165013
Wang Y, Zhao F, Luo L, Li X. A Review on Recent Advances in Signal Processing in Interferometry. Sensors. 2025; 25(16):5013. https://doi.org/10.3390/s25165013
Chicago/Turabian StyleWang, Yifeng, Fangyuan Zhao, Linbin Luo, and Xinghui Li. 2025. "A Review on Recent Advances in Signal Processing in Interferometry" Sensors 25, no. 16: 5013. https://doi.org/10.3390/s25165013
APA StyleWang, Y., Zhao, F., Luo, L., & Li, X. (2025). A Review on Recent Advances in Signal Processing in Interferometry. Sensors, 25(16), 5013. https://doi.org/10.3390/s25165013





