Vehicle Load Information Acquisition Using Roadside Micro-Electromechanical Systems Accelerometers
Abstract
1. Introduction
2. Methodology
2.1. Theoretical Analysis
2.1.1. Pavement Vibration Analysis Based on Vehicle–Road Interactions
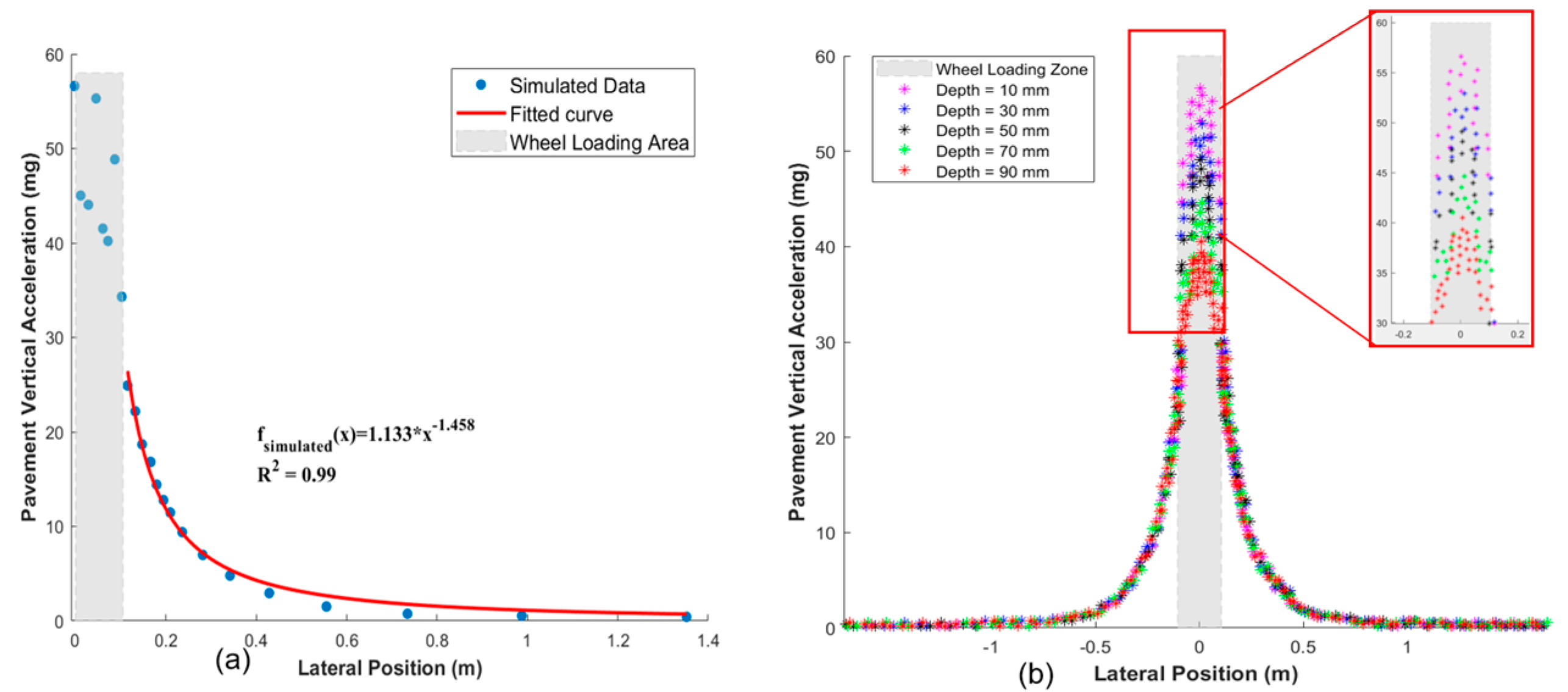
2.1.2. Pavement Vibration Distribution in Lateral and Vertical Direction
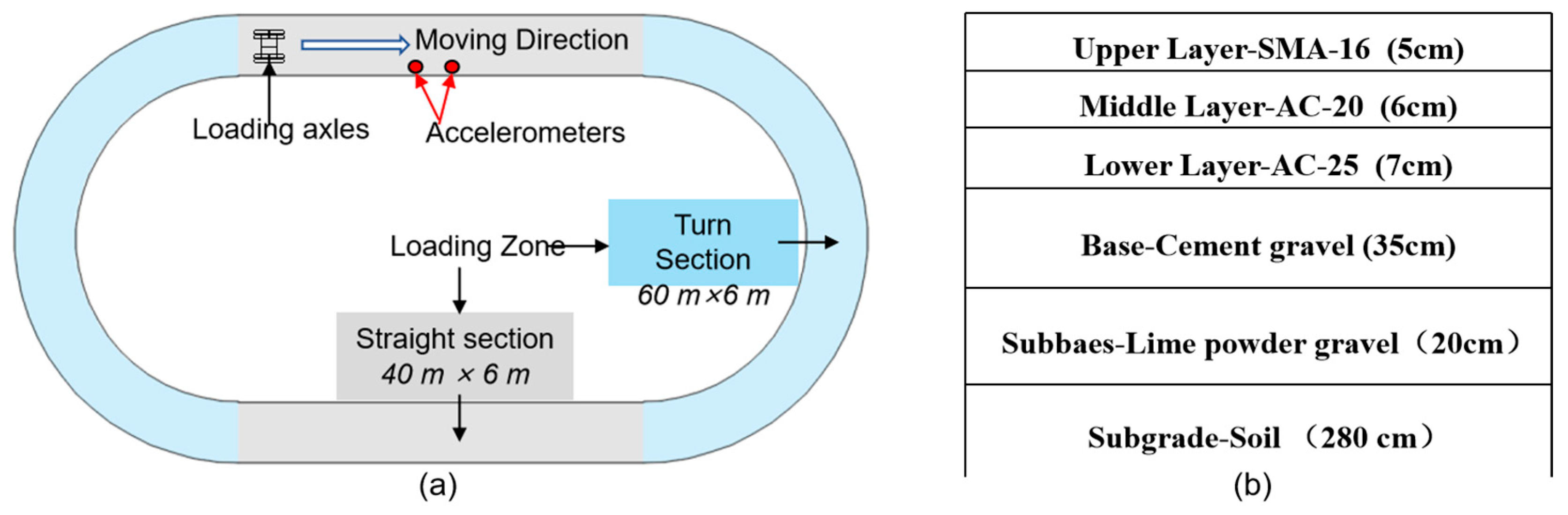
2.2. Full-Scale Accelerated Pavement Testing
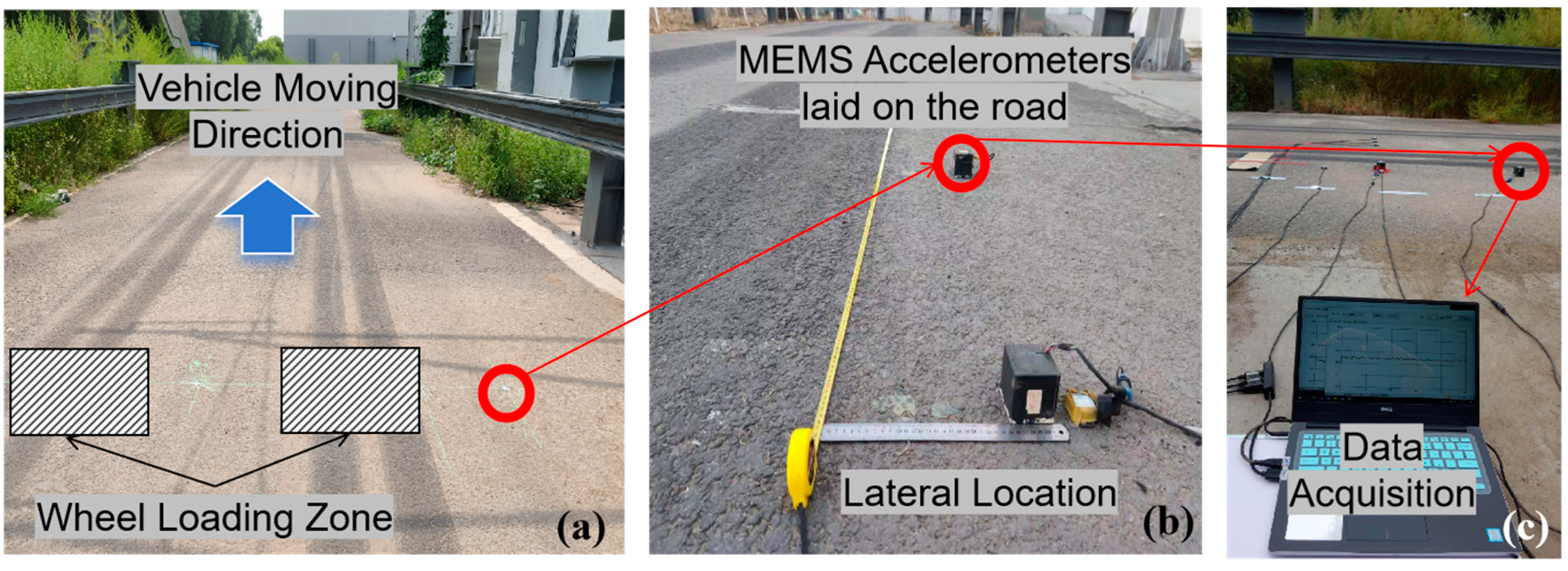
2.2.1. Field Test of Full-Scale Accelerated Pavement Testing
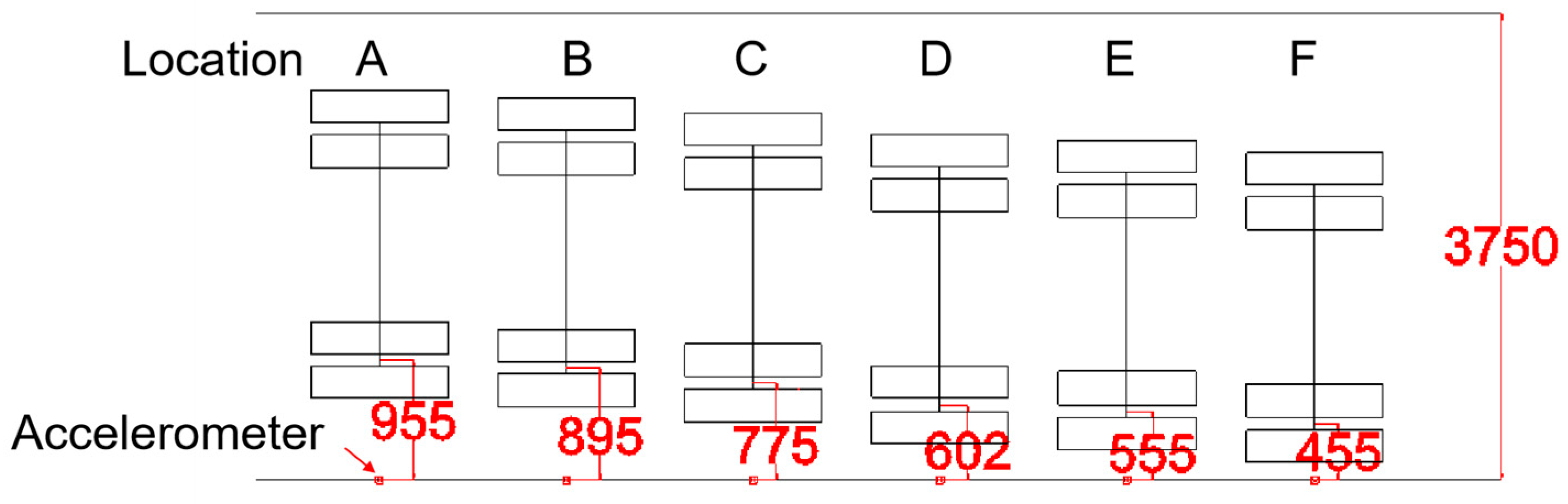
2.2.2. Layout of the MEMS Accelerometer
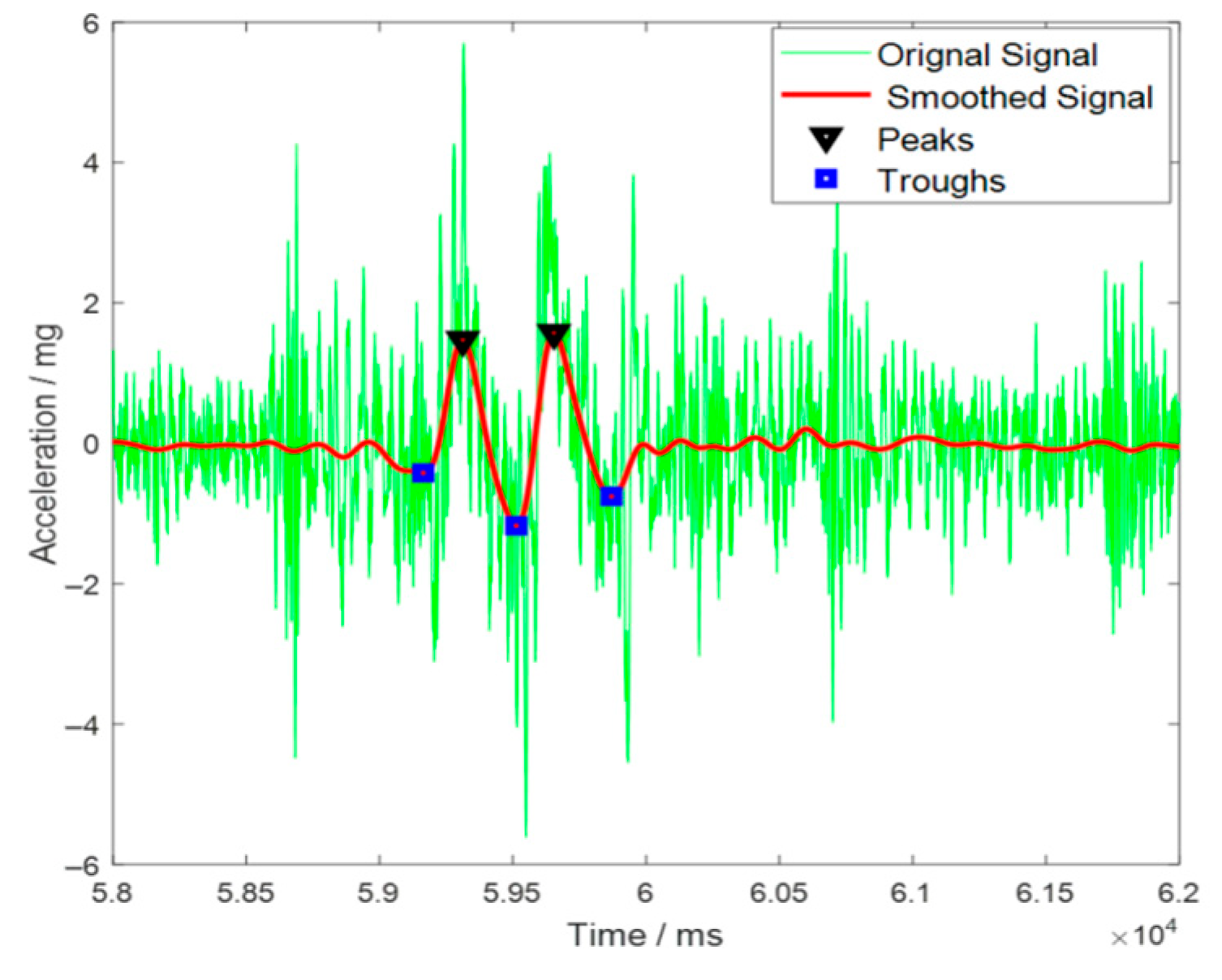
2.3. Vibration Signal Acquisition and Processing
- (1)
- Data windowing.
- (2)
- Baseline correction.
- (3)
- Data filtering.
- (4)
- Feature value extraction.
3. Experimental Results and Discussion
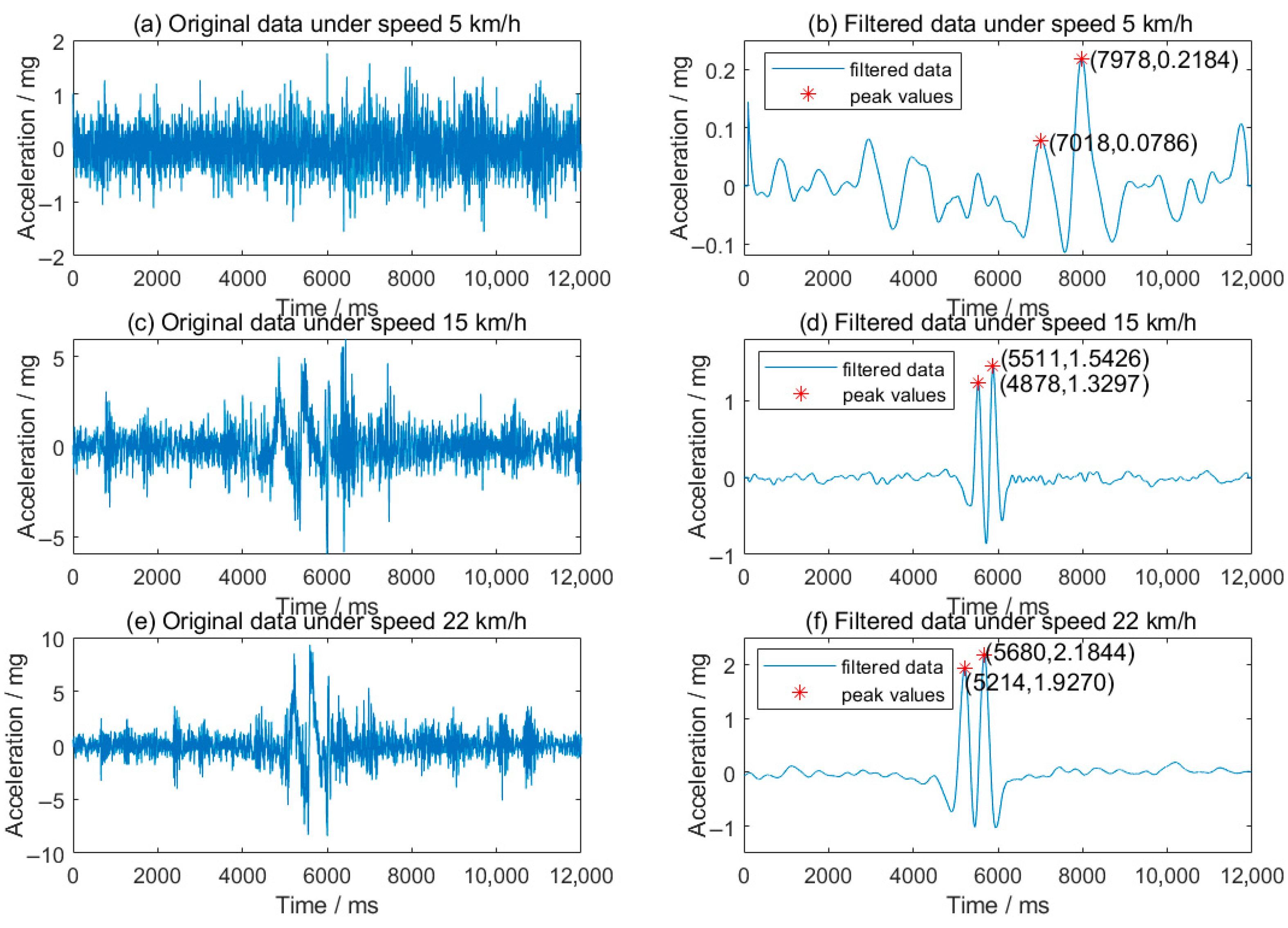
3.1. Acceleration Under Different Loading Speeds
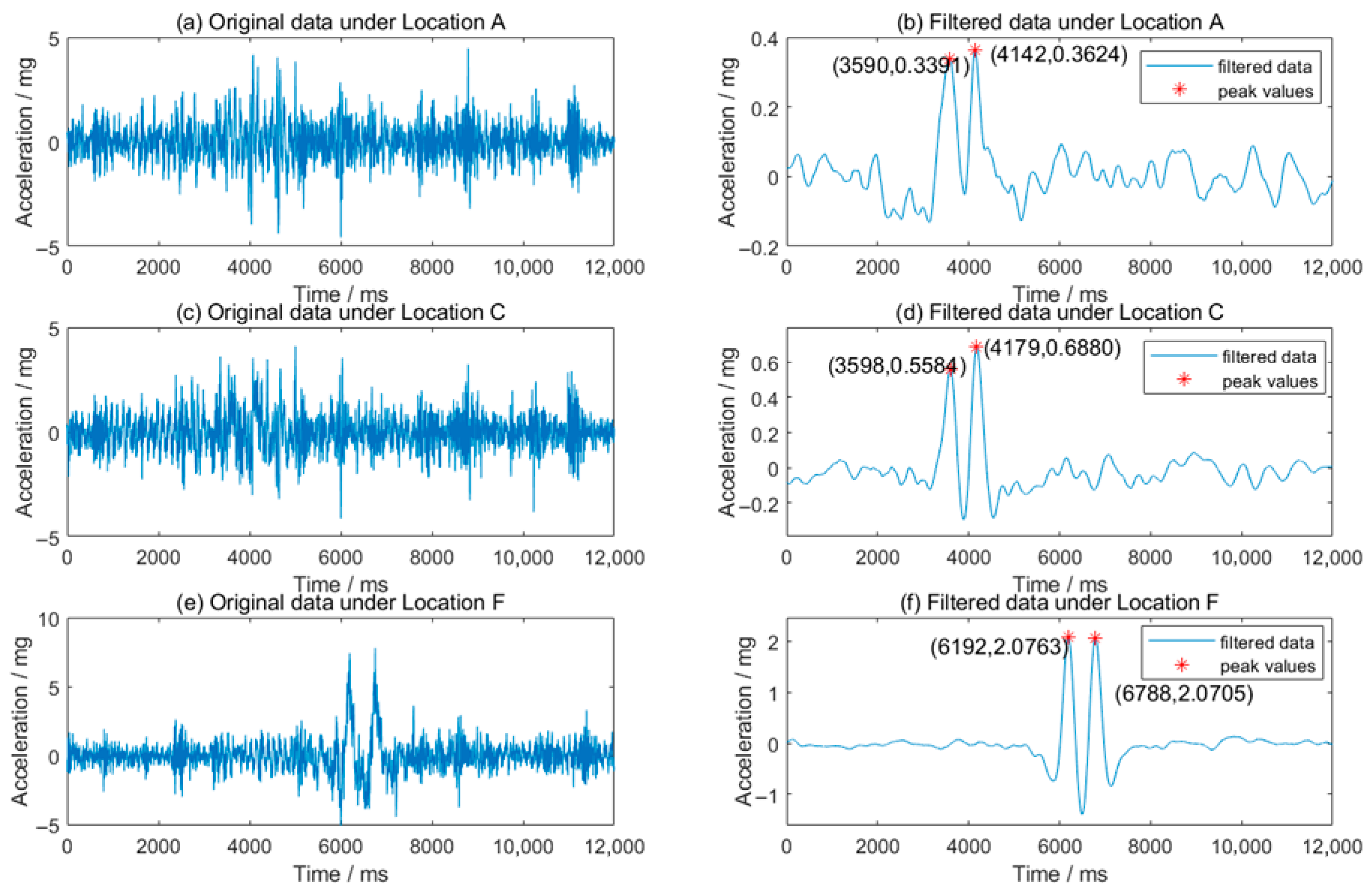
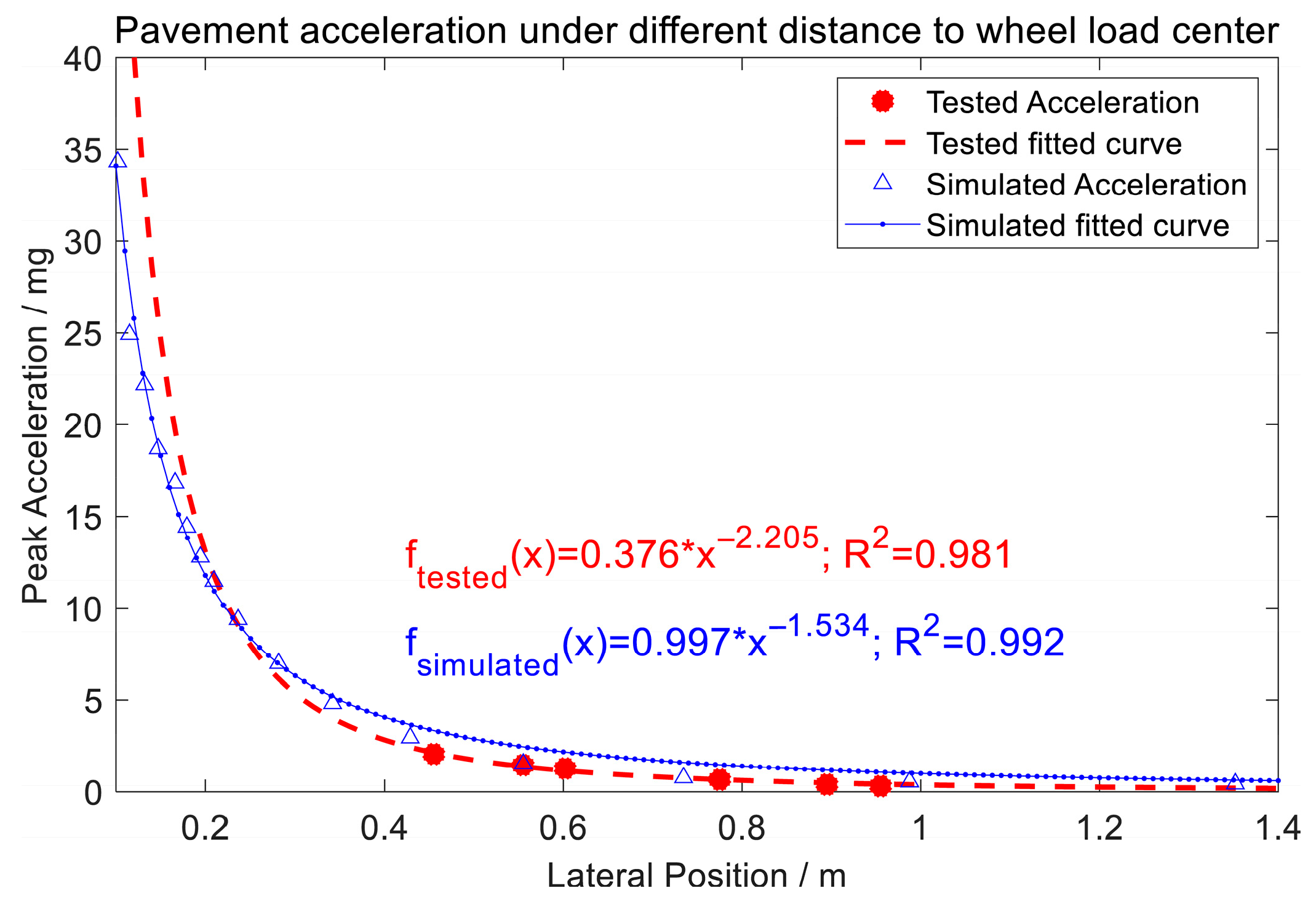
3.2. Acceleration Under Loads with Different Lateral Locations (Wandering)
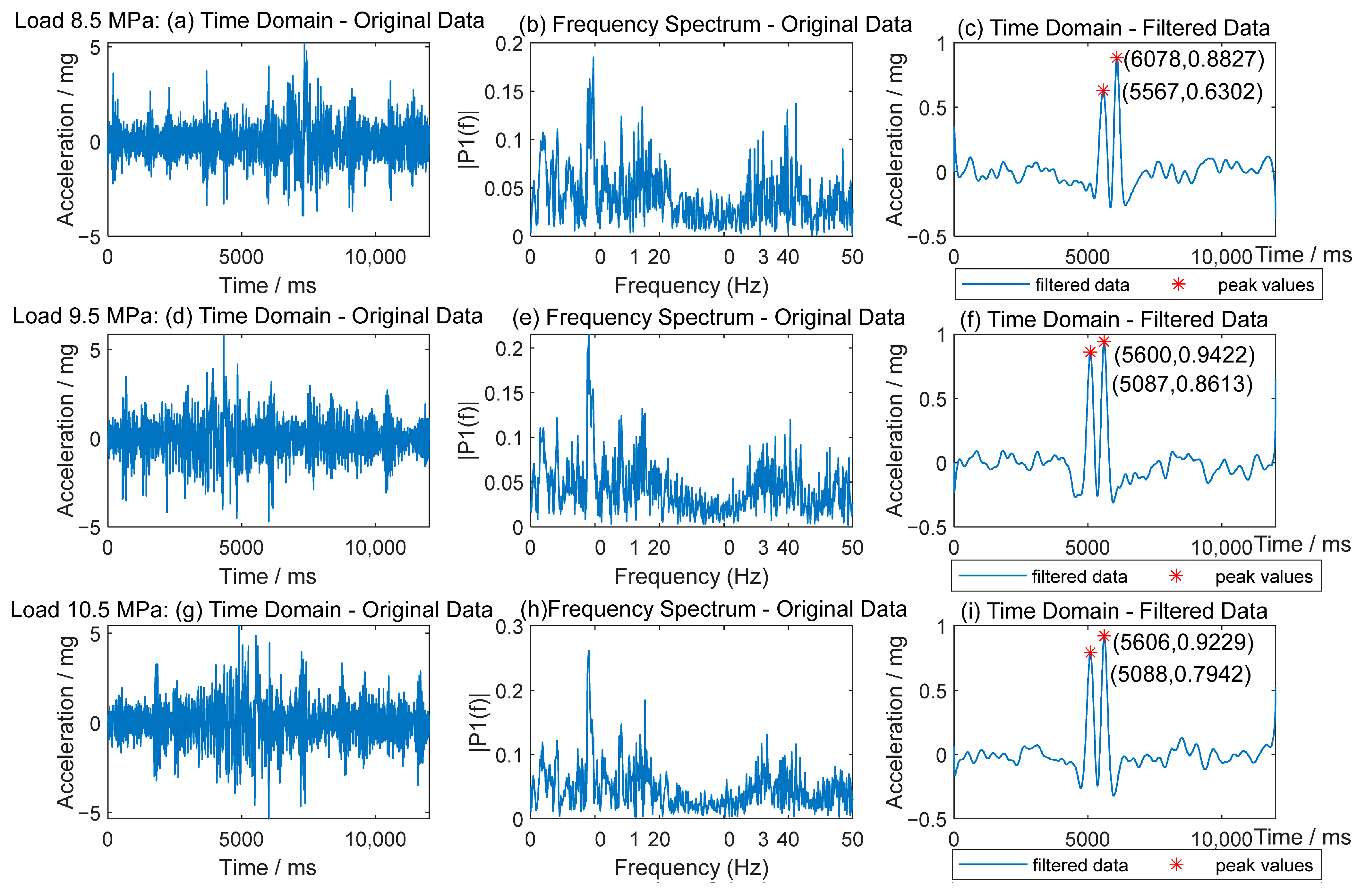
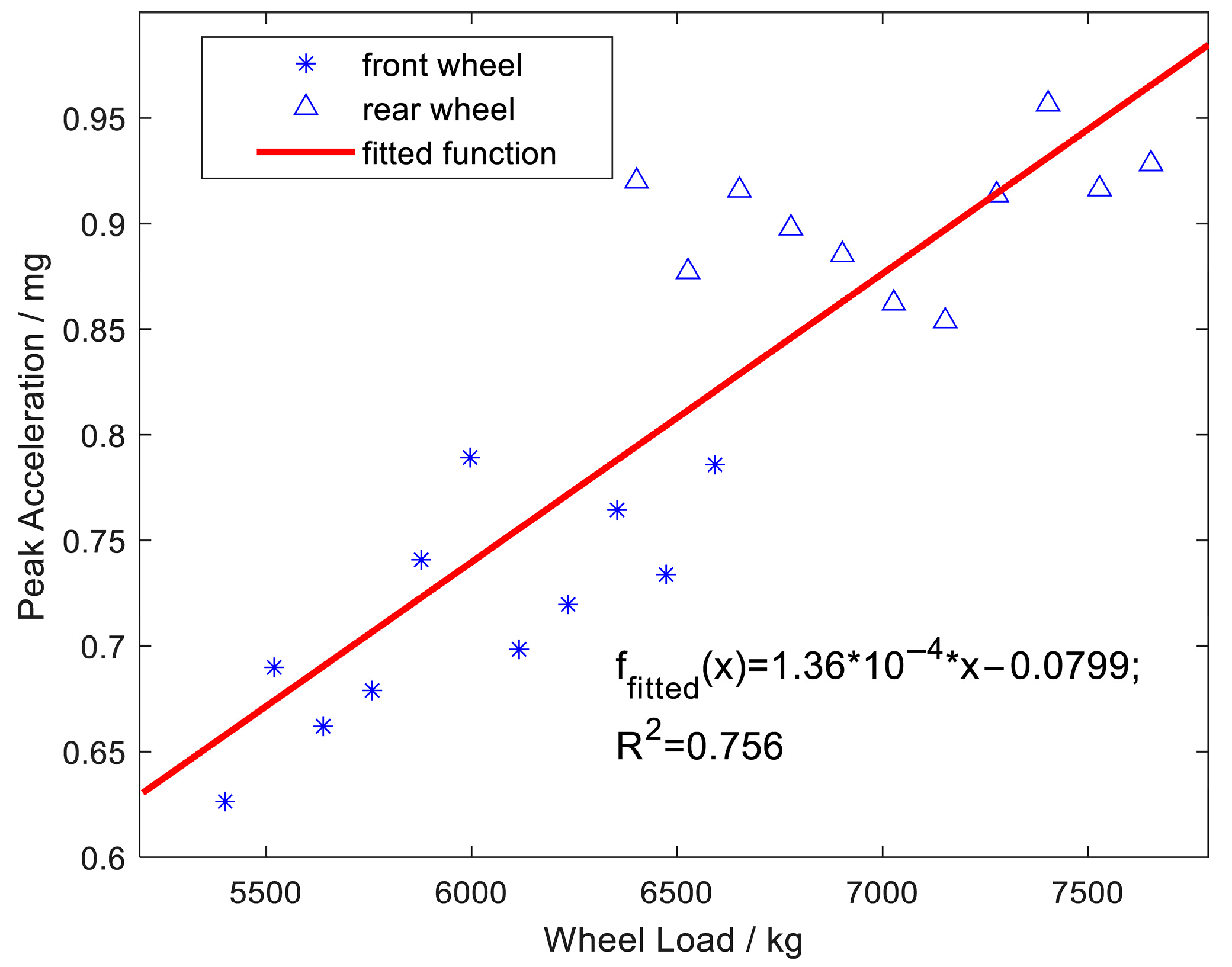
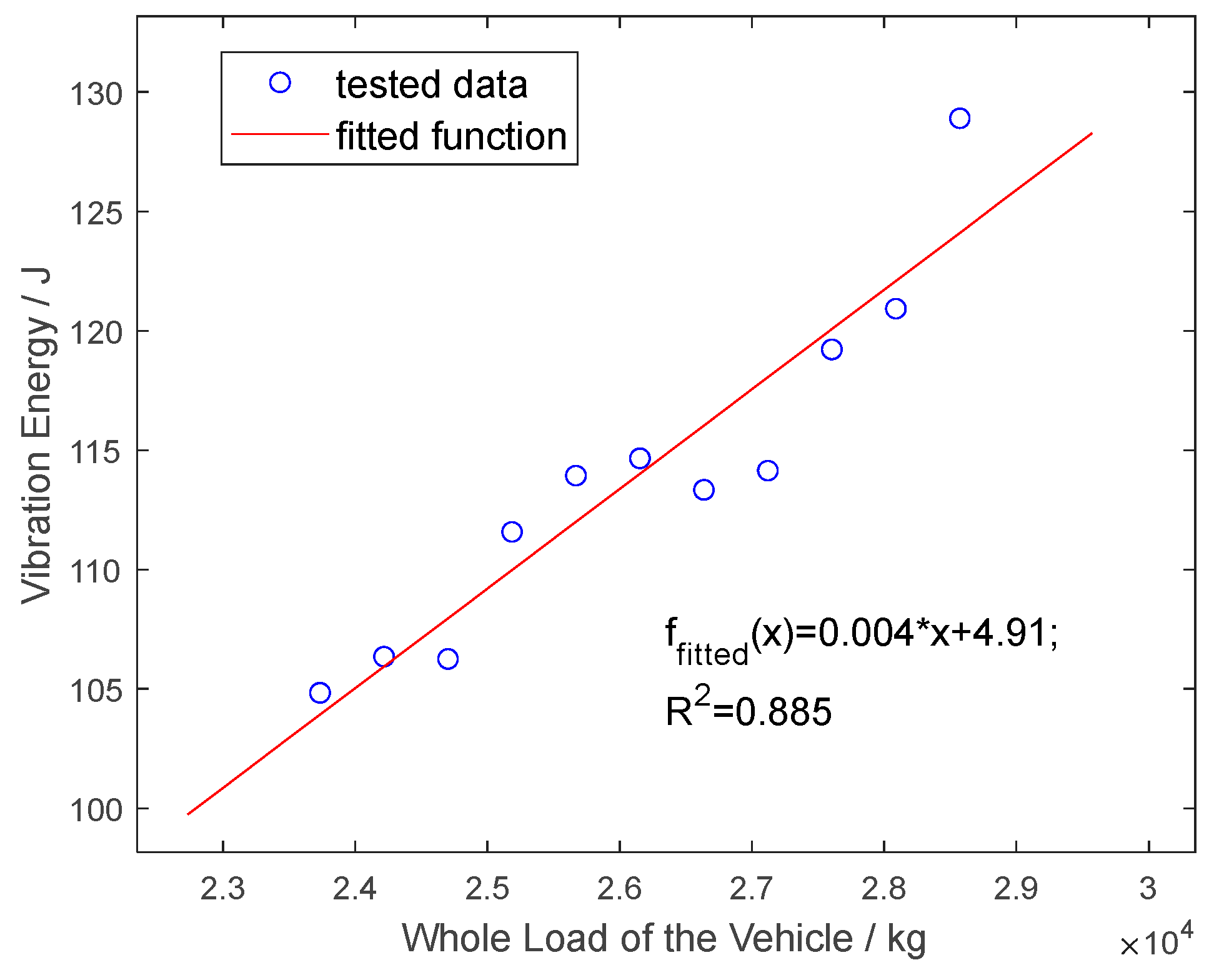
3.3. Acceleration Under Different Loads
4. Conclusions
- (1)
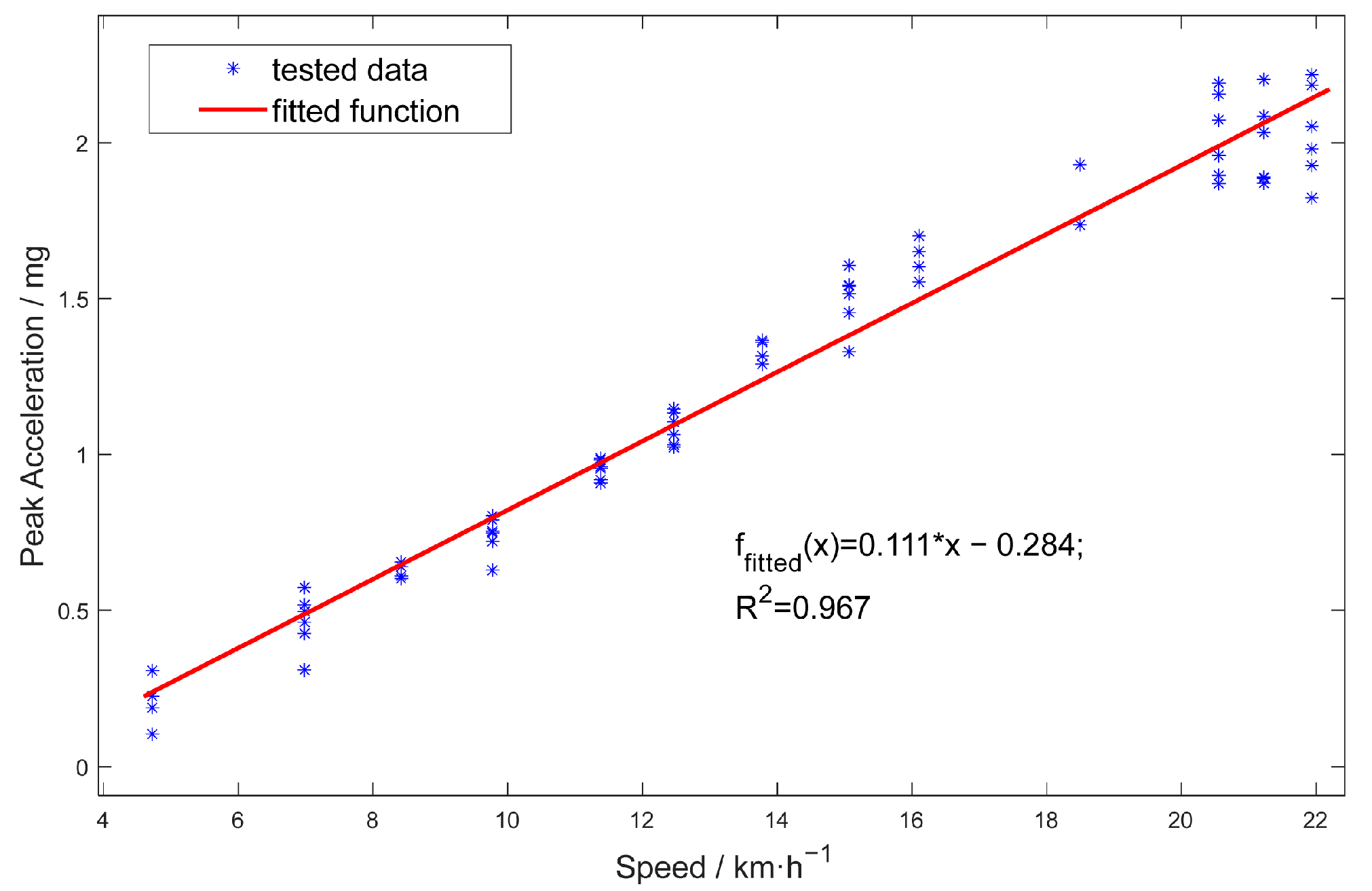
- The peak acceleration of roadside vibrations exhibits a strong linear correlation with vehicle speed in the range of 5–22 km/h, with a high correlation coefficient (R2 = 96.5%).
- (2)
- As the lateral distance between the wheel center and the monitoring point increases, the peak acceleration decreases following a power law, with a fitting coefficient of 98%, which is consistent with the FEM simulation results.
- (3)
- The relationship between the peak acceleration and the wheel load is approximately linear, with a fitting coefficient of 75.6%. Taking the vibration energy of the original signal as an index, there is a positive linear correlation between the vibration energy and the total vehicle load of the tandem axles, with a correlation coefficient of 88.5%, validating the feasibility of monitoring vehicle loads using roadside vibration sensors.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, Z.; Mohammadi, M.; Wang, H.; Tsai, Y.C.J. A feature-based pavement image registration method for precise pavement deterioration monitoring. Comput. Aided Civ. Inf. 2025, 40, 1276–1294. [Google Scholar] [CrossRef]
- Rose, C.; Britt, J.; Allen, J.; Bevly, D. An Integrated Vehicle Navigation System Utilizing Lane-Detection and Lateral Position Estimation Systems in Difficult Environments for GPS. IEEE Trans. Intell. Transp. 2014, 15, 2615–2629. [Google Scholar] [CrossRef]
- Mohsen, I.; Ditchi, T.; Holé, S.; Géron, E. Lateral Position Measurement Based on Vehicles’ Longitudinal Displacement. Sensors 2020, 20, 7183. [Google Scholar] [CrossRef]
- Jihanny, J.; Subagio, B.S.; Hariyadi, E.S.; Roosmini, D.; Pribadi, K.; Sugeng, B.; Hadihardaja, I.K. The analysis of overloaded trucks in indonesia based on weigh in motion data (east of sumatera national road case study). MATEC Web Conf. 2018, 147, 2006. [Google Scholar] [CrossRef]
- Khavassefat, P.; Jelagin, D.; Birgisson, B. Dynamic response of flexible pavements at vehicle-road interaction. Road Mater. Pavement 2015, 16, 256–276. [Google Scholar] [CrossRef]
- Tao, H.; Ju, S. Traffic Load Analysis of Highway One in Togo Based on Weigh-In-Motion Data. Highway 2020, 65, 222–225. [Google Scholar]
- Gao, J.; Sha, A.; Huang, Y.; Liu, Z.; Hu, L.; Jiang, W.; Yun, D.; Tong, Z.; Wang, Z. Cycling comfort on asphalt pavement: Influence of the pavement-tyre interface on vibration. J. Clean. Prod. 2019, 223, 323–341. [Google Scholar] [CrossRef]
- Lam, P.T.; Lee, J.; Lee, Y.; Nguyen, X.T.; Vy, V.; Han, K.; Yoon, H. A vision-based weigh-in-motion approach for vehicle load tracking and identification. Comput.-Aided Civ. Inf. 2025, 40, 1466–1489. [Google Scholar] [CrossRef]
- Fernández Llorca, D.; Hernández Martínez, A.; García Daza, I. Vision-based vehicle speed estimation: A survey. IET Intell. Transp. Syst. 2021, 15, 987–1005. [Google Scholar] [CrossRef]
- Zhang, R.; Zou, Z.; Shen, S.; Liu, H.X. Design, Implementation, and Evaluation of a Roadside Cooperative Perception System. Transp. Res. Rec. 2022, 2676, 273–284. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, Q.; Suo, C. A Novel Vehicle Classification Using Embedded Strain Gauge Sensors. Sensors 2008, 8, 6952–6971. [Google Scholar] [CrossRef]
- Xue, W.; Wang, L.; Wang, D.; Druta, C. Pavement Health Monitoring System Based on an Embedded Sensing Network. J. Mater. Civ. Eng. 2014, 26, 4014071–4014072. [Google Scholar] [CrossRef]
- Bian, Z.; Zeng, M.; Zhao, H.; Guo, M.; Cai, J. Temporal Convolutional Network-Based Axle Load Estimation from Pavement Vibration Data. Appl. Sci. 2023, 13, 13264. [Google Scholar] [CrossRef]
- Al-Tarawneh, M.; Huang, Y.; Lu, P.; Bridgelall, R. Weigh-In-Motion System in Flexible Pavements Using Fiber Bragg Grating Sensors Part A: Concept. IEEE Trans. Intell. Transp. 2020, 21, 5136–5147. [Google Scholar] [CrossRef]
- Dan, D.; Ge, L.; Yan, X. Identification of moving loads based on the information fusion of weigh-in-motion system and multiple camera machine vision. Meas. J. Int. Meas. Confed. 2019, 144, 155–166. [Google Scholar] [CrossRef]
- Zhao, D.; He, W.; Deng, L.; Wu, Y.; Xie, H.; Dai, J. Trajectory Tracking and Load Monitoring for Moving Vehicles on Bridge Based on Axle Position and Dual Camera Vision. Remote Sens. 2021, 13, 4868. [Google Scholar] [CrossRef]
- Ye, Z.; Xiong, H.; Wang, L. Collecting comprehensive traffic information using pavement vibration monitoring data. Comput. Aided Civ. Inf. 2019, 35, 134–149. [Google Scholar] [CrossRef]
- Liu, F.; Ye, Z.; Wang, L. Deep transfer learning-based vehicle classification by asphalt pavement vibration. Constr. Build. Mater. 2022, 342, 127997. [Google Scholar] [CrossRef]
- Chang, C.; Kong, L.; Han, L.; Li, J.; Pan, S.; Wei, Y. Vibration Analysis and Vehicle Detection by MEMS Acceleration Sensors Embedded in PCC Pavement. Sensors 2025, 25, 2898. [Google Scholar] [CrossRef]
- Shi, B.; Shen, S.; Liu, L.; Wang, X. Estimation of vehicle speed from pavement stress responses using wireless sensors. J. Transp. Eng. Part B Pavements 2021, 3, 4021028. [Google Scholar] [CrossRef]
- Verster, J.C.; Roth, T. Effects of central nervous system drugs on driving: Speed variability versus standard deviation of lateral position as outcome measure of the on-the-road driving test. Hum. Psychopharmacol. Clin. Exp. 2014, 29, 19–24. [Google Scholar] [CrossRef]
- Charly, A.; Mathew, T.V. Estimation of traffic conflicts using precise lateral position and width of vehicles for safety assessment. Accid. Anal. Prev. 2019, 132, 105264. [Google Scholar] [CrossRef]
- Zheng, Z.; Li, X. A novel vehicle lateral positioning methodology based on the integrated deep neural network. Expert. Syst. Appl. 2020, 142, 112991. [Google Scholar] [CrossRef]
- Sujon, M.; Dai, F. Application of weigh-in-motion technologies for pavement and bridge response monitoring: State-of-the-art review. Autom. Constr. 2021, 130, 103844. [Google Scholar] [CrossRef]
- MacLeod, E.; Arjomandi, K. Dynamic bridge weigh-in-motion using estimated modal parameters from ambient vibration tests. Eng. Struct. 2023, 289, 116254. [Google Scholar] [CrossRef]
- Chen, Z.; Li, H.; Bao, Y.; Li, N.; Jin, Y. Identification of spatio-temporal distribution of vehicle loads on long-span bridges using computer vision technology. Struct. Control Health Monit. 2016, 23, 517–534. [Google Scholar] [CrossRef]
- Adresi, M.; Abedi, M.; Dong, W.; Yekrangnia, M. A review of different types of weigh-in-motion sensors: State-of-the-art. Meas. J. Int. Meas. Confed. 2024, 225, 114042. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, C.; Chen, L.; Zhang, X. Phase deviation of semi-active suspension control and its compensation with inertial suspension. Acta Mech. Sin. 2024, 40, 523367. [Google Scholar] [CrossRef]
- GB/T 7031-2005/ISO 8608; Mechanical Vibration—Road Surface Profiles—Reporting of Measured Data. Standards Press of China: Beijing, China; International Organization for Standardization (ISO): Geneva, Switzerland, 1995.
- Pengfei, H.; Youqun, Z.; Changjun, D. Modeling of 3-D Virtual Road Model with Matlab and Adams. Mech. Sci. Technol. Aerosp. Eng. 2011, 30, 327–335. [Google Scholar]
- Dong, Q.; Cheng, S.; Zhang, X.; Bao, Y. Research on Vibration Response of Asphalt Concrete Pavement under Vehicle-road Coupled Load. J. Beijing Univ. Aeronaut. Astronaut. 2023, 49, 2385–2394. [Google Scholar] [CrossRef]
- Xue, W.; Wang, D.; Wang, L. Monitoring the Speed, Configurations, and Weight of Vehicles Using an In-Situ Wireless Sensing Network. IEEE Trans. Intell. Transp. 2015, 16, 1667–1675. [Google Scholar] [CrossRef]
- Yan, G.; Ye, Z.; Wang, W.; Wang, L. Numerical analysis on distribution and response of acceleration field of pavement under moving load. Int. J. Pavement Res. Technol. 2021, 14, 519–529. [Google Scholar] [CrossRef]
- Wang, W.; Yan, G.; Zhao, K.; Wang, L. Numerical Simulation and Experimental Measurements of Dynamic Responses of Asphalt Pavement in Dry and Saturated Conditions under Full-Scale Accelerated Loading. Appl. Sci. 2022, 12, 12291. [Google Scholar] [CrossRef]
- Shi, X.M.; Cai, C.S. Simulation of Dynamic Effects of Vehicles on Pavement Using a 3D Interaction Model. J. Transp. Eng. 2009, 135, 736–744. [Google Scholar] [CrossRef]
- Yoo, P.J.; Al-Qadi, I.L. Effect of Transient Dynamic Loading on Flexible Pavements. Transp. Res. Rec. J. Transp. Res. Board. 2007, 1990, 129–140. [Google Scholar] [CrossRef]
- Yang, S.L.; Wei, Y.; Ye, Z.J.; Yang, H.L.; Yang, B.Y.; Li, P.P.; Wang, L.B. Time-frequency Energy Analysis and Vehicle Speed Estimation of Cement Pavement Vibration Signals Under Vehicle Load. China J. Highw. Transp. 2024, 12, 310–325. [Google Scholar]
- Bajwa, R.; Coleri, E.; Rajagopal, R.; Varaiya, P.; Flores, C. Development of a Cost-Effective Wireless Vibration Weigh-In-Motion System to Estimate Axle Weights of Trucks. Comput. Aided Civ. Inf. 2017, 32, 443–457. [Google Scholar] [CrossRef]
- Ye, Z.; Wang, L.; Xu, W.; Gao, Z.; Yan, G. Monitoring Traffic Information with a Developed Acceleration Sensing Node. Sensors 2017, 17, 2817. [Google Scholar] [CrossRef] [PubMed]
- Zeng, M.; Zhao, H.; Gao, D.; Bian, Z.; Wu, D. Reconstruction of Vehicle-Induced Vibration on Concrete Pavement Using Distributed Fiber Optic. IEEE Trans. Intell. Transp. 2022, 23, 24305–24317. [Google Scholar] [CrossRef]
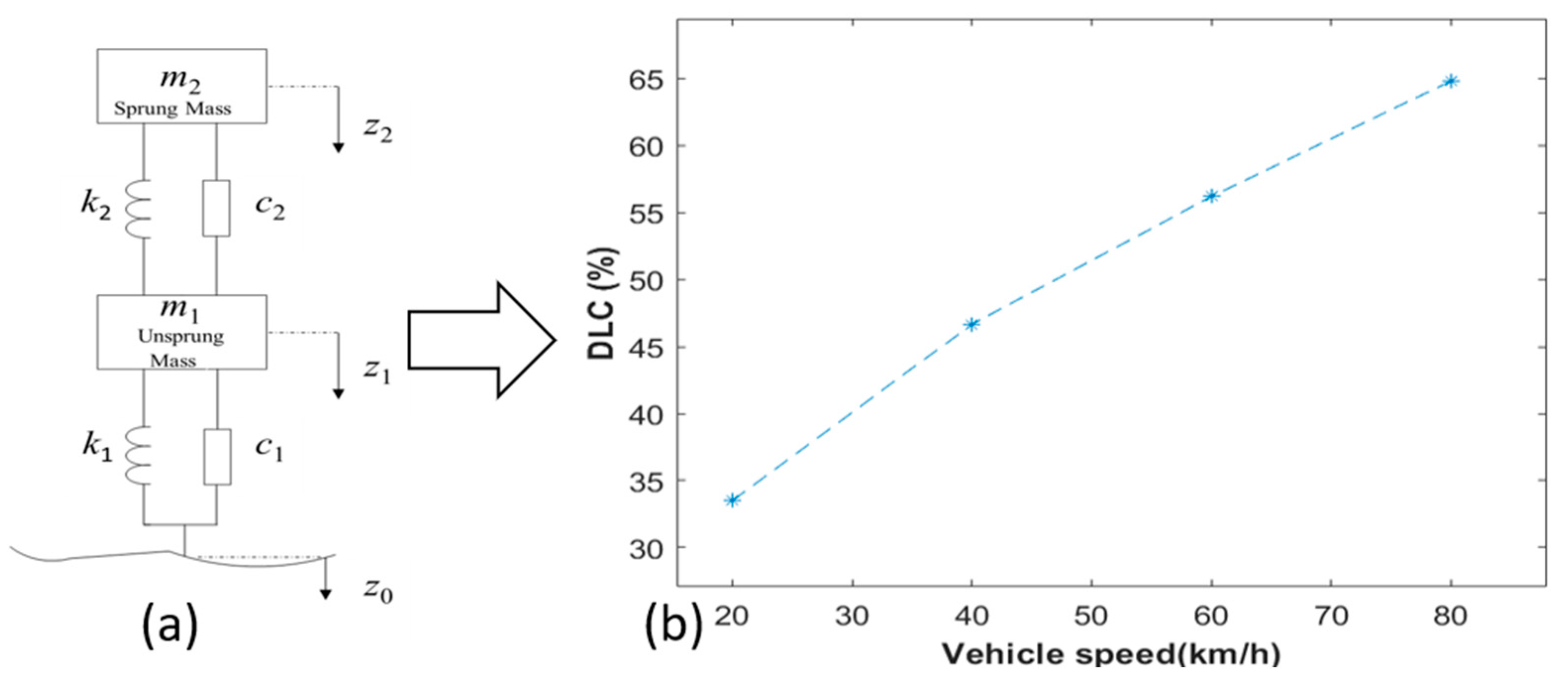



| Unsprung Mass m1/kg | Sprung Mass m2/kg | Unsprung Damping c1/(kN·s·m−1) | Sprung Damping c2/(kN·s·m−1) | Unsprung Stiffness k1/(MN·m−1) | Sprung Stiffness k2/(MN·m−1) |
|---|---|---|---|---|---|
| 550 | 4450 | 2 | 15 | 1.75 | 1 |
| Authors | Index | Model Size (L·W·H) mm | Element | Materials | Load | Validation |
|---|---|---|---|---|---|---|
| Xue et al. [32] | Horizontal strain | 2540 × 1828.8 × 254 | C3D8 | The top layer is viscoelastic, using the dynamic master curve from laboratory tests, while sublayers are elastic. | Elliptical uniform | Validated by the embedded horizontal strain in the field. |
| Yan et al. [33] | Vertical acceleration | 7500 × 3750 × 3750 | C3D8R | Elastic with Rayleigh damping model. | Rectangular nonuniformly distributed | With a speed of 10 m/s, a total load of 2000 kg and a monitoring depth of 70 mm, the simulated and measured peak acceleration are both 45 mg and the time-history curves are similar. |
| Group No. | Revolutions per Minute | Hydraulic Loading Pressure (MPa) | Lateral Loading Position (mm) |
|---|---|---|---|
| 1 | 140/200/240/280/330/360/400/440/470/540/600/620/640 | 9 | 180 |
| 2 | 540 | 8.5/8.7/8.9/9.1/9.3/9.5/9.7/9.9/10.1/10.3/10.5 | 180 |
| 3 | 470 | 9 | 0/60/180/353/400/500 |
| No. | Hydraulic Loading Pressure (MPa) | Whole Load of the Tandem Axles (kg) | Front Left Wheel (kg) | Front Right Wheel (kg) | Rare Left Wheel (kg) | Rare Right Wheel (kg) |
|---|---|---|---|---|---|---|
| 1 | 8 | 22,643.3 | 5163.3 | 5576.7 | 6093.3 | 5810 |
| 2 | 8.5 | 24,043.4 | 5470 | 5936.7 | 6446.7 | 6190 |
| 3 | 9 | 24,663.3 | 5600 | 5996.7 | 6683.3 | 6383.3 |
| 4 | 9.5 | 25,840 | 5913.3 | 6370 | 6960 | 6596.7 |
| 5 | 10 | 27,563.4 | 6376.7 | 6763.3 | 7396.7 | 7026.7 |
| 6 | 10.5 | 28,497.5 | 6572.5 | 7010 | 7665 | 7250 |
| 7 | 11 | 29,745 | 6820 | 7310 | 7960 | 7655 |
| No. | Revolutions per Minute (r/min) | Measured Speed (km/h) | No. | Revolutions per Minute (r/min) | Measured Speed (km/h) |
|---|---|---|---|---|---|
| 1 | 140 | 4.72 | 8 | 440 | 15.07 |
| 2 | 200 | 6.98 | 9 | 470 | 16.10 |
| 3 | 240 | 8.42 | 10 | 540 | 18.50 |
| 4 | 280 | 9.77 | 11 | 600 | 20.55 |
| 5 | 330 | 11.38 | 12 | 620 | 21.22 |
| 6 | 360 | 12.47 | 13 | 640 | 21.94 |
| 7 | 400 | 13.78 |
| Location | Lateral Displacement Set by the Loading System (mm) | Lateral Distance Between the Center of Wheel Loading Zone and the Accelerometer (mm) |
|---|---|---|
| A | 0 | 955 |
| B | 60 | 895 |
| C | 180 | 775 |
| D | 353 | 602 |
| E | 400 | 555 |
| F | 500 | 455 |
| Parameter | Description | Parameter | Description |
|---|---|---|---|
| Sensitivity (mV/g) | 996.1 | Analog Output Bandwidth (Hz) | 50 |
| Noise (mV) | 0.198 | Size (L × W × H, mm) | 60 × 60 × 60 |
| Resolution * (mg) | 0.199 | Maximum Allowable Compressive Strength (MPa) | 67.54 |
| Measurement Range (g) | ±2 | Waterproof Standard Grade | IPX8 |
| Default Sampling Frequency (Hz) | 1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Q.; Ye, Z.; Tan, Z.; Xu, J.; Wang, L. Vehicle Load Information Acquisition Using Roadside Micro-Electromechanical Systems Accelerometers. Sensors 2025, 25, 4901. https://doi.org/10.3390/s25164901
Zhao Q, Ye Z, Tan Z, Xu J, Wang L. Vehicle Load Information Acquisition Using Roadside Micro-Electromechanical Systems Accelerometers. Sensors. 2025; 25(16):4901. https://doi.org/10.3390/s25164901
Chicago/Turabian StyleZhao, Qian, Zhoujing Ye, Zhao Tan, Jie Xu, and Linbing Wang. 2025. "Vehicle Load Information Acquisition Using Roadside Micro-Electromechanical Systems Accelerometers" Sensors 25, no. 16: 4901. https://doi.org/10.3390/s25164901
APA StyleZhao, Q., Ye, Z., Tan, Z., Xu, J., & Wang, L. (2025). Vehicle Load Information Acquisition Using Roadside Micro-Electromechanical Systems Accelerometers. Sensors, 25(16), 4901. https://doi.org/10.3390/s25164901








