Design and Analysis of an Autonomous Active Ankle–Foot Prosthesis with 2-DoF
Abstract
1. Introduction
- –
- Has a compact and lightweight design without excessive mass;
- –
- Provides active control in both the sagittal and frontal planes;
- –
- Features low power consumption and high autonomy;
- –
- Is validated through large-scale clinical trials.
- –
- The proposed system includes a mechanical structure designed to balance reliability, low weight, and adaptability to gait dynamics;
- –
- Electronic systems and sensors ensuring precise motion control;
- –
- Intelligent control algorithms mimicking the biomechanics of natural gait;
- –
- Autonomous operation focused on minimizing power consumption and maximizing runtime without recharging.
- –
- How can we design a 2-Dof active ankle prosthesis structure that balances strength, weight, and functionality?
- –
- What kinematic and dynamic principles should guide the actuator system design for sagittal and frontal plane movements?
- –
- Which control algorithms best adapt prosthetic motion to terrain variations and user gait dynamics?
- –
- How can power consumption be minimized while maintaining a high output and system stability?
- –
- How does active ankle joint control affect gait symmetry, metabolic cost, and overall user comfort?
2. Materials and Methods
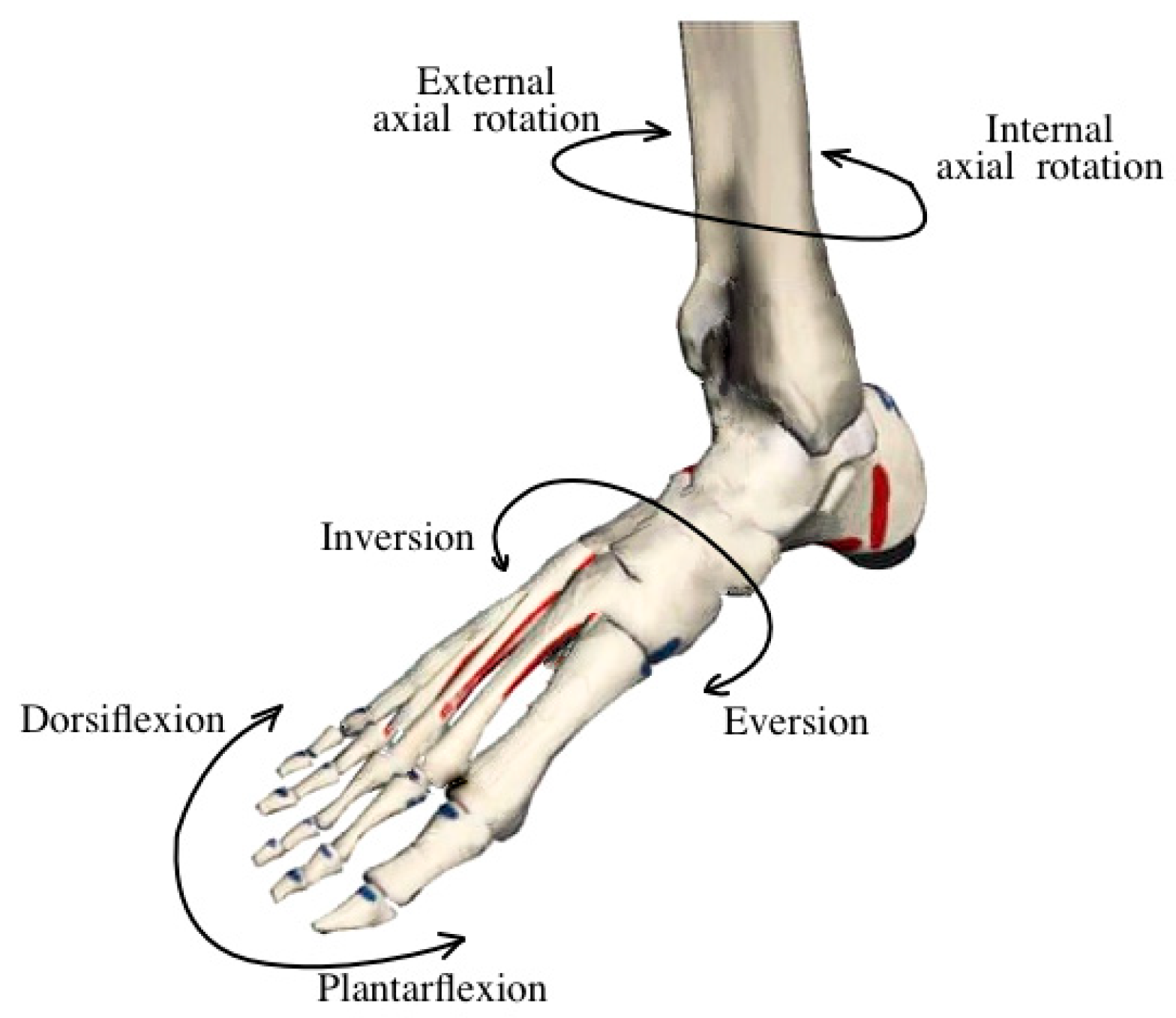
2.1. Biomechanical Requirements for Ankle–Foot Prosthesis
- –
- At heel strike, the joint absorbs impact forces and initiates plantarflexion. Dorsiflexion begins after the foot is flat and increases toward toe-off.
- –
- During mid-stance, it stabilizes the body over the supporting leg.
- –
- In the toe-off phase, it generates the necessary torque and energy to propel the body forward.
- –
- During the swing phase, it prepares the foot for the next step (Figure 2).
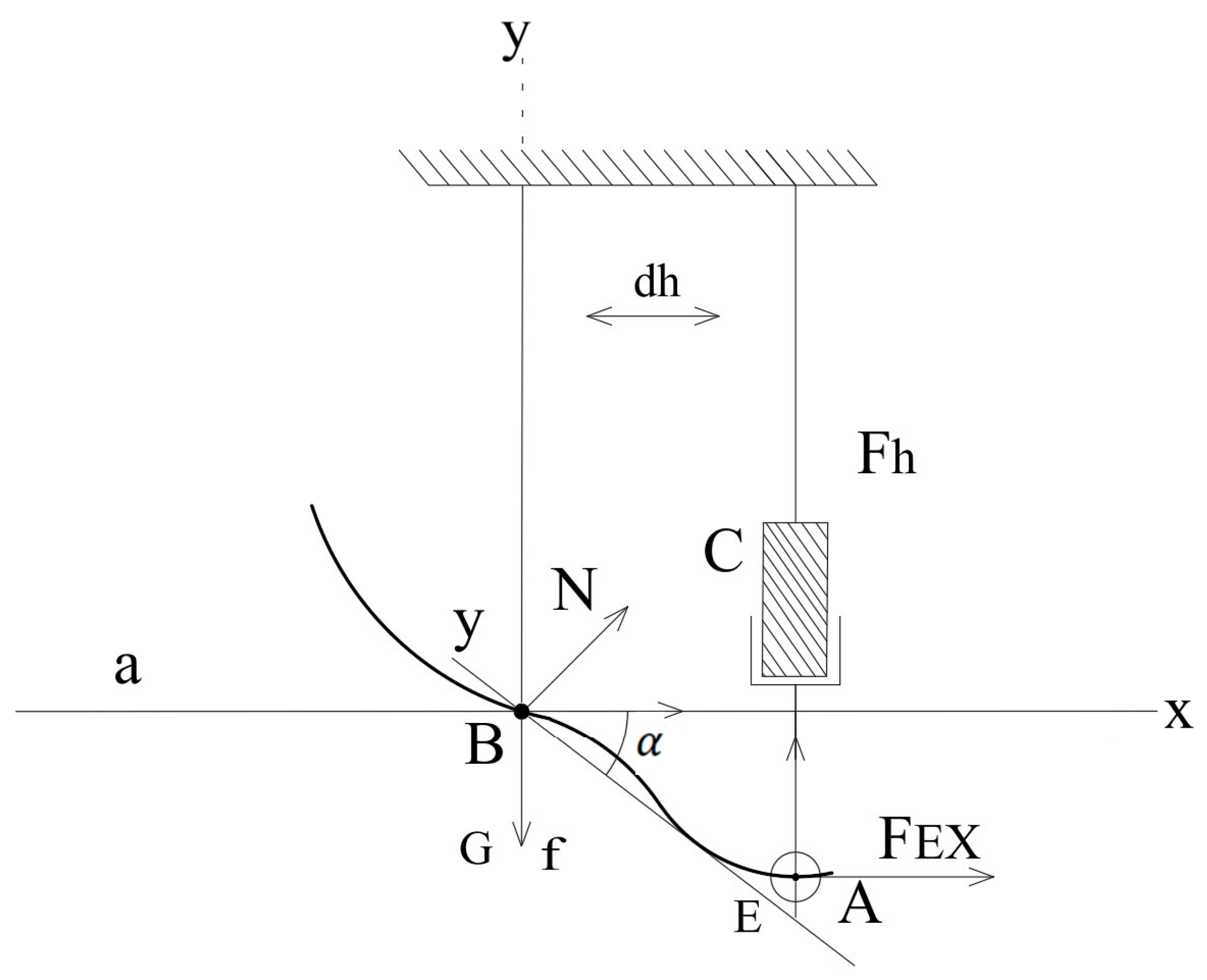
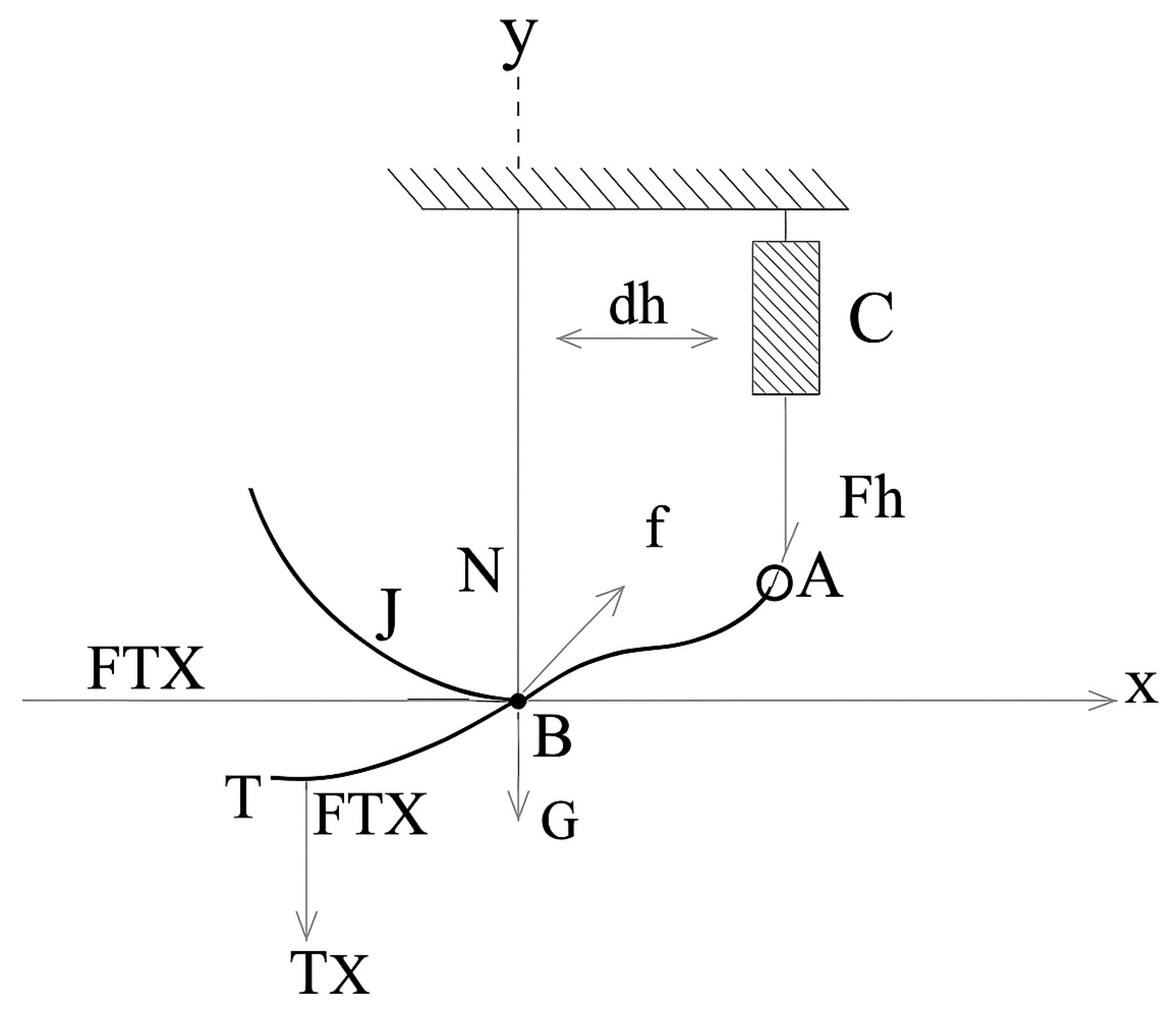
2.2. Kinematic Scheme
- (a)
- The transformation of coordinates during rotation;
- (b)
- The determination of the positions of key points a, b, and c;
- (c)
- The calculation of the relationship between angular displacement and force/torque.
- (a)
- Coordinate Transformation and Point Rotation
- (b)
- Geometric Configuration and Trajectory Parameters
- (c)
- Dynamic Equilibrium and Torque Analysis
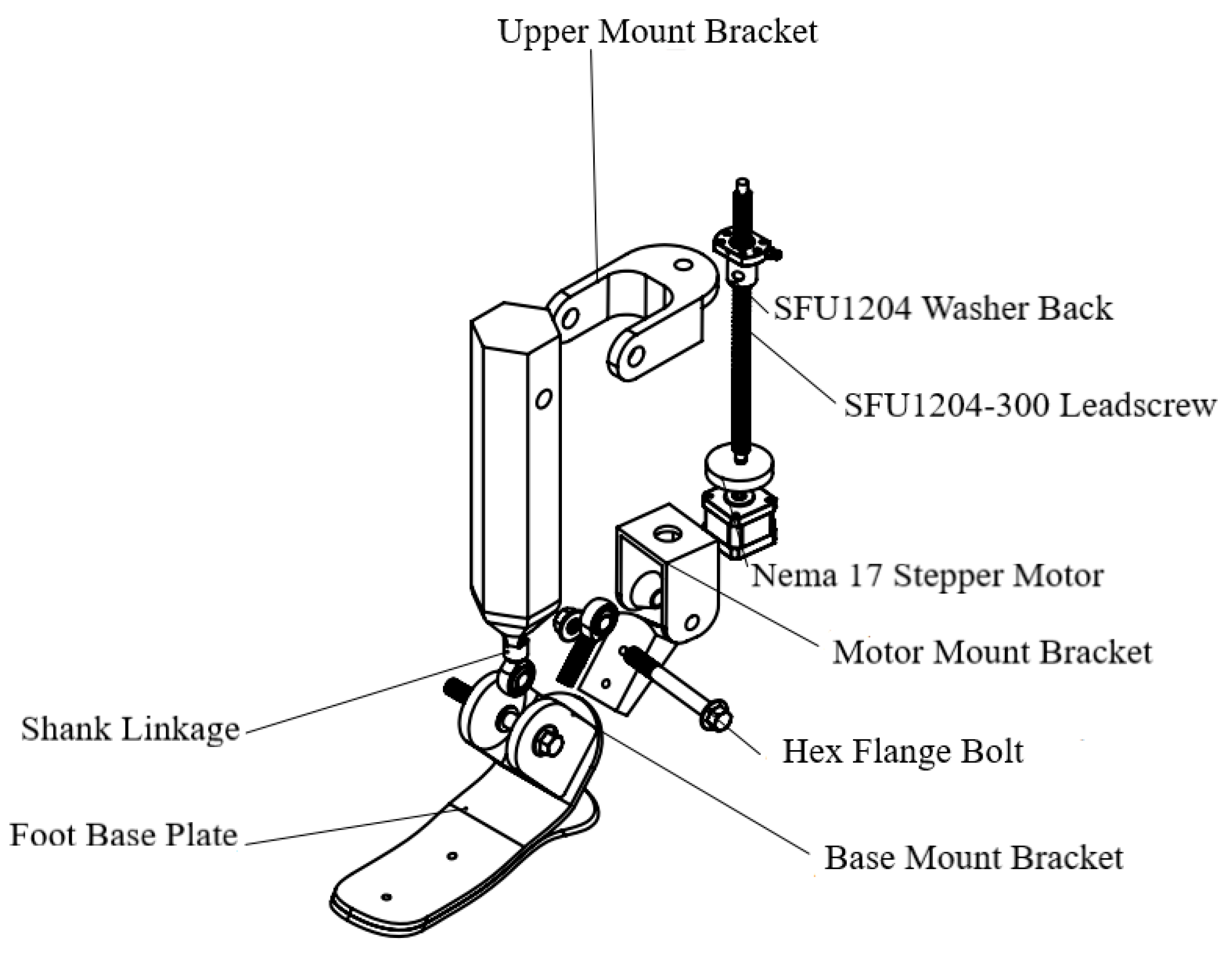
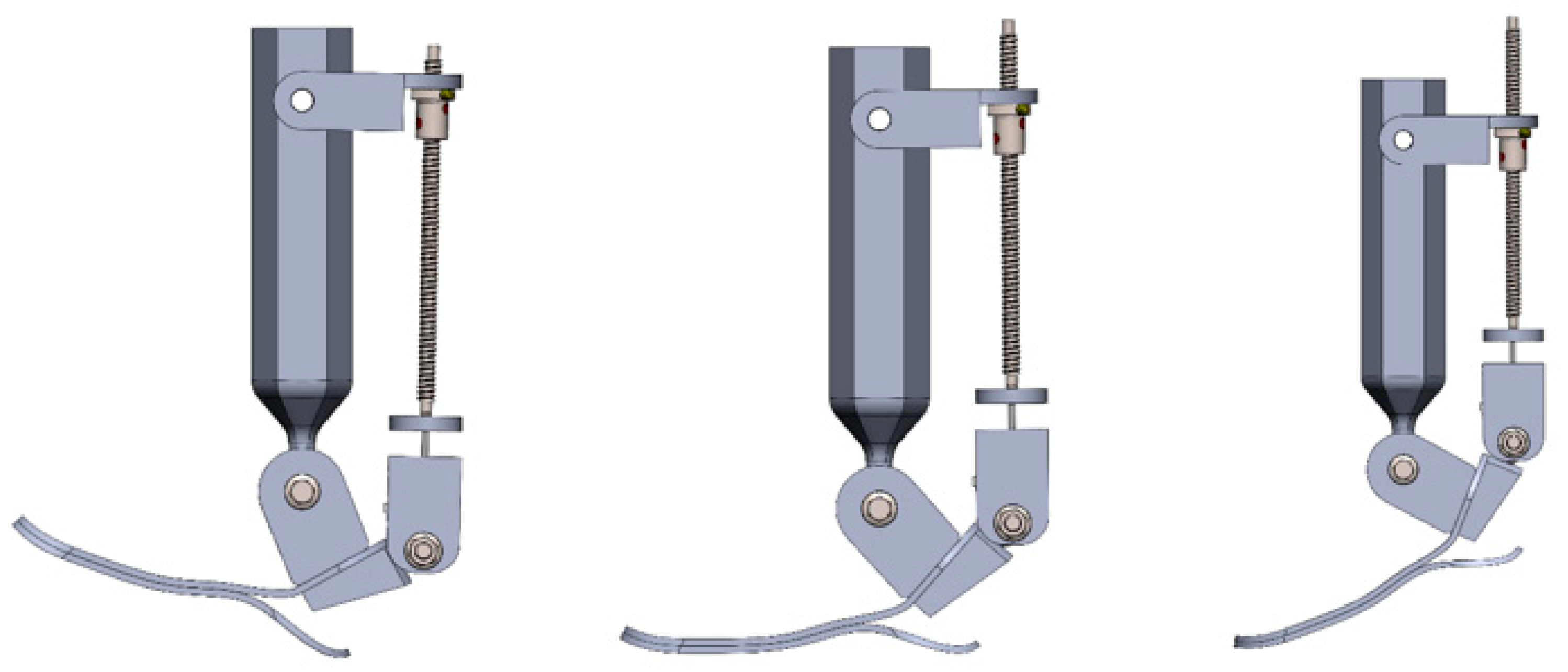
2.3. Design Using CAD Model
- –
- Foot base plate—the structural element of the foot platform that supports ground contact and connects to the lower actuator assembly.
- –
- Shank linkage—mechanical linkage that transmits motion from the actuator to the ankle joint.
- –
- Nema 17—stepper motor is responsible for generating the actuation motion.
- –
- SFU washer back/SFU1204-300—ball screw transmission that converts rotational motion into linear displacement.
- –
- Motor mount bracket, lead screw support bracket, and upper mount bracket—fastening components used to attach the drive mechanism (motor and screw) to the foot structure and the shank linkage.
- –
- Hex flange bolt—standard fasteners used to secure and stabilize movable mechanical parts.
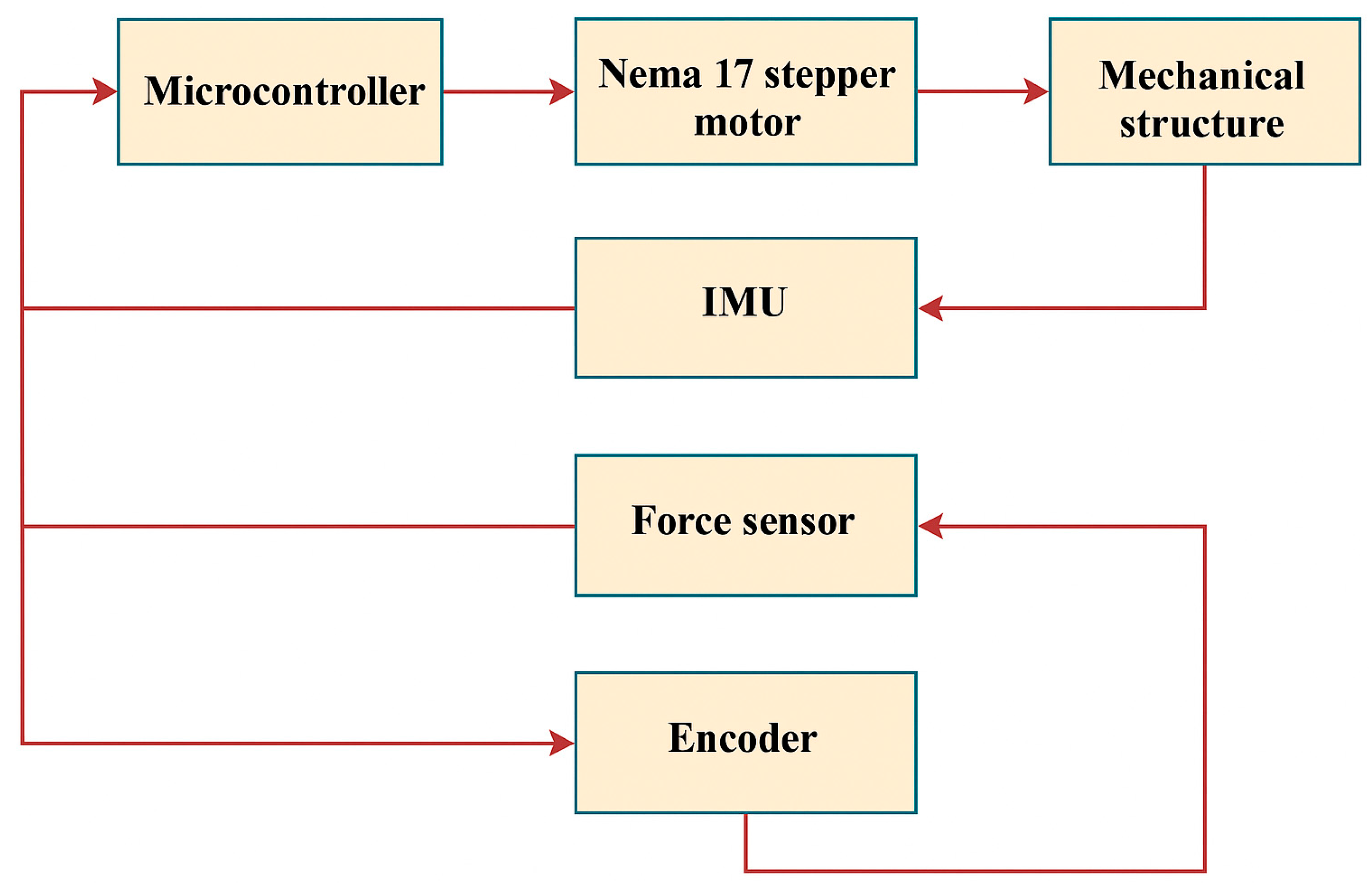
2.4. Mechanical Structure
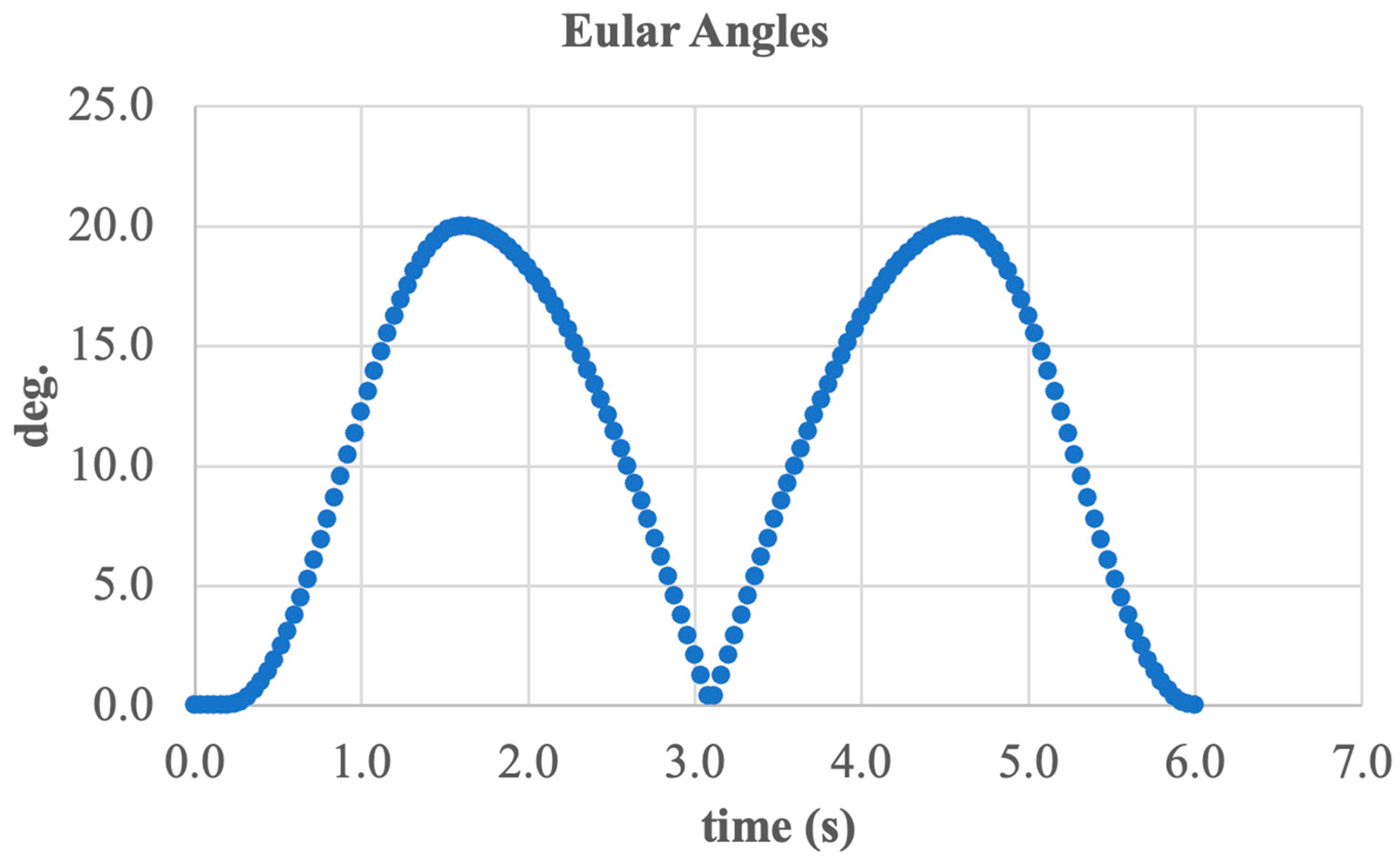
- –
- The required range of motion within physiological limits (±20–25 deg.).
- –
- Structural strength and frame rigidity underload.
- –
- Compact dimensions for ergonomic use.
- –
- Ease of assembly and modification.
3. Results
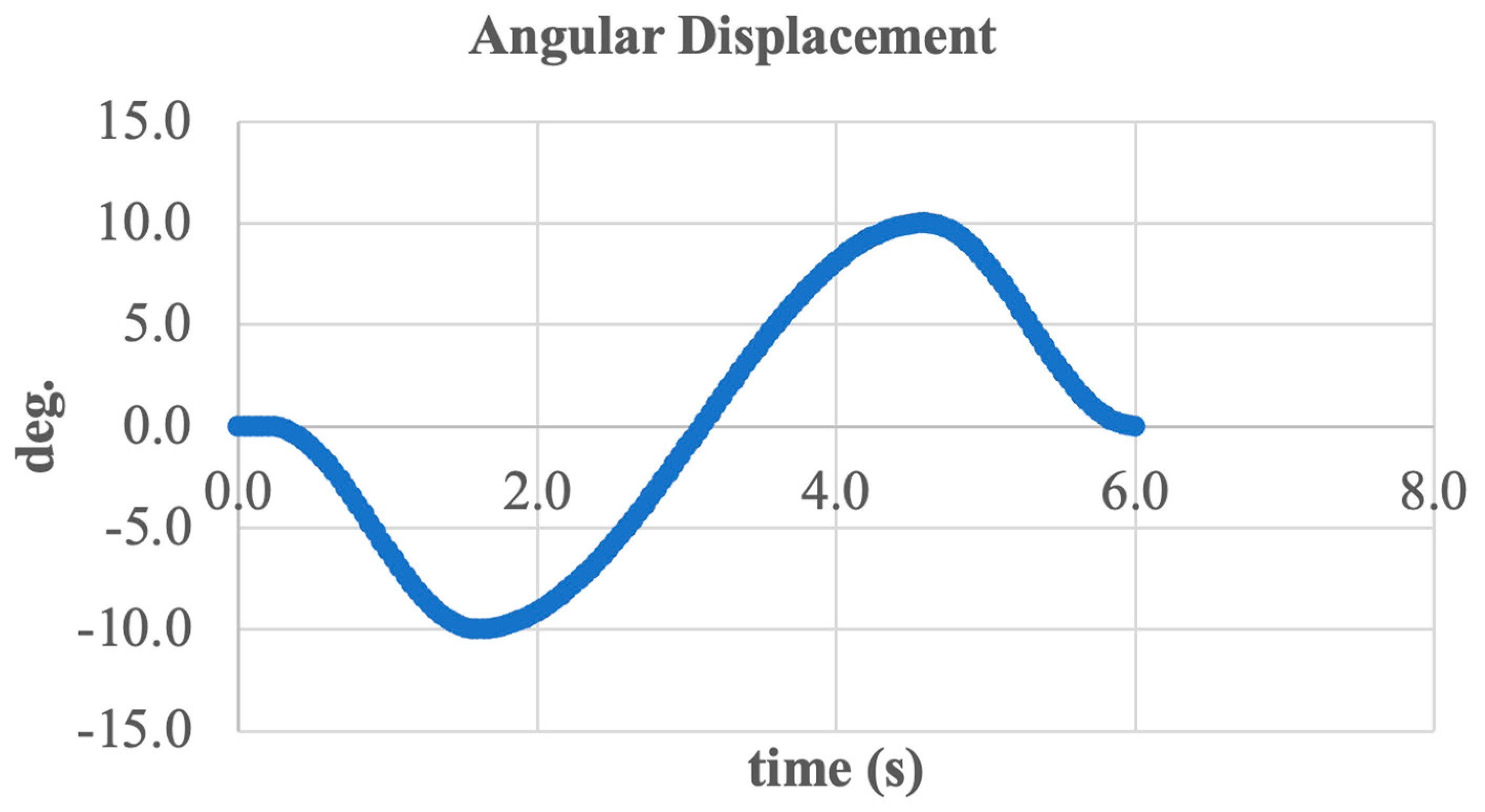
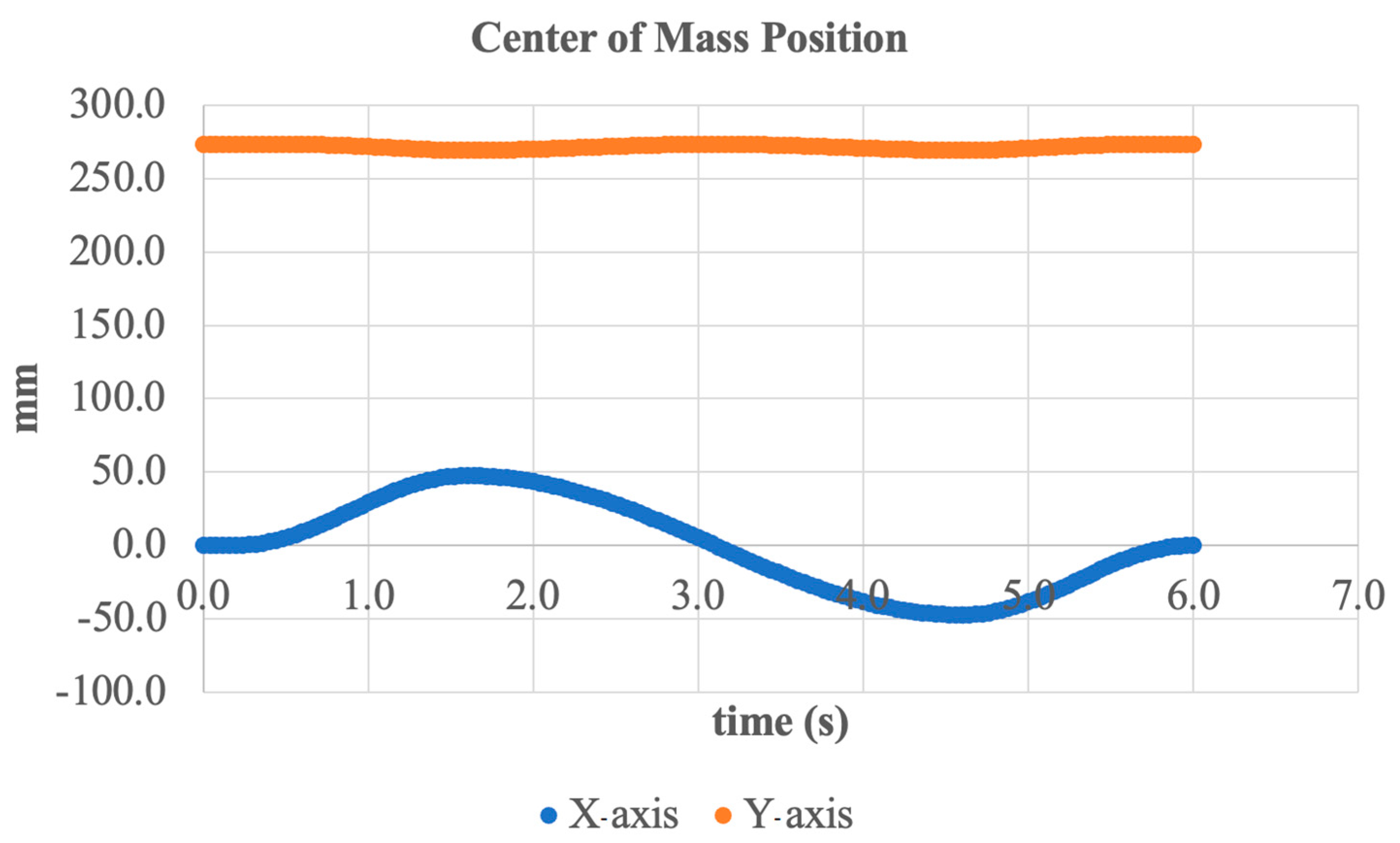
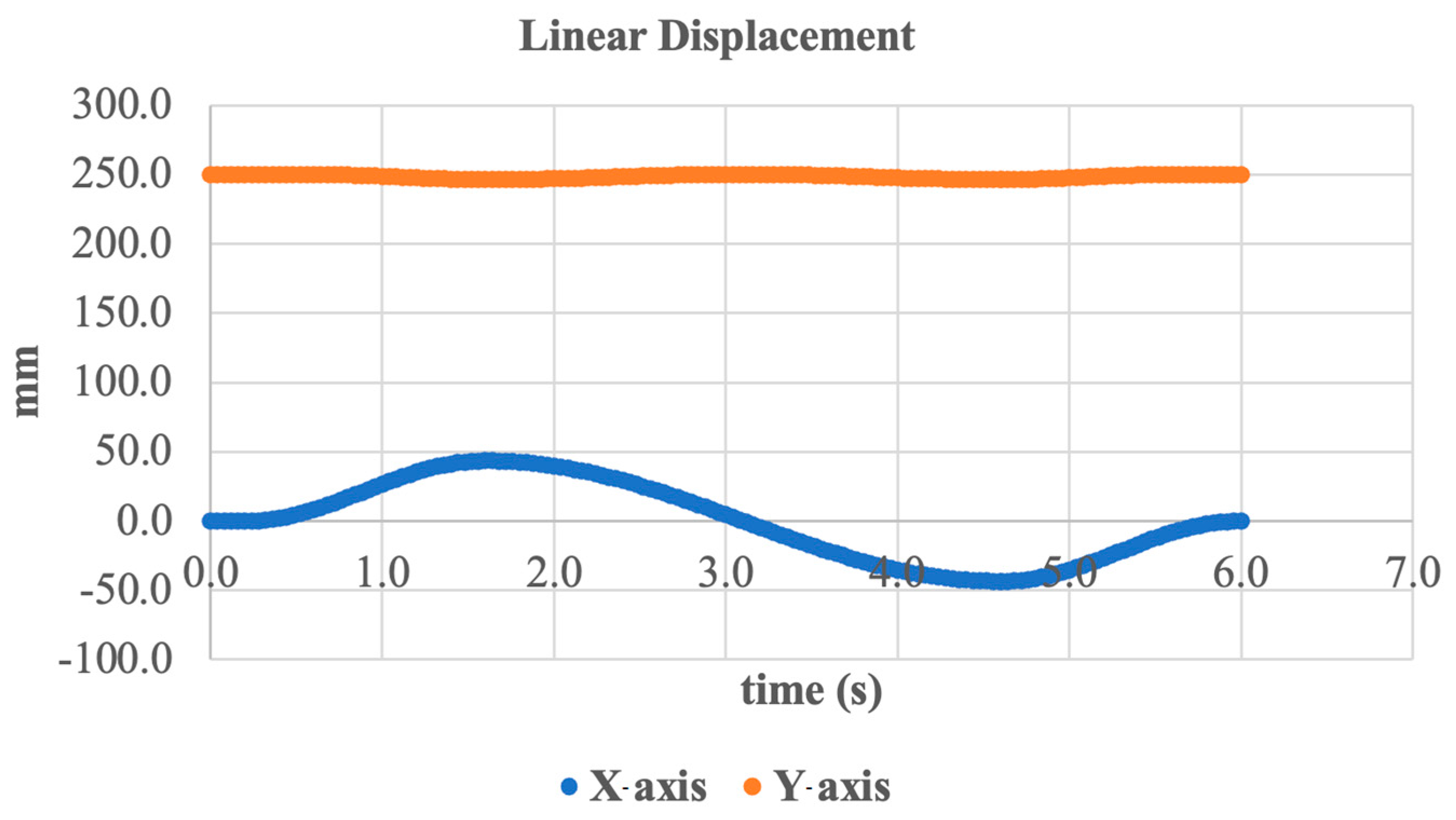
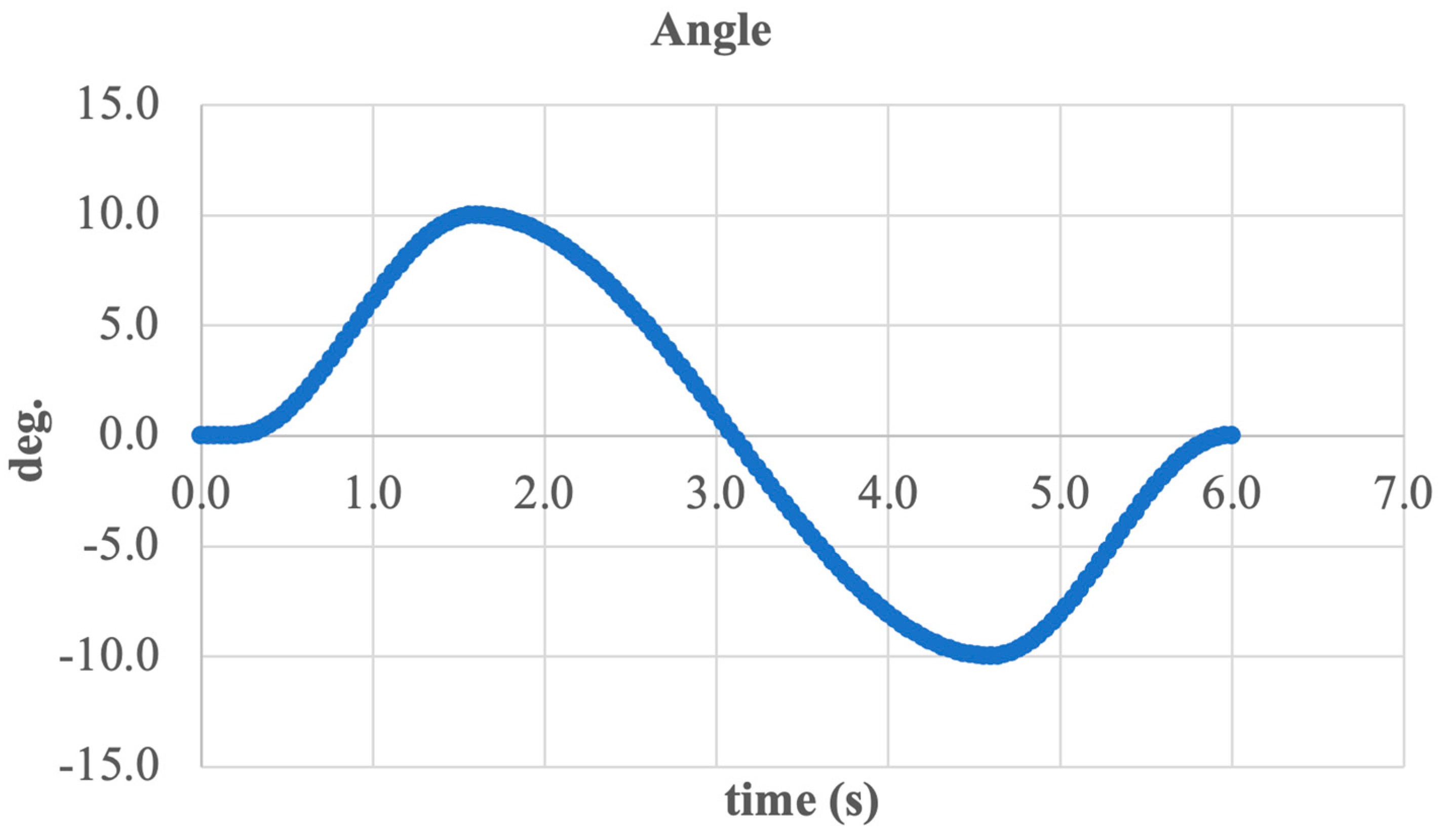
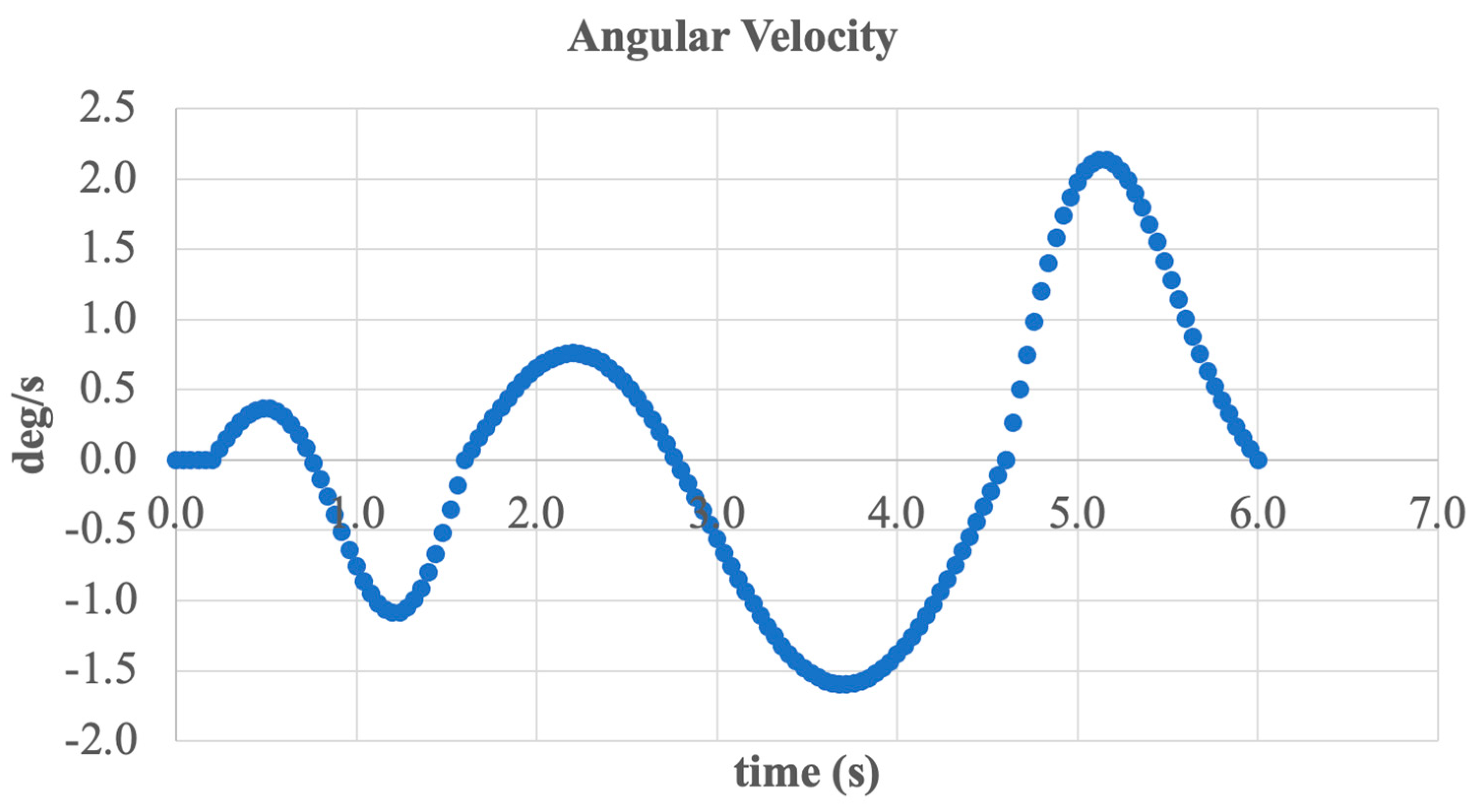
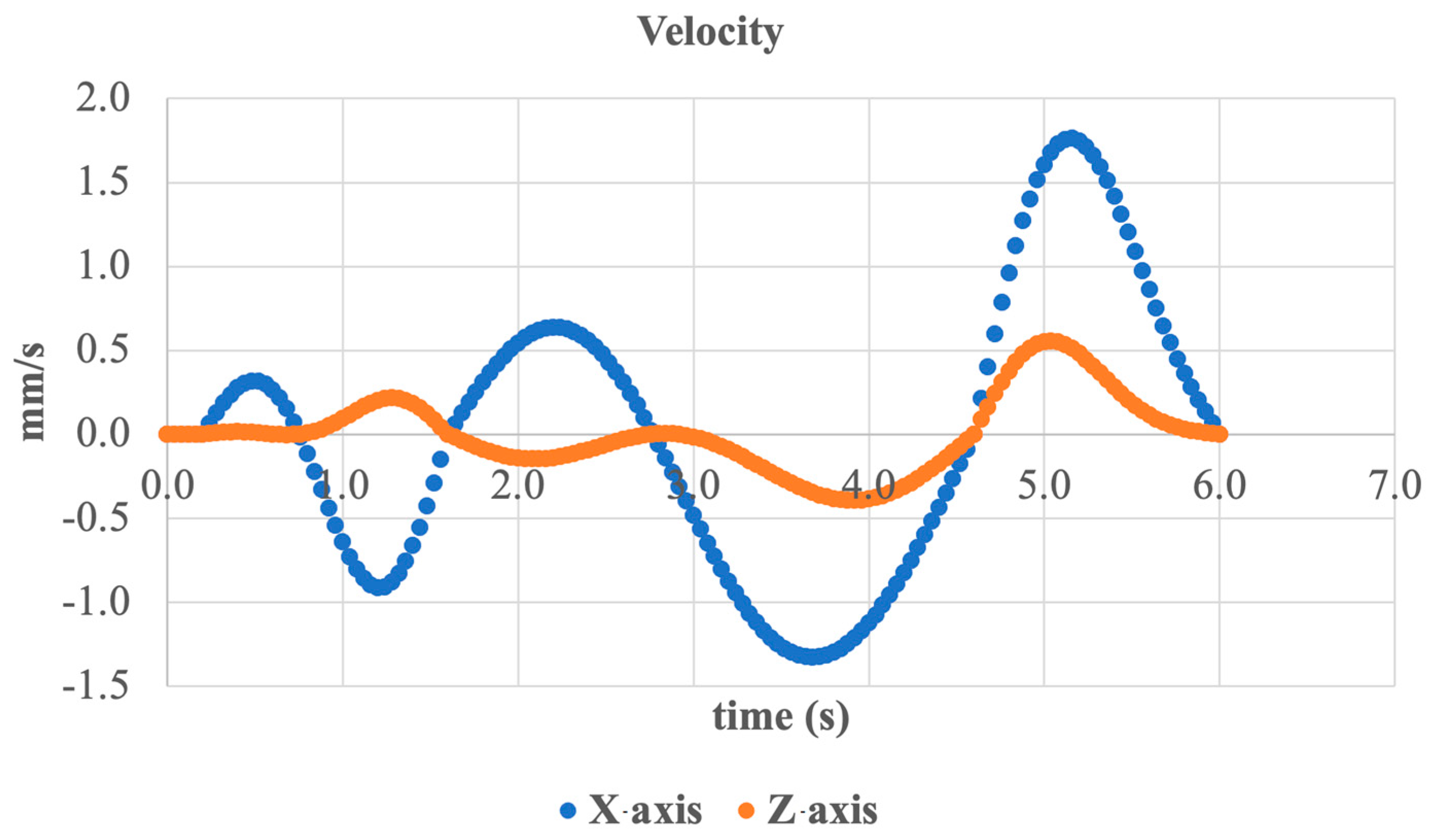
3.1. Simulation—Inversion/Eversion Movement
3.2. Simulation—Dorsiflexion and Plantarflexion Movement
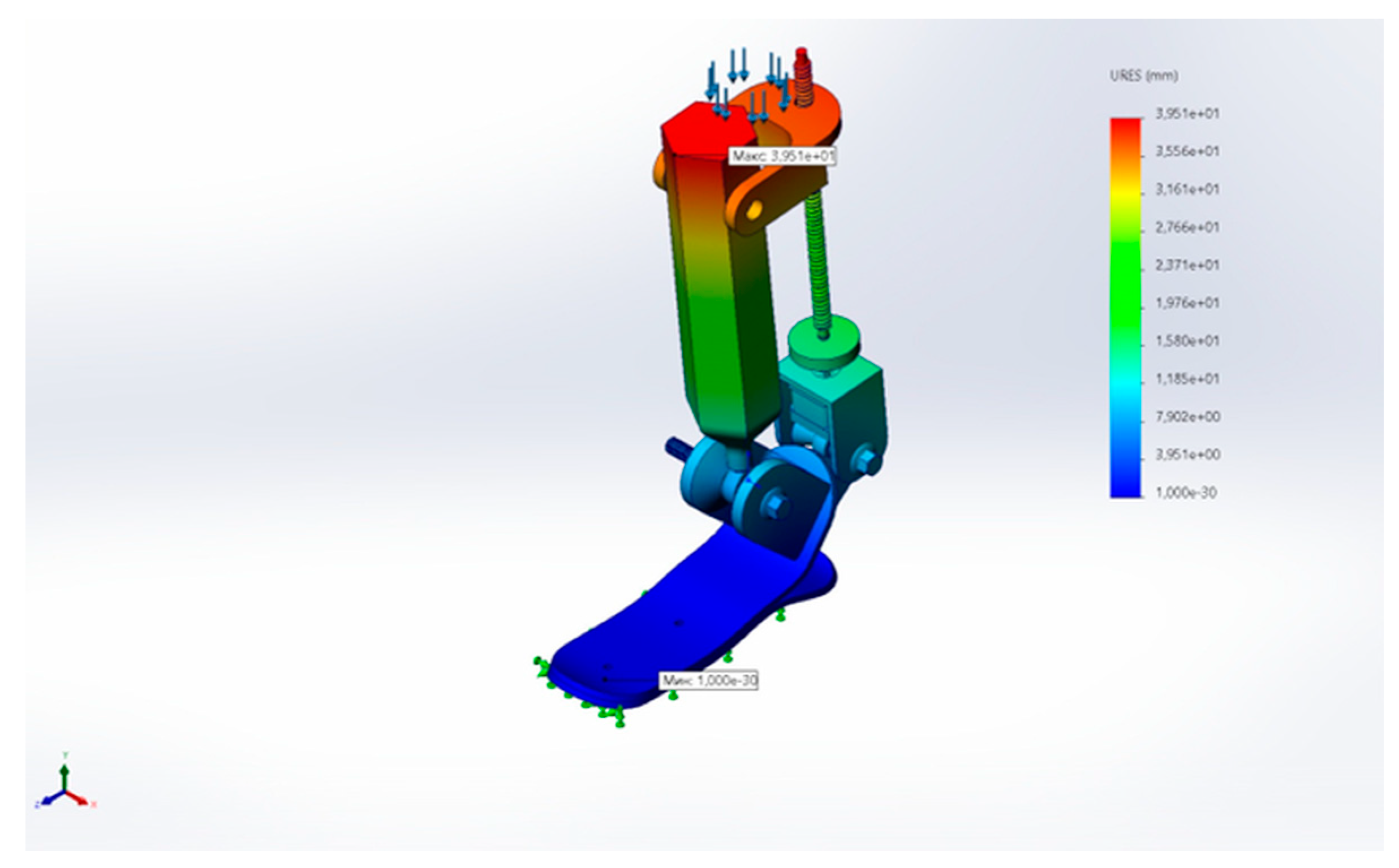
3.3. FEA
- –
- Yield strength—2.07 × 108 N/m2.
- –
- Tensile strength—5.17 × 108 N/m2.
- –
- Young’s modulus—1.9 × 1011 N/m2.
- –
- Shear modulus—7.5 × 1010 N/m2.
- –
- Poisson’s ratio—0.29.
- –
- Density—8000 kg/m3.
- –
- Thermal expansion coefficient—1.8 × 10−5 1/K.
- FEA Results Summary
- –
- Maximum von Mises stress: .
- –
- Maximum total displacement: .
- –
- Maximum equivalent strain: (dimensionless).
- –
- Safety factor:
- –
- The dynamic simulation of the full gait cycle (from heel strike to toe-off).
- –
- Fatigue strength assessment under cyclic loading.
- –
- A consideration of screw mechanism compliance and backlash in the actuator transmission model to improve simulation accuracy.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Herr, H.M.; Grabowski, A.M. Bionic Ankle-Foot Prosthesis Normalizes Walking Gait for Persons with Leg Amputation. Proc. R. Soc. 2012, 279, 457–464. [Google Scholar] [CrossRef] [PubMed]
- Montgomery, J.R.; Grabowski, A.M. Use of a powered ankle-foot prosthesis reduces the metabolic cost of uphill walking and improves leg work symmetry in people with transtibial amputations. J. R. Soc. Interface 2018, 15, 20180442. [Google Scholar] [CrossRef] [PubMed]
- Ottobock. Empower Ankle. Available online: https://www.ottobockus.com/prosthetics/lower-limb-prosthetics/solution-overview/empower-ankle/ (accessed on 15 February 2025).
- Össur. PROPRIO FOOT®. Available online: https://www.ossur.com/en-gb/prosthetics/feet/proprio-foot (accessed on 16 February 2025).
- Masum, H.; Bhaumik, S.; Ray, R. Conceptual Design of a Powered Ankle-foot Prosthesis for Walking with Inversion and Eversion, 2nd International Conference on Innovations in Automation and Mechatronics Engineering. Procedia Technol. 2014, 14, 228–235. [Google Scholar] [CrossRef]
- Tabucol, J.; Kooiman, V.G.M.; Leopaldi, M.; Brugo, T.M.; Leijendekkers, R.A.; Tagliabue, G.; Raveendranathan, V.; Sotgiu, E.; Benincasa, P.; Oddsson, M.; et al. The Functionality Verification through Pilot Human Subject Testing of MyFlex-δ: An ESR Foot Prosthesis with Spherical Ankle Joint. Appl. Sci. 2022, 12, 4575. [Google Scholar] [CrossRef]
- Au, S.K.; Weber, J.; Herr, H. Powered Ankle—Foot Prosthesis Improves Walking Metabolic Economy. IEEE Trans. Robot. 2009, 25, 51–66. [Google Scholar] [CrossRef]
- Bilal, M.; Rizwan, M.; Maqbool, H.F.; Ahsan, M.; Raza, A. Design optimization of powered ankle prosthesis to reduce peak power requirement. Sci. Prog. 2022, 105, 368504221117895. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Drăgoi, M.-V.; Hadăr, A.; Goga, N.; Baciu, F.; Ștefan, A.; Grigore, L.Ș.; Gorgoteanu, D.; Molder, C.; Oncioiu, I. Contributions to the Dynamic Regime Behavior of a Bionic Leg Prosthesis. Biomimetics 2023, 8, 414. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, T.-H.; Song, H.; Shu, T.; Qiao, J.; Yeon, S.H.; Carney, M.; Mooney, L.; Duval, J.-F.; Herr, H. Design, Characterization, and Preliminary Assessment of a Two-Degree-of-Freedom Powered Ankle–Foot Prosthesis. Biomimetics 2024, 9, 76. [Google Scholar] [CrossRef] [PubMed]
- Dong, D.; Ge, W.; Liu, S.; Xia, F.; Sun, Y. Design and optimization of a powered ankle-foot prosthesis using a geared five-bar spring mechanism. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417704545. [Google Scholar] [CrossRef]
- Barooji, H.R.; Ohadi, A.; Towhidkhah, F. Design and analysis of active transtibial prosthesis function using 7-link inverse dynamic model of gait. Robotica 2023, 41, 2337–2364. [Google Scholar] [CrossRef]
- Eilenberg, M.F.; Geyer, H.; Herr, H. Control of a powered ankle-foot prosthesis based on a neuromuscular model. IEEE Trans. Neural Syst. Rehabil. Eng. 2010, 18, 164–173. [Google Scholar] [CrossRef] [PubMed]
- Ficanha, E.M.; Ribeiro, G.A.; Dallali, H.; Rastgaar, M. Design and Preliminary Evaluation of a Two DOFs Cable-Driven Ankle–Foot Prosthesis with Active Dorsiflexion–Plantarflexion and Inversion–Eversion. Front. Bioeng. Biotechnol. 2016, 4, 36. [Google Scholar] [CrossRef] [PubMed]
- Kennedy LaPrè, A.; Umberger, B.R.; Sup, F.C., IV. A Robotic Ankle–Foot Prosthesis with Active Alignment. ASME. J. Med. Devices 2016, 10, 025001. [Google Scholar] [CrossRef]
- Jin, J.; Wang, K.; Ren, L.; Qian, Z.; Liang, W.; Xu, X.; Zhao, S.; Lu, X.; Zhao, D.; Wang, X. Design of a Flexible Bionic Ankle Prosthesis Based on Subject-specific Modeling of the Human Musculoskeletal System. J. Bionic Eng. 2023, 20, 1008–1020. [Google Scholar] [CrossRef]
- Bader, Y.; Langlois, D.; Baddour, N.; Lemaire, E.D. Development of an Integrated Powered Hip and Microprocessor-Controlled Knee for a Hip–Knee–Ankle–Foot Prosthesis. Bioengineering 2023, 10, 614. [Google Scholar] [CrossRef] [PubMed]
- Muñoz-Vásquez, S.; Mora-Pérez, Z.A.; Ospina-Henao, P.A.; Valencia-Niño, C.H.; Becker, M.; Díaz-Rodríguez, J.G. Finite Element Analysis in the Balancing Phase for an Open Source Transfemoral Prosthesis with Magneto-Rheological Damper. Inventions 2023, 8, 36. [Google Scholar] [CrossRef]
- Carney, M.E.; Shu, T.; Stolyarov, R.; Duval, J.-F.; Herr, H.M. Design and Preliminary Results of a Reaction Force Series Elastic Actuator for Bionic Knee and Ankle Prostheses. IEEE Trans. Med. Robot. Bionics 2021, 3, 542–553. [Google Scholar] [CrossRef]
- Brockett, C.L.; Chapman, G.J. Biomechanics of the ankle. Orthop. Trauma 2016, 30, 232–238. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Pirker, W.; Katzenschlager, R. Gait disorders in adults and the elderly: A clinical guide. Wien. Klin. Wochenschr. 2017, 129, 81–95. [Google Scholar] [CrossRef] [PubMed]
- Sergazin, G.; Ozhiken, A.; Zhetenbayev, N.; Ozhikenov, K.; Tursunbayeva, G.; Nurgizat, Y.; Uzbekbayev, A.; Ayazbay, A.-A. Development of an Ankle Exoskeleton: Design, Modeling, and Testing. Sensors 2025, 25, 2020. [Google Scholar] [CrossRef] [PubMed]

















| Study | DoF | Mass [kg] | Torque [Nm] | ROM [deg] | Power Draw [W] |
|---|---|---|---|---|---|
| [5] | 2 | N/A | N/A | ±15 | High (external) |
| [6] | 1 | N/A | N/A | ±10 | Passive |
| [7] | 1 | 1.93 | 130 | ±20 | Battery |
| [8] | 1 | 2.2 | 120 | ±25 | Low |
| [9] | 2 | Light | N/A | ±18 | Low |
| [10] | 2 | 3.1 | 90 | ±18 | Moderate |
| [11] | 1 | N/A | N/A | ±16 | Moderate |
| [12] | 1 | N/A | N/A | ±17 | High |
| [13] | 1 | N/A | N/A | ±15 | Moderate |
| [14] | 2 | 3.7 | 100 | ±22 | Low |
| [15] | 1 | N/A | N/A | ±12 | Compressed Air |
| [16] | 1 | 1.9 | N/A | ±10 | None |
| [17] | 4 | N/A | N/A | ±30 | High |
| [18] | 1 | 3.2 | N/A | ±14 | High |
| [19] | 2 | 3.4 | 80 | ±20 | High |
| Parameter | Biological Joint | Prosthesis Requirements |
|---|---|---|
| Dorsiflexion | ~20° | ≥20°, with adaptive modulation |
| Plantarflexion | 25–30° | ≥25–30°, with controlled dynamics |
| Inversion / Eversion | ±10–15° | ±10–15°, with lateral shift compensation |
| Torque | 100–150 N/m | ≥120 N/m, with adaptive regulation |
| Mechanical Work | Up to 0.2 J/kg per step | Comparable level with high energy efficiency |
| Stability | Surface adaptation | Dynamic stabilization with feedback |
| Shock Absorption | Impact attenuation | Active and passive damping |
| Gait Synchronization | Automatic | Intelligent, with phase prediction |
| Response to External Forces | Immediate adaptation | Adaptive control with predictive capabilities |
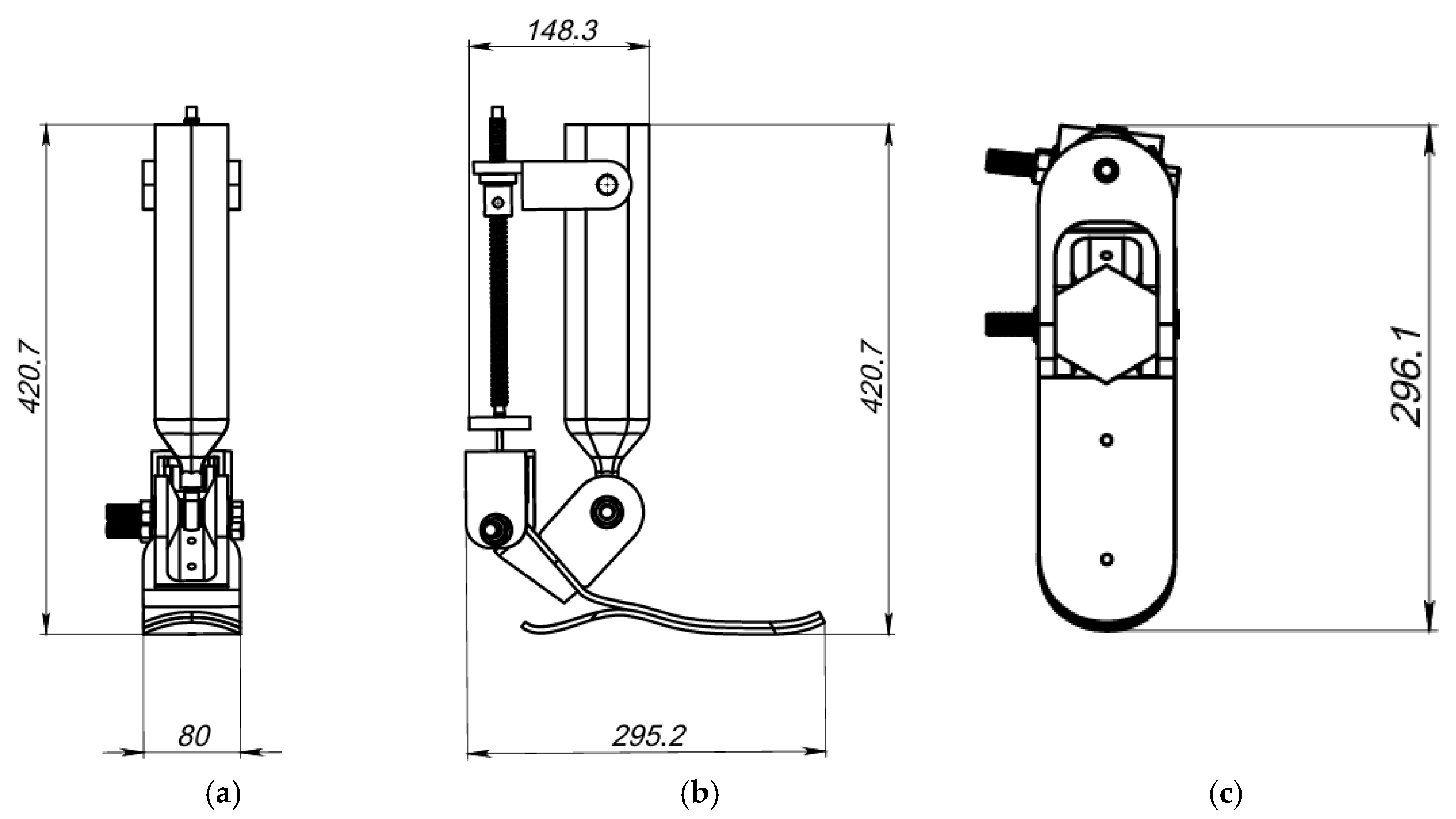
| Parameter | Value (mm) |
|---|---|
| Total height | 420.7 |
| Foot length | 295.2 |
| Foot width | 80 |
| Platform height to foot | 296.1 |
| Upper mounting length | 148.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akhmejanov, S.; Zhetenbayev, N.; Sultan, A.; Zhauyt, A.; Nurgizat, Y.; Ozhikenov, K.; Ayazbay, A.-A.; Uzbekbayev, A. Design and Analysis of an Autonomous Active Ankle–Foot Prosthesis with 2-DoF. Sensors 2025, 25, 4881. https://doi.org/10.3390/s25164881
Akhmejanov S, Zhetenbayev N, Sultan A, Zhauyt A, Nurgizat Y, Ozhikenov K, Ayazbay A-A, Uzbekbayev A. Design and Analysis of an Autonomous Active Ankle–Foot Prosthesis with 2-DoF. Sensors. 2025; 25(16):4881. https://doi.org/10.3390/s25164881
Chicago/Turabian StyleAkhmejanov, Sayat, Nursultan Zhetenbayev, Aidos Sultan, Algazy Zhauyt, Yerkebulan Nurgizat, Kassymbek Ozhikenov, Abu-Alim Ayazbay, and Arman Uzbekbayev. 2025. "Design and Analysis of an Autonomous Active Ankle–Foot Prosthesis with 2-DoF" Sensors 25, no. 16: 4881. https://doi.org/10.3390/s25164881
APA StyleAkhmejanov, S., Zhetenbayev, N., Sultan, A., Zhauyt, A., Nurgizat, Y., Ozhikenov, K., Ayazbay, A.-A., & Uzbekbayev, A. (2025). Design and Analysis of an Autonomous Active Ankle–Foot Prosthesis with 2-DoF. Sensors, 25(16), 4881. https://doi.org/10.3390/s25164881









