Uncertainty Evaluation of Two-Dimensional Horizontal Distributed Photometric Sensor Based on MCM for Illuminance Measurement Task
Abstract
1. Introduction
2. Working Principle and System Composition
2.1. Working Principle
2.2. System Composition
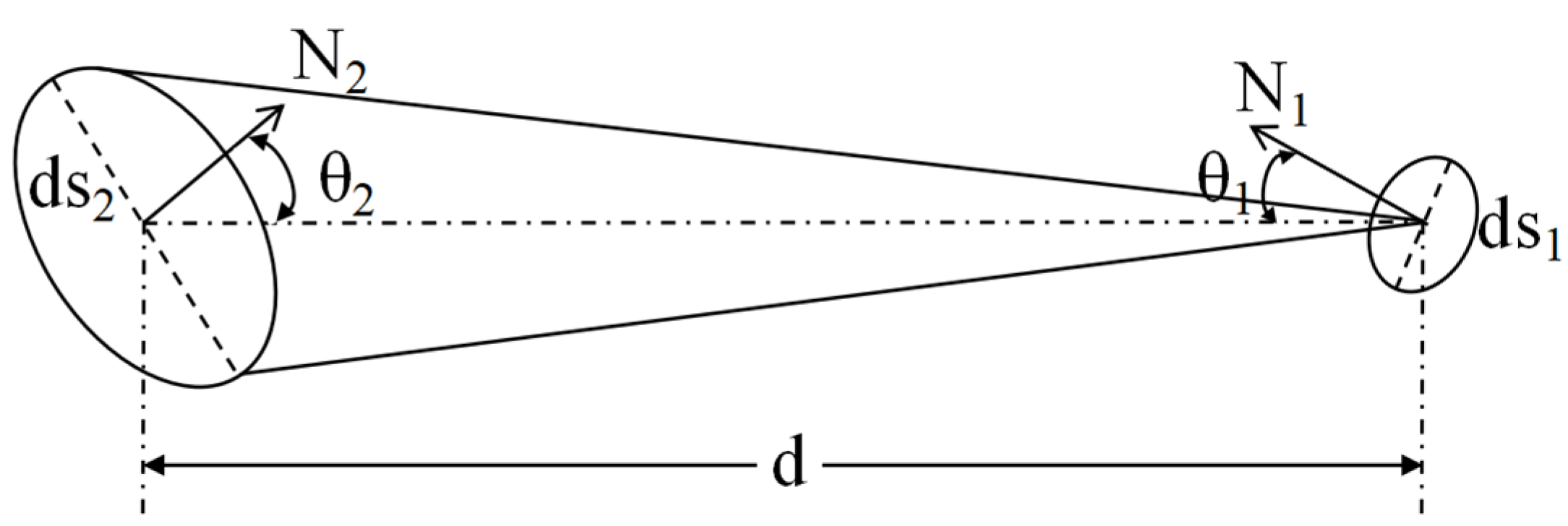
2.3. Deduction of Integral Formula for Illumination of Surface Light Source
3. Uncertainty Evaluation Method
3.1. GUM Method
3.2. MCM Method
3.3. Uncertainty Analysis
4. Experimental Analysis
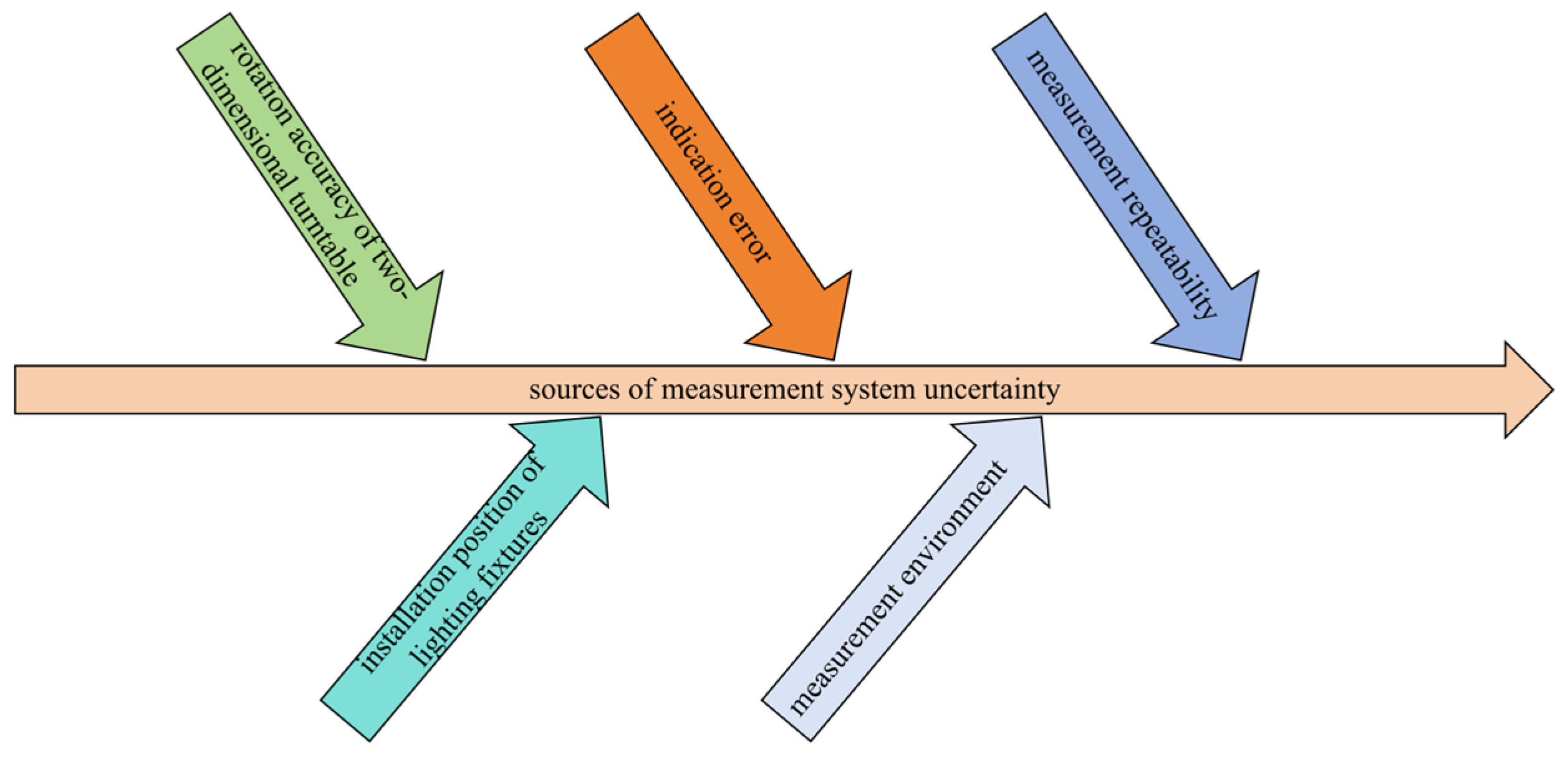
4.1. Uncertainty Evaluation of Measurement System
4.1.1. Installation Position of Lighting Fixtures
4.1.2. Rotation Accuracy of Two-Dimensional Turntable
4.1.3. Measurement Repeatability
4.1.4. Uncertainty Introduced by the Inaccurate Indication
4.1.5. Uncertainty Introduced by Measurement Environment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GUM | Guide to the Expression of Uncertainty in Measurement |
| MCM | Monte Carlo Method |
References
- Tanane, B.; Bentaha, L.M.; Dafflon, B.; Moalla, N. Bridging the gap between Industry 4.0 and manufacturing SMEs: A framework for an end-to-end Total Manufacturing Quality 4.0’s implementation and adoption. J. Ind. Inf. Integr. 2025, 45, 100833. [Google Scholar] [CrossRef]
- International Organization for Standardization. ISO 9001: 2015, Quality Management Systems: Requirements; ISO: Switzerland, Geneva, 2015. [Google Scholar]
- Wang, Z.; Zhang, D.; Li, J.; Zhang, W. An Intelligent Controller of LED Street Light Based on Discrete Devices. Energies, 2024; in press. [Google Scholar]
- Gao, W.; Zeng, X.; Yang, H.; Chen, F.; Pan, A.; Fang, Y.; Wang, Y.; Li, H.; Ren, Z.; Zhang, G.; et al. Green manufacturing evaluation of light-emitting diodes lamps production: Resource and environmental assessment. Renew. Sustain. Energy Rev. 2025, 211, 115317. [Google Scholar] [CrossRef]
- Li, L.; Wang, J.; Yang, S.; Gong, H. Binocular stereo vision based illuminance measurement used for intelligent lighting with LED. Optik 2021, 237, 166651. [Google Scholar] [CrossRef]
- Xu, S.; Zou, N.; He, Q.; He, X.; Li, K.; Cheng, M.; Liu, K. Design and Application Research of a UAV-Based Road Illuminance Measurement System. Automation 2024, 5, 407–431. [Google Scholar] [CrossRef]
- Medina, C.; Avrenli, A.; Benekohal, F. Field and Software Evaluation of Illuminance from LED Luminaires for Roadway Applications. Transp. Res. Rec. 2013, 2384, 55–64. [Google Scholar] [CrossRef]
- Mahlab, F.; Yamaguchi, H.; Shimozima, Y.; Yoshizawa, N.; Cai, H. A joint validation study on camera-aided illuminance measurement. Light. Res. Technol. 2023, 55, 571–593. [Google Scholar] [CrossRef]
- Omar, G.; Andres, S.; David, G.; Manuel, G.; Diego, G. A Low-Cost Luxometer Benchmark for Solar Illuminance Measurement System Based on the Internet of Things. Sensors 2022, 22, 7107. [Google Scholar] [CrossRef]
- Zhang, L.; Gao, Y.; Zhang, Z.; Zou, N. A lightweight distributed measurement method used to study illuminance estimation. Optik 2020, 223, 165590. [Google Scholar] [CrossRef]
- Gao, Y.; Cheng, Y.; Zhang, H.; Zou, N. Dynamic illuminance measurement and control used for smart lighting with LED. Measurement 2019, 139, 380–386. [Google Scholar] [CrossRef]
- Wang, X.; Huang, L.; Li, M.; Han, C.; Liu, X.; Nie, T. Fast, Zero-Reference Low-Light Image Enhancement with Camera Response Model. Sensors 2024, 24, 5019. [Google Scholar] [CrossRef]
- Miguel, J.; Steendam, H. On the Optimisation of Illumination LEDs for VLP Systems. Photonics 2022, 9, 750. [Google Scholar] [CrossRef]
- Yan, S.; Sun, M.; Chen, W.; Li, L. Illumination Calibration for Computational Ghost Imaging. Photonics 2021, 8, 59. [Google Scholar] [CrossRef]
- Yoo, Y.; Im, J.; Paik, J. Low-Light Image Enhancement Using Adaptive Digital Pixel Binning. Sensors 2015, 15, 14917–14931. [Google Scholar] [CrossRef]
- Petzi, M.; Liemert, A.; Ott, F.; Reitzle, D.; Kienle, A. Radiance and fluence in a scattering disc under Lambertian illumination. J. Quant. Spectrosc. Radiat. Transf. 2023, 310, 108728. [Google Scholar] [CrossRef]
- Efremova, N. Use of the Concept of Measurement Uncertainty in Applied Problems of Metrology. Meas. Tech. 2018, 61, 335–341. [Google Scholar] [CrossRef]
- International Organization for Standardization/International Electrotechnical Commission. ISO/IEC GUIDE 98-3: 2008, Uncertainty of Measurement-Part 3: Guide to the Expression of Uncertainty in Measurement; ISO/CASCO: Switzerland, Geneva, 2008. [Google Scholar]
- Zhao, Y.; Zhang, F.; Ai, Y.; Tian, J.; Wang, Z. Comparison of Guide to Expression of Uncertainty in Measurement and Monte Carlo Method for Evaluating Gauge Factor Calibration Test Uncertainty of High-Temperature Wire Strain Gauge. Sensors 2025, 25, 1633. [Google Scholar] [CrossRef]
- Jamroz, F.; Williams, F. Consistency in Monte Carlo uncertainty analyses. Metrologia 2020, 57, 65008. [Google Scholar] [CrossRef]
- Zhang, K.; Su, K.; Yao, Y.; Li, Q.; Chen, S. Dynamic evaluation and analysis of the uncertainty of roundness error measurement by Markov Chain Monte Carlo method. Measurement 2022, 201, 111771. [Google Scholar] [CrossRef]
- Harris, P.; Cox, M. On a Monte Carlo method for measurement uncertainty evaluation and its implementation. Metrologia 2014, 51, S176–S182. [Google Scholar] [CrossRef]
- Li, Y.; Lin, M.; Xu, L.; Luo, R.; Zhang, Y.; Ni, Q.; Liu, Y. Monte Carlo method for evaluation of surface emission rate measurement uncertainty. Nucl. Sci. Tech. 2024, 35, 118. [Google Scholar] [CrossRef]
- ISO/IEC 17025: 2017; Accreditation Criteria for the Competence of Testing and Calibration Laboratories. ISO/CASCO (International Organization for Standardization/International Electrotechnical Commission): Switzerland, Geneva, 2017.




| Sequence | Brightness Level | ||
|---|---|---|---|
| Level 1 | Level 50 | Level 99 | |
| 1 | 0.651 | 132.28 | 243.32 |
| 2 | 0.633 | 132.29 | 243.43 |
| 3 | 0.632 | 132.35 | 243.27 |
| 4 | 0.659 | 132.26 | 243.49 |
| 5 | 0.622 | 132.34 | 243.38 |
| 6 | 0.643 | 132.37 | 243.26 |
| 7 | 0.639 | 132.26 | 243.35 |
| 8 | 0.652 | 132.29 | 243.40 |
| 9 | 0.623 | 132.38 | 243.29 |
| 10 | 0.629 | 132.24 | 243.47 |
| average value | 0.638 | 132.306 | 243.366 |
| standard deviation | 0.0127 | 0.050 | 0.082 |
| Brightness Level | Expanded Uncertainty | ||
|---|---|---|---|
| level 1 | 0.638 | 0.000100 | 0.00020 |
| level 50 | 132.306 | 0.030 | 0.061 |
| level 99 | 243.366 | 0.056 | 0.112 |
| Uncertainty Component | Source | Expectation | Standard Deviation | Distribution |
|---|---|---|---|---|
| 0 | 0.056 | uniform distribution | ||
| 0 | 0.00080 | uniform distribution | ||
| 0 | 0.026 | normal distribution | ||
| 0 | 1.15 | uniform distribution | ||
| 0 | 0.0157 | uniform distribution |
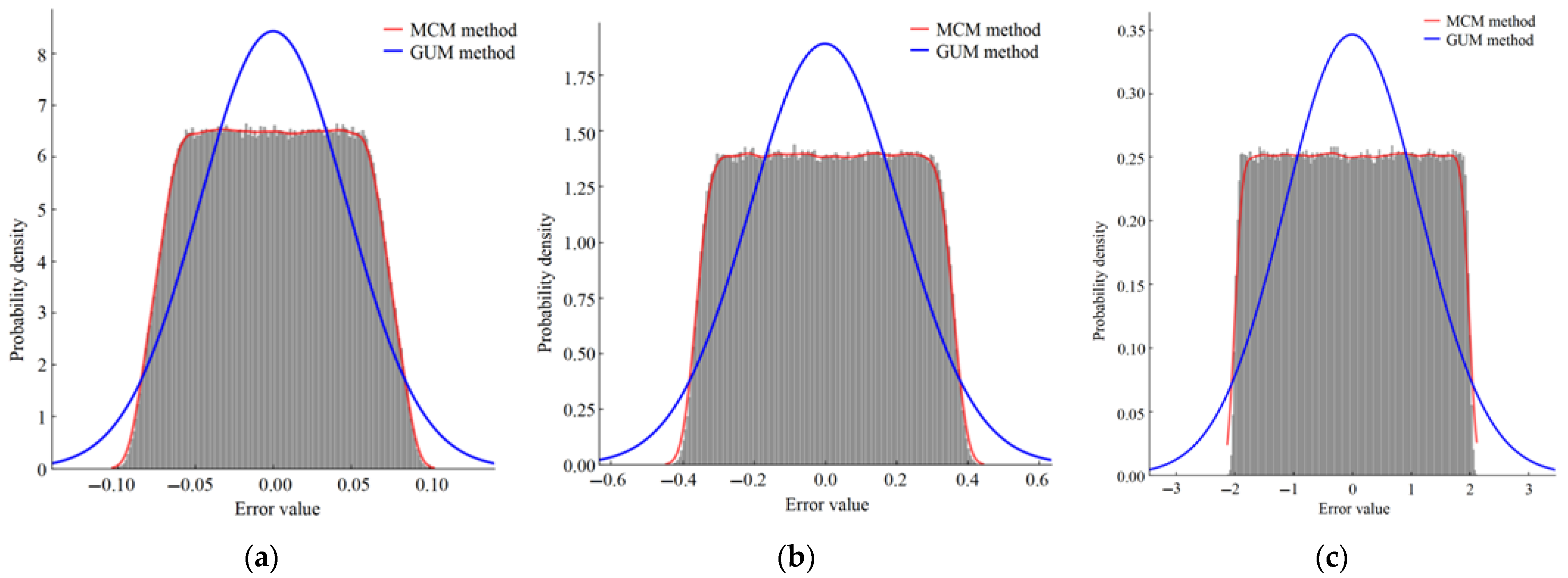
| Uncertainty Information | GUM Method | MCM Method |
|---|---|---|
| standard uncertainty | 1.15 lx | 1.15 lx |
| p = 68.27% | p = 57.70% | |
| extended uncertainty U (p = 95%) | 2.3 lx | 1.90 lx |
| k = 2 | k = 1.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Wang, Y.; Cheng, Y.; Zhu, G.; Shao, J.; Sha, Y. Uncertainty Evaluation of Two-Dimensional Horizontal Distributed Photometric Sensor Based on MCM for Illuminance Measurement Task. Sensors 2025, 25, 4648. https://doi.org/10.3390/s25154648
Sun J, Wang Y, Cheng Y, Zhu G, Shao J, Sha Y. Uncertainty Evaluation of Two-Dimensional Horizontal Distributed Photometric Sensor Based on MCM for Illuminance Measurement Task. Sensors. 2025; 25(15):4648. https://doi.org/10.3390/s25154648
Chicago/Turabian StyleSun, Jianguo, Yueyao Wang, Yinbao Cheng, Guanghu Zhu, Jianwen Shao, and Yuebing Sha. 2025. "Uncertainty Evaluation of Two-Dimensional Horizontal Distributed Photometric Sensor Based on MCM for Illuminance Measurement Task" Sensors 25, no. 15: 4648. https://doi.org/10.3390/s25154648
APA StyleSun, J., Wang, Y., Cheng, Y., Zhu, G., Shao, J., & Sha, Y. (2025). Uncertainty Evaluation of Two-Dimensional Horizontal Distributed Photometric Sensor Based on MCM for Illuminance Measurement Task. Sensors, 25(15), 4648. https://doi.org/10.3390/s25154648






