Infrared Small Target Detection via Modified Fast Saliency and Weighted Guided Image Filtering
Abstract
1. Introduction
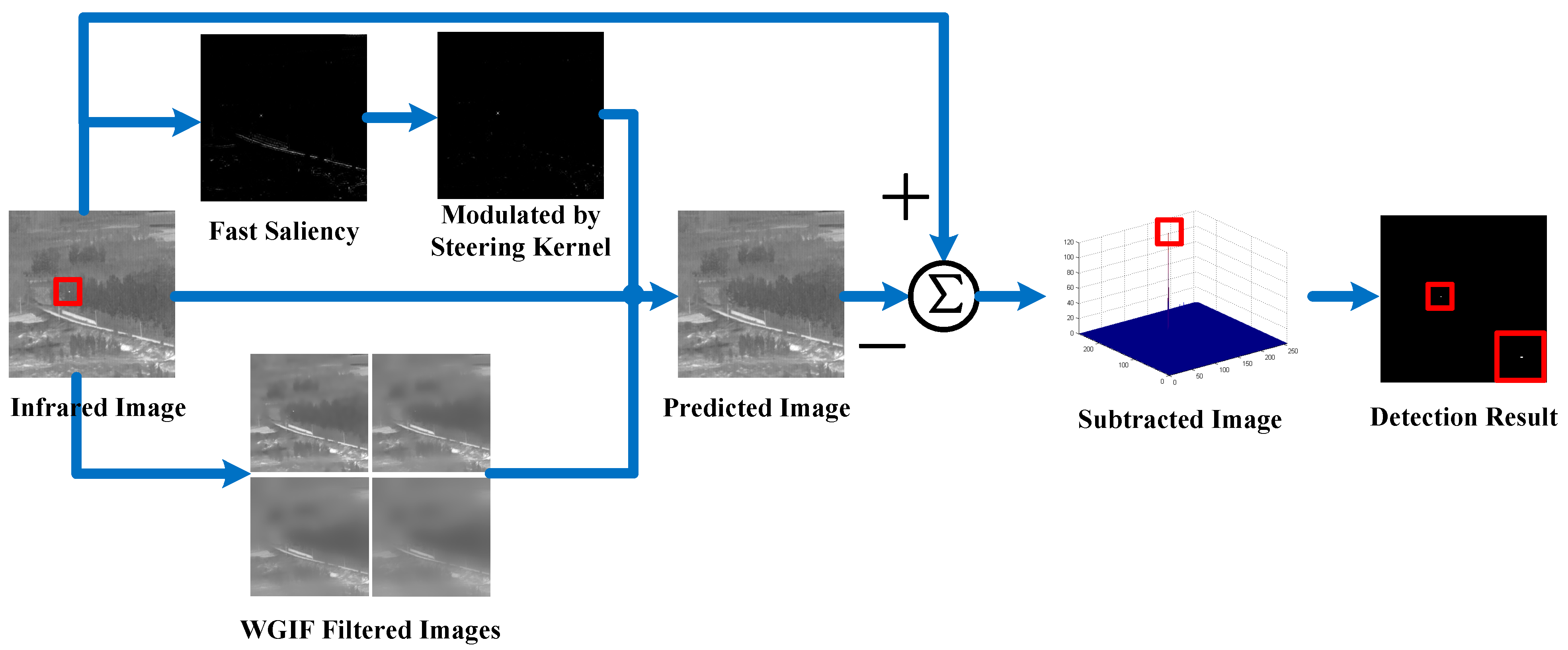
2. Proposed Algorithm
2.1. Saliency Map Calculation
2.2. Weighted Self-Guided Image Filtering
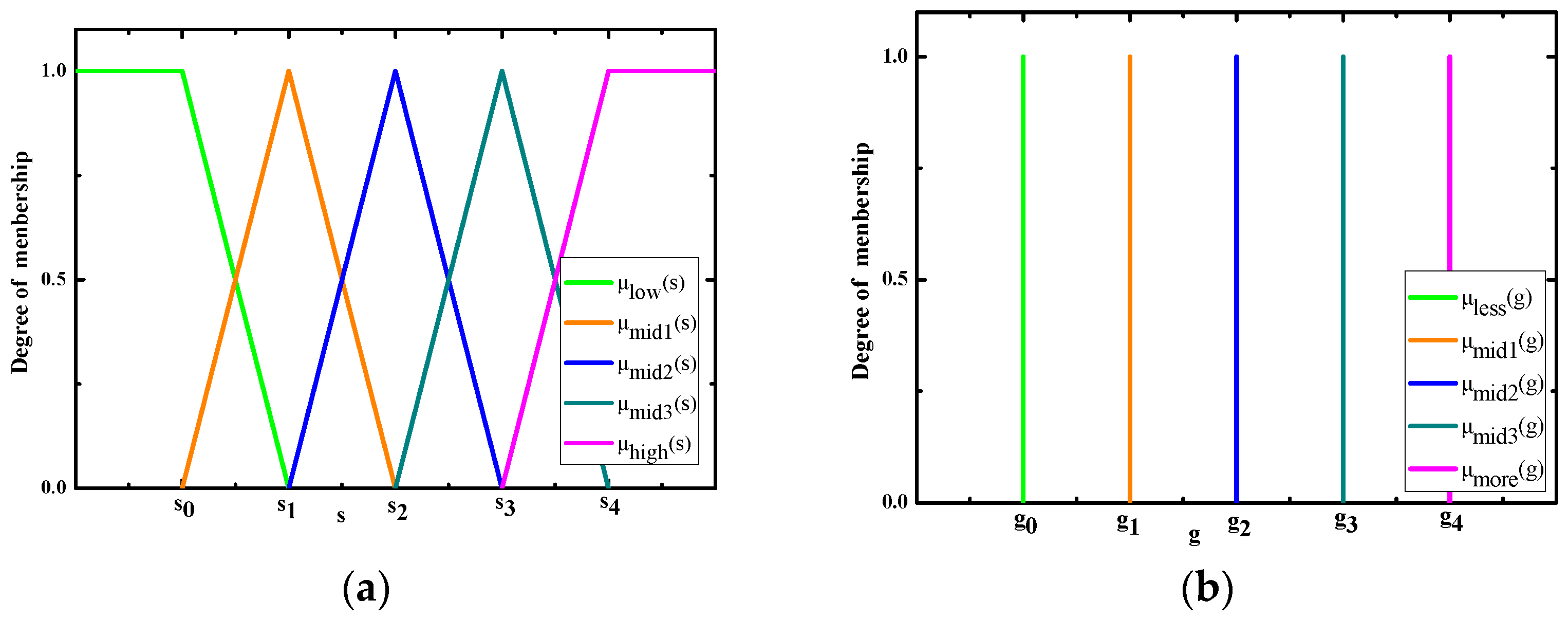
2.3. Background Prediction Using Fuzzy Sets
2.4. Target Detection
3. Experimental and Analysis
3.1. Evaluation Metrics and Comparison Methods
3.2. Experimental Results and Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, C.; Meng, D.; Yang, Y.; Wang, Y.; Zhou, X.; Hauptmann, A.G. Infrared Patch-Image Model for Small Target Detection in a Single Image. IEEE Trans. Image Process. 2013, 22, 4996–5009. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Ni, H.; Liu, S.; Xu, G.; Deng, L. TNLRS: Target-Aware Non-Local Low-Rank Modeling With Saliency Filtering Regularization for Infrared Small Target Detection. IEEE Trans. Image Process. 2020, 29, 9546–9558. [Google Scholar] [CrossRef]
- Li, L.; Li, Z.; Li, Y.; Chen, C.; Yu, J.; Zhang, C. Small Infrared Target Detection Based on Local Difference Adaptive Measure. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1258–1262. [Google Scholar] [CrossRef]
- Deshpande, S.D.; Er, M.H.; Venkateswarlu, R.; Chan, P.; Drummond, O.E. Max-mean and max-median filters for detection of small targets. In Proceedings of the SPIE’s International Symposium on Optical Science, Engineering, and Instrumentation, Denver, CO, USA, 18–23 July 1999; Volume 3809, pp. 74–84. [Google Scholar]
- Cao, Y.; Liu, R.; Yang, J. Small Target Detection Using Two-Dimensional Least Mean Square (TDLMS) Filter Based on Neighborhood Analysis. Int. J. Infrared Millim. Waves 2008, 29, 188–200. [Google Scholar] [CrossRef]
- Bae, T.-W.; Zhang, F.; Kweon, I.-S. Edge directional 2D LMS filter for infrared small target detection. Infrared Phys. Technol. 2012, 55, 137–145. [Google Scholar] [CrossRef]
- Bae, T.-W.; Sohng, K.-I. Small Target Detection Using Bilateral Filter Based on Edge Component. J. Infrared Millim. Terahertz Waves 2010, 31, 735–743. [Google Scholar] [CrossRef]
- Tom, V.T.; Peli, T.; Leung, M.; Bondaryk, J.E. Morphology-based algorithm for point target detection in infrared backgrounds. In Proceedings of the Signal and Data Processing of Small Targets, Orlando, FL, USA, 22 October 1993; Volume 1954, pp. 2–11. [Google Scholar]
- Bai, X.; Zhou, F. Analysis of new top-hat transformation and the application for infrared dim small target detection. Pattern Recognit. 2010, 43, 2145–2156. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, J.; Xu, G.; Deng, L. Balanced Ring Top-Hat Transformation for Infrared Small-Target Detection With Guided Filter Kernel. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3892–3903. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L. Multidirectional Ring Top-Hat Transformation for Infrared Small Target Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8077–8088. [Google Scholar] [CrossRef]
- Deng, L.; Xu, G.; Zhang, J.; Zhu, H. Entropy-Driven Morphological Top-Hat Transformation for Infrared Small Target Detection. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 962–975. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y.; Song, Y. Infrared small target and background separation via column-wise weighted robust principal component analysis. Infrared Phys. Technol. 2016, 77, 421–430. [Google Scholar] [CrossRef]
- Zhang, L.; Peng, L.; Zhang, T.; Cao, S.; Peng, Z. Infrared Small Target Detection via Non-Convex Rank Approximation Minimization Joint l(2,1) Norm. Remote Sens. 2018, 10, 1821. [Google Scholar] [CrossRef]
- Zhang, L.; Peng, Z. Infrared Small Target Detection Based on Partial Sum of the Tensor Nuclear Norm. Remote Sens. 2019, 11, 382. [Google Scholar] [CrossRef]
- Zhang, X.; Ding, Q.; Luo, H.; Hui, B.; Chang, Z.; Zhang, J. Infrared small target detection based on an image-patch tensor model. Infrared Phys. Technol. 2019, 99, 55–63. [Google Scholar] [CrossRef]
- Kong, X.; Yang, C.; Cao, S.; Li, C.; Peng, Z. Infrared Small Target Detection via Nonconvex Tensor Fibered Rank Approximation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–21. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, L.; Wang, X.; Shen, F.; Pu, T.; Fei, C. Edge and Corner Awareness-Based Spatial–Temporal Tensor Model for Infrared Small-Target Detection. IEEE Trans. Geosci. Remote Sens. 2021, 59, 10708–10724. [Google Scholar] [CrossRef]
- Huang, S.; Liu, Y.; He, Y.; Zhang, T.; Peng, Z. Structure-Adaptive Clutter Suppression for Infrared Small Target Detection: Chain-Growth Filtering. Remote Sens. 2020, 12, 47. [Google Scholar] [CrossRef]
- Chen, C.L.P.; Li, H.; Wei, Y.; Xia, T.; Tang, Y.Y. A Local Contrast Method for Small Infrared Target Detection. IEEE Trans. Geosci. Remote Sens. 2014, 52, 574–581. [Google Scholar] [CrossRef]
- Wei, Y.; You, X.; Li, H. Multiscale patch-based contrast measure for small infrared target detection. Pattern Recognit. 2016, 58, 216–226. [Google Scholar] [CrossRef]
- Han, J.; Liang, K.; Zhou, B.; Zhu, X.; Zhao, J.; Zhao, L. Infrared Small Target Detection Utilizing the Multiscale Relative Local Contrast Measure. IEEE Geosci. Remote Sens. Lett. 2018, 15, 612–616. [Google Scholar] [CrossRef]
- Bai, X.; Bi, Y. Derivative Entropy-Based Contrast Measure for Infrared Small-Target Detection. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2452–2466. [Google Scholar] [CrossRef]
- Han, J.; Moradi, S.; Faramarzi, I.; Liu, C.; Zhang, H.; Zhao, Q. A Local Contrast Method for Infrared Small-Target Detection Utilizing a Tri-Layer Window. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1822–1826. [Google Scholar] [CrossRef]
- Wu, L.; Ma, Y.; Fan, F.; Wu, M.; Huang, J. A Double-Neighborhood Gradient Method for Infrared Small Target Detection. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1476–1480. [Google Scholar] [CrossRef]
- Li, Z.; Liao, S.; Zhao, T. Infrared Dim and Small Target Detection Based on Strengthened Robust Local Contrast Measure. IEEE Geosci. Remote Sens. Lett. 2022, 19, 7506005. [Google Scholar] [CrossRef]
- Qiu, Z.; Ma, Y.; Fan, F.; Huang, J.; Wu, M. Adaptive Scale Patch-Based Contrast Measure for Dim and Small Infrared Target Detection. IEEE Geosci. Remote Sens. Lett. 2022, 19, 7000305. [Google Scholar] [CrossRef]
- Zhang, C.; He, Y.; Tang, Q.; Chen, Z.; Mu, T. Infrared Small Target Detection via Interpatch Correlation Enhancement and Joint Local Visual Saliency Prior. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5001314. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, L.; Wang, L. Miss Detection vs. False Alarm: Adversarial Learning for Small Object Segmentation in Infrared Images. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 8508–8517. [Google Scholar]
- Hou, Q.; Wang, Z.; Tan, F.; Zhao, Y.; Zheng, H.; Zhang, W. RISTDnet: Robust Infrared Small Target Detection Network. IEEE Geosci. Remote Sens. Lett. 2022, 19, 7000805. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, C.; Fu, Q.; Han, Z. A Novel Pattern for Infrared Small Target Detection With Generative Adversarial Network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4481–4492. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y.; Zhou, F.; Barnard, K. Attentional Local Contrast Networks for Infrared Small Target Detection. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9813–9824. [Google Scholar] [CrossRef]
- Bai, Y.; Li, R.; Gou, S.; Zhang, C.; Chen, Y.; Zheng, Z. Cross-Connected Bidirectional Pyramid Network for Infrared Small-Dim Target Detection. IEEE Geosci. Remote Sens. Lett. 2022, 19, 7506405. [Google Scholar] [CrossRef]
- Zhao, M.; Li, W.; Li, L.; Hu, J.; Ma, P.; Tao, R. Single-Frame Infrared Small-Target Detection: A survey. IEEE Geosci. Remote Sens. Mag. 2022, 10, 87–119. [Google Scholar] [CrossRef]
- Qi, S.; Xu, G.; Mou, Z.; Huang, D.; Zheng, X. A fast-saliency method for real-time infrared small target detection. Infrared Phys. Technol. 2016, 77, 440–450. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, J.; Zhu, Z.; Yao, W.; Wu, S. Weighted Guided Image Filtering. IEEE Trans. Image Process. 2015, 24, 120–129. [Google Scholar]
- Liu, Y.; Peng, Z. Infrared Small Target Detection Based on Resampling-Guided Image Model. IEEE Geosci. Remote Sens. Lett. 2022, 19, 7002405. [Google Scholar] [CrossRef]
- Takeda, H.; Farsiu, S.; Milanfar, P. Kernel regression for image processing and reconstruction. IEEE Trans. Image Process. 2007, 16, 349–366. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y. Robust infrared small target detection using local steering kernel reconstruction. Pattern Recognit. 2018, 77, 113–125. [Google Scholar] [CrossRef]
- He, K.; Sun, J.; Tang, X. Guided Image Filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1397–1409. [Google Scholar] [CrossRef]
- A Dataset for Dim-Small Target Detection and Tracking of Aircraft in Infrared Image Sequences. Available online: http://www.csdata.org/p/387/1 (accessed on 23 June 2020).
- Zhang, H.; Zhang, L.; Yuan, D.; Chen, H. Infrared small target detection based on local intensity and gradient properties. Infrared Phys. Technol. 2018, 89, 88–96. [Google Scholar] [CrossRef]
- Gao, C.; Wang, L.; Xiao, Y.; Zhao, Q.; Meng, D. Infrared small-dim target detection based on Markov random field guided noise modeling. Pattern Recognit. 2018, 76, 463–475. [Google Scholar] [CrossRef]




| Sequence | Size/Pixels | Length/Frames | Target Description | Background Description |
|---|---|---|---|---|
| Seq.1 | 256 × 200 | 30 | Single, relatively large, moving along cloud edges | Heavy cloud sky |
| Seq.2 | 256 × 256 | 80 | Single, tiny, low nonlocal contrast | Complex road and forest |
| Seq.3 | 256 × 256 | 80 | Single, tiny, varying size | Much target-like clutter |
| Seq.4 | 256 × 256 | 80 | Single, a little long strip, varying size | Mountain and artificial structures |
| No. | Method | Parameter Settings |
|---|---|---|
| 1 | LCM | Largest scale S = 4 size: 3 × 3, 5 × 5, 7 × 7, 9 × 9 |
| 2 | MPCM | Mean filter size: 3 × 3, N = 3,5,7,9 |
| 3 | TLLCM | Core layer size: 3 × 3, Reserve layer size: 5 × 5, 7 × 7, 9 × 9 |
| 4 | LIG | Sliding window size: 11 × 11, k = 0.2 |
| 5 | IPI | Patch size: 50 × 50, step:10 |
| 6 | PSTNN | Patch size: 40 × 40, step:40 |
| 7 | NTFRA | Patch size: 40 × 40, step:40 |
| 8 | Proposed | Fuzzy set parameters: 0.4,0.5,0.6,0.7,0.8 |
| Methods | Without SK | Without Weighting | Proposed | |
|---|---|---|---|---|
| Seq 1 | Inf | Inf | Inf | |
| Seq 2 | Inf | Inf | Inf | |
| Seq 3 | Inf | Inf | Inf | |
| Seq 4 | Inf | Inf | Inf | |
| Seq 1 | Inf | Inf | Inf | |
| Seq 2 | 9.339 | 24.959 | Inf | |
| Seq 3 | Inf | Inf | Inf | |
| Seq 4 | 36.312 | 48.393 | 58.503 | |
| Seq 1 | 2.368 | 2.728 | 3.198 | |
| Seq 2 | 0.768 | 1.455 | 1.510 | |
| Seq 3 | 0.904 | 0.830 | 1.767 | |
| Seq 4 | 0.991 | 1.163 | 1.488 |
| No. | Filter Parameters | Fuzzy Set Parameters |
|---|---|---|
| Group 1 | 0.4,0.5,0.6,0.7,0.8 | |
| Group 2 | 0.4,0.5,0.6,0.7,0.8 | |
| Group 3 | 0.4,0.5,0.6,0.7,0.8 | |
| Group 4 | 0.4,0.5,0.6,0.7,0.8 | |
| Group 5 | 0.1,0.3,0.5,0.7,0.9 | |
| Group 6 | 0.5,0.55,0.6,0.65,0.7 | |
| Adopted | 0.4,0.5,0.6,0.7,0.8 |
| Parameters | Group 1 | Group 2 | Group 3 | Group 4 | Group 5 | Group 6 | Adopted | |
|---|---|---|---|---|---|---|---|---|
| Seq 1 | Inf | Inf | Inf | Inf | Inf | Inf | Inf | |
| Seq 2 | Inf | Inf | Inf | Inf | 173.22 | Inf | Inf | |
| Seq 3 | Inf | Inf | Inf | Inf | Inf | Inf | Inf | |
| Seq 4 | Inf | Inf | Inf | Inf | 106.05 | Inf | Inf | |
| Seq 1 | Inf | Inf | Inf | Inf | Inf | Inf | Inf | |
| Seq 2 | 114.73 | 90.617 | 129.08 | 67.432 | 21.977 | Inf | Inf | |
| Seq 3 | Inf | Inf | Inf | Inf | 107.01 | Inf | Inf | |
| Seq 4 | 162.51 | 49.14 | 45.647 | 380.51 | 38.99 | Inf | 58.503 | |
| Seq 1 | 3.167 | 3.235 | 3.006 | 2.967 | 3.346 | 3.099 | 3.198 | |
| Seq 2 | 1.469 | 1.493 | 1.486 | 1.518 | 1.681 | 1.418 | 1.510 | |
| Seq 3 | 1.691 | 1.739 | 1.717 | 1.787 | 1.867 | 1.662 | 1.767 | |
| Seq 4 | 1.311 | 1.451 | 1.541 | 1.468 | 1.566 | 1.407 | 1.488 |
| Methods | LCM | MPCM | TLLCM | LIG | IPI | PSTNN | NTFRA | Proposed | |
|---|---|---|---|---|---|---|---|---|---|
| Seq 1 | 1.563 | 1.656 | Inf | 52.325 | 9.130 | Inf | 8.875 | Inf | |
| Seq 2 | 1.638 | 1.496 | 17.972 | 131.880 | Inf | Inf | Inf | Inf | |
| Seq 3 | 0.533 | 2.131 | Inf | 23.649 | 7.656 | Inf | 4.330 | Inf | |
| Seq 4 | 0.320 | 1.695 | 4.394 | 38.384 | 5.106 | Inf | 6.140 | Inf | |
| Seq 1 | 0.706 | 2.135 | 13.132 | 10.070 | 16.186 | Inf | 10.875 | Inf | |
| Seq 2 | 0.889 | 4.097 | 8.151 | 3.895 | 14.771 | 3.323 | 1.309 | Inf | |
| Seq 3 | 1.612 | 6.904 | 29.250 | 10.141 | 34.615 | 15.666 | 4.999 | Inf | |
| Seq 4 | 1.984 | 7.818 | 42.535 | 12.850 | 19.539 | 10.391 | 2.645 | 58.503 | |
| Seq 1 | 3.306 | 1.172 | 2.264 | 2.857 | 2.591 | 3.328 | 4.320 | 3.198 | |
| Seq 2 | 3.972 | 0.888 | 1.837 | 1.219 | 1.235 | 1.482 | 1.911 | 1.510 | |
| Seq 3 | 1.421 | 0.661 | 1.309 | 1.464 | 1.261 | 1.575 | 1.729 | 1.767 | |
| Seq 4 | 1.475 | 0.775 | 1.332 | 1.306 | 1.161 | 1.408 | 1.407 | 1.488 | |
| Seq 1 | 0.0786 | 0.0837 | 2.041 | 1.270 | 6.311 | 0.0634 | 1.211 | 0.715 | |
| Seq 2 | 0.0902 | 0.0901 | 2.773 | 1.647 | 8.553 | 0.282 | 1.827 | 0.894 | |
| Seq 3 | 0.0877 | 0.0899 | 2.864 | 1.667 | 9.007 | 0.229 | 1.902 | 0.968 | |
| Seq 4 | 0.0899 | 0.0925 | 2.752 | 1.674 | 10.055 | 0.253 | 1.793 | 0.901 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Y.; Lei, T.; Chen, G.; Zhang, Y.; Zhang, G.; Hao, X. Infrared Small Target Detection via Modified Fast Saliency and Weighted Guided Image Filtering. Sensors 2025, 25, 4405. https://doi.org/10.3390/s25144405
Cui Y, Lei T, Chen G, Zhang Y, Zhang G, Hao X. Infrared Small Target Detection via Modified Fast Saliency and Weighted Guided Image Filtering. Sensors. 2025; 25(14):4405. https://doi.org/10.3390/s25144405
Chicago/Turabian StyleCui, Yi, Tao Lei, Guiting Chen, Yunjing Zhang, Gang Zhang, and Xuying Hao. 2025. "Infrared Small Target Detection via Modified Fast Saliency and Weighted Guided Image Filtering" Sensors 25, no. 14: 4405. https://doi.org/10.3390/s25144405
APA StyleCui, Y., Lei, T., Chen, G., Zhang, Y., Zhang, G., & Hao, X. (2025). Infrared Small Target Detection via Modified Fast Saliency and Weighted Guided Image Filtering. Sensors, 25(14), 4405. https://doi.org/10.3390/s25144405






