Miniaturizing Controlled-Source EM Transmitters for Urban Underground Surveys: A Bipolar Square-Wave Inverter Approach with SiC-MOSFETs
Abstract
1. Introduction
- (1)
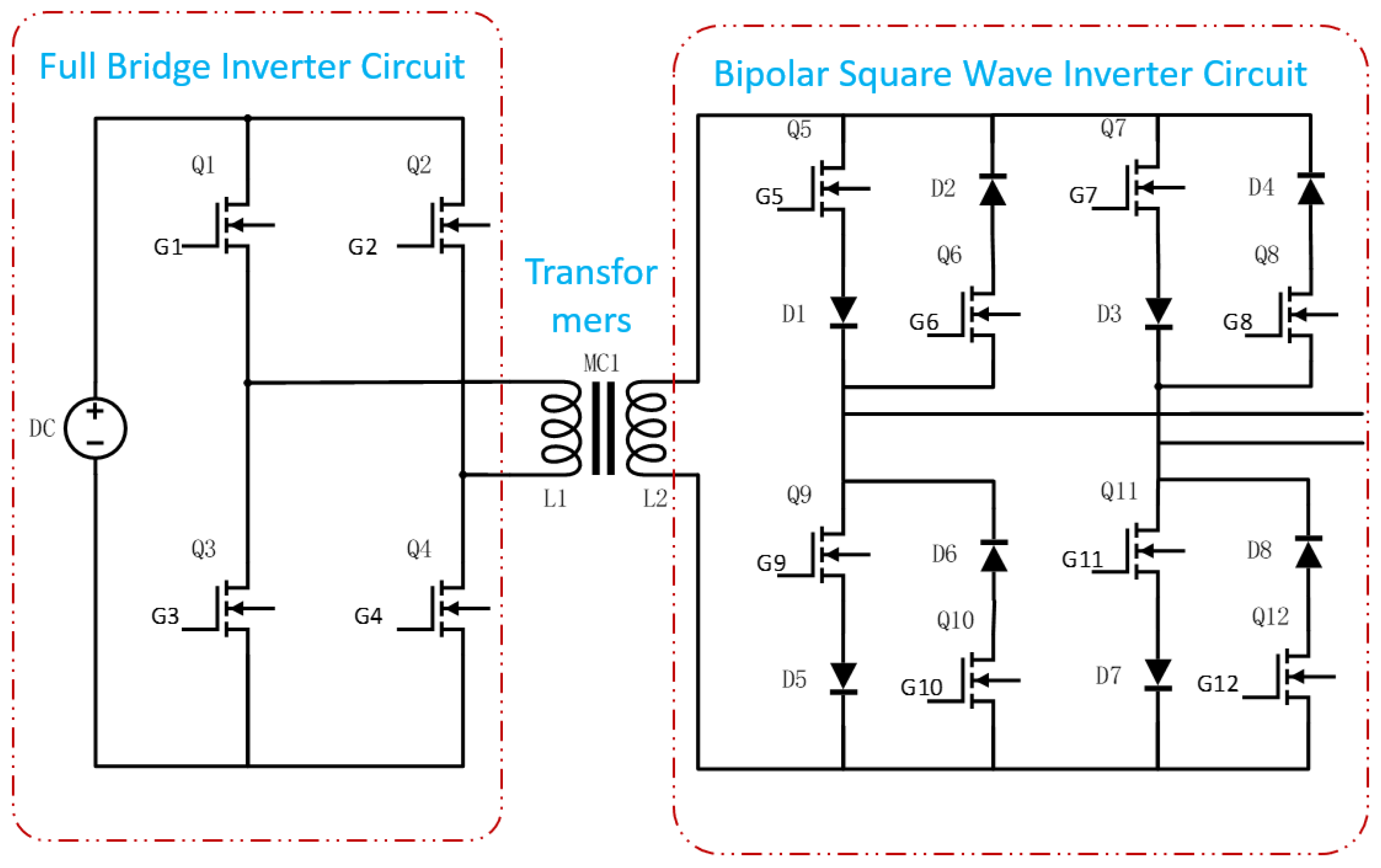
- By directly inverting the AC voltage output from the transformer using a bipolar square wave inverter circuit, the rectification and filtering stages are eliminated, reducing energy loss and achieving a 70% reduction in system volume and weight compared to traditional high-frequency transmitters.
- (2)
- The utilization of SiC-MOSFETs combined with transformers enables a reduction in the required number of winding turns or the magnetic core cross-sectional area for the transformer design under identical output power and other constant parameters as the operating frequency increases [18]. This facilitates a 40% reduction in weight and volume, consequently enhancing power density.
- (3)
- A complementary timing control strategy with optimized dead time is introduced to ensure circuit stability under filterless operation. Simulation and experimental results demonstrate that the proposed system can reliably output square-wave signals in the 10–100 kHz range with efficiencies of up to 92%, providing a lightweight, reliable solution for urban subsurface exploration with millimeter-scale resolution.
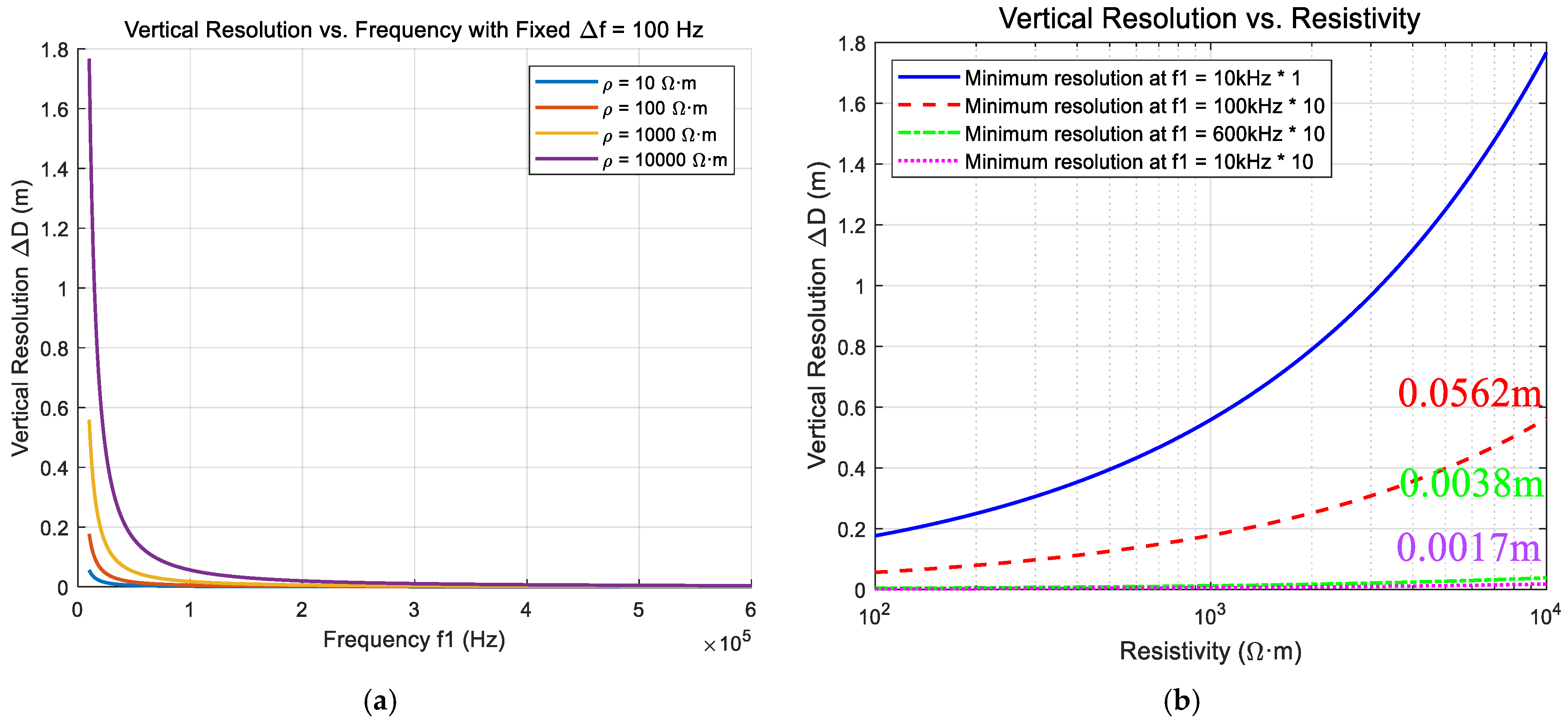
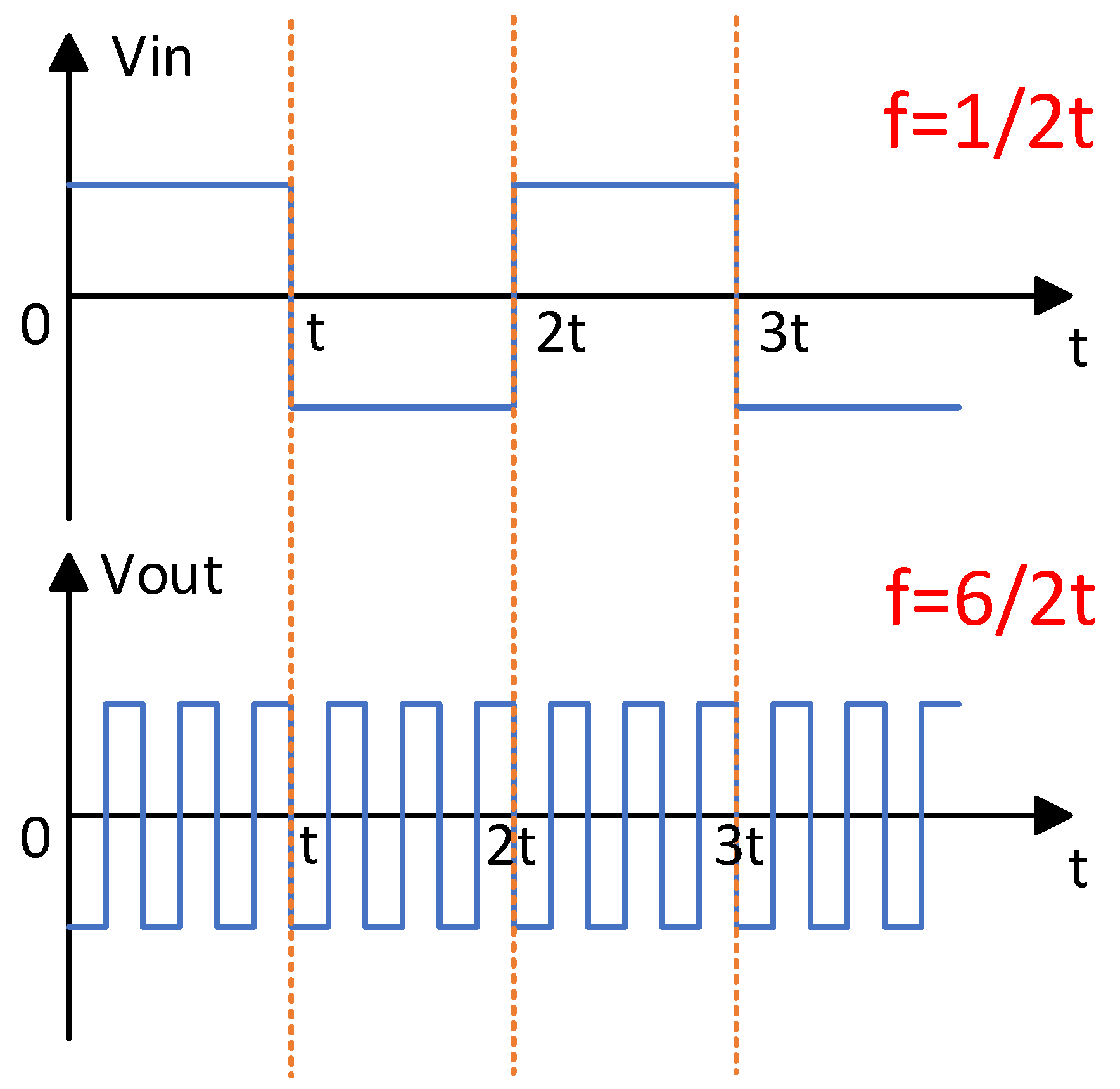
2. Theoretical Basis for High-Frequency Transmitter Design
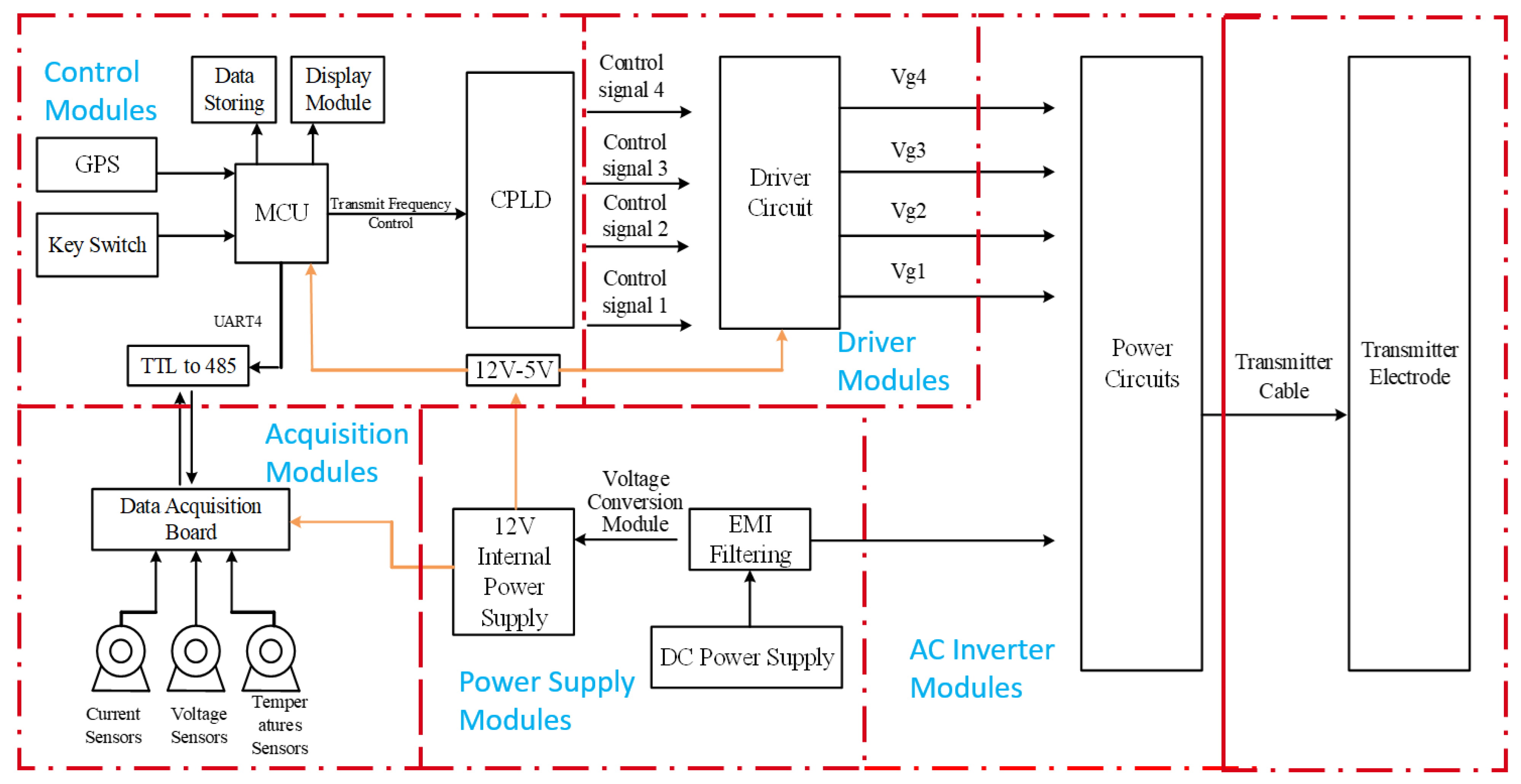
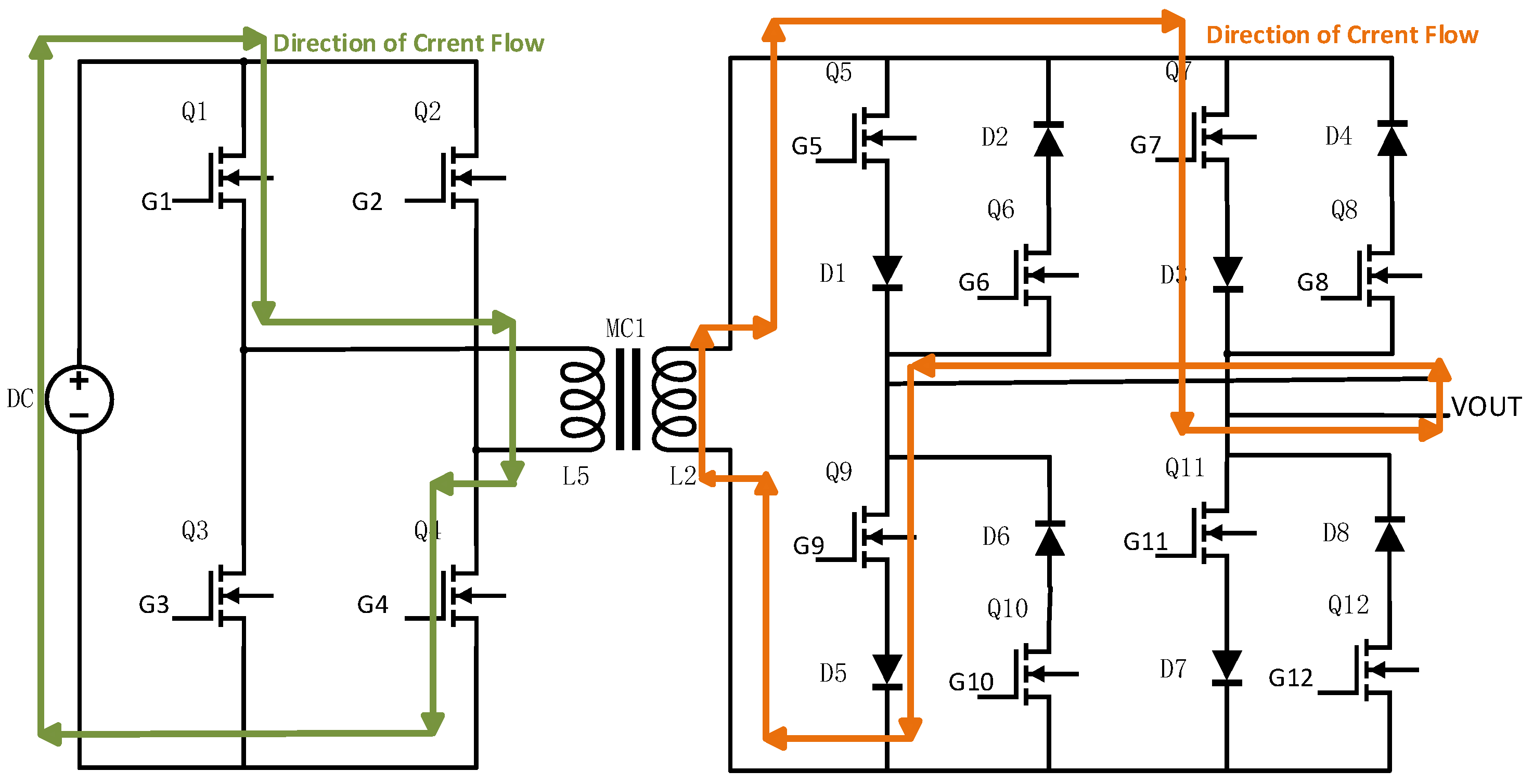
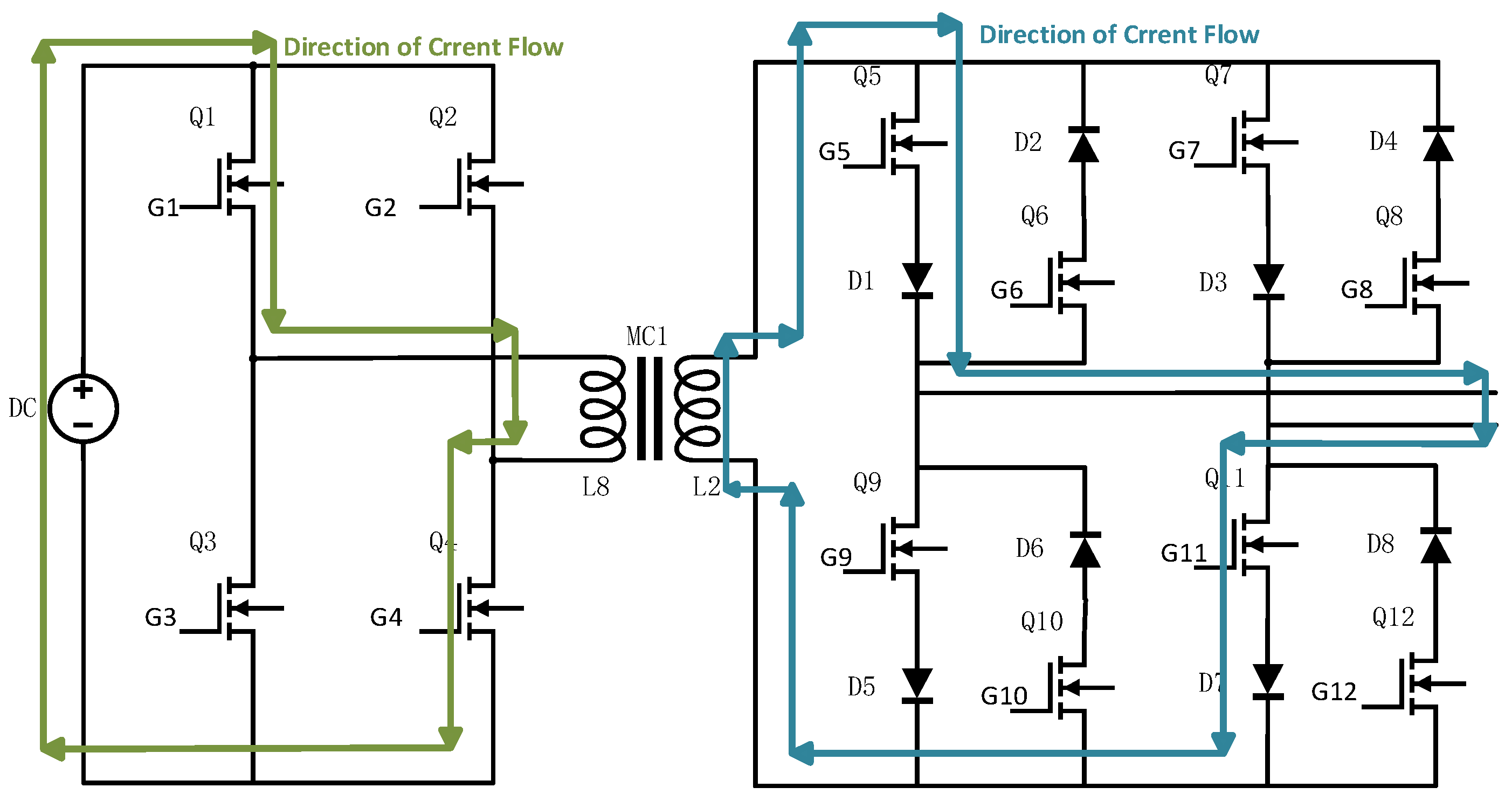
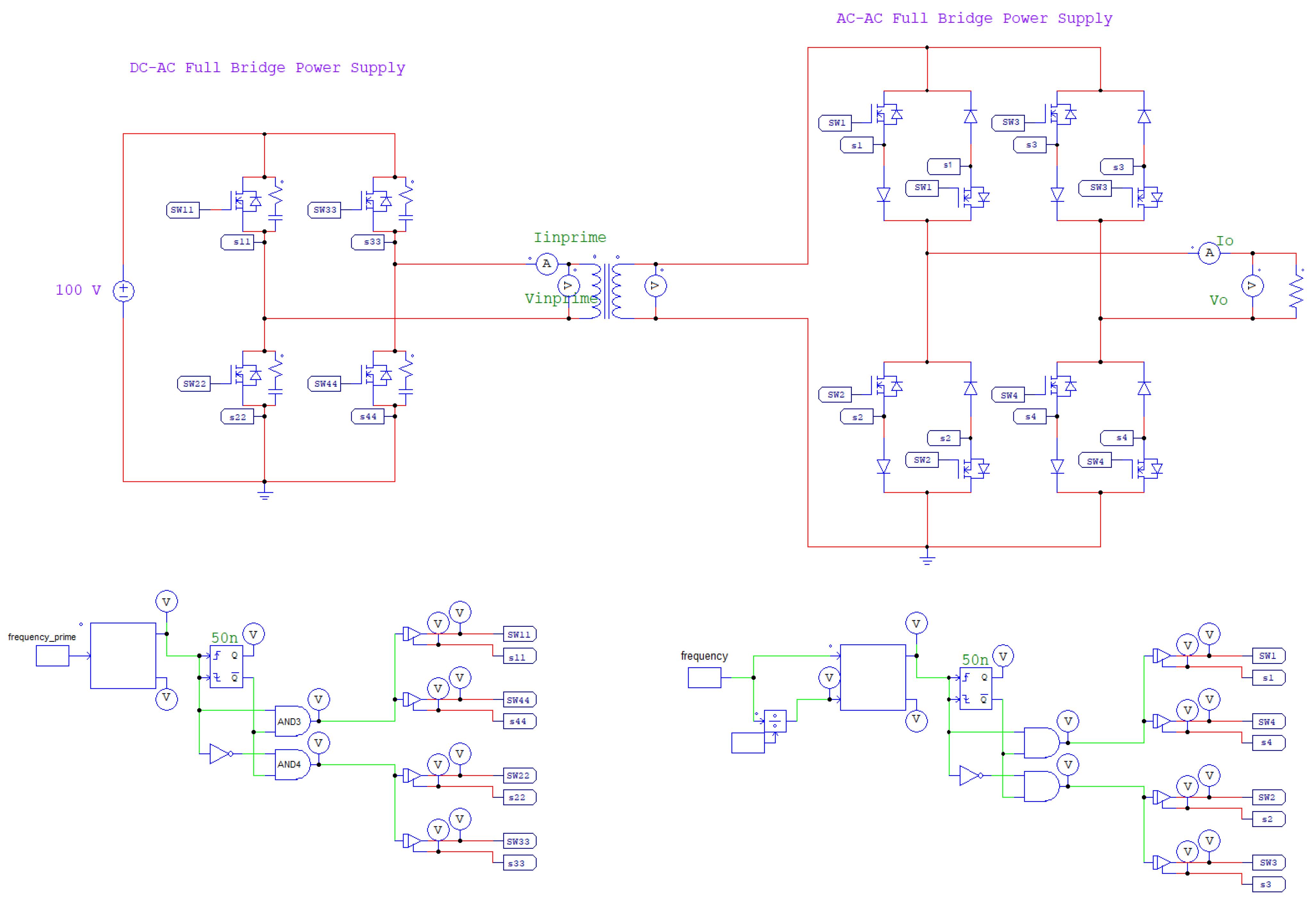
3. Design of the Controlled-Source Electromagnetic Transmitter Circuit
Power Circuit Design
4. Circuit Efficiency Analysis
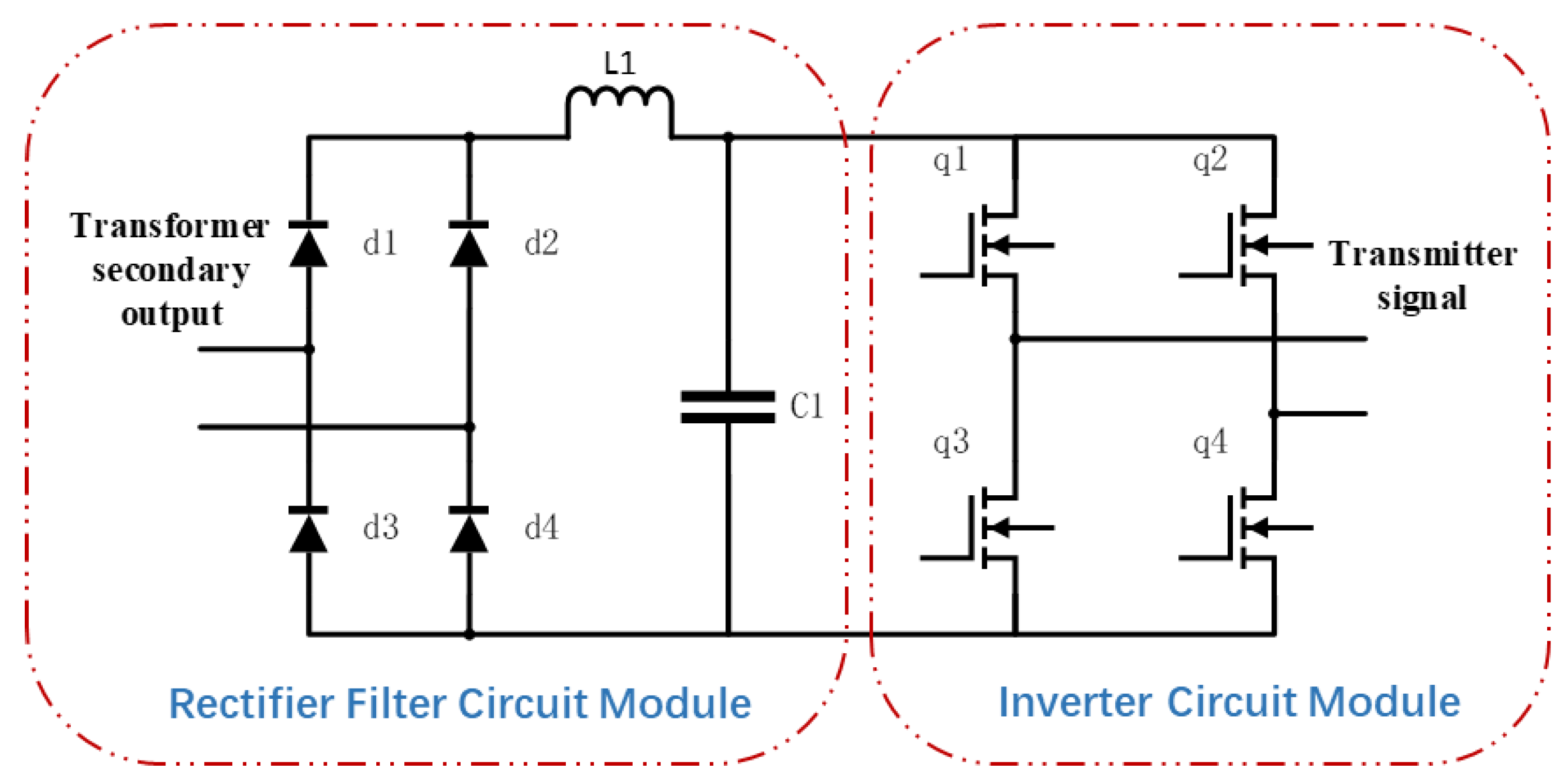
4.1. Comparative Analysis Between the Bipolar Square-Wave Inverter and Traditional Transmitter Topologies
4.2. Theoretical Efficiency Analysis of the Bipolar Square-Wave Inverter Circuit
5. Simulation and Experimental Validation
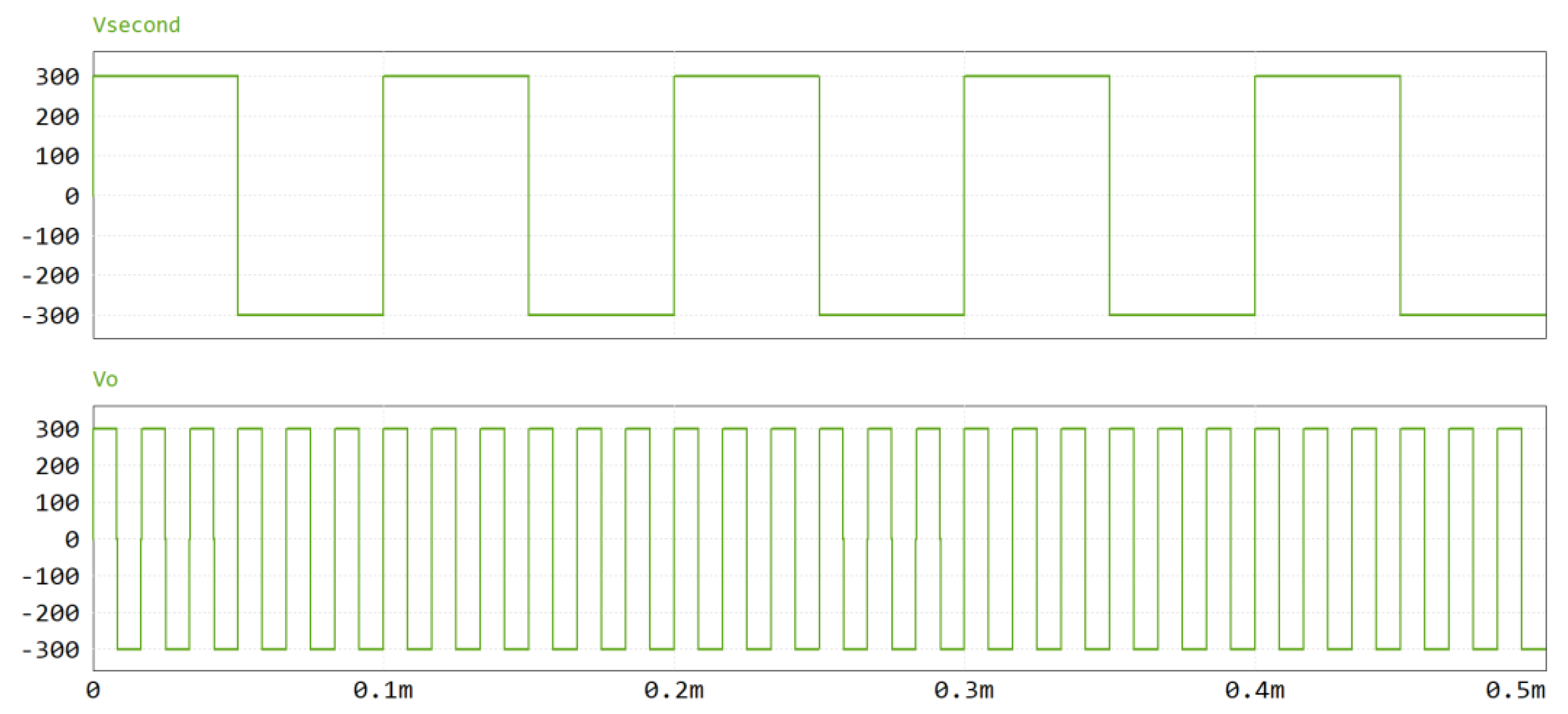
5.1. Simulation Verification
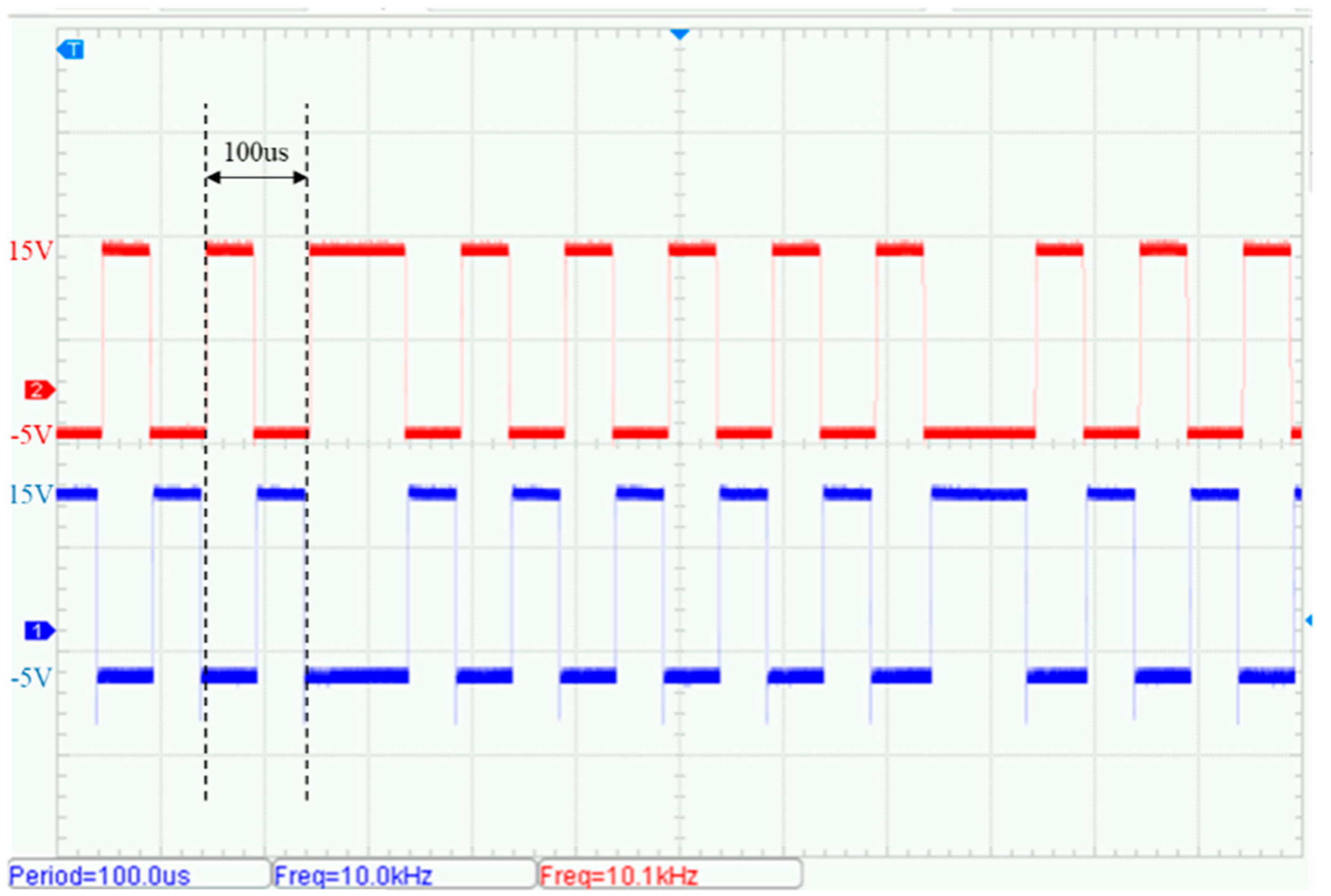
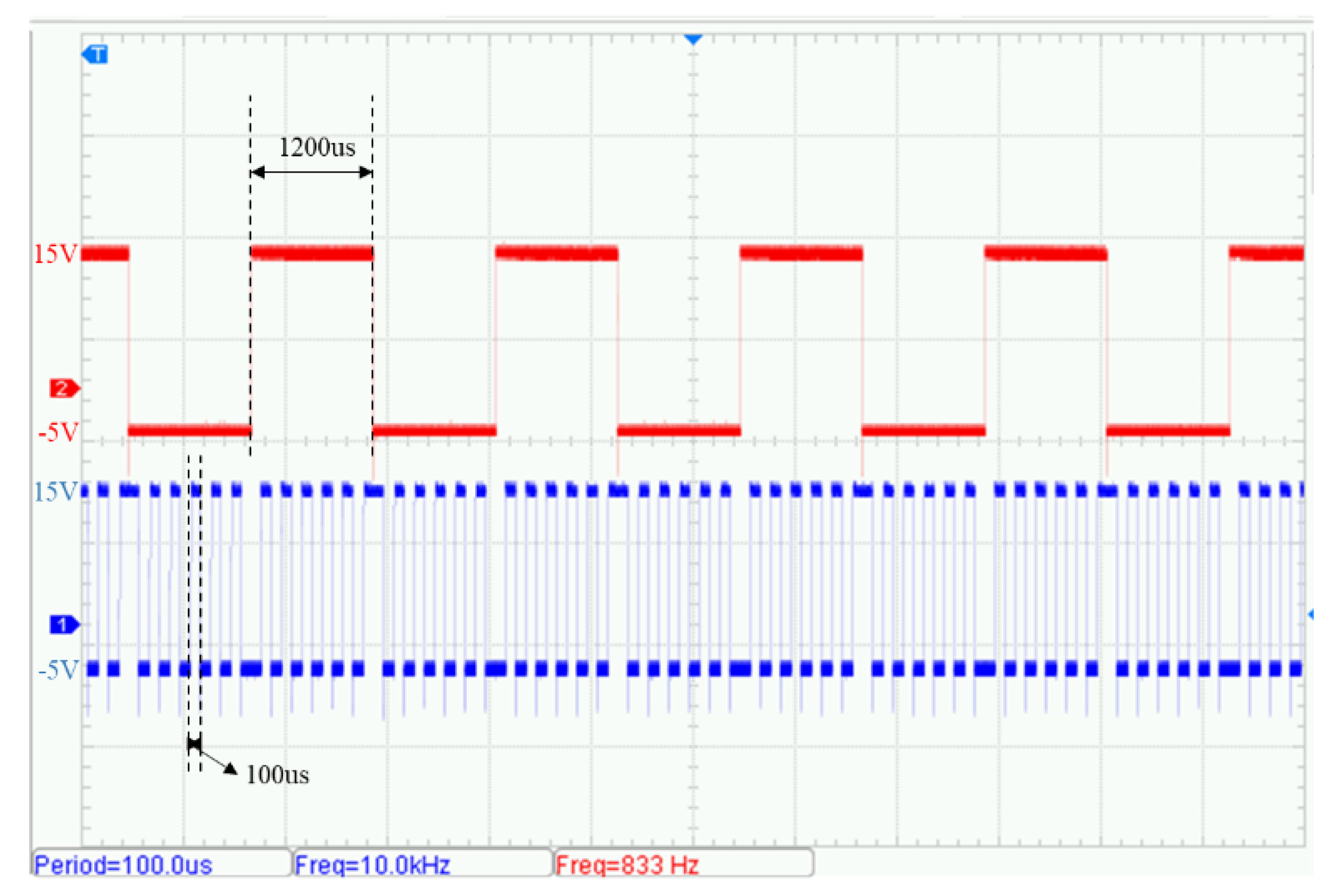
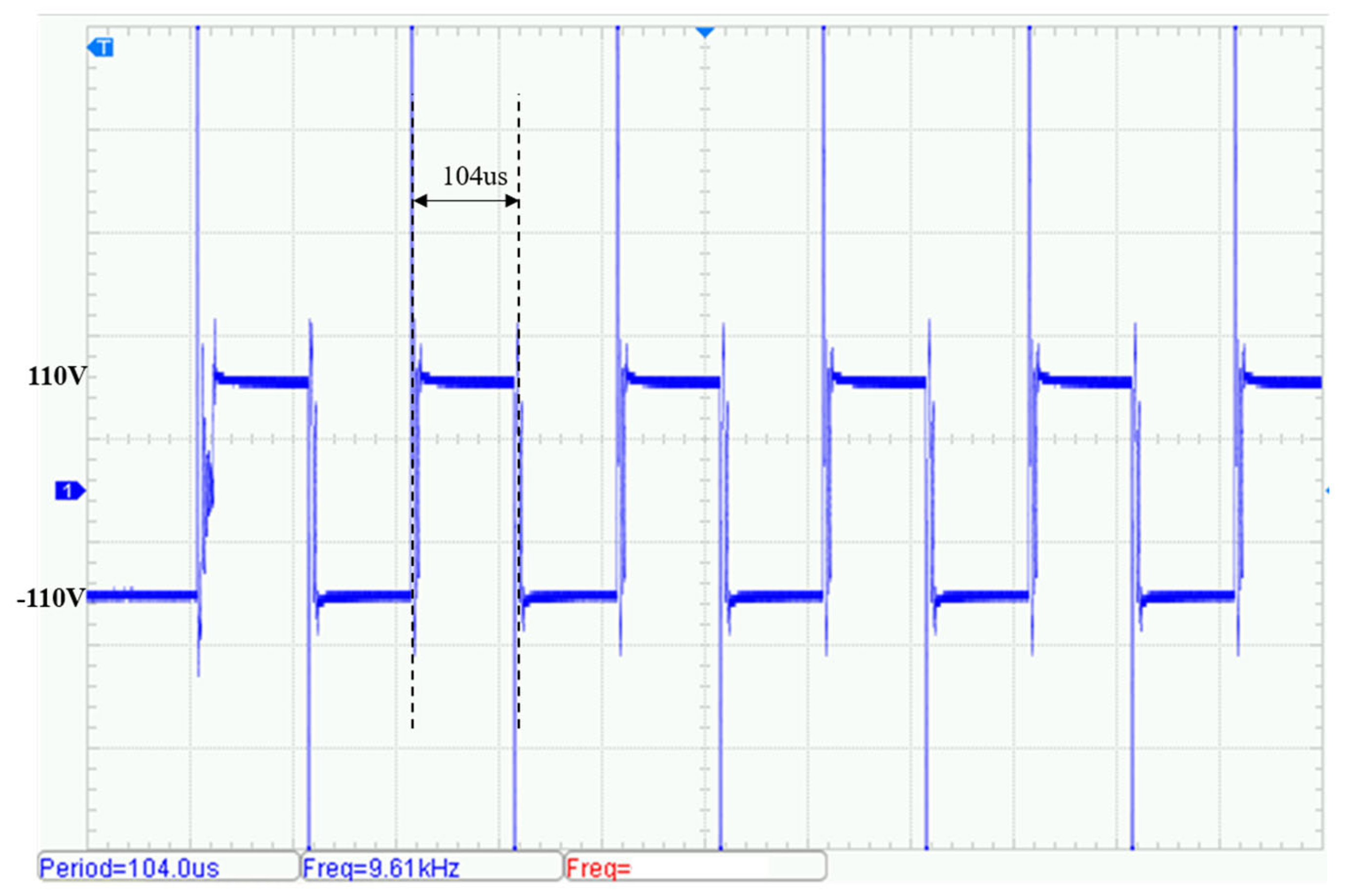
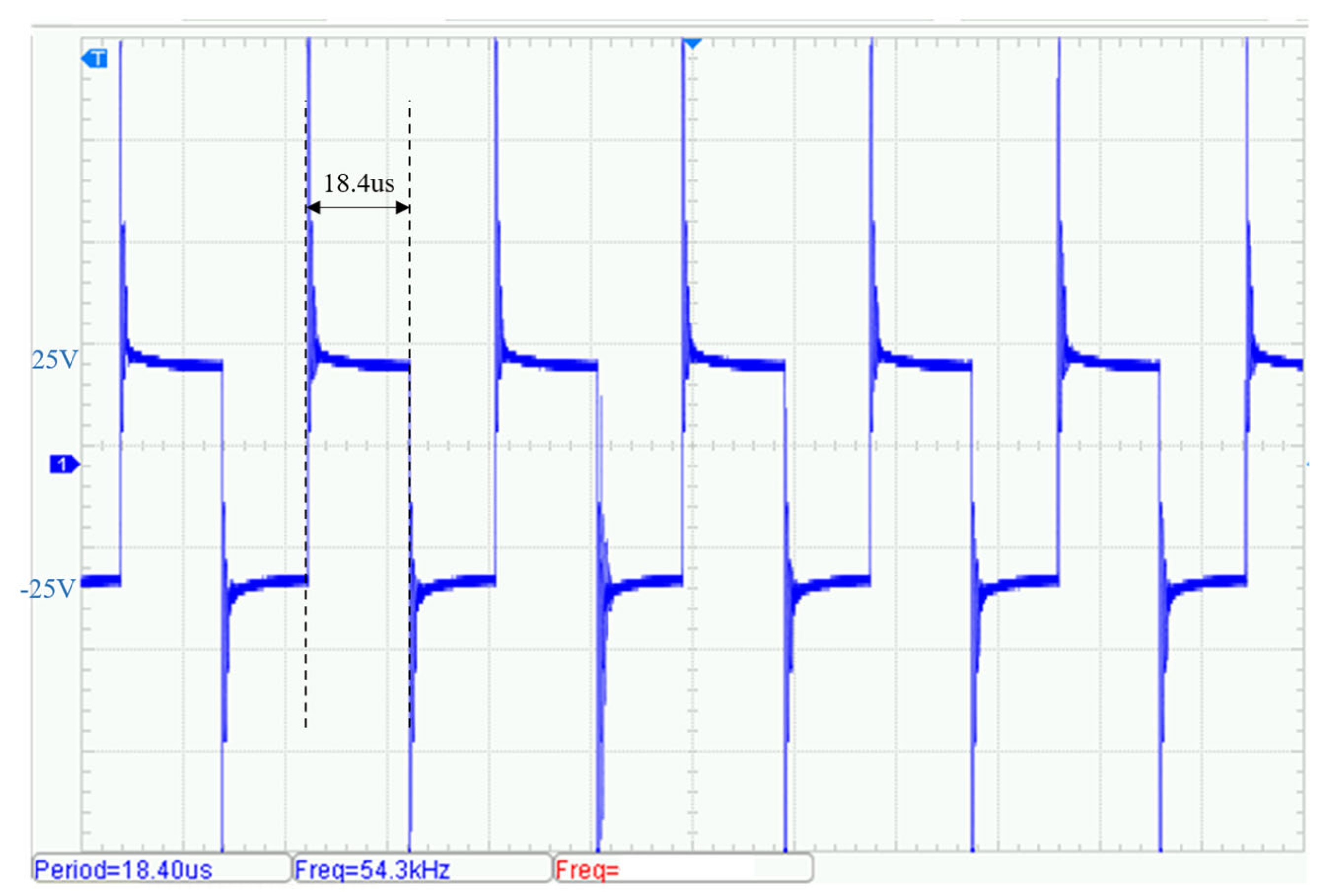
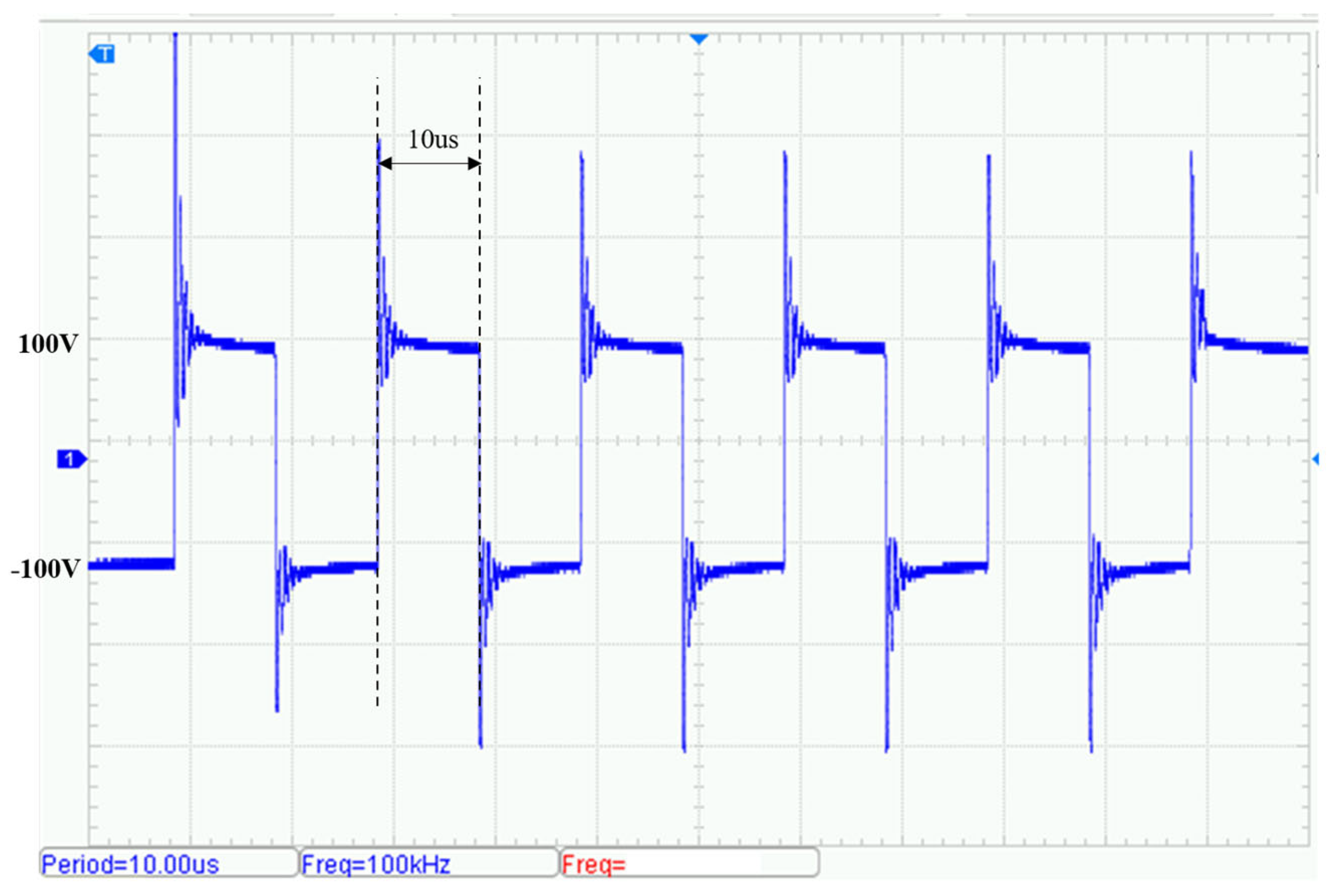
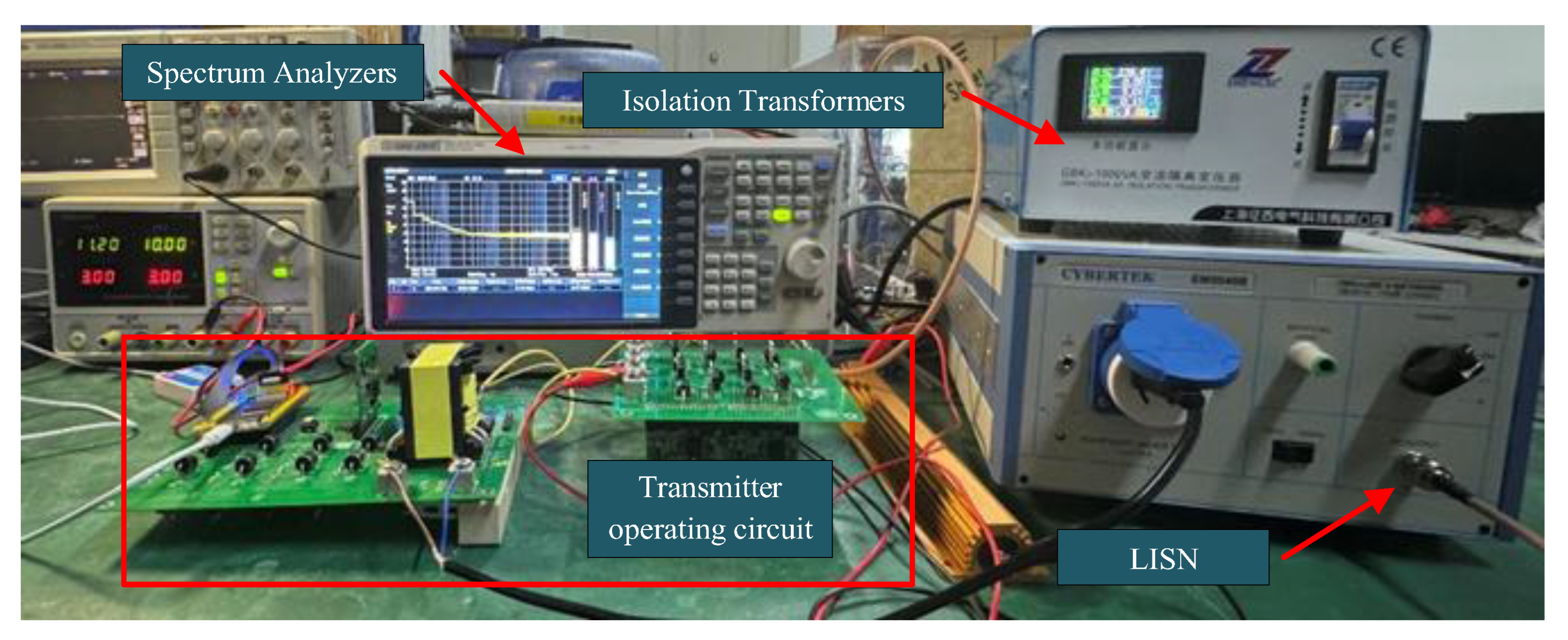
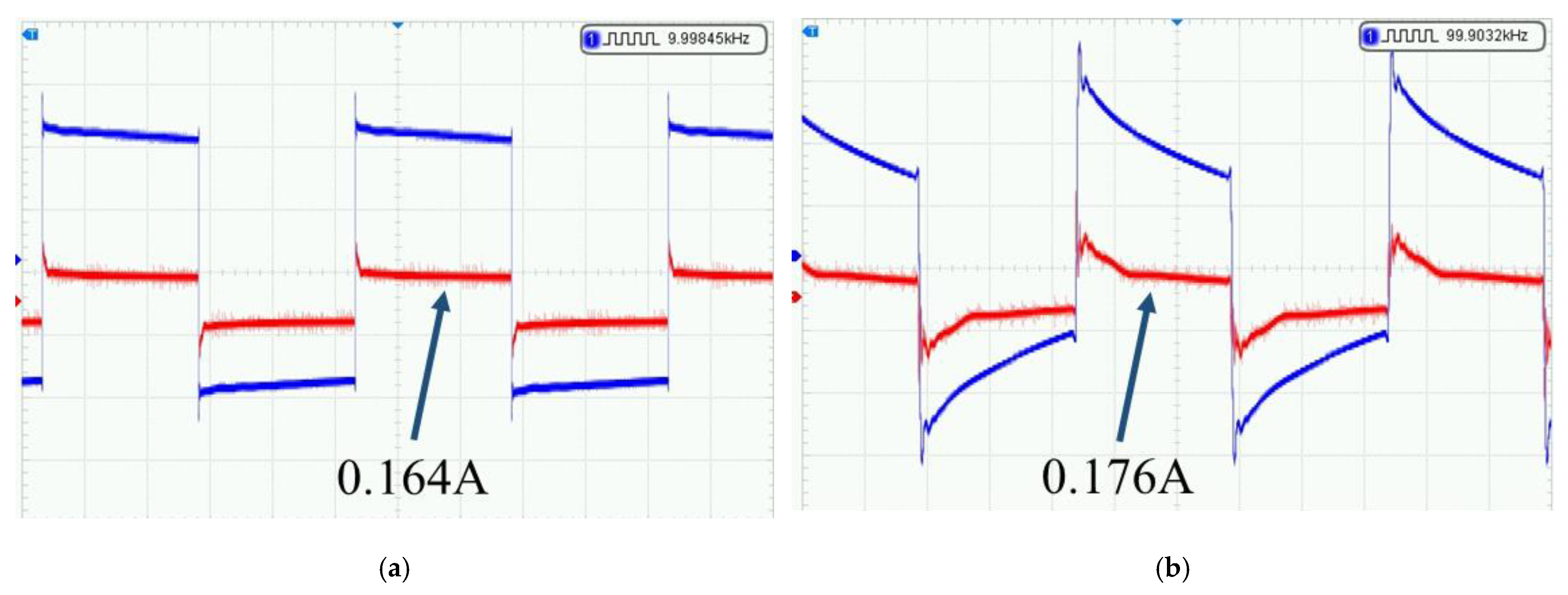
5.2. Laboratory Transmission Testing
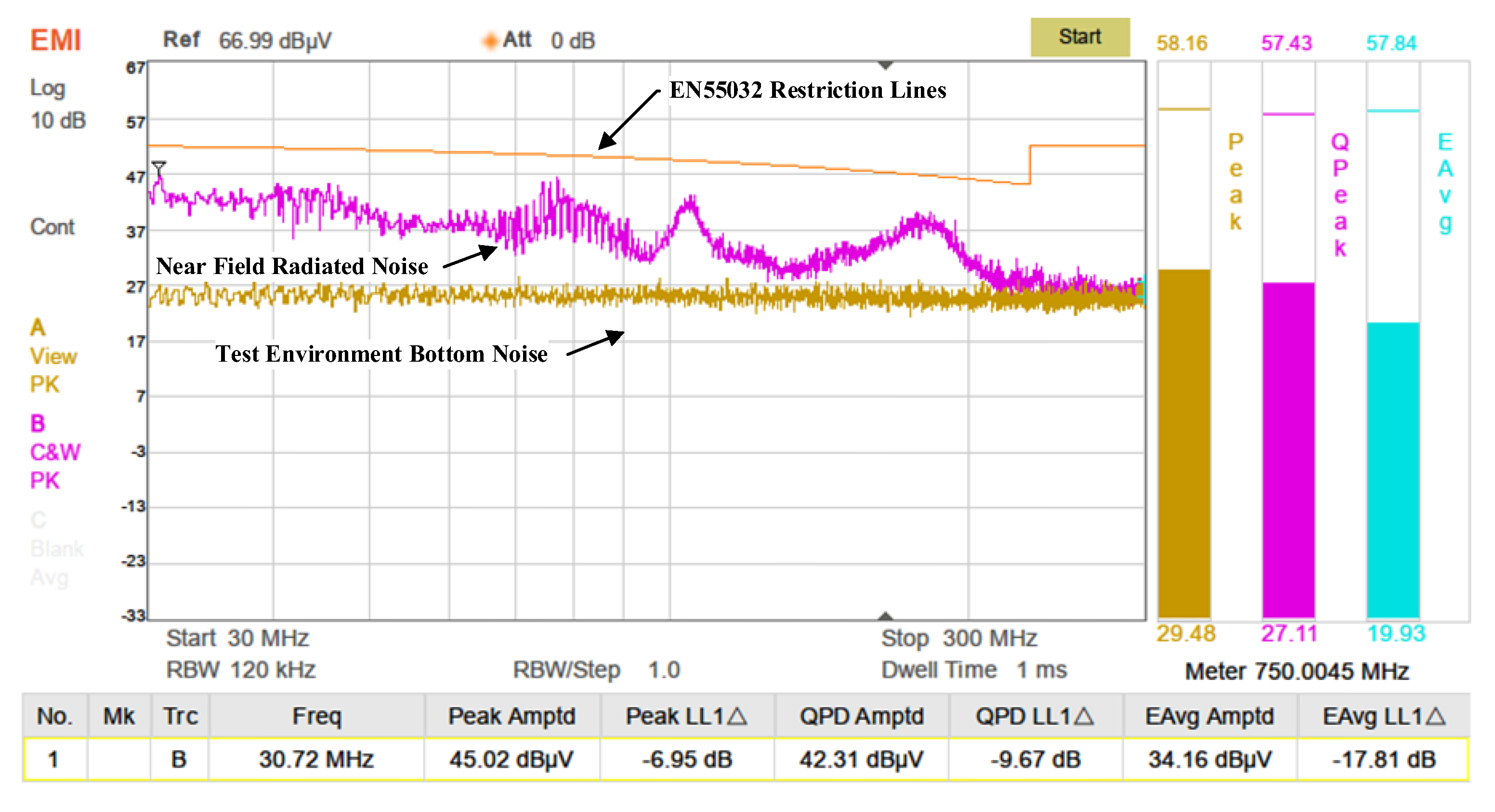
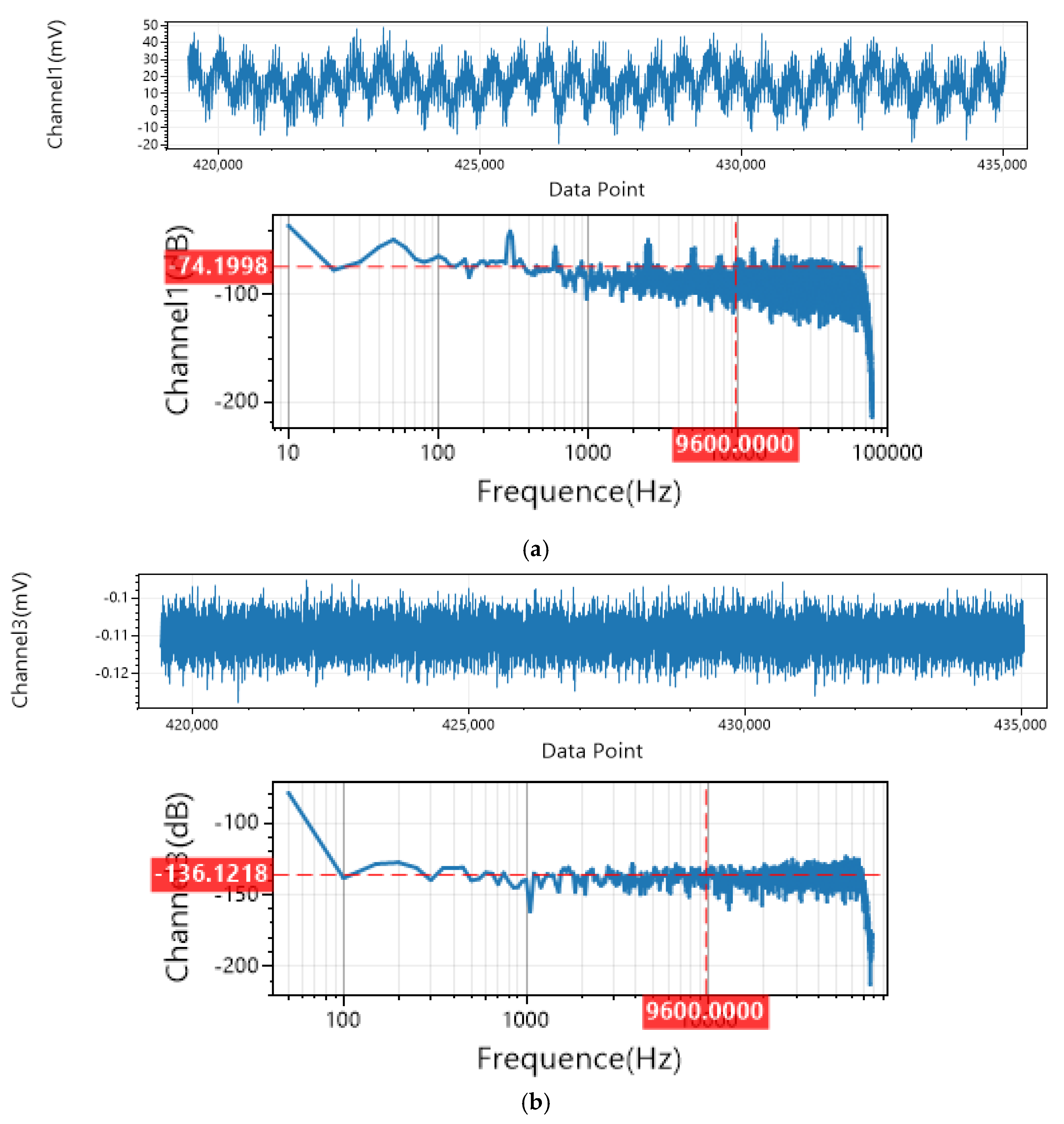
5.3. EMI Near-Field Radiation and Conducted Emission Testing
6. Joint Field Survey with High-Frequency Receiver
7. Conclusions
- (1)
- For the first time, a novel bipolar square-wave inverter topology is proposed. This architecture replaces the traditional DC–DC boost stage and multi-stage inversion by directly converting the transformer’s secondary-side AC square-wave output. By eliminating the rectification and filtering stages, the circuit is significantly simplified, laying the foundation for miniaturization and high efficiency.
- (2)
- Laboratory tests with a 25 Ω resistive load, as well as field surveys with a high-frequency receiver, confirm that the transmitter can reliably output square-wave signals across the 10–100 kHz range, achieving an efficiency of up to 92%.
- (3)
- EMI near-field radiation and conducted emission tests demonstrate that the transmitter complies with the EN55032 Class A standard for industrial equipment.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ye, W.; Huang, J.; Xu, P.; Yuan, J.; Zeng, L.; Zhang, Y.; Wang, Y.; Wang, S.; Xu, X.; Guo, Z.; et al. Suitability Evaluation of Underground Space Development by Considering Socio-Economic Factors—An Empirical Study from Longgang Region of China. Sustainability 2025, 17, 2788. [Google Scholar] [CrossRef]
- Yang, M.; Zhu, Y.; Ji, X.; Wang, J.; Fang, H. Study on Development Pattern and Comprehensive Evaluation of Integration of Urban Underground Space and Rail Transit in China. Sustainability 2025, 17, 2497. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, S.; Chen, A.; Chen, Q.; Xiong, F.; Wang, Y.; Chen, H. Underground Anomaly Detection in GPR Data by Learning in the C3 Model Space. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–11. [Google Scholar] [CrossRef]
- Zonge, K.L.; Hughes, L.J. Controlled source audio-frequency magnetotellurics (CSAMT). In Electromagnetic Methods in Applied Geophysics: Volume 2, Application, Parts A and B; Nabighian, M.N., Ed.; Society of Exploration Geophysicists: Houston, TX, USA, 1991; pp. 713–809. [Google Scholar]
- Cheng, S.; Zhang, Z.-Y.; Zhou, F.; Li, M.; Chen, H.; Shi, F.-S.; Huang, L.-P.; Li, Y. 3D Step-by-step inversion strategy for audio magnetotellurics data based on unstructured mesh. Appl. Geophys. 2021, 18, 375–385. [Google Scholar] [CrossRef]
- Xu, Z.; Liao, X.; Liu, L.; Fu, N.; Fu, Z. Research on Small-Loop Transient Electromagnetic Method Forward and Nonlinear Optimization Inversion Method. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–13. [Google Scholar]
- Sanny, T.A. Identification of Lembang fault, West-Java Indonesia by using controlled source audio-magnetotelluric (CSAMT). AIP Conf. Proc. 2017, 1861, 030002. [Google Scholar]
- Zhang, J.; Zeng, Z.; Zhao, X.; Li, J.; Zhou, Y.; Gong, M. Deep mineral exploration of the jinchuan Cu–Ni sulfide deposit based on aeromagnetic, gravity, and csamt methods. Minerals 2020, 10, 168. [Google Scholar] [CrossRef]
- Hu, X.; Peng, R.; Wu, G.; Wang, W.; Huo, G.; Han, B. Mineral Exploration using CSAMT data: Application to Longmen region metallogenic belt, Guangdong Province, China. Geophysics 2013, 78, B111–B119. [Google Scholar]
- Zhang, K.; Lin, N.; Wan, X.; Yang, J.; Wang, X.; Tian, G. An approach for predicting geothermal reservoirs distribution using wavelet transform and self-organizing neural network: A case study of radon and CSAMT data from Northern Jinan, China. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 156. [Google Scholar] [CrossRef]
- Tao, H.; Yang, N.; Wang, H. Cascaded controllable source circuit and control of electromagnetic transmitters for deep sea exploration. J. Power Electron. 2024, 24, 1–11. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, R.; Wang, M.; Lin, Z.; Zhang, Q.; Jing, J.; Li, F.; Yang, S. Controlled source ultra-audio frequency magnetotellurics transmitter for high-resolution detection of urban shallow underground space. Measurement 2025, 256, 118144. [Google Scholar] [CrossRef]
- Winter, H. Mitsubishi Electric to Ship Samples of SBD-embedded SiCMOSFET Module. Electron. Newsweekly 2023, 123–124. [Google Scholar]
- Walter, M.; Bakran, M.-M. Enhancing Hybrid Inverter Performance Through Inductive Decoupling of Silicon and Silicon Carbide Devices. IEEE Trans. Ind. Appl. 2025, 61, 1–14. [Google Scholar] [CrossRef]
- Zhu, P.; Liu, X.; Yu, Z.; Zhao, L.; Li, X. Application of phase-shifted full-bridge soft-switch technology in suspension chopper. Meas. Control. 2023, 56, 1487–1498. [Google Scholar] [CrossRef]
- Cheng, X.; Liu, C.; Wang, D.; Zhang, Y. State-of-The-Art Review on Soft-Switching Technologies for Non-Isolated DC-DC Converters. J. IEEE Access. 2021, 9, 1. [Google Scholar] [CrossRef]
- Yang, F.; Lv, Z.; Song, Z.; Li, H.; Zhang, Z.; Dong, B. Optimization Design of Magnetic Integrated Planar Transformer for Bidirectional CLLC Resonant Converter. J. Electr. Eng. Technol. 2025, 20, 2331–2342. [Google Scholar] [CrossRef]
- Liu, C.; Qi, L.; Cui, X. Design Considerations on Voltage and Current Transfer Ratio of High-Frequency Transformers. CSEE J. Power Energy Syst. 2025, 11, 447–457. [Google Scholar]
- Xie, M.; Tan, H.; Wang, K.; Guo, C.; Zhang, Z.; Li, Z. Study on the characteristics of 3D CSAMT tensor impedance data. Prog. Geophys. 2017, 32, 522–530. [Google Scholar]
- Zhen, Q.-H.; Di, Q.-Y.; Liu, H.-B. Key technology study on CSAMT transmitter with excitation control. Chin. J. Geophys.-Chin. Ed. 2013, 56, 3751–3760. [Google Scholar]
- Liu, X.; Gao, S. Response characteristics of 3D tensor CSAMT in axis anisotropic media. Front. Earth Sci. 2024, 12, 1449515. [Google Scholar] [CrossRef]
- Hasan, M.; Su, L.; Cui, P.; Shang, Y. Development of deep-underground engineering structures via 2D and 3D RQD prediction using non-invasive CSAMT. Sci. Rep. 2025, 15, 1403. [Google Scholar] [CrossRef] [PubMed]
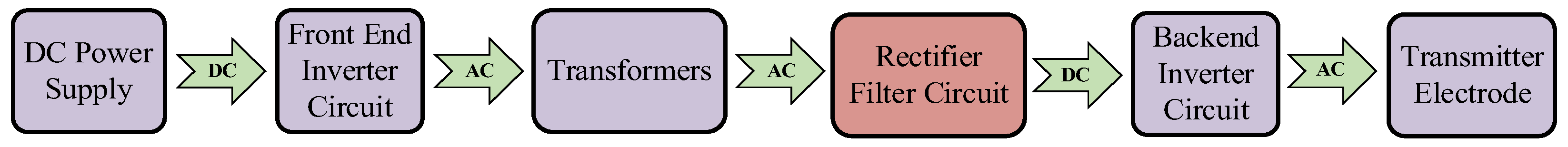









| Parameter | Core (Bobbin) Model | Operating Frequency | Maximum Input Voltage | Maximum Output Voltage/ Current | Reverse Breakdown Voltage of Switch | Maximum Duty Cycle | Minimum Duty Cycle | Voltage Withstand Rating | Turns Ratio |
|---|---|---|---|---|---|---|---|---|---|
| Design Specification | BDV0PQ050001 | 100 kHz | 50 V | 150 V/15 A | 600 V | 0.8 | 0.2 | 600 V | 1:3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Zhang, K.; Zhang, R.; Lin, Z.; Wang, M.; Wang, Y.; Zhang, Q. Miniaturizing Controlled-Source EM Transmitters for Urban Underground Surveys: A Bipolar Square-Wave Inverter Approach with SiC-MOSFETs. Sensors 2025, 25, 4183. https://doi.org/10.3390/s25134183
Wu Z, Zhang K, Zhang R, Lin Z, Wang M, Wang Y, Zhang Q. Miniaturizing Controlled-Source EM Transmitters for Urban Underground Surveys: A Bipolar Square-Wave Inverter Approach with SiC-MOSFETs. Sensors. 2025; 25(13):4183. https://doi.org/10.3390/s25134183
Chicago/Turabian StyleWu, Zhongping, Kuiyuan Zhang, Rongbo Zhang, Zucan Lin, Meng Wang, Yongqing Wang, and Qisheng Zhang. 2025. "Miniaturizing Controlled-Source EM Transmitters for Urban Underground Surveys: A Bipolar Square-Wave Inverter Approach with SiC-MOSFETs" Sensors 25, no. 13: 4183. https://doi.org/10.3390/s25134183
APA StyleWu, Z., Zhang, K., Zhang, R., Lin, Z., Wang, M., Wang, Y., & Zhang, Q. (2025). Miniaturizing Controlled-Source EM Transmitters for Urban Underground Surveys: A Bipolar Square-Wave Inverter Approach with SiC-MOSFETs. Sensors, 25(13), 4183. https://doi.org/10.3390/s25134183






