Wavelet-Based P-Wave Detection in High-Rate GNSS Data: A Novel Approach for Rapid Earthquake Monitoring in Tsunamigenic Settings
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Acquisition and Sources
2.2. GNSS Data Processing
2.3. P-Wave Detection Using Dynamic Wavelet Thresholding
3. Results
3.1. Padang Earthquake—30 September 2009 (Mw 7.6)
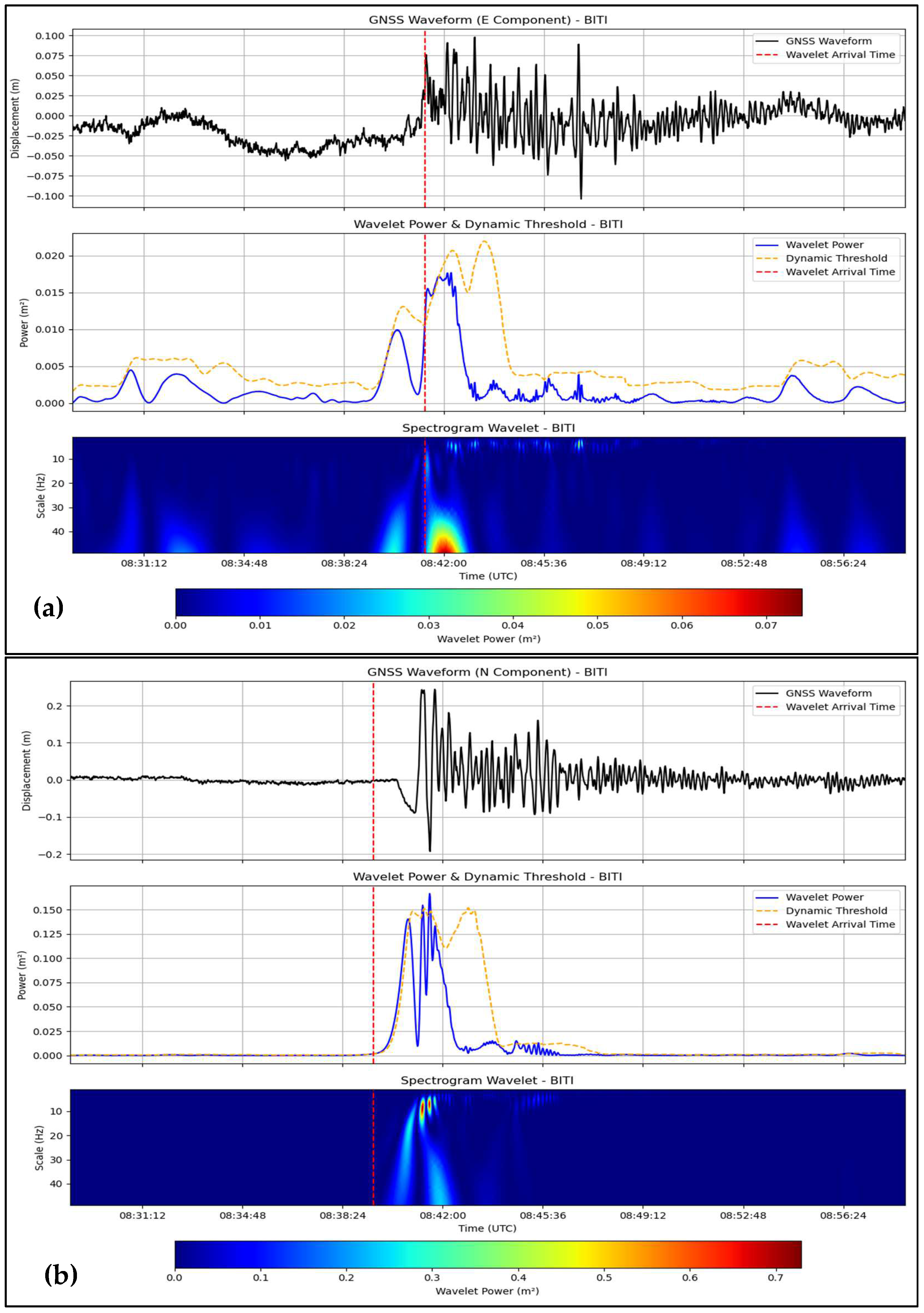
3.2. Simeulue Earthquake—11 April 2012 (Mw 8.6)
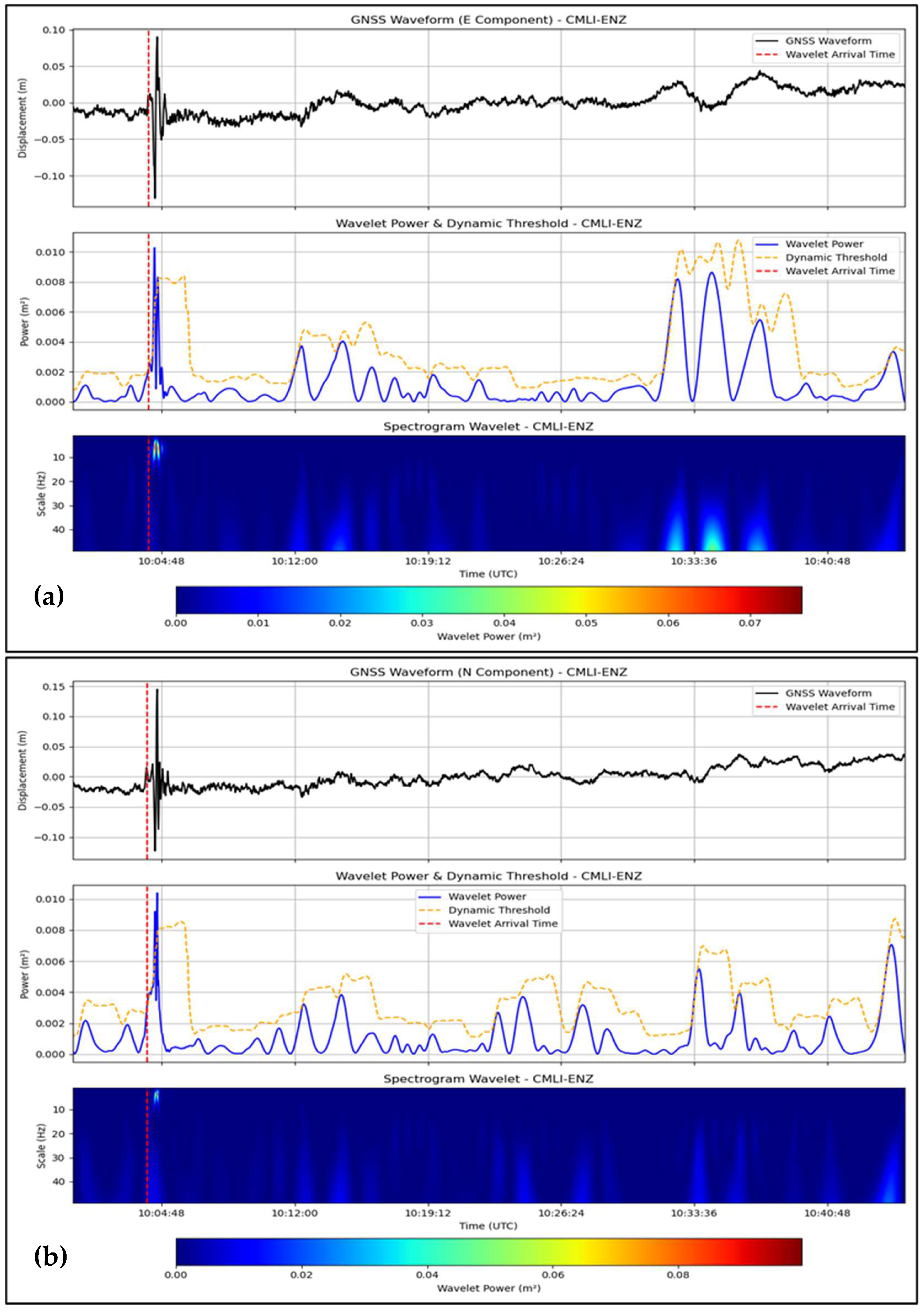
3.3. Palu Earthquake—28 September 2018 (Mw 7.5)
3.4. Comparison with STA/LTA Method
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stein, S.; Wysession, M. An Introduction to Seismology, Earthquakes, and Earth Structure, 2nd ed.; Blackwell Publishing: Hoboken, NJ, USA, 2003; ISBN 0865420785/9780865420786. [Google Scholar]
- Shearer, P.M. Introduction to Seismology; Cambridge University Press: Cambridge, UK, 2009; ISBN 0521882109/9780521882101. [Google Scholar]
- Juhel, K.; Ampuero, J.P.; Barsuglia, M.; Bernard, P.; Chassande-Mottin, E.; Fiorucci, D.; Harms, J.; Montagner, J.-P.; Vallée, M.; Whiting, B.F. Earthquake Early Warning Using Future Generation Gravity Strainmeters. J. Geophys. Res. Solid. Earth 2018, 123, 10889–10902. [Google Scholar] [CrossRef]
- Licciardi, A.; Bletery, Q.; Rouet-Leduc, B.; Ampuero, J.-P.; Juhel, K. Instantaneous Tracking of Earthquake Growth with Elastogravity Signals. Nature 2022, 606, 319–324. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhang, M.; Tian, X. Real-Time Earthquake Early Warning with Deep Learning: Application to the 2016 M 6.0 Central Apennines, Italy Earthquake. Geophys. Res. Lett. 2021, 48, 2020GL089394. [Google Scholar] [CrossRef]
- Kodera, Y. Real-Time Detection of Rupture Development: Earthquake Early Warning Using P Waves from Growing Ruptures. Geophys. Res. Lett. 2018, 45, 156–165. [Google Scholar] [CrossRef]
- van den Ende, M.P.A.; Ampuero, J.-P. Evaluating Seismic Beamforming Capabilities of Distributed Acoustic Sensing Arrays. Solid Earth 2021, 12, 915–934. [Google Scholar] [CrossRef]
- Chakraborty, M.; Fenner, D.; Li, W.; Faber, J.; Zhou, K.; Rümpker, G.; Stoecker, H.; Srivastava, N. CREIME—A Convolutional Recurrent Model for Earthquake Identification and Magnitude Estimation. J. Geophys. Res. Solid. Earth 2022, 127, e2022JB024595. [Google Scholar] [CrossRef]
- Seo, J.; Kim, Y.; Ha, J.; Kwak, D.; Ko, M.; Yoo, M. Unsupervised Anomaly Detection for Earthquake Detection on Korea High-Speed Trains Using Autoencoder-Based Deep Learning Models. Sci. Rep. 2024, 14, 639. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.; Du, F.; Shu, Y.; Zhang, H.; Shi, Y. Regularized Reconstruction of Peak Ground Velocity and Acceleration from Very High-Rate GNSS Precise Point Positioning with Applications to the 2013 Lushan Mw6.6 Earthquake. J. Geod. 2021, 95, 17. [Google Scholar] [CrossRef]
- Wang, S.; Song, C.; Li, S.; Li, X. Resolving Co- and Early Post-Seismic Slip Variations of the 2021 MW 7.4 Maduo Earthquake in East Bayan Har Block with a Block-Wide Distributed Deformation Mode from Satellite Synthetic Aperture Radar Data. Earth Planet. Phys. 2022, 6, 106–120. [Google Scholar] [CrossRef]
- Gao, Z.; Li, Y.; Shan, X.; Zhu, C. Earthquake Magnitude Estimation from High-Rate GNSS Data: A Case Study of the 2021 Mw 7.3 Maduo Earthquake. Remote Sens. 2021, 13, 4478. [Google Scholar] [CrossRef]
- Wilkinson, M.W.; McCaffrey, K.J.W.; Jones, R.R.; Roberts, G.P.; Holdsworth, R.E.; Gregory, L.C.; Walters, R.J.; Wedmore, L.; Goodall, H.; Iezzi, F. Near-Field Fault Slip of the 2016 Vettore Mw 6.6 Earthquake (Central Italy) Measured Using Low-Cost GNSS. Sci. Rep. 2017, 7, 4612. [Google Scholar] [CrossRef] [PubMed]
- Ravanelli, M.; Occhipinti, G.; Savastano, G.; Komjathy, A.; Shume, E.B.; Crespi, M. GNSS Total Variometric Approach: First Demonstration of a Tool for Real-Time Tsunami Genesis Estimation. Sci. Rep. 2021, 11, 3114. [Google Scholar] [CrossRef] [PubMed]
- Ruhl, C.J.; Melgar, D.; Grapenthin, R.; Allen, R.M. The Value of Real-time GNSS to Earthquake Early Warning. Geophys. Res. Lett. 2017, 44, 8311–8319. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Bock, Y. Self-contained Local Broadband Seismogeodetic Early Warning System: Detection and Location. J. Geophys. Res. Solid. Earth 2017, 122, 3197–3220. [Google Scholar] [CrossRef]
- Zhang, H. Automatic P-Wave Arrival Detection and Picking with Multiscale Wavelet Analysis for Single-Component Recordings. Bull. Seismol. Soc. Am. 2003, 93, 1904–1912. [Google Scholar] [CrossRef]
- Shang, X.; Li, X.; Weng, L. Enhancing Seismic P Phase Arrival Picking Based on Wavelet Denoising and Kurtosis Picker. J. Seismol. 2018, 22, 21–33. [Google Scholar] [CrossRef]
- Akram, J.; Eaton, D.W. A Review and Appraisal of Arrival-Time Picking Methods for Downhole Microseismic Data. Geophysics 2016, 81, KS71–KS91. [Google Scholar] [CrossRef]
- Zeng, C.; Lin, H.; Jiang, Q.; Xu, M. QRS Complex Detection Using Combination of Mexican-Hat Wavelet and Complex Morlet Wavelet. J. Comput. 2013, 8, 2951–2958. [Google Scholar] [CrossRef]
- Singh, A.; Rawat, A. The Mexican Hat Wavelet Stieltjes Transform. Filomat 2023, 37, 2717–2730. [Google Scholar] [CrossRef]
- Singh, A.; Rawat, A.; Raghuthaman, N. Mexican Hat Wavelet Transform and Its Applications. In Methods of Mathematical Modelling and Computation for Complex Systems; Singh, J., Dutta, H., Kumar, D., Baleanu, D., Hristov, J., Eds.; Springer: Cham, Switzerland, 2022; pp. 299–317. ISBN 978-3-030-77169-0. [Google Scholar]
- Geng, J.; Chen, X.; Pan, Y.; Mao, S.; Li, C.; Zhou, J.; Zhang, K. PRIDE PPP-AR: An Open-Source Software for GPS PPP Ambiguity Resolution. GPS Solut. 2019, 23, 91. [Google Scholar] [CrossRef]
- Beyreuther, M.; Barsch, R.; Krischer, L.; Megies, T.; Behr, Y.; Wassermann, J. ObsPy: A Python Toolbox for Seismology. Seismol. Res. Lett. 2010, 81, 530–533. [Google Scholar] [CrossRef]
- Megies, T.; Beyreuther, M.; Barsch, R.; Krischer, L.; Wassermann, J. ObsPy—What can it do for data centers and observatories? Ann. Geophys. 2011, 54, 47–58. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array Programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Lee, S.L. Wavelets: A Tool for Efficient Data Representation. In Proceedings of the International Conference on Computer Graphics, Imaging and Visuualization, CGIV 2004, Penang, Malaysia, 2 July 2004; p. 199. [Google Scholar]
- Mallat, S. A Wavelet Tour of Signal Processing: The Sparse Way; Academic Press: Cambridge, MA, USA, 2009; Volume 3. [Google Scholar]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Li, X.; Zheng, K.; Li, X.; Liu, G.; Ge, M.; Wickert, J.; Schuh, H. Real-Time Capturing of Seismic Waveforms Using High-Rate BDS, GPS and GLONASS Observations: The 2017 Mw 6.5 Jiuzhaigou Earthquake in China. GPS Solut. 2019, 23, 17. [Google Scholar] [CrossRef]
- Fuchs, M.J.; Rexer, M.; Schaider, F. Detection and Analysis of Seismic Induced GNSS Station Motion in a North American Network Following the 2017 Chiapas Earthquake. J. Geodyn. 2022, 149, 101881. [Google Scholar] [CrossRef]
- Ringler, A.T.; Wilson, D.C.; Storm, T.; Marshall, B.; Hutt, C.R.; Holland, A.A. Noise Reduction in Long-Period Seismograms by Way of Array Summing. Bull. Seismol. Soc. Am. 2016, 106, 1991–1997. [Google Scholar] [CrossRef]
- Hameed, M.S.; Li, Z.; Zheng, K. Damage Detection Method Based on Continuous Wavelet Transformation of Lamb Wave Signals. Appl. Sci. 2020, 10, 8610. [Google Scholar] [CrossRef]
- Moya-Cessa, H.M. The Illustrated Wavelet Transform Handbook: Introductory Theory and Applications in Science, Engineering, Medicine and Finance, 2nd Edition, by P. S. Addison. Contemp. Phys. 2018, 59, 100. [Google Scholar] [CrossRef]
- Murray, J.R.; Bartlow, N.; Bock, Y.; Brooks, B.A.; Foster, J.; Freymueller, J.; Hammond, W.C.; Hodgkinson, K.; Johanson, I.; López-Venegas, A.; et al. Regional Global Navigation Satellite System Networks for Crustal Deformation Monitoring. Seismol. Res. Lett. 2019, 91, 552–572. [Google Scholar] [CrossRef]
- Kawamoto, S.; Hiyama, Y.; Ohta, Y.; Nishimura, T. First Result from the GEONET Real-Time Analysis System (REGARD): The Case of the 2016 Kumamoto Earthquakes. Earth Planets Space 2016, 68, 190. [Google Scholar] [CrossRef]
- Melgar, D.; Melbourne, T.I.; Crowell, B.W.; Geng, J.; Szeliga, W.; Scrivner, C.; Santillan, M.; Goldberg, D.E. Real-Time High-Rate GNSS Displacements: Performance Demonstration during the 2019 Ridgecrest, California, Earthquakes. Seismol. Res. Lett. 2020, 91, 1943–1951. [Google Scholar] [CrossRef]
- Crowell, B.W.; Bock, Y.; Squibb, M.B. Demonstration of Earthquake Early Warning Using Total Displacement Waveforms from Real-Time GPS Networks. Seismol. Res. Lett. 2009, 80, 772–782. [Google Scholar] [CrossRef]
- Cremen, G.; Galasso, C.; Zuccolo, E. Investigating the Potential Effectiveness of Earthquake Early Warning across Europe. Nat. Commun. 2022, 13, 639. [Google Scholar] [CrossRef]
- Jakka, R.S.; Garg, S. Suitable Triggering Algorithms for Detecting Strong Ground Motions Using MEMS Accelerometers. Earthq. Eng. Eng. Vib. 2015, 14, 27–35. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Melgar, D.; Hayes, G.P.; Crowell, B.W.; Sahakian, V.J. A Ground-Motion Model for GNSS Peak Ground Displacement. Bull. Seismol. Soc. Am. 2021, 111, 2393–2407. [Google Scholar] [CrossRef]
- Crowell, B.W.; Melgar, D.; Bock, Y.; Haase, J.S.; Geng, J. Earthquake Magnitude Scaling Using Seismogeodetic Data. Geophys. Res. Lett. 2013, 40, 6089–6094. [Google Scholar] [CrossRef]
- Zhao, H.; Bai, T.; Chen, Y. Background Noise Suppression for DAS-VSP Records Using GC-AB-Unet. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Sasikala, S.; Sivaranjani, P.; Meeradevi, T.; Udhayasuriyan, V. Two Stage Step-Size Adaptive Filter Design for ECG Denoising. In Proceedings of the 2024 15th International Conference on Computing Communication and Networking Technologies (ICCCNT), Kamand, India, 24–28 June 2024; pp. 1–7. [Google Scholar]
- Oboué, Y.A.S.I.; Chen, Y.; Fomel, S.; Chen, Y. Protecting the Weak Signals in Distributed Acoustic Sensing Data Processing Using Local Orthogonalization: The FORGE Data Example. Geophysics 2024, 89, V103–V118. [Google Scholar] [CrossRef]
- Chen, J.; Chen, G.; Li, J.; Du, R.; Qi, Y.; Li, C.; Wang, N. Efficient Seismic Data Denoising via Deep Learning with Improved MCA-SCUNet. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–14. [Google Scholar] [CrossRef]
- Xiong, F.Q.; Ao, B.Q. The Simulation and Application in Eliminating Noise of Adaptive Filter. Appl. Mech. Mater. 2013, 364, 449–452. [Google Scholar] [CrossRef]
- Zhang, H.; Dong, Y.; Pang, S.; Li, S. Research on Neural Network Adaptive Noise Cancellation Technique Based on BP Algorithm. In Proceedings of the 2024 8th International Conference on High Performance Compilation, Computing and Communications, Guangzhou China, 7–9 June 2024; ACM: New York, NY, USA, 2024; pp. 76–81. [Google Scholar]
- Li, X.; Ge, M.; Dai, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Accuracy and Reliability of Multi-GNSS Real-Time Precise Positioning: GPS, GLONASS, BeiDou, and Galileo. J. Geod. 2015, 89, 607–635. [Google Scholar] [CrossRef]


| Events | Stations GNSS | Distance | Components | P Arrival Time (Wavelet) | Stations Seismic BMKG | Distance (Km) | P Arrival Time (Seismic) |
|---|---|---|---|---|---|---|---|
| Padang 30 September 2009 Mw 7.6 | PSKI | 69.62 | E | 10:16:47.00 | PDSI | 66.6 | 10:16:26.0 |
| N | 10:16:56.00 | ||||||
| U | 10:06:41.00 | ||||||
| PKRT | 162.26 | E | 10:16:10.00 | SDSI | 177.6 | 10:16:37.6 | |
| N | 10:16:10.00 | ||||||
| U | 10:06:44.00 | ||||||
| Simelue 11 April 2012 Mw 8.6 | PBLI | 483.33 | E | 8:38:37.00 | TPTI | 466.2 | 8:39:37.20 |
| N | 8:39:12.00 | ||||||
| U | 8:40:57.00 | ||||||
| BITI | 545.94 | E | 8:41:19.00 | KCSI | 543.9 | 8:39:47.90 | |
| N | 8:39:30.00 | ||||||
| U | 8:54:24.00 | ||||||
| Palu 28 September 2018 Mw 7.5 | CMLI | 297.62 | E | 10:04:07.00 | SRSI | 277.5 | 10:03:24.9 |
| N | 10:04:00.00 | ||||||
| U | 10:00:50.00 | ||||||
| CBAL | 352.43 | E | 10:06:56.00 | BKB | 344.1 | 10:03:31.2 | |
| N | 10:04:39.00 | ||||||
| U | 10:06:53.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sudrajat, A.; Meilano, I.; Abidin, H.Z.; Susilo, S.; Hardy, T.; Samapta, B.T.; Kautsar, M.A.; Kambali, R.A.P. Wavelet-Based P-Wave Detection in High-Rate GNSS Data: A Novel Approach for Rapid Earthquake Monitoring in Tsunamigenic Settings. Sensors 2025, 25, 3860. https://doi.org/10.3390/s25133860
Sudrajat A, Meilano I, Abidin HZ, Susilo S, Hardy T, Samapta BT, Kautsar MA, Kambali RAP. Wavelet-Based P-Wave Detection in High-Rate GNSS Data: A Novel Approach for Rapid Earthquake Monitoring in Tsunamigenic Settings. Sensors. 2025; 25(13):3860. https://doi.org/10.3390/s25133860
Chicago/Turabian StyleSudrajat, Ajat, Irwan Meilano, Hasanuddin Z. Abidin, Susilo Susilo, Thomas Hardy, Brilian Tatag Samapta, Muhammad Al Kautsar, and Retno Agung P. Kambali. 2025. "Wavelet-Based P-Wave Detection in High-Rate GNSS Data: A Novel Approach for Rapid Earthquake Monitoring in Tsunamigenic Settings" Sensors 25, no. 13: 3860. https://doi.org/10.3390/s25133860
APA StyleSudrajat, A., Meilano, I., Abidin, H. Z., Susilo, S., Hardy, T., Samapta, B. T., Kautsar, M. A., & Kambali, R. A. P. (2025). Wavelet-Based P-Wave Detection in High-Rate GNSS Data: A Novel Approach for Rapid Earthquake Monitoring in Tsunamigenic Settings. Sensors, 25(13), 3860. https://doi.org/10.3390/s25133860







