Improving High-Precision BDS-3 Satellite Orbit Prediction Using a Self-Attention-Enhanced Deep Learning Model
Abstract
1. Introduction
2. Methodology
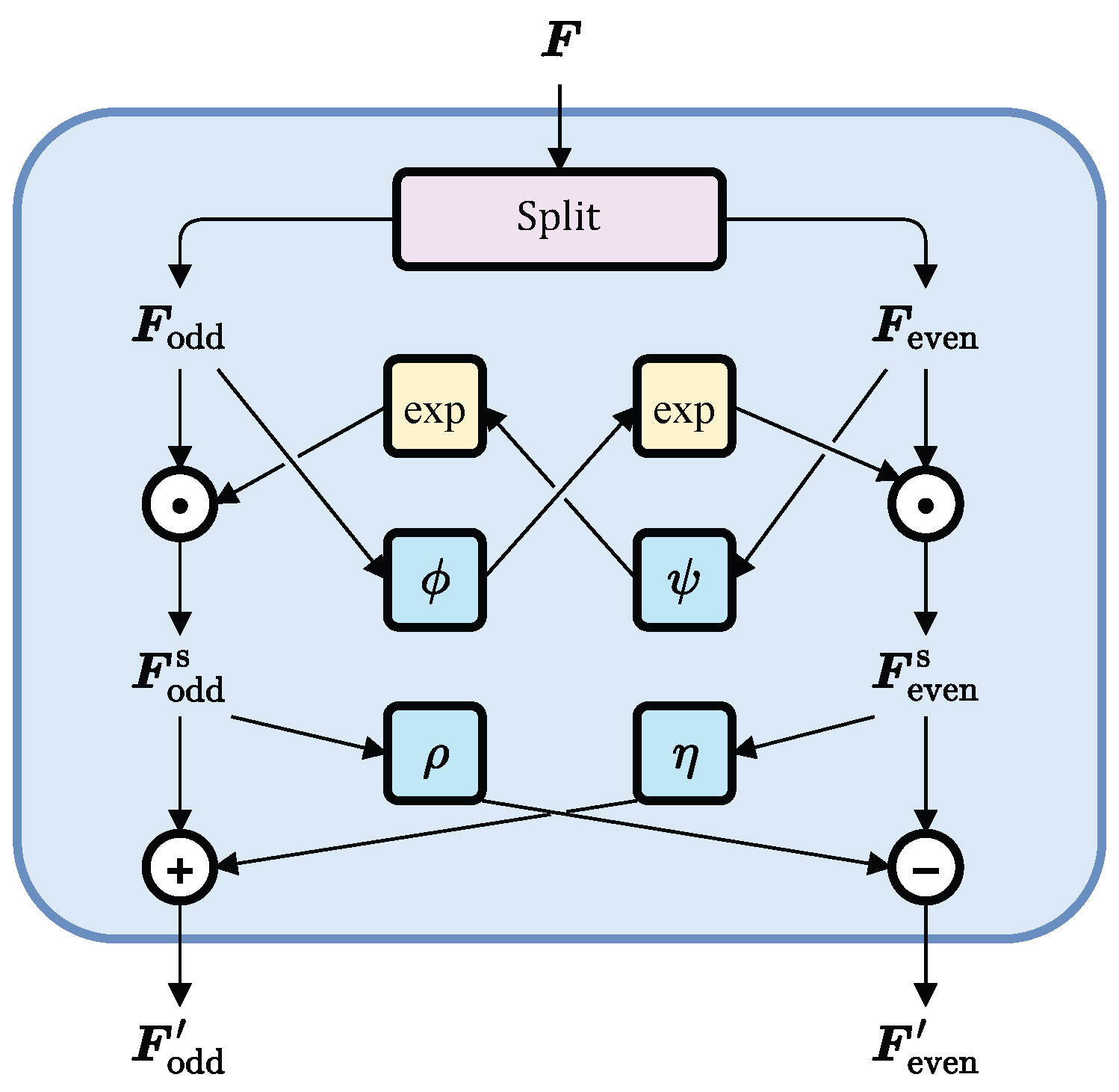
2.1. SCINet-SA
2.1.1. SCINet Module
2.1.2. Attention Module
2.2. Workflow of the Algorithm
2.2.1. Ephemeris File Reading
2.2.2. Data Pre-Processing
2.2.3. Model Training/Prediction
3. Experiments
3.1. Model Evaluation Strategy
3.2. Results and Analyses
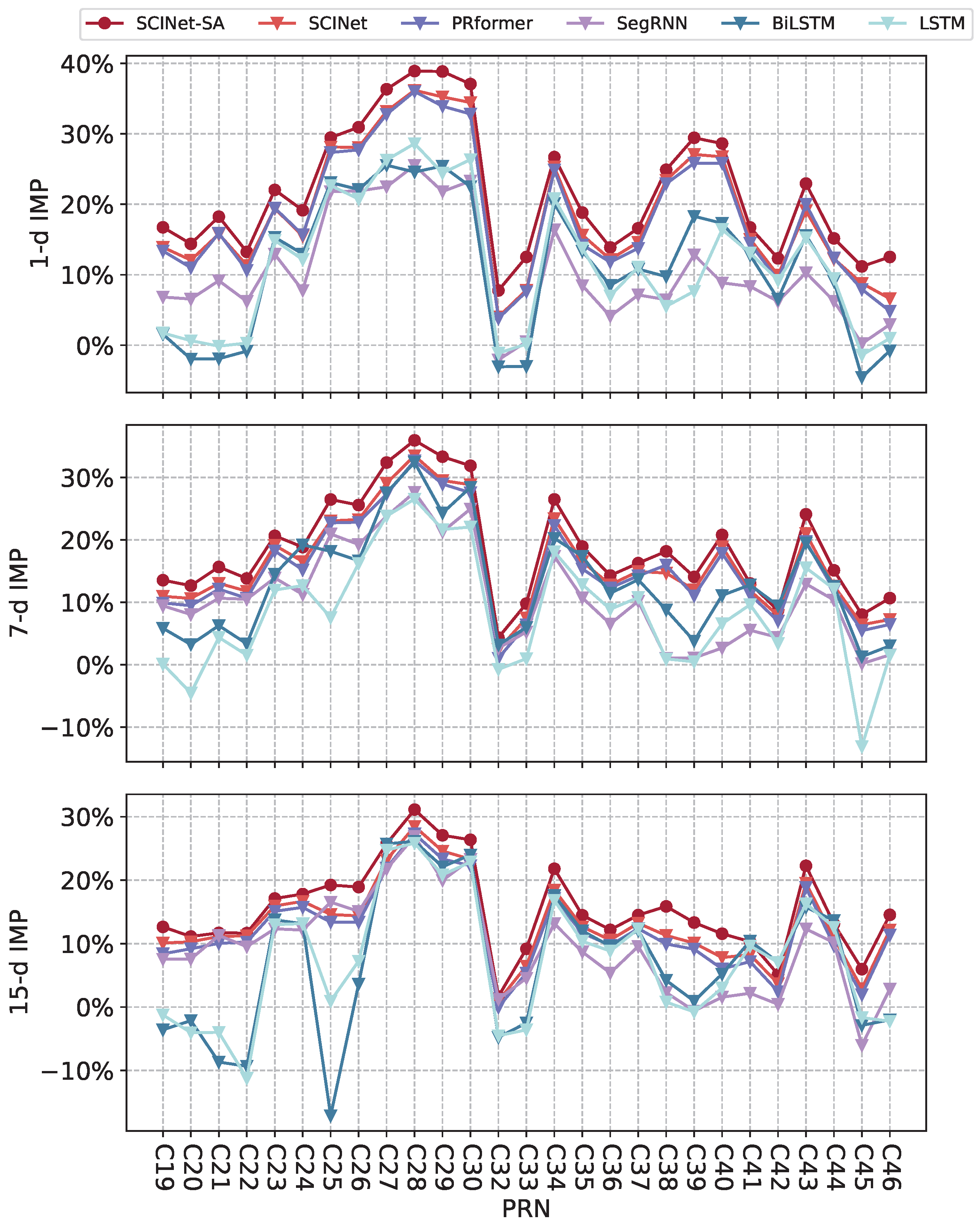
3.2.1. Performance Comparison of SCINet-SA with Other Models
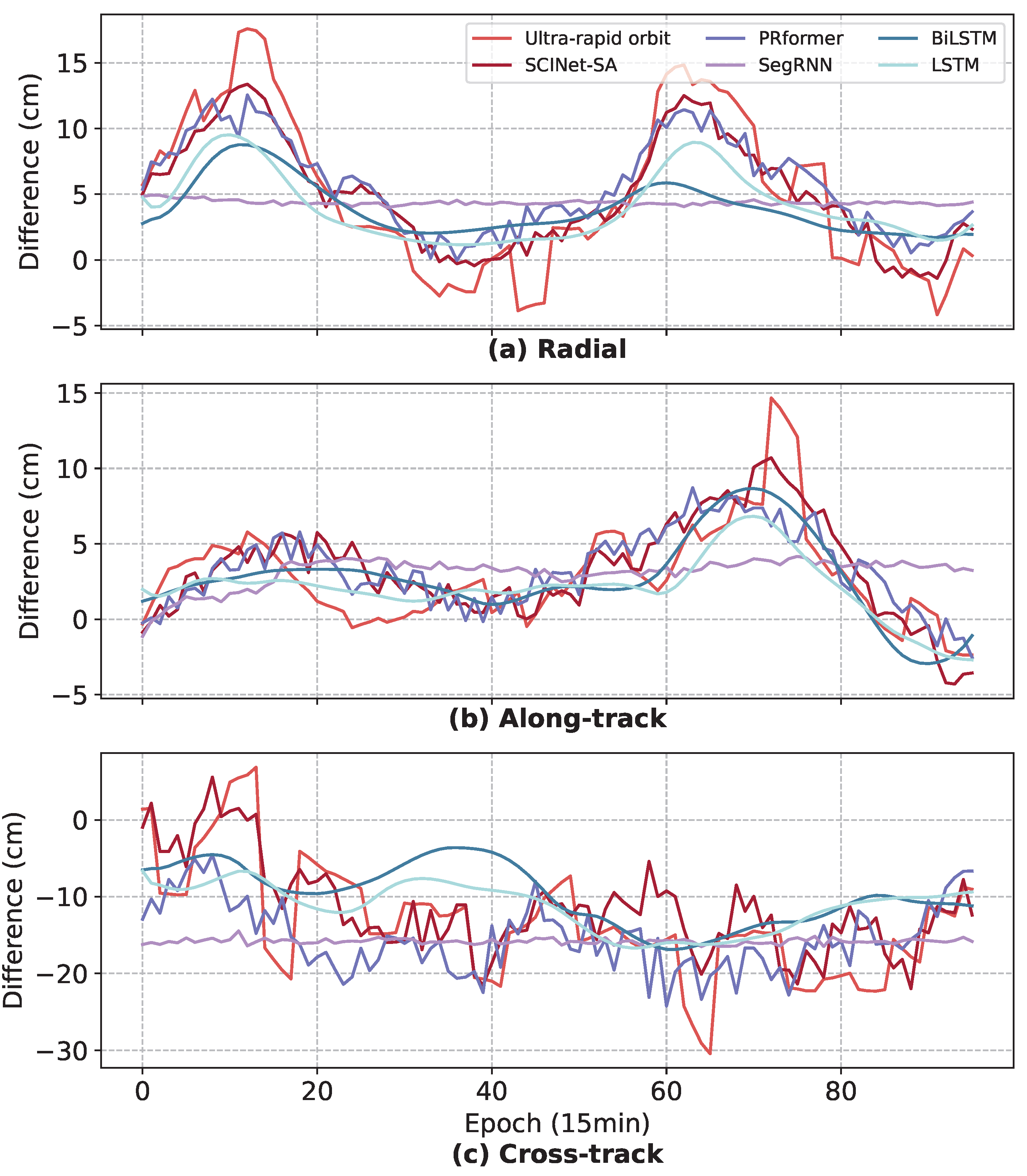
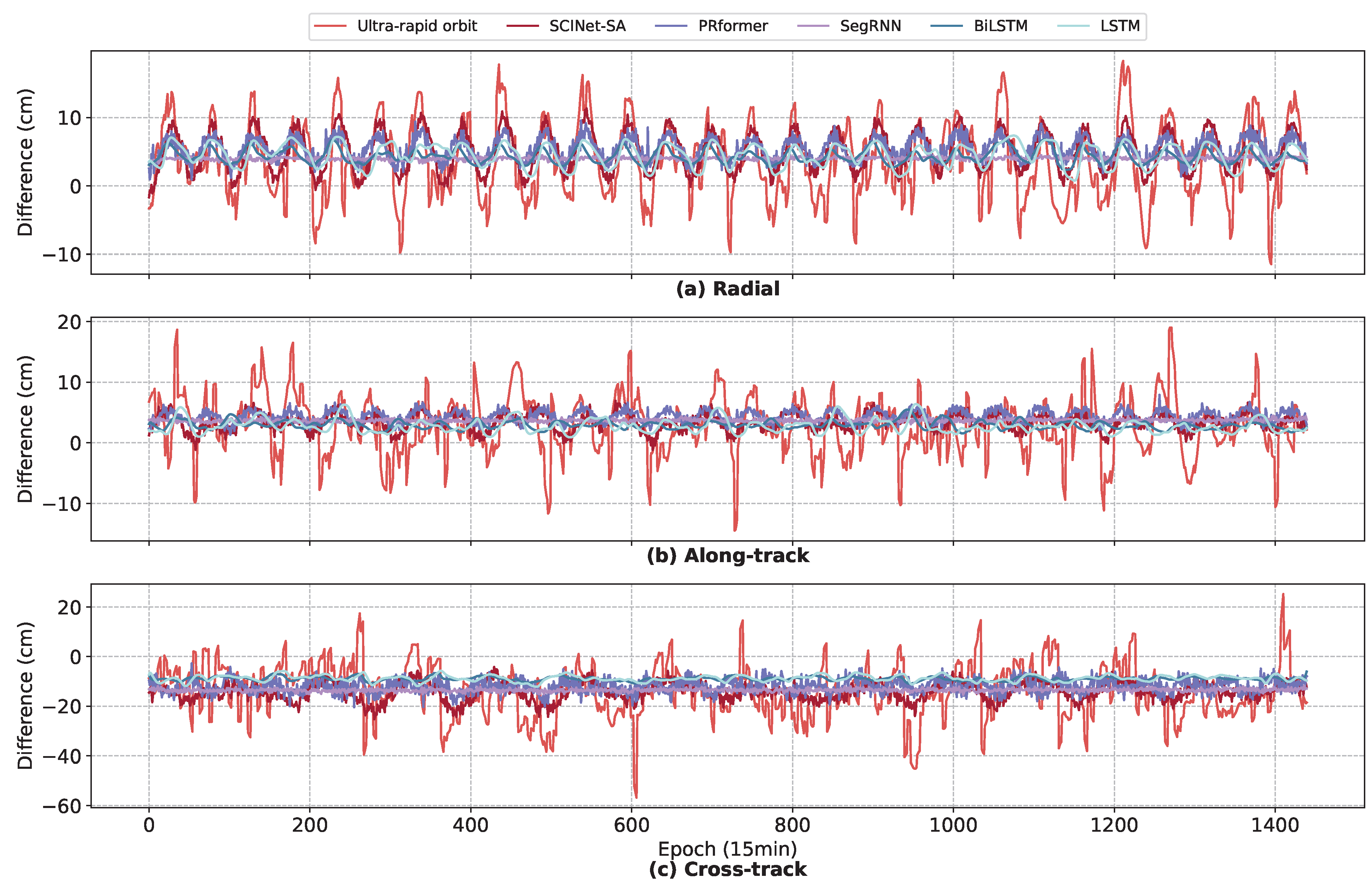
3.2.2. Analysis of RTN Differences Prediction Results
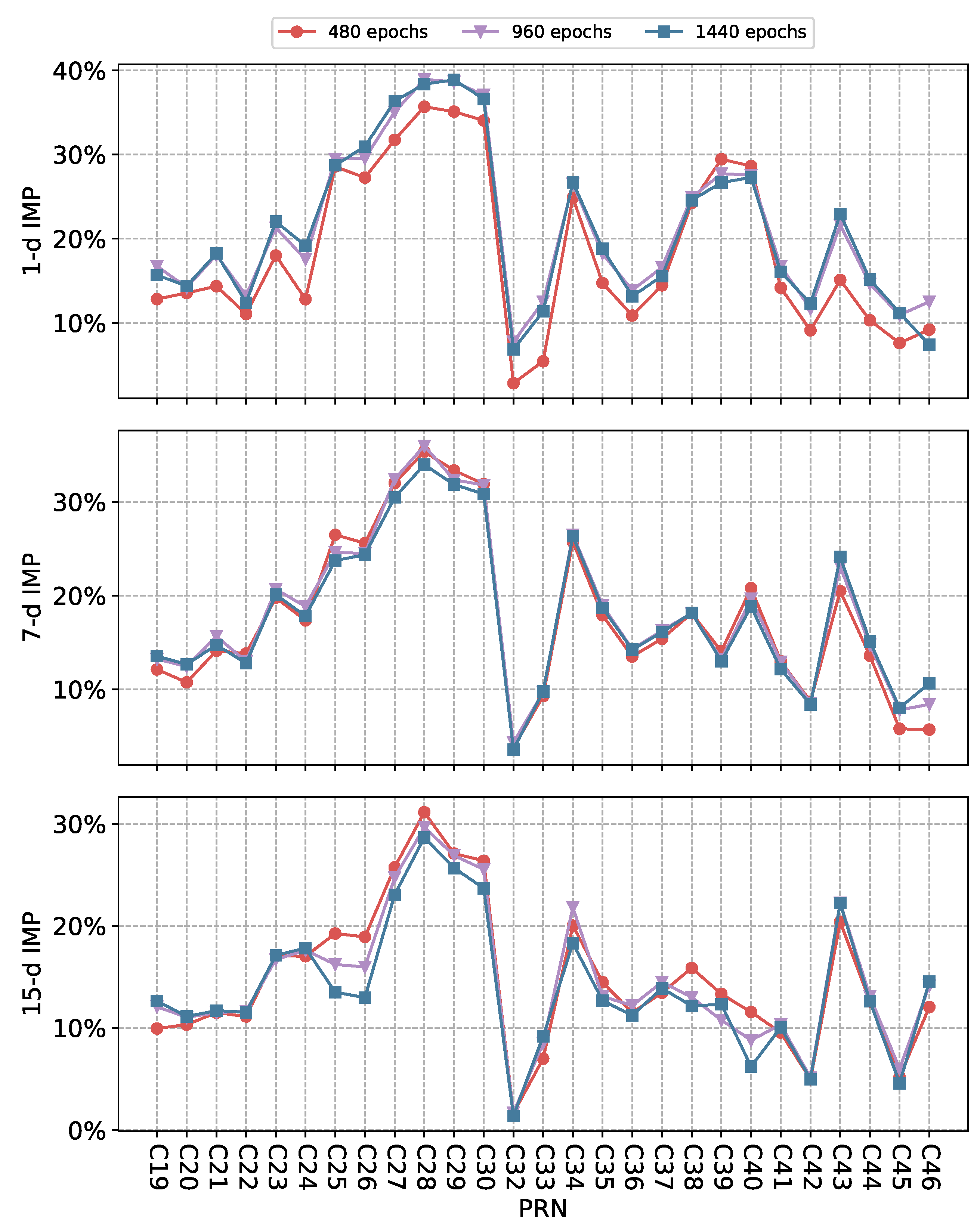
3.2.3. Performance Comparison of SCINet-SA with Different Observation Windows
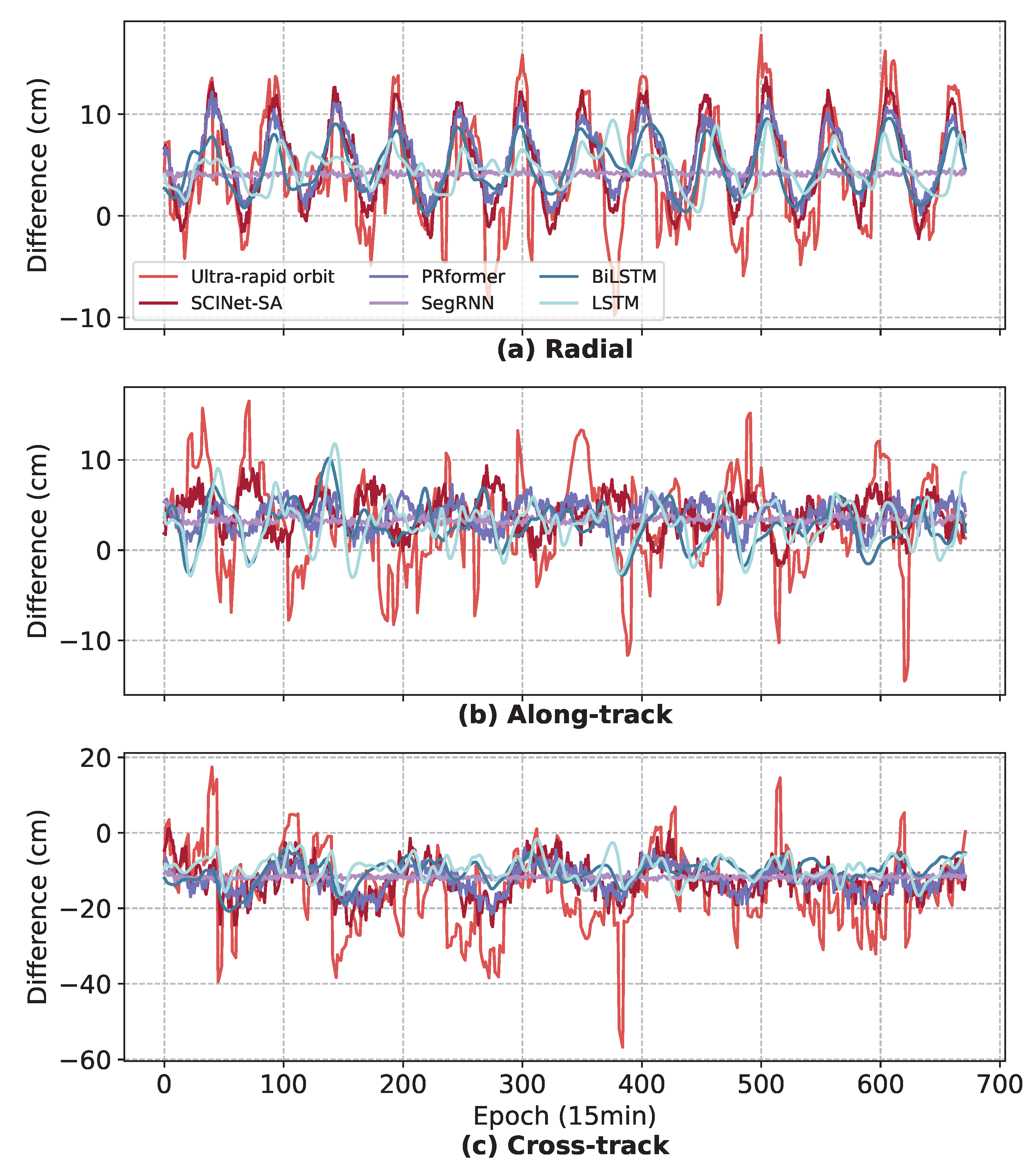
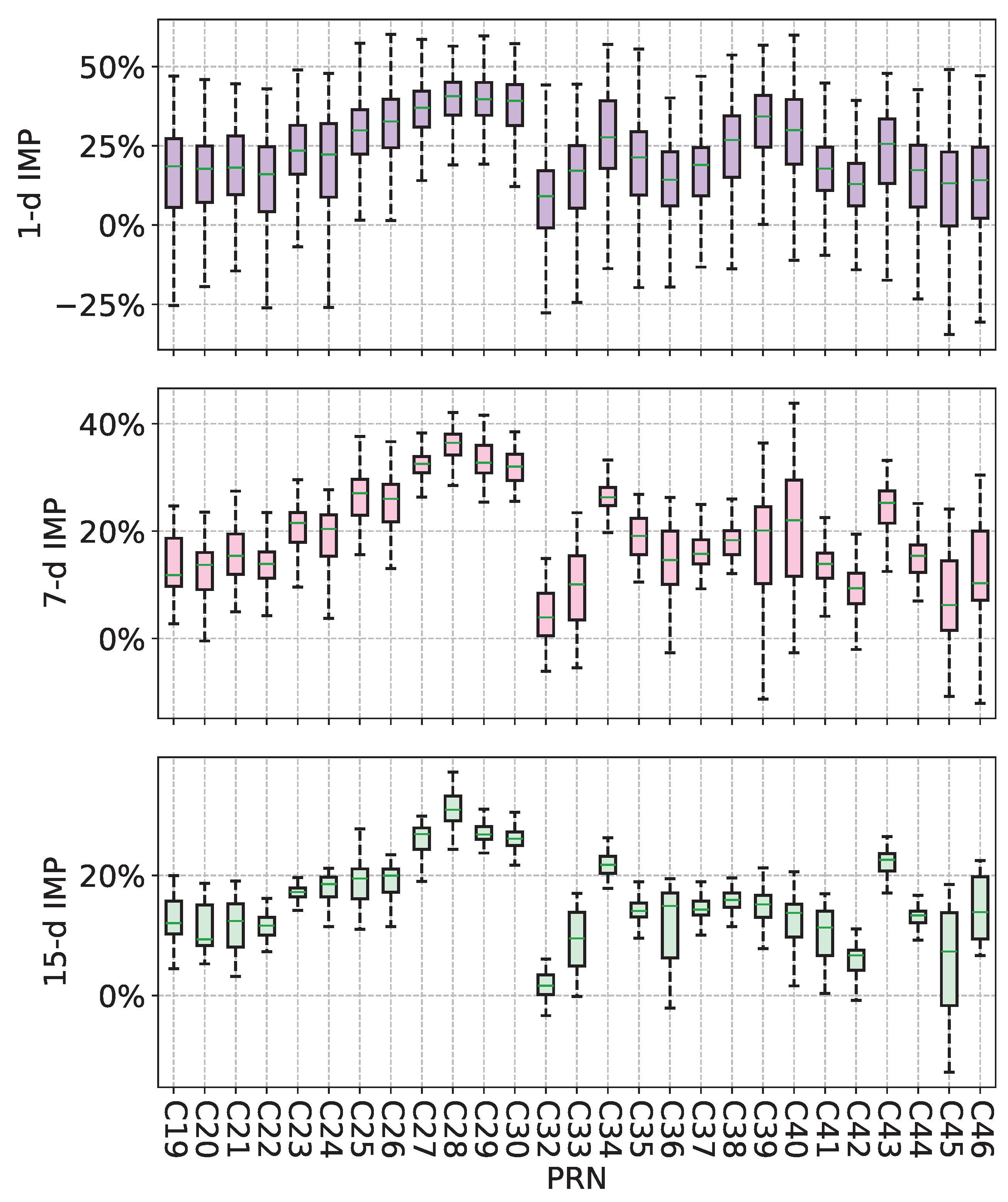
3.2.4. Reliability Analysis of SCINet-SA
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | Analysis Centers |
| AI | Artificial intelligence |
| BDS | BeiDou Navigation Satellite System |
| BiLSTM | Bidirectional Long Short-Term Memory |
| BP | Back Propagation |
| CNN | Convolutional Neural Networks |
| DBSCAN | Density-Based Spatial Clustering of Applications with Noise |
| DL | Deep learning |
| ECEF | Earth-Centered Earth-Fixed |
| ECI | Earth-Centered Inertial |
| EOP | Earth Orientation Parameters |
| FNN | Feed-Forward Neural Networks |
| GNSS | Global Navigation Satellite System |
| GPS | Global Positioning System |
| IERS | International Earth Rotation and Reference Systems Service |
| IGS | International GNSS Service |
| IGSO | Inclined Geosynchronous Orbit |
| ILRS | International Laser Ranging Service |
| IMP | Improvement |
| LSTM | Long-Short Term Memory |
| MAE | Mean Absolute Error |
| MEO | Medium Earth Orbit |
| MGEX | Multi-GNSS Experiment |
| ML | Machine learning |
| PRformer | Pyramidal Recurrent Transformer |
| PRN | Pseudo-Random Noise |
| RNN | Recurrent Neural Networks |
| RTN | Radial, Along-Track, Cross-Track |
| SCINet-SA | Sample Convolution and Interaction Network with Self-Attention |
| SGD | Stochastic Gradient Descent |
| SGP4 | Simplified General Perturbations Model 4 |
| SegRNN | Segment Recurrent Neural Network |
| SVM | Support Vector Machine |
| TLE | Two-Line Orbital Element |
| UT1 | Universal Time |
| UTC | Coordinated Universal Time |
| WHU | Wuhan University |
| 3D | Three-Dimensional |
Appendix A. Hyperparameters for SCINet-SA
| Hyperparameter | Description | Value |
|---|---|---|
| level | The level count of SCI-Blocks | 4 |
| kernel | Convolution kernel size of convolutional filters | 5 |
| dilation | Whether to use dilation convolution | True |
| optimizer | Optimizer used | Adam |
| lr | Learning rate | |
| dropout | Dropout value in convolutional filters | 0.5 |
| loss | Loss function | MAE |
| n_head | Number of attention heads | 1 |
| batch_size | Batch size value | 128 |
| patience | Threshold for early stopping strategy | 3 |
| d_model | Input dimension of the attention module | 3 |
| input_len | Input length of SCINet-SA | 480/960/1440 |
| output_len | Output length of SCINet-SA | 96/672/1440 |
References
- Li, X.; Wang, H.; Li, S.; Feng, S.; Wang, X.; Liao, J. GIL: A Tightly Coupled GNSS PPP/INS/LiDAR Method for Precise Vehicle Navigation. Satell. Navig. 2021, 2, 26. [Google Scholar] [CrossRef]
- Li, S.; Li, X.; Wang, H.; Zhou, Y.; Shen, Z. Multi-GNSS PPP/INS/Vision/LiDAR Tightly Integrated System for Precise Navigation in Urban Environments. Inf. Fusion 2023, 90, 218–232. [Google Scholar] [CrossRef]
- Huang, G.; Du, S.; Wang, D. GNSS Techniques for Real-Time Monitoring of Landslides: A Review. Satell. Navig. 2023, 4, 5. [Google Scholar] [CrossRef]
- Wang, D.; Huang, G.; Du, Y.; Zhang, Q.; Bai, Z.; Tian, J. Stability Analysis of Reference Station and Compensation for Monitoring Stations in GNSS Landslide Monitoring. Satell. Navig. 2023, 4, 29. [Google Scholar] [CrossRef]
- Nijak, M.; Skrzypczyński, P.; Ćwian, K.; Zawada, M.; Szymczyk, S.; Wojciechowski, J. On the Importance of Precise Positioning in Robotised Agriculture. Remote Sens. 2024, 16, 985. [Google Scholar] [CrossRef]
- Geng, T.; Zhang, P.; Wang, W.; Xie, X. Comparison of Ultra-Rapid Orbit Prediction Strategies for GPS, GLONASS, Galileo and BeiDou. Sensors 2018, 18, 477. [Google Scholar] [CrossRef]
- Yigit, C.O.; El-Mowafy, A.; Bezcioglu, M.; Dindar, A.A. Investigating the Effects of Ultra-Rapid, Rapid vs. Final Precise Orbit and Clock Products on High-Rate GNSS-PPP for Capturing Dynamic Displacements. Struct. Eng. Mech. 2020, 73, 427–436. [Google Scholar] [CrossRef]
- Li, B.; Ge, H.; Bu, Y.; Zheng, Y.; Yuan, L. Comprehensive Assessment of Real-Time Precise Products from IGS Analysis Centers. Satell. Navig. 2022, 3, 12. [Google Scholar] [CrossRef]
- Dai, X.; Ge, M.; Lou, Y.; Shi, C.; Wickert, J.; Schuh, H. Estimating the Yaw-Attitude of BDS IGSO and MEO Satellites. J. Geod. 2015, 89, 1005–1018. [Google Scholar] [CrossRef]
- Xia, F.; Ye, S.; Chen, D.; Jiang, N. Observation of BDS-2 IGSO/MEOs Yaw-Attitude Behavior during Eclipse Seasons. GPS Solut. 2019, 23, 71. [Google Scholar] [CrossRef]
- Guo, J.; Chen, G.; Zhao, Q.; Liu, J.; Liu, X. Comparison of Solar Radiation Pressure Models for BDS IGSO and MEO Satellites with Emphasis on Improving Orbit Quality. GPS Solut. 2017, 21, 511–522. [Google Scholar] [CrossRef]
- Chen, X.; Ge, M.; Liu, Y.; He, L.; Schuh, H. Adapting Empirical Solar Radiation Pressure Model for BDS-3 Medium Earth Orbit Satellites. GPS Solut. 2023, 27, 183. [Google Scholar] [CrossRef]
- Levit, C.; Marshall, W. Improved Orbit Predictions Using Two-Line Elements. Adv. Space Res. 2011, 47, 1107–1115. [Google Scholar] [CrossRef]
- Bennett, J.C.; Sang, J.; Smith, C.; Zhang, K. Improving Low-Earth Orbit Predictions Using Two-Line Element Data with Bias Correction. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, Maui, HI, USA, 11–14 September 2012; Volume 1, p. 46. [Google Scholar]
- San-Juan, J.F.; Pérez, I.; San-Martín, M.; Vergara, E.P. Hybrid SGP4 Orbit Propagator. Acta Astronaut. 2017, 137, 254–260. [Google Scholar] [CrossRef]
- Sang, J.; Li, B.; Chen, J.; Zhang, P.; Ning, J. Analytical Representations of Precise Orbit Predictions for Earth Orbiting Space Objects. Adv. Space Res. 2017, 59, 698–714. [Google Scholar] [CrossRef]
- Vallado, D.; Crawford, P. SGP4 orbit determination. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; p. 6770. [Google Scholar] [CrossRef]
- Peng, H.; Bai, X. Exploring Capability of Support Vector Machine for Improving Satellite Orbit Prediction Accuracy. J. Aerosp. Inf. Syst. 2018, 15, 366–381. [Google Scholar] [CrossRef]
- Peng, H.; Bai, X. Machine Learning Approach to Improve Satellite Orbit Prediction Accuracy Using Publicly Available Data. J. Astronaut. Sci. 2020, 67, 762–793. [Google Scholar] [CrossRef]
- San-Juana, J.F.; Pérezb, I.; Vergarac, E.; San Martınd, M.; Lópeze, R.; Wittigf, A.; Izzog, D. Hybrid SGP4 Propagator Based on Machine-Learning Techniques Applied to GALILEO-type Orbits. In Proceedings of the 69th International Astronautical Congress, Bremen, Germany, 1–5 October 2018; Volume 4. [Google Scholar]
- Curzi, G.; Modenini, D.; Tortora, P. Two-Line-Element Propagation Improvement and Uncertainty Estimation Using Recurrent Neural Networks. CEAS Space J. 2022, 14, 197–204. [Google Scholar] [CrossRef]
- Azmi, N.F.M.; Yuhaniz, S.S. An Adaptation of Deep Learning Technique in Orbit Propagation Model Using Long Short-Term Memory. In Proceedings of the 2021 International Conference on Electrical, Communication, and Computer Engineering (ICECCE), Kuala Lumpur, Malaysia, 12–13 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Shin, Y.; Park, E.J.; Woo, S.S.; Jung, O.; Chung, D. Selective Tensorized Multi-Layer Lstm for Orbit Prediction. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta, GA, USA, 17–21 October 2022; pp. 3495–3504. [Google Scholar]
- Li, B.; Zhang, Y.; Huang, J.; Sang, J. Improved Orbit Predictions Using Two-Line Elements through Error Pattern Mining and Transferring. Acta Astronaut. 2021, 188, 405–415. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, Z.; Gao, J.; Xu, C. Forecast Methods for Time Series Data: A Survey. IEEE Access 2021, 9, 91896–91912. [Google Scholar] [CrossRef]
- Pihlajasalo, J.; Leppäkoski, H.; Ali-Löytty, S.; Piché, R. Improvement of GPS and BeiDou Extended Orbit Predictions with CNNs. In Proceedings of the 2018 European Navigation Conference (ENC), Gothenburg, Sweden, 14–17 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 54–59. [Google Scholar]
- Chen, H.; Niu, F.; Su, X.; Geng, T.; Liu, Z.; Li, Q. Initial Results of Modeling and Improvement of BDS-2/GPS Broadcast Ephemeris Satellite Orbit Based on BP and PSO-BP Neural Networks. Remote Sens. 2021, 13, 4801. [Google Scholar] [CrossRef]
- Rothacher, M. Orbits of Satellite Systems in Space Geodesy; Institut ftlr Geodlsie mid Photogrammetrie: Zurich, Switzerland, 1992; Volume 46. [Google Scholar]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations Using RNN Encoder-Decoder for Statistical Machine Translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Liu, M.; Zeng, A.; Chen, M.; Xu, Z.; Lai, Q.; Ma, L.; Xu, Q. SCINet: Time Series Modeling and Forecasting with Sample Convolution and Interaction. Adv. Neural Inf. Process. Syst. 2022, 35, 5816–5828. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 1–11. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Hu, Y.; Xiao, F. Network Self Attention for Forecasting Time Series. Appl. Soft Comput. 2022, 124, 109092. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar]
- Shi, C.; Li, M.; Zhao, Q.; Geng, J.; Zhang, Q. Wuhan University Analysis Center Technical Report; IGS Central Bureau: Pasadena, CA, USA, 2022; p. 105. [Google Scholar]
- Kaplan, E.D.; Hegarty, C. Understanding GPS/GNSS: Principles and Applications; Artech House: Norwood, MA, USA, 2017. [Google Scholar]
- Montenbruck, O.; Gill, E.; Lutze, F. Satellite orbits: Models, methods, and applications. Appl. Mech. Rev. 2002, 55, B27–B28. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS Conventions (2010); Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt, Germany, 2010. [Google Scholar]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Kdd, Portland, OR, USA, 2–4 August 1996; Volume 96, pp. 226–231. [Google Scholar]
- Al Shalabi, L.; Shaaban, Z.; Kasasbeh, B. Data Mining: A Preprocessing Engine. J. Comput. Sci. 2006, 2, 735–739. [Google Scholar] [CrossRef]
- Ruder, S. An Overview of Gradient Descent Optimization Algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Willmott, C.J.; Matsuura, K. Advantages of the Mean Absolute Error (MAE) over the Root Mean Square Error (RMSE) in Assessing Average Model Performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.; Lin, W.; Wu, W.; Zhao, F.; Mo, R.; Zhang, H. Segrnn: Segment Recurrent Neural Network for Long-Term Time Series Forecasting. arXiv 2023, arXiv:2308.11200. [Google Scholar]
- Yu, Y.; Yu, W.; Nie, F.; Li, X. PRformer: Pyramidal Recurrent Transformer for Multivariate Time Series Forecasting. arXiv 2024, arXiv:2408.10483. [Google Scholar]




| PRN | C19 | C20 | C21 | C22 | C23 | C24 | C25 | C26 | C27 |
| C28 | C29 | C30 | C32 | C33 | C34 | C35 | C36 | C37 | |
| C38 * | C39 * | C40 * | C41 | C42 | C43 | C44 | C45 | C46 | |
| Time range | [9 April 2020 01:15, 4 January 2023 22:45] | ||||||||
| Total sample size | 2,405,507 | ||||||||
| Data partition | Training/Validation/Testing: 6/2/2 | ||||||||
| Model | Horizon | Radial | Along-Track | Cross-Track | 3D |
|---|---|---|---|---|---|
| SCINet-SA | 1 | 29.77 | 19.14 | 15.22 | 21.69 |
| 7 | 25.48 | 14.49 | 15.60 | 18.66 | |
| 15 | 20.73 | 8.88 | 13.54 | 15.42 | |
| SCINet | 1 | 27.51 | 17.16 | 12.38 | 18.96 |
| 7 | 22.98 | 12.20 | 13.41 | 16.28 | |
| 15 | 18.28 | 5.58 | 11.72 | 13.07 | |
| PRformer | 1 | 26.77 | 16.62 | 11.78 | 18.39 |
| 7 | 22.27 | 11.35 | 12.53 | 15.41 | |
| 15 | 17.23 | 4.52 | 10.74 | 12.02 | |
| SegRNN | 1 | 12.33 | 12.93 | 5.69 | 10.49 |
| 7 | 9.26 | 9.76 | 9.82 | 10.90 | |
| 15 | 7.24 | 5.47 | 8.99 | 9.32 | |
| BiLSTM | 1 | 16.77 | 4.54 | 8.35 | 11.08 |
| 7 | 19.76 | 4.55 | 12.80 | 13.12 | |
| 15 | 12.51 | −10.35 | 10.46 | 6.82 | |
| LSTM | 1 | 17.16 | 6.01 | 8.72 | 11.36 |
| 7 | 11.05 | 0.18 | 9.37 | 8.59 | |
| 15 | 11.29 | −6.20 | 9.82 | 7.16 |
| Horizon | Window | Radial | Along-Track | Cross-Track | 3D |
|---|---|---|---|---|---|
| 1 | 480 | 27.27 | 17.15 | 11.51 | 18.37 |
| 960 | 29.48 | 19.03 | 14.75 | 21.25 | |
| 1440 | 29.28 | 18.31 | 14.70 | 21.03 | |
| 7 | 480 | 25.11 | 14.17 | 14.37 | 17.73 |
| 960 | 25.08 | 13.72 | 15.35 | 18.22 | |
| 1440 | 24.79 | 12.71 | 15.24 | 17.93 | |
| 15 | 480 | 20.80 | 8.66 | 12.63 | 14.78 |
| 960 | 20.21 | 6.70 | 13.30 | 14.63 | |
| 1440 | 19.22 | 4.74 | 12.93 | 13.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, S.; Li, J.; Cai, J. Improving High-Precision BDS-3 Satellite Orbit Prediction Using a Self-Attention-Enhanced Deep Learning Model. Sensors 2025, 25, 2844. https://doi.org/10.3390/s25092844
Xie S, Li J, Cai J. Improving High-Precision BDS-3 Satellite Orbit Prediction Using a Self-Attention-Enhanced Deep Learning Model. Sensors. 2025; 25(9):2844. https://doi.org/10.3390/s25092844
Chicago/Turabian StyleXie, Shengda, Jianwen Li, and Jiawei Cai. 2025. "Improving High-Precision BDS-3 Satellite Orbit Prediction Using a Self-Attention-Enhanced Deep Learning Model" Sensors 25, no. 9: 2844. https://doi.org/10.3390/s25092844
APA StyleXie, S., Li, J., & Cai, J. (2025). Improving High-Precision BDS-3 Satellite Orbit Prediction Using a Self-Attention-Enhanced Deep Learning Model. Sensors, 25(9), 2844. https://doi.org/10.3390/s25092844







