Research on Centrifugal Pump Speed Measurement Based on Vibration Measurement
Abstract
1. Introduction
2. Materials and Methods
2.1. Methods for Measuring Rotational Speed
2.2. Wavelet Denoising
2.3. Fourier Transform
| Algorithm 1: Zoom-FFT with Wavelet Denoising |
| Input: Vibration signal data, [f_low, f_high], noise_level = 0.05, zoom_factor = 10 |
| Output: Enhanced Zoom-FFT spectrum |
| Procedure: |
| 1. Signal Acquisition: |
| - Read time(t) and vibration(z_data) from file |
| - Compute fs = 1/Δt |
| 2. Preprocessing: |
| - Add noise: z_noisy ← z_data + N(0, noise_level2) |
| - Wavelet denoising (db4, level = 5): |
| * Estimate threshold via median absolute deviation |
| * Apply soft-thresholding (α = 2) |
| * Reconstruct z_denoised |
| 3. Zoom-FFT Core: |
| a. Frequency shift to baseband: |
| z_shifted←z_denoised · e^{−j2πf_center t} |
| where f_center = (f_high + f_low)/2 |
| b. FIR lowpass filtering (order = 100, cutoff = bandwidth/2) |
| c. Downsample by decimation_factor = max (1, ⌊fs/(2·bandwidth·zoom_factor)⌋) |
| d. Apply Hamming window and compute FFT |
| e. Adjust frequency axis: f_zoom = f_center + (k·fs_new/N − fs_new/2) |
| 4. Comparison: |
| - Compute conventional FFT with same window |
| - Plot both spectra over [f_low, f_high] with matched axes (0–0.008) |
| Critical Parameters: |
| - Bandwidth = f_high - f_low |
| - fs_new = fs/decimation_factor |
| - Threshold: σ = median(|cD1|)/0.6745 |
3. Experimental Setup and Method
3.1. Experimental Setup
3.2. Experimental Method
4. Results and Discussion
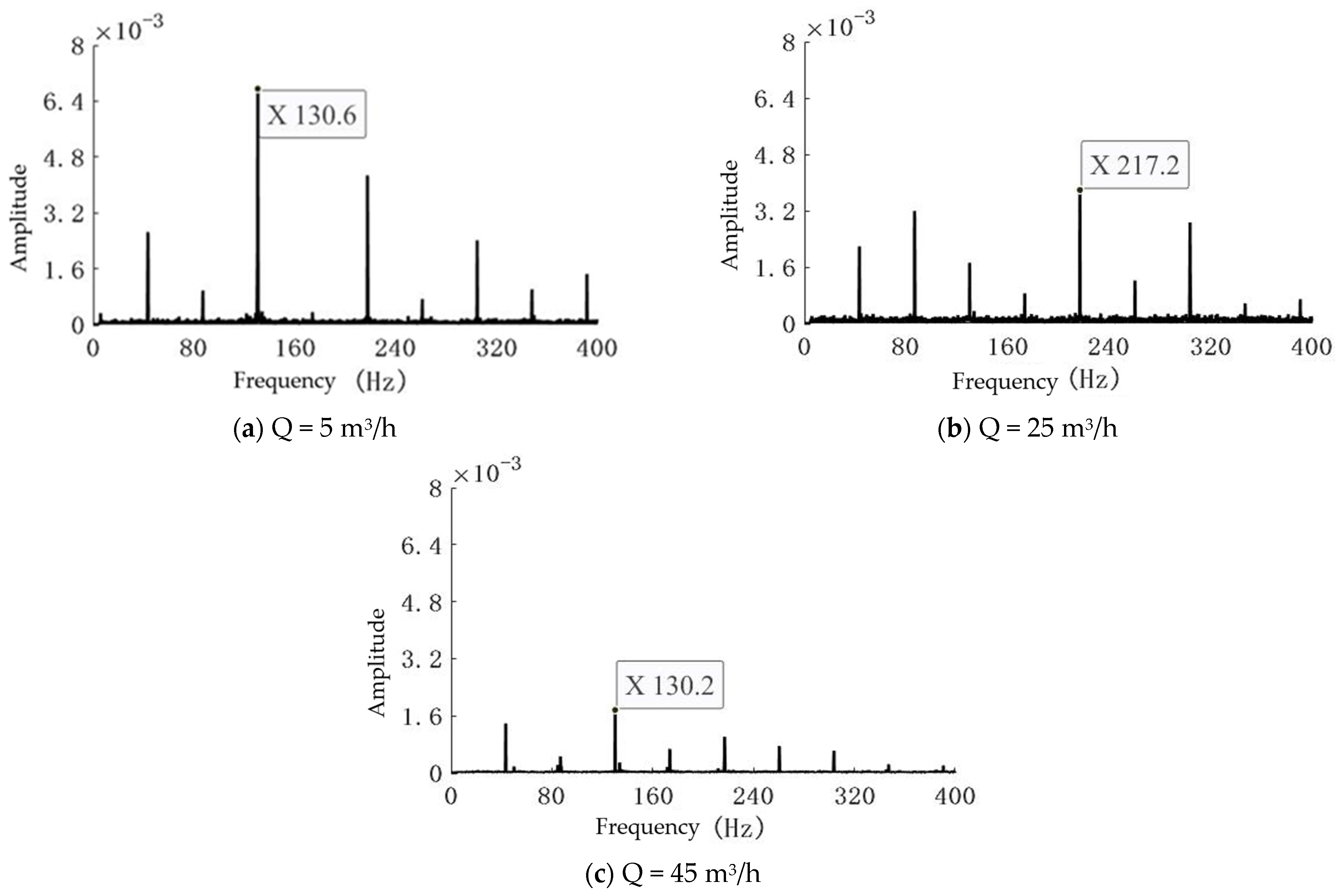
4.1. Data Processing
4.2. Error Validation
5. Conclusions
- This research systematically compared the Fourier Transform (FT) with the refined Zoom-Fast Fourier Transform (Zoom-FFT) and provided a detailed explanation of the principles underlying Zoom-FFT. The comparative analysis highlighted the significant advantages of Zoom-FFT in handling high-frequency details and enhancing the spectral resolution. These findings establish a solid theoretical basis for a subsequent vibration signal analysis.
- By analyzing the vibration characteristics of centrifugal pumps, it was observed that the dominant frequency is an integer multiple of the pump shaft rotation frequency, directly reflecting the pump’s rotational speed. Based on this observation, a rotational speed calculation formula was proposed, enabling the precise determination of the actual speed of the centrifugal pump.
- The experimental data analysis compared the results of the dominant frequency extraction and the rotational speed calculation with the actual operating conditions of the pump equipment. As demonstrated by the data in Table 4, the computational results show excellent agreement with the actual pump operating speeds, achieving a remarkable calculation accuracy of 0.27%, which exceeds the precision standards of conventional measurement methods.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Q.; Yi, D.; Hu, C.; Chen, H.; Song, J. Research on the Method of Measuring the Rotational Speed of Medical Centrifuges Based on Vibration Frequency Analysis. China Insp. Test. 2022, 30, 20–22. [Google Scholar]
- Jaehong, K.; Usama, M.; Nam, K. Precise rotor speed measurement method with sinusoidal coded gearwheel encoder for spindle motor drive. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020. [Google Scholar]
- Guo, Y.; Yuan, S.; Luo, Y.; Sun, H.; Yin, J. Experimental analysis on the characteristics of the transient rotational speed of centrifugal pumps Vibration and Shock. J. Vib. Shock. 2018, 37, 187–193. [Google Scholar]
- Wang, A.; Wang, X.; Zhang, Y.; Yin, J.; Zhai, Z.; Wang, H. Research of Engine Rotation Speed Measurement Based on Vibration Signal Precise Basic-frequency. Instrum. Tech. Sens. 2023, 115–120. [Google Scholar]
- Hao, S.; Tang, Z.; Guo, S.; Ding, Z.; Su, Z. Model and Method of Fault Signal Diagnosis for Blockage and Slippage of Rice Threshing Drum. Agriculture 2022, 12, 1968. [Google Scholar] [CrossRef]
- Antoni, J.; Bonnardot, F.; Raad, A.; El Badaoui, M. Cyclostationary modelling of rotating machine vibration signals. Mech. Syst. Signal Process. 2004, 18, 1285–1314. [Google Scholar] [CrossRef]
- Sun, B.; Li, H.; Wang, C.; Zhang, K.; Chen, S. Current-Aided Dynamic Time Warping for Planetary Gearbox Fault Detection at Time-Varying Speeds. IEEE Sens. J. 2023, 24, 390–402. [Google Scholar] [CrossRef]
- Pan, Z.Y.; Ni, Y.Y.; Yuan, S.Q.; Li, H. Experiment and Mechanism of Centriugal Pumps Rotation Speed Measurement Based on Rotor-stator Interaction. J. Agric. Mach. 2010, 41, 81–85. [Google Scholar]
- Tian, L.; Wu, J. Fault Diagnosis and Analysis of Sewage Pumps Based on Zoom-FFT. J. Mach. Des. Res. 2018, 34, 171–174. [Google Scholar]
- Zhang, Z.; Wang, H.; Zhang, Z. Propeller Shaft Number Extraction of Underwater Acoustic Target Based on Zoom-FFT Spectrum Zooming. Command. Inf. Syst. Technol. 2020, 11, 84–88. [Google Scholar]
- Shan, X.; Tang, L.; Wen, H.; Martinek, R.; Smulko, J. Analysis of vibration and acoustic signals for noncontact measurement of engine rotation speed. Sensors 2020, 20, 683. [Google Scholar] [CrossRef] [PubMed]
- Deng, L.; Leng, K. Application of two spectrum refinement methods in frequency estimation. J. Phys. Conf. Ser. 2022, 2290, 012070. [Google Scholar] [CrossRef]
- Yu, Z.; Li, Y.; Du, X.; Liu, Y. Threshing Cylinder Unbalance Detection Using a Signal Extraction Method Based on Parameter-Adaptive Variational Mode Decomposition. Biosyst. Eng. 2024, 244, 26–41. [Google Scholar] [CrossRef]
- Qi, P.; Zheng, J.; Pan, H.; Cheng, J.; Tong, J. Waveform adaptive wavelet decomposition and its Application in rolling bearing fault diagnosis. J. Vib. Eng. 2025, 05 04, 1–9. [Google Scholar]
- Yang, H. Application Research of Fast Fourier Transform in Detection of Concrete Defects by Impact-Echo. Method Ind. Technol. Vocat. Educ. 2023, 21, 17–21. [Google Scholar]
- Wang, Y.; Zheng, L.; Gao, Y.; Li, S. Vibration signal extraction based on FFT and least square method. IEEE Access 2020, 8, 224092–224107. [Google Scholar] [CrossRef]
- Wang, A.; Wang, F. The Algorithm Researcher of Frequency Shift Param eters Based on ZOOM—FFT. Microprocessors 2011, 32, 37–40. [Google Scholar]
- Zhang, Y.; Zhang, Q.; Lin, M. Analysis and Simulation of ZFFT Algorithm based on Complex Analytical Bandpass filter. Parts Appl. 2022, 46, 112–114+123. [Google Scholar]
- Meng, Z.; Lu, J.; Xin, P. Research on signal separation method of micro-speed difference dual-rotor based on ZFFT and FT algorithm. J. Vib. Control 2023, 30, 2200–2213. [Google Scholar] [CrossRef]
- Runde, C. Acquisition and processing analysis of Underwater Acoustic Communication Signal. Master’s Thesis, Qinghai Normal University, Xining, China, 2020. [Google Scholar]
- Lin, H.; Xu, P.T.; Sun, L.; Bi, X.K.; Zhao, J.W.; Cai, J.R. Identification of eggshell crack using multiple vibration sensors and correlative information analysis. J. Food Process Eng. 2018, 41, e12894.1–e12894.9. [Google Scholar] [CrossRef]
- ISO 16063-21:2003; Methods for the Calibration of Vibration and Shock Transducers—Part 21: Vibration Calibration by Comparison to a Reference Transducer. ISO: Geneva, Switzerland, 2003.
- Faheem, M.; Liu, J.; Chang, G.; Abbas, I.; Xie, B.; Shan, Z.; Yang, K. Experimental Research on Grape Cluster Vibration Signals during Transportation and Placing for Harvest and Post-Harvest Handling. Agriculture 2021, 11, 902. [Google Scholar] [CrossRef]

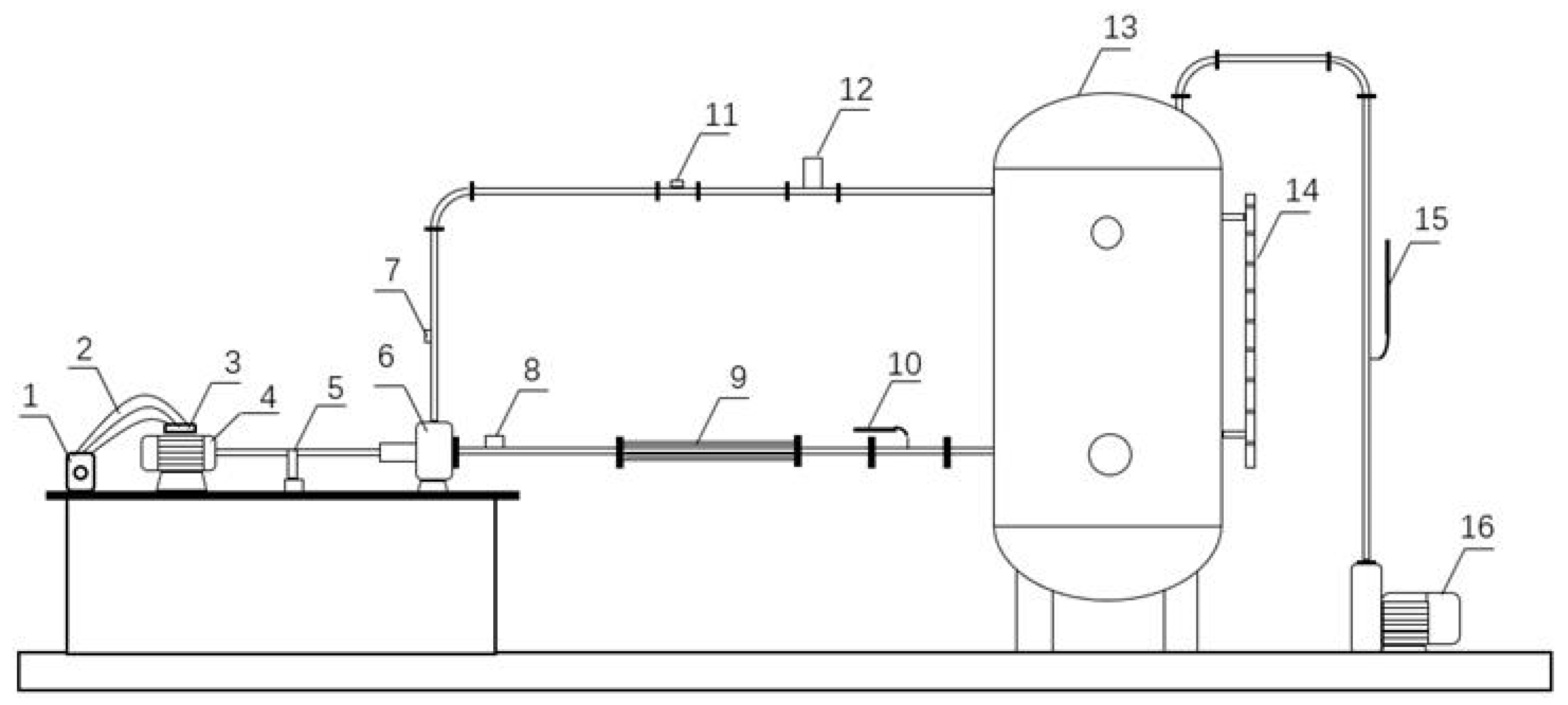




| Parameter | Symbol and Unit | Value |
|---|---|---|
| Design flow rate | Q/m3/h | 50 |
| Design head | H/m | 34 |
| Rotational speed | r/min | 2950 |
| Specific speed | 81.5 | |
| Number of blades | Z | 6 |
| Parameter | Symbol and Unit | Value |
|---|---|---|
| Rated voltage | U/V | 380 |
| Rated rotational speed | n/r/min | 2950 |
| Rated efficiency | /% | 89.4 |
| Rated power | P/kW | 15 |
| Flow Rate (m3/h) | Calculated Rotational Speed (r/min) | Error (%) |
|---|---|---|
| 5 | 2612 | 0.04 |
| 25 | 2606 | 0.02 |
| 45 | 2604 | 0.01 |
| Actual Rotational Speed (r/min) | Calculated Rotational Speed (r/min) | Error (%) |
|---|---|---|
| 2400 | 2367 | 0.11 |
| 2600 | 2607 | 0.27 |
| 2800 | 2805 | 0.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Y.; Yan, H. Research on Centrifugal Pump Speed Measurement Based on Vibration Measurement. Sensors 2025, 25, 3095. https://doi.org/10.3390/s25103095
Luo Y, Yan H. Research on Centrifugal Pump Speed Measurement Based on Vibration Measurement. Sensors. 2025; 25(10):3095. https://doi.org/10.3390/s25103095
Chicago/Turabian StyleLuo, Yin, and Hang Yan. 2025. "Research on Centrifugal Pump Speed Measurement Based on Vibration Measurement" Sensors 25, no. 10: 3095. https://doi.org/10.3390/s25103095
APA StyleLuo, Y., & Yan, H. (2025). Research on Centrifugal Pump Speed Measurement Based on Vibration Measurement. Sensors, 25(10), 3095. https://doi.org/10.3390/s25103095




