Effect of Rare-Earth Co-Doping on the Trap Level Concentrations in Silica Glasses: Experimental and Theoretical Study of the Light Emission Under X-Rays for Dosimetry Applications
Abstract
1. Introduction
2. Materials and Methods
2.1. Studied Samples
2.2. TL and Initial Rise Experimental Setup
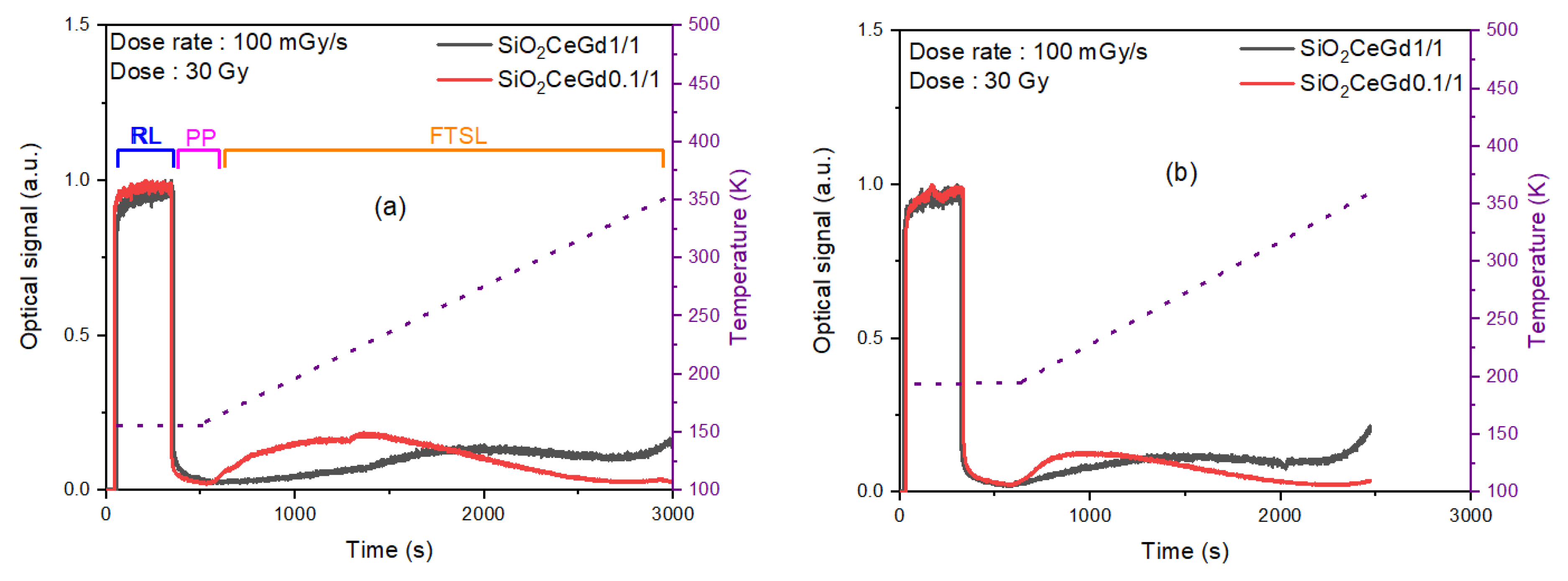
2.3. RL, PP and FTSL Measurements
3. Experimental Results
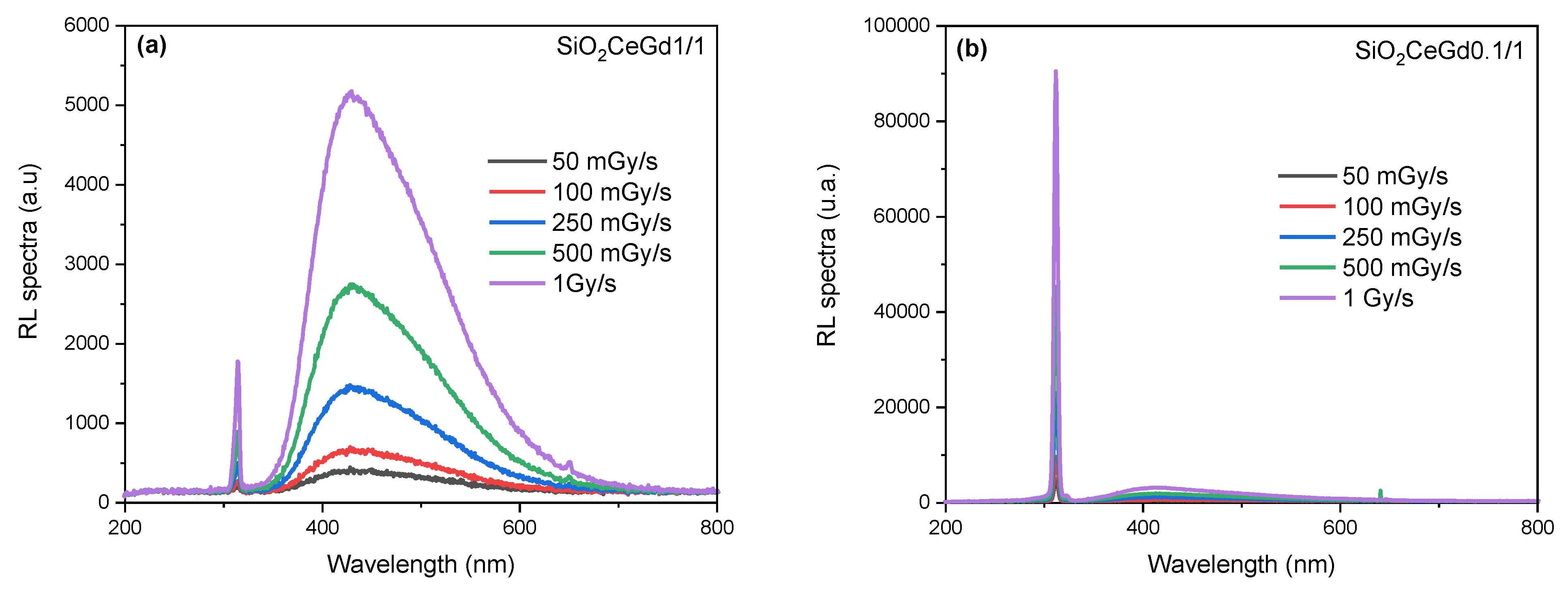
3.1. RL Spectra
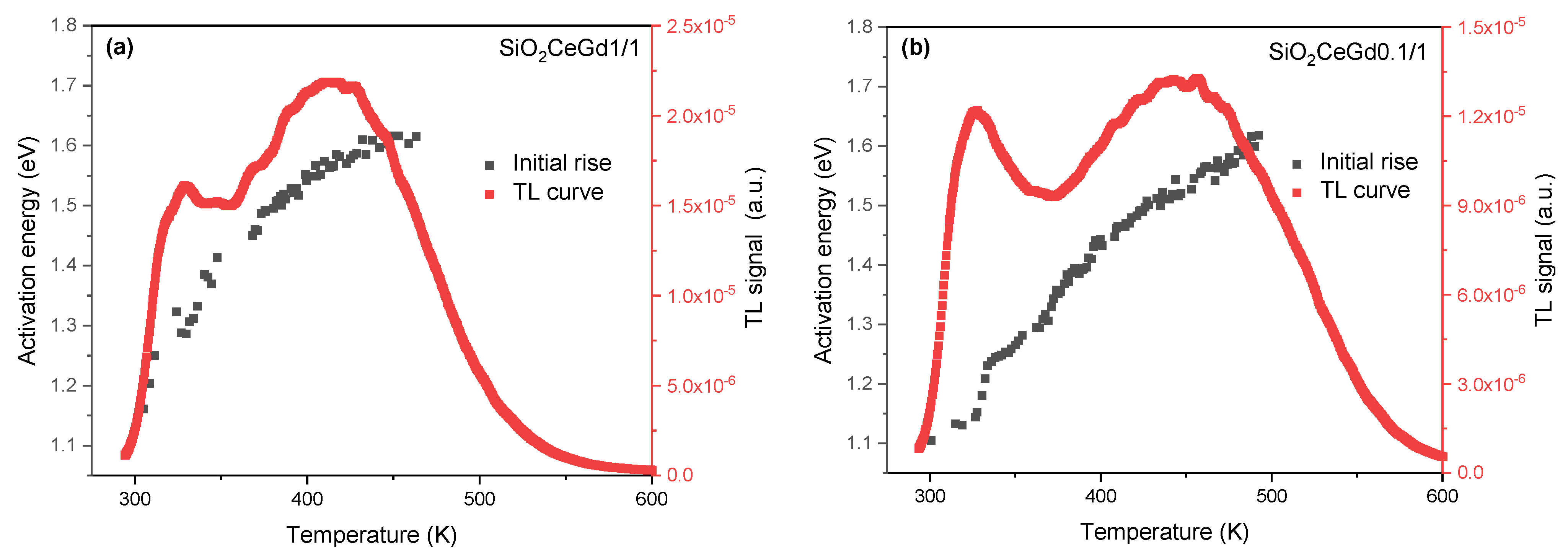
3.2. TL and Initial Rise
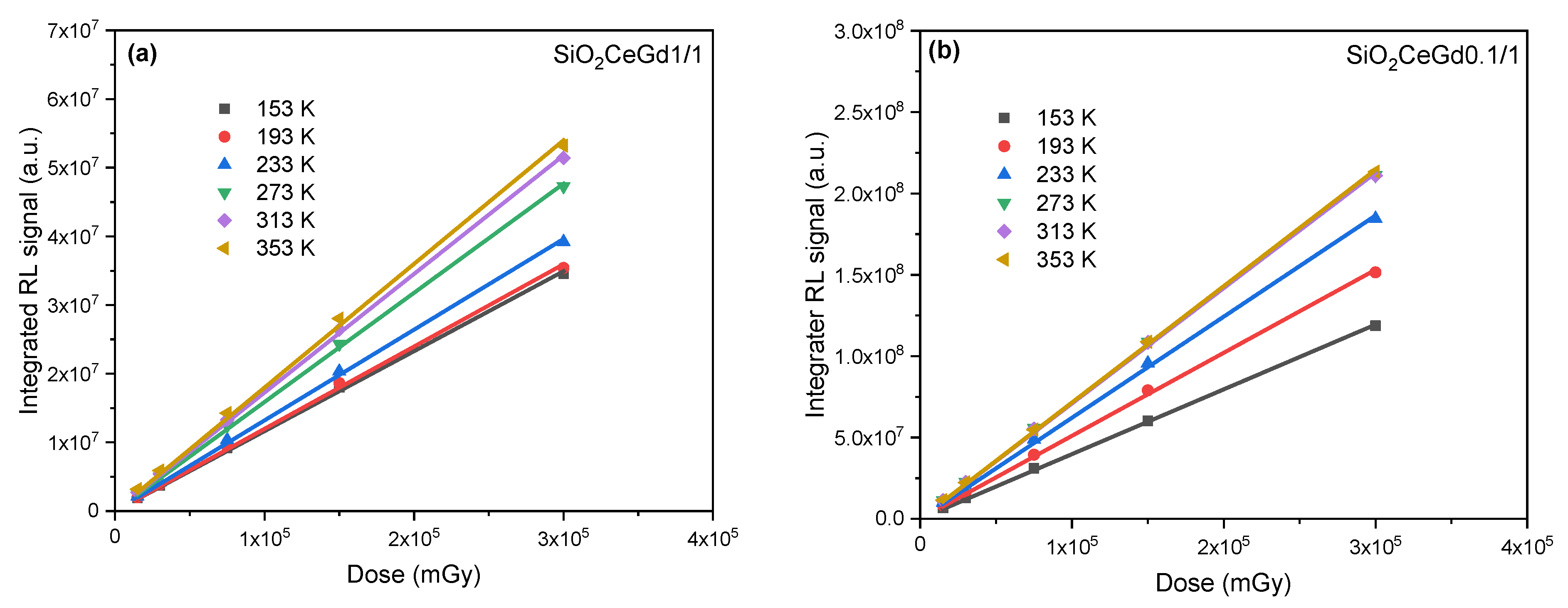
3.3. RL, PP, and FTSL Signal
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- El Hamzaoui, H.; Capoen, B.; Al Helou, N.; Bouwmans, G.; Ouerdane, Y.; Boukenter, A.; Girard, S.; Marcandella, C.; Duhamel, O.; Chadeyron, G.; et al. Cerium-activated sol–gel silica glasses for radiation dosimetry in harsh environment. Mater. Res. Express 2016, 3, 046201. [Google Scholar] [CrossRef]
- Girard, S.; Capoen, B.; El Hamzaoui, H.; Bouazaoui, M.; Bouwmans, G.; Morana, A.; Di Francesca, D.; Boukenter, A.; Duhamel, O.; Paillet, P.; et al. Potential of Copper- and Cerium-Doped Optical Fiber Materials for Proton Beam Monitoring. IEEE Trans. Nucl. Sci. 2017, 64, 567–573. [Google Scholar] [CrossRef]
- Veronese, I.; Chiodini, N.; Cialdi, S.; d’Ippolito, E.; Fasoli, M.; Gallo, S.; La Torre, S.; Mones, E.; Vedda, A.; Loi, G. Real-time dosimetry with Yb-doped silica optical fibres. Phys. Med. Biol. 2017, 62, 4218–4236. [Google Scholar] [CrossRef] [PubMed]
- Söderström, D.; Timonen, O.; Kettunen, H.; Kronholm, R.; El Hamzaoui, H.; Capoen, B.; Ouerdane, Y.; Morana, A.; Javanainen, A.; Bouwmans, G.; et al. Properties of Gd-Doped Sol-Gel Silica Glass Radioluminescence under Electron Beams. Sensors 2022, 22, 9248. [Google Scholar] [CrossRef]
- Hoehr, C.; Morana, A.; Duhamel, O.; Capoen, B.; Trinczek, M.; Paillet, P.; Duzenli, C.; Bouazaoui, M.; Bouwmans, G.; Cassez, A.; et al. Novel Gd3+-doped silica-based optical fiber material for dosimetry in proton therapy. Sci. Rep. 2019, 9, 16376. [Google Scholar] [CrossRef]
- Zubair, H.T.; Oresegun, A.; Rahman, A.K.M.M.; Ung, N.M.; Mat Sharif, K.A.; Zulkifli, M.I.; Yassin, S.Z.M.; Maah, M.J.; Yusoff, Z.; Abdul-Rashid, H.A.; et al. Real-time radiation dosimetry using P-doped silica optical fiber. Measurement 2019, 146, 119–124. [Google Scholar] [CrossRef]
- Shen, H.; Huang, C.; Dong, Y.; Wen, J.; Zhang, X.; Pang, F.; Wang, T. Radiation Sensitive Long-Period Fiber Grating Based on Tb-Doped Silica Fiber. IEEE Trans. Nucl. Sci. 2023, 70, 228–234. [Google Scholar] [CrossRef]
- Ashurov, M.; Baydjanov, M.; Gasanov, E.; Nuritdinov, I.; Shikama, T.; Salikhbayev, U. Influence of γ-Radiation Dose Growth and Dose Rates on Luminescence Properties of Pure Silica Core Fibers with High-OH Group Content. Jpn. J. Appl. Phys. 2011, 50, 012501. [Google Scholar] [CrossRef]
- Gurzhiev, A.N.; Turchanovich, L.K.; Vasil’chenko, V.G.; Bogatyrjov, V.A.; Mashinsky, V.M. Radiation damage in optical fibers. Nucl. Instrum. Methods Phys. Res. A 1997, 391, 417–422. [Google Scholar] [CrossRef]
- Toh, K.; Sakasai, K.; Nakamura, T.; Soyama, K.; Shikama, T. Effects of neutrons and gamma-rays on polymethylmethacrylate plastic optical fiber. J. Nucl. Mater. 2011, 417, 814–817. [Google Scholar] [CrossRef]
- Prajzler, V.; Masopoustova, K.; Sarsounova, Z. Gamma radiation effects on plastic optical fibers. Opt. Fiber Technol. 2022, 72, 102995. [Google Scholar] [CrossRef]
- Begum, M.; Rahman, A.; Zubair, H.T.; Abdul-Rashid, H.A.; Yusoff, Z.; Begum, M.; Alkhorayef, M.; Alzimami, K.; Bradley, D.A. The effect of different dopant concentration of tailor-made silica fibers in radiotherapy dosimetry. Radiat. Phys. Chem. 2017, 141, 73–77. [Google Scholar] [CrossRef]
- Al Helou, N.; El Hamzaoui, H.; Capoen, B.; Bouwmans, G.; Cassez, A.; Ouerdane, Y.; Boukenter, A.; Girard, S.; Chadeyron, G.; Mahiou, R.; et al. Radioluminescence and Optically Stimulated Luminescence Responses of a Cerium-Doped Sol-Gel Silica Glass Under X-Ray Beam Irradiation. IEEE Trans. Nucl. Sci. 2018, 65, 1591–1597. [Google Scholar] [CrossRef]
- Oresegun, A.; Basaif, A.; Tarif, Z.H.; Abdul-Rashid, H.A.; Hashim, S.A.; Bradley, D.A. Radioluminescence of silica optical fibre scintillators for real-time industrial radiation dosimetry. Radiat. Phys. Chem. 2021, 188, 109684. [Google Scholar] [CrossRef]
- Zghari, I.; El Hamzaoui, H.; Morana, A.; Ouerdane, Y.; Capoen, B.; Cieslikiewicz-Bouet, M.; Andrieux, V.; Girard, S.; Boukenter, A.; Mélin, G.; et al. Ce/Gd-codoped sol-gel silica glasses: Towards temperature-independent radiation dosimeters. IEEE Sensors J. 2024, 24, 10068–10075. [Google Scholar] [CrossRef]
- Bahout, J.; Bahout, J.; Ouerdane, Y.; El Hamzaoui, H.; Bouwmans, G.; Bouazaoui, M.; Cassez, A.; Baudelle, K.; Habert, R.; Morana, A.; et al. Cu/Ce-co-Doped Silica Glass as Radioluminescent Material for Ionizing Radiation Dosimetry. Materials 2020, 13, 2611. [Google Scholar] [CrossRef]
- Rahman, A.K.M.M.; Begum, M.; Zubair, H.T.; Abdul-Rashid, H.A.; Yusoff, Z.; Ung, N.M.; Bradley, D.A. Ge-doped silica optical fibres as RL/OSL dosimeters for radiotherapy dosimetry. Sens. Actuators A Phys. 2017, 264, 30–39. [Google Scholar] [CrossRef]
- Chiodini, N.; Vedda, A.; Veronese, I. Rare Earth Doped Silica Optical Fibre Sensors for Dosimetry in Medical and Technical Applications. Adv. Opt. 2014, 2014, 974584. [Google Scholar] [CrossRef]
- Braccini, S.; Ereditato, A.; Giacoppo, F.; Kreslo, I.; Nesteruk, K.P.; Nirkko, M.; Weber, M.; Scampoli, P.; Neff, M.; Pilz, S.; et al. A beam monitor detector based on doped silica and optical fibres. J. Instrum. 2012, 7, T02001. [Google Scholar] [CrossRef]
- Dohler, D.; Alshut, L.; König, L.; Teichmann, T.; Werner, T.; Kormoll, T. Characterization of a Fiber Optic Radiation Sensor Prototype for Nuclear Dismantling. IEEE Trans. Nucl. Sci. 2022, 69, 1884–1892. [Google Scholar] [CrossRef]
- Wu, J.; Wang, M.; Zhao, K.; Huang, S.; Zaghloul, M.A.; Cao, R.; Carpenter, D.; Zheng, G.; Rountree, S.D.; Chen, K.P. Distributed Fiber Sensors with High Spatial Resolution in Extreme Radiation Environments in Nuclear Reactor Cores. J. Light. Technol. 2021, 39, 4873–4883. [Google Scholar] [CrossRef]
- Girard, S.; Alessi, A.; Richard, N.; Martin-Samos, L.; De Michele, V.; Giacomazzi, L.; Agnello, S.; Francesca, D.D.; Morana, A.; Winkler, B.; et al. Overview of radiation induced point defects in silica-based optical fibers. Rev. Phys. 2019, 4, 100032. [Google Scholar] [CrossRef]
- Sui, Z.; Qian, S.; Niu, L.; Hu, P.; Hua, Z.; Zheng, X.; Sun, X.; Tang, G.; Cai, H.; Yang, D.; et al. Glass scintillator: A window to future high-energy radiation detection. Innov. 2025, 6, 100878. [Google Scholar] [CrossRef]
- Beckurts, K.H.; Wirts, K. Neutron Physics; Springer: Berlin/Heidelberg, Germany, 1964. [Google Scholar] [CrossRef]
- Rawat, N.S.; Kulkarni, M.S.; Mishra, D.R.; Bhatt, B.C.; Sunta, C.M.; Gupta, S.K.; Sharma, D.N. Use of initial rise method to analyze a general-order kinetic thermoluminescence glow curve. Nucl. Instrum. Methods Phys. Res. B 2009, 267, 3475–3479. [Google Scholar] [CrossRef]
- Bahout, J.; Ouerdane, Y.; El Hamzaoui, H.; Bouwmans, G.; Bouazaoui, M.; Cassez, A.; Baudelle, K.; Habert, R.; Morana, A.; Boukenter, A.; et al. Remote Measurements of X-Rays Dose Rate Using a Cerium-Doped Air-Clad Optical Fiber. IEEE Trans. Nucl. Sci. 2020, 67, 1658–1662. [Google Scholar] [CrossRef]
- Cieslikiewicz-Bouet, M.; El Hamzaoui, H.; Ouerdane, Y.; Mahiou, R.; Chadeyron, G.; Bigot, L.; Delplace-Baudelle, K.; Habert, R.; Plus, S.; Cassez, A.; et al. Investigation of the Incorporation of Cerium Ions in MCVD-Silica Glass Preforms for Remote Optical Fiber Radiation Dosimetry. Sensors 2021, 21, 3362. [Google Scholar] [CrossRef]
- Malashkevich, G.E.; Poddenezhny, E.N.; Melnichenko, I.M.; Boiko, A.A. Optical centers of cerium in silica glasses obtained by the sol-gel process. J. Non-Cryst. Solids 1995, 188, 107–117. [Google Scholar] [CrossRef]
- Dormenev, V.; Amelina, A.; Auffray, E.; Brinkmann, K.-T.; Dosovitskiy, G.; Cova, F.; Fedorov, A.; Gundacker, S.; Kazlou, D.; Korjik, M.; et al. Multipurpose Ce-doped Ba-Gd silica glass scintillator for radiation measurements. Nucl. Instrum. Methods Phys. Res. A 2021, 1015, 165762. [Google Scholar] [CrossRef]
- Zatsepin, A.F.; Zatsepin, D.; Boukhvalov, D.; Kuznetsova, Y.A.; Gavrilov, N.; Shur, V.Y.; Esin, A. Local atomic configurations, energy structure, and optical properties of implantation defects in Gd-doped silica glass: An XPS, PL, and DFT study. J. Alloys Compd. 2019, 796, 77–85. [Google Scholar] [CrossRef]
- Jiménez, J.A.; Crawford, C.L. Optical spectroscopy assessment of the impact of γ-ray irradiation on Gd3+-doped phosphate glass. Chem. Phys. Impact 2023, 6, 100198. [Google Scholar] [CrossRef]
- Qiuqiu, L.; Zhao, H.; He, J.; Wang, Y.; Xiang, Y.; Qu, H.; Zhong, Q.; Sun, Y.; Tenglong, Z. An in situ hydrothermally self-crystallized dense ceria-based barrier layer for solid oxide fuel cells. J. Mater. Chem. A 2024, 12, 9778–9786. [Google Scholar] [CrossRef]
- Gao, P.; Liu, Q.; Wu, J.; Jing, J.; Zhang, W.; Zhang, J.; Jiang, T.; Wang, J.; Qi, Y.; Li, Z. Enhanced Fluorescence Characteristics of SrAl2O4: Eu2+, Dy3+ Phosphor by Co-Doping Gd3+ and Anti-Counterfeiting Application. Nanomaterials 2023, 13, 2034. [Google Scholar] [CrossRef] [PubMed]
- Benabdesselam, M.; Bahout, J.; Mady, M.; Blanc, W.; El Hamzaoui, H.; Cassez, A.; Delplace-Baudelle, K.; Habert, R.; Bouwmans, G.; Bouazaoui, M.; et al. TL Properties of RE-Doped and Co-Doped Sol-Gel Silica Rods. Application to Passive (OSL) and Real-Time (RL) Dosimetry. IEEE Sensors J. 2021, 21, 27465–27472. [Google Scholar] [CrossRef]
- Mady, F.; Gutilla, A.; Benabdesselam, M.; Wilfried, G.; Girard, S.; Ouerdane, Y.; Boukenter, A.; Desjonquères, H.; Louvet, C.M. Optical fibers under irradiation: Quantitative assessment of the energy distribution of radiation-induced trapped states. In Fiber Lasers and Glass Photonics: Materials Through Applications II; SPIE: Washington, DC, USA, 2020; Volume 1357. [Google Scholar] [CrossRef]
- Cova, F.; Moretti, F.; Dujardin, C.; Chiodini, N.; Vedda, A. Trapping Mechanisms and Delayed Recombination Processes in Scintillating Ce-Doped Sol–Gel Silica Fibers. J. Phys. Chem. C 2021, 125, 11489–11498. [Google Scholar] [CrossRef]
- Zghari, I.; El Hamzaoui, H.; Capoen, B.; Cassez, A.; Bouwmans, G.; Hay, L.; Ouerdane, Y.; Morana, A.; Girard, S.; Boukenter, A.; et al. Radioluminescence Processes in Cerium-Doped Silica Glasses. IEEE Trans. Nucl. Sci. 2023, 70, 1933–1941. [Google Scholar] [CrossRef]
- Zghari, I.; El Hamzaoui, H.; Capoen, B.; Mady, F.; Benabdesselam, M.; Bouwmans, G.; Labat, D.; Ouerdane, Y.; Morana, A.; Girard, S.; et al. Effects of Measurement Temperature on Radioluminescence Processes in Cerium-Activated Silica Glasses for Dosimetry Applications. Sensors 2023, 23, 4785. [Google Scholar] [CrossRef]
- Zghari, I.; Morana, A.; El Hamzaoui, H.; Capoen, C.; Cassez, A.; Ouerdane, Y.; Girard, S.; Boukenter, A.; Mady, F.; Benabdesselam, M.; et al. Combined Theoretical and Experimental Study on Luminescence of Gd3+-Doped Silica Glass under Ionizing Radiation. Opt. Express 2025, 33, 16987–17001. [Google Scholar] [CrossRef]
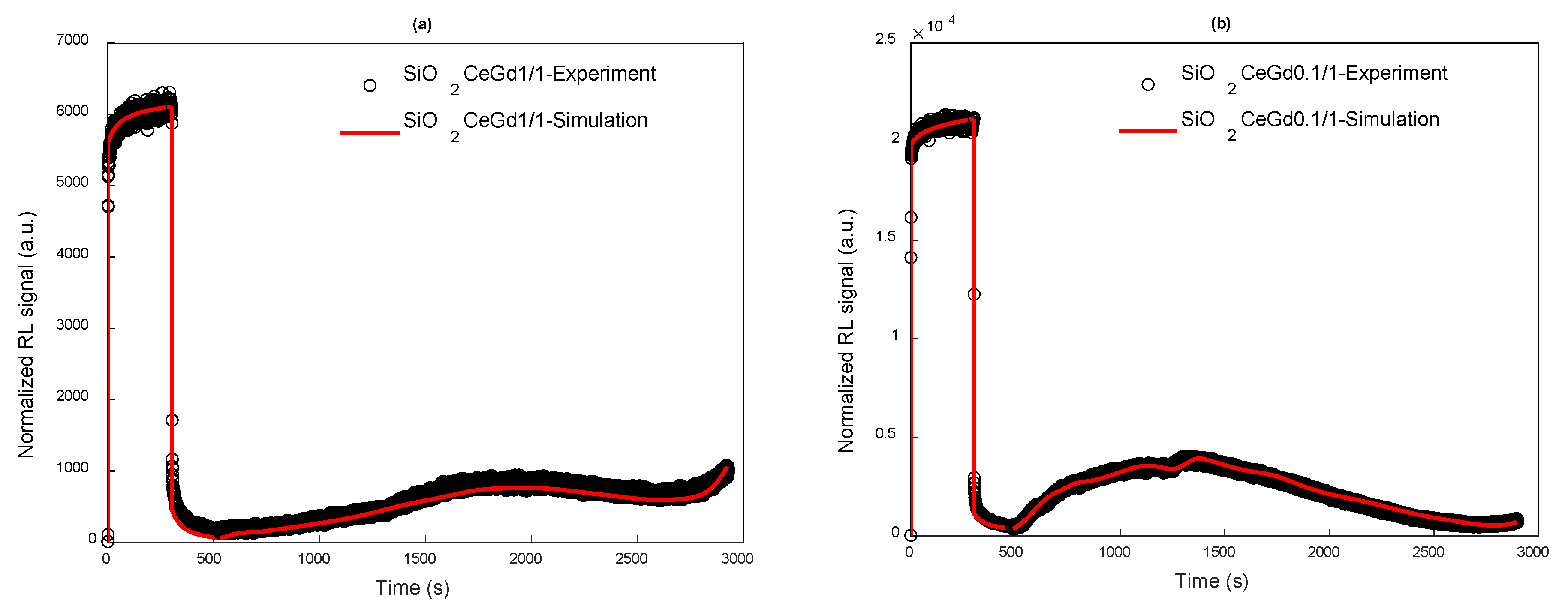
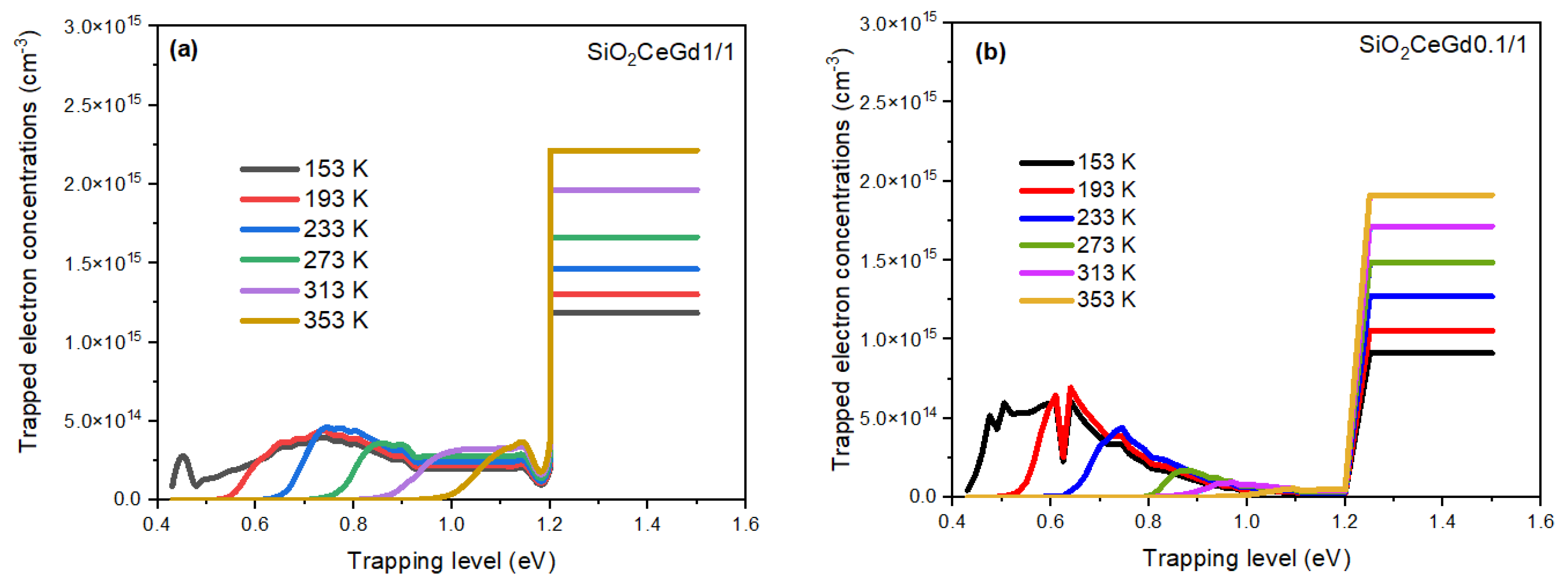
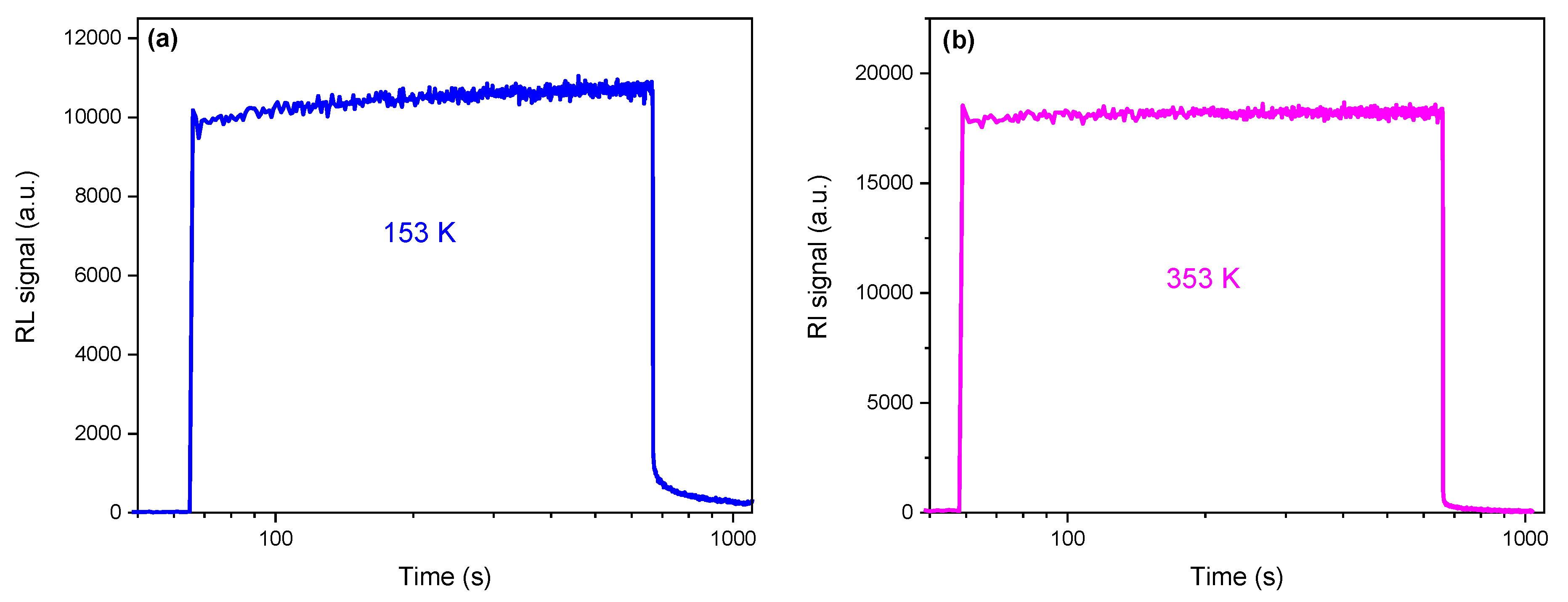
| Symbol | [Ce] (wt.%) | [Gd] (wt.%) |
|---|---|---|
| SiO2-CeGd1/1 | 0.07 | 0.08 |
| SiO2-CeGd0.1/1 | 0.008 | 0.13 |
| Parameter | Status | Description | Value for k = 50 (Number of Electron Traps) SiO2CeGd1/1 | Value for k = 50 (Number of Electron Traps) SiO2CeGd0.1/1 |
|---|---|---|---|---|
| Fixed | Trapping level | 0.43, 0.445, 0.46, 0.475, 0.49, 0.505, 0.52, 0.535, 0.55, 0.565, 0.58, 0.595, 0.61, 0.625, 0.64, 0.655, 0.67, 0.685, 0.7, 0.715, 0.73, 0.745, 0.76, 0.775, 0.79, 0.805, 0.82, 0.835, 0.85, 0.865, 0.88, 0.895, 0.91, 0.925, 0.94, 0.955, 0.97, 0.985, 1, 1.08, 1.095, 1.11, 1.125, 1.15, 1.2, 1.25, 1.3, 1.35, 1.4, 1.5 | 0.43, 0.445, 0.46, 0.475, 0.49, 0.505, 0.52, 0.535, 0.55, 0.565, 0.58, 0.595, 0.61, 0.625, 0.64, 0.655, 0.67, 0.685, 0.7, 0.715, 0.73, 0.745, 0.76, 0.775, 0.79, 0.805, 0.82, 0.835, 0.85, 0.865, 0.88, 0.895, 0.91, 0.925, 0.94, 0.955, 0.97, 0.985, 1, 1.08, 1.095, 1.11, 1.125, 1.15, 1.2, 1.25, 1.3, 1.35, 1.4, 1.5 | |
| Free | Concentrations of electrons traps | 4.5 × 1019, 4.5 × 1019, 2 × 1019, 6 × 1018, 6.5 × 1018, 7 × 1018, 7.5 × 1018, 8.5 × 1018, 9.5 × 1018, 1 × 1019, 1.1 × 1019, 1.2 × 1019, 1.3 × 1019, 1.4 × 1019, 1.6×1019, 1.7 × 1019, 1.7 × 1019, 1.8 × 1019, 1.8 × 1019, 1.9 × 1019, 2 × 1019, 2 × 1019, 1.9 × 1019, 1.9 × 1019, 1.8 × 1019, 1.8 × 1019, 1.7 × 1019, 1.6 × 1019, 1.5 × 1019, 1.4 × 1019, 1.3 × 1019, 1.3 × 1019, 1.2 × 1019, 1 × 1019, 1 × 1019, 1 × 1019, 1 × 1019, 1 × 1019, 1 × 1019, 1 × 1019, 1 × 1019, 1 × 1019, 1 × 1019, 1 × 1019, 1 × 1019, 6 × 1019, 6 × 1019, 6 × 1019, 6 × 1019, 6 × 1019 | 4 × 1019, 4 × 1019, 4 × 1019, 5 × 1019, 4 × 1019; 5 × 1019, 4 × 1019, 5.5 × 1019, 4.5 × 1019, 4.5 × 1019, 4.5 × 1019, 4.5 × 1019, 4.5 × 1019, 2 × 1019, 4.5 × 1019, 4 × 1019, 3.5 × 1019, 3.2 × 1019, 3 × 1019, 2.5 × 1019, 2.4 × 1019, 2.3 × 1019, 2.1 × 1019, 1.9 × 1019, 1.65 × 1019, 1.45 × 1019, 1.3 × 1019, 1.2 × 1019, 1.1 × 1019, 9.5 × 1018, 8.5 × 1018, 7.5 × 1018, 6.5 × 1018, 5.5 × 1018; 5 × 1018, 4.5 × 1018, 4 × 1018, 3.5 × 1018, 3 × 1018, 2.5 × 1018, 2 × 1018, 1.5 × 1018, 1.5 × 1019, 1.5 × 1019, 1.5 × 1019, 6 × 1019, 6 × 1019, 6 × 1019, 6 × 1019, 6 × 1019 | |
| Fixed | Frequency factors | 5 × 1012 | 5 × 1012 | |
| Free | Ratio between recombination and trapping coefficients | ~10−3 | ~10−3 | |
| Fixed | Rate of electron–hole pairs production | 100 mGy(SiO2)/s → 8.44 × 1013 | 100 mGy(SiO2)/s → 8.44 × 1013 | |
| Fixed | Concentration of radiative hole center | Ce3+: 6.62 × 1018 Gd3+: 6.74 × 1018 | Ce3+: 7.5 × 1017 Gd3+: 1 × 1019 | |
| Fixed | Boltzmann constant | 8.617330 × 10−5 eV. K−1 | 8.617330 × 10−5 eV. K−1 | |
| Fixed | Irradiation time | 300 | 300 | |
| Fixed | Afterglow time | 180 | 180 | |
| and | Free | Density of electrons in and CB, respectively | Evolves over time | Evolves over time |
| and | Free | Density of holes in RC and VB, respectively | Evolves over time | Evolves over time |
| Fixed | Emission ratio | ; | ; |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zghari, I.; El Hamzaoui, H.; Morana, A.; Ouerdane, Y.; Capoen, B.; Garzandat, S.; Girard, S.; Boukenter, A.; Mady, F.; Benabdesselam, M.; et al. Effect of Rare-Earth Co-Doping on the Trap Level Concentrations in Silica Glasses: Experimental and Theoretical Study of the Light Emission Under X-Rays for Dosimetry Applications. Sensors 2025, 25, 3005. https://doi.org/10.3390/s25103005
Zghari I, El Hamzaoui H, Morana A, Ouerdane Y, Capoen B, Garzandat S, Girard S, Boukenter A, Mady F, Benabdesselam M, et al. Effect of Rare-Earth Co-Doping on the Trap Level Concentrations in Silica Glasses: Experimental and Theoretical Study of the Light Emission Under X-Rays for Dosimetry Applications. Sensors. 2025; 25(10):3005. https://doi.org/10.3390/s25103005
Chicago/Turabian StyleZghari, Ismail, Hicham El Hamzaoui, Adriana Morana, Youcef Ouerdane, Bruno Capoen, Sarah Garzandat, Sylvain Girard, Aziz Boukenter, Franck Mady, Mourad Benabdesselam, and et al. 2025. "Effect of Rare-Earth Co-Doping on the Trap Level Concentrations in Silica Glasses: Experimental and Theoretical Study of the Light Emission Under X-Rays for Dosimetry Applications" Sensors 25, no. 10: 3005. https://doi.org/10.3390/s25103005
APA StyleZghari, I., El Hamzaoui, H., Morana, A., Ouerdane, Y., Capoen, B., Garzandat, S., Girard, S., Boukenter, A., Mady, F., Benabdesselam, M., Mélin, G., & Bouazaoui, M. (2025). Effect of Rare-Earth Co-Doping on the Trap Level Concentrations in Silica Glasses: Experimental and Theoretical Study of the Light Emission Under X-Rays for Dosimetry Applications. Sensors, 25(10), 3005. https://doi.org/10.3390/s25103005










