Focusing on Cracks with Instance Normalization Wavelet Layer
Abstract
1. Introduction
- We propose a framework for crack detection. Our framework is proficient at capturing the thin features, owing to the INW layer, deformable convolution layer and, and fusion layer.
- We design the INW layer, motivated by the wavelet transform mechanism. Based on the corresponding a priori knowledge, we calculate the inner products between the adaptive wavelets and the features and normalize the representation, refining and denoising the features.
- Comprehensive experiments verify the performance of the presented framework on the aspects of detection and convergence. The ablation studies demonstrate the effectiveness of the designed module.
2. Related Work
2.1. Crack Detection
2.2. Application of Wavelet Transform in Vision
3. Proposed Method
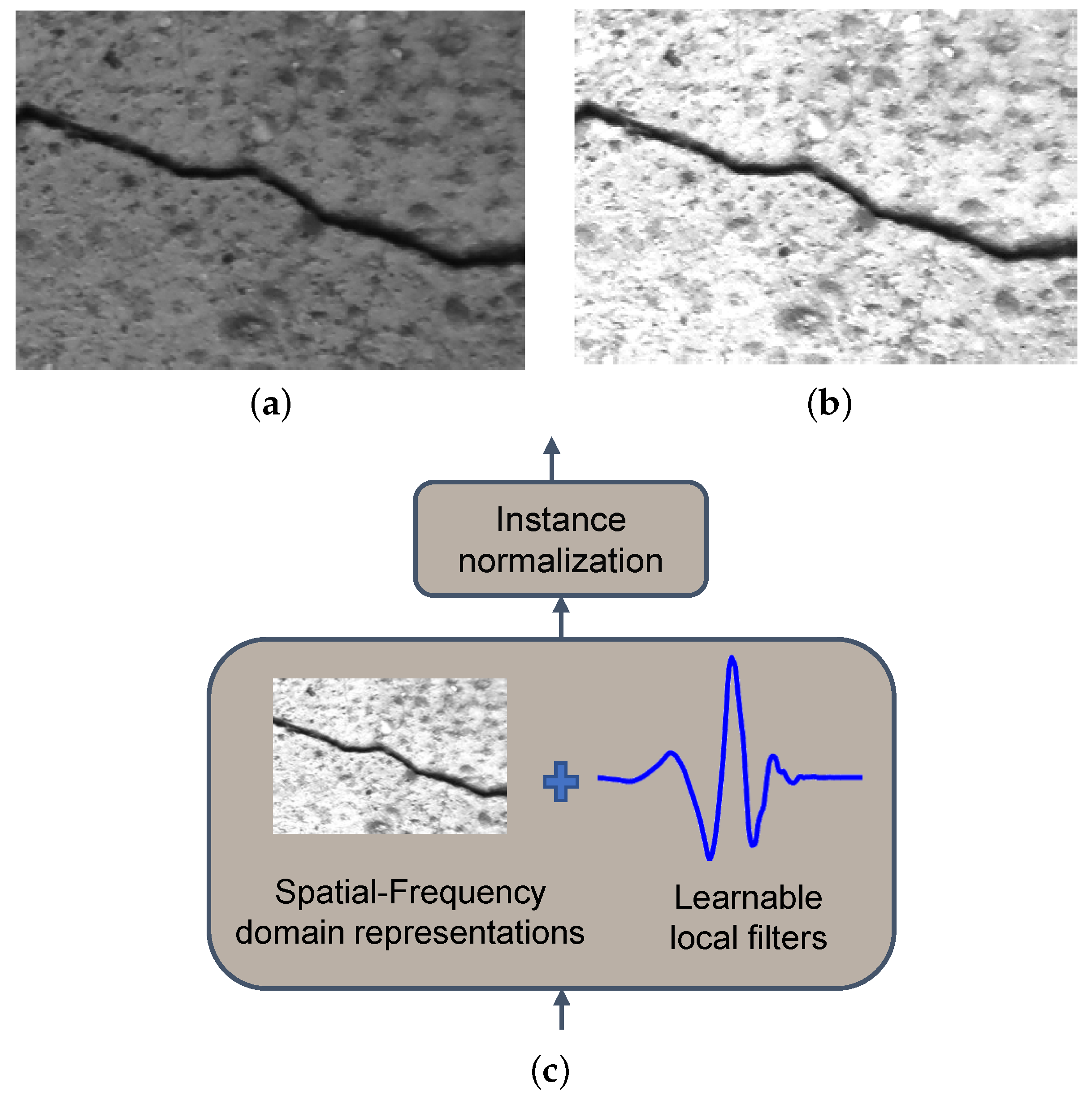
3.1. Instance Normalization Wavelet Layer
3.2. Fusion Layer
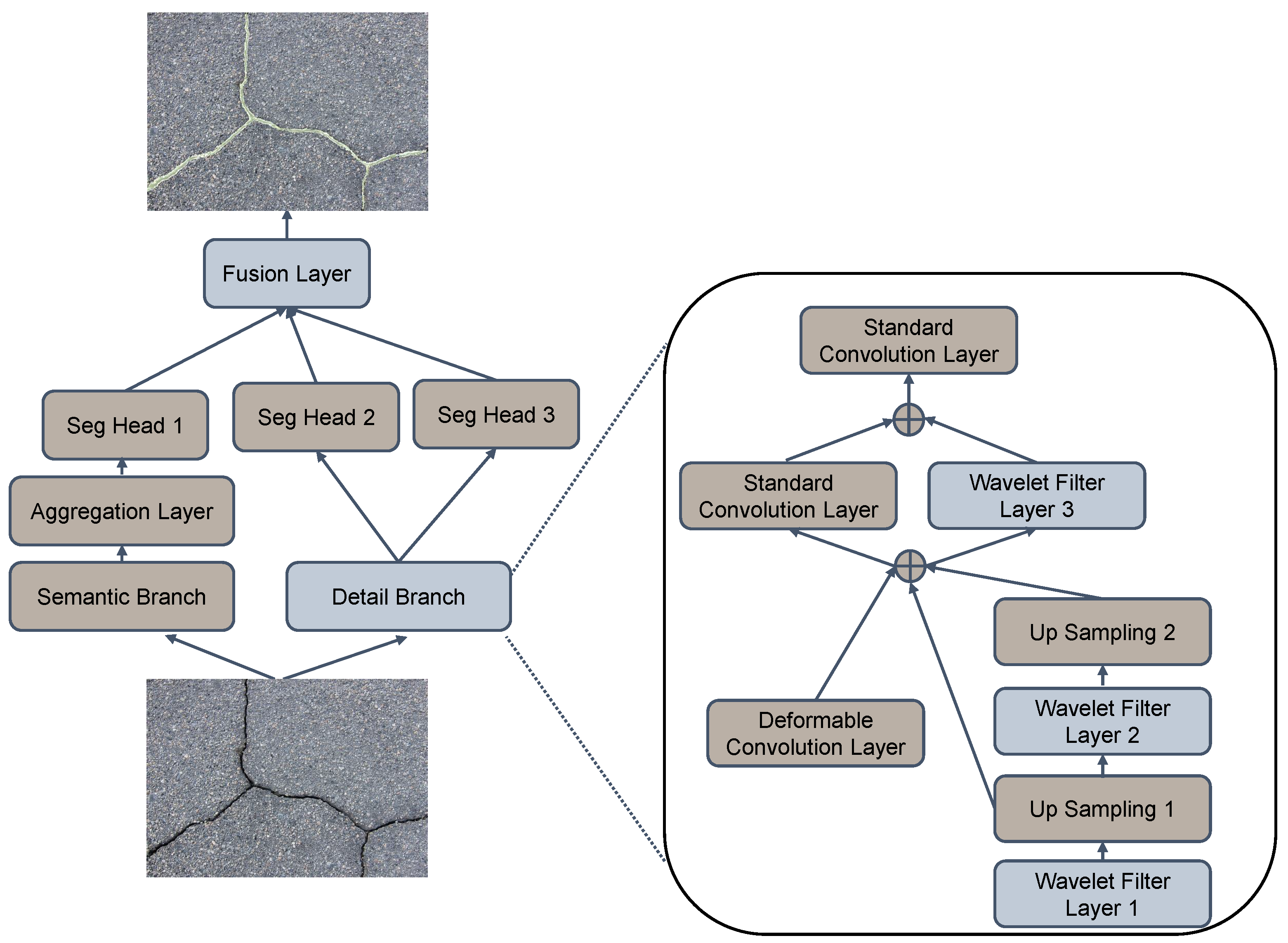
3.3. INWB Architecture
| Algorithm 1: The training algorithm of INWB. |
|
4. Experiments
4.1. Datasets and Implementation Details
4.2. Evaluation Metrics
4.3. Ablation Studies
- (1)
- Impact of INW structure
- (2)
- Feature visualization
- (3)
- Module analysis
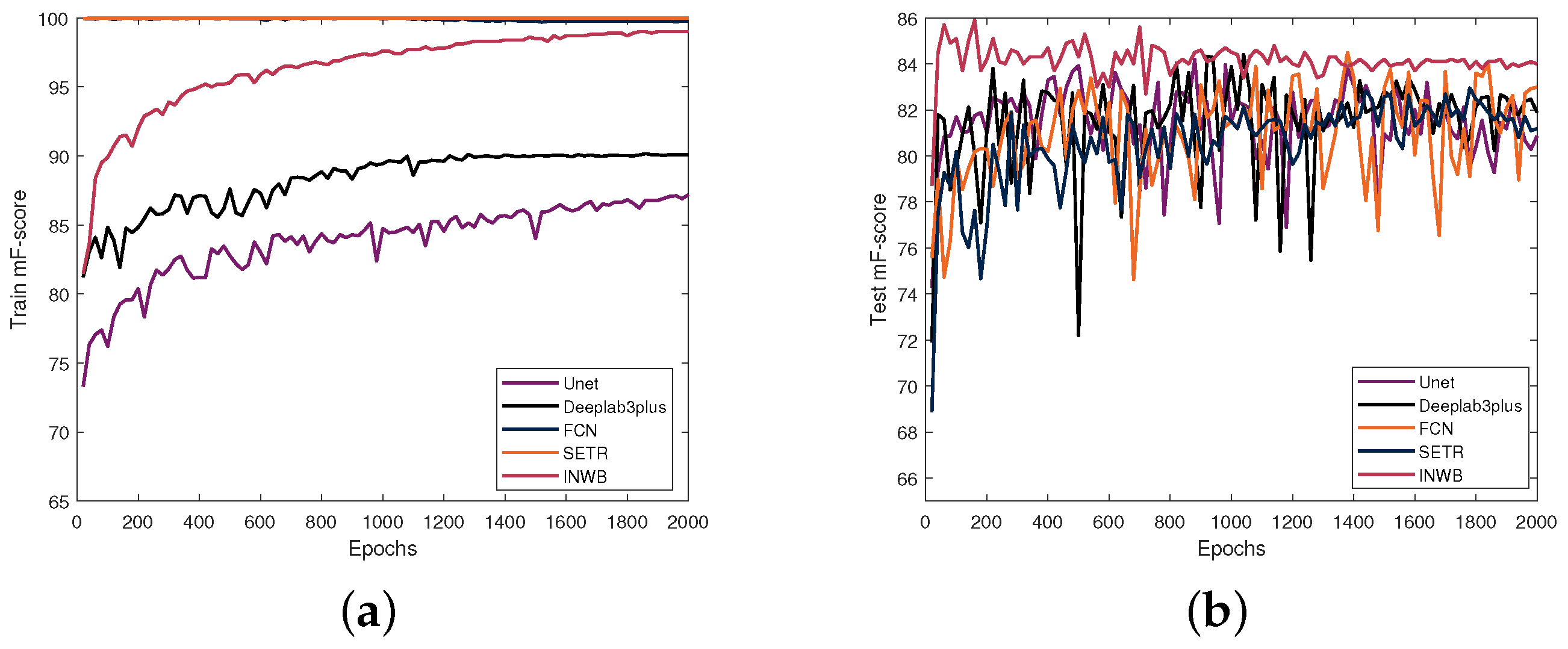
4.4. Main Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yuan, J.; Ren, Q.; Jia, C.; Zhang, J.; Fu, J.; Li, M. Automated pixel-level crack detection and quantification using deep convolutional neural networks for structural condition assessment. In Proceedings of the Structures; Elsevier: Amsterdam, The Netherlands, 2024; Volume 59, p. 105780. [Google Scholar]
- Dorafshan, S.; Thomas, R.J.; Maguire, M. Comparison of deep convolutional neural networks and edge detectors for image-based crack detection in concrete. Constr. Build. Mater. 2018, 186, 1031–1045. [Google Scholar] [CrossRef]
- Zhang, A.; Wang, K.C.; Fei, Y.; Liu, Y.; Chen, C.; Yang, G.; Li, J.Q.; Yang, E.; Qiu, S. Automated pixel-level pavement crack detection on 3D asphalt surfaces with a recurrent neural network. Comput.-Aided Civ. Infrastruct. Eng. 2019, 34, 213–229. [Google Scholar] [CrossRef]
- Liu, F.; Wang, L. UNet-based model for crack detection integrating visual explanations. Constr. Build. Mater. 2022, 322, 126265. [Google Scholar] [CrossRef]
- Gao, X.; Tong, B. MRA-UNet: Balancing speed and accuracy in road crack segmentation network. Signal Image Video Process. 2023, 17, 2093–2100. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, J.; Lu, X.; Xie, R.; Li, L. DeepCrack: A deep hierarchical feature learning architecture for crack segmentation. Neurocomputing 2019, 338, 139–153. [Google Scholar] [CrossRef]
- Ye, W.; Deng, S.; Ren, J.; Xu, X.; Zhang, K.; Du, W. Deep learning-based fast detection of apparent concrete crack in slab tracks with dilated convolution. Constr. Build. Mater. 2022, 329, 127157. [Google Scholar] [CrossRef]
- Wang, X.; Mao, Z.; Liang, Z.; Shen, J. Multi-Scale Semantic Map Distillation for Lightweight Pavement Crack Detection. IEEE Trans. Intell. Transp. Syst. 2024, 25, 15081–15093. [Google Scholar] [CrossRef]
- Geng, M.; Ma, H.; Wang, J.; Liu, S.; Li, J.; Ai, Y.; Zhang, W. A deep learning framework for predicting slab transverse crack using multivariate LSTM-FCN in continuous casting. Expert Syst. Appl. 2024, 260, 125413. [Google Scholar] [CrossRef]
- Yu, C.; Gao, C.; Wang, J.; Yu, G.; Shen, C.; Sang, N. Bisenet v2: Bilateral network with guided aggregation for real-time semantic segmentation. Int. J. Comput. Vis. 2021, 129, 3051–3068. [Google Scholar] [CrossRef]
- Munawar, H.S.; Hammad, A.W.; Haddad, A.; Soares, C.A.P.; Waller, S.T. Image-based crack detection methods: A review. Infrastructures 2021, 6, 115. [Google Scholar] [CrossRef]
- Kamaliardakani, M.; Sun, L.; Ardakani, M.K. Sealed-crack detection algorithm using heuristic thresholding approach. J. Comput. Civ. Eng. 2016, 30, 04014110. [Google Scholar] [CrossRef]
- Zhang, D.; Li, Q.; Chen, Y.; Cao, M.; He, L.; Zhang, B. An efficient and reliable coarse-to-fine approach for asphalt pavement crack detection. Image Vis. Comput. 2017, 57, 130–146. [Google Scholar] [CrossRef]
- Zou, Q.; Cao, Y.; Li, Q.; Mao, Q.; Wang, S. CrackTree: Automatic crack detection from pavement images. Pattern Recognit. Lett. 2012, 33, 227–238. [Google Scholar] [CrossRef]
- Salman, M.; Mathavan, S.; Kamal, K.; Rahman, M. Pavement crack detection using the Gabor filter. In Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems (ITSC 2013), The Hague, The Netherlands, 6–9 October 2013; pp. 2039–2044. [Google Scholar]
- Wu, S.; Liu, Y. A segment algorithm for crack dection. In Proceedings of the 2012 IEEE Symposium on Electrical & Electronics Engineering (EEESYM), Kuala Lumpur, Malaysia, 24–27 June 2012; pp. 674–677. [Google Scholar]
- Dais, D.; Bal, İ.E.; Smyrou, E.; Sarhosis, V. Automatic crack classification and segmentation on masonry surfaces using convolutional neural networks and transfer learning. Autom. Constr. 2021, 125, 103606. [Google Scholar] [CrossRef]
- Cui, X.; Wang, Q.; Dai, J.; Xue, Y.; Duan, Y. Intelligent crack detection based on attention mechanism in convolution neural network. Adv. Struct. Eng. 2021, 24, 1859–1868. [Google Scholar] [CrossRef]
- Zhou, Q.; Qu, Z.; Cao, C. Mixed pooling and richer attention feature fusion for crack detection. Pattern Recognit. Lett. 2021, 145, 96–102. [Google Scholar] [CrossRef]
- Li, H.; Peng, T.; Qiao, N.; Guan, Z.; Feng, X.; Guo, P.; Duan, T.; Gong, J. CrackTinyNet: A novel deep learning model specifically designed for superior performance in tiny road surface crack detection. IET Intell. Transp. Syst. 2024, 18, 2693–2712. [Google Scholar] [CrossRef]
- SwinCrack: Pavement crack detection using convolutional swin-transformer networkImage 1. Digit. Signal Process. 2024, 145, 104297. [CrossRef]
- Mallat, S. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Vonesch, C.; Blu, T.; Unser, M. Generalized Daubechies Wavelet Families. Trans. Sig. Proc. 2007, 55, 4415–4429. [Google Scholar] [CrossRef]
- Kamiński, M. Homogenization-based finite element analysis of unidirectional composites by classical and multiresolutional techniques. Comput. Methods Appl. Mech. Eng. 2005, 194, 2147–2173. [Google Scholar] [CrossRef]
- Othman, G.; Zeebaree, D.Q. The applications of discrete wavelet transform in image processing: A review. J. Soft Comput. Data Min. 2020, 1, 31–43. [Google Scholar]
- Singh, A.; Rawat, A.; Raghuthaman, N. Mexican Hat Wavelet Transform and Its Applications. In Methods of Mathematical Modelling and Computation for Complex Systems; Singh, J., Dutta, H., Kumar, D., Baleanu, D., Hristov, J., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 299–317. [Google Scholar] [CrossRef]
- Nikolov, S.; Hill, P.; Bull, D.; Canagarajah, N. Wavelets for Image Fusion. In Wavelets in Signal and Image Analysis: From Theory to Practice; Petrosian, A.A., Meyer, F.G., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 2001; pp. 213–241. [Google Scholar]
- Shen, L.; Bai, L. A review on Gabor wavelets for face recognition. Pattern Anal. Appl. 2006, 9, 273–292. [Google Scholar] [CrossRef]
- Zhou, W.; Sun, F.; Jiang, Q.; Cong, R.; Hwang, J.N. WaveNet: Wavelet Network with Knowledge Distillation for RGB-T Salient Object Detection. IEEE Trans. Image Process. 2023, 32, 3027–3039. [Google Scholar] [CrossRef]
- Williams, T.; Li, R. Wavelet pooling for convolutional neural networks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Yao, T.; Pan, Y.; Li, Y.; Ngo, C.W.; Mei, T. Wave-ViT: Unifying Wavelet and Transformers for Visual Representation Learning. In Proceedings of the Computer Vision—ECCV 2022, Tel Aviv, Israel, 23–27 October 2022; pp. 328–345. [Google Scholar]
- Liu, J.; Zhao, H.; Chen, Z.; Wang, Q.; Shen, X.; Zhang, H. A Dynamic Weights-Based Wavelet Attention Neural Network for Defect Detection. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 16211–16221. [Google Scholar] [CrossRef]
- Lei, D.; Yang, L.; Xu, W.; Zhang, P.; Huang, Z. Experimental study on alarming of concrete micro-crack initiation based on wavelet packet analysis. Constr. Build. Mater. 2017, 149, 716–723. [Google Scholar] [CrossRef]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Instance normalization: The missing ingredient for fast stylization. arXiv 2016, arXiv:1607.08022. [Google Scholar]
- Shrivastava, A.; Gupta, A.; Girshick, R. Training Region-Based Object Detectors with Online Hard Example Mining. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27 June–1 July 2016; pp. 761–769. [Google Scholar]
- Yang, F.; Zhang, L.; Yu, S.; Prokhorov, D.; Mei, X.; Ling, H. Feature pyramid and hierarchical boosting network for pavement crack detection. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1525–1535. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Xie, E.; Wang, W.; Yu, Z.; Anandkumar, A.; Alvarez, J.M.; Luo, P. SegFormer: Simple and efficient design for semantic segmentation with transformers. Adv. Neural Inf. Process. Syst. 2021, 34, 12077–12090. [Google Scholar]
| Wavelet Component | Precision | Recall | F-Score |
|---|---|---|---|
| LL | 0.858 | 0.860 | 0.859 |
| HH | 0.733 | 0951 | 0.801 |
| LL, LH, HL | 0.821 | 0.873 | 0.846 |
| LL, LH, HL, HH | 0.829 | 0.882 | 0.855 |
| Wavelet Family | Precision | Recall | F-Score |
|---|---|---|---|
| haar | 0.819 | 0.887 | 0.852 |
| db | 0.822 | 0.884 | 0.852 |
| rbio | 0.831 | 0.878 | 0.854 |
| bior | 0.858 | 0.860 | 0.859 |
| Methods | INW | Fusion Layer | Precision | Recall | F-Score |
|---|---|---|---|---|---|
| Baseline | − | − | 0.803 | 0.818 | 0.810 |
| +INW | ✓ | − | 0.841 | 0.841 | 0.840 |
| +Fusion Layer | − | ✓ | 0.770 | 0.898 | 0.829 |
| All | ✓ | ✓ | 0.858 | 0.860 | 0.859 |
| Methods | Precision | Recall | F-Score | FLOPs |
|---|---|---|---|---|
| Unet | 0.849 | 0.835 | 0.842 | 0.162T |
| Deeplabv3plusFree | 0.880 | 0.810 | 0.844 | 0.141T |
| Deeplabv3plusFrozen | 0.858 | 0.842 | 0.850 | 0.141T |
| FCN | 0.857 | 0.834 | 0.845 | 0.158T |
| SETR | 0.887 | 0.779 | 0.830 | 0.284T |
| INWB | 0.858 | 0.860 | 0.859 | 0.158T |
| Methods | Precision | Recall | F-Score | FLOPs |
|---|---|---|---|---|
| Unet | 0.703 | 0.673 | 0.688 | 0.190T |
| Deeplabv3plusFree | 0.724 | 0.707 | 0.715 | 0.155T |
| Deeplabv3plusFrozen | 0.760 | 0.741 | 0.750 | 0.155T |
| FCN | 0.720 | 0.733 | 0.726 | 0.174T |
| SETR | 0.640 | 0.693 | 0.665 | 0.325T |
| INWB | 0.693 | 0.921 | 0.791 | 0.186T |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, L.; Xiong, F.; Cao, Y.; Xue, H.; Cui, L.; Han, X. Focusing on Cracks with Instance Normalization Wavelet Layer. Sensors 2025, 25, 146. https://doi.org/10.3390/s25010146
Guo L, Xiong F, Cao Y, Xue H, Cui L, Han X. Focusing on Cracks with Instance Normalization Wavelet Layer. Sensors. 2025; 25(1):146. https://doi.org/10.3390/s25010146
Chicago/Turabian StyleGuo, Lei, Fengguang Xiong, Yaming Cao, Hongxin Xue, Lei Cui, and Xie Han. 2025. "Focusing on Cracks with Instance Normalization Wavelet Layer" Sensors 25, no. 1: 146. https://doi.org/10.3390/s25010146
APA StyleGuo, L., Xiong, F., Cao, Y., Xue, H., Cui, L., & Han, X. (2025). Focusing on Cracks with Instance Normalization Wavelet Layer. Sensors, 25(1), 146. https://doi.org/10.3390/s25010146






