Data-Driven Enhancements for MPC-Based Path Tracking Controller in Autonomous Vehicles
Abstract
1. Introduction
- In response to the challenge that the relationship between the lateral force and slip angle becomes nonlinear as the tires exhibit nonlinear characteristics, this study employs the KAN network to estimate the lateral forces to correct the tire cornering stiffness, thereby enhancing the accuracy of the predictive model.
- GPR is utilized to learn the residual dynamics between the simplified mechanistic model and the actual vehicle state. This strategy significantly enhances the predictive model accuracy of the MPC and further improves the precision of path tracking.
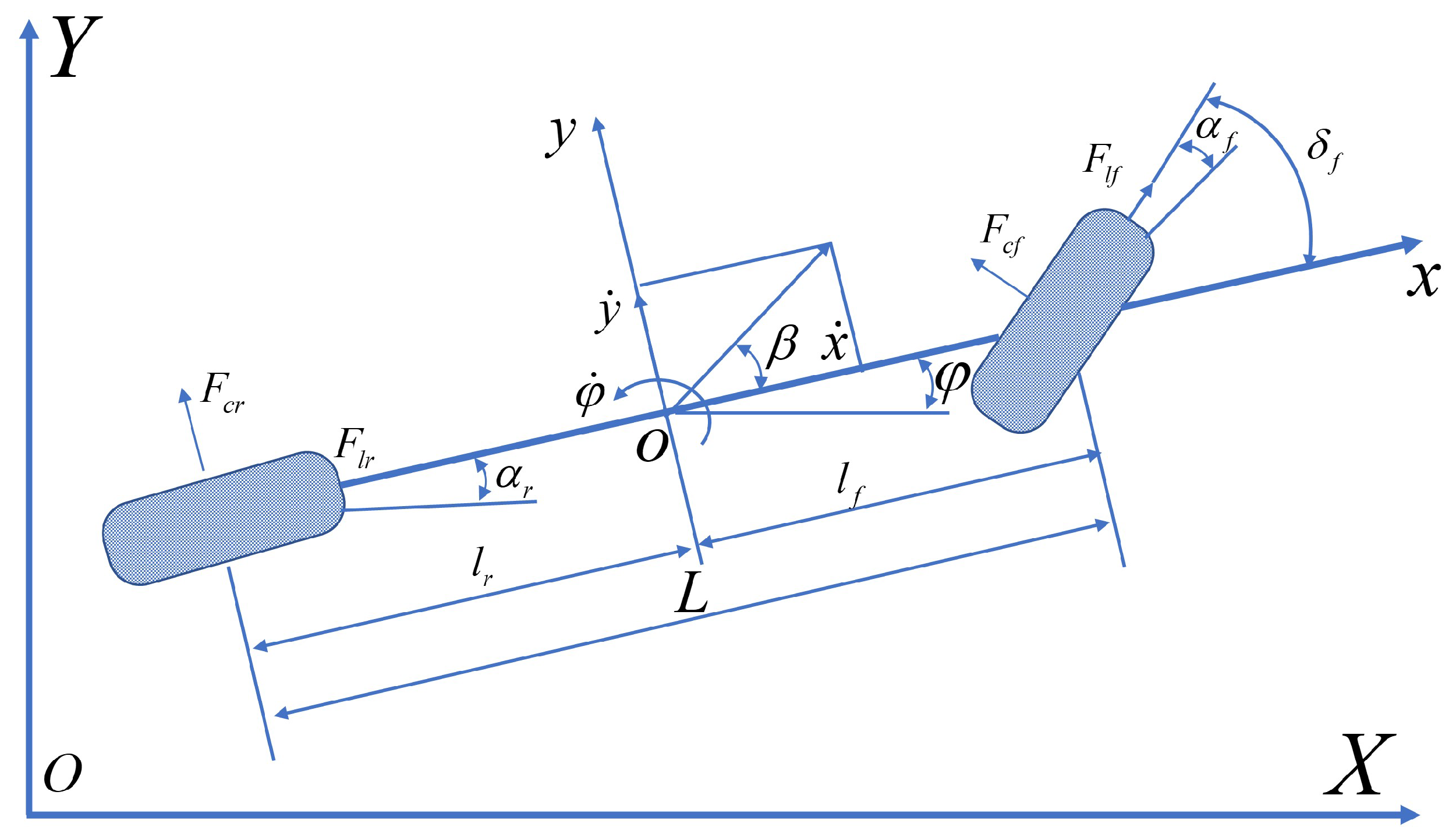
2. Nominal Vehicle Dynamics Model
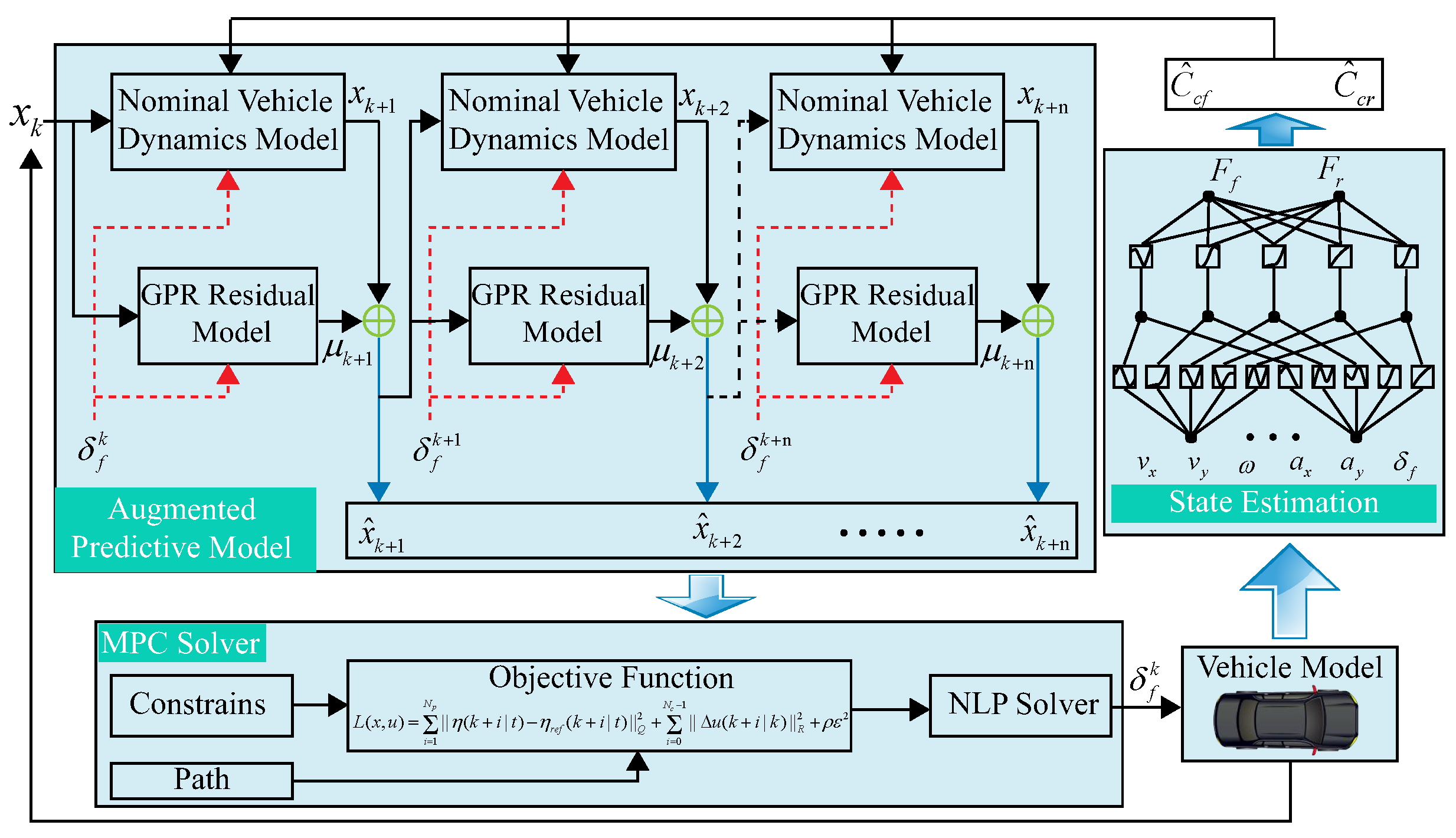
3. DD-PTC Architecture
3.1. Augmented Predictive Model Layer
3.1.1. Gaussian Process Regression
3.1.2. Data Collection and Practical Implementation
3.2. State Estimation Layer
3.3. MPC Solver Layer
4. Simulation and Analysis
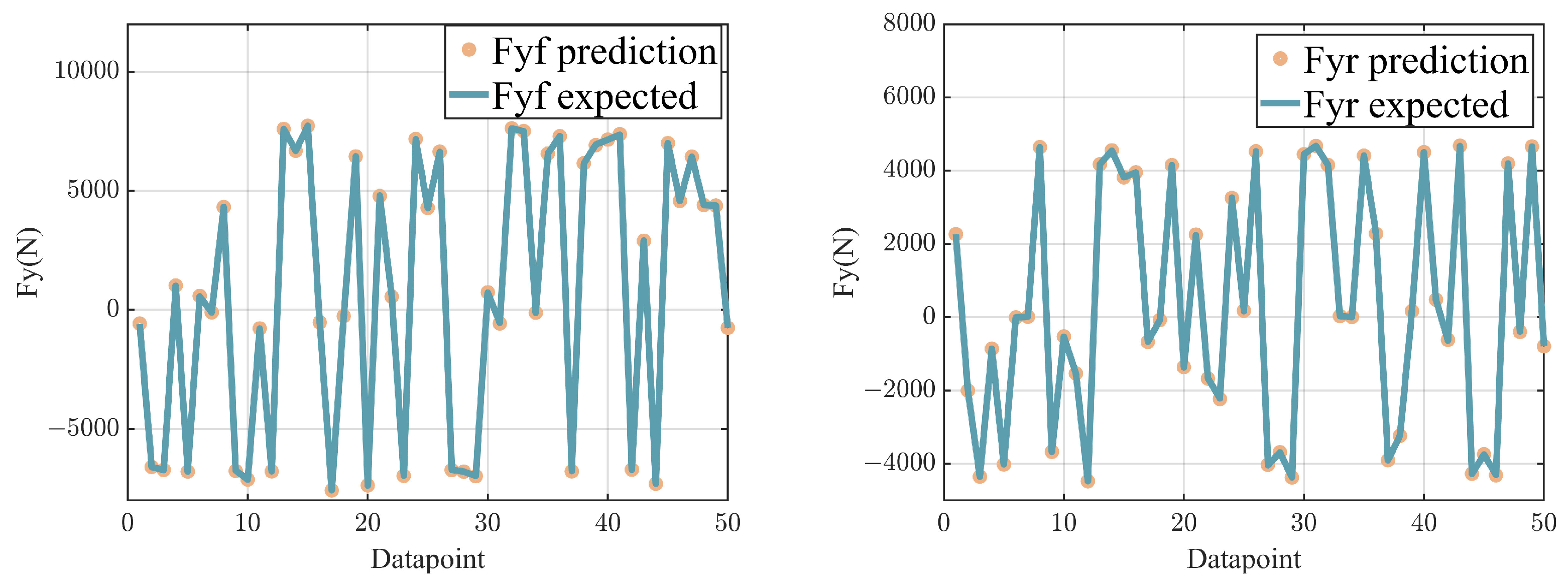
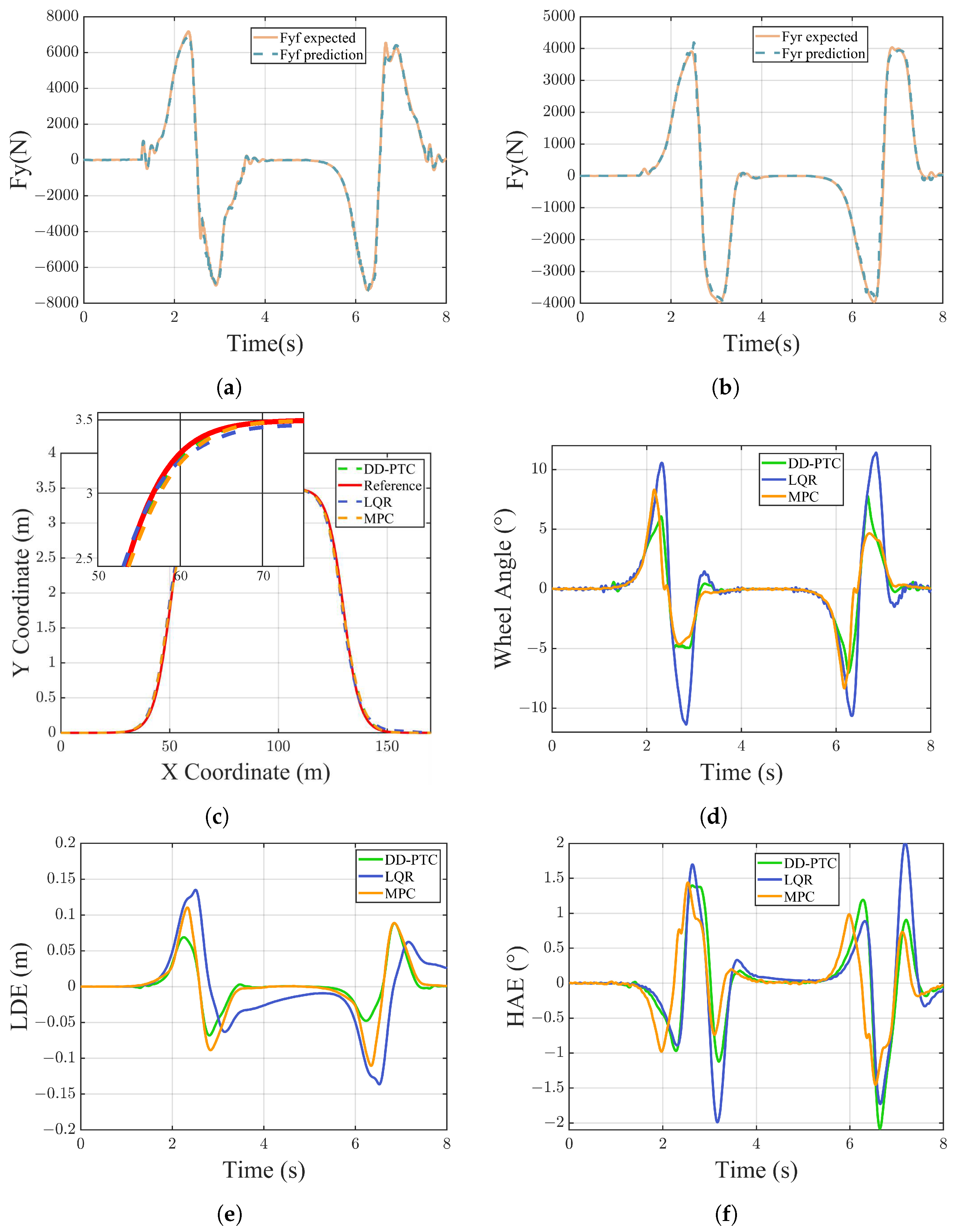
4.1. Estimation Results of the KAN Model
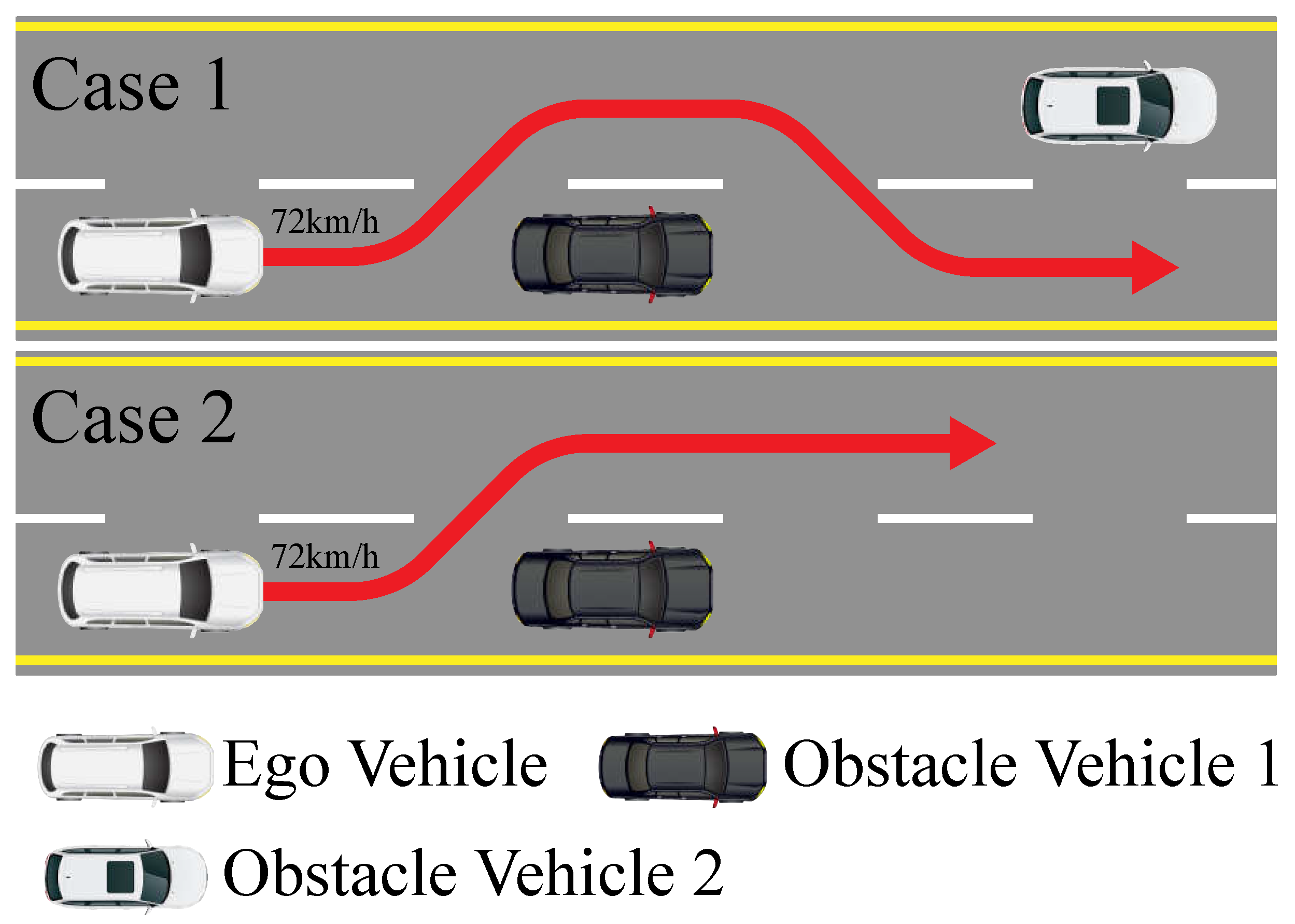
4.2. Double-Lane Change
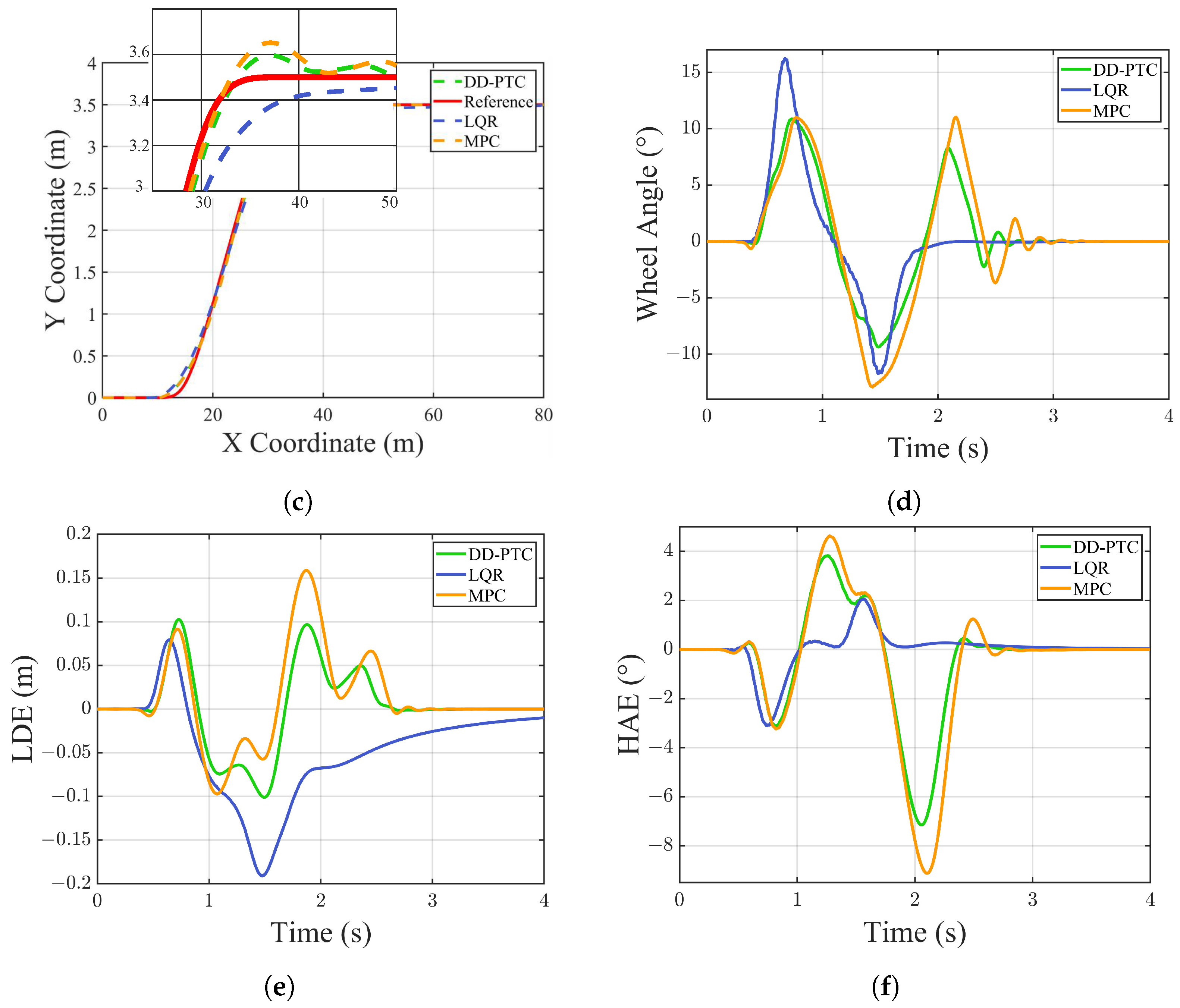
4.3. Single-Lane Change
4.4. Ablation Experiment
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Teng, S.; Hu, X.; Deng, P.; Li, B.; Li, Y.; Ai, Y.; Yang, D.; Li, L.; Xuanyuan, Z.; Zhu, F.; et al. Motion planning for autonomous driving: The state of the art and future perspectives. IEEE Trans. Intell. Veh. 2023, 8, 3692–3711. [Google Scholar] [CrossRef]
- Rokonuzzaman, M.; Mohajer, N.; Nahavandi, S.; Mohamed, S. Review and performance evaluation of path tracking controllers of autonomous vehicles. IET Intell. Transp. Syst. 2021, 15, 646–670. [Google Scholar] [CrossRef]
- Stano, P.; Montanaro, U.; Tavernini, D.; Tufo, M.; Fiengo, G.; Novella, L.; Sorniotti, A. Model predictive path tracking control for automated road vehicles: A review. Annu. Rev. Control 2023, 55, 194–236. [Google Scholar] [CrossRef]
- Kong, J.; Pfeiffer, M.; Schildbach, G.; Borrelli, F. Kinematic and dynamic vehicle models for autonomous driving control design. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Republic of Korea, 28 June–1 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1094–1099. [Google Scholar]
- Taherian, S.; Montanaro, U.; Dixit, S.; Fallah, S. Integrated trajectory planning and torque vectoring for autonomous emergency collision avoidance. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 2714–2721. [Google Scholar]
- Law, C.K.; Dalal, D.; Shearrow, S. Robust model predictive control for autonomous vehicles/self driving cars. arXiv 2018, arXiv:1805.08551. [Google Scholar]
- Tang, L.; Yan, F.; Zou, B.; Wang, K.; Lv, C. An improved kinematic model predictive control for high-speed path tracking of autonomous vehicles. IEEE Access 2020, 8, 51400–51413. [Google Scholar] [CrossRef]
- Vallon, C.; Ercan, Z.; Carvalho, A.; Borrelli, F. A machine learning approach for personalized autonomous lane change initiation and control. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1590–1595. [Google Scholar]
- Xie, J.; Xu, X.; Wang, F.; Tang, Z.; Chen, L. Coordinated control based path following of distributed drive autonomous electric vehicles with yaw-moment control. Control Eng. Pract. 2021, 106, 104659. [Google Scholar] [CrossRef]
- Hang, P.; Xia, X.; Chen, G.; Chen, X. Active safety control of automated electric vehicles at driving limits: A tube-based MPC approach. IEEE Trans. Transp. Electrif. 2021, 8, 1338–1349. [Google Scholar] [CrossRef]
- Kabzan, J.; Valls, M.I.; Reijgwart, V.J.; Hendrikx, H.F.; Ehmke, C.; Prajapat, M.; Bühler, A.; Gosala, N.; Gupta, M.; Sivanesan, R.; et al. AMZ driverless: The full autonomous racing system. J. Field Robot. 2020, 37, 1267–1294. [Google Scholar] [CrossRef]
- Wu, H.; Si, Z.; Li, Z. Trajectory tracking control for four-wheel independent drive intelligent vehicle based on model predictive control. IEEE Access 2020, 8, 73071–73081. [Google Scholar] [CrossRef]
- Hamid, U.Z.A.; Ariff, M.H.M.; Zamzuri, H.; Saito, Y.; Zakaria, M.A.; Rahman, M.A.A.; Raksincharoensak, P. Piecewise trajectory replanner for highway collision avoidance systems with safe-distance based threat assessment strategy and nonlinear model predictive control. J. Intell. Robot. Syst. 2018, 90, 363–385. [Google Scholar] [CrossRef]
- Yuan, H.; Sun, X.; Gordon, T. Unified decision-making and control for highway collision avoidance using active front steer and individual wheel torque control. Veh. Syst. Dyn. 2018, 57, 1188–1205. [Google Scholar] [CrossRef]
- Subosits, J.K.; Gerdes, J.C. Impacts of model fidelity on trajectory optimization for autonomous vehicles in extreme maneuvers. IEEE Trans. Intell. Veh. 2021, 6, 546–558. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, W.; Yang, C.; Ma, M. An adaptive model predictive control strategy for path following of autonomous vehicles based on tire cornering stiffness estimation. In Proceedings of the 2021 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1904–1909. [Google Scholar]
- Xie, H.; Xi, Y.; Song, K.; Guo, F. A Trajectory Tracking Control Algorithm of Self-driving Tractor-trailer Based on Online Estimation of Cornering Stiffness. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 5414–5419. [Google Scholar]
- Wang, Y.; Duan, Y.; Zhang, Y. Local Path Planning and Tracking Control Considering Tire Cornering Stiffness Uncertainty; Technical Report, SAE Technical Paper; SAE International: Warrendale, PA, USA, 2021. [Google Scholar]
- Chu, Z.; Chen, N.; Zhang, N.; Li, G. Path-tracking for autonomous vehicles with on-line estimation of axle cornering stiffnesses. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 6651–6657. [Google Scholar]
- Zhang, Z.; Zheng, L.; Li, Y.; Li, S.; Liang, Y. Cooperative strategy of trajectory tracking and stability control for 4WID autonomous vehicles under extreme conditions. IEEE Trans. Veh. Technol. 2023, 72, 3105–3118. [Google Scholar] [CrossRef]
- Hewing, L.; Kabzan, J.; Zeilinger, M.N. Cautious model predictive control using gaussian process regression. IEEE Trans. Control Syst. Technol. 2019, 28, 2736–2743. [Google Scholar] [CrossRef]
- Kabzan, J.; Hewing, L.; Liniger, A.; Zeilinger, M.N. Learning-based model predictive control for autonomous racing. IEEE Robot. Autom. Lett. 2019, 4, 3363–3370. [Google Scholar] [CrossRef]
- Saviolo, A.; Li, G.; Loianno, G. Physics-inspired temporal learning of quadrotor dynamics for accurate model predictive trajectory tracking. IEEE Robot. Autom. Lett. 2022, 7, 10256–10263. [Google Scholar] [CrossRef]
- Torrente, G.; Kaufmann, E.; Föhn, P.; Scaramuzza, D. Data-driven MPC for quadrotors. IEEE Robot. Autom. Lett. 2021, 6, 3769–3776. [Google Scholar] [CrossRef]
- Salzmann, T.; Kaufmann, E.; Arrizabalaga, J.; Pavone, M.; Scaramuzza, D.; Ryll, M. Real-time neural MPC: Deep learning model predictive control for quadrotors and agile robotic platforms. IEEE Robot. Autom. Lett. 2023, 8, 2397–2404. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. Kan: Kolmogorov-arnold networks. arXiv 2024, arXiv:2404.19756. [Google Scholar]
- Pinkus, A. Approximation theory of the MLP model in neural networks. Acta Numer. 1999, 8, 143–195. [Google Scholar] [CrossRef]




| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Vehicle mass (kg) | 1270 | Yaw moment of inertia (kg·m2) | 1536.7 |
| Wheelbase (m) | 2.910 | Wheel track (mm) | 1.675 (front, rear) |
| Distance from front axle to center of mass (m) | 1.015 | Distance from rear axle to center of mass (m) | 1.895 |
| Centroid height (m) | 0.54 | Rolling radius (m) | 0.325 |
| Front axle cornering stiffness (N/rad) | 60,000 | Rear axle cornering stiffness (N/rad) | 40,000 |
| LDE (m) | HAE (°) | |
|---|---|---|
| Max/Avg. | Max/Avg. | |
| DD-PTC | 0.0885/0.0162 | 2.0818/0.3564 |
| LQR | 0.1362/0.0357 | 2.0139/0.4071 |
| MPC | 0.1104/0.0230 | 1.4532/0.3080 |
| LDE (m) | HAE (°) | |
|---|---|---|
| Max/Avg. | Max/Avg. | |
| DD-PTC | 0.1025/0.0331 | 7.1496/1.4074 |
| LQR | 0.1908/0.0520 | 3.1016/0.3942 |
| MPC | 0.1521/0.0378 | 9.1182/1.8024 |
| Test Scenarios | LDE (m) | HAE (°) | |
|---|---|---|---|
| Max/Avg. | Max/Avg. | ||
| Stiff Corr–MPC | Double-lane | 0.1062/0.0194 | 2.1643/0.3705 |
| Single-lane | 0.1181/0.0297 | 5.8537/1.1589 | |
| GP-MPC | Double-lane | 0.0891/0.0178 | 1.6996/0.3610 |
| Single-lane | 0.1213/0.0350 | 8.8269/1.7213 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Xie, Z.; Liu, M.; Hu, J.; Dai, Z.; Guo, J. Data-Driven Enhancements for MPC-Based Path Tracking Controller in Autonomous Vehicles. Sensors 2024, 24, 7657. https://doi.org/10.3390/s24237657
Guo J, Xie Z, Liu M, Hu J, Dai Z, Guo J. Data-Driven Enhancements for MPC-Based Path Tracking Controller in Autonomous Vehicles. Sensors. 2024; 24(23):7657. https://doi.org/10.3390/s24237657
Chicago/Turabian StyleGuo, Jianhua, Zhihao Xie, Ming Liu, Jincheng Hu, Zhiyuan Dai, and Jinqiu Guo. 2024. "Data-Driven Enhancements for MPC-Based Path Tracking Controller in Autonomous Vehicles" Sensors 24, no. 23: 7657. https://doi.org/10.3390/s24237657
APA StyleGuo, J., Xie, Z., Liu, M., Hu, J., Dai, Z., & Guo, J. (2024). Data-Driven Enhancements for MPC-Based Path Tracking Controller in Autonomous Vehicles. Sensors, 24(23), 7657. https://doi.org/10.3390/s24237657





