Pixel-Based Long-Wave Infrared Spectral Image Reconstruction Using a Hierarchical Spectral Transformer
Abstract
1. Introduction
- We propose training the neural network on pixel-based LWIR spectra and integrating an LWIR spectral noise model into the USIRS data simulation pipeline. This approach reduces the need for high-quality paired data for training on LWIR spectral images.
- We introduce the Hierarchical Spectral Transformer (HST), designed to effectively learn and preserve both global and local spectral information, thus mitigating the large amount of noise and enhancing the reconstruction accuracy.
- We evaluate our pipeline using both synthetic and experimental data to demonstrate its effectiveness in handling real-world scenarios.
2. Materials and Methods
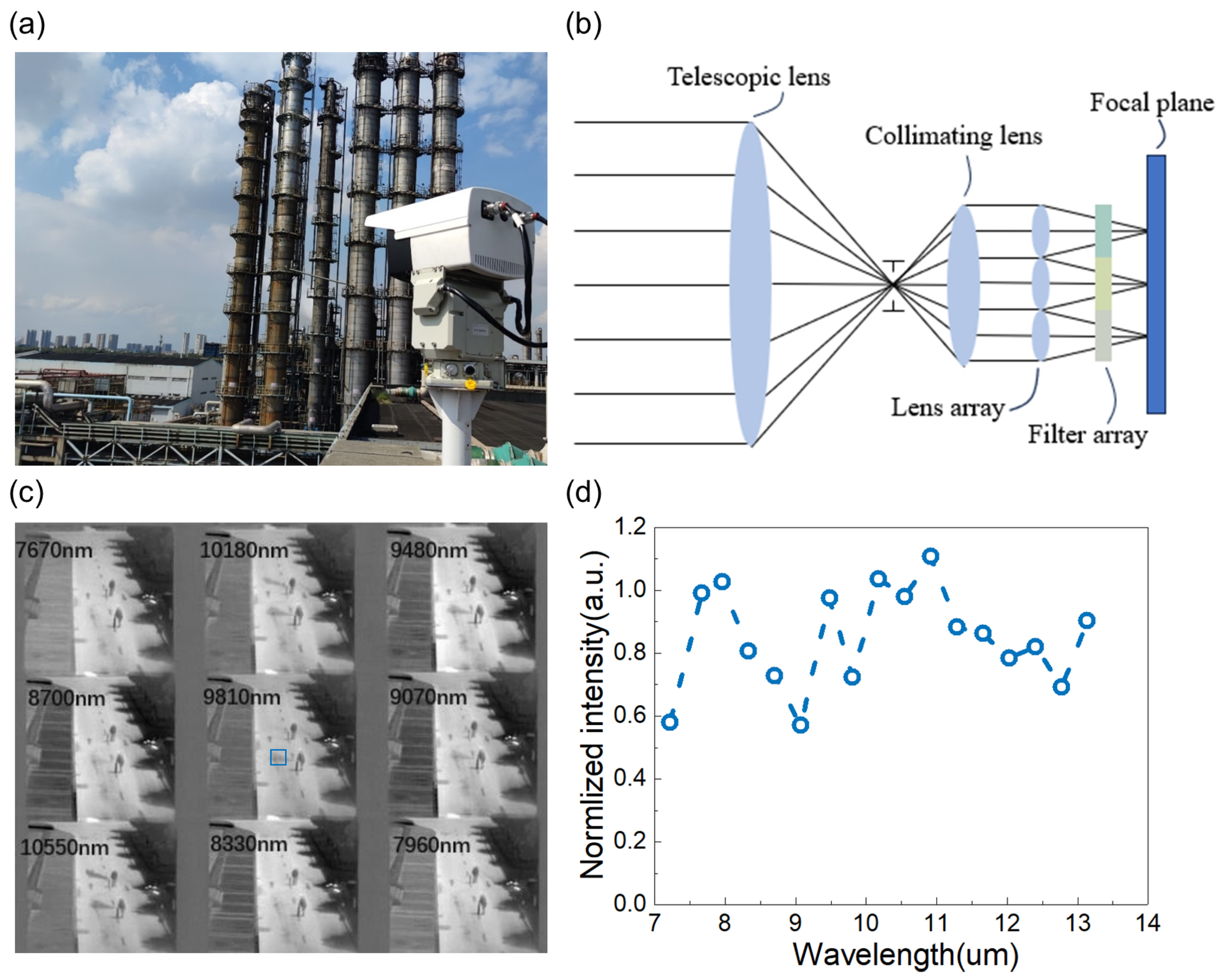
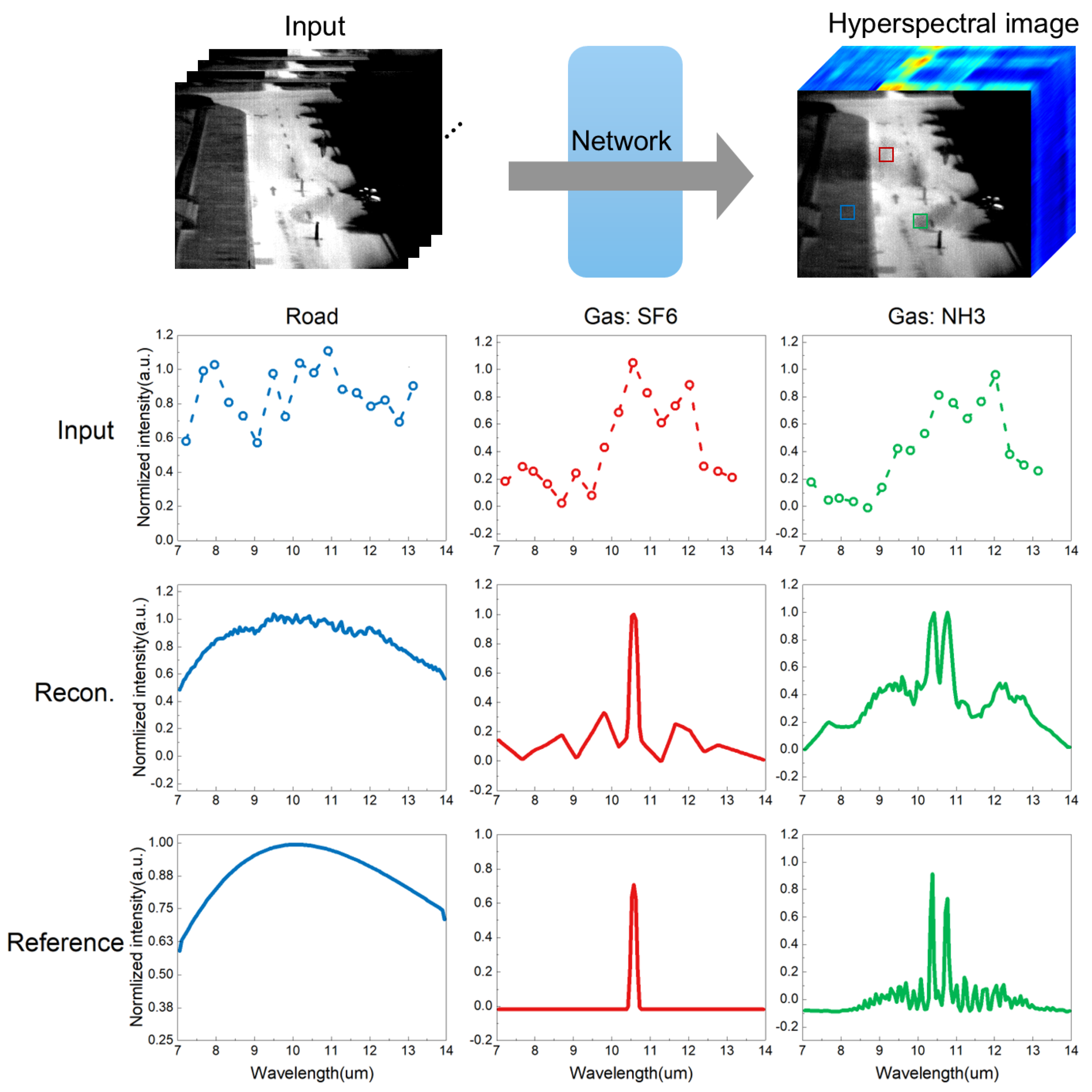
2.1. The USIRS
2.2. Imaging and Noise Model
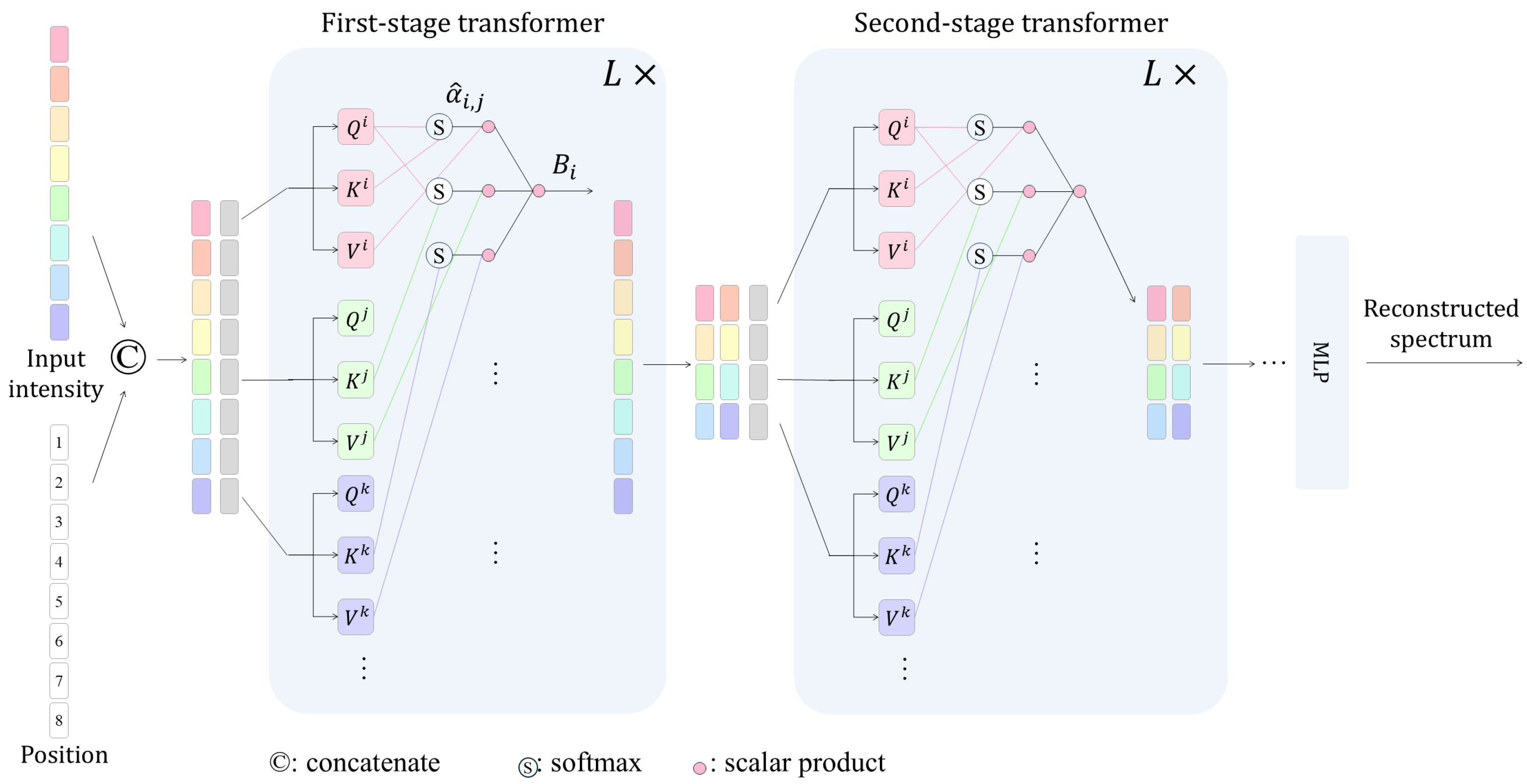
2.3. Pixel-Based Hierarchical Spectral Transformer
2.3.1. Positional Encoding
2.3.2. Hierarchical Representation
2.3.3. Attention Mechanism in Transformer
2.3.4. Implementation Details
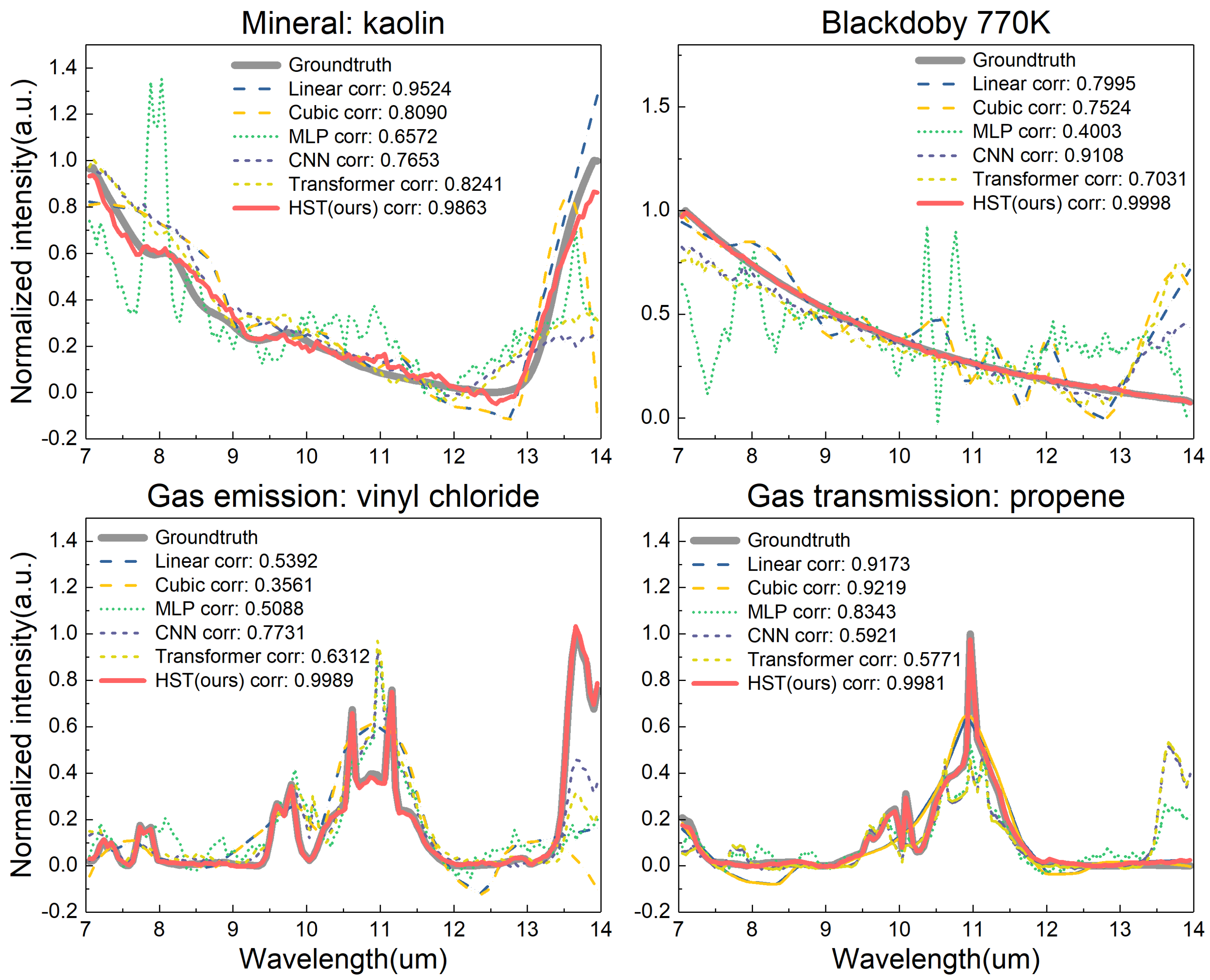
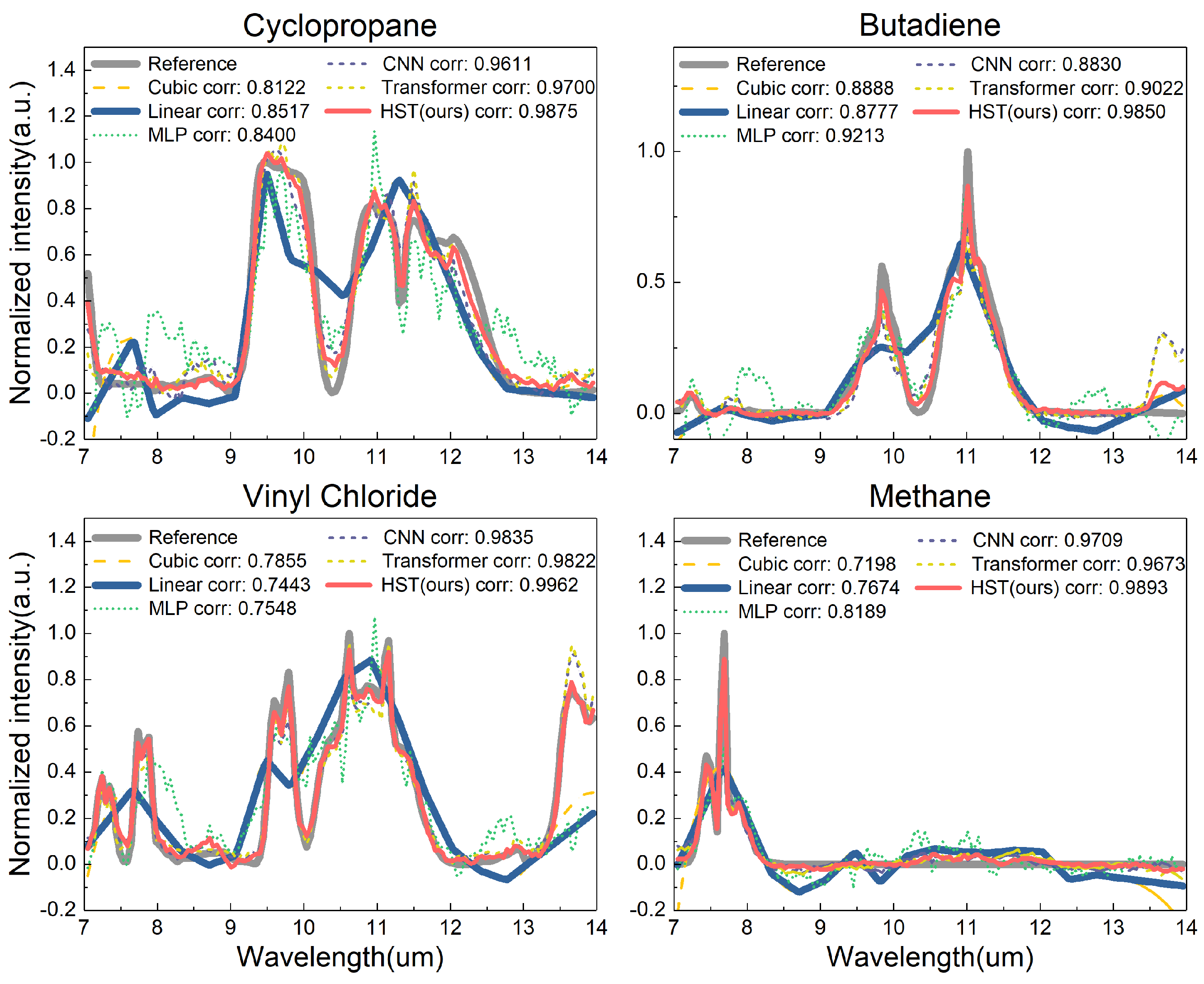
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Greek Symbol | Meaning | ||
| photon noise | |||
| response | |||
| variance | |||
| mean | |||
| attention weight | |||
| Lowercase Label | Meaning | Uppercase Label | Meaning |
| t | target | L | radiation |
| p | background | M | encoding dimension |
| d | dark current | N | noise |
| q | quantization | Q | query |
| n | total number of data | K | key |
| s | spectrum | V | value |
| g | ground truth spectrum | S | network input |
| l | length of spectrum | B | concatenated attention |
References
- Shaw, G.A.; Burke, H.-H.K. Spectral Imaging for Remote Sensing. Linc. Lab. J. 2003, 14, 3–28. [Google Scholar]
- Jia, J.; Wang, Y.-M.; Chen, J.; Guo, R.; Shu, R.; Wang, J. Status and application of advanced airborne hyperspectral imaging technology: A review. Infrared Phys. Technol. 2020, 104, 103–115. [Google Scholar] [CrossRef]
- Manolakis, D.G.; Pieper, M.L.; Truslow, E.; Lockwood, R.B.; Weisner, A.; Jacobson, J.; Cooley, T.W. Longwave Infrared Hyperspectral Imaging: Principles, Progress, and Challenges. IEEE Geosci. Remote Sens. Mag. 2019, 7, 72–100. [Google Scholar] [CrossRef]
- Bacca, J.; Martinez, E.; Arguello, H. Longwave Computational Spectral Imaging: A Contemporary Overview. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2023, 40, 115–125. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Liu, S.; Wang, P.; Yuan, L.; Tang, G.; Liu, X.; Lu, J.; Kong, Y.; Li, C.; Wang, J. Uncooled Snapshot Infrared Spectrometer With Improved Sensitivity for Gas Imaging. IEEE Trans. Instrum. Meas. 2024, 73, 4506009. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Z.; Wang, P.; Tang, G.; Liu, C.; Li, C.; Wang, J. Robust gas species and concentration monitoring via cross-talk transformer with snapshot infrared spectral imager. Sens. Actuators B Chem. 2024, 413, 135780. [Google Scholar] [CrossRef]
- Oiknine, Y.; August, I.; Stern, A. Multi-aperture snapshot compressive hyperspectral camera. Opt. Lett. 2018, 43, 5042–5045. [Google Scholar] [CrossRef]
- Takasawa, S. Uncooled LWIR imaging: Applications and market analysis. Image Sens. Technol. Mater. Devices Syst. Appl. II 2015, 9481. [Google Scholar] [CrossRef]
- Vollmer, M. Infrared Thermal Imaging. In Computer Vision: A Reference Guide; Springer International Publishing: Cham, Switzerland, 2020; pp. 1–4. [Google Scholar]
- Zhang, Q.; Zheng, Y.; Yuan, Q.; Song, M.; Yu, H.; Xiao, Y. Hyperspectral Image Denoising: From Model-Driven, Data-Driven, to Model-Data-Driven. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 13143–13163. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Yuan, X.; Wu, Z.; Luo, T. Coded Aperture Snapshot Spectral Imager. In Coded Optical Imaging; Liang, J., Ed.; Springer: Cham, Switzerland, 2024. [Google Scholar]
- Yuan, Q.; Zhang, Q.; Li, J.; Shen, H.; Zhang, L. Hyperspectral Image Denoising Employing a Spatial–Spectral Deep Residual Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1205–1218. [Google Scholar] [CrossRef]
- Wang, L.; Sun, C.; Fu, Y.; Kim, M.H.; Huang, H. Hyperspectral Image Reconstruction Using a Deep Spatial-Spectral Prior. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 8024–8033. [Google Scholar]
- Cai, Y.; Lin, J.; Hu, X.; Wang, H.; Yuan, X.; Zhang, Y.; Timofte, R.; Gool, L.V. Mask-guided Spectral-wise Transformer for Efficient Hyperspectral Image Reconstruction. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 17481–17490. [Google Scholar]
- Cai, Y.; Lin, J.; Hu, X.; Wang, H.; Yuan, X.; Zhang, Y.; Timofte, R.; Gool, L.V. Coarse-to-Fine Sparse Transformer for Hyperspectral Image Reconstruction. In Proceedings of the 2022 European Conference on Computer Vision (ECCV), Tel Aviv, Israel, 23–27 October 2022; Volume 13677. [Google Scholar]
- Shi, Q.; Tang, X.; Yang, T.; Liu, R.; Zhang, L. Hyperspectral Image Denoising Using a 3-D Attention Denoising Network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 10348–10363. [Google Scholar] [CrossRef]
- Xiong, F.; Zhou, J.; Zhou, J.; Lu, J.; Qian, Y. Multitask Sparse Representation Model Inspired Network for Hyperspectral Image Denoising. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5518515. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, X.; Bao, J. Denoising autoencoder aided spectrum reconstruction for colloidal quantum dot spectrometers. IEEE Sens. 2021, 21, 6450–6458. [Google Scholar] [CrossRef]
- Brown, C.; Goncharov, A.; Ballard, Z.S.; Fordham, M.; Clemens, A.; Qiu, Y.; Rivenson, Y.; Ozcan, A. Neural network-based on-chip spectroscopy using a scalable plasmonic encoder. ACS Nano 2021, 15, 6305–6315. [Google Scholar] [CrossRef]
- Zhang, W.; Song, H.; He, X.; Huang, L.; Zhang, X.; Zheng, J.; Shen, W.; Hao, X.; Liu, X. Deeply learned broadband encoding stochastic hyperspectral imaging. Light Sci. Appl. 2021, 10, 108. [Google Scholar] [CrossRef]
- Wang, J.; Pan, B.; Wang, Z.; Zhang, J.; Zhou, Z.; Yao, L.; Wu, Y.; Ren, W.; Wang, J.; Ji, H.; et al. Single-pixel p-graded-n junction spectrometers. Nat. Commun. 2024, 15, 1773. [Google Scholar] [CrossRef]
- Wen, J.; Hao, L.; Gao, C.; Wang, H.; Mo, K.; Yuan, W.; Chen, X.; Wang, Y.; Zhang, Y.; Shao, Y.; et al. Deep learning-based miniaturized all-dielectric ultracompact film spectrometer. Acs Photonics 2022, 10, 225–233. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, X.; Bao, J. Solver-informed neural networks for spectrum reconstruction of colloidal quantum dot spectrometers. Opt. Express 2020, 28, 33656–33672. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 1, 25. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Luo, W.; Li, Y.; Urtasun, R.; Zemel, R.S. Understanding the Effective Receptive Field in Deep Convolutional Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Barcelona, Spain, 5–8 December 2016; Volume 29. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Gardner, M.W.; Dorling, S.R. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks and Learning Machines, 3/E; Pearson Education India: Noida, Uttar Pradesh, India, 2009. [Google Scholar]
- Cherubini, D.; Fanni, A.; Montisci, A.; Testoni, P. Inversion of MLP neural networks for direct solution of inverse problems. IEEE Trans. Magn. 2005, 41, 1784–1787. [Google Scholar] [CrossRef]
- Baldridge, A.M.; Hook, S.J.; Grove, C.I.; Rivera, G. The ASTER spectral library version 2.0. Remote Sens. Environ. 2009, 113, 711–715. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.M.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All you Need. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Yoon, H.H.; Fernandez, H.A.; Nigmatulin, F.; Cai, W.; Yang, Z.; Cui, H.; Ahmed, F.; Cui, X.; Uddin, M.G.; Minot, E.D.; et al. Miniaturized spectrometers with a tunable van der Waals junction. Science 2022, 378, 296–299. [Google Scholar] [CrossRef]

| Noise Level | 0 | 0.1 | 0.2 | 0.5 | |
|---|---|---|---|---|---|
| Linear interp. | RMSE | 0.1133 | 0.1346 | 0.1793 | 0.3532 |
| Correlation | 0.9558 | 0.9433 | 0.9134 | 0.8008 | |
| PSNR | 17.54 | 16.28 | 13.98 | 8.16 | |
| Cubic interp. | RMSE | 0.1139 | 0.1686 | 0.2629 | 0.5953 |
| Correlation | 0.9593 | 0.9180 | 0.8420 | 0.6868 | |
| PSNR | 17.93 | 14.33 | 10.13 | 2.75 | |
| MLP [32] | RMSE | 0.1208 | 0.1130 | 0.1767 | 0.2153 |
| Correlation | 0.9568 | 0.9599 | 0.9011 | 0.8420 | |
| PSNR | 18.04 | 18.35 | 14.63 | 12.83 | |
| CNN [26] | RMSE | 0.0103 | 0.0233 | 0.0428 | 0.1076 |
| Correlation | 0.9989 | 0.9968 | 0.9906 | 0.9565 | |
| PSNR | 33.87 | 29.22 | 24.53 | 18.03 | |
| Transformer [35] | RMSE | 0.0061 | 0.0238 | 0.0436 | 0.1089 |
| Correlation | 0.9994 | 0.9970 | 0.9904 | 0.9563 | |
| PSNR | 36.51 | 29.46 | 24.45 | 17.99 | |
| HST (ours) | RMSE | 0.0059 | 0.0212 | 0.0378 | 0.1074 |
| Correlation | 0.9995 | 0.9976 | 0.9929 | 0.9566 | |
| PSNR | 37.16 | 30.41 | 25.74 | 18.02 |
| Method | Metric | Performance |
|---|---|---|
| Linear interp. | RMSE | 0.1149 |
| Correlation | 0.9386 | |
| PSNR | 18.30 | |
| Cubic interp. | RMSE | 0.1338 |
| Correlation | 0.9059 | |
| PSNR | 16.28 | |
| MLP [32] | RMSE | 0.1241 |
| Correlation | 0.9248 | |
| PSNR | 17.67 | |
| CNN [26] | RMSE | 0.0437 |
| Correlation | 0.9866 | |
| PSNR | 24.87 | |
| Transformer [35] | RMSE | 0.0422 |
| Correlation | 0.9880 | |
| PSNR | 25.32 | |
| HST (ours) | RMSE | 0.0333 |
| Correlation | 0.9915 | |
| PSNR | 26.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Yang, Y.; Yuan, L.; Li, C.; Wang, J. Pixel-Based Long-Wave Infrared Spectral Image Reconstruction Using a Hierarchical Spectral Transformer. Sensors 2024, 24, 7658. https://doi.org/10.3390/s24237658
Wang Z, Yang Y, Yuan L, Li C, Wang J. Pixel-Based Long-Wave Infrared Spectral Image Reconstruction Using a Hierarchical Spectral Transformer. Sensors. 2024; 24(23):7658. https://doi.org/10.3390/s24237658
Chicago/Turabian StyleWang, Zi, Yang Yang, Liyin Yuan, Chunlai Li, and Jianyu Wang. 2024. "Pixel-Based Long-Wave Infrared Spectral Image Reconstruction Using a Hierarchical Spectral Transformer" Sensors 24, no. 23: 7658. https://doi.org/10.3390/s24237658
APA StyleWang, Z., Yang, Y., Yuan, L., Li, C., & Wang, J. (2024). Pixel-Based Long-Wave Infrared Spectral Image Reconstruction Using a Hierarchical Spectral Transformer. Sensors, 24(23), 7658. https://doi.org/10.3390/s24237658







