Piezo-VFETs: Vacuum Field Emission Transistors Controlled by Piezoelectric MEMS Sensors as an Artificial Mechanoreceptor with High Sensitivity and Low Power Consumption
Abstract
1. Introduction
2. Structure Design of the VFET and the Piezo-VFETs
2.1. Design and Model of the VFET for the Artificial Mechanoreceptor
2.2. Implementation of the Piezo-VFETs
3. Characteristics of the Piezo-VFETs as Artificial Mechanoreceptors for Sensing
3.1. Sensitivity Adjustment Through Parameter Modifications
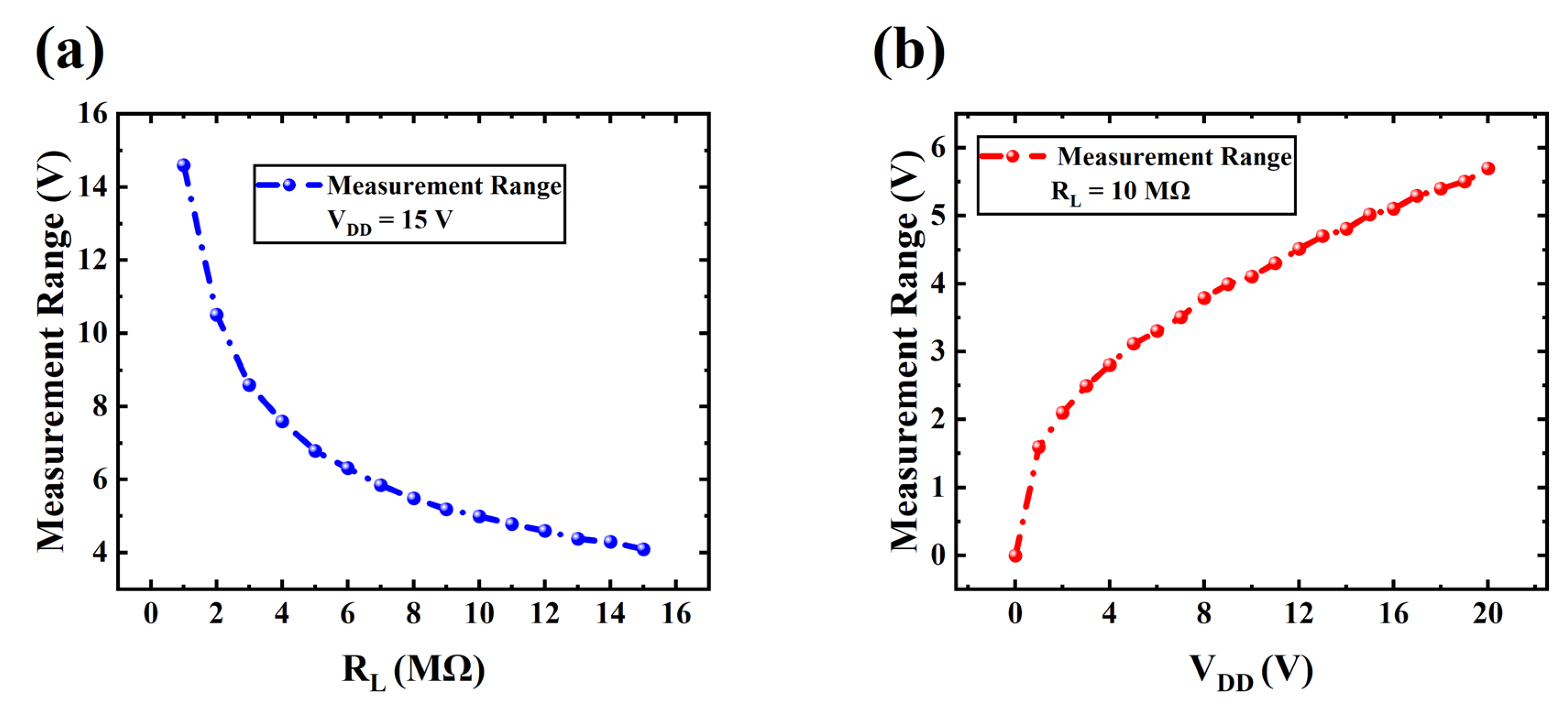
3.2. Measurement Range Adjustable from the Power Supply and Load Resistance
3.3. Impact of VFET Array on the Characteristics of the Piezo-VFETs
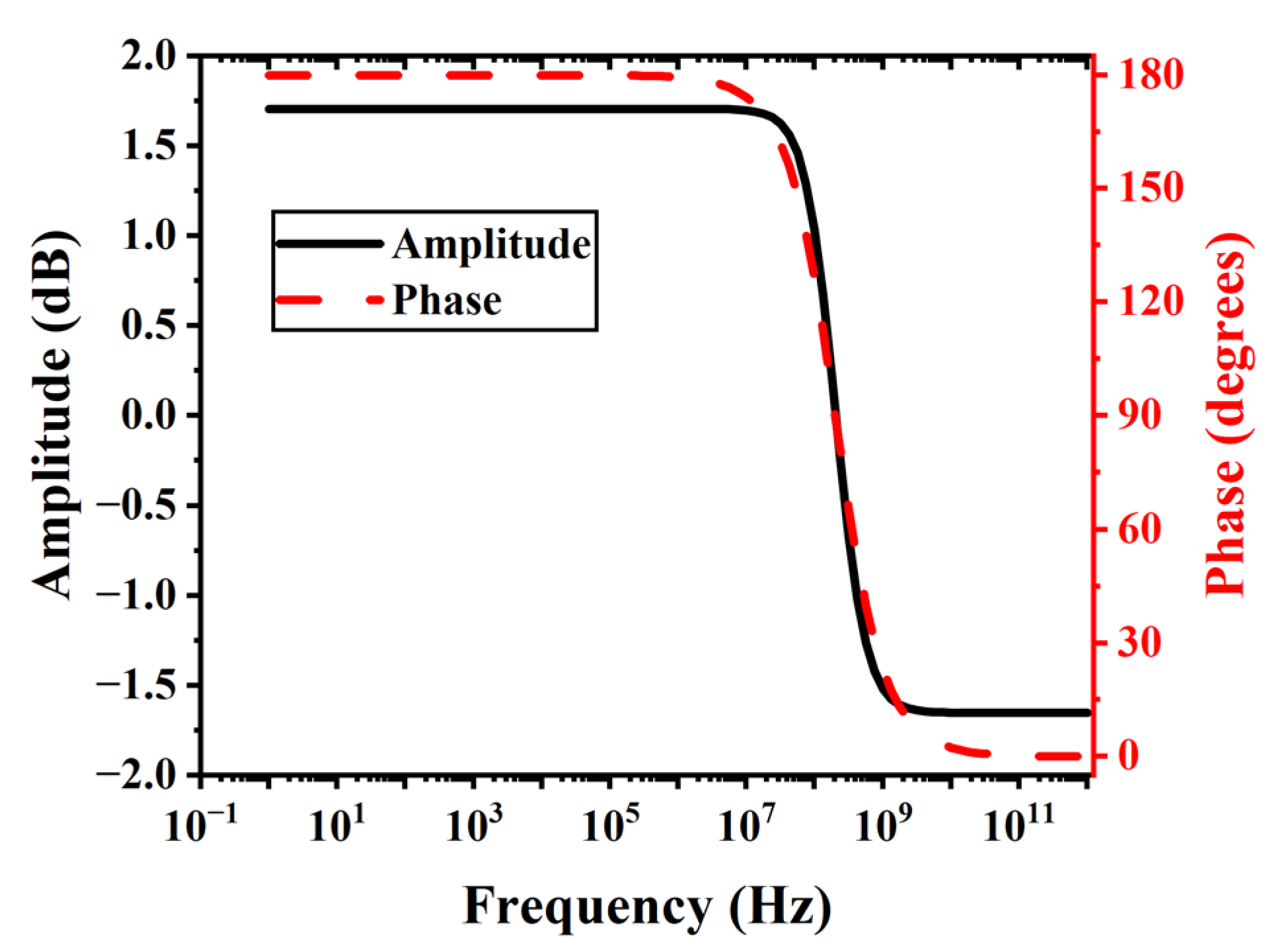
3.4. Bandwidth of the Piezo-VFETs
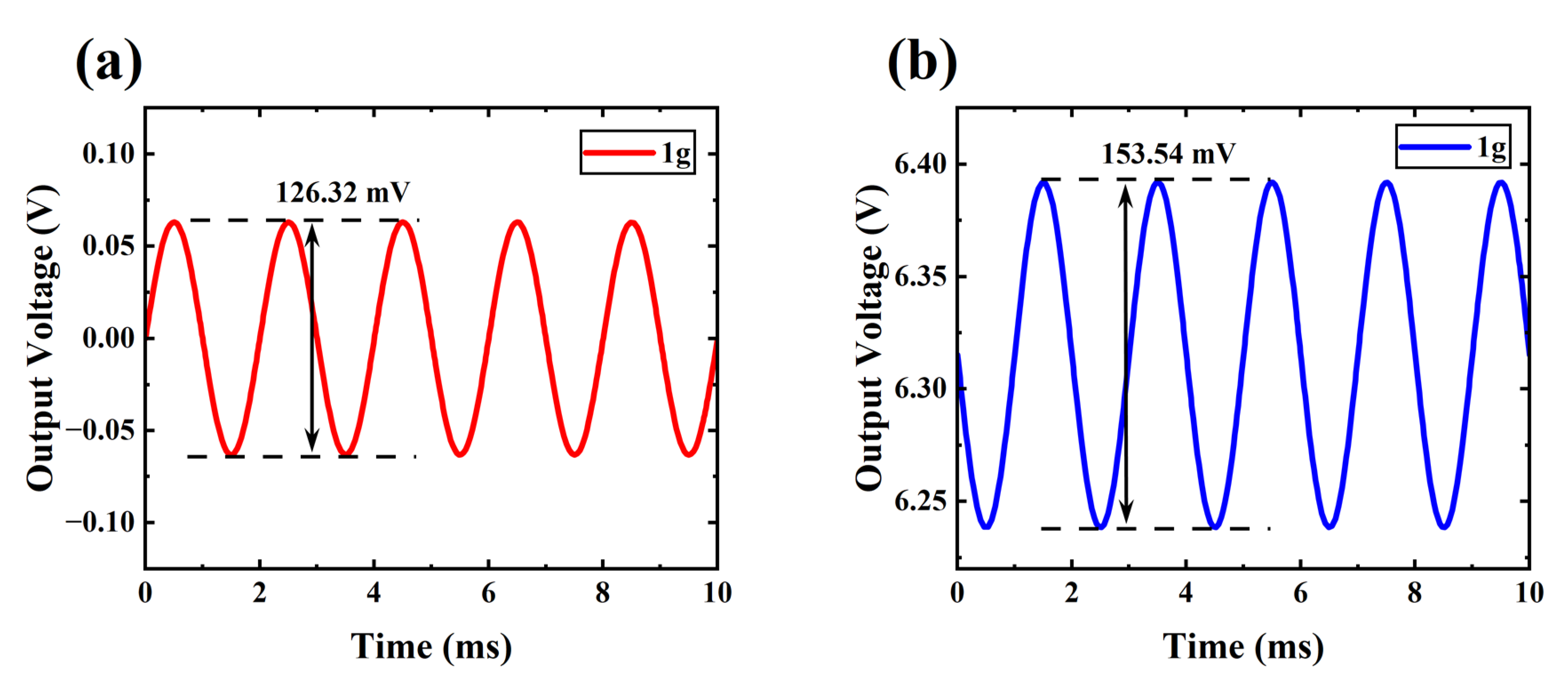
3.5. Noise of the Piezo-VFETs as an Artificial Mechanoreceptor
4. Application Potential of Piezo-VFETs as Artificial Mechanoreceptors for Sensing Purposes
4.1. Increment of Sensitivity, Bandwidth, and Degree of Miniaturization
4.2. Reduced Power Consumption than Piezo-FETs
5. Method
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Armstrong, C.M.; Kowalczyk, R.; Zubyk, A.; Berg, K.; Meadows, C.; Chan, D.; Schoemehl, T.; Duggal, R.; Hinch, N.; True, R.B.; et al. A Compact Extremely High Frequency MPM Power Amplifier. IEEE Trans. Electron Devices 2018, 65, 2183–2188. [Google Scholar] [CrossRef]
- Pan, P.; Tang, Y.; Bian, X.; Zhang, L.; Lu, Q.; Li, Y.; Feng, Y.; Feng, J. A G-Band Traveling Wave Tube With 20 W Continuous Wave Output Power. IEEE Electron Device Lett. 2020, 41, 1833–1836. [Google Scholar] [CrossRef]
- Symons, R.S. Tubes: Still vital after all these years. IEEE Spectrum 1998, 35, 52–63. [Google Scholar] [CrossRef]
- De Rose, L.B.; Jones, W.M.; Scherer, A. Lateral nanoscale field emission comb for frequency mixing. Appl. Phys. Lett. 2023, 123, 013505. [Google Scholar] [CrossRef]
- Han, J.-W.; Oh, J.S.; Meyyappan, M. Vacuum nanoelectronics: Back to the future?—Gate insulated nanoscale vacuum channel transistor. Appl. Phys. Lett. 2012, 100, 213505. [Google Scholar] [CrossRef]
- Fan, L.; Zhao, B.; Chen, B.; Ma, Y.; Bi, J.; Zhao, F. Radiation Immune-Planar Two-Terminal Nanoscale Air Channel Devices toward Space Applications. ACS Appl. Nano Mater. 2023, 6, 22080–22087. [Google Scholar] [CrossRef]
- Han, J.-W.; Moon, D.-I.; Meyyappan, M. Nanoscale Vacuum Channel Transistor. Nano Lett. 2017, 17, 2146–2151. [Google Scholar] [CrossRef]
- Wei, Y.; Chen, F.; Huang, R.; Zhao, J.; Zhao, H.; Wang, J.; Li, M.; Zhang, J. Fast Response GaN Nanoscale Air Channel Diodes with Highly Stable 10 mA Output Current toward Wafer-Scale Fabrication. Adv. Sci. 2023, 10, 2206385. [Google Scholar] [CrossRef]
- Stoner, B.R.; Glass, J.T. Nothing is like a vacuum. Nat. Nanotechnol. 2012, 7, 485–487. [Google Scholar] [CrossRef]
- de Heer, W.A.; Châtelain, A.; Ugarte, D. A Carbon Nanotube Field-Emission Electron Source. Science 1995, 270, 1179–1180. [Google Scholar] [CrossRef]
- Hsu, S.H.; Kang, W.P.; Raina, S.; Huang, J.H. Nanodiamond vacuum field emission device with gate modulated triode characteristics. Appl. Phys. Lett. 2013, 102, 203105. [Google Scholar] [CrossRef]
- Nirantar, S.; Patil, B.; Tripathi, D.C.; Sethu, N.; Narayanan, R.V.; Tian, J.; Bhaskaran, M.; Walia, S.; Sriram, S. Metal-Air Field Emission Devices—Nano Electrode Geometries Comparison of Performance and Stability. Small 2022, 18, 2203234. [Google Scholar] [CrossRef] [PubMed]
- Shih, P.-C.; Perozek, J.; Akinwande, A.I.; Palacios, T. Anode-Integrated GaN Field Emitter Arrays for Compact Vacuum Transistors. IEEE Electron Device Lett. 2023, 44, 1895–1898. [Google Scholar] [CrossRef]
- Wang, X.; Zheng, C.; Xue, T.; Shen, Z.; Long, M.; Wu, S. Nanoscale Vacuum Field Emission Triode with a Double Gate Structure. IEEE Electron Device Lett. 2022, 43, 292–295. [Google Scholar] [CrossRef]
- Xu, J.; Hu, H.; Yang, W.; Li, C.; Shi, Y.; Shi, Y.; Wang, Q.; Zhang, X. Nanoscale vacuum channel transistor with in-plane collection structure. Nanotechnology 2020, 31, 065202. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, G.; Zhan, F.; He, Y. Planar nanoscale vacuum channel transistors based on resistive switching. Nanotechnology 2024, 35, 215205. [Google Scholar] [CrossRef]
- Han, J.-W.; Seol, M.-L.; Moon, D.-I.; Hunter, G.; Meyyappan, M. Nanoscale vacuum channel transistors fabricated on silicon carbide wafers. Nat. Electron. 2019, 2, 405–411. [Google Scholar] [CrossRef]
- Nirantar, S.; Ahmed, T.; Ren, G.; Gutruf, P.; Xu, C.; Bhaskaran, M.; Walia, S.; Sriram, S. Metal–Air Transistors: Semiconductor-Free Field-Emission Air-Channel Nanoelectronics. Nano Lett. 2018, 18, 7478–7484. [Google Scholar] [CrossRef]
- Wu, G.; Wei, X.; Zhang, Z.; Chen, Q.; Peng, L. A Graphene-Based Vacuum Transistor with a High ON/OFF Current Ratio. Adv. Funct. Mater. 2015, 25, 5972–5978. [Google Scholar] [CrossRef]
- Heo, S.J.; Shin, J.H.; Jun, B.O.; Jang, J.E. Vacuum Tunneling Transistor with Nano Vacuum Chamber for Harsh Environments. ACS Nano 2023, 17, 19696–19708. [Google Scholar] [CrossRef]
- Xu, J.; Qin, Y.; Shi, Y.; Shi, Y.; Yang, Y.; Zhang, X. Design and circuit simulation of nanoscale vacuum channel transistors. Nanoscale Adv. 2020, 2, 3582–3587. [Google Scholar] [CrossRef] [PubMed]
- Chang, W.-T.; Cheng, M.-C.; Chuang, T.-Y.; Tsai, M.-Y. Field Emission Air-Channel Devices as a Voltage Adder. Nanomaterials 2020, 10, 2378. [Google Scholar] [CrossRef] [PubMed]
- Han, J.-W.; Seol, M.-L.; Kim, J.; Meyyappan, M. Nanoscale Complementary Vacuum Field Emission Transistor. ACS Appl. Nano Mater. 2020, 3, 11481–11488. [Google Scholar] [CrossRef]
- Bhattacharya, R.; Han, J.W.; Browning, J.; Meyyappan, M. Complementary Vacuum Field Emission Transistor. IEEE Trans. Electron. Devices 2021, 68, 5244–5249. [Google Scholar] [CrossRef]
- Zhu, J.; Yao, K.; Dong, X.S.; Huang, Q.W.; Liu, R.H. Pull-in behavior of electrostatically actuated stepped microbeams. Int. J. Mod. Phys. B 2018, 32, 1850180. [Google Scholar] [CrossRef]
- Chen, Y.B.; Yan, Z. Investigation of pull-in behaviors of a nanoswitch tuned by piezoelectric and flexoelectric effects. Int. J. Mech. Sci. 2019, 161, 105032. [Google Scholar] [CrossRef]
- Cai, T.; Fang, Y.M.; Fang, Y.L.; Li, R.Z.; Yu, Y.; Huang, M.Y. Electrostatic pull-in application in flexible devices: A review. Beilstein J. Nanotechnol. 2022, 13, 390–403. [Google Scholar] [CrossRef]
- Dehkordi, M.F.; Beni, Y.T.; Dashtaki, P.M.; Vanani, S.M.F. Effect of flexoelectricity on the Pull-in instability of beam-type NEMS. Eng. Anal. Bound. Elem. 2023, 155, 87–107. [Google Scholar] [CrossRef]
- French, A.S.; Torkkeli, P.H. Chapter 36—Sensory Receptors and Mechanotransduction. In Cell Physiology Source Book, 4th ed.; Sperelakis, N., Ed.; Academic Press: San Diego, CA, USA, 2012; pp. 633–647. [Google Scholar]
- Yogeswaran, N.; Hosseini, E.S.; Dahiya, R. Graphene Based Low Voltage Field Effect Transistor Coupled with Biodegradable Piezoelectric Material Based Dynamic Pressure Sensor. ACS Appl. Mater. Interfaces 2020, 12, 54035–54040. [Google Scholar] [CrossRef]
- Wang, J.C.; Jiang, Y.P.; Lin, C.H.; Chan, S.H.; Wu, M.C. Enhanced piezoelectric tactile sensing behaviors of high-density and low-damage CF4-plasma-treated IGZO thin-film transistors coated by P(VDF-TrFE) copolymers. Sens. Actuator A Phys. 2020, 304, 9. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, J.F.; Zhang, C.C.; Sun, M.Y.; Han, S.W.; Zhang, R.T.; Liang, N.; Sun, D.H.; Liu, H. Energy-efficient, fully flexible, high-performance tactile sensor based on piezotronic effect: Piezoelectric signal amplified with organic field-effect transistors. Nano Energy 2020, 76, 8. [Google Scholar] [CrossRef]
- Wang, F.L.; Jiang, J.F.; Liu, Q.L.; Zhang, Y.; Wang, J.J.; Wang, S.H.; Han, L.; Liu, H.; Sang, Y.H. Piezopotential gated two-dimensional InSe field-effect transistor for designing a pressure sensor based on piezotronic effect. Nano Energy 2020, 70, 8. [Google Scholar] [CrossRef]
- Meng, Z.M.; Zhang, H.; Zhu, M.; Wei, X.Y.; Cao, J.P.; Murtaza, I.; Ali, M.U.; Meng, H.; Xu, J.Y. Lead Zirconate Titanate (a piezoelectric ceramic)-Based thermal and tactile bimodal organic transistor sensors. Org. Electron. 2020, 80, 5. [Google Scholar] [CrossRef]
- Zhu, M.J.; Inomata, N.; Adachi, N.; Sakurai, A.; Nomura, M.; Ono, T. High-Gauge Factor Strain Sensor Based on Piezoelectric Aluminum Nitride Coupled to MOSFET. IEEE Sens. J. 2019, 19, 3626–3632. [Google Scholar] [CrossRef]
- Sung, M.; Shin, K.; Moon, W. A micro-machined hydrophone employing a piezoelectric body combined on the gate of a field-effect transistor. Sens. Actuator A Phys. 2016, 237, 155–166. [Google Scholar] [CrossRef]
- Ueda, M.; Kaneko, Y.; Nishitani, Y.; Omote, A. Battery-less shock-recording device consisting of a piezoelectric sensor and a ferroelectric-gate field-effect transistor. Sens. Actuator A Phys. 2015, 232, 75–83. [Google Scholar] [CrossRef]
- Sung, M.; Shin, K.; Moon, W. A new transduction mechanism for hydrophones employing piezoelectricity and a field-effect transistor. Sens. Actuator A Phys. 2015, 233, 557–568. [Google Scholar] [CrossRef]
- Ai, C.P.; Zhao, X.F.; Wen, D.Z. Characteristics Research of a High Sensitivity Piezoelectric MOSFET Acceleration Sensor. Sensors 2020, 20, 14. [Google Scholar] [CrossRef]
- Ellis, R.K. Fowler-Nordheim emission from non-planar surfaces. IEEE Electron Device Lett. 1982, 3, 330–332. [Google Scholar] [CrossRef]
- Forbes, R.G.; Deane, J.H.B. Reformulation of the standard theory of Fowler–Nordheim tunnelling and cold field electron emission. Proc. R. Soc. A. 2007, 463, 2907–2927. [Google Scholar] [CrossRef]
- Kosmahl, H.G. Analytic evaluation of field emission enhancement factors for ellipsoidal cones and elliptic cross-section wedges. IEEE Trans. Electron Devices 1991, 38, 1534–1537. [Google Scholar] [CrossRef]
- Lenzlinger, M.; Snow, E.H. Fowler-Nordheim Tunneling into Thermally Grown SiO2. J. Appl. Phys. 1969, 40, 278–283. [Google Scholar] [CrossRef]
- Fowler, R.H.; Nordheim, L. Electron Emission in Intense Electric Fields. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1928, 119, 173–181. [Google Scholar]
- Han, J.W.; Oh, J.S.; Meyyappan, M. Cofabrication of Vacuum Field Emission Transistor (VFET) and MOSFET. IEEE Trans. Nanotechnol. 2014, 13, 464–468. [Google Scholar] [CrossRef]
- Wisitsora-At, A.; Kang, W.P.; Davidson, J.L.; Li, C.; Kerns, D.V.; Howell, M. Modeling of the transistor characteristics of a monolithic diamond vacuum triode. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 2003, 21, 1665–1670. [Google Scholar] [CrossRef]
- Ge, C.; Cretu, E. A polymeric piezoelectric MEMS accelerometer with high sensitivity, low noise density, and an innovative manufacturing approach. Microsyst. Nanoeng. 2023, 9, 151. [Google Scholar] [CrossRef]
- Ge, C.; Cretu, E. Polymeric piezoelectric accelerometers with high sensitivity, broad bandwidth, and low noise density for organic electronics and wearable microsystems. Microsyst. Nanoeng. 2024, 10, 61. [Google Scholar] [CrossRef]
- Gong, X.; Kuo, Y.-C.; Zhou, G.; Wu, W.-J.; Liao, W.-H. An aerosol deposition based MEMS piezoelectric accelerometer for low noise measurement. Microsyst. Nanoeng. 2023, 9, 23. [Google Scholar] [CrossRef]
- Hewa-Kasakarage, N.N.; Kim, D.; Kuntzman, M.L.; Hall, N.A. Micromachined Piezoelectric Accelerometers via Epitaxial Silicon Cantilevers and Bulk Silicon Proof Masses. J. Microelectromech. Syst. 2013, 22, 1438–1446. [Google Scholar] [CrossRef]
- Lee, Y.-C.; Tsai, C.-C.; Li, C.-Y.; Liou, Y.-C.; Hong, C.-S.; Chu, S.-Y. Fabrication and function examination of PZT-based MEMS accelerometers. Ceram. Int. 2021, 47, 24458–24465. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, B.; Cai, Y.; Liu, W.; Tovstopyat, A.; Sun, C. A Novel Tri-Axial Piezoelectric MEMS Accelerometer with Folded Beams. Sensors 2021, 21, 453. [Google Scholar] [CrossRef] [PubMed]
- Udvardi, P.; Radó, J.; Straszner, A.; Ferencz, J.; Hajnal, Z.; Soleimani, S.; Schneider, M.; Schmid, U.; Révész, P.; Volk, J. Spiral-Shaped Piezoelectric MEMS Cantilever Array for Fully Implantable Hearing Systems. Micromachines 2017, 8, 311. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Hu, B.; Lu, L.; Wang, Z.; Liu, W.; Sun, C. A Miniaturized Piezoelectric MEMS Accelerometer with Polygon Topological Cantilever Structure. Micromachines 2022, 13, 1608. [Google Scholar] [CrossRef] [PubMed]
- Pogorelov, E.G.; Zhbanov, A.; Chang, Y.-C.J.U. Field enhancement factor and field emission from a hemi-ellipsoidal metallic needle. Ultramicroscopy 2008, 109, 373–378. [Google Scholar] [CrossRef]
- Debnath, B.; Kumar, R. Single-axis low acceleration sensing using an enhanced piezoelectric vibration energy harvester. Microsyst. Technol. 2021, 27, 3171–3181. [Google Scholar] [CrossRef]
- Nyquist, H. Thermal Agitation of Electric Charge in Conductors. Phys. Rev. 1928, 32, 110–113. [Google Scholar] [CrossRef]
- Yang, T.; Wang, Q.; Zhang, Z.; Liao, Z.; Zhao, Y.; Li, Y.; Zang, J.; Gao, R.; Cui, D.; Xue, C. Design and Implementation of 6 × 6 Array Piezoelectric AlN Hydrophone with High Sensitivity. IEEE Sens. J. 2021, 21, 26615–26623. [Google Scholar] [CrossRef]
- Minh, L.V.; Hara, M.; Kuwano, H. Lead-Free (K,Na)NbO3 Impact-Induced-Oscillation Microenergy Harvester. J. Microelectromech. Syst. 2015, 24, 1887–1895. [Google Scholar] [CrossRef]
- Ali, W.R.; Prasad, M. Piezoelectric Based MEMS Acoustic Sensor for Wide Frequency Applications. IEEE Sens. J. 2021, 21, 27352–27360. [Google Scholar] [CrossRef]
- Prasad, M.; Aditi; Khanna, V.K. Development of MEMS Acoustic Sensor with Microtunnel for High SPL Measurement. IEEE Trans. Ind. Electron. 2022, 69, 3142–3150. [Google Scholar] [CrossRef]
- Levinzon, F.A. Fundamental noise limit of piezoelectric accelerometer. IEEE Sens. J. 2004, 4, 108–111. [Google Scholar] [CrossRef]
- Dahiya, R.S.; Metta, G.; Valle, M.; Adami, A.; Lorenzelli, L. Piezoelectric Oxide Semiconductor Field Effect Transistor Touch Sensing Devices. Appl. Phys. Lett. 2009, 95, 3. [Google Scholar] [CrossRef]
- Maita, F.; Maiolo, L.; Minotti, A.; Pecora, A.; Ricci, D.; Metta, G.; Scandurra, G.; Giusi, G.; Ciofi, C.; Fortunato, G. Ultraflexible Tactile Piezoelectric Sensor Based on Low-Temperature Polycrystalline Silicon Thin-Film Transistor Technology. IEEE Sens. J. 2015, 15, 3819–3826. [Google Scholar] [CrossRef]
- Viola, F.A.; Spanu, A.; Ricci, P.C.; Bonfiglio, A.; Cosseddu, P. Ultrathin, Flexible and Multimodal Tactile Sensors Based on Organic Field-Effect Transistors. Sci. Rep. 2018, 8, 8. [Google Scholar] [CrossRef] [PubMed]
- Hsu, Y.J.; Jia, Z.; Kymissis, I. A Locally Amplified Strain Sensor Based on A Piezoelectric Polymer and Organic Field-Effect Transistors. IEEE Trans. Electron Devices 2011, 58, 910–917. [Google Scholar] [CrossRef]




| Research | Piezoelectric Material | Sensor Types | Bandwidth | Resonance Frequency |
|---|---|---|---|---|
| Ali et al. [60] | ZnO | Acoustic sensor | 15 kHz | 78 kHz |
| Prasad et al. [61] | ZnO | Acoustic sensor | 8 kHz | 42.875 kHz |
| Minh et al. [59] | (K, Na) NbO3 | Energy harvester | 150 Hz | 3.094 kHz |
| Ge et al. [47] | PVDF | Accelerometer | 58.6 Hz | 128.95 Hz |
| Gong et al. [49] | PZT | Accelerometer | 200 Hz | 857.4 Hz |
| Yang et al. [58] | AlN | Hydrophone | 2 kHz | 479 kHz |
| Researchers | Sensor Types | Semiconductor Material | Continuous Current | Sensitivity | Operating Voltage | Power Consumption | Fabrication Complexity | Cost |
|---|---|---|---|---|---|---|---|---|
| Dahiya et al. [63] | Tactile | Silicon | 3~4 mA | 50 mV/N (Load: 100 kΩ) | VSS = −5 V | 15~20 mW | Middle | Low |
| Maita et al. [64] | Tactile | Silicon | ~40 µA | 430 mV/N (Load: 270 kΩ) | VDD = 20 V, VG = 9 V | ~0.8 mW | Middle | Low |
| Viola et al. [65] | Tactile | Polyethylene naphthalene (PEN) | −3~−4 µA | 0.15 nA/kPa | VDD = VG = −2 V | 6~8 µW | Easy | Low |
| Wang et al. [33] | Tactile | InSe | ~1 mA | 0.1 mA/N | Vds = 1 V | ~1 mW | Difficult | High |
| Wang et al. [32] | Tactile | Pentacene | 1~2 µA | 21 nA/N | Vds = −40 V | 40~80 µW | Middle | High |
| Yogeswaran et al. [30] | Tactile | Graphene | 8~10 µA | 2.7 × 10−4 kPa−1 (ΔI/I0) | Vds = 50 mV | 0.4 µW | Difficult | High |
| Hsu et al. [66] | Strain gauge | Pentacene | ~100 nA | 0.182 µA/strain | Vds = 35 V | 3.5 µW | Easy | Low |
| Zhu et al. [35] | Strain gauge | Silicon | ~1 mA | 1340 ppm | Vds = 3 V, VG = 3.15 V | ~3 mW | Middle | Middle |
| Ueda et al. [37] | Inertial | ZnO | ~10 µA | N/A | Vds = 0.1 V | ~1 µW | Easy | Low |
| Ai et al. [39] | Inertial | Silicon | ~100 mA | 2.05 V/g | VDD = 5 V | 500 mW | Easy | Low |
| This work | Inertial | Silicon | ~5.58 µA | 1.216 V/g | VDD = 15 V | 83.7 µW | Easy | Middle |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, C.; Chen, Y.; Yu, D.; Liu, Z.; Xu, J. Piezo-VFETs: Vacuum Field Emission Transistors Controlled by Piezoelectric MEMS Sensors as an Artificial Mechanoreceptor with High Sensitivity and Low Power Consumption. Sensors 2024, 24, 6764. https://doi.org/10.3390/s24206764
Ge C, Chen Y, Yu D, Liu Z, Xu J. Piezo-VFETs: Vacuum Field Emission Transistors Controlled by Piezoelectric MEMS Sensors as an Artificial Mechanoreceptor with High Sensitivity and Low Power Consumption. Sensors. 2024; 24(20):6764. https://doi.org/10.3390/s24206764
Chicago/Turabian StyleGe, Chang, Yuezhong Chen, Daolong Yu, Zhixia Liu, and Ji Xu. 2024. "Piezo-VFETs: Vacuum Field Emission Transistors Controlled by Piezoelectric MEMS Sensors as an Artificial Mechanoreceptor with High Sensitivity and Low Power Consumption" Sensors 24, no. 20: 6764. https://doi.org/10.3390/s24206764
APA StyleGe, C., Chen, Y., Yu, D., Liu, Z., & Xu, J. (2024). Piezo-VFETs: Vacuum Field Emission Transistors Controlled by Piezoelectric MEMS Sensors as an Artificial Mechanoreceptor with High Sensitivity and Low Power Consumption. Sensors, 24(20), 6764. https://doi.org/10.3390/s24206764







