Light Field Image Super-Resolution Using Deep Residual Networks on Lenslet Images
Abstract
:1. Introduction
- We propose a different paradigm to increase the spatial-angular interaction by processing the Lenslet image and sub-aperture images to incorporate more information for LFSR.
- We propose a CNN-based network to work for LFSR using Lenslet Images with superior performance over the state-of-the-art methods in the case of small-baseline LFSR.
- The remainder of the paper is structured as follows: Section 2 briefly examines the related work. In Section 3, we present our technique for LFSR. Section 4 introduces the conducted experiments to compare our work with the state-of-the-art and discusses the meaning of the obtained results. Finally, Section 5 brings this paper to a close and presents future work to improve the proposed work.
2. Related Work
3. Our Approach
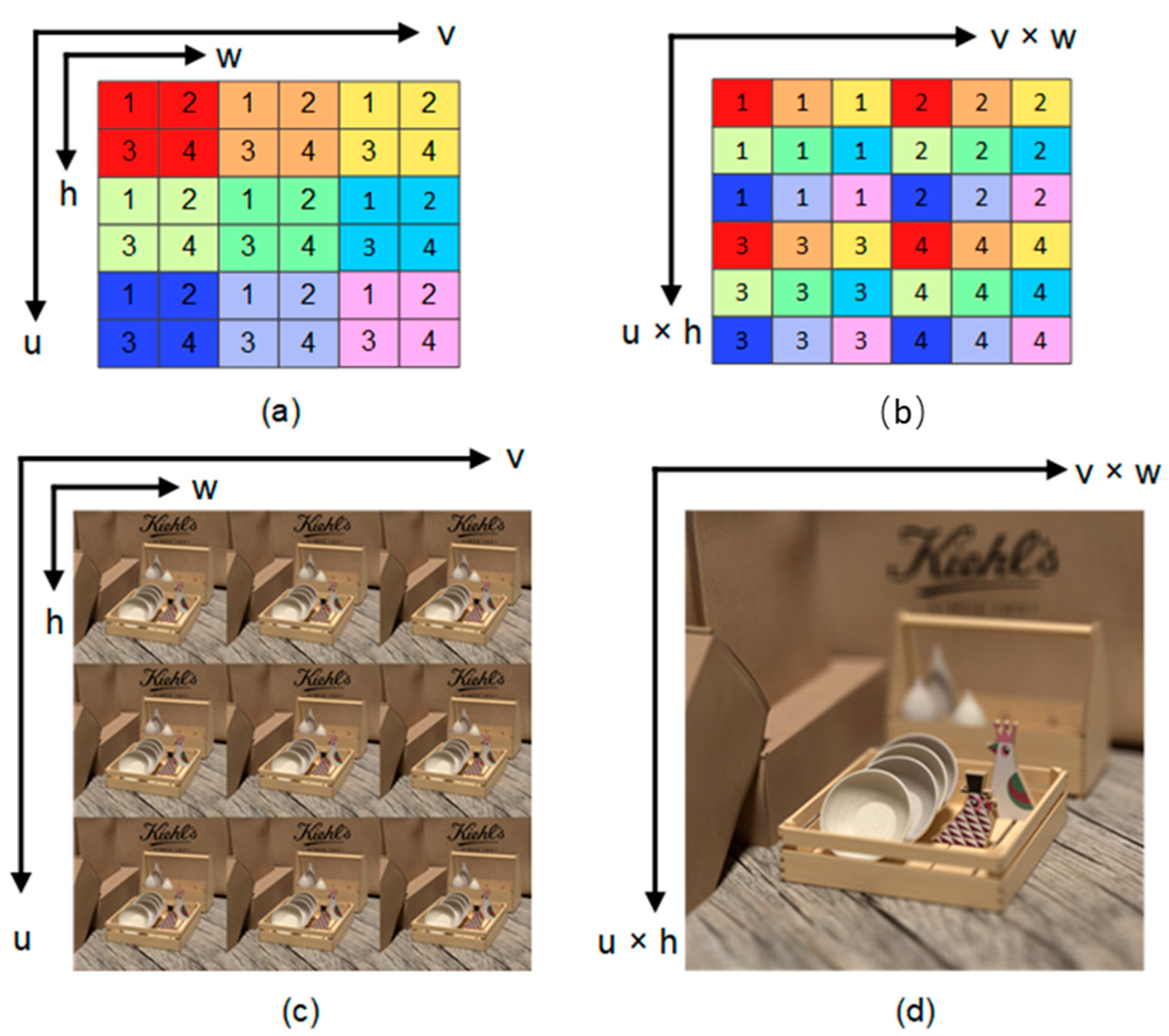
3.1. Problem Formulation
3.2. Features Extractors
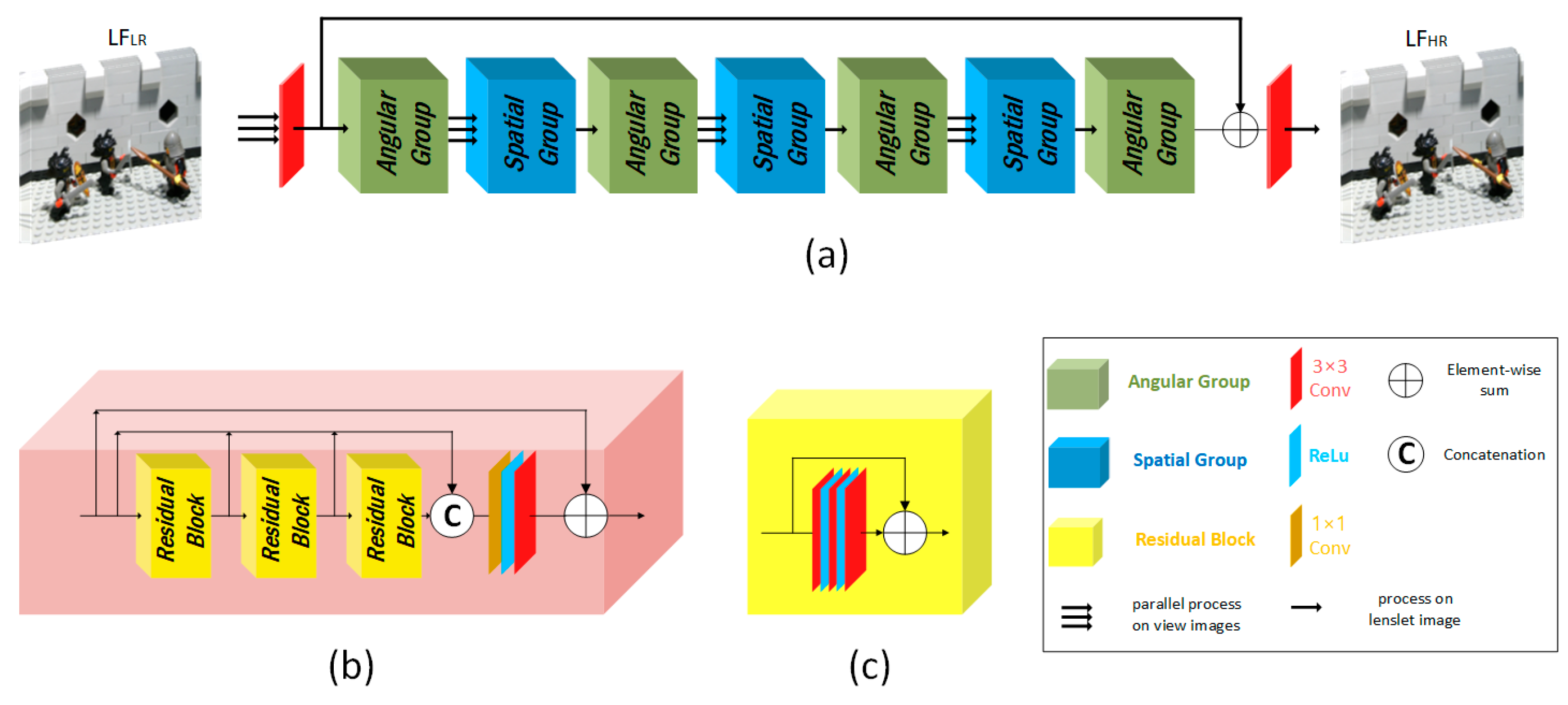
3.3. Network Overview
3.4. Loss Function and Training Details
4. Experiments and Discussion
4.1. Comparison with the State-of-the-Art Methods
4.1.1. Quantitative Comparison
4.1.2. Qualitative Comparison
4.1.3. Model Efficiency
4.2. Ablation Study
4.2.1. Feature Extractors
4.2.2. Patch Size
5. Conclusions and Future Work
- Shear LF images into different disparity levels; after shearing, the disparity value will become smaller, then our network can extract better features, as proposed in [38].
- Use a parallax-attention module (PAM) as a final stage, where PAM was designed to capture a global correspondence in stereo images super-resolution [39].
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, G.; Masia, B.; Jarabo, A.; Zhang, Y.; Wang, L.; Dai, Q.; Chai, T.; Liu, Y. Light field image processing: An overview. IEEE J. Sel. Top. Signal Process. 2017, 11, 926–954. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Liang, Z.; Yang, J.; An, W.; Guo, Y. Occlusion-Aware Cost Constructor for Light Field Depth Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–20 June 2022; pp. 19809–19818. [Google Scholar]
- Gao, M.; Deng, H.; Xiang, S.; Wu, J.; He, Z. EPI Light Field Depth Estimation Based on a Directional Relationship Model and Multiviewpoint Attention Mechanism. Sensors 2022, 22, 6291. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Yang, W.; Xu, Z.; Chen, Z.; Shi, Z.; Zhang, Y.; Huang, L. Mask4D: 4D convolution network for light field occlusion removal. In Proceedings of the ICASSP 2021—2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 2480–2484. [Google Scholar]
- Wang, Y.; Wu, T.; Yang, J.; Wang, L.; An, W.; Guo, Y. DeOccNet: Learning to see through foreground occlusions in light fields. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Snowmass Village, CO, USA, 1–5 March 2020; pp. 118–127. [Google Scholar]
- Zhang, M.; Ji, W.; Piao, Y.; Li, J.; Zhang, Y.; Xu, S.; Lu, H. LFNet: Light field fusion network for salient object detection. IEEE Trans. Image Process. 2020, 29, 6276–6287. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Chen, G.; Chen, Q.; Sun, Y.; Xia, Y.; Deforges, O.; Hamidouche, W.; Zhang, L. Learning synergistic attention for light field salient object detection. arXiv 2021, arXiv:2104.13916. [Google Scholar]
- Jayaweera, S.S.; Edussooriya, C.U.; Wijenayake, C.; Agathoklis, P.; Bruton, L.T. Multi-volumetric refocusing of light fields. IEEE Signal Process. Lett. 2020, 28, 31–35. [Google Scholar] [CrossRef]
- RayTrix. 3D Light Field Camera Technology. Available online: http://www.raytrix.de/ (accessed on 30 November 2022).
- Bishop, T.E.; Favaro, P. The light field camera: Extended depth of field, aliasing, and superresolution. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 34, 972–986. [Google Scholar] [CrossRef] [PubMed]
- Mitra, K.; Veeraraghavan, A. Light field denoising, light field superresolution and stereo camera based refocussing using a GMM light field patch prior. In Proceedings of the 2012 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Providence, RI, USA, 16–21 June 2012; pp. 22–28. [Google Scholar]
- Wanner, S.; Goldluecke, B. Variational light field analysis for disparity estimation and super-resolution. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 36, 606–619. [Google Scholar] [CrossRef] [PubMed]
- Rossi, M.; Frossard, P. Graph-based light field super-resolution. In Proceedings of the 2017 IEEE 19th International Workshop on Multimedia Signal Processing (MMSP), Luton, UK, 16–18 October 2017; pp. 1–6. [Google Scholar]
- Zhang, S.; Lin, Y.; Sheng, H. Residual networks for light field image super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 11046–11055. [Google Scholar]
- Zhang, S.; Chang, S.; Lin, Y. End-to-end light field spatial super-resolution network using multiple epipolar geometry. IEEE Trans. Image Process. 2021, 30, 5956–5968. [Google Scholar] [CrossRef] [PubMed]
- Jin, J.; Hou, J.; Chen, J.; Kwong, S. Light field spatial super-resolution via deep combinatorial geometry embedding and structural consistency regularization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2260–2269. [Google Scholar]
- Yeung, H.W.F.; Hou, J.; Chen, X.; Chen, J.; Chen, Z.; Chung, Y.Y. Light field spatial super-resolution using deep efficient spatial-angular separable convolution. IEEE Trans. Image Process. 2018, 28, 2319–2330. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Yang, J.; Wang, L.; Ying, X.; Wu, T.; An, W.; Guo, Y. Light field image super-resolution using deformable convolution. IEEE Trans. Image Process. 2020, 30, 1057–1071. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, L.; Yang, J.; An, W.; Yu, J.; Guo, Y. Spatial-angular interaction for light field image super-resolution. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 November 2020; pp. 290–308. [Google Scholar]
- Liu, G.; Yue, H.; Wu, J.; Yang, J. Intra-inter view interaction network for light field image super-resolution. IEEE Trans. Multimedia 2021, 25, 256–266. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Wu, G.; Yang, J.; An, W.; Yu, J.; Guo, Y. Disentangling light fields for super-resolution and disparity estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 425–443. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zhou, T.; Lu, Y.; Di, H. Detail preserving transformer for light field image super-resolution. Proc. Conf. AAAI Artif. Intell. 2022, 36, 2522–2530. [Google Scholar] [CrossRef]
- Liang, Z.; Wang, Y.; Wang, L.; Yang, J.; Zhou, S. Light field image super-resolution with transformers. IEEE Signal Process. Lett. 2022, 29, 563–567. [Google Scholar] [CrossRef]
- Honauer, K.; Johannsen, O.; Kondermann, D.; Goldluecke, B. A dataset and evaluation methodology for depth estimation on 4D light fields. In Proceedings of the Asian Conference on Computer Vision, Taipei, Taiwan, 20–24 November 2016; pp. 19–34. [Google Scholar]
- Rerabek, M.; Ebrahimi, T. New light field image dataset. In Proceedings of the 8th International Conference on Quality of Multimedia Experience (QoMEX), Lisbon, Portugal, 6–8 June 2016. [Google Scholar]
- Wanner, S.; Meister, S.; Goldluecke, B. Datasets and benchmarks for densely sampled 4D light fields. In Vision Modeling and Visualization; The Eurographics Association: Munich, Germany, 2013; pp. 225–226. [Google Scholar]
- Le Pendu, M.; Jiang, X.; Guillemot, C. Light field inpainting propagation via low rank matrix completion. IEEE Trans. Image Process. 2018, 27, 1981–1993. [Google Scholar] [CrossRef] [PubMed]
- Vaish, V.; Adams, A. The (new) stanford light field archive. Comput. Graph. Lab. Stanf. Univ. 2008, 6, 3. [Google Scholar]
- Salem, A.; Ibrahem, H.; Kang, H.-S. Light Field Reconstruction Using Residual Networks on Raw Images. Sensors 2022, 22, 1956. [Google Scholar] [CrossRef] [PubMed]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S. An image is worth 16 × 16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 10–13 September 2018; pp. 286–301. [Google Scholar]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar]
- Wang, L.; Guo, Y.; Lin, Z.; Deng, X.; An, W. Learning for video super-resolution through HR optical flow estimation. In Proceedings of the Asian Conference on Computer Vision, Perth, Australia, 2–6 December 2018; pp. 514–529. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th {USENIX} Symposium on Operating Systems Design and Implementation ({OSDI} 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Mu Lee, K. Enhanced deep residual networks for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 136–144. [Google Scholar]
- Wu, G.; Liu, Y.; Dai, Q.; Chai, T. Learning sheared EPI structure for light field reconstruction. IEEE Trans. Image Process. 2019, 28, 3261–3273. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Wang, Y.; Liang, Z.; Lin, Z.; Yang, J.; An, W.; Guo, Y. Learning parallax attention for stereo image super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 12250–12259. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Virtual, 11–17 October 2021; pp. 10012–10022. [Google Scholar]


| Dataset | Training | Testing | Disparity | Data Type |
|---|---|---|---|---|
| HCInew [24] | 20 | 4 | [−4, 4] | Synthetic |
| HCIold [26] | 10 | 2 | [−3, 3] | Synthetic |
| EPFL [25] | 70 | 10 | [−1, 1] | Real-world |
| INRIA [27] | 35 | 5 | [−1, 1] | Real-world |
| STFgantry [28] | 9 | 2 | [−7, 7] | Real-world |
| Dataset | EPFL | HCInew | HCIold | INRIA | STFgantry | Average |
|---|---|---|---|---|---|---|
| Bicubic | 29.74/0.941 | 31.89/0.939 | 37.69/0.979 | 31.33/0.959 | 31.06/0.954 | 32.34/0.954 |
| VDSR [36] | 32.50/0.960 | 34.37/0.956 | 40.61/0.987 | 34.43/0.974 | 35.54/0.979 | 35.49/0.971 |
| EDSR [37] | 33.09/0.963 | 34.83/0.959 | 41.01/0.988 | 34.97/0.977 | 36.29/0.982 | 36.04/0.974 |
| RCAN [31] | 33.16/0.964 | 34.98/0.960 | 41.05/0.988 | 35.01/0.977 | 36.33/0.983 | 36.11/0.974 |
| resLF [14] | 33.62/0.971 | 36.69/0.974 | 43.42/0.993 | 35.39/0.981 | 38.36/0.990 | 37.50/0.982 |
| LFSSR [17] | 33.68/0.974 | 36.81/0.975 | 43.81/0.994 | 35.28/0.983 | 37.95/0.990 | 37.51/0.983 |
| MEG-Net [15] | 34.30/0.977 | 37.42/0.978 | 44.08/0.994 | 36.09/0.985 | 38.77/0.991 | 38.13/0.985 |
| LF-ATO [16] | 34.27/0.976 | 37.24/0.977 | 44.20/0.994 | 36.15/0.984 | 39.64/0.993 | 38.30/0.985 |
| LF-InterNet [19] | 34.14/0.972 | 37.28/0.977 | 44.45/0.995 | 35.80/0.985 | 38.72/0.992 | 38.08/0.984 |
| LF-DFnet [18] | 34.44/0.977 | 37.44/0.979 | 44.23/0.994 | 36.36/0.984 | 39.61/0.993 | 38.42/0.985 |
| LF-IINet [20] | 34.68/0.977 | 37.74/0.979 | 44.84/0.995 | 36.57/0.985 | 39.86/0.994 | 38.74/0.986 |
| DPT [22] | 34.48/0.976 | 37.35/0.977 | 44.31/0.994 | 36.40/0.984 | 39.52/0.993 | 38.41/0.984 |
| LFT [23] | 34.80/0.978 | 37.84/0.979 | 44.52/0.995 | 36.59/0.986 | 40.51/0.994 | 38.85/0.986 |
| DistgSSR [21] | 34.80/0.979 | 37.95/0.980 | 44.92/0.995 | 36.58/0.986 | 40.37/0.994 | 38.92/0.987 |
| Ours | 35.76/0.979 | 37.49/0.979 | 44.50/0.994 | 38.44/0.986 | 39.16/0.993 | 39.05/0.986 |
| Dataset | EPFL | HCInew | HCIold | INRIA | STFgantry | Average |
|---|---|---|---|---|---|---|
| Bicubic | 25.14/0.833 | 27.61/0.853 | 32.42/0.931 | 26.82/0.886 | 25.93/0.847 | 27.58/0.870 |
| VDSR [36] | 27.25/0.878 | 29.31/0.883 | 34.81/0.952 | 29.19/0.921 | 28.51/0.901 | 29.81/0.907 |
| EDSR [37] | 27.84/0.886 | 29.60/0.887 | 35.18/0.954 | 29.66/0.926 | 28.70/0.908 | 30.20/0.912 |
| RCAN [31] | 27.88/0.886 | 29.63/0.888 | 35.20/0.954 | 29.76/0.927 | 28.90/0.911 | 30.27/0.913 |
| resLF [14] | 28.27/0.904 | 30.73/0.911 | 36.71/0.968 | 30.34/0.941 | 30.19/0.937 | 31.25/0.932 |
| LFSSR [17] | 28.27/0.908 | 30.72/0.912 | 36.70/0.969 | 30.31/0.945 | 30.15/0.939 | 31.23/0.935 |
| MEG-Net [15] | 28.74/0.916 | 31.10/0.918 | 37.28/0.972 | 30.66/0.949 | 30.77/0.945 | 31.71/0.940 |
| LF-ATO [16] | 28.52/0.912 | 30.88/0.914 | 37.00/0.970 | 30.71/0.949 | 30.61/0.943 | 31.54/0.938 |
| LF-InterNet [19] | 28.67/0.914 | 30.98/0.917 | 37.11/0.972 | 30.64/0.949 | 30.53/0.943 | 31.59/0.939 |
| LF-DFnet [18] | 28.77/0.917 | 31.23/0.920 | 37.32/0.972 | 30.83/0.950 | 31.15/0.949 | 31.86/0.942 |
| LF-IINet [20] | 29.11/0.920 | 31.36/0.921 | 37.62/0.974 | 31.08/0.952 | 31.21/0.950 | 32.08/0.943 |
| DPT [22] | 28.93/0.917 | 31.19/0.919 | 37.39/0.972 | 30.96/0.950 | 31.14/0.949 | 31.92/0.941 |
| LFT [23] | 29.25/0.921 | 31.46/0.922 | 37.63/0.974 | 31.20/0.952 | 31.86/0.955 | 32.28/0.945 |
| DistgSSR [21] | 28.98/0.919 | 31.38/0.922 | 37.55/0.973 | 30.99/0.952 | 31.63/0.953 | 32.11/0.944 |
| Ours | 29.48/0.922 | 31.01/0.921 | 37.17/0.971 | 32.08/0.953 | 30.83/0.951 | 32.26/0.944 |
| Dataset | 2× | 4× | ||||
|---|---|---|---|---|---|---|
| #Param. | PSNR | SSIM | #Param. | PSNR | SSIM | |
| EDSR [37] | 38.6 M | 36.04 | 0.974 | 38.9 M | 30.20 | 0.912 |
| RCAN [31] | 15.3 M | 36.11 | 0.974 | 15.4 M | 30.27 | 0.913 |
| resLF [14] | 6.35 M | 37.50 | 0.982 | 6.79 M | 31.25 | 0.932 |
| LFSSR [17] | 0.81 M | 37.51 | 0.983 | 1.61 M | 31.23 | 0.935 |
| MEG-Net [15] | 1.69 M | 38.13 | 0.985 | 1.77 M | 31.71 | 0.940 |
| LF-ATO [16] | 1.51 M | 38.30 | 0.985 | 1.66 M | 31.54 | 0.938 |
| LF-InterNet [19] | 4.80 M | 38.08 | 0.984 | 5.23 M | 31.59 | 0.939 |
| LF-DFnet [18] | 3.94 M | 38.42 | 0.985 | 3.99 M | 31.86 | 0.942 |
| LF-IINet [20] | 4.84 M | 38.74 | 0.986 | 4.89 M | 32.08 | 0.943 |
| DPT [22] | 3.73 M | 38.41 | 0.984 | 3.78 M | 31.92 | 0.941 |
| LFT [23] | 1.11 M | 38.85 | 0.986 | 1.16 M | 32.28 | 0.945 |
| DistgSSR [21] | 3.53 M | 38.92 | 0.987 | 3.58 M | 32.11 | 0.944 |
| Ours | 3.21 M | 39.05 | 0.986 | 3.21 M | 32.26 | 0.944 |
| Dataset | EPFL | HCInew | HCIold | INRIA | STFgantry | Average |
|---|---|---|---|---|---|---|
| Spatial | 33.35/0.964 | 34.55/0.960 | 40.68/0.987 | 35.58/0.977 | 35.99/0.983 | 36.03/0.974 |
| Lenslet | 35.06/0.976 | 36.40/0.975 | 43.35/0.993 | 37.63/0.985 | 36.95/0.989 | 37.88/0.984 |
| Both | 35.76/0.979 | 37.49/0.979 | 44.50/0.994 | 38.44/0.986 | 39.16/0.993 | 39.05/0.986 |
| Dataset | EPFL | HCInew | HCIold | INRIA | STFgantry | Average |
|---|---|---|---|---|---|---|
| 16 × 16 | 35.78/0.980 | 37.46/0.979 | 44.34/0.994 | 38.47/0.987 | 39.36/0.993 | 39.08/0.987 |
| 32 × 32 | 35.76/0.979 | 37.49/0.979 | 44.50/0.994 | 38.44/0.986 | 39.16/0.993 | 39.05/0.986 |
| 64 × 64 | 35.46/0.977 | 37.17/0.977 | 44.14/0.994 | 38.11/0.985 | 38.98/0.993 | 38.77/0.985 |
| Dataset | EPFL | HCInew | HCIold | INRIA | STFgantry | Average |
|---|---|---|---|---|---|---|
| 16 × 16 | 29.33/0.918 | 30.63/0.912 | 36.63/0.967 | 31.44/0.949 | 30.21/0.940 | 31.65/0.937 |
| 32 × 32 | 29.48/0.922 | 31.01/0.921 | 37.17/0.971 | 32.08/0.953 | 30.83/0.951 | 32.26/0.944 |
| 64 × 64 | 29.34/0.918 | 30.80/0.919 | 36.77/0.969 | 31.84/0.951 | 30.51/0.948 | 31.85/0.941 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salem, A.; Ibrahem, H.; Kang, H.-S. Light Field Image Super-Resolution Using Deep Residual Networks on Lenslet Images. Sensors 2023, 23, 2018. https://doi.org/10.3390/s23042018
Salem A, Ibrahem H, Kang H-S. Light Field Image Super-Resolution Using Deep Residual Networks on Lenslet Images. Sensors. 2023; 23(4):2018. https://doi.org/10.3390/s23042018
Chicago/Turabian StyleSalem, Ahmed, Hatem Ibrahem, and Hyun-Soo Kang. 2023. "Light Field Image Super-Resolution Using Deep Residual Networks on Lenslet Images" Sensors 23, no. 4: 2018. https://doi.org/10.3390/s23042018
APA StyleSalem, A., Ibrahem, H., & Kang, H.-S. (2023). Light Field Image Super-Resolution Using Deep Residual Networks on Lenslet Images. Sensors, 23(4), 2018. https://doi.org/10.3390/s23042018






