Model of the Performance Based on Artificial Intelligence–Fuzzy Logic Description of Physical Activity
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Material
2.2. Methods
- Easy and precise alignment of the dynamometer’s axis of motion with that of the joint being tested/exercised;
- Repeatability of the dynamometer setting;
- Force torque measurement during acceleration and deceleration phases of movement;
- Fully adjustable adjustment for assessment and training of different joints and muscle groups;
- Torque measurement range: concentric operation from 0 to 680 Nm, eccentric operation from 0 to 544 Nm;
- Range of motion speed measurement: concentric operation up to 500 deg/s, eccentric operation up to 300 deg/s;
- Minimum movement speed (for passive movement): from 0.25 deg/s;
- Minimum force torque (for passive movement): 0.68 Nm and above;
- Minimum force torque value (for isotonic operation): 0.68 Nm and above.
- Away (extension)—movement of the lower limb at the knee joint in the sagittal plane between 90 and 0 degrees—as straightening;
- Toward (flexion)—(movement in the opposite direction to away) as bending after previous straightening.
- PEAKTQ (R, L)—peak torque value (R—lower limb right, L—lower limb left) (Nm);
- PEAKTQ/BM—the ratio of peak torque to body mass (Nm/kg);
- H/Q—the ratio of peak torque of hamstring to quadriceps (flexors to extensors of lower limb) (%);
2.3. Statistical Analysis
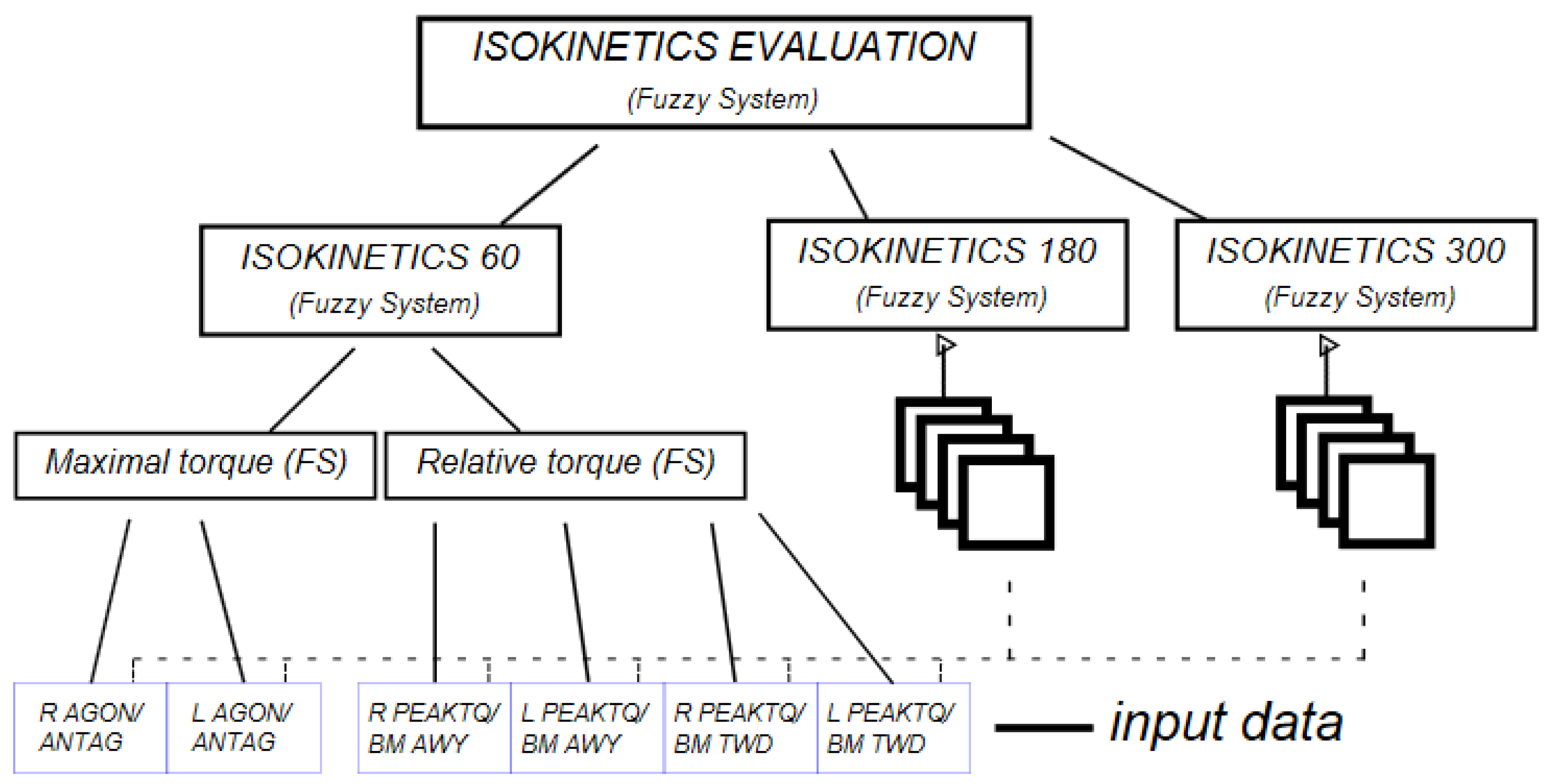
2.4. Computational Analysis
- Two evaluation systems, including one with detailed data (both legs), and another simpler one where only the data for the leading leg were considered to see if the results were similar;
- A comparative evaluation between hearing players and deaf players—more than one fuzzy system to indicate a better structure of the algorithm.
- R AGON/ANTAG (denoted in fuzzy system by XRMT)—the ratio of extensor to flexor muscles for a right leg,
- L AGON/ANTAG(XLMT)—as per previous, but for a left leg.
- R PEAKTQ/BM AWY(XRAWYRT)—peak torque relative to body mass for a right leg during away move,
- L PEAKTQ/BM AWY (XLAWYRT)—as per previous, but for a left leg,
- R PEAKTQ/BM TWD (XRTWDRT)—peak torque relative to body mass for a right leg during toward move,
- L PEAKTQ/BM TWD (XLTWDRT)—as per previous, but for a left leg.
XRT = {XRAWYRT, XLAWYRT, XRTWDRT, XLTWDRT},
XRAWYRT: lowXRAWYRT = (0;0;0.6;3.4), highXRAWYRT = (0.6;3.4;4.5;4.5),
XRTWDRT: lowXRTWDRT = (0;0;0.4;2.2), highXRTWDRT = (0.4;2.2;3;3).
R2: IF XRMT islowXRMT AND XLMT ismedXLMT THEN eMT = Y2,
R3: IF XRMT islowXRMT AND XLMT ishighXLMT THEN eMT = Y1,
R4: IF XRMT ismedXRMT AND XLMT islowXLMT THEN eMT = Y2,
R5: IF XRMT ismedXRMT AND XLMT ismedXLMT THEN eMT = Y3,
R6: IF XRMT ismedXRMT AND XLMT ishighXLMT THEN eMT = Y2,
R7: IF XRMT ishighXRMT AND XLMT islowXLMT THEN eMT = Y1,
R8: IF XRMT ishighXRMT AND XLMT ismedXLMT THEN eMT = Y2,
R9: IF XRMT ishighXRMT AND XLMT ishighXLMT THEN eMT = Y1,
R2: IF XRAWYRT islowXRAWYRT AND XLAWYRT islowXLAWYRT AND XRTWDRTislowXRTWDRT AND XLTWDRTishighXLTWDRT THEN eRT = Y2,
R3:IF XRAWYRT islowXRAWYRT AND XLAWYRT islowXLAWYRT AND XRTWDRTishighXRTWDRT AND XLTWDRTislowXLTWDRT THEN eRT = Y2,
R4: IF XRAWYRT islowXRAWYRT AND XLAWYRT islowXLAWYRT AND XRTWDRTishighXRTWDRT AND XLTWDRTishighXLTWDRT THEN eRT = Y3,
R5: IF XRAWYRT islowXRAWYRT AND XLAWYRT ishighXLAWYRT AND XRTWDRTislowXRTWDRT AND XLTWDRTislowXLTWDRT THEN eRT = Y2,
…
R16: IF XRAWYRT ishighXRAWYRT AND XLAWYRT ishighXLAWYRT AND XRTWDRTishighXRTWDRT AND XLTWDRTishighXLTWDRT THEN eRT = Y5,
EMT: lowEMT= (0;0;0;1),highEMT = (0;1;1;1),
ERT: lowERT = (0;0;0;1),highERT = (0;1;1;1).
R2: IF EMT is lowEMT AND ERT ishighERT THEN eK60 = Y2K60,
R3: IF EMT is highEMT AND ERT is lowERT THEN eK60 = Y2K60,
R4: IF EMT is highEMT AND ERTishighERT THEN eK60 = Y3K60,
EK180: lowEK180 = (0;0;0;1),highEK180 = (0;1;1;1),
EK300: lowEK300 = (0;0;0;1),highEK300 = (0;1;1;1).
O4 = (0.667,1,1,1)
R2: IF EK60 is highEK60 AND EK180 is lowEK180 AND EK300 is lowEK300 THEN o = O2,
R3: IF EK60 is lowEK60 AND EK180 is highEK180 AND EK300 is lowEK300 THEN o = O2,
R4: IF EK60 is lowEK60 AND EK180 is lowEK180 AND EK300 is highEK300 THEN o = O2,
R5: IF EK60 is highEK60 AND EK180 is highEK180 AND EK300 is lowEK300 THEN o = O3,
R6: IF EK60 is lowEK60 AND EK180 is highEK180 AND EK300 is highEK300 THEN o = O3,
R7: IF EK60 is highEK60 AND EK180 is lowEK180 AND EK300 is highEK300 THEN o = O3,
R8: IF EK60 is highEK60 AND EK180 is highEK180 AND EK300 is highEK300 THEN o = O4
3. Results
4. Discussion
Future Research Directions
- Regression model, designed to estimate each participant’s mindfulness score based on their postural cues;
- Classifier, designed to assign each participant to one of the ‘Mindful’ or ‘Non-mindful’ classes [39].
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Niespodziński, B.; Mieszkowski, J.; Sawczyn, S.; Kochanowicz, K.; Szulc, A.; Zasada, M.; Kochanowicz, A. Elbow Joint Position and Force Senses in Young and Adult Untrained People and Gymnasts. Int. J. Environ. Res. Public Health 2022, 19, 7592. [Google Scholar] [CrossRef] [PubMed]
- Danek, J.; Wojtasik, W.; Szulc, A. Measurement of maximal isometric torque and muscle fatigue index of the knee muscles in male athletes. Acta Bioeng. Biomech. 2019, 21, 31–37. [Google Scholar] [PubMed]
- Szulc, A.; Sandurska, E. Deaf and hearing Basketball National Teams at the 2019 World Championships: Discriminant analysis of game-related statistics between the winning and the defeated. Acta Kinesiol. 2021, 15, 82–91. [Google Scholar] [CrossRef]
- Buśko, K.; Kopczyńska, J.; Szulc, A. Physical fitness of deaf females. Biomed. Hum. Kinet. 2020, 12, 101–104. [Google Scholar] [CrossRef]
- Mikołajewska, E.; Prokopowicz, P.; Mikołajewski, D. Computational gait analysis using fuzzy logic for everyday clinical purposes—Preliminary findings. Bio-Algorithms Med. Syst. 2017, 13, 37–42. [Google Scholar] [CrossRef]
- Prokopowicz, P.; Mikołajewski, D.; Tyburek, K.; Mikołajewska, E. Computational gait analysis for post-stroke rehabilitation purposes using fuzzy numbers, fractal dimension and neural networks. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 191–198. [Google Scholar]
- Zhang, J.; Lockhart, T.E.; Soangra, R. Classifying lower extremity muscle fatigue during walking using machine learning and inertial sensors. Ann. Biomed. Eng. 2014, 42, 600–612. [Google Scholar] [CrossRef]
- Prokopowicz, P.; Mikołajewski, D. Fuzzy Approach to Computational Classification of Burnout—Preliminary Findings. Appl. Sci. 2022, 12, 3767. [Google Scholar] [CrossRef]
- Mikołajewski, D.; Prokopowicz, P. Effect of COVID-19 on Selected Characteristics of Life Satisfaction Reflected in a FuzzyModel. Appl. Sci. 2022, 12, 7376. [Google Scholar] [CrossRef]
- Feldman, A.G. The Relationship Between Postural and Movement Stability. Adv. Exp. Med. Biol. 2016, 957, 105–120. [Google Scholar]
- Horak, F.B. Postural orientation and equilibrium: What do we need to know about neural control of balance to prevent falls? Age Ageing 2006, 35 (Suppl. 2), ii7–ii11. [Google Scholar] [CrossRef] [PubMed]
- Koshio, Y.; Samukawa, M.; Chida, S.; Okada, S.; Tanaka, H.; Watanabe, K.; Chijimatsu, M.; Yamanaka, M.; Tohyama, H. Postural Stability and Muscle Activation Onset during Double-to Single-LegStanceTransitioninFlat-FootedIndividuals. J. Sports Sci. Med. 2020, 19, 662–669. [Google Scholar]
- Wojciechowska-Maszkowska, B.; Marcinów, R.; Iskra, J.; Tataruch, R. Postural Stability in Athletes during Special HurdleTests without a Definite Dominant Leg. Int. J. Environ. Res. Public Health 2020, 18, 172. [Google Scholar] [CrossRef]
- McIntyre, C.C.; Richardson, S.J.; Frankemolle, A.M.; Varga, G.; Noecker, A.M.; Alberts, J.L. Improving postural stability viacomputational modeling approach to deep brain stimulation programming. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2011, 2011, 675–676. [Google Scholar] [PubMed]
- Asgari, M.; Crouch, D.L. Estimating Human Upper Limb Impedance Parameters Froma State-of-the-Art Computational Neuromusculoskeletal Model. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2021, 2021, 4820–4823. [Google Scholar] [PubMed]
- Chopp-Hurley, J.N.; Langenderfer, J.E.; Dickerson, C.R. Probabilistic evaluation of predicted force sensitivity to muscle attachment and glenohumeral stability uncertainty. Ann. Biomed. Eng. 2014, 42, 1867–1879. [Google Scholar] [CrossRef]
- Mouchnino, L.; Robert, G.; Ruget, H.; Blouin, J.; Simoneau, M. Online control of anticipated postural adjustments in step initiation: Evidence from behavioral and computational approaches. Gait Posture 2012, 35, 616–620. [Google Scholar] [CrossRef]
- Vlamou, E.; Papadopoulos, B. Fuzzy logic systems and medical applications. AIMS Neurosci. 2019, 6, 266–272. [Google Scholar]
- Arani, L.A.; Sadoughi, F.; Langarizadeh, M. An Expert System to Diagnose Pneumonia Using Fuzzy Logic. Acta Inf. Med. 2019, 27, 103–107. [Google Scholar] [CrossRef]
- Thukral, S.; Rana, V. Versatility of fuzzy logic in chronic diseases: A review. Med. Hypotheses. 2019, 122, 150–156. [Google Scholar] [CrossRef]
- Farzandipour, M.; Nabovati, E.; Saeedi, S.; Fakharian, E. Fuzzy decision support systems to diagnose musculoskeletal disorders: A systematic literature review. Comput. Methods Programs Biomed. 2018, 163, 101–109. [Google Scholar] [CrossRef] [PubMed]
- Murugesan, G.; Ahmed, T.I.; Bhola, J.; Shabaz, M.; Singla, J.; Rakhra, M.; More, S.; Samori, I.A. Fuzzy Logic-Based Systemsfor the Diagnosis of Chronic Kidney Disease. Biomed. Res. Int. 2022, 2022, 2653665. [Google Scholar] [CrossRef]
- Ahmadi, H.; Gholamzadeh, M.; Shahmoradi, L.; Nilashi, M.; Rashvand, P. Diseases diagnosis using fuzzy logic methods: A systematic and meta-analysis review. Comput. Methods Programs Biomed. 2018, 161, 145–172. [Google Scholar] [CrossRef] [PubMed]
- Iancu, I. Heart disease diagnosis based on mediative fuzzy logic. Artif. Intell. Med. 2018, 89, 51–60. [Google Scholar] [CrossRef]
- Ahmedov, S.; Amirjanov, A. Genetic-fuzzy logic model for a non-invasive measurement of a stroke volume. Comput. Methods Programs Biomed. 2021, 203, 106046. [Google Scholar] [CrossRef]
- Dumitrescu, C.; Ciotirnae, P.; Vizitiu, C. Fuzzy Logic for Intelligent Control System Using Soft Computing Applications. Sensors 2021, 21, 2617. [Google Scholar] [CrossRef]
- Prokopowicz, P. The use of Ordered Fuzzy Numbers for modeling changes in dynamic processes. Inf. Sci. 2019, 470, 1–14. [Google Scholar] [CrossRef]
- Prokopowicz, P.; Golsefid, S.M.M. Aggregation Operatorfor Ordered Fuzzy Numbers Concerning the Direction. In ArtificialIntelligence and Soft Computing; ICAISC 2014. Lecture Notes in Computer Science; Rutkowski, L., Korytkowski, M., Scherer, R., Tadeusiewicz, R., Zadeh, L.A., Zurada, J.M., Eds.; Springer: Cham, Switzerland, 2014; Volume 8467. [Google Scholar]
- Prokopowicz, P.; Czerniak, J.; Mikołajewski, D.; Apiecionek, Ł.; Ślęzak, D. Theory and Applications of Ordered Fuzzy Numbers; Studies in Fuzziness and Soft Computing Book Series (STUDFUZZ); Springer: Berlin/Heidelberg, Germany, 2017; Volume 356. [Google Scholar]
- Li, Y.; Mache, M.A.; Todd, T.A. Automated identification of postural controlforchildrenwithautismspectrumdisorderusingamachinelearningapproach. J. Biomech. 2020, 113, 110073. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, S.; Odeh, C. Automated Classification of Postural Control for Individuals with Parkinson’s Disease Usinga Machine Learning Approach: A Preliminary Study. J. Appl. Biomech. 2020, 1–6. [Google Scholar] [CrossRef]
- Brown, L.E. Isokinetics in Human Performance; Florida Atlantic University: Boca Raton, FL, USA, 2000. [Google Scholar]
- Szulc, A.; Buśko, K.; Sandurska, E.; Kołodziejczyk, M. The biomechanical characteristics of elite deaf and hearing female soccer players: Comparative analysis. Acta Bioeng. Biomech. 2017, 19, 127–133. [Google Scholar]
- Cometti, G.; Maffiuletti, N.A.; Pousson, M.; Chatard, J.-C.; Maffuli, N. Isokinetics strength and anaerobic power of elite, subelite and amateur French soccer players. Int. J. Sport. Med. 2001, 22, 45–51. [Google Scholar] [CrossRef] [PubMed]
- Fousekis, K.; Tsepis, E.; Vagenas, G. Lower limb strength in professional soccer players: Profile, asymmetry, and training age. J. Sport Sci. Med. 2010, 9, 364–373. [Google Scholar]
- Akbas, K.; Mummolo, C. A Computational Framework Towards the Tele-Rehabilitation of Balance Control Skills. Front. Robot AI 2021, 8, 648485. [Google Scholar] [CrossRef] [PubMed]
- Rosiak, O.; Puzio, A.; Kaminska, D.; Zwolinski, G.; Jozefowicz-Korczynska, M. Virtual Reality - A Supplement to Posturography or a Novel Balance Assessment Tool? Sensors 2022, 22, 7904. [Google Scholar] [CrossRef] [PubMed]
- Błaszczyk, J.W. The use of force-plate posturography in the assessment of postural instability. Gait Posture 2016, 44, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Verdonk, C.; Trousselard, M.; Medani, T.; Vialatte, F.; Dreyfus, G. Probing the posture with machine learning provides physiological evidence supporting the enhanced body awareness hypothesis in trait mindfulness. Front. Physiol. 2022, 13, 915134. [Google Scholar] [CrossRef]
- Adkin, A.L.; Carpenter, M.G. New insights on emotional contributions to human postural control. Front. Neurol. 2018, 9, 789. [Google Scholar] [CrossRef]
| Parameter | Group 1 Deaf Soccer Players (n = 28) | Group 2 Hearing Soccer Players (n = 19) | Group 3 Deaf Untrained (n = 46) |
|---|---|---|---|
| Age [years] | |||
| Mean | 20.00 | 19.63 | 21.89 |
| SD | 3.50 | 1.95 | 4.40 |
| Min | 17 | 17 | 17 |
| Q1 | 18 | 18 | 18 |
| Median | 19 | 19 | 22 |
| Q3 | 21 | 21 | 25 |
| Max | 30 | 23 | 32 |
| Body height [cm] | |||
| Mean | 175.36 | 172.96 | 179.63 |
| SD | 4.13 | 9.43 | 6.01 |
| Min | 166.80 | 151.30 | 165.00 |
| Q1 | 172.60 | 167.10 | 175.60 |
| Median | 174.80 | 173.50 | 179.40 |
| Q3 | 178.50 | 180.10 | 184.20 |
| Max | 184.60 | 191.70 | 190.00 |
| Shin length [cm] | |||
| Mean | 38.55 | 38.45 | 39.56 |
| SD | 1.80 | 2.18 | 2.62 |
| Min | 33.50 | 35.50 | 34.80 |
| Q1 | 37.50 | 36.50 | 38.00 |
| Median | 38.00 | 37.80 | 39.60 |
| Q3 | 40.00 | 40.00 | 41.50 |
| Max | 42.00 | 43.10 | 44.50 |
| Body mass [kg] | |||
| Mean | 70.19 | 66.71 | 73.67 |
| SD | 9.63 | 17.13 | 8.38 |
| Min | 57.70 | 41.60 | 60.10 |
| Q1 | 64.40 | 55.80 | 67.90 |
| Median | 68.20 | 62.90 | 74.30 |
| Q3 | 75.40 | 75.40 | 78.80 |
| Max | 92.90 | 103.30 | 94.50 |
| Dominant leg | |||
| L | 4 (14.29%) | 3 (15.79%) | 7 (15.22%) |
| R | 24 (85.71%) | 16 (84.21%) | 39 (84.78%) |
| Parameter | Low Values | Medium Values | High Values | Linguistic Interpretation |
|---|---|---|---|---|
| Isokinetic mode 60 deg/s | ||||
| R AGON/ANTAG | 0–50 | 45–65 | 60–100 | the medium values are good, but low and high are bad |
| L AGON/ANTAG | 0–50 | 45–65 | 60–100 | the medium values are good, but low and high are bad |
| R PEAKTQ/BM AWY | 0–1.2 | 1.0–2.4 | 2.3–4.5 | the more, the better |
| L PEAKTQ/BM AWY | 0–1.2 | 1.0–2.4 | 2.3–4.5 | the more, the better |
| R PEAKTQ/BM TWD | 0–0.8 | 0.7–1.5 | 1.4–3.0 | the more, the better |
| L PEAKTQ/BM TWD | 0–0.8 | 0.7–1.5 | 1.4–3.0 | the more, the better |
| Isokinetic mode 180 deg/s | ||||
| R AGON/ANTAG | 0–50 | 45–65 | 60–100 | the medium values are good, but low and high are bad |
| L AGON/ANTAG | 0–50 | 45–65 | 60–100 | the medium vales are good, but low and high are bad |
| R PEAKTQ/BM AWY | 0–0.90 | 0.8–1.7 | 1.6–3.0 | the more, the better |
| L PEAKTQ/BM AWY | 0–0.90 | 0.8–1.7 | 1.6–3.0 | the more, the better |
| R PEAKTQ/BM TWD | 0–0.7 | 0.6–1.3 | 1.2–3.0 | the more, the better |
| L PEAKTQ/BM TWD | 0–0.7 | 0.6–1.3 | 1.2–3.0 | the more, the better |
| Isokinetic mode 300 deg/s | ||||
| R AGON/ANTAG | 0–60 | 55–90 | 85–150 | the medium values are good, but low and high are bad |
| L AGON/ANTAG | 0–60 | 55–90 | 85–150 | the medium values are good, but low and high are bad |
| R PEAKTQ/BM AWY | 0–0.7 | 0.60–1.30 | 1.20–2.8 | the more, the better |
| L PEAKTQ/BM AWY | 0–0.7 | 0.60–1.30 | 1.20–2.8 | the more, the better |
| R PEAKTQ/BM TWD | 0–0.7 | 0.60–1.30 | 1.20–2.8 | the more, the better |
| L PEAKTQ/BM TWD | 0–0.7 | 0.60–1.30 | 1.20–2.8 | the more, the better |
| No. of Participant/Parameter | Value |
|---|---|
| 1 | 0.76734109 |
| 2 | 0.65589328 |
| 3 | 0.64234552 |
| 4 | 0.69709596 |
| 5 | 0.73758406 |
| 6 | 0.68142442 |
| 7 | 0.60856813 |
| 8 | 0.60663099 |
| 9 | 0.53337415 |
| 10 | 0.65551133 |
| 11 | 0.60379564 |
| 12 | 0.67940767 |
| 13 | 0.6983585 |
| 14 | 0.75756501 |
| 15 | 0.74477273 |
| 16 | 0.74373664 |
| 17 | 0.69312008 |
| 18 | 0.64302757 |
| 19 | 0.64844364 |
| 20 | 0.71791784 |
| 21 | 0.6558216 |
| 22 | 0.62666147 |
| 23 | 0.6727858 |
| 24 | 0.70166569 |
| 25 | 0.73768627 |
| 26 | 0.65344389 |
| 27 | 0.61765752 |
| 28 | 0.74812219 |
| Mean | 0.67606281 |
| SD (Standard Deviation) | 0.0565327 |
| Min | 0.53337415 |
| Q1 (Lower quartile) | 0.64285706 |
| Median | 0.67609673 |
| Q3 (Upper quartile) | 0.7228344 |
| Max | 0.76734109 |
| No. of Participant/Parameter | Value |
|---|---|
| 1 | 0.56585384 |
| 2 | 0.64469192 |
| 3 | 0.54099616 |
| 4 | 0.61011369 |
| 5 | 0.56910691 |
| 6 | 0.58987825 |
| 7 | 0.56994588 |
| 8 | 0.5731141 |
| 9 | 0.56502047 |
| 10 | 0.61102068 |
| 11 | 0.54596697 |
| 12 | 0.61948461 |
| 13 | 0.62375196 |
| 14 | 0.66939015 |
| 15 | 0.575458 |
| 16 | 0.58376321 |
| 17 | 0.59714431 |
| 18 | 0.59057348 |
| 19 | 0.58581099 |
| Mean | 0.59110977 |
| SD (Standard Deviation) | 0.03258833 |
| Min | 0.54099616 |
| Q1 (Lower quartile) | 0.5695264 |
| Median | 0.58581099 |
| Q3 (Upper quartile) | 0.61056719 |
| Max | 0.66939015 |
| No. of Participant/Parameter | Value |
|---|---|
| 1 | 0.80400957 |
| 2 | 0.76927435 |
| 3 | 0.62282284 |
| 4 | 0.74328593 |
| 5 | 0.74373664 |
| 6 | 0.70207034 |
| 7 | 0.64074447 |
| 8 | 0.73227387 |
| 9 | 0.70003183 |
| 10 | 0.72986779 |
| 11 | 0.70734059 |
| 12 | 0.69860786 |
| 13 | 0.65737016 |
| 14 | 0.66614456 |
| 15 | 0.69351383 |
| 16 | 0.67523309 |
| 17 | 0.68521024 |
| 18 | 0.66333946 |
| 19 | 0.71704625 |
| 20 | 0.67574448 |
| 21 | 0.70851757 |
| 22 | 0.74564416 |
| 23 | 0.68427606 |
| 24 | 0.64150353 |
| 25 | 0.71149862 |
| 26 | 0.6788365 |
| 27 | 0.68999421 |
| 28 | 0.72515522 |
| 29 | 0.61814783 |
| 30 | 0.7283098 |
| 31 | 0.70268278 |
| 32 | 0.60633094 |
| 33 | 0.61681826 |
| 34 | 0.64672526 |
| 35 | 0.67162273 |
| 36 | 0.73704441 |
| 37 | 0.69031519 |
| 38 | 0.6860709 |
| 39 | 0.77480748 |
| 40 | 0.73948592 |
| 41 | 0.82803729 |
| 42 | 0.75687176 |
| 43 | 0.65334806 |
| 44 | 0.65969457 |
| 45 | 0.69795882 |
| 46 | 0.77084335 |
| Mean | 0.69996107 |
| SD (Standard Deviation) | 0.0490296 |
| Min | 0.60633094 |
| Q1 (Lower quartile) | 0.6675141 |
| Median | 0.69828334 |
| Q3 (Upper quartile) | 0.73167235 |
| Max | 0.82803729 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szulc, A.; Prokopowicz, P.; Buśko, K.; Mikołajewski, D. Model of the Performance Based on Artificial Intelligence–Fuzzy Logic Description of Physical Activity. Sensors 2023, 23, 1117. https://doi.org/10.3390/s23031117
Szulc A, Prokopowicz P, Buśko K, Mikołajewski D. Model of the Performance Based on Artificial Intelligence–Fuzzy Logic Description of Physical Activity. Sensors. 2023; 23(3):1117. https://doi.org/10.3390/s23031117
Chicago/Turabian StyleSzulc, Adam, Piotr Prokopowicz, Krzysztof Buśko, and Dariusz Mikołajewski. 2023. "Model of the Performance Based on Artificial Intelligence–Fuzzy Logic Description of Physical Activity" Sensors 23, no. 3: 1117. https://doi.org/10.3390/s23031117
APA StyleSzulc, A., Prokopowicz, P., Buśko, K., & Mikołajewski, D. (2023). Model of the Performance Based on Artificial Intelligence–Fuzzy Logic Description of Physical Activity. Sensors, 23(3), 1117. https://doi.org/10.3390/s23031117






