FilterformerPose: Satellite Pose Estimation Using Filterformer
Abstract
:1. Introduction
- A new end-to-end satellite pose estimation network is proposed, which incorporates an improved transformer model and employs a dual-channel network structure. This effectively decouples the translation information and orientation information of the satellite objects;
- A filterformer network structure is designed, which effectively integrates the advantages of the transformer encoder and the filter, enabling the network to adapt to complex background environments and effectively improving the satellite pose inference accuracy;
- The effectiveness of the method is verified in different computer vision downstream tasks.
2. Related Work
2.1. Satellite Pose Estimation Network
2.1.1. Direct End-to-End Approaches
2.1.2. Hybrid Modular Approaches
2.2. Transformer
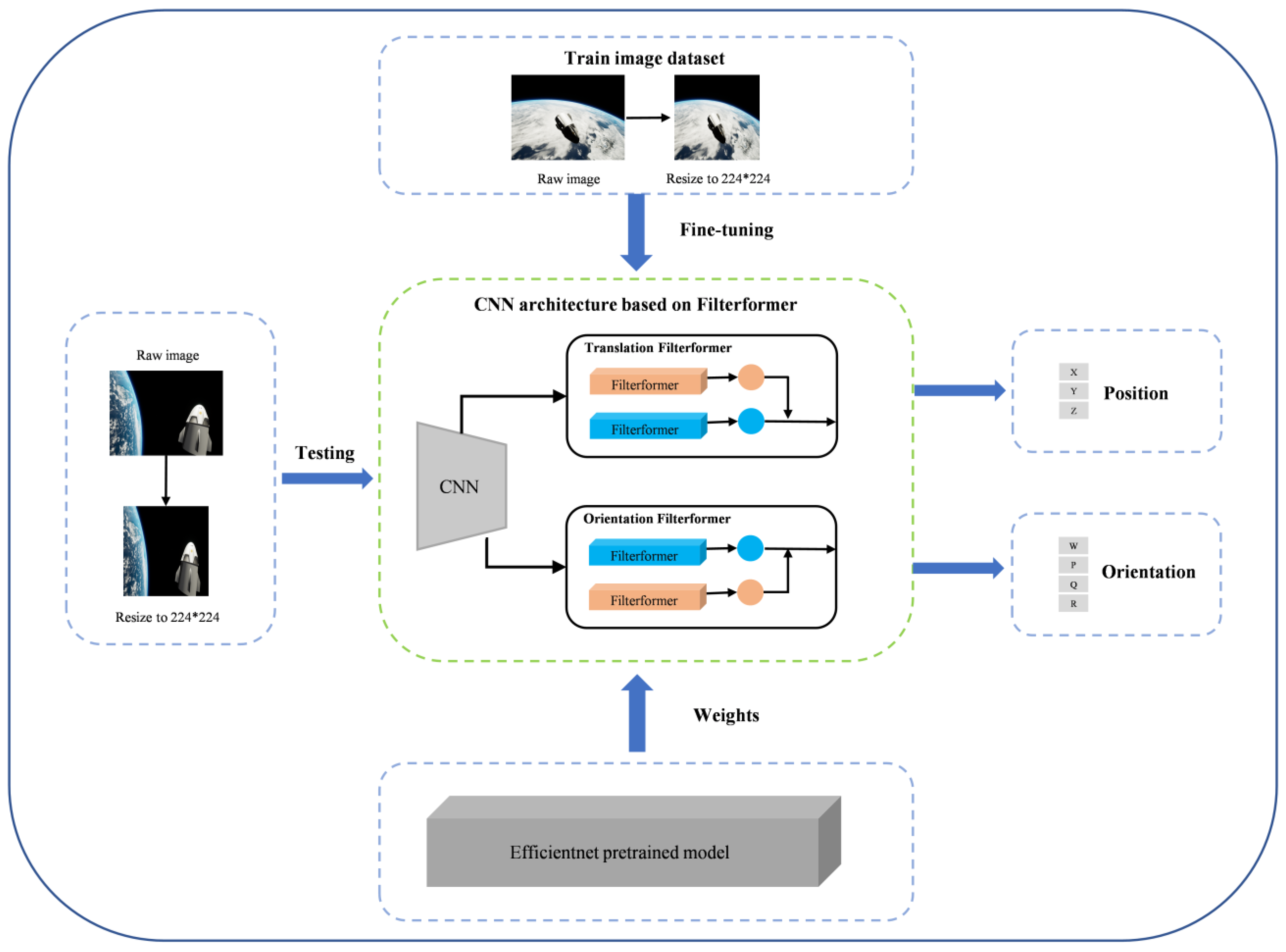
3. FilterformerPose
3.1. Network Architecture
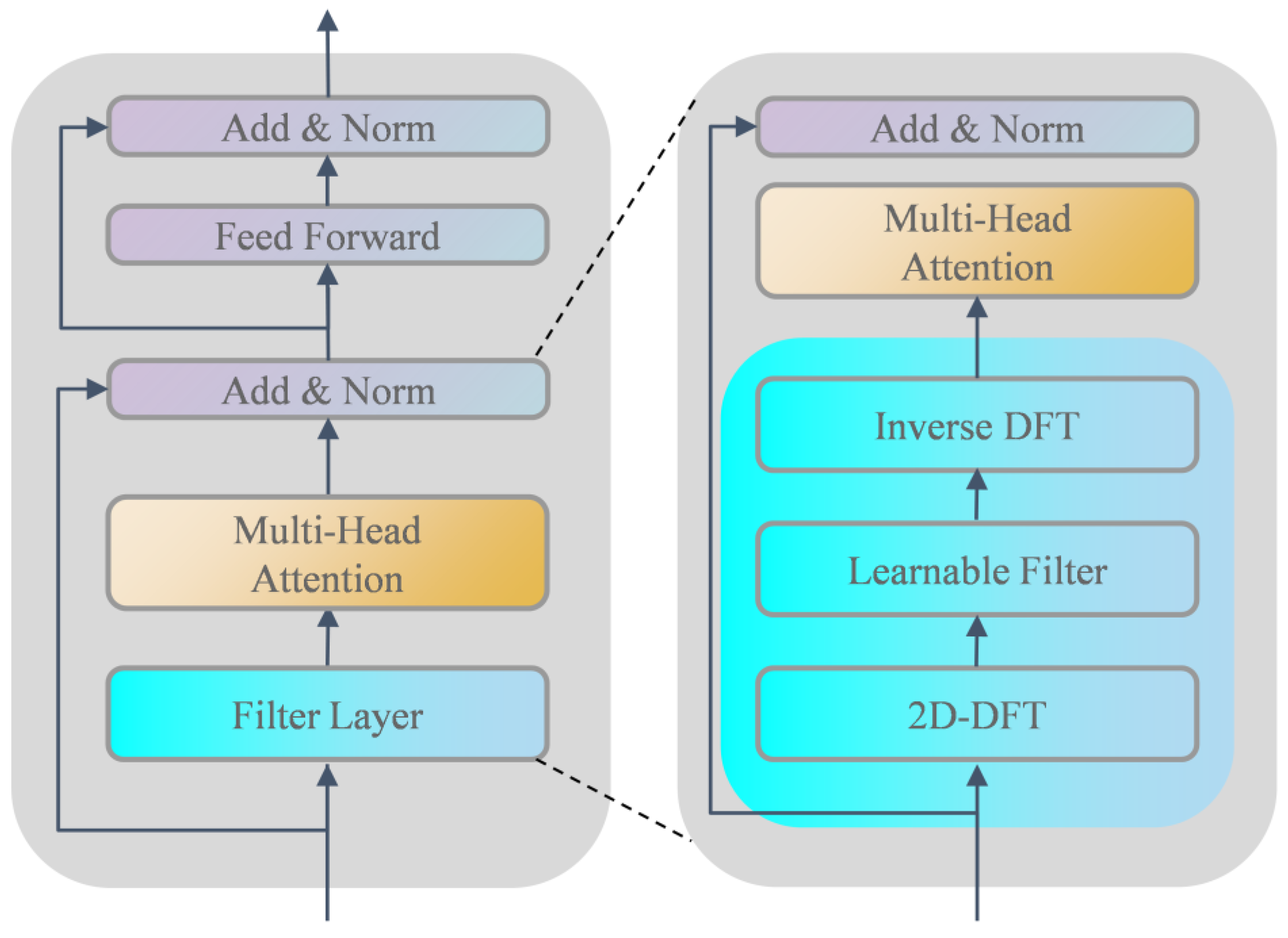
3.1.1. Filter Layer
3.1.2. Self-Attention
3.1.3. Multi-Head Attention
3.2. Quaternion Activation Function
3.3. The Joint Loss Function of Pose
4. Experimental Results
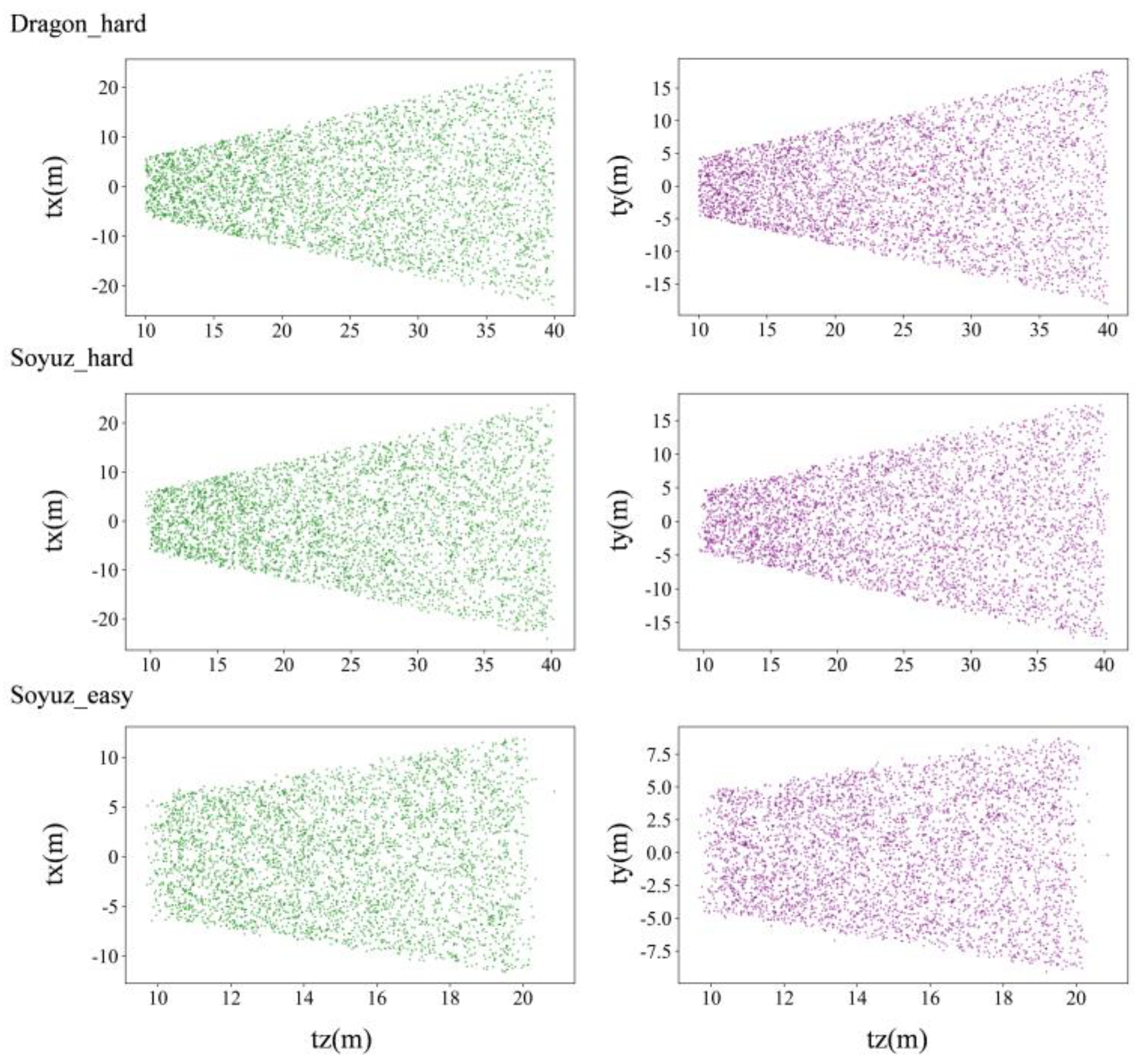
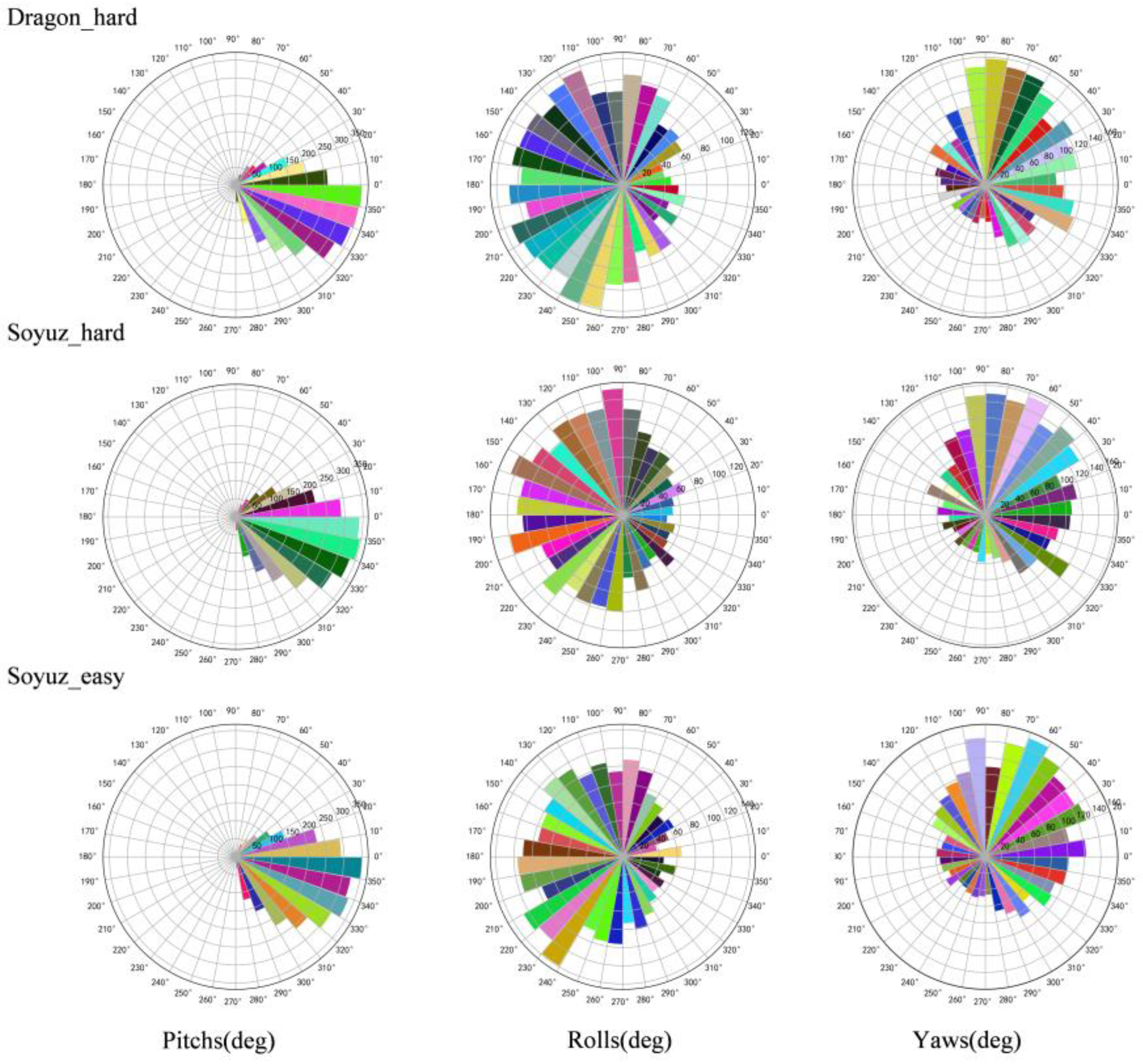
4.1. URSO Analysis
4.2. Evaluation Metrics
4.3. Training Details
4.4. Ablation Study
4.4.1. MLP Dimensions
4.4.2. The Number of Filterformer Components
4.4.3. Filter Layer
4.5. Results
4.6. Evaluation of Cambridge Landmarks
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CNNs | Convolutional neural networks |
| URSO | Unreal rendered spacecraft on-orbit |
| SFF | Spacecraft formation flying |
| OOM | On-orbit maintenance |
| ADR | Active debris removal |
| 6-DoF | Six-degrees of freedom |
| PnP | Perspective-n-Points |
| RANSAC | Random sample consensus |
| SPN | Spacecraft pose network |
| RoI | Regions of interest |
| ViT | Vision transformer |
| TFPose | Transformer pose |
| HRFormer | High-resolution transformer |
| HRNet | High-resolution network |
| KDN | Keypoint Detection Network |
| MLP | Multi-layer perception |
| SA | Self-attention mechanism |
| MHA | Multi-head attention |
| LN | Residual connection and layer normalization |
| FFN | Feed forward network |
| 2D-DFT | Two-dimensional discrete Fourier transform |
| Inverse 2D-DFT | Inverse Two-dimensional discrete Fourier transform |
References
- Dony, M.; Dong, W.J. Distributed Robust Formation Flying and Attitude Synchronization of Spacecraft. J. Aerosp. Eng. 2021, 34, 04021015. [Google Scholar] [CrossRef]
- Xu, J.; Song, B.; Yang, X.; Nan, X. An Improved Deep Keypoint Detection Network for Space Targets Pose Estimation. Remote Sens. 2020, 12, 3857. [Google Scholar] [CrossRef]
- Liu, X.; Wang, H.Y.; Chen, X.L.; Chen, W.C.; Xie, Z.Y. Position Awareness Network for Noncooperative Spacecraft Pose Estimation Based on Point Cloud. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 507–518. [Google Scholar] [CrossRef]
- De Jongh, W.C.; Jordaan, H.W.; Van Daalen, C.E. Experiment for pose estimation of uncooperative space debris using stereo vision. Acta Astronaut. 2020, 168, 164–173. [Google Scholar] [CrossRef]
- Opromolla, R.; Vela, C.; Nocerino, A.; Lombardi, C. Monocular-based pose estimation based on fiducial markers for space robotic capture operations in GEO. Remote Sens. 2022, 14, 4483. [Google Scholar] [CrossRef]
- Park, T.H.; Märtens, M.; Lecuyer, G.; Izzo, D.; Amico, S.D. SPEED+: Next-Generation Dataset for Spacecraft Pose Estimation across Domain Gap. In Proceedings of the 2022 IEEE Aerospace Conference (AERO), Big Sky, MT, USA, 5–12 March 2022; pp. 1–15. [Google Scholar]
- Bechini, M.; Lavagna, M.; Lunghi, P. Dataset generation and validation for spacecraft pose estimation via monocular images processing. Acta Astronaut. 2023, 204, 358–369. [Google Scholar] [CrossRef]
- Liu, Y.; Xie, Z.; Liu, H. Three-line structured light vision system for non-cooperative satellites in proximity operations. Chin. J. Aeronaut. 2020, 33, 1494–1504. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, Z. Multi-view space object recognition and pose estimation based on kernel regression. Chin. J. Aeronaut. 2014, 27, 1233–1241. [Google Scholar] [CrossRef]
- Hu, Y.; Speierer, S.; Jakob, W.; Fua, P.; Salzmann, M. Wide-Depth-Range 6D Object Pose Estimation in Space. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 15865–15874. [Google Scholar]
- Yang, Z.; Yu, X.; Yang, Y. DSC-PoseNet: Learning 6DoF Object Pose Estimation via Dual-scale Consistency. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 3906–3915. [Google Scholar]
- Xu, W.; Yan, L.; Hu, Z.; Liang, B. Area-oriented coordinated trajectory planning of dual-arm space robot for capturing a tumbling target. Chin. J. Aeronaut. 2019, 32, 2151–2163. [Google Scholar] [CrossRef]
- Wang, C.; Xu, D.; Zhu, Y.; Martín-Martín, R.; Lu, C.; Fei-Fei, L.; Savarese, S. DenseFusion: 6D Object Pose Estimation by Iterative Dense Fusion. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 3338–3347. [Google Scholar]
- Ren, H.; Lin, L.; Wang, Y.; Dong, X. Robust 6-DoF Pose Estimation under Hybrid Constraints. Sensors 2022, 22, 8758. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Wang, P.; Wang, F.; Tian, W.; Xiong, L.; Li, H. EPro-PnP: Generalized End-to-End Probabilistic Perspective-n-Points for Monocular Object Pose Estimation. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 2771–2780. [Google Scholar]
- Chen, W.; Jia, X.; Chang, H.J.; Duan, J.; Leonardis, A. G2L-Net: Global to Local Network for Real-Time 6D Pose Estimation with Embedding Vector Features. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 4232–4241. [Google Scholar]
- Wang, H.; Sridhar, S.; Huang, J.; Valentin, J.; Song, S.; Guibas, L.J. Normalized Object Coordinate Space for Category-Level 6D Object Pose and Size Estimation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June; pp. 2637–2646.
- Sharma, S.; Beierle, C.; Amico, S.D. Pose estimation for non-cooperative spacecraft rendezvous using convolutional neural networks. In Proceedings of the 2018 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2018; pp. 1–12. [Google Scholar]
- Xiang, Y.; Schmidt, T.; Narayanan, V.; Fox, D. Posecnn: A convolutional neural network for 6d object pose estimation in cluttered scenes. arXiv 2017, arXiv:1711.00199. [Google Scholar]
- Peng, S.; Liu, Y.; Huang, Q.; Zhou, X.; Bao, H. PVNet: Pixel-Wise Voting Network for 6DoF Pose Estimation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 4556–4565. [Google Scholar]
- Proença, P.F.; Gao, Y. Deep Learning for Spacecraft Pose Estimation from Photorealistic Rendering. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 6007–6013. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
- Huang, R.; Chen, T. Landslide recognition from multi-feature remote sensing data based on improved transformers. Remote Sens. 2023, 15, 3340. [Google Scholar] [CrossRef]
- Zheng, F.; Lin, S.; Zhou, W.; Huang, H. A lightweight dual-branch swin transformer for remote sensing scene classification. Remote Sens. 2023, 15, 2865. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S. An image is worth 16x16 words: Transformers for image recognition at scale. In Proceedings of the 2020 International Conference on Learning Representations(ICLR), Addis Ababa, Ethiopia, 30 April 2020; pp. 1–21. [Google Scholar]
- Xie, T.; Zhang, Z.; Tian, J.; Ma, L. Focal DETR: Target-Aware Token Design for Transformer-Based Object Detection. Sensors 2022, 22, 8686. [Google Scholar] [CrossRef] [PubMed]
- Chauhan, V.K.; Zhou, J.; Lu, P.; Molaei, S.; Clifton, D.A.J.A. A Brief Review of Hypernetworks in Deep Learning. arXiv 2023, arXiv:2306.06955. [Google Scholar]
- Garcia, A.; Musallam, M.A.; Gaudilliere, V.; Ghorbel, E.; Ismaeil, K.A.; Perez, M.; Aouada, D. LSPnet: A 2D Localization-oriented Spacecraft Pose Estimation Neural Network. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Nashville, TN, USA, 19–25 June 2021; pp. 2048–2056. [Google Scholar]
- Park, T.H.; D’Amico, S. Robust multi-task learning and online refinement for spacecraft pose estimation across domain gap. Adv. Space Res. 2023, in press. [Google Scholar] [CrossRef]
- Chen, B.; Cao, J.; Parra, A.; Chin, T.J. Satellite Pose Estimation with Deep Landmark Regression and Nonlinear Pose Refinement. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Republic of Korea, 27–28 October 2019; pp. 2816–2824. [Google Scholar]
- Cosmas, K.; Kenichi, A. Utilization of FPGA for Onboard Inference of Landmark Localization in CNN-Based Spacecraft Pose Estimation. Aerospace 2020, 7, 159. [Google Scholar] [CrossRef]
- Li, K.; Zhang, H.; Hu, C. Learning-Based Pose Estimation of Non-Cooperative Spacecrafts with Uncertainty Prediction. Aerospace 2022, 9, 592. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Z.; Sun, X.; Li, Z.; Yu, Q. Revisiting Monocular Satellite Pose Estimation With Transformer. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 4279–4294. [Google Scholar] [CrossRef]
- Zou, L.; Huang, Z.; Gu, N.; Wang, G. 6D-ViT: Category-Level 6D Object Pose Estimation via Transformer-Based Instance Representation Learning. IEEE Trans. Image Process 2022, 31, 6907–6921. [Google Scholar] [CrossRef]
- Tan, M.; Le, Q. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. In Proceedings of the 36th International Conference on Machine Learning, Proceedings of Machine Learning Research, Long Beach, CA, USA, 9–15 June 2019; pp. 6105–6114. [Google Scholar]
- Shavit, Y.; Ferens, R.; Keller, Y. Learning Multi-Scene Absolute Pose Regression with Transformers. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 10–17 October 2021; pp. 2713–2722. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the ICML’15: Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lille, France, 6–11 July 2015. [Google Scholar]
- Kendall, A.; Cipolla, R. Geometric Loss Functions for Camera Pose Regression with Deep Learning. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6555–6564. [Google Scholar]
- Kendall, A.; Grimes, M.; Cipolla, R. PoseNet: A Convolutional Network for Real-Time 6-DOF Camera Relocalization. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 2938–2946. [Google Scholar]
- Walch, F.; Hazirbas, C.; Leal-Taixé, L.; Sattler, T.; Hilsenbeck, S.; Cremers, D. Image-Based Localization Using LSTMs for Structured Feature Correlation. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 627–637. [Google Scholar]
- Brahmbhatt, S.; Gu, J.; Kim, K.; Hays, J.; Kautz, J. Geometry-Aware Learning of Maps for Camera Localization. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2616–2625. [Google Scholar]
- Kendall, A.; Cipolla, R. Modelling uncertainty in deep learning for camera relocalization. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 4762–4769. [Google Scholar]
- Naseer, T.; Burgard, W. Deep regression for monocular camera-based 6-DoF global localization in outdoor environments. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 1525–1530. [Google Scholar]
- Cai, M.; Shen, C.; Reid, I.D. A hybrid probabilistic model for camera relocalization. In Proceedings of the British Machine Vision Conference, Newcastle upon Tyne, UK, 3–6 September 2018; pp. 1–12. [Google Scholar]
- Shavit, Y.; Ferens, R. Do We Really Need Scene-specific Pose Encoders? In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 3186–3192. [Google Scholar]
- Pepe, A.; Lasenby, J. CGA-PoseNet: Camera Pose Regression via a 1D-Up Approach to Conformal Geometric Algebra. arXiv 2023, arXiv:2302.05211. [Google Scholar]




| MLP Dimensions (Translation/Orientation) | Translation (Meters) | Orientation (Degrees) |
|---|---|---|
| 128/128 | 0.8956 | 6.3023 |
| 128/256 | 0.8735 | 5.8025 |
| 256/256 | 0.8546 | 6.1258 |
| Filterformer Numbers | Translation (Meters) | Orientation (Degrees) | Inference Time (ms) |
|---|---|---|---|
| N = 3 | 1.0125 | 6.5437 | 61.61 |
| N = 4 | 0.9233 | 5.9961 | 64.89 |
| N = 5 | 0.8735 | 5.8025 | 68.11 |
| N = 6 | 0.8155 | 5.3566 | 71.46 |
| N = 7 | 0.7541 | 5.2023 | 74.73 |
| N = 8 | 0.7623 | 5.3562 | 78.01 |
| N = 9 | 0.7496 | 5.3534 | 81.49 |
| Dataset | TransformerPose (Translation/Orientation) | FilterformerPose (Translation/Orientation) |
|---|---|---|
| Soyuz_easy | 0.5103 m, 5.1259° | 0.4918 m, 4.6122° |
| Soyuz_hard | 0.7283 m, 6.3654° | 0.7541 m, 5.2023° |
| Dragon_hard | 0.8076 m, 7.9168° | 0.8160 m, 5.5256° |
| Dataset | Method | Translation (Meters) | Orientation (Degrees) |
|---|---|---|---|
| Soyuz_easy | UrsoNet | 0.5288 | 5.3342 |
| Soyuz_easy | FilterformerPose (ours) | 0.4918 | 4.6122 |
| Soyuz_hard | UrsoNet | 0.8133 | 7.7207 |
| Soyuz_hard | FilterformerPose (ours) | 0.7541 | 5.2023 |
| Dragon_hard | UrsoNet | 0.8909 | 13.9480 |
| Dragon_hard | FilterformerPose (ours) | 0.8160 | 5.5256 |
| Method | K.College | Old Hospital | Shop Facade | St.Mary | Avg. | Ranks |
|---|---|---|---|---|---|---|
| PoseNet [39] | 1.92 m, 5.40° | 2.31 m, 5.38° | 1.46 m, 8.08° | 2.56 m, 8.48° | 2.08 m, 6.83° | 9/10 |
| LSTM-PN [40] | 0.99 m, 3.65° | 1.51 m, 4.29° | 1.18 m, 7.44° | 1.52 m, 6.68° | 1.30 m, 5.57° | 3/8 |
| MapNet [41] | 1.07 m, 1.89° | 1.94 m, 3.91° | 1.49 m, 4.22° | 2.00 m, 4.53° | 1.62 m, 3.64° | 6/5 |
| BayesianPN [42] | 1.74 m, 4.06° | 2.57 m, 5.14° | 1.25 m, 7.54° | 2.11 m, 8.38° | 1.91 m, 6.28° | 7/9 |
| SVS-Pose [43] | 1.06 m, 2.81° | 1.50 m, 4.03° | 0.63 m, 5.73° | 2.11 m, 8.11° | 1.32 m, 5.17° | 4/7 |
| GPoseNet [44] | 1.61 m, 2.29° | 2.62 m, 3.89° | 1.14 m, 5.73° | 2.93 m, 6.46° | 2.07 m, 4.59° | 8/6 |
| IRPNet [45] | 1.18 m, 2.19° | 1.87 m, 3.38° | 0.72 m, 3.47° | 1.87 m, 4.94° | 1.41 m, 3.50° | 5/4 |
| CGA-PoseNet [46] | 1.36 m, 1.85° | 2.52 m, 2.90° | 0.74 m, 5.84° | 2.12 m, 2.97° | 2.84 m, 3.39° | 10/3 |
| MS-Trans [36] | 0.83 m, 1.47° | 1.81 m, 2.39° | 0.86 m, 3.07° | 1.62 m, 3.99° | 1.14 m, 2.73° | 2/1 |
| FilterformerPose (Ours) | 0.67 m, 2.57° | 1.88 m, 3.38° | 0.73 m, 3.59° | 1.08 m, 3.94° | 1.09 m, 3.37° | 1/2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, R.; Wang, L.; Ren, Y.; Wang, Y.; Chen, X.; Liu, Y. FilterformerPose: Satellite Pose Estimation Using Filterformer. Sensors 2023, 23, 8633. https://doi.org/10.3390/s23208633
Ye R, Wang L, Ren Y, Wang Y, Chen X, Liu Y. FilterformerPose: Satellite Pose Estimation Using Filterformer. Sensors. 2023; 23(20):8633. https://doi.org/10.3390/s23208633
Chicago/Turabian StyleYe, Ruida, Lifen Wang, Yuan Ren, Yujing Wang, Xiaocen Chen, and Yufei Liu. 2023. "FilterformerPose: Satellite Pose Estimation Using Filterformer" Sensors 23, no. 20: 8633. https://doi.org/10.3390/s23208633
APA StyleYe, R., Wang, L., Ren, Y., Wang, Y., Chen, X., & Liu, Y. (2023). FilterformerPose: Satellite Pose Estimation Using Filterformer. Sensors, 23(20), 8633. https://doi.org/10.3390/s23208633




