Entropy-Based Machine Learning Model for Fast Diagnosis and Monitoring of Parkinson’s Disease
Abstract
:1. Introduction
- A comparative analysis of the effectiveness of various methods for calculating entropy for identifying PD was carried out;
- The most significant frequency ranges and EEG channels were identified, as well as their combinations;
- A study was conducted to reduce computational costs by selecting the most significant features and reducing the length of the EEG segments analyzed;
- A method of monitoring a patient’s condition based on entropy values was developed;
- We propose a machine learning model for monitoring the health status of Parkinson’s patients using an IoT environment based on low-performance sensors.
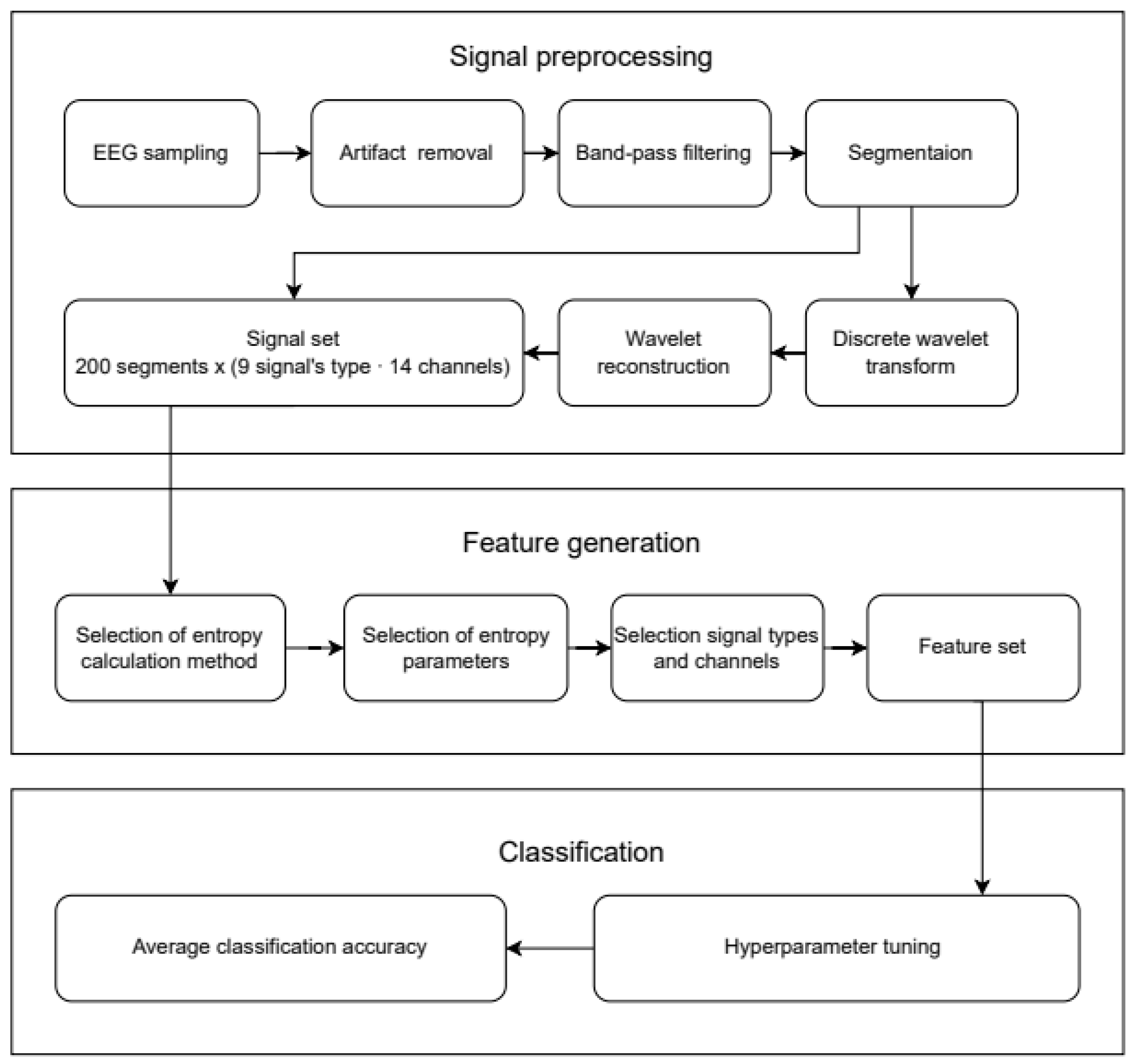
2. Materials and Methods
2.1. Dataset
2.2. Signal Preprocessing
- Original (O) signal; frequency ranges: (0–64 Hz);
- Signals reconstructed based on approximation coefficients (cA1–cA4); frequency ranges: (cA1 (0–32 Hz), cA2 (0–16 Hz), cA3 (0–8 Hz), cA4 (0–4 Hz));
- Signals reconstructed based on detail coefficients (cD1–cD4); frequency ranges: (cD1 (32–64 Hz), cD2 (16–32 Hz), cD3 (8–16 Hz), cD4 (4–8 Hz)).
2.3. Feature Generation
2.3.1. SVDEn
2.3.2. PermEn
2.3.3. SampEn
2.3.4. CoSiEn
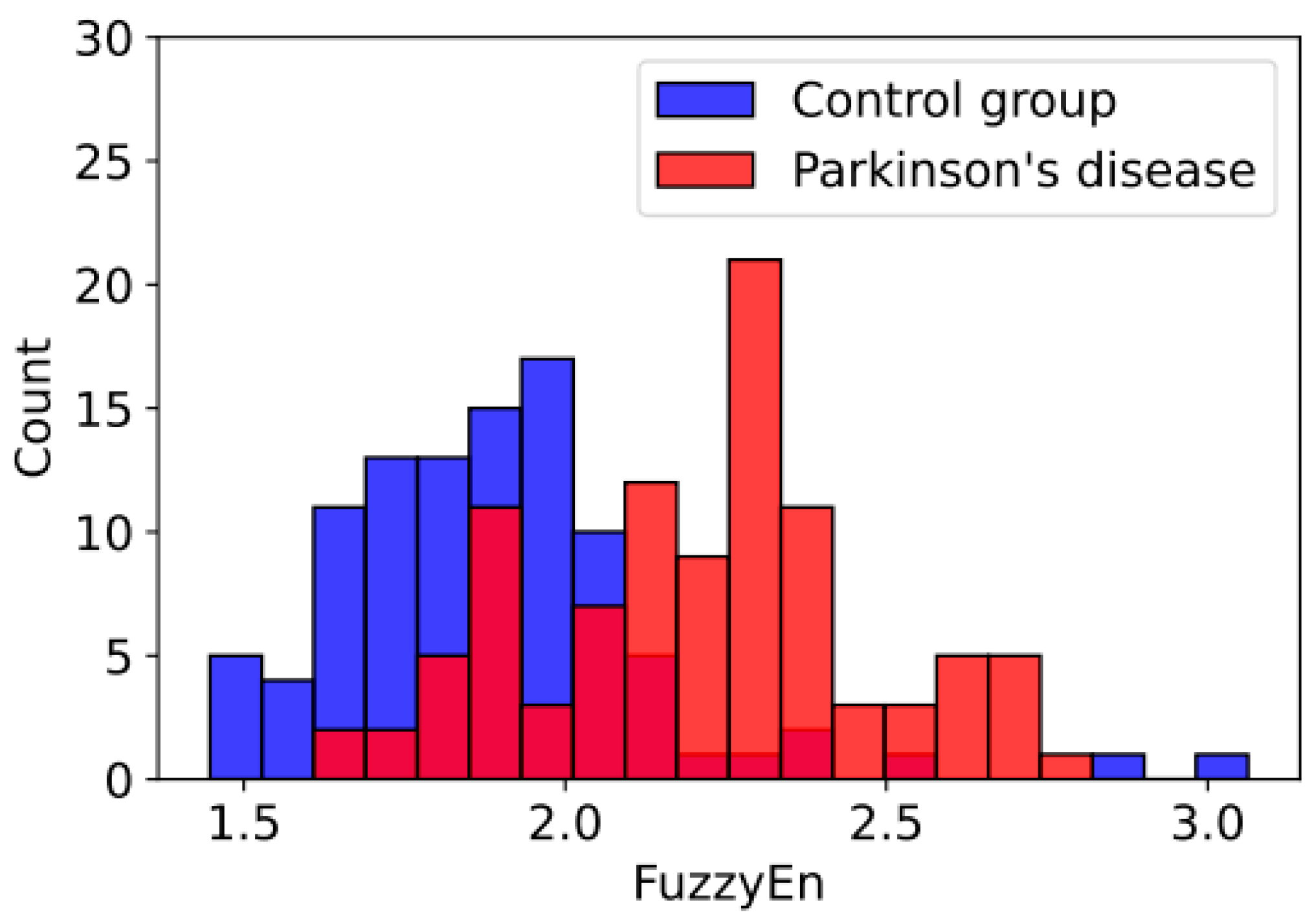
2.3.5. FuzzyEn
2.3.6. PhaseEn
2.3.7. AttnEn
2.4. Assessment of Classification Accuracy
3. Experimental Results and Discussion
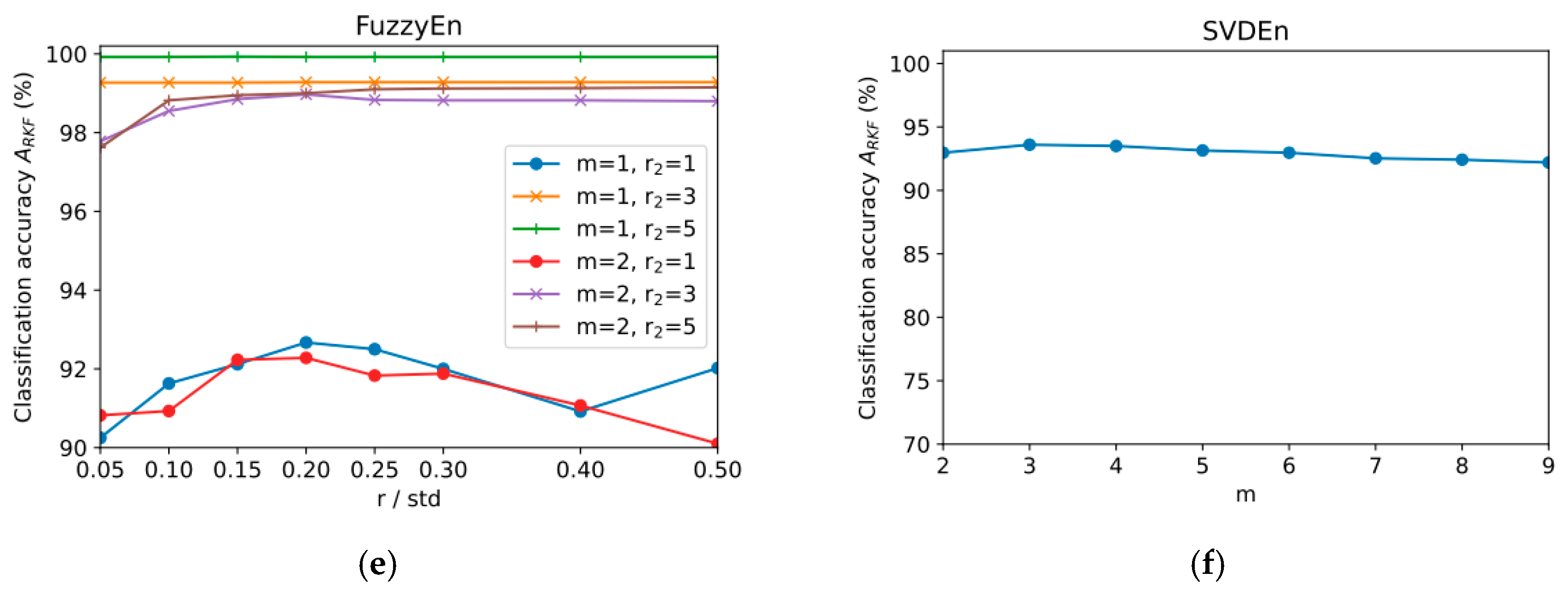
3.1. Classification Accuracy Using One Method for Calculating the Entropy
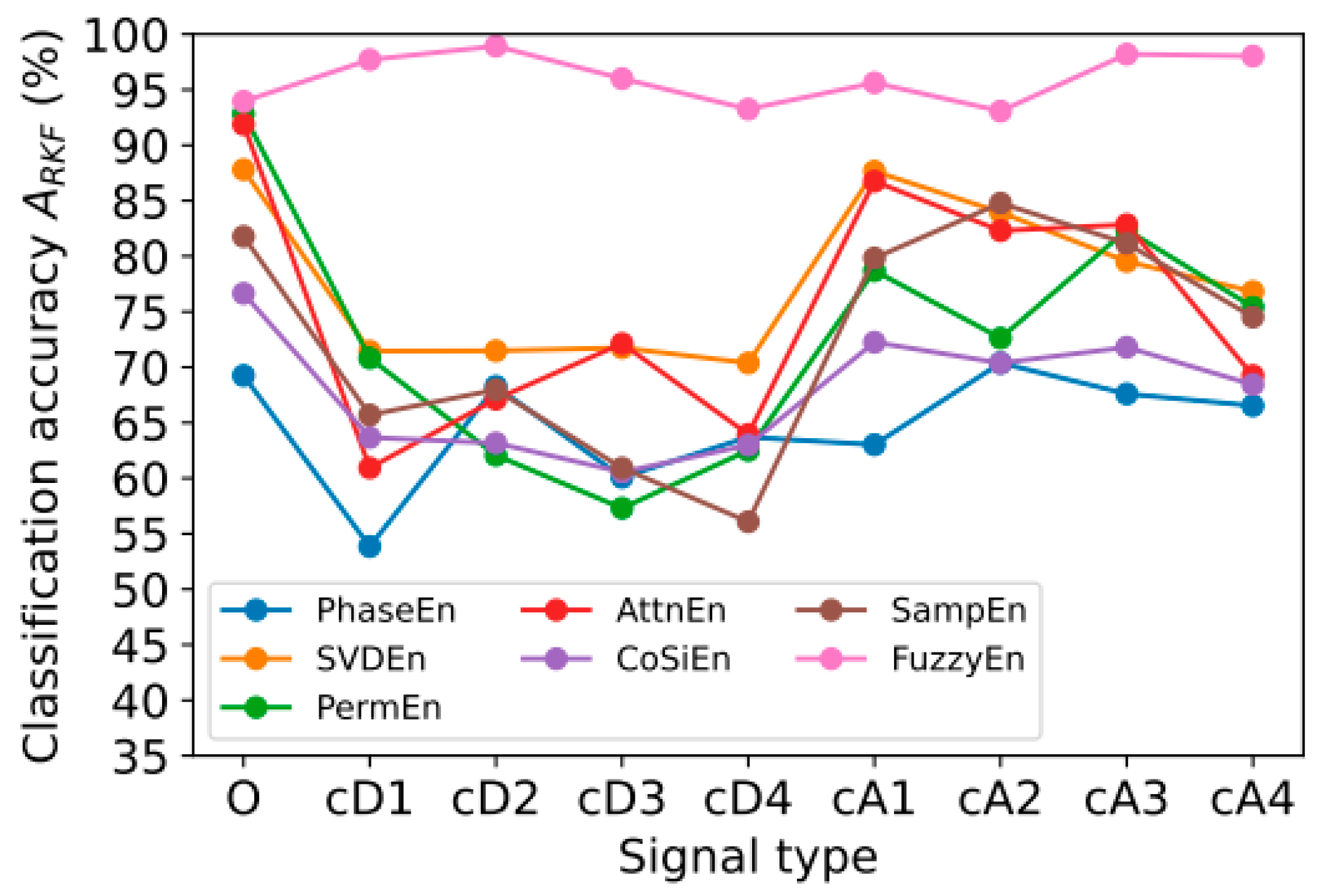
3.2. Classification Accuracy Using One Type of Signal
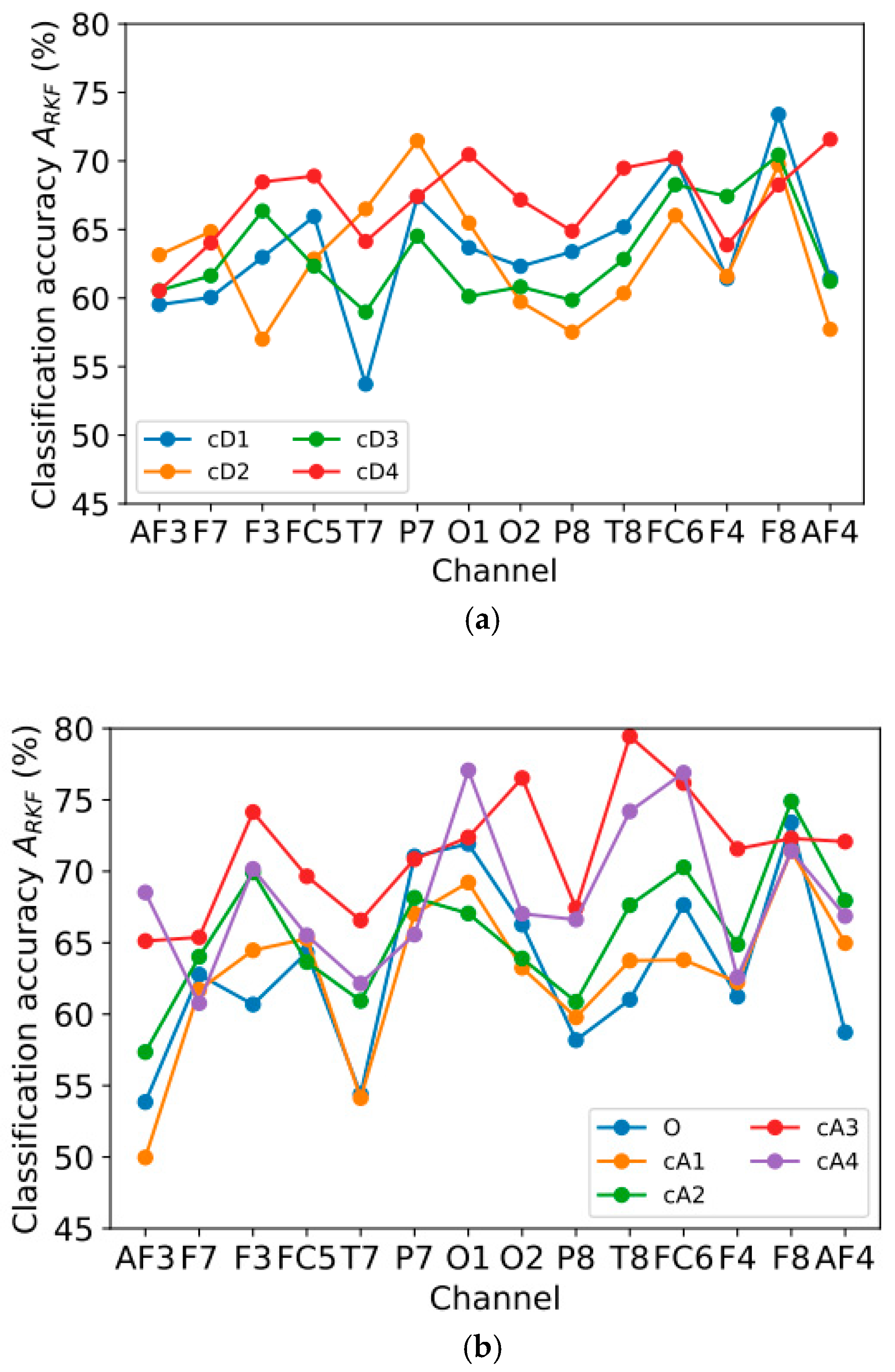
3.3. Classification Accuracy Using a Single Channel
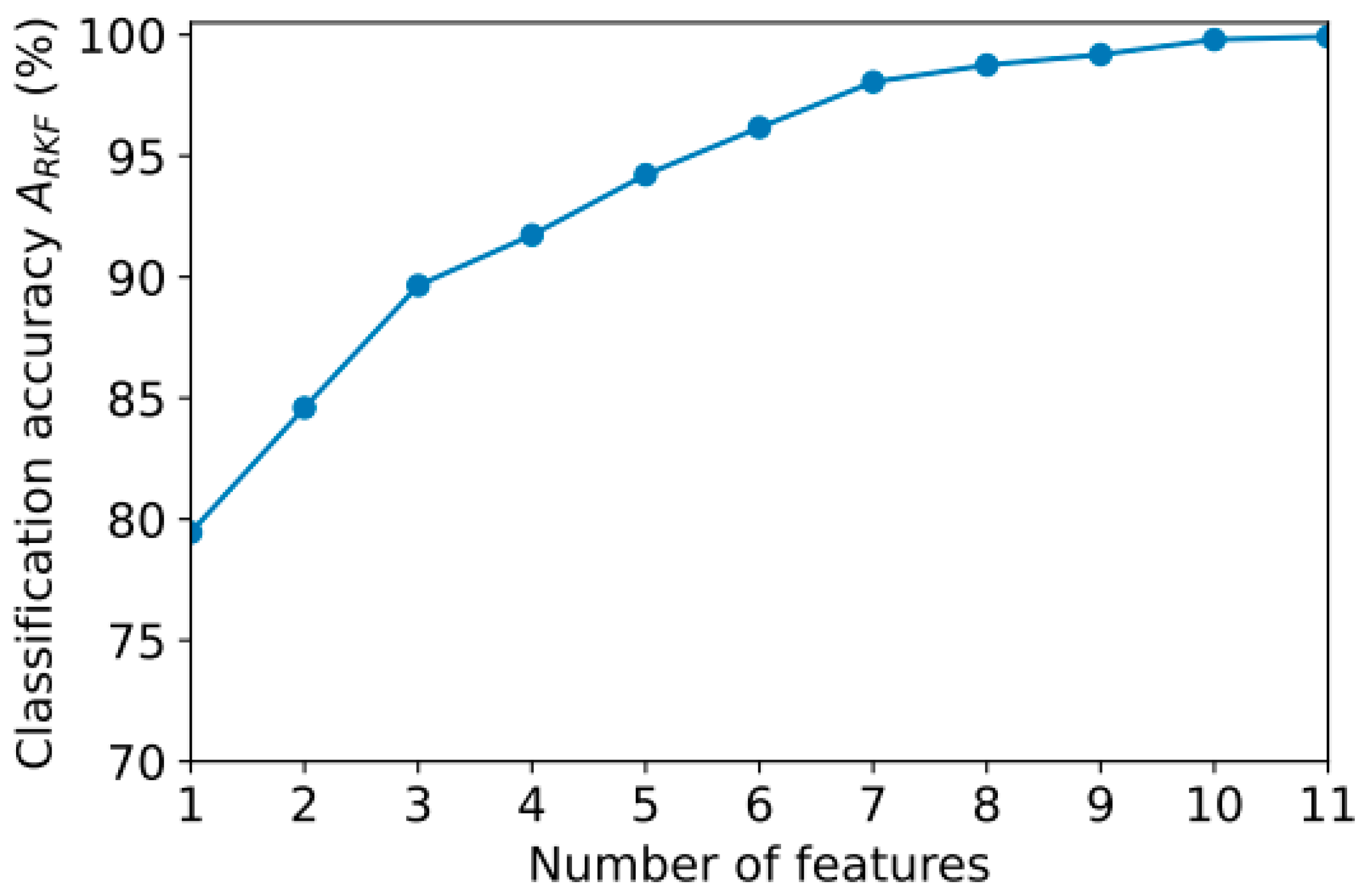
3.4. Classification Accuracy Using One Feature
- Group 1 consists of signals based on detail wavelet coefficients, as follows: cD1 (32–64 Hz), cD2 (16–32 Hz), cD3 (8–16 Hz), and cD4 (4–8 Hz);
- Group 2 consists of the original signal and signals based on approximation wavelet coefficients, as follows: O (0–64 Hz), cA1 (0–32 Hz), cA2 (0–16 Hz), cA3 (0–8 Hz), and cA4 (0–4 Hz).
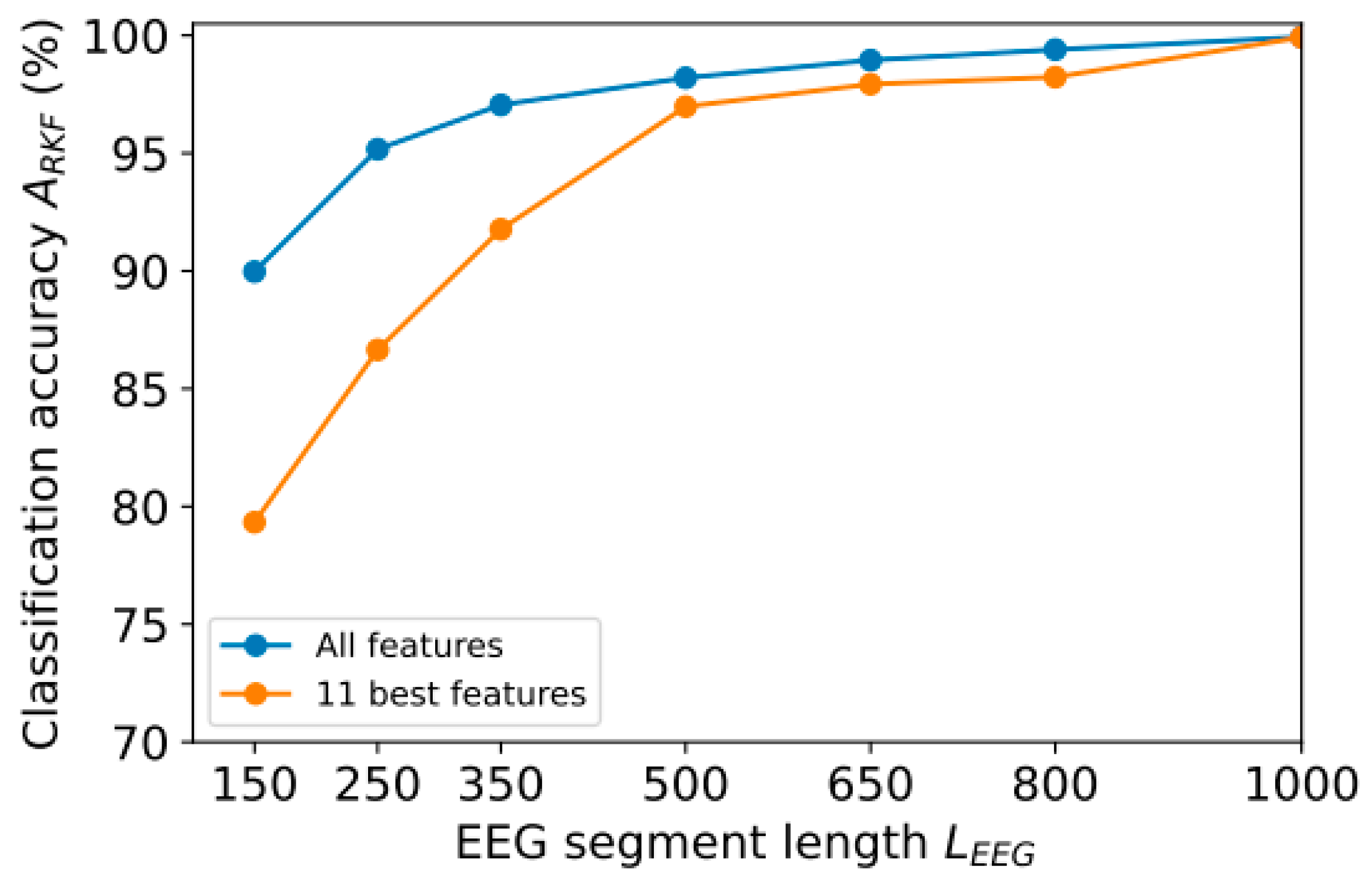
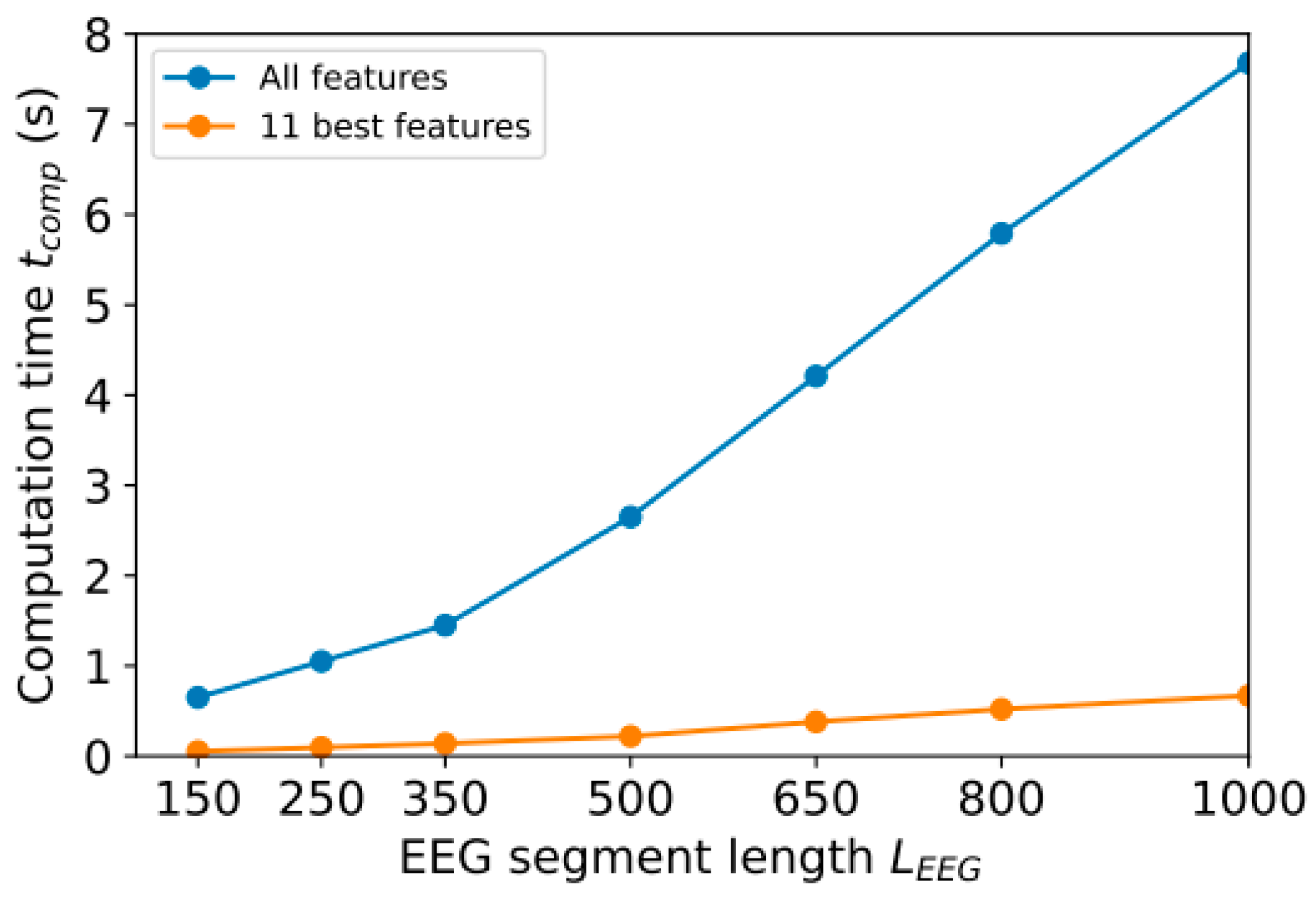
4. Model Optimization
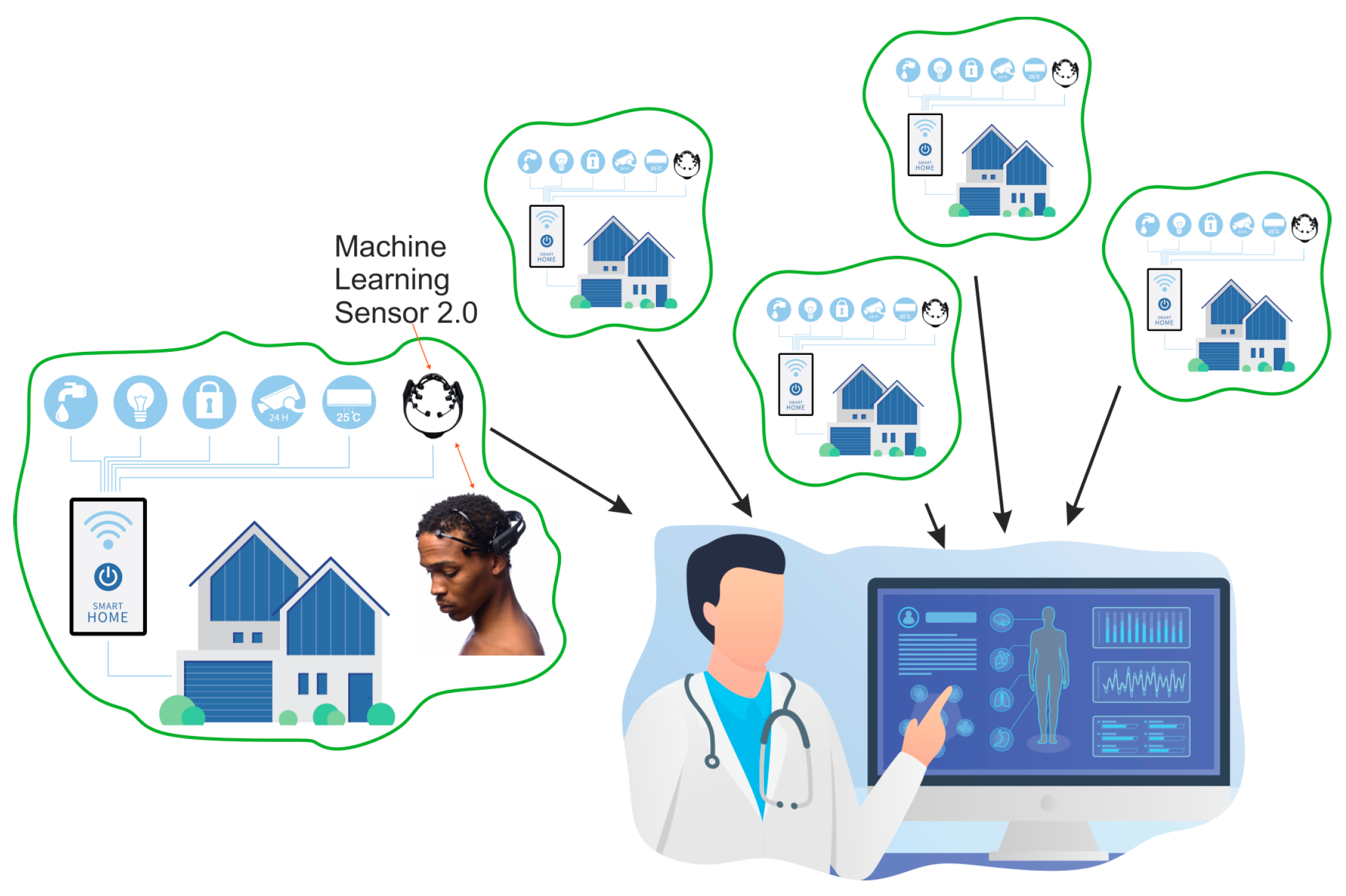
5. Future Work: Smart IoT Environment Concept for Patient Health Monitoring
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Health Organization. Aging and Health. Available online: https://www.who.int/news-room/fact-sheets/detail/ageing-and-health (accessed on 1 June 2023).
- Mayne, K.; White, J.A.; McMurran, C.E.; Rivera, F.J.; de la Fuente, A.G. Aging and Neurodegenerative Disease: Is the Adaptive Immune System a Friend or Foe? Front. Aging Neurosci. 2020, 12, 572090. [Google Scholar] [CrossRef] [PubMed]
- Hou, Y.; Dan, X.; Babbar, M.; Wei, Y.; Hasselbalch, S.G.; Croteau, D.L.; Bohr, V.A. Ageing as a risk factor for neurodegenerative disease. Nat. Rev. Neurol. 2019, 15, 565–581. [Google Scholar] [CrossRef] [PubMed]
- Erkkinen, M.G.; Kim, M.-O.; Geschwind, M.D. Clinical Neurology and Epidemiology of the Major Neurodegenerative Diseases. Cold Spring Harb. Perspect. Biol. 2018, 10, a033118. [Google Scholar] [CrossRef] [PubMed]
- Gomez, C.; Chessa, S.; Fleury, A.; Roussos, G.; Preuveneers, D. Internet of Things for enabling smart environments: A technology-centric perspective. J. Ambient Intell. Smart Environ. 2019, 11, 23–43. [Google Scholar] [CrossRef]
- Cook, D.J.; Das, S.K. How smart are our environments? An updated look at the state of the art. Pervasive Mob. Comput. 2007, 3, 53–73. [Google Scholar] [CrossRef]
- Gopi, R.; Veena, S.; Balasubramanian, S.; Ramya, D.; Ilanchezhian, P.; Harshavardhan, A.; Gupta, Z. IoT Based Disease Prediction Using Mapreduce and LSQN3 Techniques. Intell. Autom. Soft Comput. 2022, 34, 1215–1230. [Google Scholar] [CrossRef]
- Mohammed, M.N.; Desyansah, S.F.; Al-Zubaidi, S.; Yusuf, E. An internet of things-based smart homes and healthcare monitoring and management system: Review. J. Phys. Conf. Ser. 2020, 1450, 012079. [Google Scholar] [CrossRef]
- Korzun, D.G. Internet of Things Meets Mobile Health Systems in Smart Spaces: An Overview BT—Internet of Things and Big Data Technologies for Next Generation Healthcare; Bhatt, C., Dey, N., Ashour, A.S., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 111–129. ISBN 978-3-319-49736-5. [Google Scholar]
- Kumar, M.; Kumar, A.; Verma, S.; Bhattacharya, P.; Ghimire, D.; Kim, S.; Hosen, A.S.M.S. Healthcare Internet of Things (H-IoT): Current Trends, Future Prospects, Applications, Challenges, and Security Issues. Electronics 2023, 12, 2050. [Google Scholar] [CrossRef]
- Avinashiappan, A.; Mayilsamy, B. Internet of Medical Things: Security Threats, Security Challenges, and Potential Solutions BT—Internet of Medical Things: Remote Healthcare Systems and Applications; Hemanth, D.J., Anitha, J., Tsihrintzis, G.A., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 1–16. ISBN 978-3-030-63937-2. [Google Scholar]
- Velichko, A.; Huyut, M.T.; Belyaev, M.; Izotov, Y.; Korzun, D. Machine Learning Sensors for Diagnosis of COVID-19 Disease Using Routine Blood Values for Internet of Things Application. Sensors 2022, 22, 7886. [Google Scholar] [CrossRef] [PubMed]
- Pang, T.; Zhao, X.; He, X.; Kan, C.N.; Venketasubramanian, N.; Cheng, C.-Y.; Yuan, C.; Chen, C.; Xu, X. The discriminant validity of single-question assessments of subjective cognitive complaints in an Asian older adult population. Front. Aging Neurosci. 2022, 14, 901592. [Google Scholar] [CrossRef]
- Parnetti, L.; Gaetani, L.; Eusebi, P.; Paciotti, S.; Hansson, O.; El-Agnaf, O.; Mollenhauer, B.; Blennow, K.; Calabresi, P. CSF and blood biomarkers for Parkinson’s disease. Lancet Neurol. 2019, 18, 573–586. [Google Scholar] [CrossRef] [PubMed]
- Ma, W.; Li, M.; Wu, J.; Zhang, Z.; Jia, F.; Zhang, M.; Bergman, H.; Li, X.; Ling, Z.; Xu, X. Multiple step saccades in simply reactive saccades could serve as a complementary biomarker for the early diagnosis of Parkinson’s disease. Front. Aging Neurosci. 2022, 14, 912967. [Google Scholar] [CrossRef] [PubMed]
- Ali, N.; Liu, J.; Tian, H.; Pan, W.; Tang, Y.; Zhong, Q.; Gao, Y.; Xiao, M.; Wu, H.; Sun, C.; et al. A novel dual-task paradigm with story recall shows significant differences in the gait kinematics in older adults with cognitive impairment: A cross-sectional study. Front. Aging Neurosci. 2022, 14, 992873. [Google Scholar] [CrossRef]
- Rossini, P.M.; Di Iorio, R.; Vecchio, F.; Anfossi, M.; Babiloni, C.; Bozzali, M.; Bruni, A.C.; Cappa, S.F.; Escudero, J.; Fraga, F.J.; et al. Early diagnosis of Alzheimer’s disease: The role of biomarkers including advanced EEG signal analysis. Report from the IFCN-sponsored panel of experts. Clin. Neurophysiol. 2020, 131, 1287–1310. [Google Scholar] [CrossRef] [PubMed]
- Giannakopoulou, K.-M.; Roussaki, I.; Demestichas, K. Internet of Things Technologies and Machine Learning Methods for Parkinson’s Disease Diagnosis, Monitoring and Management: A Systematic Review. Sensors 2022, 22, 1799. [Google Scholar] [CrossRef] [PubMed]
- Savadkoohi, M.; Oladunni, T.; Thompson, L. A machine learning approach to epileptic seizure prediction using Electroencephalogram (EEG) Signal. Biocybern. Biomed. Eng. 2020, 40, 1328–1341. [Google Scholar] [CrossRef] [PubMed]
- Samiee, K.; Kovacs, P.; Gabbouj, M. Epileptic Seizure Classification of EEG Time-Series Using Rational Discrete Short-Time Fourier Transform. IEEE Trans. Biomed. Eng. 2015, 62, 541–552. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, Z.; Frounchi, J.; Amiri, M. Wavelet-based emotion recognition system using EEG signal. Neural Comput. Appl. 2017, 28, 1985–1990. [Google Scholar] [CrossRef]
- Lopes da Silva, F. Neural mechanisms underlying brain waves: From neural membranes to networks. Electroencephalogr. Clin. Neurophysiol. 1991, 79, 81–93. [Google Scholar] [CrossRef]
- Nawaz, R.; Cheah, K.H.; Nisar, H.; Yap, V.V. Comparison of different feature extraction methods for EEG-based emotion recognition. Biocybern. Biomed. Eng. 2020, 40, 910–926. [Google Scholar] [CrossRef]
- Stancin, I.; Cifrek, M.; Jovic, A. A Review of EEG Signal Features and Their Application in Driver Drowsiness Detection Systems. Sensors 2021, 21, 3786. [Google Scholar] [CrossRef]
- Boonyakitanont, P.; Lek-uthai, A.; Chomtho, K.; Songsiri, J. A review of feature extraction and performance evaluation in epileptic seizure detection using EEG. Biomed. Signal Process. Control 2020, 57, 101702. [Google Scholar] [CrossRef]
- Maitín, A.M.; García-Tejedor, A.J.; Muñoz, J.P.R. Machine Learning Approaches for Detecting Parkinson’s Disease from EEG Analysis: A Systematic Review. Appl. Sci. 2020, 10, 8662. [Google Scholar] [CrossRef]
- Myszczynska, M.A.; Ojamies, P.N.; Lacoste, A.M.B.; Neil, D.; Saffari, A.; Mead, R.; Hautbergue, G.M.; Holbrook, J.D.; Ferraiuolo, L. Applications of machine learning to diagnosis and treatment of neurodegenerative diseases. Nat. Rev. Neurol. 2020, 16, 440–456. [Google Scholar] [CrossRef]
- Yuvaraj, R.; Rajendra Acharya, U.; Hagiwara, Y. A novel Parkinson’s Disease Diagnosis Index using higher-order spectra features in EEG signals. Neural Comput. Appl. 2018, 30, 1225–1235. [Google Scholar] [CrossRef]
- Khare, S.K.; Bajaj, V.; Acharya, U.R. Detection of Parkinson’s disease using automated tunable Q wavelet transform technique with EEG signals. Biocybern. Biomed. Eng. 2021, 41, 679–689. [Google Scholar] [CrossRef]
- Jeong, D.-H.; Kim, Y.-D.; Song, I.-U.; Chung, Y.-A.; Jeong, J. Wavelet Energy and Wavelet Coherence as EEG Biomarkers for the Diagnosis of Parkinson’s Disease-Related Dementia and Alzheimer’s Disease. Entropy 2015, 18, 8. [Google Scholar] [CrossRef]
- Aljalal, M.; Aldosari, S.A.; Molinas, M.; AlSharabi, K.; Alturki, F.A. Detection of Parkinson’s disease from EEG signals using discrete wavelet transform, different entropy measures, and machine learning techniques. Sci. Rep. 2022, 12, 22547. [Google Scholar] [CrossRef]
- Aoki, Y.; Takahashi, R.; Suzuki, Y.; Pascual-Marqui, R.D.; Kito, Y.; Hikida, S.; Maruyama, K.; Hata, M.; Ishii, R.; Iwase, M.; et al. EEG resting-state networks in Alzheimer’s disease associated with clinical symptoms. Sci. Rep. 2023, 13, 3964. [Google Scholar] [CrossRef] [PubMed]
- Han, C.-X.; Wang, J.; Yi, G.-S.; Che, Y.-Q. Investigation of EEG abnormalities in the early stage of Parkinson’s disease. Cogn. Neurodyn. 2013, 7, 351–359. [Google Scholar] [CrossRef] [PubMed]
- Oh, S.L.; Hagiwara, Y.; Raghavendra, U.; Yuvaraj, R.; Arunkumar, N.; Murugappan, M.; Acharya, U.R. A deep learning approach for Parkinson’s disease diagnosis from EEG signals. Neural Comput. Appl. 2020, 32, 10927–10933. [Google Scholar] [CrossRef]
- Bhurane, A.A.; Dhok, S.; Sharma, M.; Yuvaraj, R.; Murugappan, M.; Acharya, U.R. Diagnosis of Parkinson’s disease from electroencephalography signals using linear and self-similarity features. Expert Syst. 2022, 39, e12472. [Google Scholar] [CrossRef]
- Miltiadous, A.; Tzimourta, K.D.; Giannakeas, N.; Tsipouras, M.G.; Afrantou, T.; Ioannidis, P.; Tzallas, A.T. Alzheimer’s disease and frontotemporal dementia: A robust classification method of EEG signals and a comparison of validation methods. Diagnostics 2021, 11, 1437. [Google Scholar] [CrossRef] [PubMed]
- van der Zande, J.J.; Gouw, A.A.; van Steenoven, I.; Scheltens, P.; Stam, C.J.; Lemstra, A.W. EEG Characteristics of Dementia with Lewy Bodies, Alzheimer’s Disease and Mixed Pathology. Front. Aging Neurosci. 2018, 10, 190. [Google Scholar] [CrossRef] [PubMed]
- Faiman, I.; Smith, S.; Hodsoll, J.; Young, A.H.; Shotbolt, P. Resting-state EEG for the diagnosis of idiopathic epilepsy and psychogenic nonepileptic seizures: A systematic review. Epilepsy Behav. 2021, 121, 108047. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Parkinson Disease. Available online: https://www.who.int/news-room/fact-sheets/detail/parkinson-disease (accessed on 1 June 2023).
- Yuvaraj, R.; Murugappan, M.; Omar, M.I.; Ibrahim, N.M.; Sundaraj, K.; Mohamad, K.; Satiyan, M. Emotion processing in Parkinson’s disease: An EEG spectral power study. Int. J. Neurosci. 2014, 124, 491–502. [Google Scholar] [CrossRef] [PubMed]
- Yuvaraj, R.; Murugappan, M.; Palaniappan, R. The Effect of Lateralization of Motor Onset and Emotional Recognition in PD Patients Using EEG. Brain Topogr. 2017, 30, 333–342. [Google Scholar] [CrossRef] [PubMed]
- Dar, M.N.; Akram, M.U.; Yuvaraj, R.; Gul Khawaja, S.; Murugappan, M. EEG-based emotion charting for Parkinson’s disease patients using Convolutional Recurrent Neural Networks and cross dataset learning. Comput. Biol. Med. 2022, 144, 105327. [Google Scholar] [CrossRef]
- Wang, T.; Guan, S.-U.; Man, K.L.; Ting, T.O. EEG Eye State Identification Using Incremental Attribute Learning with Time-Series Classification. Math. Probl. Eng. 2014, 2014, 365101. [Google Scholar] [CrossRef]
- Başar, E.; Başar-Eroglu, C.; Karakaş, S.; Schürmann, M. Gamma, alpha, delta, and theta oscillations govern cognitive processes. Int. J. Psychophysiol. 2001, 39, 241–248. [Google Scholar] [CrossRef] [PubMed]
- Başar, E.; Güntekin, B. Review of delta, theta, alpha, beta, and gamma response oscillations in neuropsychiatric disorders. Suppl. Clin. Neurophysiol. 2013, 62, 303–341. [Google Scholar] [PubMed]
- Murugappan, M.; Baharuddin, N.Q.I.; Jerritta, S. DWT and MFCC based human emotional speech classification using LDA. In Proceedings of the 2012 International Conference on Biomedical Engineering (ICoBE), Penang, Malaysia, 27–28 February 2012; pp. 203–206. [Google Scholar]
- Li, S.; Yang, M.; Li, C.; Cai, P. Analysis of heart rate variability based on singular value decomposition entropy. J. Shanghai Univ. 2008, 12, 433–437. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation Entropy: A Natural Complexity Measure for Time Series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Chanwimalueang, T.; Mandic, D. Cosine Similarity Entropy: Self-Correlation-Based Complexity Analysis of Dynamical Systems. Entropy 2017, 19, 652. [Google Scholar] [CrossRef]
- Xie, H.-B.; Chen, W.-T.; He, W.-X.; Liu, H. Complexity analysis of the biomedical signal using fuzzy entropy measurement. Appl. Soft Comput. 2011, 11, 2871–2879. [Google Scholar] [CrossRef]
- Rohila, A.; Sharma, A. Phase entropy: A new complexity measure for heart rate variability. Physiol. Meas. 2019, 40, 105006. [Google Scholar] [CrossRef]
- Yang, J.; Choudhary, G.I.; Rahardja, S.; Fränti, P. Classification of Interbeat Interval Time-Series Using Attention Entropy. IEEE Trans. Affect. Comput. 2023, 14, 321–330. [Google Scholar] [CrossRef]
- Flood, M.W.; Grimm, B. EntropyHub: An open-source toolkit for entropic time series analysis. PLoS ONE 2021, 16, e0259448. [Google Scholar] [CrossRef] [PubMed]
- Vallat, R. AntroPy: Entropy and Complexity of (EEG) Time-Series in Python. Available online: https://github.com/raphaelvallat/antropy (accessed on 1 June 2023).
- Kim, J.-H. Estimating classification error rate: Repeated cross-validation, repeated hold-out and bootstrap. Comput. Stat. Data Anal. 2009, 53, 3735–3745. [Google Scholar] [CrossRef]
- Meigal, A.Y.; Korzun, D.G.; Moschevikin, A.P.; Reginya, S.; Gerasimova-Meigal, L.I. Ambient Assisted Living At-Home Laboratory for Motor Status Diagnostics in Parkinson’s Disease Patients and Aged People. In Research Anthology on Supporting Healthy Aging in a Digital Society; IGI Global: Hershey, PA, USA, 2022; pp. 836–862. [Google Scholar] [CrossRef]
- Machine Learning Sensors: Truly Data-Centric AI|Towards Data Science. Available online: https://towardsdatascience.com/machine-learning-sensors-truly-data-centric-ai-8f6b9904633a (accessed on 23 August 2022).
- Warden, P.; Stewart, M.; Plancher, B.; Banbury, C.; Prakash, S.; Chen, E.; Asgar, Z.; Katti, S.; Reddi, V.J. Machine Learning Sensors. arXiv 2022, arXiv:2206.03266. [Google Scholar] [CrossRef]
- Peng, Y.; Zhao, W.; Cai, W.; Su, J.; Han, B.; Liu, Q. Evaluating deep learning for image classification in adversarial environment. IEICE Trans. Inf. Syst. 2020, E103D, 825–837. [Google Scholar] [CrossRef]
- Ehatisham-Ul-Haq, M.; Javed, A.; Azam, M.A.; Malik, H.M.A.; Irtaza, A.; Lee, I.H.; Mahmood, M.T. Robust Human Activity Recognition Using Multimodal Feature-Level Fusion. IEEE Access 2019, 7, 60736–60751. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, P.; Zhang, Y.; Miyazaki, K. Gait Analysis Using Stereo Camera in Daily Environment. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1471–1475. [Google Scholar]
- Ballard, Z.; Brown, C.; Madni, A.M.; Ozcan, A. Machine learning and computation-enabled intelligent sensor design. Nat. Mach. Intell. 2021, 3, 556–565. [Google Scholar] [CrossRef]
- Chinchole, S.; Patel, S. Artificial intelligence and sensors based assistive system for the visually impaired people. In Proceedings of the 2017 International Conference on Intelligent Sustainable Systems (ICISS), Palladam, India, 7–8 December 2017; pp. 16–19. [Google Scholar]
- Gulzar Ahmad, S.; Iqbal, T.; Javaid, A.; Ullah Munir, E.; Kirn, N.; Ullah Jan, S.; Ramzan, N. Sensing and Artificial Intelligent Maternal-Infant Health Care Systems: A Review. Sensors 2022, 22, 4362. [Google Scholar] [CrossRef] [PubMed]



| Entropy Name | Parameter Range |
|---|---|
| SVDEn | order m = 2…10, delay = 1 |
| PermEn | order m = 2…10, delay = 1 |
| SampEn | order m = 1…3, tolerance r = 0.05…0.5 × std |
| CoSiEn | order m = 2…3, tolerance r = 0.05…0.5 |
| FuzzyEn | order m = 1…2, tolerance r = 0.05…0.5 × std, exponent membership function of order r2 = 1…5 |
| PhaseEn | K = 2…10 |
| AttnEn | no parameters |
| Channel | Signal Type | ARKF, % |
|---|---|---|
| T8 | cA3 | 79.5 |
| O1 | cA4 | 77.1 |
| FC6 | cA4 | 76.9 |
| O2 | cA3 | 76.5 |
| FC6 | cA3 | 76.2 |
| F8 | cA2 | 74.9 |
| T8 | cA4 | 74.2 |
| F3 | cA3 | 74.2 |
| F8 | O | 73.4 |
| F8 | cD1 | 73.4 |
| O1 | cA3 | 72.4 |
| F8 | cA3 | 72.3 |
| AF4 | cA3 | 72.1 |
| O1 | O | 71.9 |
| AF4 | cD4 | 71.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belyaev, M.; Murugappan, M.; Velichko, A.; Korzun, D. Entropy-Based Machine Learning Model for Fast Diagnosis and Monitoring of Parkinson’s Disease. Sensors 2023, 23, 8609. https://doi.org/10.3390/s23208609
Belyaev M, Murugappan M, Velichko A, Korzun D. Entropy-Based Machine Learning Model for Fast Diagnosis and Monitoring of Parkinson’s Disease. Sensors. 2023; 23(20):8609. https://doi.org/10.3390/s23208609
Chicago/Turabian StyleBelyaev, Maksim, Murugappan Murugappan, Andrei Velichko, and Dmitry Korzun. 2023. "Entropy-Based Machine Learning Model for Fast Diagnosis and Monitoring of Parkinson’s Disease" Sensors 23, no. 20: 8609. https://doi.org/10.3390/s23208609
APA StyleBelyaev, M., Murugappan, M., Velichko, A., & Korzun, D. (2023). Entropy-Based Machine Learning Model for Fast Diagnosis and Monitoring of Parkinson’s Disease. Sensors, 23(20), 8609. https://doi.org/10.3390/s23208609









