Improved Calibration of Eye-in-Hand Robotic Vision System Based on Binocular Sensor
Abstract
:1. Introduction
- (1)
- A circle of confusion rectification method is proposed. The position of the pixel is rectified based on the Gaussian energy distribution model to obtain a geometric feature close to the real one and improve the accuracy of the 3D reconstruction of the binocular sensor.
- (2)
- Based on the strong geometric constraint of the standard multi-target reference calibrator on the observed error, a transformation correction method is developed. The observed error is introduced to the calibration matrix updating model, and the observed error is constrained according to the standard geometric relationship of the calibrator.
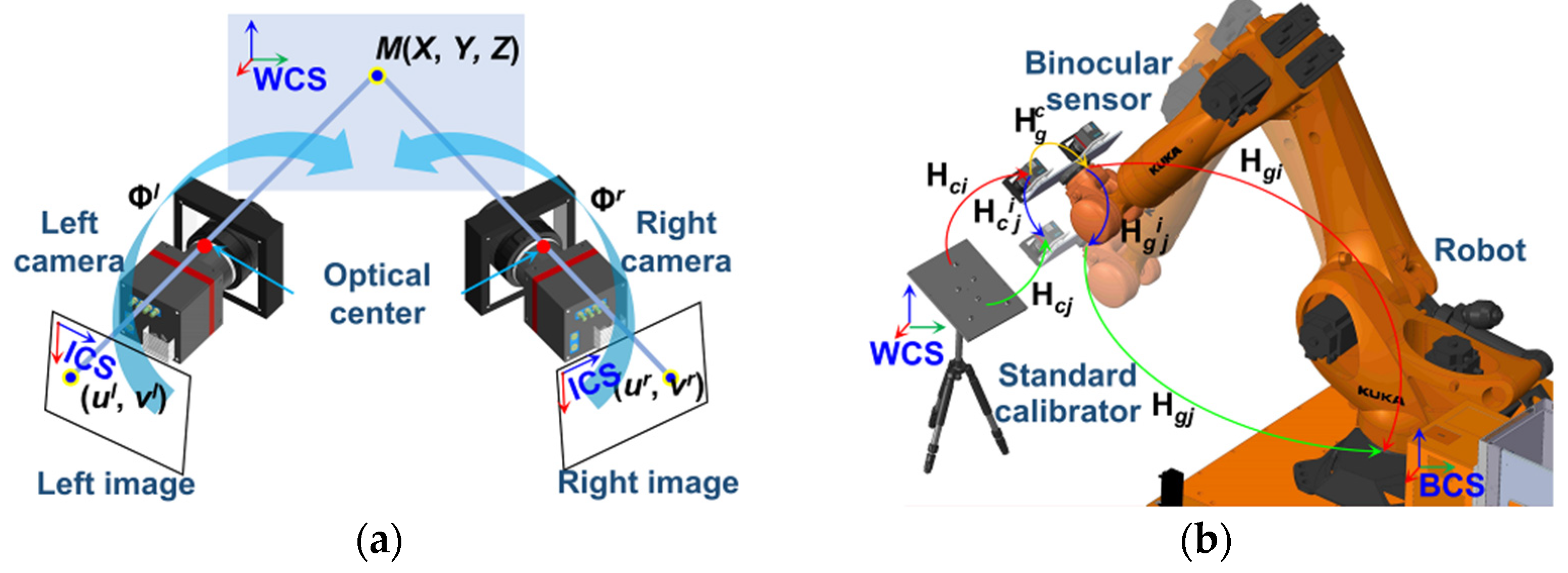
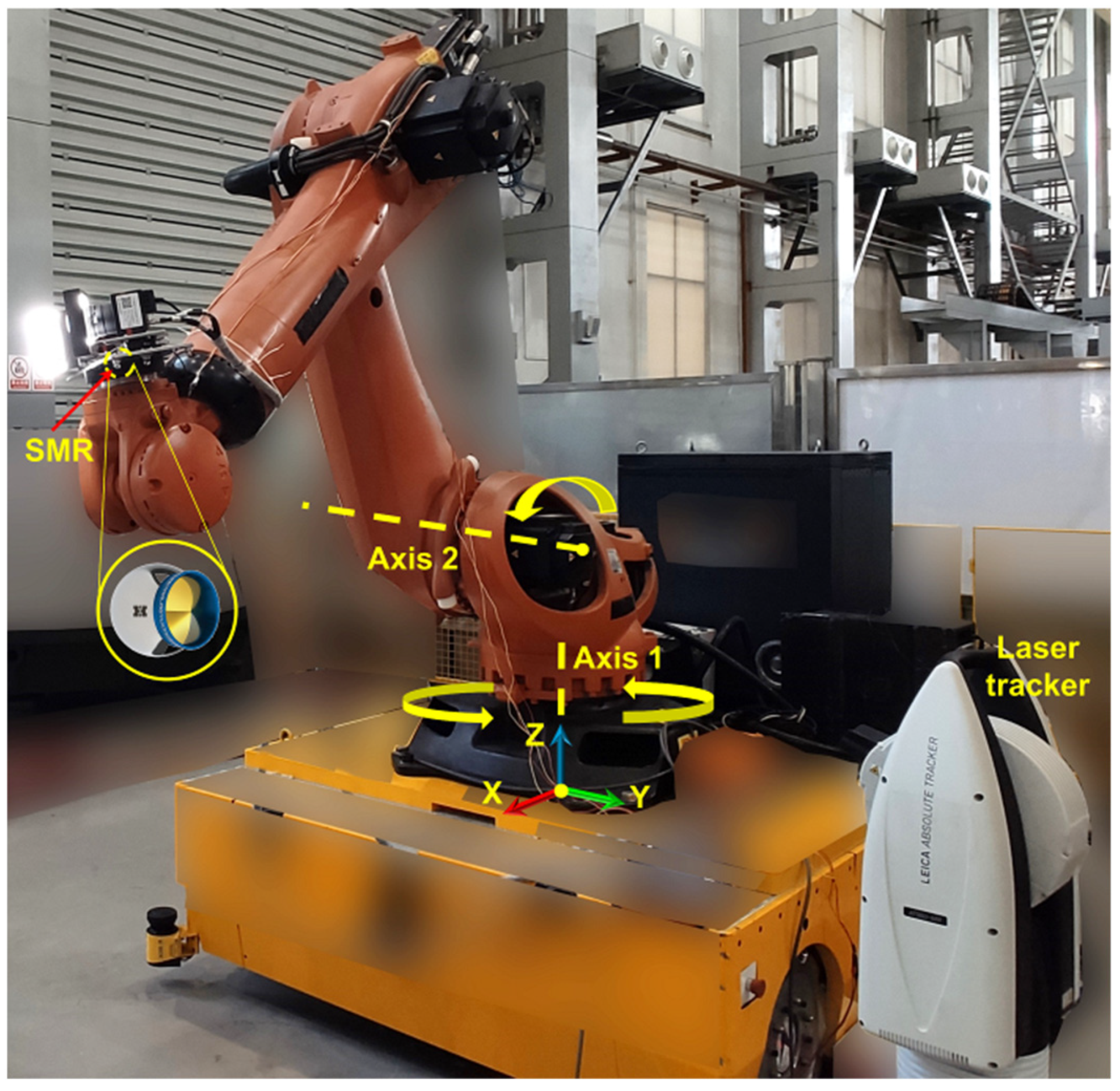
2. System Description
3. Improved Calibration Method
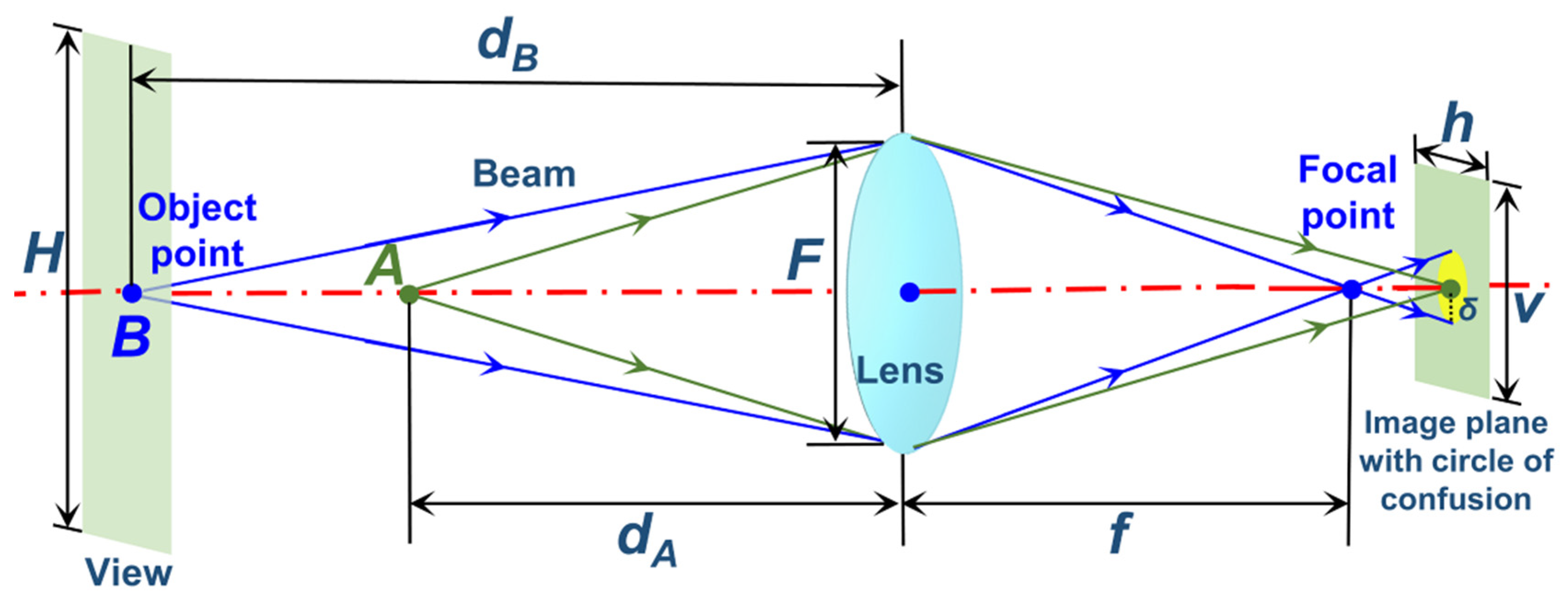
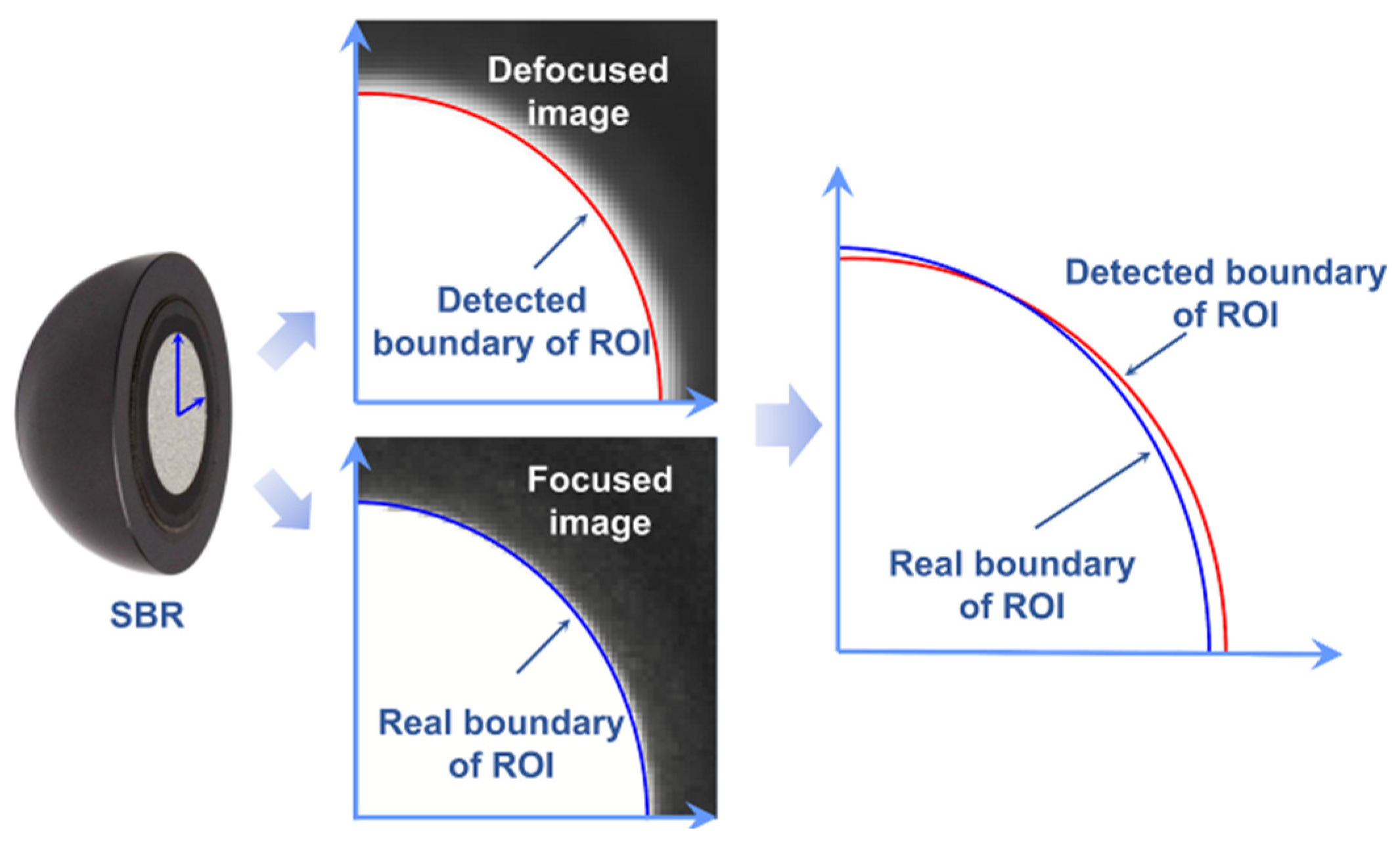
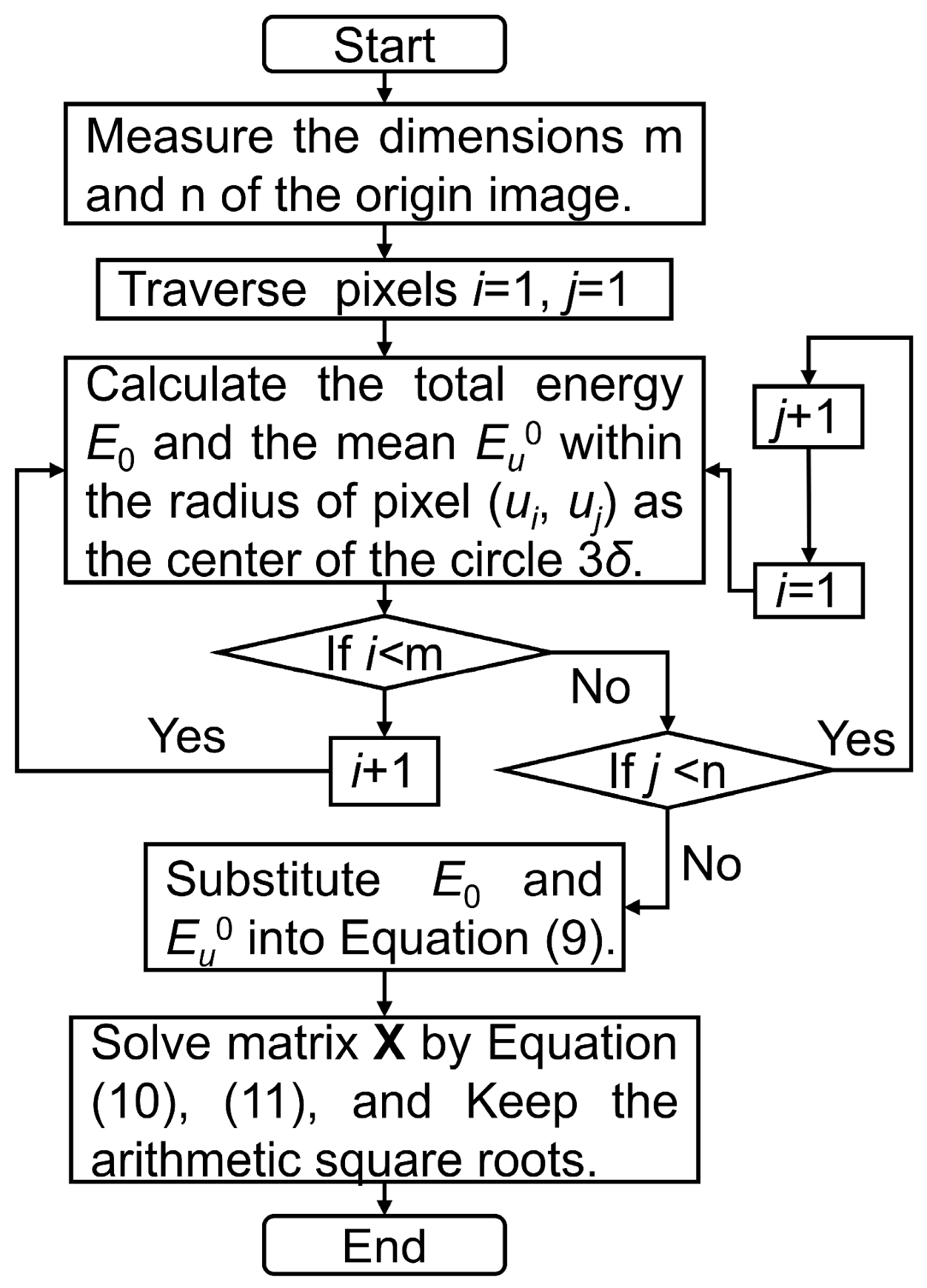
3.1. Circle of Confusion Rectification
3.2. Transformation Error Correction
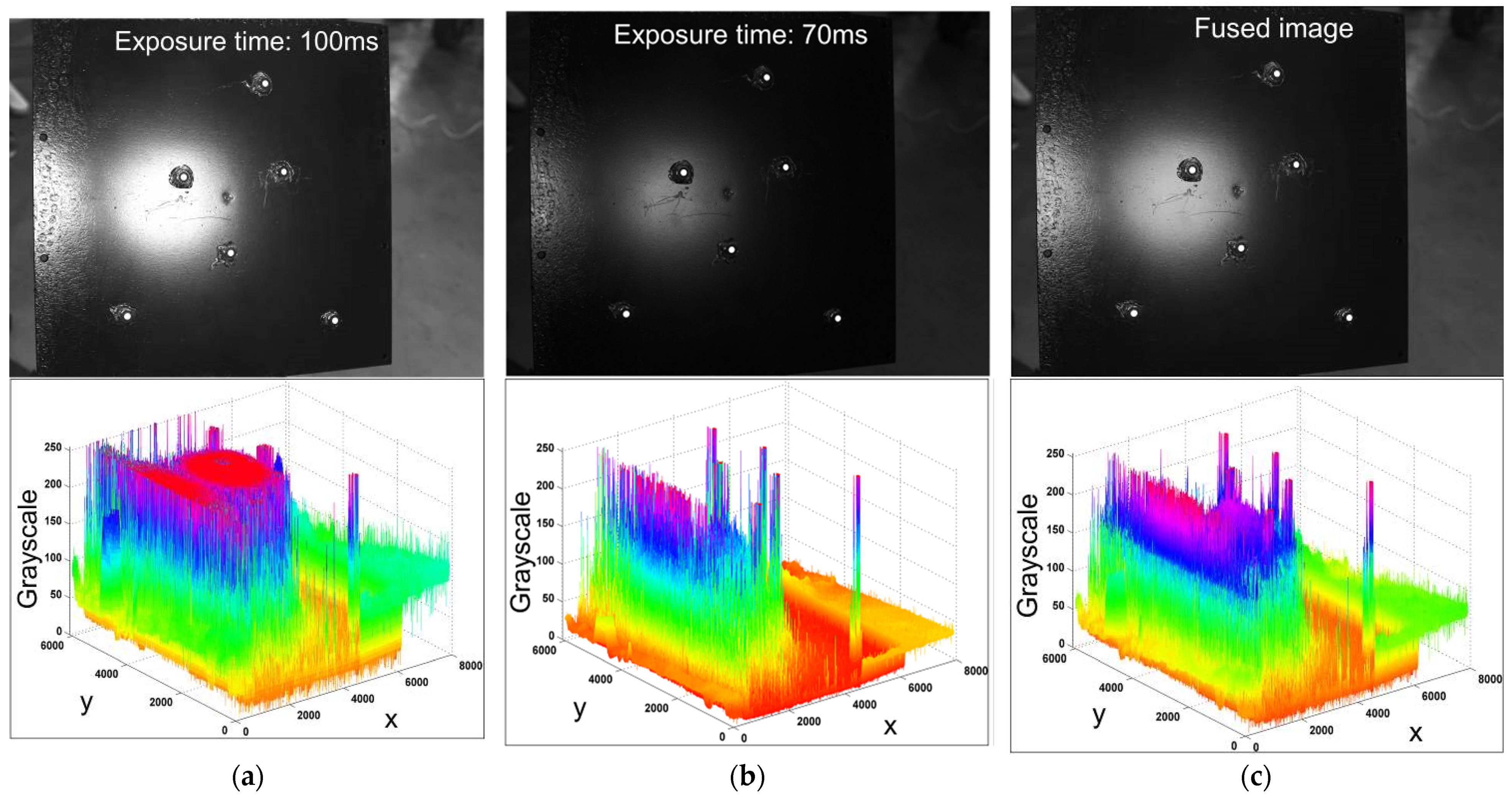
4. Experimental Validation
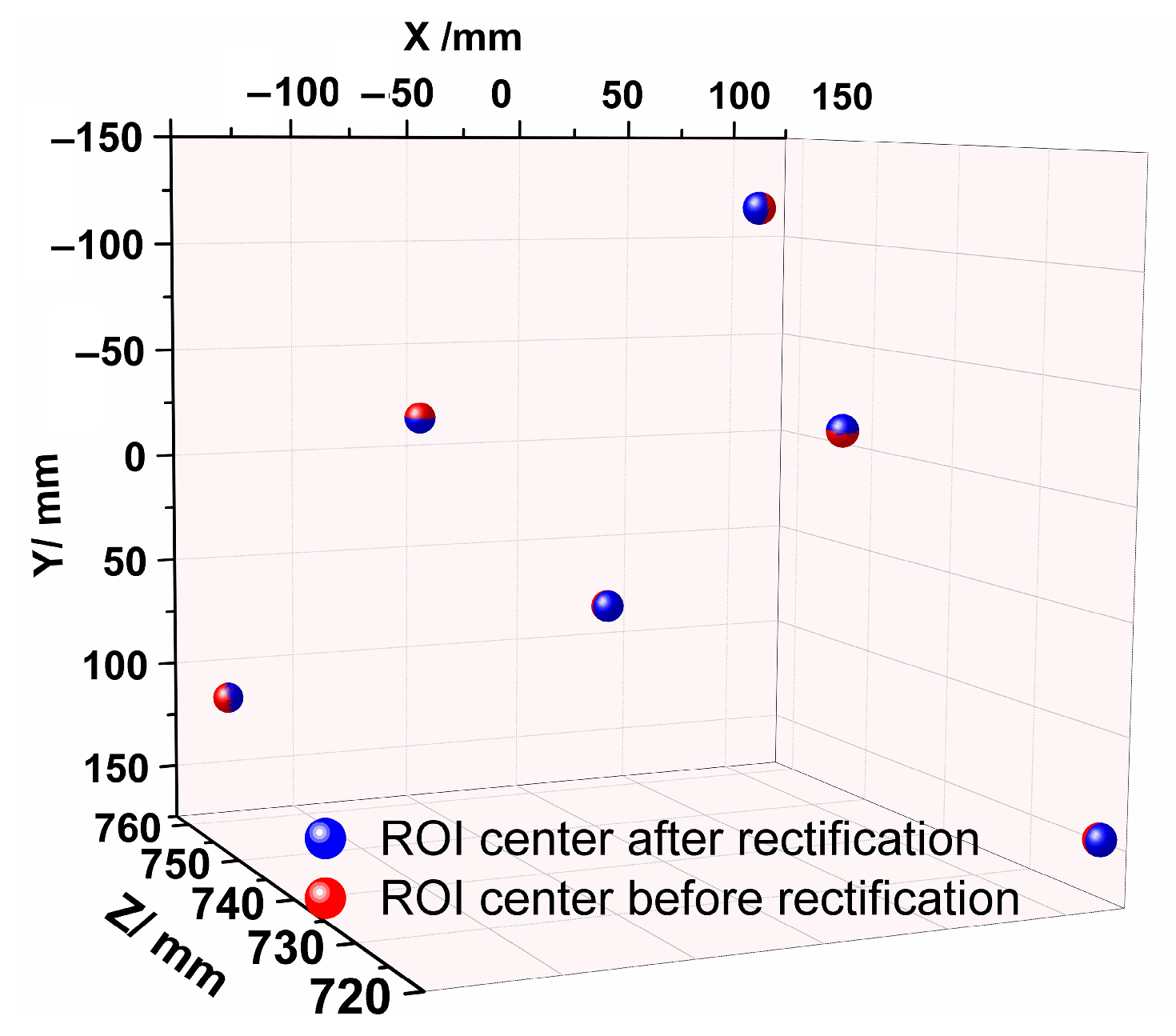
4.1. Experiment of Circle of Confusion Rectification
4.2. Experiment of Transformation Error Correction
4.3. Experiment of Measurement Applicability
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Phan, N.D.M.; Quinsat, Y.; Lartigue, C. Optimal scanning strategy for on–machine inspection with laser–plane sensor. Int. J. Adv. Manuf. Technol. 2019, 103, 4563–4576. [Google Scholar] [CrossRef]
- Vasilev, M.; MacLeod, C.N.; Loukas, C. Sensor-Enabled Multi-Robot System for Automated Welding and In-Process Ultrasonic NDE. Sensors 2021, 21, 5077. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.S.; Shah, S.H.; Yen, S.H.; Ahmad, A.R.; Lin, C.Y. Enhancing Robotic-Based Propeller Blade Sharpening Efficiency with a Laser-Vision Sensor and a Force Compliance Mechanism. Sensors 2023, 23, 5320. [Google Scholar] [CrossRef]
- Jiang, T.; Cui, H.H.; Cheng, X.S. A calibration strategy for vision–guided robot assembly system of large cabin. Measurement 2020, 163, 107991. [Google Scholar] [CrossRef]
- Yu, C.; Ji, F.; Xue, J.; Wang, Y. Adaptive Binocular Fringe Dynamic Projection Method for High Dynamic Range Measurement. Sensors 2019, 19, 4023. [Google Scholar] [CrossRef]
- Hu, J.B.; Sun, Y.; Li, G.F.; Jiang, G.Z.; Tao, B. Probability analysis for grasp planning facing the field of medical robotics. Measurement 2019, 141, 227–234. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, Y.; Shi, W.; Nie, M. Laser Ranging-Assisted Binocular Visual Sensor Tracking System. Sensors 2020, 20, 688. [Google Scholar] [CrossRef] [PubMed]
- Li, M.Y.; Du, Z.J.; Ma, X.X.; Dong, W.; Gao, Y.Z. A robot hand–eye calibration method of line laser sensor based on 3D reconstruction. Robot. Comput. Integr. Manuf. 2021, 71, 102136. [Google Scholar] [CrossRef]
- Zhang, Y.; Qiu, Z.C.; Zhang, X.M. Calibration method for hand–eye system with rotation and translation couplings. Appl. Opt. 2019, 58, 5375–5387. [Google Scholar]
- Yang, L.X.; Cao, Q.X.; Lin, M.J.; Zhang, H.R.; Ma, Z.M. Robotic hand–eye calibration with depth camera: A sphere model approach. In Proceedings of the IEEE International Conference on Control Automation and Robotics (ICCAR), Auckland, New Zealand, 20–23 April 2018. [Google Scholar]
- Wu, J.; Liu, M.; Qi, Y.H. Computationally efficient robust algorithm for generalized sensor calibration. IEEE Sens. J. 2019, 19, 9512–9521. [Google Scholar] [CrossRef]
- Tsai, R.Y.; Lenz, R.K. A new technique for fully autonomous and efficient 3d robotics hand eye calibration. IEEE Trans. Robot. Autom. 1989, 5, 345–358. [Google Scholar] [CrossRef]
- Higuchi, Y.; Inoue, K.T. Probing supervoids with weak lensing. Mon. Not. R. Astron. Soc. 2018, 476, 359–365. [Google Scholar] [CrossRef]
- Liao, K.; Lin, C.Y.; Zhao, Y. DR–GAN: Automatic radial distortion rectification using conditional GAN in real–time. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 725–733. [Google Scholar] [CrossRef]
- Xu, F.; Wang, H.S.; Liu, Z.; Chen, W.D. Adaptive visual servoing for an underwater soft robot considering refraction effects. IEEE Trans. Ind. Electron. 2020, 67, 10575–10586. [Google Scholar] [CrossRef]
- Tang, Z.W.; Von Gioi, R.G.; Monasse, P.; Morel, J.M. A precision analysis of camera distortion models. IEEE Trans. Image Process. 2017, 26, 2694–2704. [Google Scholar] [CrossRef]
- Er, X.Z.; Rogers, A. Two families of elliptical plasma lenses. Mon. Not. R. Astron. Soc. 2019, 488, 5651–5664. [Google Scholar] [CrossRef]
- Deng, F.; Zhang, L.L.; Gao, F.; Qiu, H.B.; Gao, X.; Chen, J. Long–range binocular vision target geolocation using handheld electronic devices in outdoor environment. IEEE Trans. Image Process. 2020, 29, 5531–5541. [Google Scholar] [CrossRef] [PubMed]
- Shi, B.W.; Liu, Z.; Zhang, G.J. Online stereo vision measurement based on correction of sensor structural parameters. Opt. Express 2021, 29, 37987–38000. [Google Scholar] [CrossRef] [PubMed]
- Kong, S.H.; Fang, X.; Chen, X.Y.; Wu, Z.X.; Yu, J.Z. A NSGA–II–based calibration algorithm for underwater binocular vision measurement system. IEEE Trans. Instrum. Meas. 2020, 69, 794–803. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.J. On–line three–dimensional coordinate measurement of dynamic binocular stereo vision based on rotating camera in large FOV. Opt. Express 2021, 29, 4986–5005. [Google Scholar] [CrossRef]
- Yang, Y.; Peng, Y.; Zeng, L.; Zhao, Y.; Liu, F. Rendering Circular Depth of Field Effect with Integral Image. In Proceedings of the 11th International Conference on Digital Image Processing (ICDIP), Guangzhou, China, 10–13 May 2019. [Google Scholar]
- Miks, A.; Novak, J. Dependence of depth of focus on spherical aberration of optical systems. Appl. Opt. 2016, 55, 5931–5935. [Google Scholar] [CrossRef]
- Miks, A.; Novak, J. Third-order aberration design of optical systems optimized for specific object distance. Appl. Opt. 2013, 52, 8554–8561. [Google Scholar] [CrossRef] [PubMed]
- Deger, F.; Mansouri, A.; Pedersen, M.; Hardeberg, J.Y.; Voisin, Y. A sensor–data–based denoising framework for hyperspectral images. Opt. Express 2015, 23, 1938–1950. [Google Scholar] [CrossRef]
- Zhang, W.L.; Sang, X.Z.; Gao, X.; Yu, X.B.; Yan, B.B.; Yu, C.X. Wavefront aberration correction for integral imaging with the pre–filtering function array. Opt. Express 2018, 26, 27064–27075. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, C.X.; Ng, M.K. Variational model for simultaneously image denoising and contrast enhancement. Opt. Express 2020, 28, 18751–18777. [Google Scholar] [CrossRef]
- Camboulives, M.; Lartigue, C.; Bourdet, P.; Salgado, J. Calibration of a 3D working space multilateration. Precis. Eng. 2016, 44, 163–170. [Google Scholar] [CrossRef]
- Franceschini, F.; Galetto, M.; Maisano, D.; Mastrogiacomo, L. Combining multiple large volume metrology systems: Competitive versus cooperative data fusion. Precis. Eng. 2016, 43, 514–524. [Google Scholar] [CrossRef]
- Wendt, K.; Franke, M.; Hartig, H. Measuring large 3D structures using four portable tracking laser interferometers. Measurement 2012, 45, 2339–2345. [Google Scholar] [CrossRef]
- Urban, S.; Wursthorn, S.; Leitloff, J.; Hinz, S. MultiCol bundle adjustment: A generic method for pose estimation, simultaneous self–calibration and reconstruction for arbitrary multi–camera systems. Int. J. Comput. Vis. 2017, 121, 234–252. [Google Scholar] [CrossRef]
- Verykokou, S.; Ioannidis, C. Exterior orientation estimation of oblique aerial images using SfM–based robust bundle adjustment. Int. J. Remote Sens. 2020, 41, 7233–7270. [Google Scholar] [CrossRef]
- Qu, Y.F.; Huang, J.Y.; Zhang, X. Rapid 3D reconstruction for image sequence acquired from UAV camera. Sensors 2018, 18, 225. [Google Scholar] [CrossRef] [PubMed]
- Mertens, T.; Kautz, J.; Van Reeth, F. Exposure fusion. In Proceedings of the 15th Pacific Conference on Computer Graphics and Applications (PG’07), Maui, HI, USA, 2 November 2007. [Google Scholar]
- Zhang, Z.Y. Flexible camera calibration by viewing a plane from unknown orientations. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999. [Google Scholar]
- Quine, B.M.; Tarasyuk, V.; Mebrahtu, H.; Hornsey, R. Determining star–image location: A new sub–pixel interpolation technique to process image centroids. Comput. Phys. Commun. 2007, 177, 700–706. [Google Scholar] [CrossRef]
- Shiu, Y.C.; Ahmad, S. Calibration of wrist–mounted robotic sensors by solving homogeneous transform equations of the form AX = XB. IEEE Trans. Robot. Autom. 1989, 5, 16–29. [Google Scholar] [CrossRef]
- VDI/VDE 2634; Part 1. Optical 3D Measuring Systems–Imaging Systems with Point-By-Point Probing. Verein Deutscher Ingenieure & Verband Der Elektrotechnik Elektronik Informationstechnik: Berlin, Germany, 2002.





| Parameter | Left Camera | Right Camera |
|---|---|---|
| k1 | –0.1820 | –0.1790 |
| k2 | 0.0382 | 0.0410 |
| p1 | –1.2323 × 10–4 | –1.3870 × 10–4 |
| p2 | –2.086 × 10–3 | 6.1797 × 10–4 |
| Intrinsic matrix | Left: | |
| Right: | ||
| Extrinsic matrix | ||
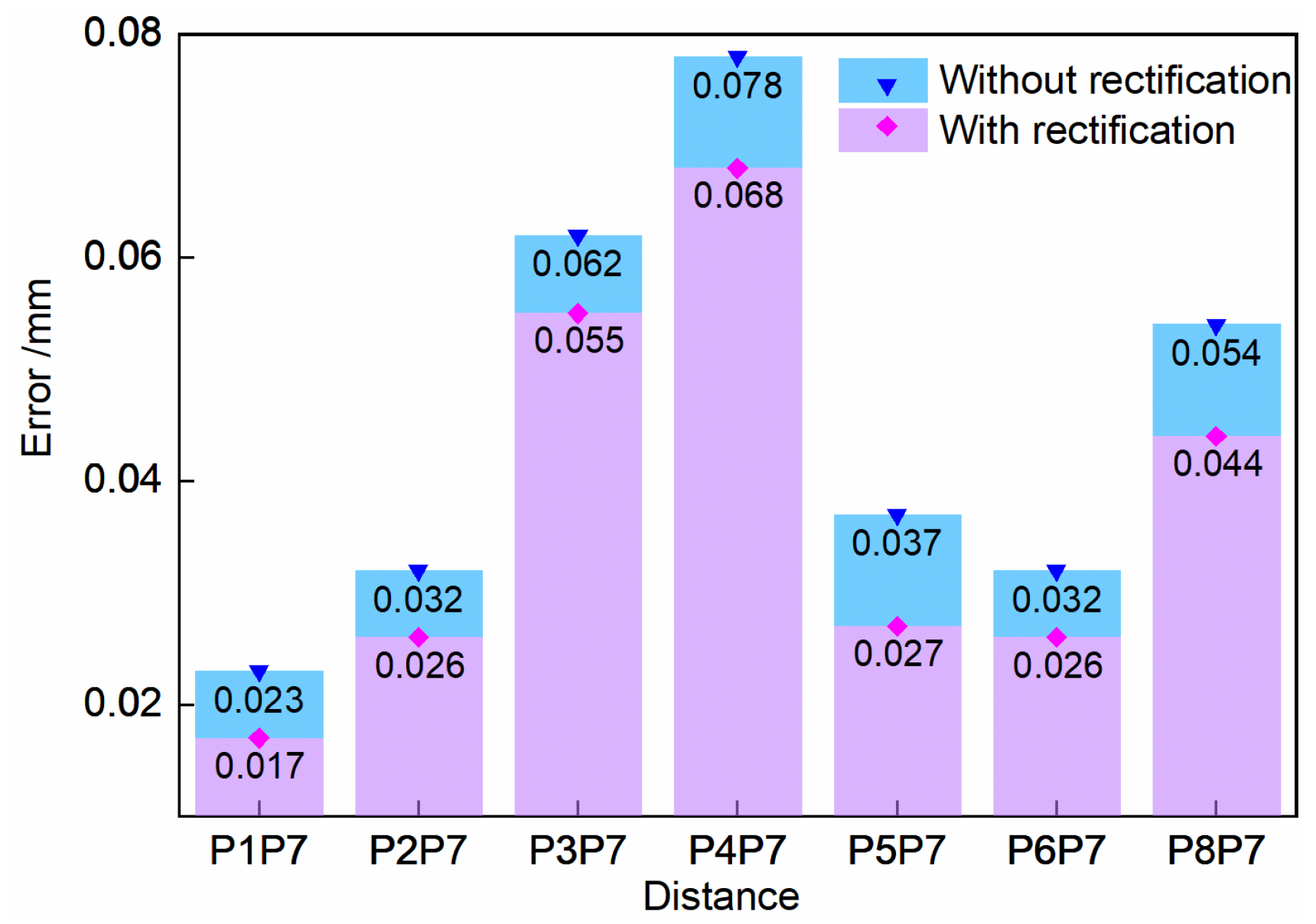
| No. | Standard Distance (mm) | Control Group 1 (mm) | Experimental Group 1 (mm) |
|---|---|---|---|
| P1P7 | 162.085 | 162.108 | 162.068 |
| P2P7 | 58.853 | 58.821 | 58.827 |
| P3P7 | 55.181 | 55.243 | 55.236 |
| P4P7 | 130.546 | 130.468 | 130.478 |
| P5P7 | 64.765 | 64.728 | 64.738 |
| P6P7 | 178.467 | 178.499 | 178.493 |
| P8P7 | 43.745 | 43.799 | 43.789 |
| No. | Standard Distance (mm) | Control Group 2 (mm) | Experimental Group 2 (mm) |
|---|---|---|---|
| P1P7 | 162.085 | 162.068 | 162.075 |
| P2P7 | 58.853 | 58.827 | 58.870 |
| P3P7 | 55.181 | 55.236 | 55.134 |
| P4P7 | 130.546 | 130.478 | 130.488 |
| P5P7 | 64.765 | 64.738 | 64.783 |
| P6P7 | 178.467 | 178.493 | 178.450 |
| P8P7 | 43.745 | 43.789 | 43.709 |
| Calibration Matrix | |
|---|---|
| Preliminary | |
| Updated |
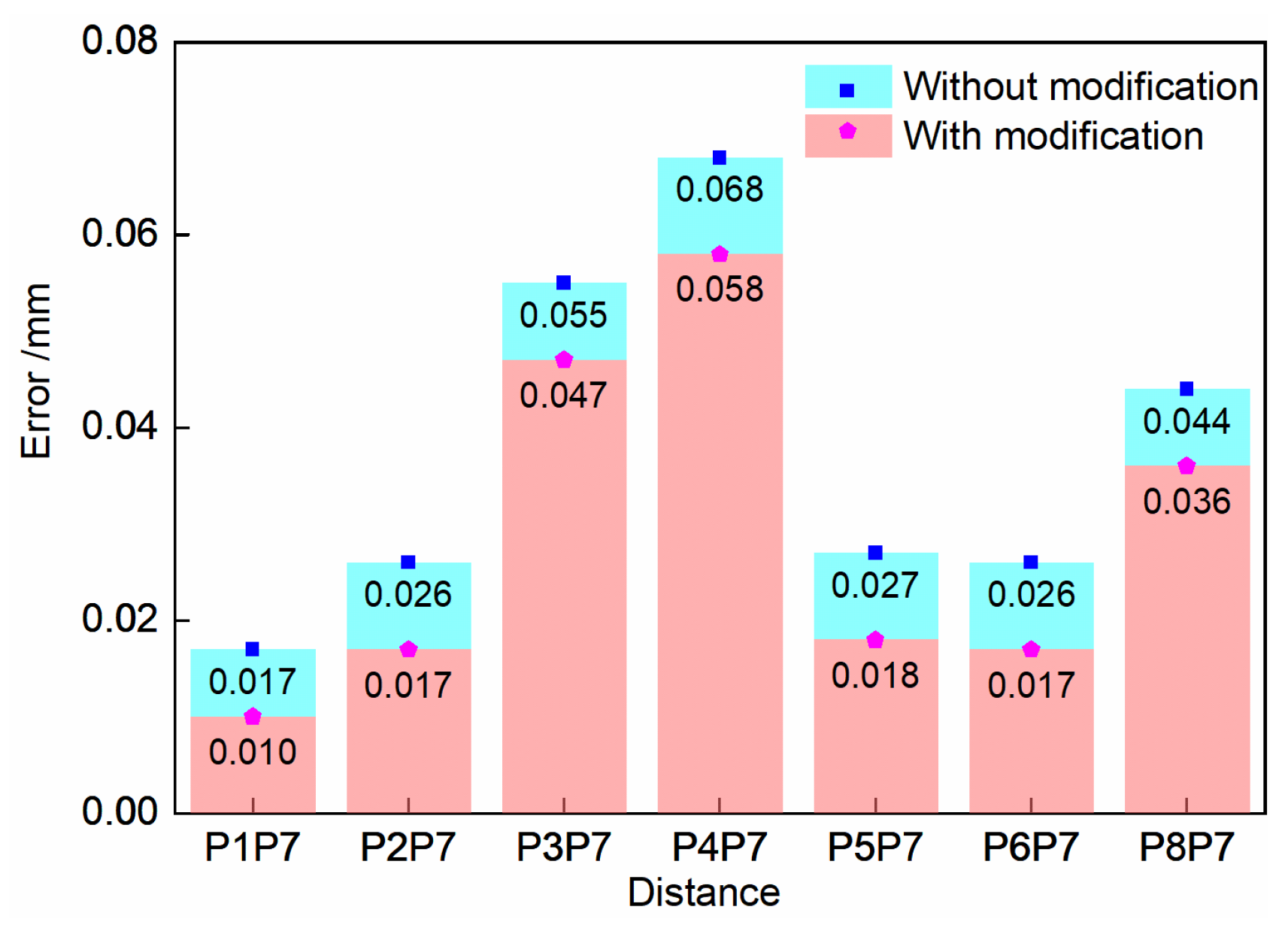
| Region | No. | Standard Distance (mm) | Observation with Preliminary Calibration (mm) | Observation with Updated Calibration (mm) | Preliminary Error (mm) | Updated Error (mm) |
|---|---|---|---|---|---|---|
| Region 1 | P1P6 | 58.224 | 58.289 | 58.279 | 0.065 | 0.054 |
| P2P6 | 54.532 | 54.596 | 54.588 | 0.064 | 0.056 | |
| P3P6 | 56.970 | 57.038 | 57.027 | 0.068 | 0.058 | |
| P4P6 | 59.835 | 59.773 | 59.782 | 0.062 | 0.053 | |
| P5P6 | 66.761 | 66.823 | 66.813 | 0.063 | 0.052 | |
| RMSE (mm) | 0.064 | 0.055 | ||||
| Region 2 | Q1Q6 | 50.030 | 50.092 | 50.081 | 0.062 | 0.051 |
| Q2Q6 | 56.000 | 55.937 | 55.946 | 0.063 | 0.054 | |
| Q3Q6 | 54.755 | 54.694 | 54.703 | 0.061 | 0.053 | |
| Q4Q6 | 54.766 | 54.703 | 54.712 | 0.064 | 0.055 | |
| Q5Q6 | 61.848 | 61.915 | 61.904 | 0.067 | 0.057 | |
| RMSE (mm) | 0.063 | 0.054 | ||||
| Region 3 | M1M6 | 59.476 | 59.541 | 59.534 | 0.065 | 0.058 |
| M2M6 | 64.325 | 64.265 | 64.274 | 0.060 | 0.051 | |
| M3M6 | 63.382 | 63.319 | 63.327 | 0.063 | 0.055 | |
| M4M6 | 50.038 | 49.977 | 49.984 | 0.061 | 0.054 | |
| M5M6 | 61.609 | 61.676 | 61.665 | 0.067 | 0.056 | |
| RMSE (mm) | 0.063 | 0.055 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, B.; Liu, W.; Yue, Y. Improved Calibration of Eye-in-Hand Robotic Vision System Based on Binocular Sensor. Sensors 2023, 23, 8604. https://doi.org/10.3390/s23208604
Yu B, Liu W, Yue Y. Improved Calibration of Eye-in-Hand Robotic Vision System Based on Binocular Sensor. Sensors. 2023; 23(20):8604. https://doi.org/10.3390/s23208604
Chicago/Turabian StyleYu, Binchao, Wei Liu, and Yi Yue. 2023. "Improved Calibration of Eye-in-Hand Robotic Vision System Based on Binocular Sensor" Sensors 23, no. 20: 8604. https://doi.org/10.3390/s23208604
APA StyleYu, B., Liu, W., & Yue, Y. (2023). Improved Calibration of Eye-in-Hand Robotic Vision System Based on Binocular Sensor. Sensors, 23(20), 8604. https://doi.org/10.3390/s23208604





