Continual Deep Learning for Time Series Modeling
Abstract
1. Introduction
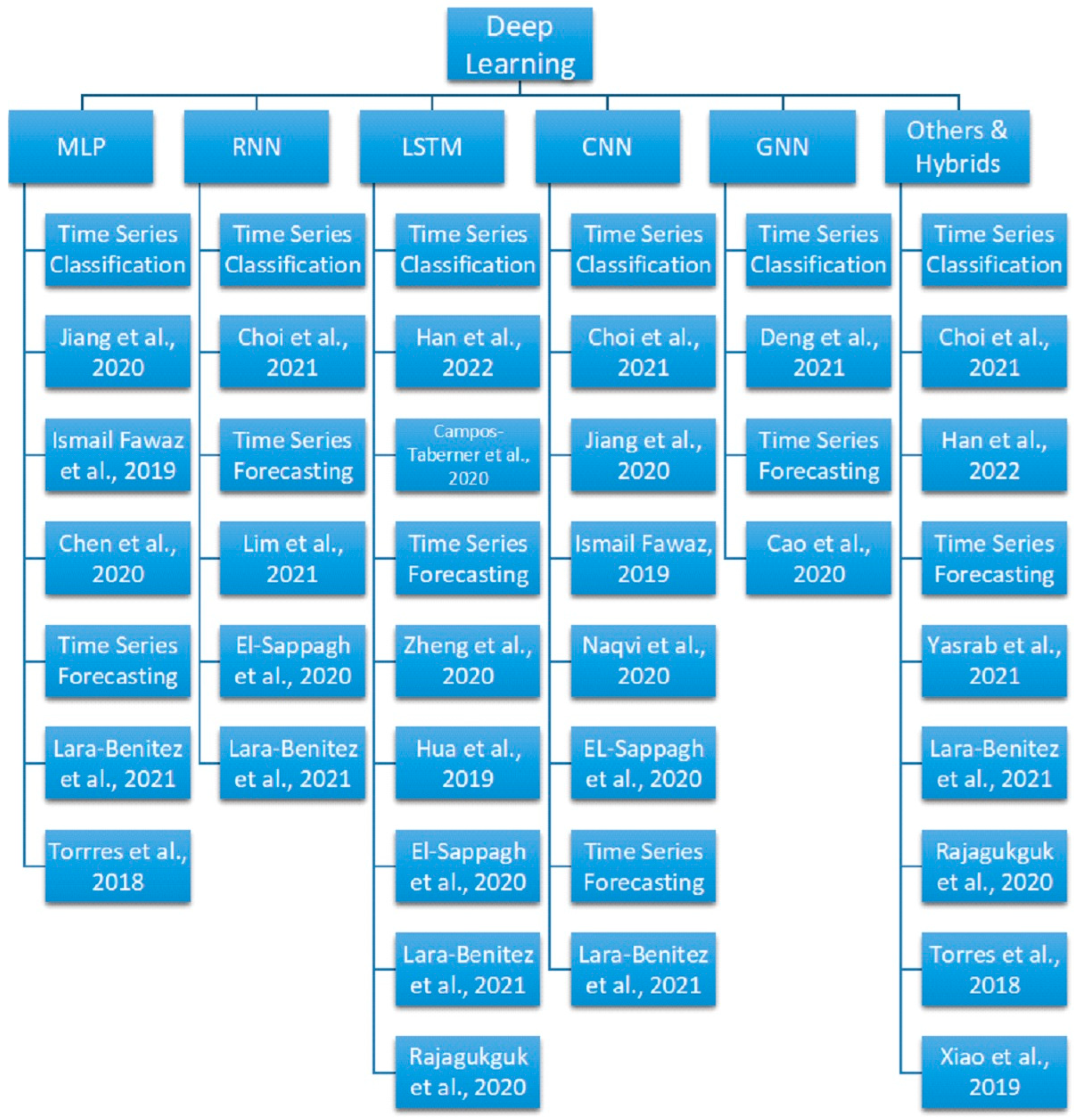
2. Advances in Deep Learning Methods for Time Series Modeling
2.1. Multi-Layer Perceptron
2.2. Recurrent Neural Network
2.3. Long Short-Term Memory
2.4. Convolutional Neural Network
2.5. Graph Neural Network
2.6. Others and Hybrids
2.7. Advanced Preprocessing and Deep Learning Applications
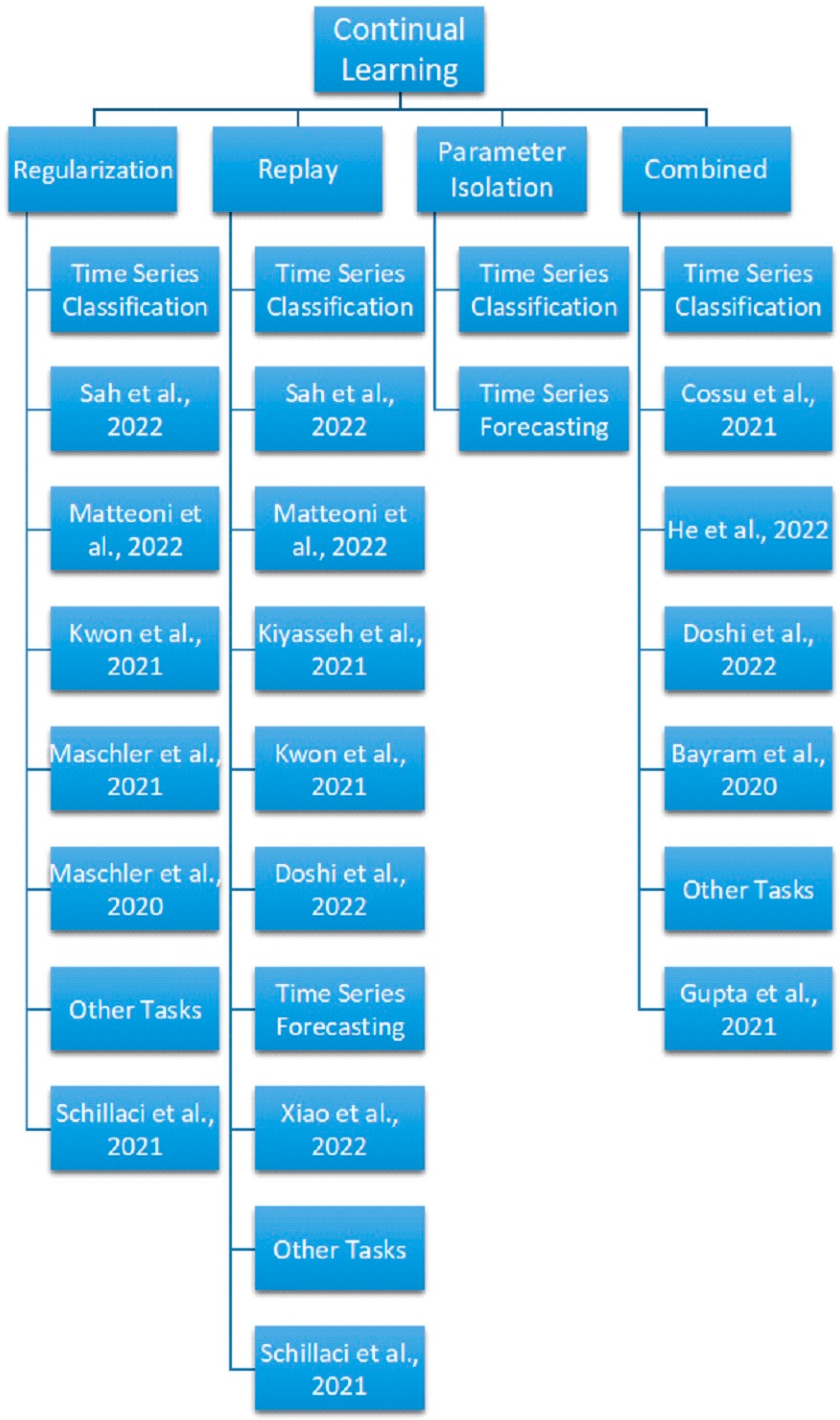
3. Advances in Continual Learning Methods for Time Series Modeling
3.1. Regularization-Based Methods
3.2. Replay Methods
3.3. Parameter Isolation Methods
3.4. Combined Approaches
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Asadi, R.; Regan, A. A Spatial-Temporal Decomposition Based Deep Neural Network for Time Series Forecasting. Appl. Soft Comput. 2020, 87, 105963. [Google Scholar] [CrossRef]
- Ao, S.I. Applied Time Series Analysis and Innovative Computing; Springer: Dordrecht, The Netherlands, 2010; ISBN 978-90-481-8768-3. [Google Scholar] [CrossRef]
- Plageras, A.P.; Psannis, K.E.; Stergiou, C.; Wang, H.; Gupta, B.B. Efficient IoT-Based Sensor Big Data Collection-Processing and Analysis in Smart Buildings. Future Gener. Comput. Syst. 2018, 82, 349–357. [Google Scholar] [CrossRef]
- Ao, S.I.; Gelman, L.; Karimi, H.R.; Tiboni, M. Advances in Machine Learning for Sensing and Condition Monitoring. Appl. Sci. 2022, 12, 12392. [Google Scholar] [CrossRef]
- Ao, S.I. Data Mining and Applications in Genomics; Springer: Dordrecht, The Netherlands, 2008; ISBN 978-1402089749. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Zheng, X.C.; Wang, M.; Ordieres-Meré, J. Comparison of Data Preprocessing Approaches for Applying Deep Learning to Human Activity Recognition in the Context of Industry 4.0. Sensors 2018, 18, 2146. [Google Scholar] [CrossRef] [PubMed]
- Dablander, F.; Bury, T. Deep Learning for Tipping Points: Preprocessing Matters. Proc. Natl. Acad. Sci. USA 2022, 119, e2207720119. [Google Scholar] [CrossRef]
- Livieris, I.E.; Stavroyiannis, S.; Pintelas, E.; Pintelas, P. A Novel Validation Framework to Enhance Deep Learning Models in Time-Series Forecasting. Neural Comput. Appl. 2020, 32, 17149–17167. [Google Scholar] [CrossRef]
- Guerrier, S.; Molinari, R.; Xu, H.; Zhang, Y. Applied Time Series Analysis with R. 2019. Available online: http://ts.smac-group.com (accessed on 28 July 2023).
- Rhif, M.; Abbes, A.B.; Farah, I.R.; Martinez, B.; Sang, Y. Wavelet Transform Application for/in Non-Stationary Time-Series Analysis: A Review. Appl. Sci. 2019, 9, 1345. [Google Scholar] [CrossRef]
- Mahmoud, A.; Mohammed, A. A Survey on Deep Learning for Time-Series Forecasting. Machine Learning and Big Data Analytics Paradigms: Analysis, Applications and Challenges. Stud. Big Data 2021, 77, 365–392. [Google Scholar]
- French, R. Catastrophic Forgetting in Connectionist Networks. Trends Cogn. Sci. 1999, 3, 128–135. [Google Scholar] [CrossRef]
- Lee, S.; Goldt, S.; Saxe, A. Continual Learning in the Teacher-Student Setup: Impact of Task Similarity. In Proceedings of the 38th International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; Volume 139. [Google Scholar]
- Shin, H.; Lee, J.K.; Kim, J.; Kim, J. Continual Learning with Deep Generative Replay. arXiv 2017, arXiv:1705.08690. [Google Scholar]
- De Lange, M.; Aljundi, R.; Masana, M.; Parisot, S.; Jia, X.; Leonardis, A.; Slabaugh, G.; Tuytelaars, T. A Continual Learning Survey: Defying Forgetting in Classification Tasks. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 3366–3385. [Google Scholar]
- Wang, L.; Zhang, X.; Su, H.; Zhu, J. A Comprehensive Survey of Continual Learning: Theory, Method and Application. arXiv 2023, arXiv:2302.00487v2. [Google Scholar]
- Hadsell, R.; Rao, D.; Rusu, A.A.; Pascanu, R. Embracing Change: Continual Learning in Deep Neural Networks. Trends Cogn. Sci. 2020, 24, 1028–1040. [Google Scholar] [CrossRef]
- Hayes, T.L.; Krishnan, G.P.; Bazhenov, M.; Siegelmann, H.T.; Sejnowski, T.J.; Kanan, C. Replay in Deep Learning: Current Approaches and Missing Biological Elements. Neural Comput. 2021, 33, 2908–2950. [Google Scholar] [PubMed]
- Jedlicka, P.; Tomko, M.; Robins, A.; Abraham, W.C. Contributions by Metaplasticity to Solving the Catastrophic Forgetting Problem. Trends Neurosci. 2022, 45, 656–666. [Google Scholar] [CrossRef] [PubMed]
- Kudithipudi, D.; Aguilar-Simon, M.; Babb, J.; Bazhenov, M.; Blackiston, D.; Bongard, J.; Brna, A.P.; Chakravarthi Raja, S.; Cheney, N.; Clune, J.; et al. Biological Underpinnings for Lifelong Learning Machines. Nat. Mach. Intell. 2022, 4, 196–210. [Google Scholar] [CrossRef]
- Kilickaya, M.; Weijer, J.V.; Asano, Y. Towards Label-Efficient Incremental Learning: A survey. arXiv 2023, arXiv:2302.00353. [Google Scholar]
- Mai, Z.; Li, R.; Jeong, J.; Quispe, D.; Kim, H.; Sanner, S. Online Continual Learning in Image Classification: An Empirical Survey. Neurocomputing 2022, 469, 28–51. [Google Scholar] [CrossRef]
- Masana, M.; Twardowski, B.; Weijer, J.V. On Class Orderings for Incremental Learning. arXiv 2020, arXiv:2007.02145. [Google Scholar]
- Qu, H.; Rahmani, H.; Xu, L.; Williams, B.; Liu, J. Recent Advances of Continual Learning in Computer Vision: An Overview. arXiv 2021, arXiv:2109.11369. [Google Scholar]
- Biesialska, M.; Biesialska, K.; Costajussa, M.R. Continual Lifelong Learning in Natural Language Processing: A survey. In Proceedings of the 28th International Conference on Computational Linguistics, Barcelona, Spain, 8–13 December 2020; pp. 6523–6541. [Google Scholar]
- Ke, Z.; Liu, B. Continual Learning of Natural Language Processing Tasks: A Survey. arXiv 2022, arXiv:2211.12701. [Google Scholar]
- Khetarpal, K.; Riemer, M.; Rish, I.; Precup, D. Towards Continual Reinforcement Learning: A Review and Perspectives. J. Artif. Intell. Res. 2022, 75, 1401–1476. [Google Scholar] [CrossRef]
- Rajagukguk, R.A.; Ramadhan, R.A.A.; Lee, H.J. A Review on Deep Learning Models for Forecasting Time Series Data of Solar Irradiance and Photovoltaic Power. Energies 2020, 13, 6623. [Google Scholar] [CrossRef]
- Cai, M.; Pipattanasomporn, M.; Rahman, S. Day-Ahead Building-Level Load Forecasts using Deep Learning vs. Traditional Time-Series Techniques. Appl. Energy 2019, 236, 1078–1088. [Google Scholar] [CrossRef]
- Choi, K.; Yi, J.; Park, C.; Yoon, S. Deep Learning for Anomaly Detection in Time-Series Data: Review, Analysis, and Guidelines. IEEE Access 2021, 9, 120043–120065. [Google Scholar]
- Deng, A.; Hooi, B. Graph Neural Network-Based Anomaly Detection in Multivariate Time Series. In Proceedings of the Thirty-Fifth AAAI Conference on Artificial Intelligence, Online, 2–9 February 2021. [Google Scholar]
- Jiang, W. Time Series Classification: Nearest Neighbor versus Deep Learning Models. SN Appl. Sci. 2020, 2, 721. [Google Scholar]
- Ismail Fawaz, H.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.A. Deep Learning for Time Series Classification: A Review. Data Min. Knowl. Discov. 2019, 33, 917–963. [Google Scholar]
- Han, T.; Sanchez-Azofeifa, G.A. A Deep Learning Time Series Approach for Leaf and Wood Classification from Terrestrial LiDAR Point Clouds. Remote Sens. 2022, 14, 3157. [Google Scholar] [CrossRef]
- Campos-Taberner, M.; García-Haro, F.J.; Martínez, B.; Izquierdo-Verdiguier, E.; Atzberger, C.; Camps-Valls, G.; Gilabert, M.A. Understanding Deep Learning in Land Use Classification Based on Sentinel-2 Time Series. Sci. Rep. 2020, 10, 17188. [Google Scholar]
- Naqvi, R.A.; Arsalan, M.; Rehman, A.; Rehman, A.U.; Loh, W.K.; Paul, A. Deep Learning-Based Drivers Emotion Classification System in Time Series Data for Remote Applications. Remote Sens. 2020, 12, 587. [Google Scholar] [CrossRef]
- Zheng, J.; Huang, M. Traffic Flow Forecast through Time Series Analysis Based on Deep Learning. IEEE Access 2020, 8, 82562–82570. [Google Scholar] [CrossRef]
- Hua, Y.; Zhao, Z.; Li, R.; Chen, X.; Liu, Z.; Zhang, H. Deep Learning with Long Short-Term Memory for Time Series Prediction. IEEE Commun. Mag. 2019, 57, 114–119. [Google Scholar] [CrossRef]
- Chen, B.; Liu, Y.; Zhang, C.; Wang, Z. Time Series Data for Equipment Reliability Analysis with Deep Learning. IEEE Access 2020, 8, 105484–105493. [Google Scholar] [CrossRef]
- Lim, B.; Zohren, S. Time Series Forecasting with Deep Learning: A Survey. Phil. Trans. R. Soc. A 2021, 379, 20200209. [Google Scholar]
- Yasrab, R.; Zhang, J.; Smyth, P.; Pound, M. Predicting Plant Growth from Time-Series Data Using Deep Learning. Remote Sens. 2021, 13, 331. [Google Scholar] [CrossRef]
- El-Sappagh, S.; Abuhmed, T.; Riazul Islam, S.M.; Kwak, K.S. Multimodal Multitask Deep Learning Model for Alzheimer’s Disease Progression Detection Based on Time Series Data. Neurocomputing 2020, 412, 197–215. [Google Scholar]
- Lara-Benitez, P.; Carranza-Garcia, M.; Riquelme, J. An Experimental Review on Deep Learning Architectures for Time Series Forecasting. Int. J. Neural Syst. 2021, 31, 2130001. [Google Scholar] [CrossRef]
- Cao, D.; Wang, Y.; Duan, J.; Zhang, C.; Zhu, X.; Huang, C.; Tong, Y.; Xu, B.; Bai, J.; Tong, J.; et al. Spectral Temporal Graph Neural Network for Multivariate Time-series Forecasting. In Proceedings of the 34th Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 6–12 December 2020. [Google Scholar]
- Torres, J.F.; Troncoso, A.; Koprinska, I.; Wang, Z.; Martínez-Álvarez, F. Deep Learning for Big Data Time Series Forecasting Applied to Solar Power. In Proceedings of the International Joint Conference SOCO’18-CISIS’18-ICEUTE’18. SOCO’18-CISIS’18-ICEUTE’18 2018, San Sebastián, Spain, 6–8 June 2018; Advances in Intelligent Systems and Computing. Springer: Cham, Switzerland, 2019; Volume 771. [Google Scholar]
- Xiao, C.; Chen, N.; Hu, C.; Wang, K.; Xu, Z.; Gai, Y.; Xu, L.; Chen, Z.; Gong, J. A Spatiotemporal Deep Learning Model for Sea Surface Temperature Field Prediction using Time-series Satellite Data. Environ. Model. Softw. 2019, 120, 104502. [Google Scholar] [CrossRef]
- Dau, H.A.; Keogh, E.; Kamgar, K.; Yeh, C.C.M.; Zhu, Y.; Gharghabi, S.; Ratanamahatana, C.A.; Chen, Y.; Hu, B.; Begum, N.; et al. The UCR Time Series Classification Archive. 2018. Available online: https://www.cs.ucr.edu/~eamonn/time_series_data_2018/ (accessed on 20 May 2023).
- Jaeger, H.; Haas, H. Harnessing Nonlinearity: Predicting Chaotic Systems and Saving Energy in Wireless Communication. Science 2004, 304, 78–80. [Google Scholar]
- Bagnall, A.; Lines, J.; Bostrom, A.; Large, J.; Keogh, E. The Great Time Series Classification Bake off: A Review and Experimental Evaluation of Recent Algorithmic Advances. Data Min. Knowl. Discov. 2017, 31, 606–660. [Google Scholar] [PubMed]
- Baydogan, M.G. Multivariate Time Series Classification Datasets. 2015. Available online: http://www.mustafabaydogan.com (accessed on 28 February 2019).
- Borovykh, A.; Bohte, S.; Oosterlee, C.W. Conditional Time Series Forecasting with Convolutional Neural Networks. arXiv 2017, arXiv:1703.04691. [Google Scholar]
- Torres, J.F.; Hadjout, D.; Sebaa, A.; Martinez-Alvarez, F.; Troncoso, A. Deep Learning for Time Series Forecasting: A Survey. Big Data 2021, 9, 3–21. [Google Scholar] [PubMed]
- Climate Commission. The Critical Decade: Australia’s Future—Solar Energy; Climate Commission: Manila, Philippines, 2013.
- Chollet, F.; Allaire, J. Deep Learning with R; Manning Publications: Shelter Island, NY, USA, 2018. [Google Scholar]
- Fan, C.; Wang, J.; Gang, W.; Li, S. Assessment of deep recurrent neural network-based strategies for short-term building energy predictions. Appl. Energy 2019, 236, 700–710. [Google Scholar] [CrossRef]
- Barrera-Animas, A.Y.; Oyedele, L.O.; Bilal, M.; Akinosho, T.D.; Delgado, J.M.D.; Akanbi, L.A. Rainfall prediction: A comparative analysis of modern machine learning algorithms for time-series forecasting. Mach. Learn. Appl. 2022, 7, 100204. [Google Scholar]
- Smyl, S. A Hybrid Method of Exponential Smoothing and Recurrent Neural Networks for Time Series Forecasting. Int. J. Forecast. 2020, 36, 75–85. [Google Scholar] [CrossRef]
- Dang, H.V.; MKohsin, R.; Nguyen, T.V.; Bui-Tien, T.; Nguyen, H.X. Deep Learning-Based Detection of Structural Damage using Time-Series Data. Structure and Infrastructure Engineering. Struct. Infrastruct. Eng. 2021, 17, 1474–1493. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; Van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 14–21 October 2014; pp. 1724–1734. [Google Scholar]
- Wang, F.; Yu, Y.; Zhang, Z.; Li, J.; Zhen, Z.; Li, K. Wavelet Decomposition and Convolutional LSTM Networks Based Improved Deep Learning Model for Solar Irradiance Forecasting. Appl. Sci. 2018, 8, 1286. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. Indian J. Chem.-Sect. B Org. Med. Chem. 2015, 45, 1951–1954. [Google Scholar]
- Uhlig, S.; Quoitin, B.; Lepropre, J.; Balon, S. Providing Public Intradomain Traffic Matrices to the Research Community. SIGCOMM Comput. Commun. Rev. 2006, 36, 83–86. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM Network: A Machine Learning Approach for Precipitation nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28, 802–810. [Google Scholar]
- Yamashita, R.; Nishio, M.; Do, R.K.G.; Togashi, K. Convolutional Neural Networks: An Overview and Application in Radiology. Insights Imaging 2018, 9, 611–629. [Google Scholar] [PubMed]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M. The Graph Neural Network Model. IEEE Trans. Neural Netw. 2009, 20, 61–80. [Google Scholar] [CrossRef] [PubMed]
- Velickovic, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph Attention Networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Ma, M.; Sun, C.; Chen, X. Deep Coupling Autoencoder for Fault Diagnosis with Multimodal Sensory Data. IEEE Trans. Ind. Inform. 2018, 14, 1137–1145. [Google Scholar] [CrossRef]
- Lei, Y.; Karimi, H.R.; Cen, L.; Chen, X.; Xie, Y. Processes soft modeling based on stacked autoencoders and wavelet extreme learning machine for aluminum plant-wide application. Control Eng. Pract. 2021, 108, 104706. [Google Scholar] [CrossRef]
- Mohammdi Farsani, E.; Pazouki, E. A Transformer Self Attention Model for Time Series Forecasting. J. Electr. Comput. Eng. Innov. 2021, 9, 1–10. [Google Scholar]
- Elsayed, S.; Thyssens, D.; Rashed, A.; Jomaa, H.S.; Schmidt-Thieme, L. Do We Really Need Deep Learning Models for Time Series Forecasting? arXiv 2021, arXiv:2101.02118v2. [Google Scholar]
- Kanani, P.; Padole, M. ECG Heartbeat Arrhythmia Classification Using Time-Series Augmented Signals and Deep Learning Approach. Procedia Comput. Sci. 2020, 171, 524–531. [Google Scholar] [CrossRef]
- Kisa, D.H.; Ozdemir, M.A.; Guren, O.; Akan, A. EMG based Hand Gesture Classification using Empirical Mode Decomposition Time-Series and Deep Learning. In Proceedings of the 2020 Medical Technologies Congress, Antalya, Turkey, 19–20 November 2020. [Google Scholar]
- Castro Filho, H.C.; Carvalho Junior, O.A.; Carvalho, O.L.F.; Bem, P.P.; Moura, R.S.; Albuquerque, A.O.; Silva, C.R.; Ferreira, P.H.G.; Guimaraes, R.F.; Gomes, R.A.T. Rice Crop Detection Using LSTM, Bi-LSTM, and Machine Learning Models from Sentinel-1 Time Series. Remote Sens. 2020, 12, 2655. [Google Scholar] [CrossRef]
- RuBwurm, M.; Korner, M. Self-Attention for Raw Optical Satellite Time Series Classification. J. Photogramm. Remote Sens. 2020, 169, 421–435. [Google Scholar]
- Kingphai, K.; Moshfeghi, Y. EEG-based Mental Workload Level Estimation using Deep Learning Models. In Ergonomics & Human Factors; CIEHF: Birmingham, UK, 2022. [Google Scholar]
- Yokkampon, U.; Mowshowitz, A.; Chumkamon, S.; Hayashi, E. Robust Unsupervised Anomaly Detection with Variational Autoencoder in Multivariate Time Series Data. IEEE Access 2022, 10, 57835–57849. [Google Scholar] [CrossRef]
- Mishra, S.; Bordin, C.; Taharaguchi, K.; Palu, I. Comparison of Deep Learning Models for Multivariate Prediction of Time Series Wind Power Generation and Temperature. Energy Rep. 2020, 6, 273–286. [Google Scholar] [CrossRef]
- Wen, Q.S.; Sun, L.; Yang, F.; Song, X.; Gao, J.; Wang, X.; Xu, H. Time Series Data Augmentation for Deep Learning: A Survey. In Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence (IJCAI-21), Montréal, QC, Canada, 19–27 August 2021; pp. 4653–4660. [Google Scholar]
- Azar, J.; Makhoul, A.; Couturier, R.; Demerjian, J. Robust IoT Time Series Classification with Data Compression and Deep Learning. Neurocomputing 2020, 398, 222–234. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and Dierentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Mognon, A.; Jovicich, J.; Bruzzone, L.; Buiatti, M. Adjust: An Automatic EEG Artifact Detector Based on the Joint Use of Spatial and Temporal Features. Psychophysiology 2011, 48, 229–240. [Google Scholar]
- Kingphai, K.; Moshfeghi, Y. On EEG Preprocessing Role in Deep Learning Effectiveness for Mental Workload Classification. In International Symposium on Human Mental Workload: Models and Applications; Springer: Berlin/Heidelberg, Germany, 2021; pp. 81–98. [Google Scholar]
- Chalapathy, R.; Chawla, S. Deep Learning for Anomaly Detection: A Survey. arXiv 2019, arXiv:1901.03407. [Google Scholar]
- Le, T.T.; Fu, W.; Moore, J.H. Scaling Tree-Based Automated Machine Learning to Biomedical Big Data with a Feature Set Selector. Bioinformatics 2020, 36, 250–256. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Livieris, I.; Stavroyiannis, S.; Iliadis, L.; Pintelas, P. Smoothing and Stationarity Enforcement Framework for Deep Learning Time-Series Forecasting. Neural Comput. Appl. 2021, 33, 14021–14035. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Huang, Z.; Sick, B. Toward Application of Continuous Power Forecasts in a Regional Flexibility Market. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; pp. 1–8. [Google Scholar]
- Kiyasseh, D.; Zhu, T.; Clifton, D. A Clinical Deep Learning Framework for Continually Learning from Cardiac Signals across Diseases, Time, Modalities, and Institutions. Nat. Commun. 2021, 12, 4221. [Google Scholar] [CrossRef]
- Gupta, V.; Narwariya, J.; Malhotra, P.; Vig, L.; Shroff, G. Continual Learning for Multivariate Time Series Tasks with Variable Input Dimensions. In Proceedings of the 2021 IEEE International Conference on Data Mining (ICDM), Auckland, New Zealand, 7–10 December 2021; pp. 161–170. [Google Scholar]
- Flesch, T.; Balaguer, J.; Dekker, R.; Nili, H.; Summerfield, C. Comparing Continual Task Learning in Minds and Machines. Proc. Natl. Acad. Sci. USA 2018, 115, E10313–E10322. [Google Scholar] [CrossRef] [PubMed]
- Shaheen, K.; Hanif, M.A.; Hasan, O.; Shafique, M. Continual Learning for Real-World Autonomous Systems: Algorithms, Challenges and Frameworks. J. Intell. Robot. Syst. 2022, 105, 9. [Google Scholar]
- Pfulb, B.; Gepperth, A. A Comprehensive, Application-Oriented Study of Catastrophic Forgetting in DNNs. In Proceedings of the International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Prabhu, A.; Torr, P.; Dokania, P. Gdumb: A Simple Approach that Questions Our Progress in Continual Learning. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2020; pp. 524–540. [Google Scholar]
- He, Y.; Sick, B. CLeaR: An Adaptive Continual Learning Framework for Regression Tasks. AI Perspect. 2021, 3, 2. [Google Scholar]
- Philps, D.; Weyde, T.; Garcez, A.D.A.; Batchelor, R. Continual Learning Augmented Investment Decisions. arXiv 2019, arXiv:1812.02340v4. [Google Scholar]
- Chen, X.; Wang, J.; Xie, K. TrafficStream: A Streaming Traffic Flow Forecasting Framework Based on Graph Neural Networks and Continual Learning. In Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 19–27 August 2021. [Google Scholar]
- Lesort, T.; George, T.; Rish, I. Continual learning in Deep Neural Networks: An Analysis of the Last Layer. arXiv 2021, arXiv:2106.01834. [Google Scholar]
- Mundt, M.; Hong, Y.; Pliushch, I.; Ramesh, V. A Wholistic View of Continual Learning with Deep Neural Networks: Forgotten Lessons and the Bridge to Active and Open World Learning. Neural Netw. 2023, 160, 306–336. [Google Scholar]
- Bagus, B.; Gepperth, A.; Lesort, T. Beyond Supervised Continual Learning: A Review. In Proceedings of the European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, Bruges, Belgium, 5–7 October 2022. [Google Scholar]
- Pham, Q.; Liu, C.; Sahoo, D.; Hoi, S.C. Learning Fast and Slow for Online Time Series Forecasting. arXiv 2022, arXiv:2202.11672v2. [Google Scholar]
- Xiao, Y.; Liu, M.; Zhang, Z.; Jiang, L.; Yin, M.; Wang, J. Streaming Traffic Flow Prediction Based on Continuous Reinforcement Learning. arXiv 2022, arXiv:2212.12767v1. [Google Scholar]
- Sah, R.K.; Mirzadeh, S.I.; Ghasemzadeh, H. Continual Learning for Activity Recognition. In Proceedings of the 2022 44th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Scotland, UK, 11–15 July 2022; pp. 2416–2420. [Google Scholar]
- Matteoni, F.; Cossu, A.; Gallicchio, C.; Lomonaco, V.; Bacciu, D. Continual Learning for Human State Monitoring. In Proceedings of the ESANN 2022 Proceedings, European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, Bruges, Belgium, 5–7 October 2022. [Google Scholar]
- Kwon, Y.D.; Chauhan, J.; Kumar, A.; Hui, P.; Mascolo, C. Exploring System Performance of Continual Learning for Mobile and Embedded Sensing Applications. In Proceedings of the 2021 IEEE/ACM Symposium on Edge Computing (SEC), San Jose, CA, USA, 14–17 December 2021; pp. 319–332. [Google Scholar]
- Cossu, A.; Carta, A.; Lomonaco, V.; Bacciu, D. Continual Learning for Recurrent Neural Networks: An Empirical Evaluation. Neural Netw. 2021, 143, 607–627. [Google Scholar] [CrossRef] [PubMed]
- He, Y. Adaptive Explainable Continual Learning Framework for Regression Problems with Focus on Power Forecasts. arXiv 2022, arXiv:2108.10781v2. [Google Scholar]
- Doshi, K.; Yilmaz, Y. Rethinking Video Anomaly Detection—A Continual Learning Approach. In Proceedings of the 2022 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 4–8 January 2022; pp. 3036–3045. [Google Scholar]
- Maschler, B.; Pham, T.T.H.; Weyrich, M. Regularization-based Continual Learning for Anomaly Detection in Discrete Manufacturing. In Proceedings of the 54th CIRP Conference on Manufacturing Systems, Procedia CIRP, Virtual, 22–24 September 2021; Volume 104, pp. 452–457. [Google Scholar]
- Maschler, B.; Vietz, H.; Jazdi, N.; Weyrich, M. Continual Learning of Fault Prediction for Turbofan Engines using Deep Learning with Elastic Weight Consolidation. In Proceedings of the 2020 25th IEEE International Conference on Emerging Technologies and Factory Automation, Vienna, Austria, 8–11 September 2020; pp. 959–966. [Google Scholar]
- Bayram, B.; Ince, G. Real Time Auditory Scene Analysis using Continual Learning in Real Environments. Eur. J. Sci. Technol. 2020, 215–226, Ejosat Special Issue 2020 (HORA). [Google Scholar] [CrossRef]
- Schillaci, G.; Schmidt, U.; Miranda, L. Prediction Error-Driven Memory Consolidation for Continual Learning: On the Case of Adaptive Greenhouse Models. KI—Künstliche Intell. 2021, 35, 71–80. [Google Scholar]
- Knoblauch, J.; Husain, H.; Diethe, T. Optimal Continual Learning has Perfect Memory and is NP-HARD. In Proceedings of the 37th International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 5327–5337. [Google Scholar]
- Kirkpatrick, J.; Pascanu, R.; Rabinowitz, N.; Veness, J.; Desjardins, G.; Rusu, A.A.; Milan, K.; Quan, J.; Ramalho, T.; Grabska-Barwinska, A.; et al. Overcoming Catastrophic Forgetting in Neural Networks. Proc. Natl. Acad. Sci. USA 2017, 114, 3521–3526. [Google Scholar] [CrossRef]
- Li, Z.; Hoiem, D. Learning without Forgetting. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 2935–2947. [Google Scholar] [CrossRef]
- Wei, H.R.; Huang, S.; Wang, R.; Dai, X.; Chen, J. Online Distilling from Checkpoints for Neural Machine Translation. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MN, USA, 2–7 June 2019; Volume 1, pp. 1932–1941. [Google Scholar]
- Chaudhry, A.; Ranzato, M.; Rohrbach, M.; Elhoseiny, M. Efficient Lifelong Learning with A-GEM. In Proceedings of the International Conference on Learning Representations, Vancouver, Canada, 30 April-3 May 2018. [Google Scholar]
- Chaudhry, A.; Rohrbach, M.; Elhoseiny, M.; Ajanthan, T.; Dokania, P.K.; Torr, P.H.S.; Ranzato, M. On Tiny Episodic Memories in Continual Learning. arXiv 2019, arXiv:1902.10486. [Google Scholar]
- Mirzadeh, S.I.; Farajtabar, M.; Gorur, D.; Pascanu, R.; Ghasemzadeh, H. Linear Mode Connectivity in Multitask and Continual Learning. In Proceedings of the ICLR 2021: The Ninth International Conference on Learning Representations, Virtual, 3–7 May 2021. [Google Scholar]
- Reiss, A.; Stricker, D. Introducing a New Benchmarked Dataset for Activity Monitoring. In Proceedings of the 16th International Symposium on Wearable Computers, Newcastle UK, 18–22 June 2012; pp. 108–109. [Google Scholar]
- Schmidt, P.; Reiss, A.; Duerichen, R.; Marberger, C.; Van Laerhoven, K. Introducing WESAD, a Multimodal Dataset for Wearable Stress and Affect Detection. In Proceedings of the 20th ACM International Conference on Multimodal Interaction, ICMI 2018, New York, NY, USA, 16–20 October 2018; pp. 400–408. [Google Scholar]
- Subramanian, R.; Wache, J.; Abadi, M.K.; Vieriu, R.L.; Winkler, S.; Sebe, N. ASCERTAIN: Emotion and Personality Recognition using Commercial Sensors. IEEE Trans. Affect. Comput. 2018, 9, 147–160. [Google Scholar] [CrossRef]
- Lee, S.W.; Kim, J.H.; Jun, J.; Ha, J.W.; Zhang, B.T. Overcoming Catastrophic Forgetting by Incremental Moment Matching. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30, pp. 4652–4662. [Google Scholar]
- Maschler, B.; Tatiyosyan, S.; Weyrich, M. Regularization-Based Continual Learning for Fault Prediction in Lithium-Ion Batteries. Procedia CIRP 2022, 112, 513–518. [Google Scholar] [CrossRef]
- Eker, O.; Camci, F.; Jennions, I. Major Challenges in Prognostics: Study on Benchmarking Prognostics Datasets. In Proceedings of the 2012 1st European Conference of the Prognostics and Health Management Society, Dresden, Germany, 3–6 July 2012; pp. 148–155. [Google Scholar]
- Gonzalez, G.G.; Casas, P.; Fernandez, A.; Gomez, G. Steps towards Continual Learning in Multivariate Time-Series Anomaly Detection using Variational Autoencoders. In Proceedings of the 22nd ACM Internet Measurement Conference, IMC ’22, Nice, France, 25–27 October 2022. [Google Scholar]
- Saxena, A.; Goebel, K. Turbofan Engine Degradation Simulation Data Set; NASA Ames Prognostics Data Repository: Moffett Field, CA, USA, 2008.
- Glymour, C.; Zhang, K.; Spirtes, P. Review of Causal Discovery Methods Based on Graphical Models. Front. Genet. 2019, 10, 524. [Google Scholar] [CrossRef] [PubMed]
- Castri, L.; Mghames, S.; Bellotto, N. From Continual Learning to Causal Discovery in Robotics. arXiv 2023, arXiv:2301.03886v1. [Google Scholar]
- Lopez-Paz, D.; Ranzato, M. Gradient Episodic Memory for Continual Learning. Adv. Neural. Inf. Process. Syst. 2017, 30, 6467–6476. [Google Scholar]
- Aljundi, R.; Caccia, L.; Belilovsky, E.; Caccia, M.; Lin, M.; Charlin, L.; Tuytelaars, T. Online Continual Learning with Maximal Interfered Retrieval. Adv. Neural. Inf. Process. Syst. 2019, 32, 11849–11860. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-Level Control through Deep Reinforcement Learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Bengio, E.; Pineau, J.; Precup, D. Interference and Generalization in Temporal Difference Learning. arXiv 2020, arXiv:2003.06350. [Google Scholar]
- Atkinson, C.; McCane, B.; Szymanski, L.; Robins, A. Pseudo-Rehearsal: Achieving Deep Reinforcement Learning without Catastrophic Forgetting. Neurocomputing 2021, 428, 291–307. [Google Scholar]
- Rusu, A.A.; Rabinowitz, N.C.; Desjardins, G.; Soyer, H.; Kirkpatrick, J.; Kavukcuoglu, K.; Pascanu, R.; Hadsell, R. Progressive Neural Networks. arXiv 2016, arXiv:1606.04671. [Google Scholar]
- Yoon, J.; Yang, E.; Lee, J.; Hwang, S.J. Lifelong Learning with Dynamically Expandable Networks. arXiv 2017, arXiv:1708.01547. [Google Scholar]
- He, Y.; Huang, Z.; Sick, B. Design of Explainability Module with Experts in the Loop for Visualization and Dynamic Adjustment of Continual Learning. In Proceedings of the AAAI-22 Workshop on Interactive Machine Learning, Vancouver, Canada, 28 February-1 March 2022. [Google Scholar]
- Tercan, H.; Deibert, P.; Meisen, T. Continual Learning of Neural Networks for Quality Prediction in Production Using Memory Aware Synapses and Weight Transfer. J. Intell. Manuf. 2022, 33, 283–292. [Google Scholar] [CrossRef]
- Altun, K.; Barshan, B. Human Activity Recognition using Inertial/Magnetic Sensor Units. In International Workshop on Human Behavior Understanding; Springer: Berlin/Heidelberg, Germany, 2010; pp. 38–51. [Google Scholar]
- Anguita, D.; Ghio, A.; Oneto, L.; Parra, X.; Reyes-Ortiz, J.L. Human Activity Recognition on Smartphones using a Multiclass Hardware-Friendly Support Vector Machine. In International Workshop on Ambient Assisted Living; Springer: Berlin/Heidelberg, Germany, 2012; pp. 216–223. [Google Scholar]
- Saxena, A.; Goebel, K.; Simon, D.; Eklund, N. Damage Propagation Modeling for Aircraft Engine Run-to-Failure Simulation. In Proceedings of the 2008 International Conference on Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008; pp. 1–9. [Google Scholar]

| Ref. | First Author | Year | Application Field | Datasets | Deep Learning Models | Accuracy | Details |
|---|---|---|---|---|---|---|---|
| [32] | Choi | 2021 | Time series anomaly detection | Water treatment test-bed, water distribution pipelines, Mars Science Laboratory rover | RNN, CNN, hybrid, attention | No clear one-size-fits-all method | Compare DL anomaly detection time series models with benchmark datasets |
| [33] | Deng | 2021 | Detecting deviation from normal patterns | Sensor time series datasets of water treatment systems (SWaT and WADI) | Graph Deviation Network | 54% better F-measure than the next best baseline | Combine graph neural networks with structured learning approach |
| [34] | Jiang | 2020 | Time series classification | UCR Time Series Classification Archive | MLP, CNN, ResNet | Not significantly better than 1-NN classifiers with dynamic time warping | Conduct comparison between nearest neighbor and DL models |
| [35] | Ismail Fawaz | 2019 | Time series classification | Univariate time series datasets of the UCR/UEA archive | MLP, CNN, Echo State Network | SOA performance achieved with CNN and deep Residual Networks | Conduct empirical study of DNNs for TSC |
| [36] | Han | 2022 | Leaf and wood terrestrial laser scanning time series classification | Seven broad-leaved trees (Ulmus americana) with a Rigel VZ-400i | Fully Convolutional Neural Network, LSTM-FCN, ResNet | Accurate separation of leaf and woody components from point clouds | Compare DL models on leaf and wood classification with a time series of geometric features |
| [37] | Campos-Taberner | 2020 | Classification of land use | Sentinel-2 time series data | 2-layer Bi-LSTM network | Achieving best overall accuracy of 98.7% | Evaluate deep recurrent network 2-BiLSTM for land use classification |
| [38] | Naqvi | 2020 | Real-time classification of normal and abnormal driving | Database of driver facial emotion and gaze | CNN | Superior performance vs. previous methods | Apply CNN to find changes in gaze from driver’s images |
| [39] | Zheng | 2020 | Traffic flow time series forecasting | Traffic flow time series from OpenITS | LSTM | Outperform the ARIMA and BPNN | Deploy LSTM for traffic flow forecasting |
| [40] | Hua | 2019 | Traffic prediction and user mobility of telecommunication problems | Traffic time series | Random Connectivity LSTM | Reduced computing complexity by 30% | Deploy the Random Connectivity LSTM for traffic and user mobility prediction |
| [41] | Chen | 2020 | Equipment reliability prediction | Reliability test data of a cylinder in the small trolley of vehicle assembly plant | Deep Learning method based on MLP | Significant improvement over PCA and HMM | Employ DNN framework for reliability evaluation of cylinder |
| [42] | Lim | 2021 | Time series forecasting | M4 competition (Smyl, 2020) | Exponential smoothing RNN | Hybrid model with better performance than pure methods | Conduct survey of common encoders and decoders for time series forecasting |
| [43] | Yasrab | 2021 | Plant growth forecasting | Public datasets (Arabidopsis and Brassica rapa plants) | Generative Adversarial Network | Strong performance matching expert annotation | Employ generative adversarial predictive network for leaf and root predictive segmentation |
| [44] | El-Sappagh | 2020 | Alzheimer’s disease progression detection | Time series data from Alzheimer’s Disease Neuroimaging Initiative | Ensemble of stacked CNN and Bidirectional LSTM | Much better than conventional ML | Deploy deep network for detecting common patterns for classification and regression tasks |
| [45] | Lara-Benitez | 2021 | Twelve time series forecasting tasks | Twelve public datasets cover time series applications like finance, industry, solar energy, tourism, traffic, and internet traffic | MLP, Elman RNN, LSTM, Echo State Network, GRU, CNN, Temporal Convolutional Network | LSTM and CNN are the best choices | Evaluate seven popular DL models in terms of efficiency and accuracy |
| [46] | Cao | 2020 | Investigating temporal correlations of intra-series and the correlations of inter-series | Time series datasets from energy, electrocardiogram, and traffic sectors | Spectral Temporal Graph Neural Network | Outstanding forecasting results, plus advantage of interpretability | Develop the Spectral Temporal Graph Neural Network for multivariable time series forecasting |
| [30] | Rajagukguk | 2020 | Prediction of solar irradiance and photovoltaic | Time series data of temperature, humidity, and wind speed | RNN, LSTM, GRU, CNN-LSTM | Better prediction results than conventional ML | Evaluate models based on accuracy, forecasting horizon, training time, etc. |
| [47] | Torres | 2018 | Solar energy generation forecasting | Two-year time series of PV power from a rooftop PV plant | Deep Learning approach, based on the H20 package with the grid search method for hyper-parameter optimization | Particularly suitable for big solar data, given its strong computing behavior | Deploy DL approach for solar photovoltaic power forecasting for the next day |
| [48] | Xiao | 2019 | Prediction of sea surface temperature (SST) | SST time series data from 36-year observations by satellite | Convolutional Long Short-Term Memory | Outperform persistence model, SVR, and two LSTM models | Deploy ConvLSTM to capture correlations of SST across both space and time |
| Ref. | First Author | Year | Application Field | Preprocessing Methods | Deep Learning Models | Accuracy | Details |
|---|---|---|---|---|---|---|---|
| [75] | Kanani | 2020 | ECG time series signals for monitoring and classification of cardiovascular health | Squeezing and stretching of the signal along the time axis | 1D convolution | Achieved more than 99% accuracy | Develop a DL architecture for the preprocessing process for increased training stability |
| [76] | Kisa | 2020 | Surface electromyography time series of human muscles for gesture classification | Empirical mode decomposition | CNN | Worst results for original signal vs. all IMFs images | Deploy EMD to segmented signal to obtain the Intrinsic Mode Functions (IMFs) images for CNN |
| [8] | Zheng | 2018 | Classifying eight daily activities from wearable sensors | Segmentation and transformation methods | CNN | Achieved best results with multichannel method | Evaluate the impact of segmentation and transformation methods on DL models |
| [77] | Castro Filho | 2020 | Synthetic Aperture Radar images for rice crop detection | 3D-Gamma filter and method of Savitzky and Golay | LSTM, Bidirectional LSTM | High accuracy and Kappa (>97%) | Apply 3D spatial–temporal filters and smoothing with Savitzky–Golay filter to minimize noise |
| [78] | ReBwurm | 2020 | Classifying crop type based on raw and preprocessed Sentinel 2 satellite time series data | Atmospheric correction, filtering of cloud temporal observations, focusing on vegetative periods, and masking of cloud | 1D-convolutions, RNN, self-attention model | Preprocessing can increase classification performance for all models | Present the preprocessing pipeline, including atmospheric correction, temporal selection of cloud-free observations, cloud masking, etc. |
| [79] | Kingphai | 2022 | Classifying mental workload levels from EEG time series signals | Independent component analysis based on ADJUST | CNN, Stacked GRU, Bidirectional GRU, BGRU-GRU, LSTM, BiLSTM, BiLSTM-LSTM | Most effective model performance can be achieved | Deploy automatic ICA-ADJUST to remove the frequently contaminated artifacts components before applying DL models |
| [80] | Yokkampon | 2022 | Anomaly detection of multivariate sensor time series | Multi-scale attribute matrices | Multi-scale convolutional variational autoencoder | Achieved superior performance and robustness | Develop a new ERR-based threshold setting strategy to optimize anomaly detection performance |
| [58] | Barrera- Animas | 2022 | Rainfall prediction | Correlation matrix with the Pearson correlation coefficient | LSTM, Stacked-LSTM, Bidirectional LSTM | Retained the main features of DL models | Apply Pearson correlation matric for unsupervised feature selection |
| [81] | Mishra | 2020 | Wind predictions | Discrete wavelet transformation, fast Fourier Transformation, inverse transformation | Attention, DCN, DFF, RNN, LSTM | Performed best for attention and DCN with wavelet or FFT signal | Propose a preprocessing model of discrete wavelet transformation and fast Fourier transformation |
| [10] | Livieris | 2020 | Time series data from energy section, stock market, and cryptocurrency | Iterative transformations and Augmented Dickey–Fuller test | LSTM, CNN-LSTM | Considerably improved the DL forecasting performance | Propose transformation method for enforcement of stationarity of the time series |
| [1] | Asadi | 2020 | Traffic flow time series | Time series decomposition method | Convolution-LSTM | Outperformed SOA models | Deploy time series decomposition method for separating short-term, long-term, and spatial patterns |
| [82] | Wen | 2021 | Survey of data augmentation methods | Data augmentation methods (like time domain and frequency domain), decomposition-based methods, statistical generative models | Deep generative models | Show successes in time series tasks | Compare data augmentation methods for enhancing the quality of training data |
| [83] | Azar | 2020 | Wireless network with smart sensors | Discrete wavelet transform and the error-bound compressor Squeeze | Resnet, LSTM-FCN, GRU-FCN, FCN | Achieve the optimal trade-off between data compression and quality | Develop a compression approach with discrete wavelet transform and error-bound compressor |
| Ref. | First Author | Year | Application Field | Motivations for Deploying CL | Continual Learning Models | Accuracy | Details |
|---|---|---|---|---|---|---|---|
| [107] | Sah | 2022 | Wearable sensors for activity recognition | Addressing the catastrophic forgetting in the non-stationary sequential learning process | A-GEM, ER-Ring, MC-SGD | Still need improvement for multitask training | Compare CL approaches for sensor systems |
| [108] | Matteoni | 2022 | Human state monitoring of domain- incremental scenario | Overcoming the non-stationary environments | Replay, elastic weight consolidation, learning without forgetting, naive and cumulative strategies | Existing strategies struggle to accumulate knowledge | Assess the ability of existing CL methods for knowledge accumulation over time |
| [93] | Kiyasseh | 2021 | Multiple clinics with various sensors for cardiac arrhythmia classification | Temporal data in clinics are often non-stationary | Buffer strategy to construct the continual learning model CLOPS | Outperform GEM and MIR | Apply uncertainty-based acquisition functions, for instance, replay |
| [109] | Kwon | 2021 | Deployment in mobile and embedded sensing devices | Addressing the resources requirements and limitations of the mobile and embedded sensing devices | CL approaches- regularization, replay and replay with examples | Best results for replay with exemplars schemes | Compare three main CL approaches for mobile and embedded sensing applications like activity recognition |
| [110] | Cossu | 2021 | Sensors of the robotics system | Achieving walk learning in different environments | Continual learning in RNNs | Highlight the importance of a clear specification | Evaluate CL approaches in class-incremental scenarios for speech recognition and sequence classification |
| [111] | He | 2022 | Identification of anomalies | Addressing the lack of transparency for CL modules | Explainability module based on dimension reduction methods and visualization methods | Proposed evaluation score based on metric | Propose the conceptual design of explainability module for CL techniques |
| [112] | Doshi | 2022 | Video anomaly detection (VAD) | Overcoming practical VAD challenges | Incremental updating of the memory module, experience replay | Outperform existing methods significantly | Develop a two-stage CL approach with feature embedding and kNN-based RNN model |
| [113] | Maschler | 2021 | Metal-forming time series dataset of a discrete manufacturing | Providing automatic capability for adapting formerly learned knowledge to new settings | Continual learning approach based on regularization strategies | Improved performance vs. no regularization | Compare CL approaches of regularization strategies on industrial metal-forming data for fault prediction |
| [114] | Maschler | 2020 | Fault prediction in a distributed environment | Real-world restrictions like industrial espionage and legal privacy concern prevent the centralizing of data from factories for the DL training | LSTM algorithm with elastic weight consolidation | Promising results for industrial automation scenarios | Apply elastic weight consolidation for distributed, cooperative learning |
| [115] | Bayram | 2020 | Auditory scene analysis | Addressing high-value background noise and high computational demands | Continual learning approach based on Hidden Markov Model | Achieve high accuracy | Develop an HMM-based CL approach with UED and retraining for time series classification |
| [106] | Xiao | 2022 | Evolving long-term streaming traffic flow | Addressing the non-stationary data distribution during policy evolution | Prioritized experience replay strategy for transferring learned knowledge into the model | Able to continuously learn and predict traffic flow over time | Formulate the traffic flow prediction problem as continuous reinforcement learning task |
| [116] | Schillaci | 2021 | Transferring the knowledge gained from the greenhouse research facilities to greenhouses | Addressing problems like the requirement of large-scale re-training in the new facility | Continual learning RNN model with episodic memory replay and consolidation | Outperform standard memory consolidation approaches | Present a CL approach of an episodic memory system and memory consolidation |
| [94] | Gupta | 2021 | In-process quality prediction by manufacturers | Addressing the lack of practical variability among industrial sensor networks | Generator-based RNN continual learning module | Possible significant performance enhancement | Deploy task-specific generative models to augment data for target tasks |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ao, S.-I.; Fayek, H. Continual Deep Learning for Time Series Modeling. Sensors 2023, 23, 7167. https://doi.org/10.3390/s23167167
Ao S-I, Fayek H. Continual Deep Learning for Time Series Modeling. Sensors. 2023; 23(16):7167. https://doi.org/10.3390/s23167167
Chicago/Turabian StyleAo, Sio-Iong, and Haytham Fayek. 2023. "Continual Deep Learning for Time Series Modeling" Sensors 23, no. 16: 7167. https://doi.org/10.3390/s23167167
APA StyleAo, S.-I., & Fayek, H. (2023). Continual Deep Learning for Time Series Modeling. Sensors, 23(16), 7167. https://doi.org/10.3390/s23167167






