Depth-Dependent Control in Vision-Sensor Space for Reconfigurable Parallel Manipulators
Abstract
1. Introduction
1.1. Reconfiguration and Redundancy on Parallel Robots
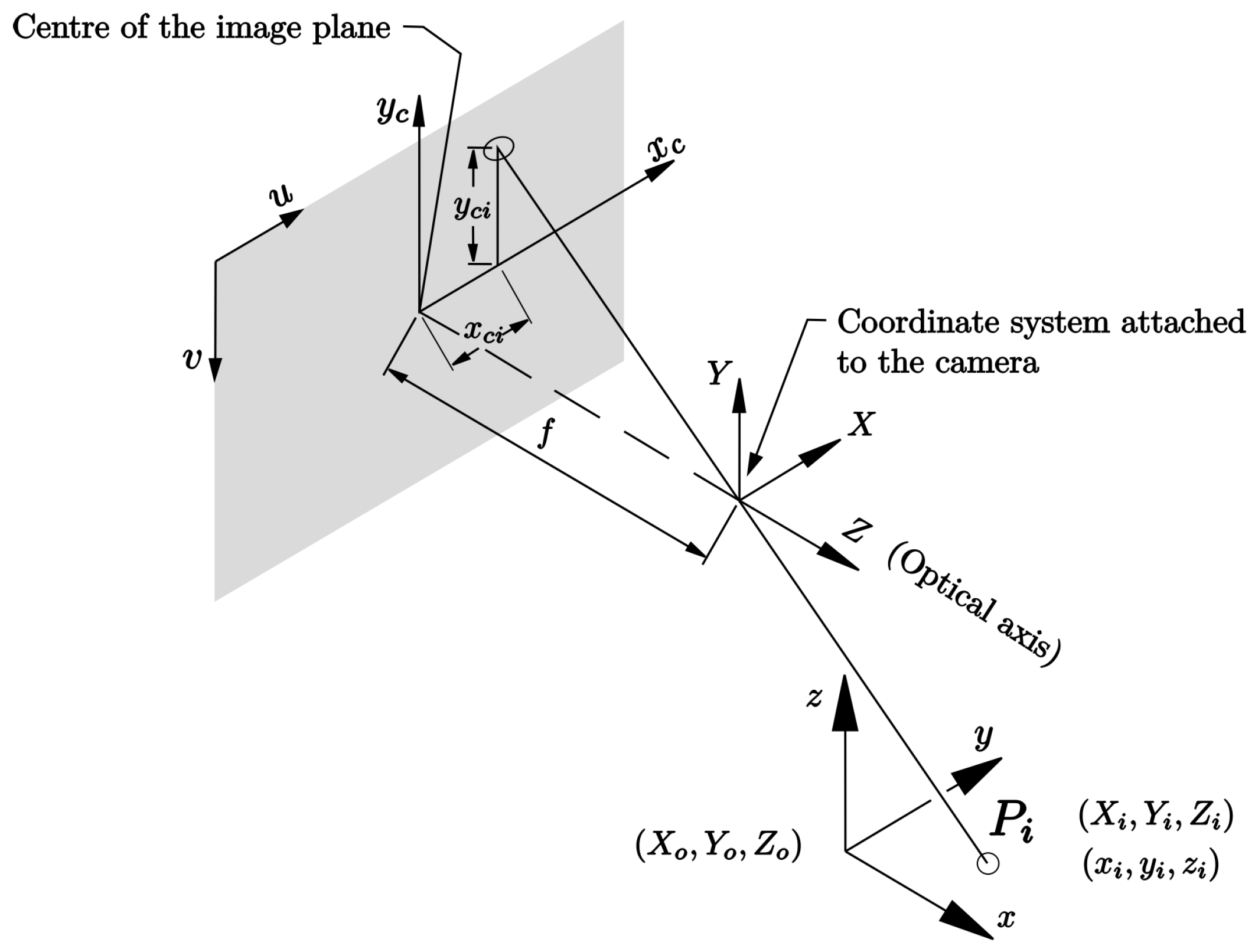
1.2. Camera Space Manipulation
2. Modeling of the Reconfigurable Delta Robot
2.1. Description of the Reconfigurable Delta Robot
2.2. Forward Geometric Model
2.3. Forward Kinematic Model
2.4. Resolution of the Redundancy Problem
2.5. Inverse Geometric Model
- (i)
- Solve the inverse kinematics for a specified value of R as if it were the original delta robot.
- (ii)
- Calculate the Jacobian matrix of the reconfigurable delta robot.
- (iii)
- Calculate the condition number and compare it with the smallest previous condition number of the Jacobian matrix. If the current one is smaller, the actual joint values are the solution.
- (iv)
- Repeat the process iteratively varying R over its entire range of motion, i.e., from 85 mm to 500 mm.
- (v)
- The solution with the smallest condition number is obtained at the end of all iterations.
3. Image Jacobian
4. Control Laws for the Reconfigurable Robot
4.1. Encoders Based Control Laws
4.2. Control Law in Vision Sensor Space
5. Experiments
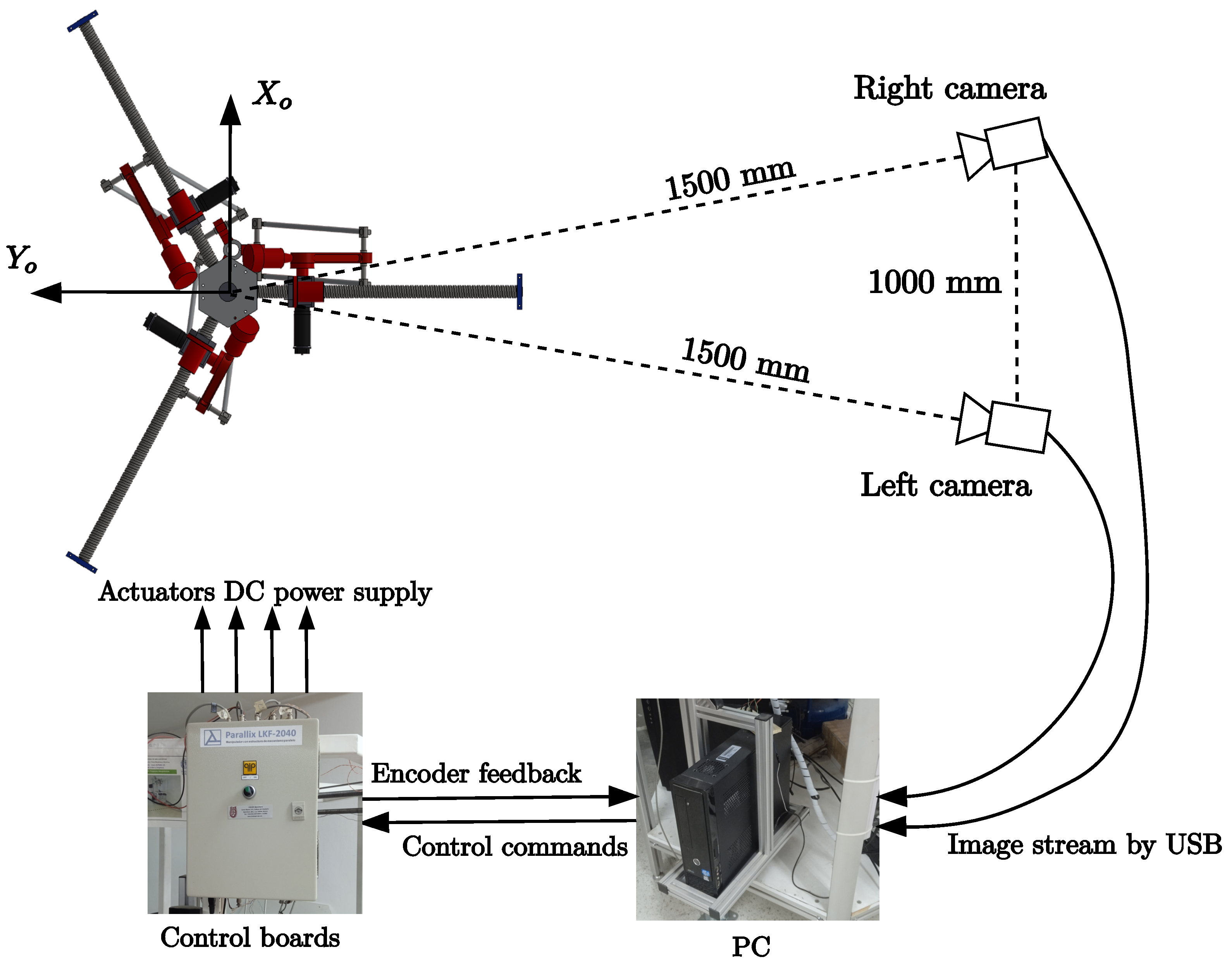
5.1. Hardware
5.2. Software
- (i)
- A main thread for all the cameras,
- (ii)
- A thread to send commands to the robot,
- (iii)
- A thread for the control law calculation.
5.3. Testing Configuration
- (i)
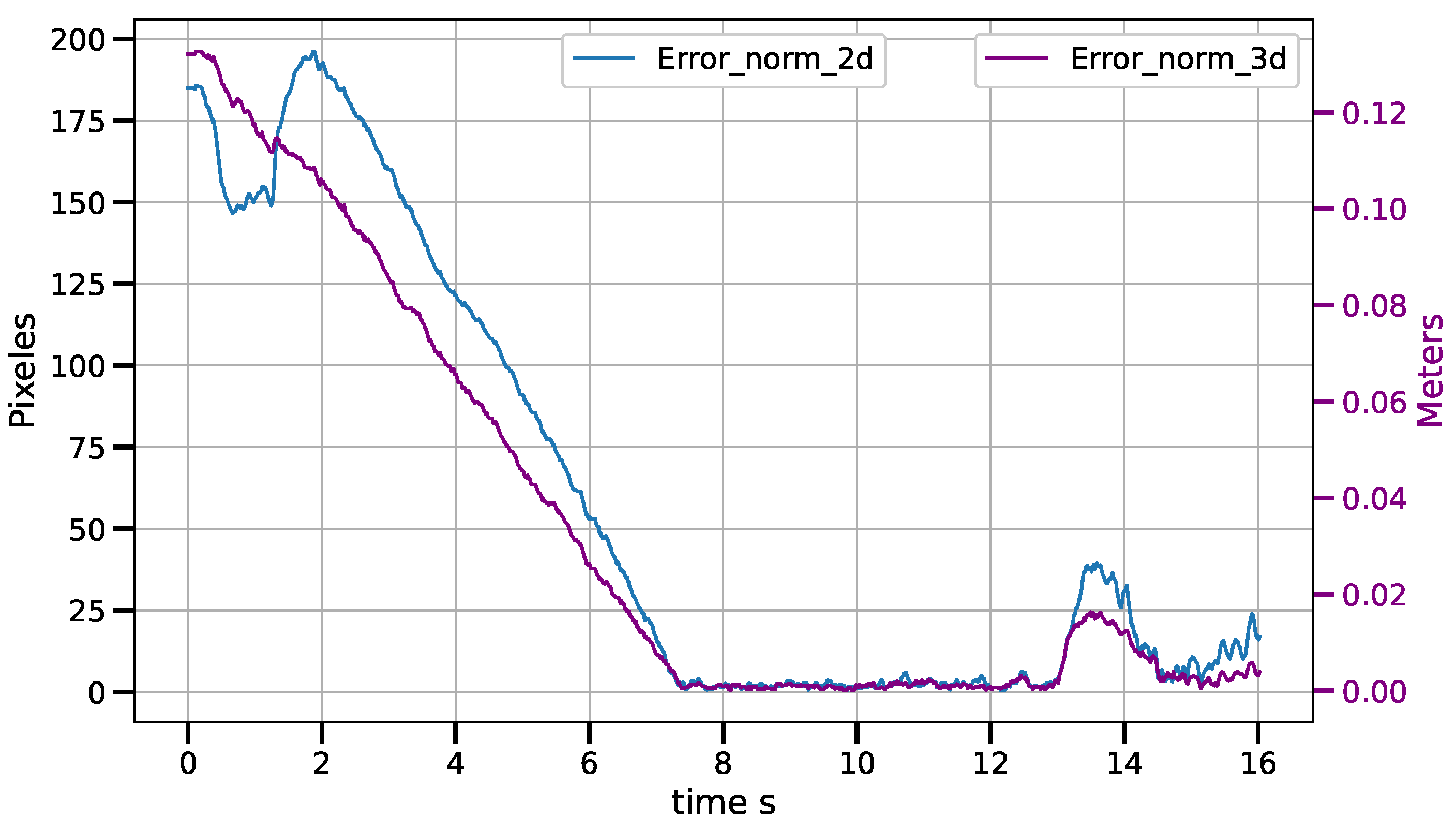
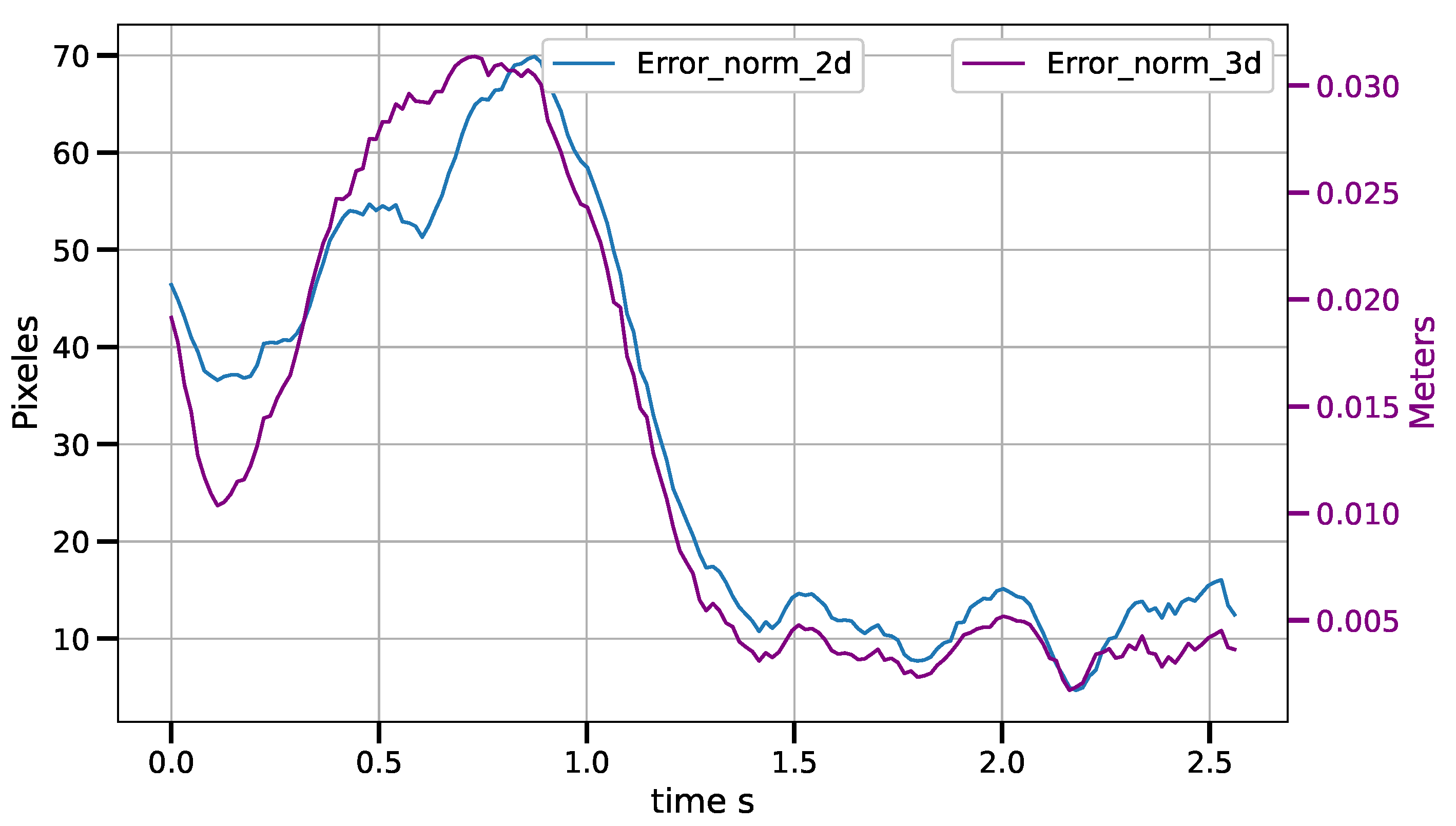
- The first set of experiments for the CSM control law consists of static positioning tasks. Four position tasks are performed three times each. The positions are chosen randomly inside the workspace of the robot. The maneuver is considered successful when an error vector norm of less than 2 pixel is achieved during, at least, 40 control cycles. This error vector contains the coordinates in image space of the two cameras. Speed compensation is set to zero to avoid noise input due to the velocity estimator.
- (ii)
- The second set of experiments for the CSM control law consists of tracking an object moving, on the conveyor, following a linear trajectory at constant speed. No a priori information about the target trajectory is used in the experiments. The target is positioned on a conveyor belt placed within the robot’s workspace. The robot first moves to the target object. The conveyor is started only once a static position has been achieved using the previously mentioned conditions. The conveyor moves at a constant speed with the robot following the object’s position. The test is stopped when the object reaches the edge of the robot’s workspace. The control law with speed compensation is used.
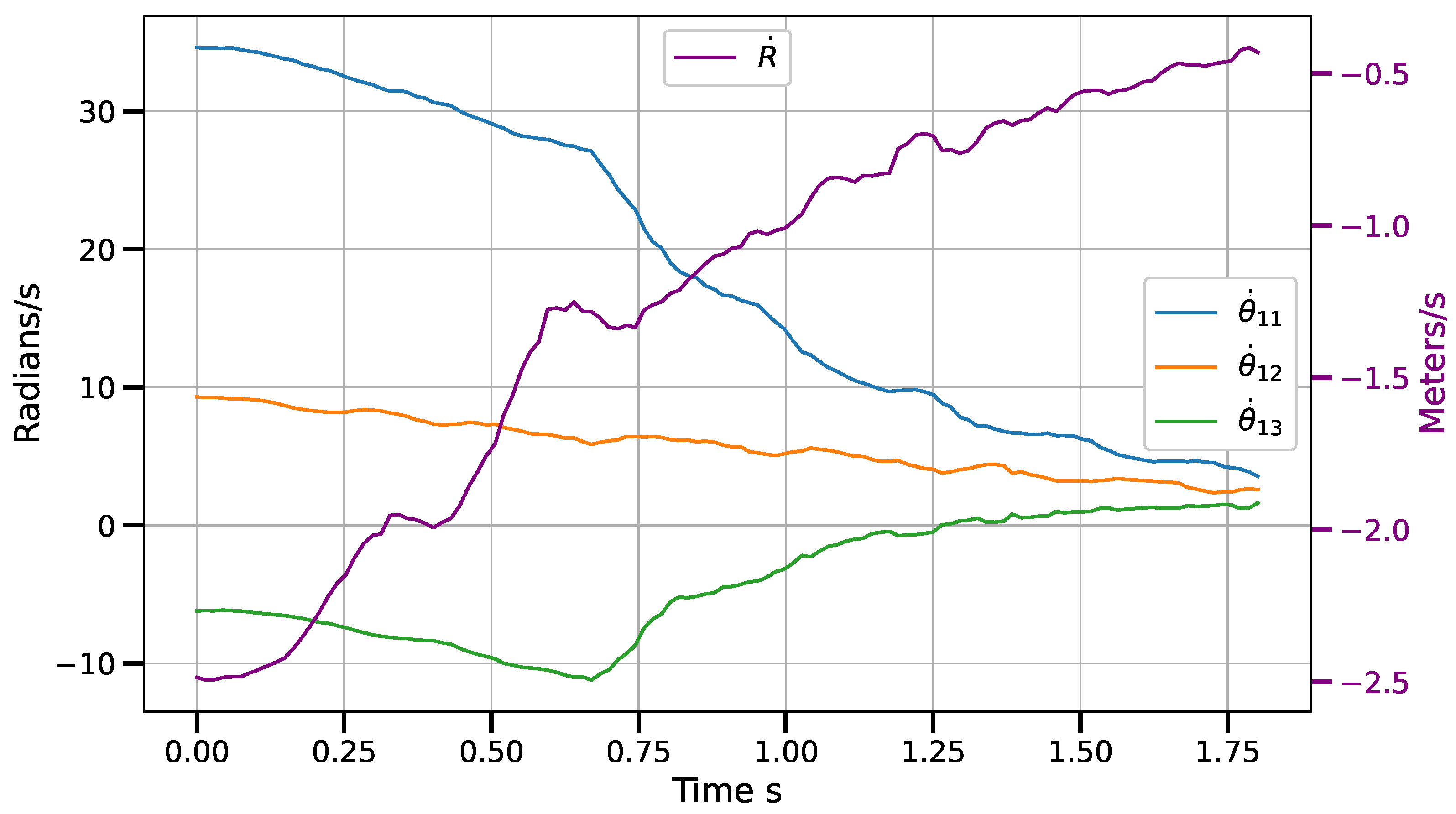
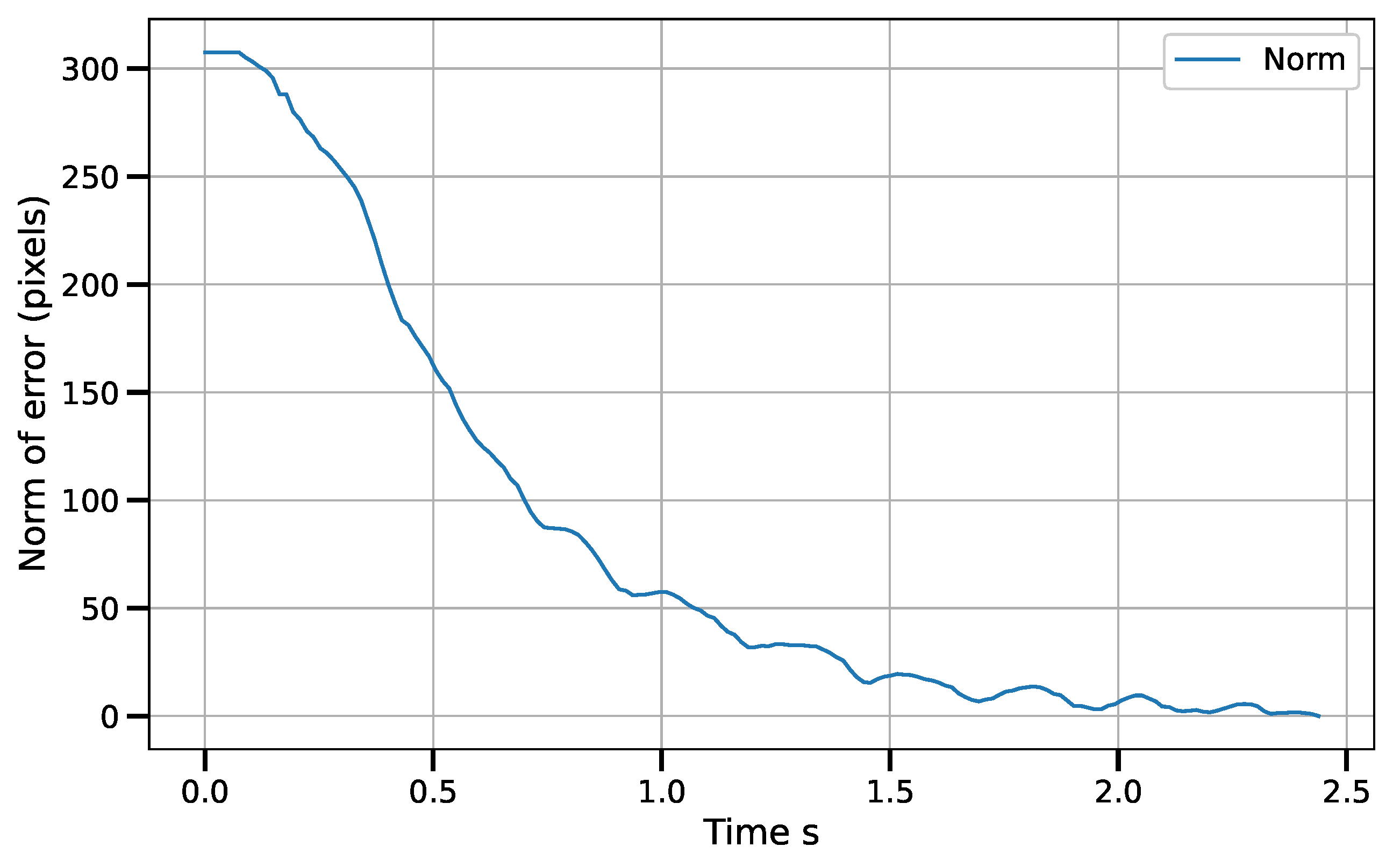
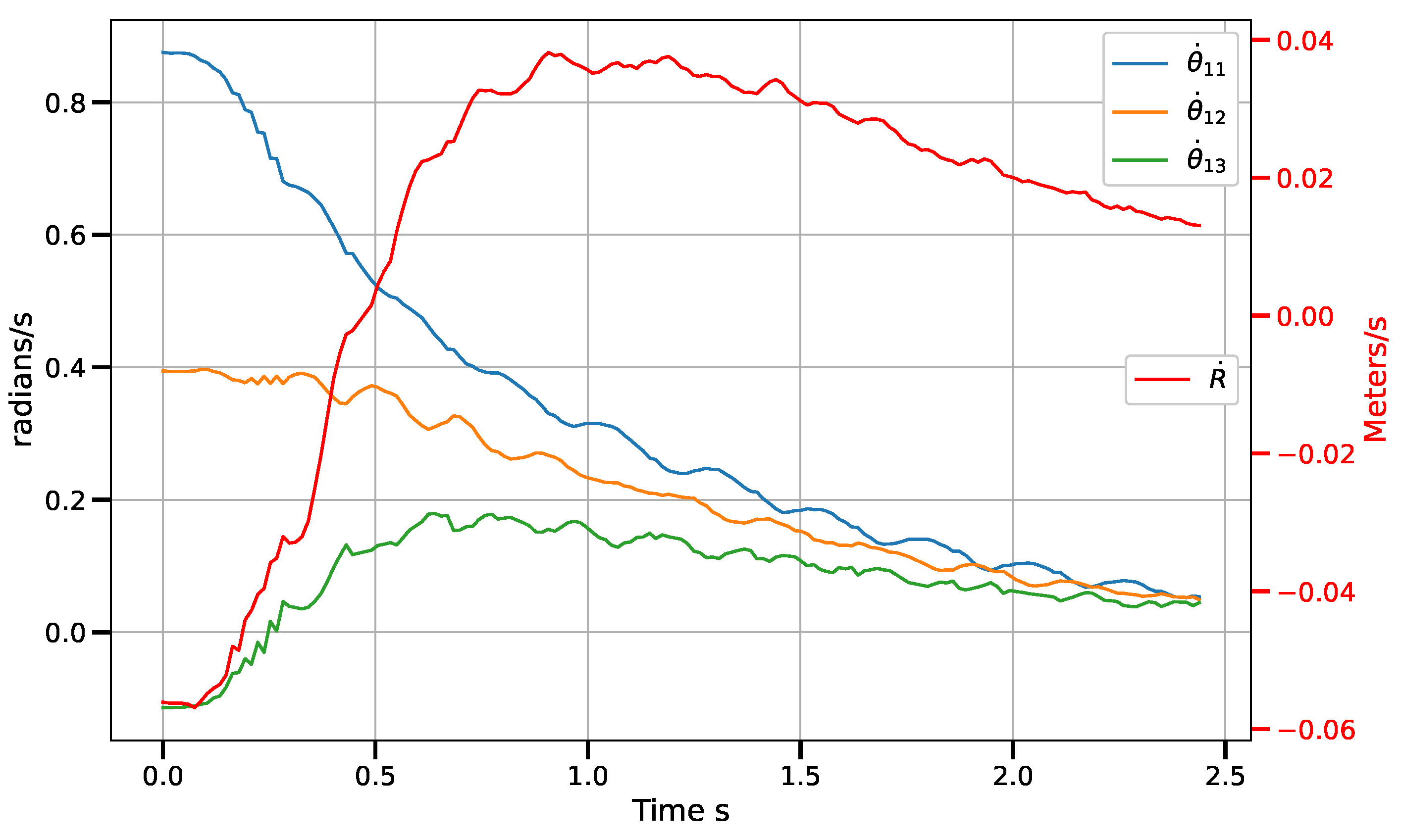
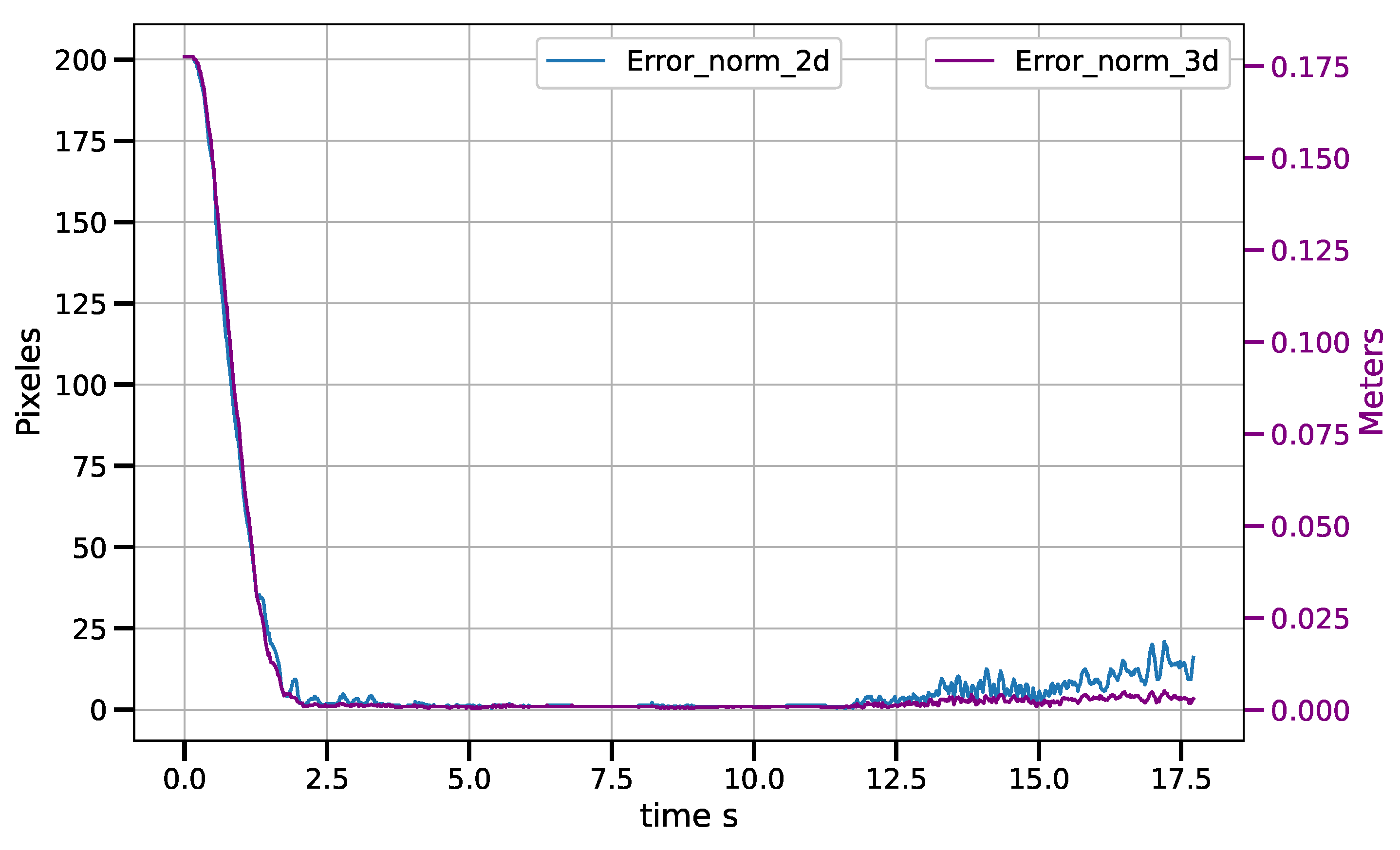
6. Results and Discussion
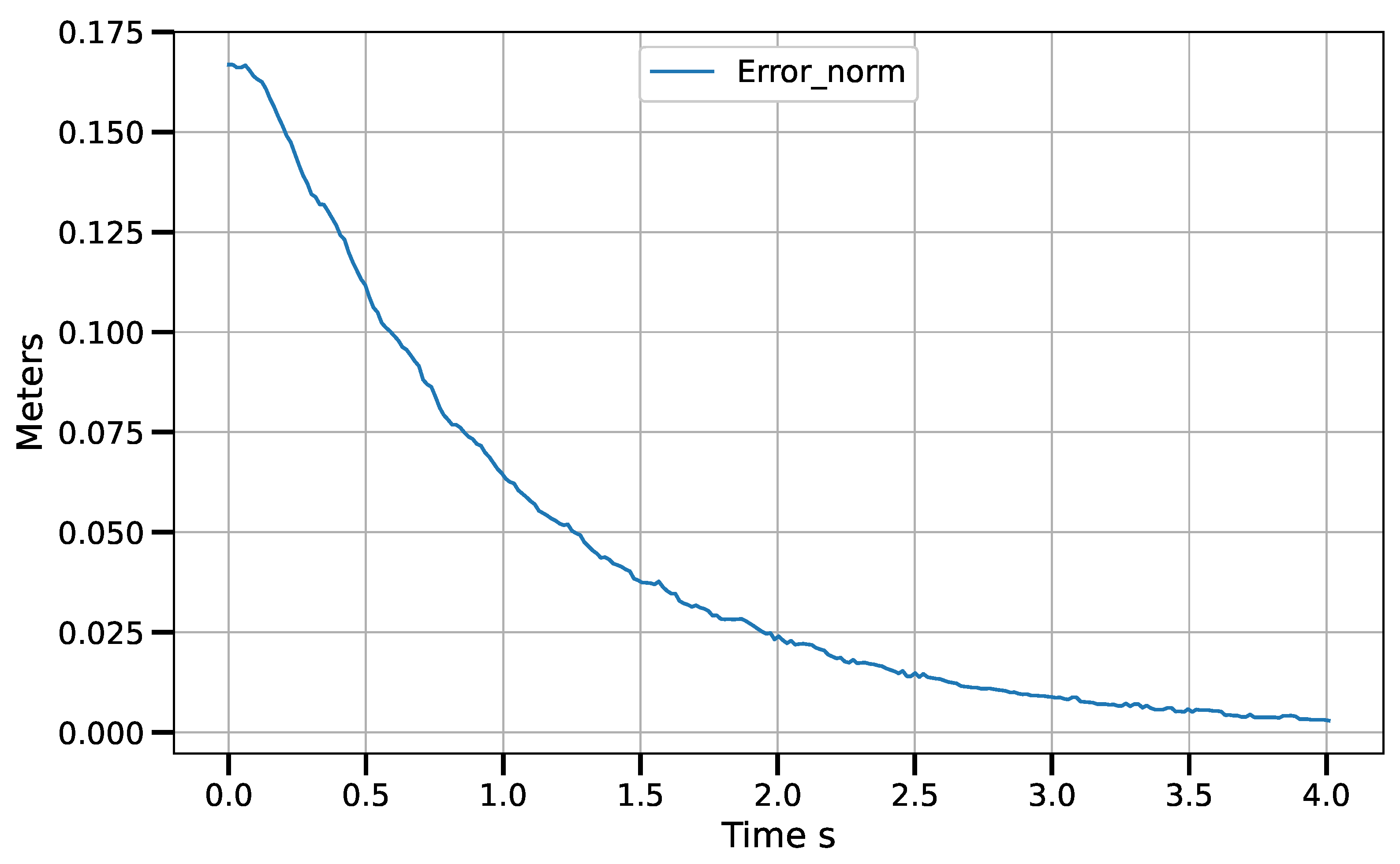
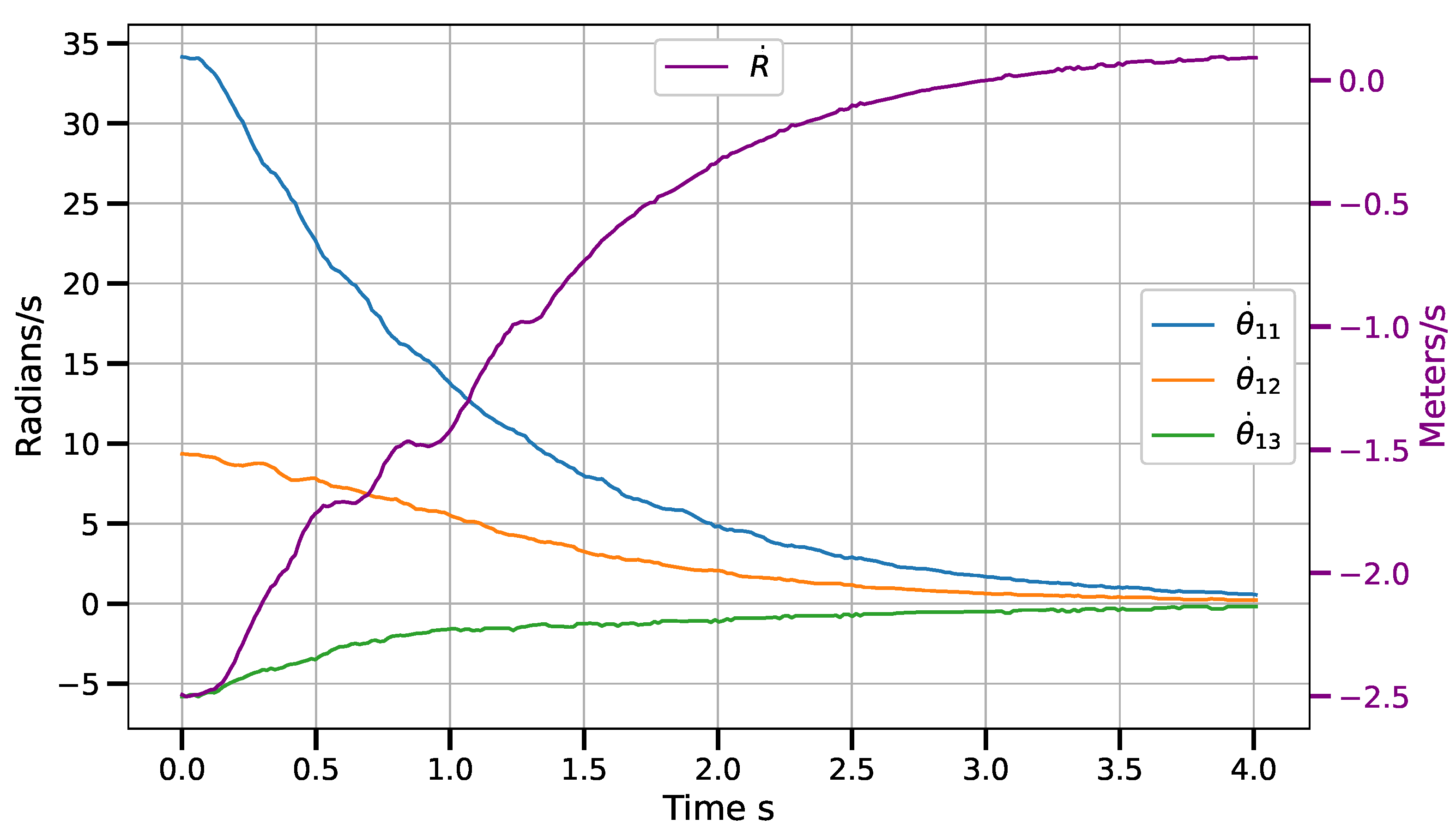
6.1. Results
6.1.1. Exponential Convergence Control Laws vs. Piece-Wise Variants
6.1.2. Control Law in Vision-Sensor Space
6.2. Discussion
7. Conclusions
Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Clavel, R. DELTA, a fast robot with parallel geometry. In Proceedings of the 18th International Symposium on Industrial Robots, Lausanne, Switzerland, 26–28 April 1988; Burckhardt, C.W., Ed.; Springer: New York, NY, USA, 1988; pp. 91–100. [Google Scholar]
- Merlet, J.P. Parallel Robots; Kluwer Academic Publishers: Alphen aan den Rijn, The Netherlands, 2006. [Google Scholar]
- Mostashiri, N.; Dhupia, J.S.; Verl, A.W.; Xu, W. A Review of Research Aspects of Redundantly Actuated Parallel Robotsw for Enabling Further Applications. IEEE/ASME Trans. Mechatronics 2018, 23, 1259–1269. [Google Scholar] [CrossRef]
- Pandilov, Z.; Dukovski, V. Comparison of the characteristics between serial and parallel robots. Acta Tech. Corviniensis-Bull. Eng. 2014, 7, 143–160. [Google Scholar]
- Zhang, H.; Fang, H.; Zou, Q. Non-singular terminal sliding mode control for redundantly actuated parallel mechanism. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420919548. [Google Scholar] [CrossRef]
- Loredo, A.; Maya, M.; González, A.; Cardenas, A.; Gonzalez-Galvan, E.; Piovesan, D. A Novel Velocity-Based Control in a Sensor Space for Parallel Manipulators. Sensors 2022, 22, 7323. [Google Scholar] [CrossRef] [PubMed]
- Pandilov, Z.; Dukovski, V. Several open problems in parallel robotics. Acta Tech. Corviniensis-Bull. Eng. 2011, 4, 77–84. [Google Scholar]
- Bentaleb, T.; Iqbal, J. On the improvement of calibration accuracy of parallel robots—Modeling and optimization. J. Theor. Appl. Mech. 2020, 58, 261–272. [Google Scholar] [CrossRef]
- Milutinović, D.; Slavković, N.; Kokotović, B.; Milutinović, M.; Živanović, S.; Dimić, Z. Kinematic modeling of reconfigurable parallel robots based on DELTA concept. In Proceedings of the 11th International Scientific Conference MMA 2012—Advanced Production Technologies, Novi Sad, Serbia, 20–21 September 2012; University of Novi Sad, Faculty of Technical Scienes, Department for Production Engineering: Novi Sad, Serbia, 2012; pp. 259–262. [Google Scholar]
- Plitea, N.; Lese, D.; Pisla, D.; Vaida, C. Structural design and kinematics of a new parallel reconfigurable robot. Robot. Comput.-Integr. Manuf. 2013, 29, 219–235. [Google Scholar] [CrossRef]
- Luces, M.; Beno Benhabib, J.K.M. A Review of Redundant Parallel Kinematic Mechanisms. J. Intell. Robot. Syst. 2017, 86, 175–198. [Google Scholar] [CrossRef]
- Gosselin, C.; Schreiber, L.T. Redundancy in Parallel Mechanisms: A Review. Appl. Mech. Rev. 2018, 70, 010802. [Google Scholar] [CrossRef]
- Mostashiri, N.; Dhupia, J.; Xu, W. Redundancy in Parallel Robots: A Case Study of Kinematics of a Redundantly Actuated Parallel Chewing Robot. In Proceedings of the RITA 2018, Kuala Lumpur, Malaysia, 16–18 December 2018; Abdul Majeed, A.P.P., Mat-Jizat, J.A., Hassan, M.H.A., Taha, Z., Choi, H.L., Kim, J., Eds.; Springer: Singapore, 2020; pp. 65–78. [Google Scholar]
- Harada, T.; Angeles, J. From the McGill pepper-mill carrier to the Kindai ATARIGI Carrier: A novel two limbs six-dof parallel robot with kinematic and actuation redundancy. In Proceedings of the 2017 IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, China, 5–8 December 2017; pp. 1328–1333. [Google Scholar] [CrossRef]
- Moosavian, A.; Xi, F.J. Modular design of parallel robots with static redundancy. Mech. Mach. Theory 2016, 96, 26–37. [Google Scholar] [CrossRef]
- Maya, M.; Castillo, E.; Lomelí, A.; González-Galván, E.; Cárdenas, A. Workspace and Payload-Capacity of a New Reconfigurable Delta Parallel Robot. Int. J. Adv. Robot. Syst. 2013, 10, 56. [Google Scholar] [CrossRef]
- Hu, L.; Gao, H.; Qu, H.; Liu, Z. Closeness to singularity based on kinematics and dynamics and singularity avoidance of a planar parallel robot with kinematic redundancy. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 3717–3730. [Google Scholar] [CrossRef]
- Pulloquinga, J.L.; Escarabajal, R.J.; Ferrándiz, J.; Vallés, M.; Mata, V.; Urízar, M. Vision-Based Hybrid Controller to Release a 4-DOF Parallel Robot from a Type II Singularity. Sensors 2021, 21, 4080. [Google Scholar] [CrossRef]
- Singh, A.; Kalaichelvi, V.; Karthikeyan, R. A survey on vision guided robotic systems with intelligent control strategies for autonomous tasks. Cogent Eng. 2022, 9, 2050020. [Google Scholar] [CrossRef]
- Cherubini, A.; Navarro-Alarcon, D. Sensor-based control for collaborative robots: Fundamentals, challenges, and opportunities. Front. Neurorobot. 2021, 14, 113. [Google Scholar] [CrossRef] [PubMed]
- Hutchinson, S.; Hager, G.D.; Corke, P.I. A tutorial on visual servo control. IEEE Trans. Robot. Autom. 1996, 12, 651–670. [Google Scholar] [CrossRef]
- Chaumette, F.; Hutchinson, S. Visual servo control. I. Basic approaches. IEEE Robot. Autom. Mag. 2006, 13, 82–90. [Google Scholar] [CrossRef]
- Ren, X.; LI, H. Uncalibrated Image-Based Visual Servoing Control with Maximum Correntropy Kalman Filter. IFAC-PapersOnLine 2020, 53, 560–565. [Google Scholar] [CrossRef]
- Skaar, S.B.; Brockman, W.H.; Hanson, R. Camera-Space Manipulation. Int. J. Robot. Res. 1987, 6, 20–32. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, W.; Zhao, C.; Skaar, S.B.; Wang, Q. A Differential Evolution Approach for Camera Space Manipulation. In Proceedings of the 2020 2nd World Symposium on Artificial Intelligence (WSAI), Karlsruhe, Germany, 14–16 September 2020; IEEE: Manhattan, NY, USA, 2020; pp. 103–107. [Google Scholar]
- Weiss, L.; Sanderson, A.; Neuman, C. Dynamic sensor-based control of robots with visual feedback. IEEE J. Robot. Autom. 1987, 3, 404–417. [Google Scholar] [CrossRef]
- Lin, C.J.; Shaw, J.; Tsou, P.C.; Liu, C.C. Vision servo based Delta robot to pick-and-place moving parts. In Proceedings of the 2016 IEEE International Conference on Industrial Technology (ICIT), Taipei, Taiwan, 14–17 March 2016; pp. 1626–1631. [Google Scholar] [CrossRef]
- Rendón-Mancha, J.M.; Cárdenas, A.; García, M.A.; Lara, B. Robot positioning using camera-space manipulation with a linear camera model. IEEE Trans. Robot. 2010, 26, 726–733. [Google Scholar] [CrossRef]
- Huynh, B.P.; Kuo, Y.L. Dynamic Hybrid Filter for Vision-Based Pose Estimation of a Hexa Parallel Robot. J. Sens. 2021, 2021, 9990403. [Google Scholar] [CrossRef]
- Amjad, J.; Humaidi, A.I.A. Design of Augmented Nonlinear PD Controller of Delta/Par4-Like Robot. J. Control Sci. Eng. 2019, 2019, 7689673. [Google Scholar] [CrossRef]
- Hoang, X.B.; Pham, P.C.; Kuo, Y.L. Collision Detection of a HEXA Parallel Robot Based on Dynamic Model and a Multi-Dual Depth Camera System. Sensors 2022, 22, 5922. [Google Scholar] [CrossRef] [PubMed]
- Kansal, S.; Mukherjee, S. Vision-based kinematic analysis of the Delta robot for object catching. Robotica 2022, 40, 2010–2030. [Google Scholar] [CrossRef]
- Huynh, B.P.; Kuo, Y.L. Dynamic Filtered Path Tracking Control for a 3RRR Robot Using Optimal Recursive Path Planning and Vision-Based Pose Estimation. IEEE Access 2020, 8, 174736–174750. [Google Scholar] [CrossRef]
- Zake, Z.; Chaumette, F.; Pedemonte, N.; Caro, S. Vision-Based Control and Stability Analysis of a Cable-Driven Parallel Robot. IEEE Robot. Autom. Lett. 2019, 4, 1029–1036. [Google Scholar] [CrossRef]
- Zake, Z.; Chaumette, F.; Pedemonte, N.; Caro, S. Robust 2½D Visual Servoing of A Cable-Driven Parallel Robot Thanks to Trajectory Tracking. IEEE Robot. Autom. Lett. 2020, 5, 660–667. [Google Scholar] [CrossRef]
- Lopez-Lara, J.G.; Maya, M.E.; González, A.; Cardenas, A.; Felix, L. Image-based control of delta parallel robots via enhanced LCM-CSM to track moving objects. Ind. Robot. Int. J. Robot. Res. Appl. 2020, 47, 559–567. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Bradski, G. The OpenCV Library. Dr. Dobb’S J. Softw. Tools Prof. Program. 2000, 25, 120–123. [Google Scholar]
- PyQt. PyQt Reference Guide. 2012. Available online: https://doc.bccnsoft.com/docs/PyQt5/ (accessed on 7 June 2023).





| Error (mm) | |
|---|---|
| Average | 0.600 |
| Max | 1.530 |
| Min | 0.172 |
| Std. Dev. | 0.445 |
| Conveyor Speed | Average Error |
|---|---|
| 6.5 cm/s | 2.5 mm |
| 9.3 cm/s | 3.9 mm |
| 12.7 cm/s | 11.5 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Franco-López, A.; Maya, M.; González, A.; Cardenas, A.; Piovesan, D. Depth-Dependent Control in Vision-Sensor Space for Reconfigurable Parallel Manipulators. Sensors 2023, 23, 7039. https://doi.org/10.3390/s23167039
Franco-López A, Maya M, González A, Cardenas A, Piovesan D. Depth-Dependent Control in Vision-Sensor Space for Reconfigurable Parallel Manipulators. Sensors. 2023; 23(16):7039. https://doi.org/10.3390/s23167039
Chicago/Turabian StyleFranco-López, Arturo, Mauro Maya, Alejandro González, Antonio Cardenas, and Davide Piovesan. 2023. "Depth-Dependent Control in Vision-Sensor Space for Reconfigurable Parallel Manipulators" Sensors 23, no. 16: 7039. https://doi.org/10.3390/s23167039
APA StyleFranco-López, A., Maya, M., González, A., Cardenas, A., & Piovesan, D. (2023). Depth-Dependent Control in Vision-Sensor Space for Reconfigurable Parallel Manipulators. Sensors, 23(16), 7039. https://doi.org/10.3390/s23167039










