Deep Learning-Aided Modulation Recognition for Non-Orthogonal Signals
Abstract
1. Introduction
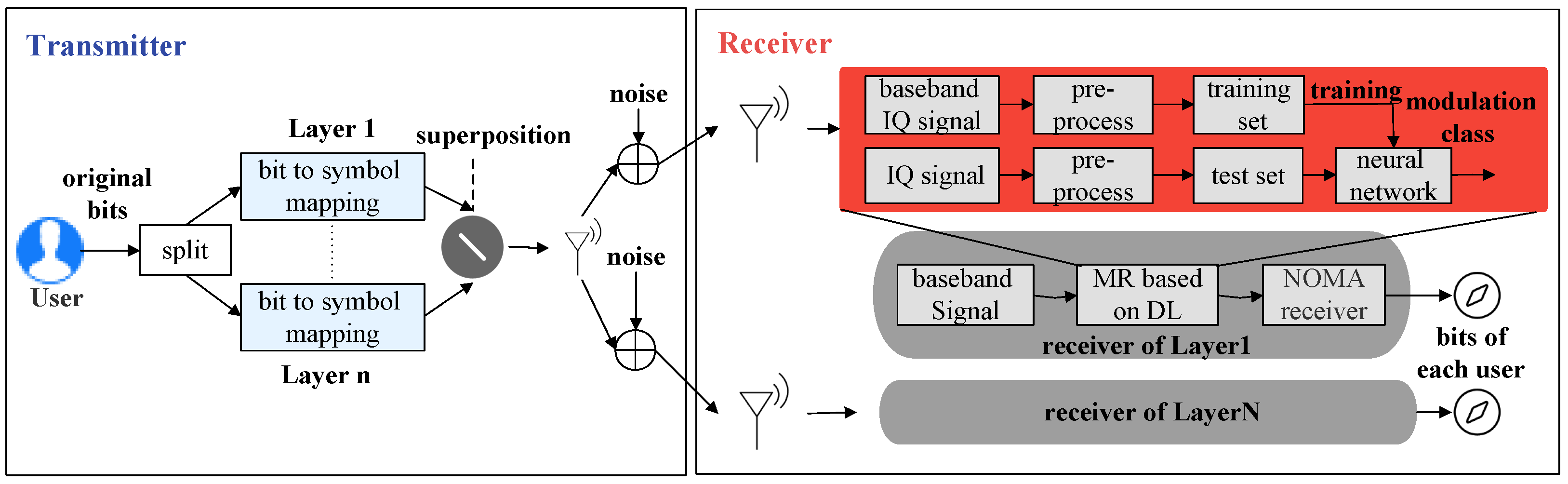
- For the downlink non-orthogonal scenario, the superposition of signals can cause irregular signal shapes. The conventional hand-crafted features become inefficient. This poses a challenge to both the feature design and signal classification stages since the learning ability of the conventional classifier is limited.
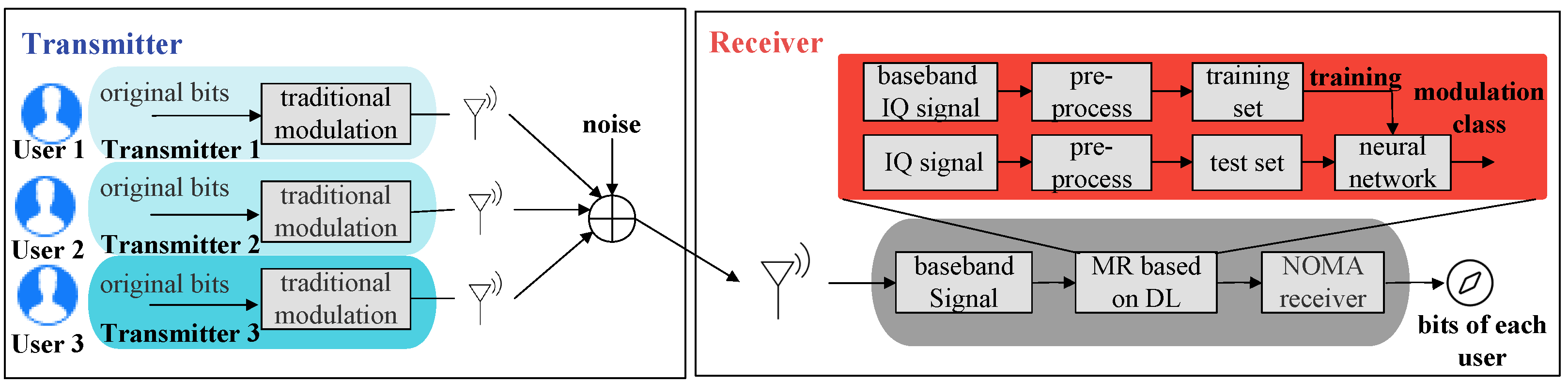
- For uplink non-orthogonal scenarios, the challenge is more significant. With the increase in the transmit signal layers, the combinatorial number of classification types explodes exponentially. Traditional classification methods thus suffer from high computational complexity and low recognition rate.
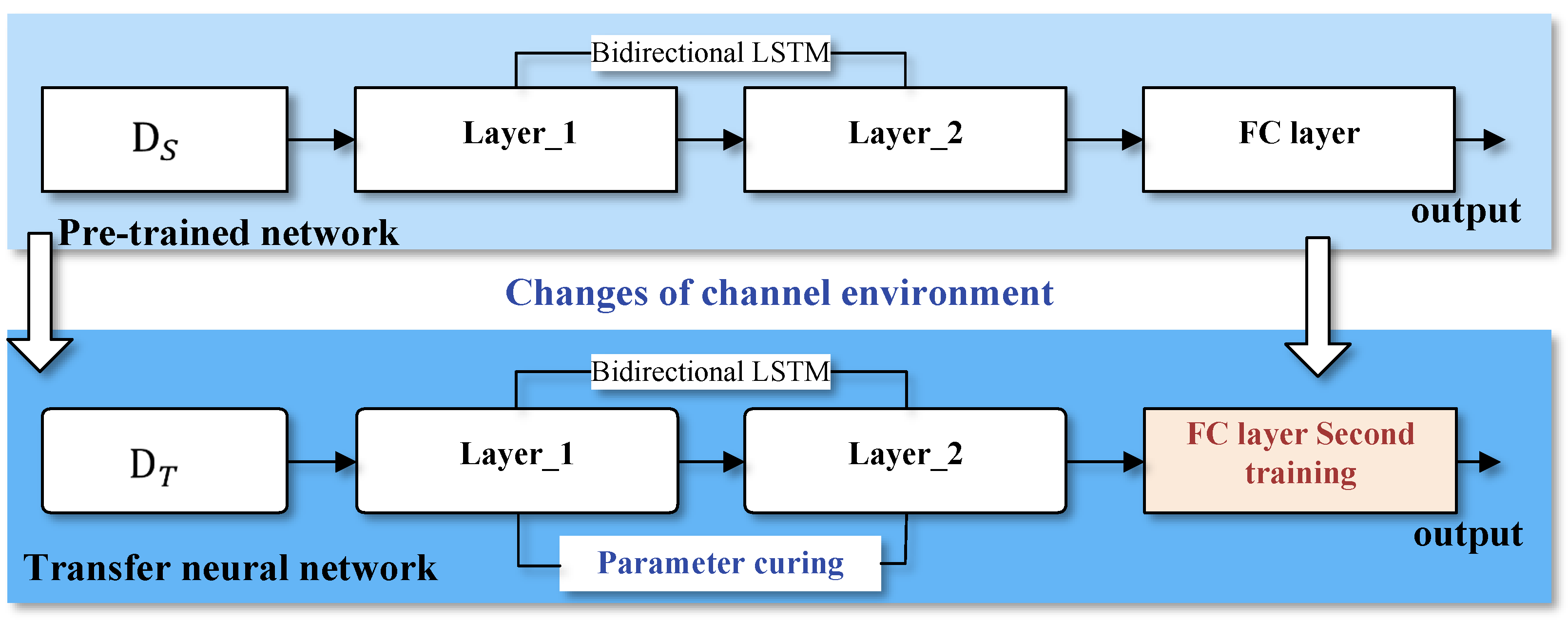
- In the downlink scenario, we propose a modulation recognition method based on BiLSTM to extract the sequential information of the superimposed signals. For the scenario where the number of training samples is insufficient, transfer learning is used to improve the network modulation recognition ability in small sample scenarios.
- In the uplink scenario, we consider Spatio-Temporal Fusion Network based on Attention Mechanism (STFAN), which can deal with the explosive increase of the combinatorial number of classification types. The spatial feature extraction module uses an Inception block to efficiently reduce the computational complexity, and the temporal feature extraction module uses BiLSTM to mine the effective signal features in the time domain.
- Experiments show that the proposed AMR methods for non-orthogonal signals outperform the conventional methods as well as vanilla DL methods, such as CNN and LSTM, under various channel conditions. Significant advantages of the proposed methods with respect to both recognition accuracy and wireless channel robustness are observed, especially in a high SNR region.
2. Signals Model for Non-Orthogonal Transmission Systems
2.1. Downlink Non-Orthogonal System Model
2.2. Uplink Non-Orthogonal System Model
3. Proposed Deep Transfer Learning Incorporated BiLSTM for Downlink AMR
3.1. Neural Network Architecture with BiLSTM
- Forget Gate
- Input Gate
- Output Gate
- Cell status update
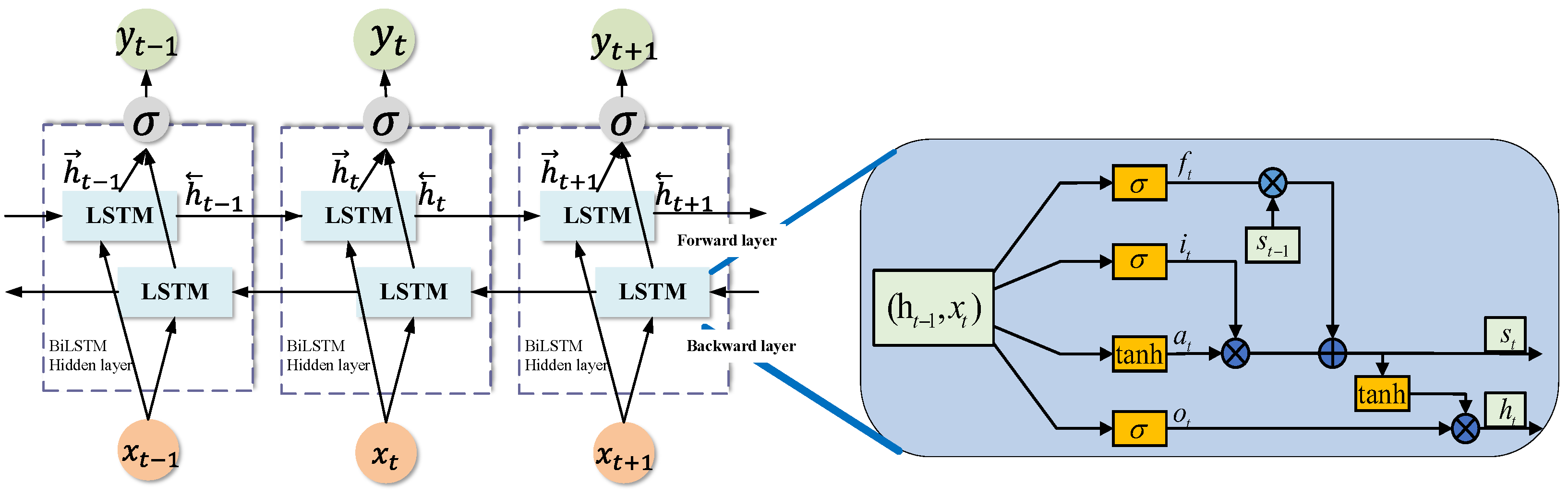
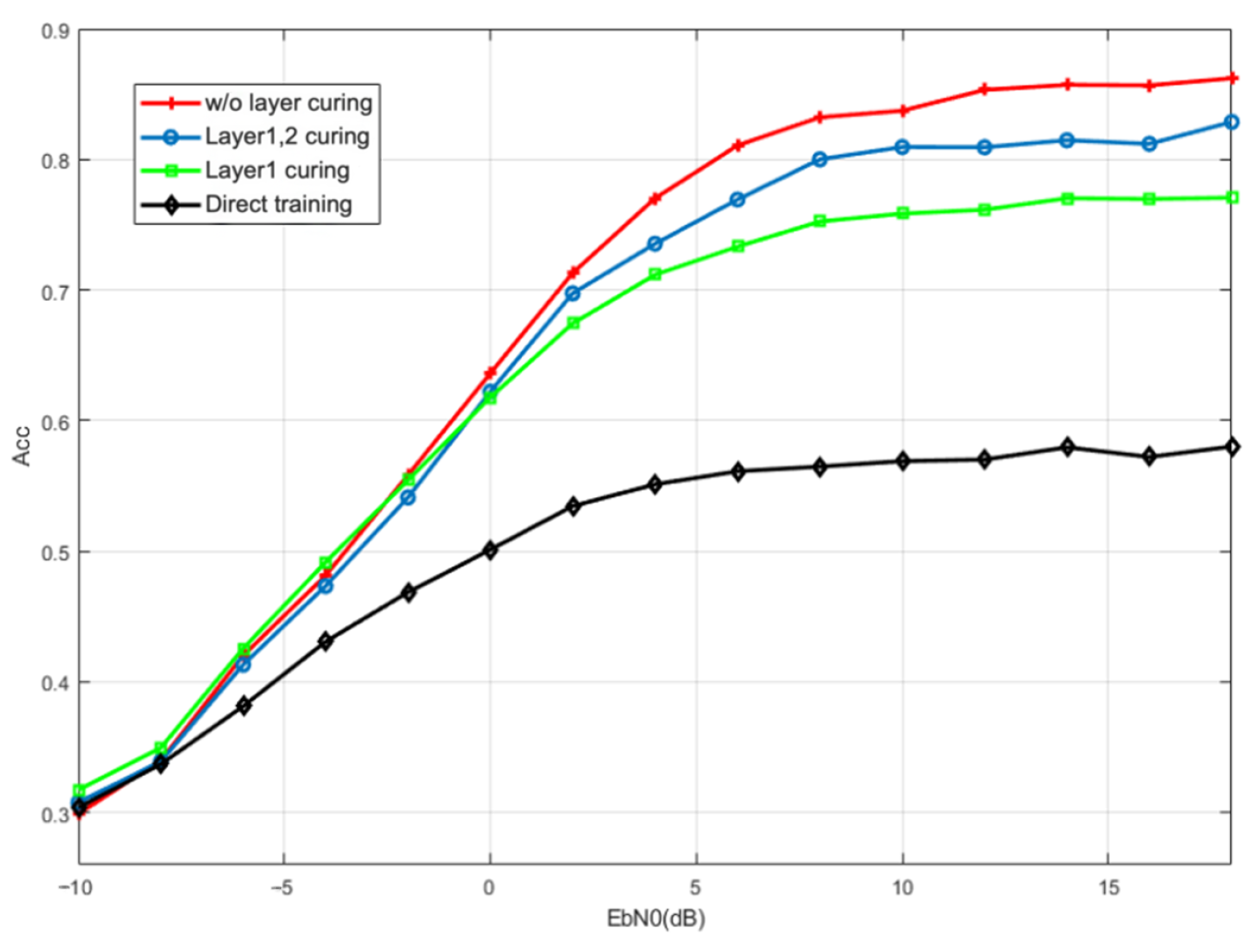
3.2. Deep Transfer Learning Enhanced BiLSTM
4. Proposed Attention-Based Spatio-Temporal Fusion Network for Uplink AMR
4.1. Proposed Neural Network Architecture
4.1.1. Spatial Feature Extraction
4.1.2. Temporal Feature Extraction
4.1.3. Feature Fusion
4.2. DNN Parameter Optimization
5. Simulation Results and Analysis
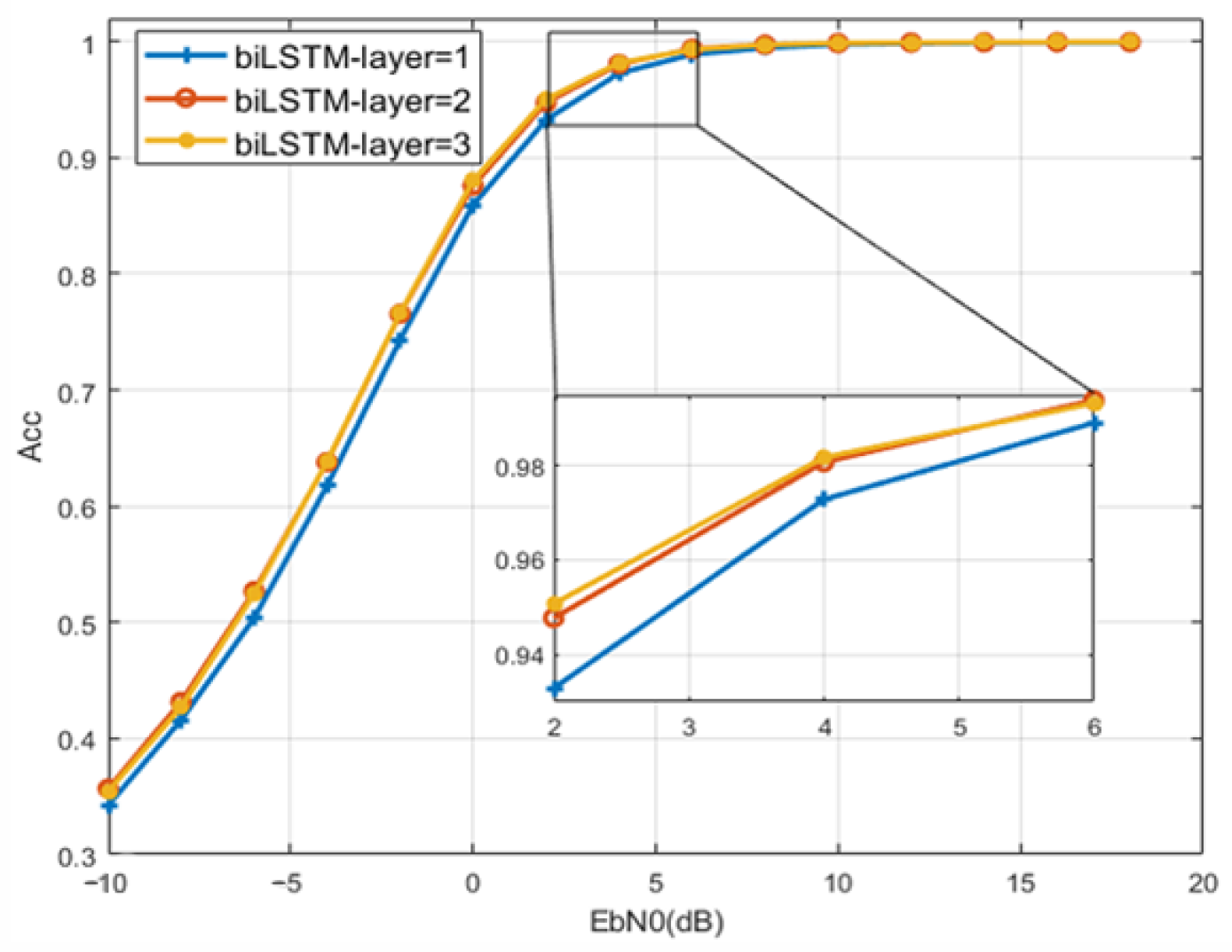
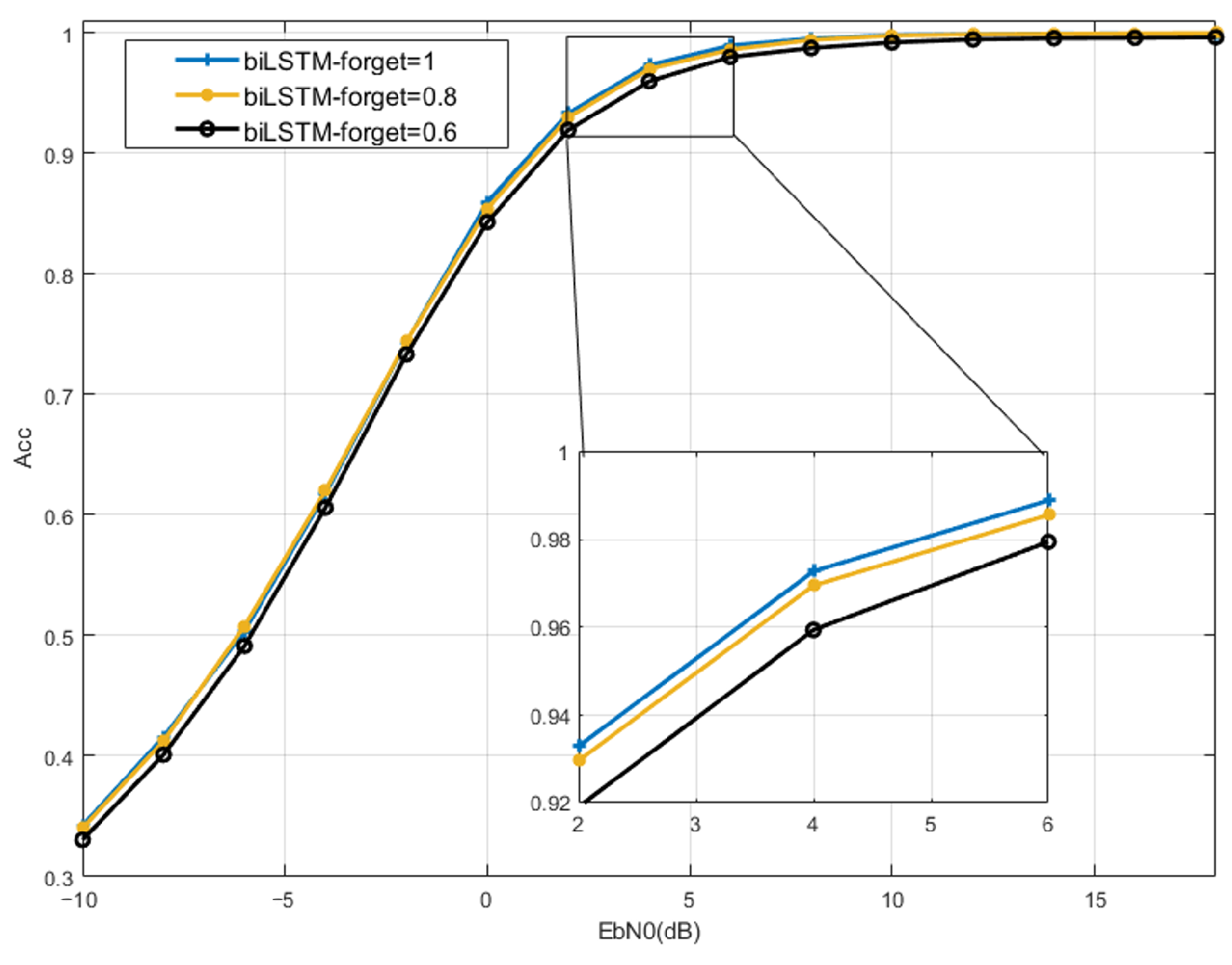
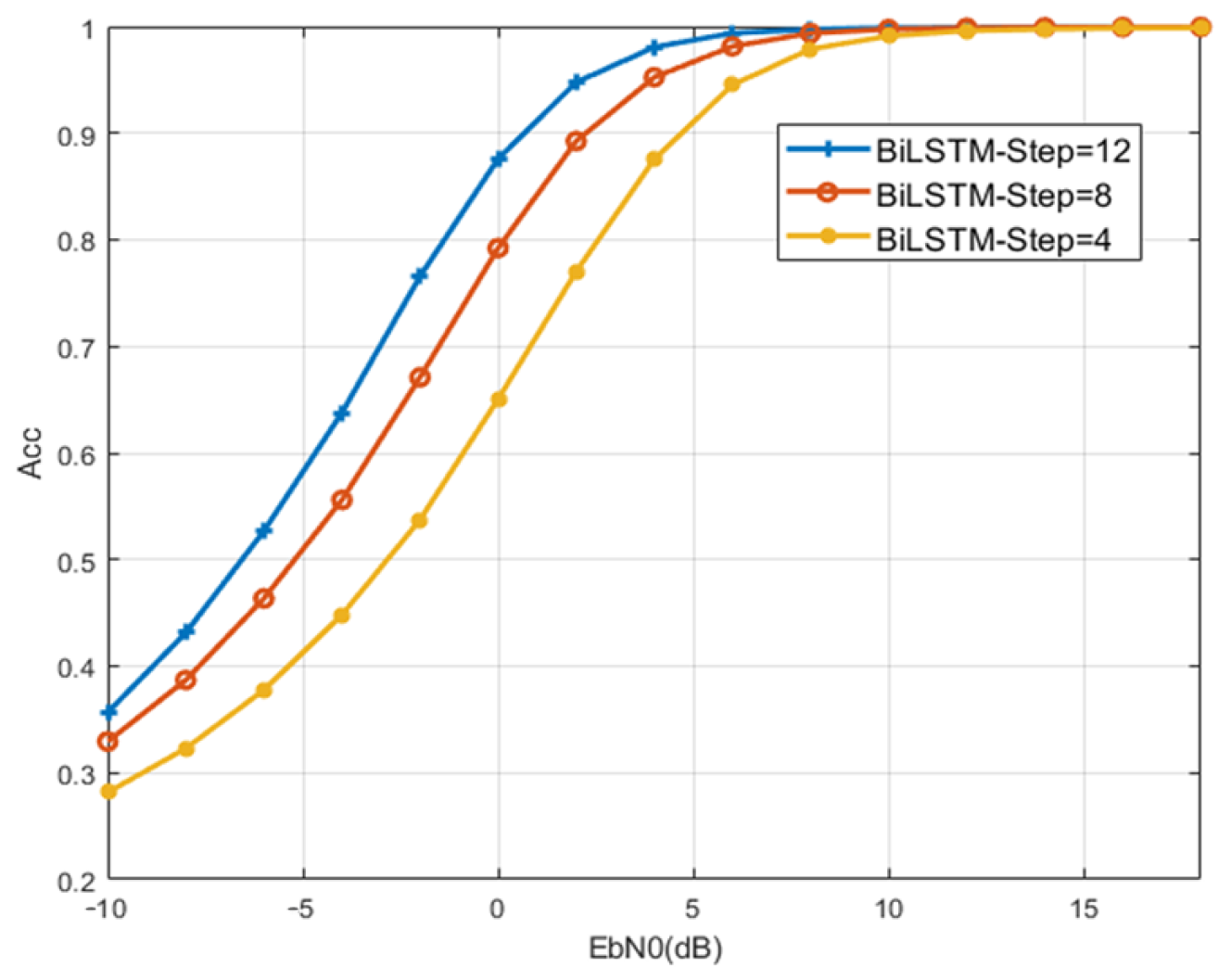
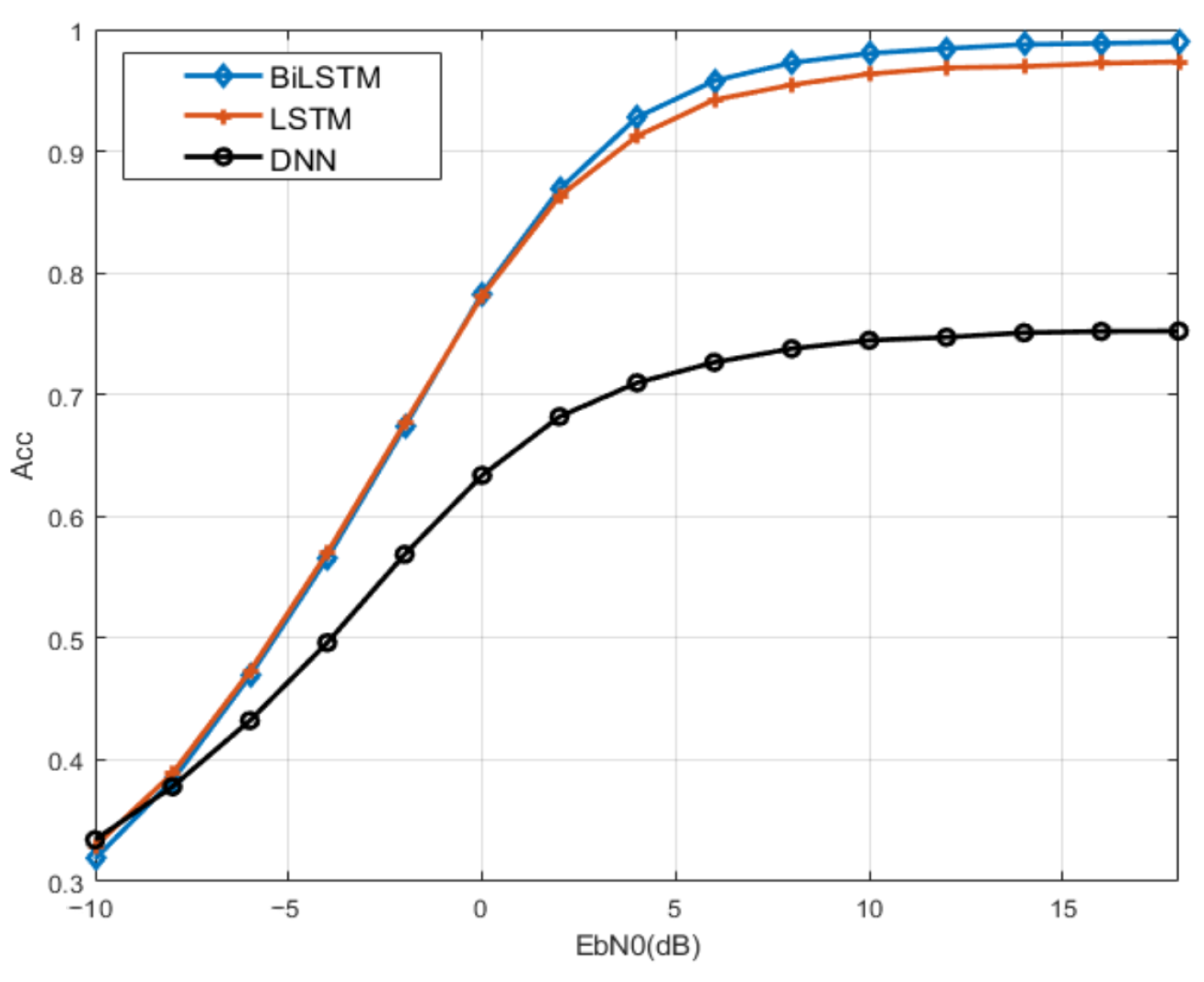
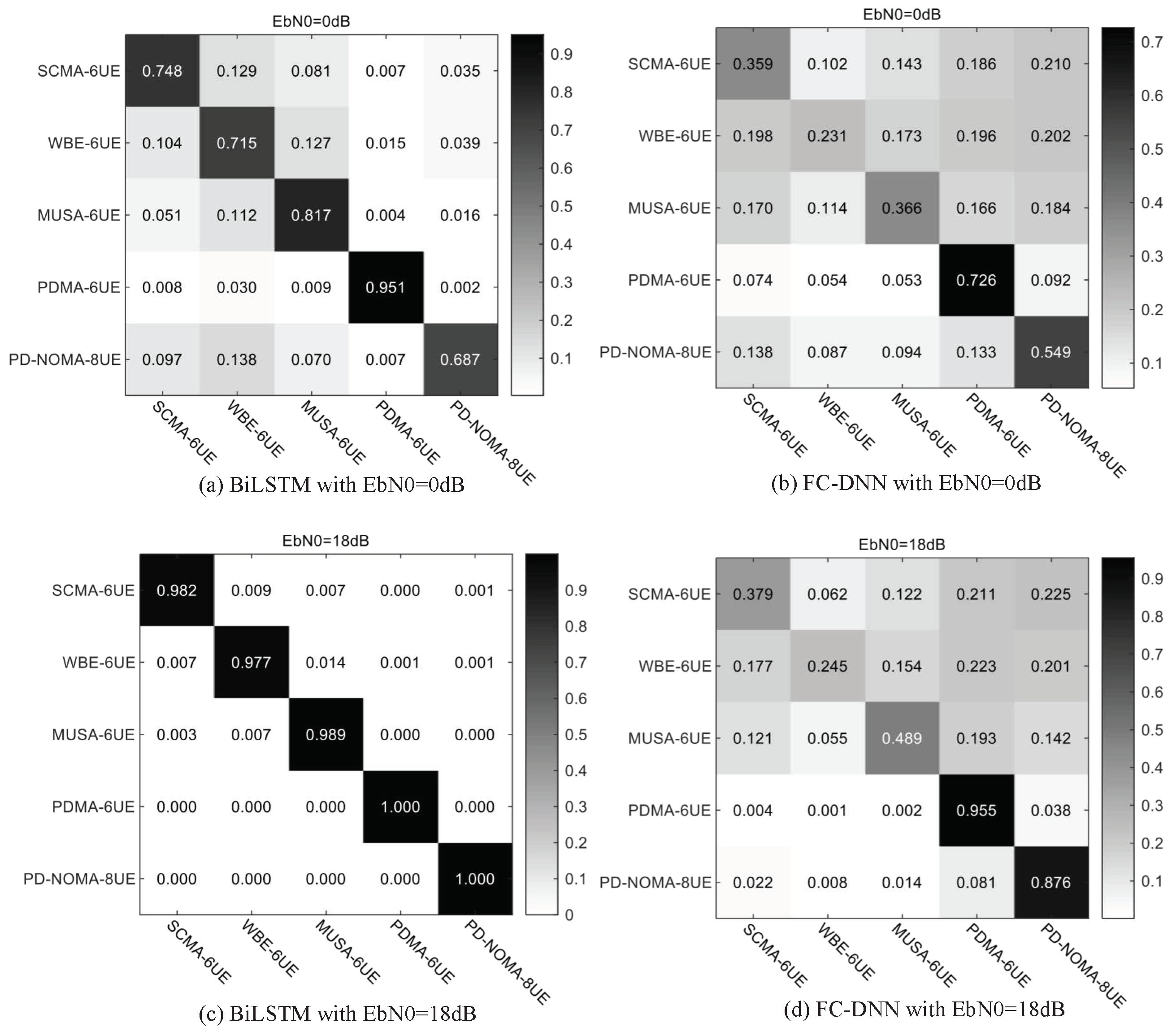
5.1. Downlink Non-Orthogonal System
5.1.1. Dataset and Parameters
5.1.2. Gaussian Channel
5.1.3. Channel with Random Phase Bias
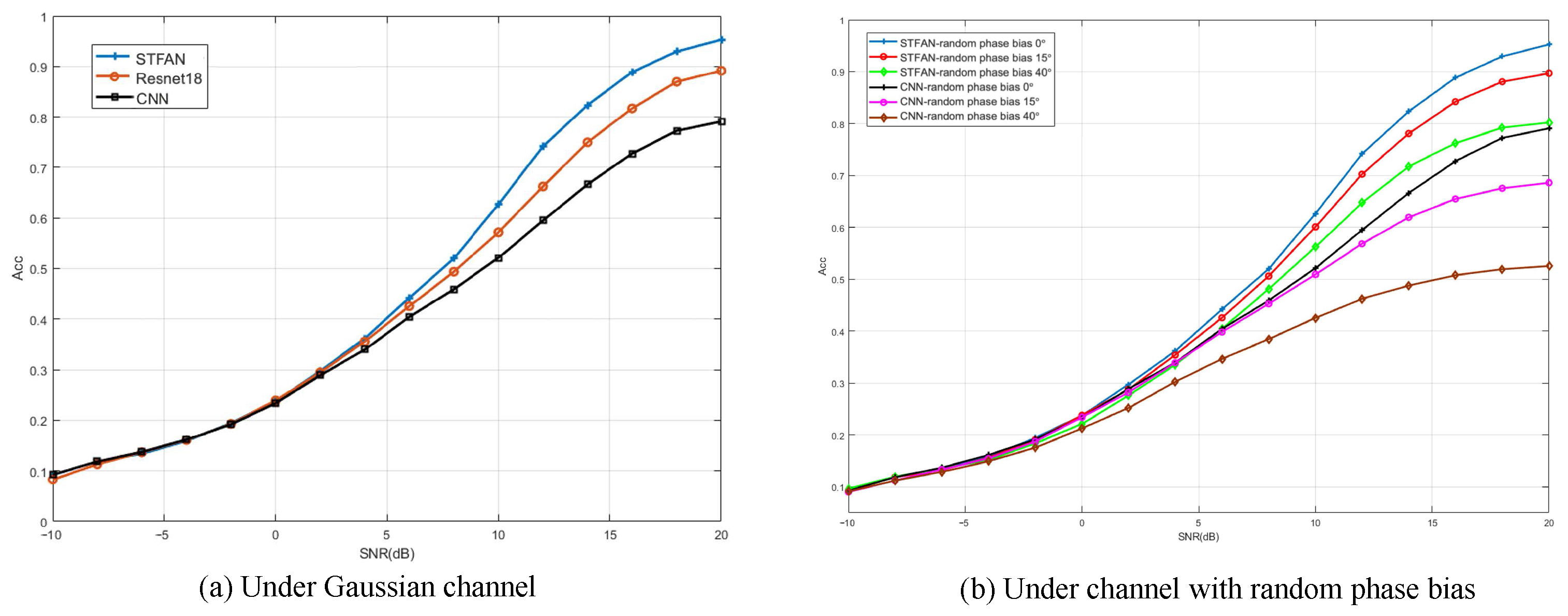
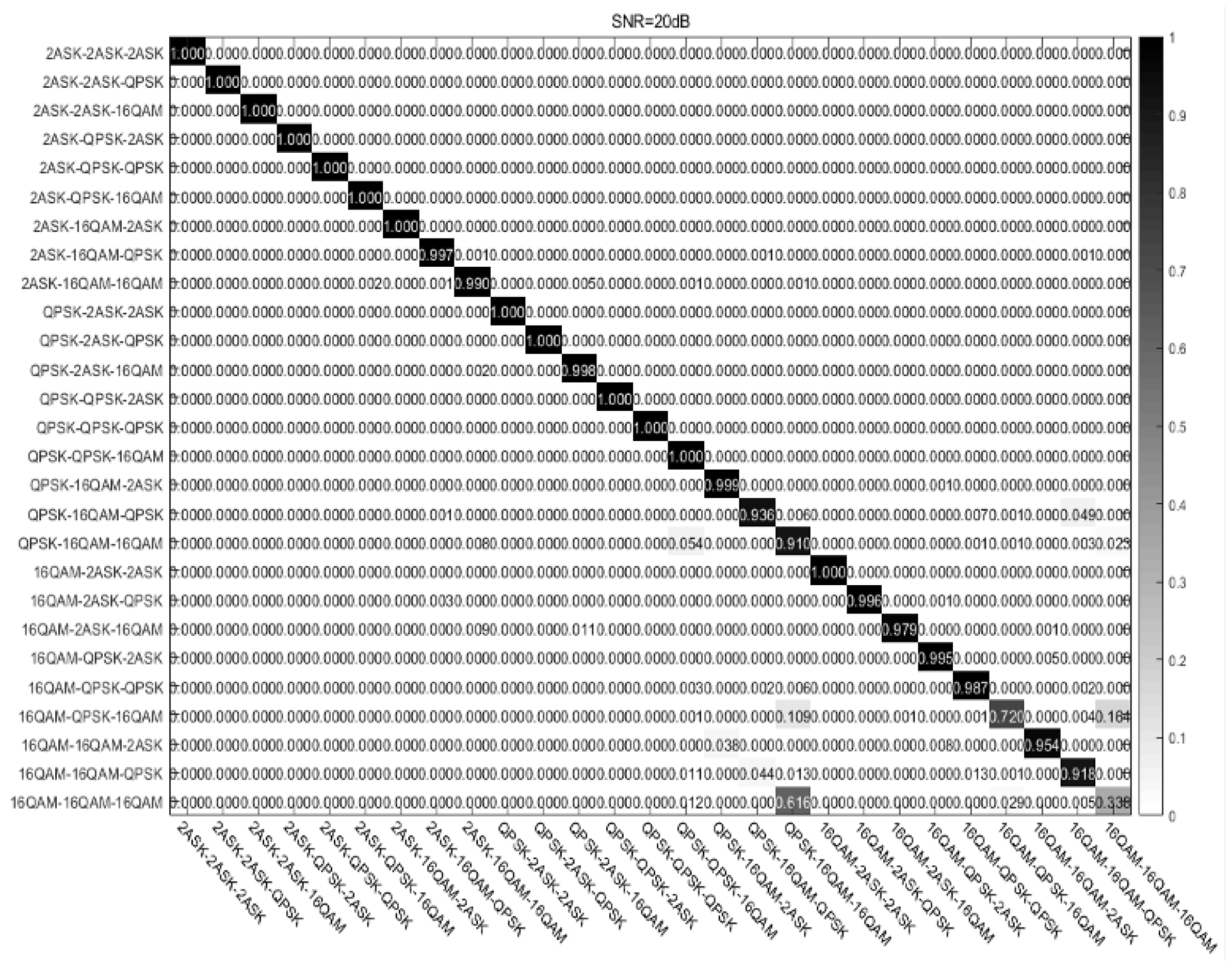
5.2. Uplink Non-Orthogonal System
5.2.1. Dataset and Parameters
5.2.2. Gaussian Channel
5.2.3. Channel with Random Phase Bias
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.; Zhao, H.; Zhu, H.; Adebisi, B.; Gui, G.; Gacanin, H.; Adachi, F. NAS-AMR: Neural Architecture Search-Based Automatic Modulation Recognition for Integrated Sensing and Communication Systems. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 1374–1386. [Google Scholar] [CrossRef]
- Qing Yang, G. Modulation classification based on extensible neural networks. Math. Probl. Eng. 2017, 2017, 6416019. [Google Scholar] [CrossRef]
- Zhou, R.; Liu, F.; Gravelle, C.W. Deep learning for modulation recognition: A survey with a demonstration. IEEE Access 2020, 8, 67366–67376. [Google Scholar] [CrossRef]
- Hou, C.; Liu, G.; Tian, Q.; Zhou, Z.; Hua, L.; Lin, Y. Multisignal Modulation Classification Using Sliding Window Detection and Complex Convolutional Network in Frequency Domain. IEEE Internet Things J. 2022, 9, 19438–19449. [Google Scholar] [CrossRef]
- Dobre, O.A.; Abdi, A.; Bar-Ness, Y.; Su, W. Survey of automatic modulation classification techniques: Classical approaches and new trends. IET Commun. 2007, 1, 137–156. [Google Scholar] [CrossRef]
- Zheng, J.; Lv, Y. Likelihood-based automatic modulation classification in OFDM with index modulation. IEEE Trans. Veh. Technol. 2018, 67, 8192–8204. [Google Scholar] [CrossRef]
- Chang, S.; Huang, S.; Zhang, R.; Feng, Z.; Liu, L. Multitask-Learning-Based Deep Neural Network for Automatic Modulation Classification. IEEE Internet Things J. 2022, 9, 2192–2206. [Google Scholar] [CrossRef]
- Jajoo, G.; Kumar, Y.; Yadav, S.K. Blind signal PSK/QAM recognition using clustering analysis of constellation signature in flat fading channel. IEEE Commun. Lett. 2019, 23, 1853–1856. [Google Scholar] [CrossRef]
- Lin, X.; Eldemerdash, Y.A.; Dobre, O.A.; Zhang, S.; Li, C. Modulation Classification Using Received Signal’s Amplitude Distribution for Coherent Receivers. IEEE Photonics Technol. Lett. 2017, 29, 1872–1875. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Zhang, W.; Yang, J.; Gui, G. Deep learning-based cooperative automatic modulation classification method for MIMO systems. IEEE Trans. Veh. Technol. 2020, 69, 4574–4579. [Google Scholar] [CrossRef]
- Liang, Z.; Tao, M.; Wang, L.; Su, J.; Yang, X. Automatic Modulation Recognition Based on Adaptive Attention Mechanism and ResNeXt WSL Model. IEEE Commun. Lett. 2021, 25, 2953–2957. [Google Scholar] [CrossRef]
- Jdid, B.; Hassan, K.; Dayoub, I.; Lim, W.H.; Mokayef, M. Machine Learning Based Automatic Modulation Recognition for Wireless Communications: A Comprehensive Survey. IEEE Access 2021, 9, 57851–57873. [Google Scholar] [CrossRef]
- Pan, J.; Ye, N.; Yu, H.; Hong, T.; Al-Rubaye, S.; Mumtaz, S.; Al-Dulaimi, A.; Chih-Lin, I. AI-Driven Blind Signature Classification for IoT Connectivity: A Deep Learning Approach. IEEE Trans. Wirel. Commun. 2022, 21, 6033–6047. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, M.; Yang, J.; Gui, G. Data-Driven Deep Learning for Automatic Modulation Recognition in Cognitive Radios. IEEE Trans. Veh. Technol. 2019, 68, 4074–4077. [Google Scholar] [CrossRef]
- Tekbıyık, K.; Ekti, A.R.; Görçin, A.; Kurt, G.K.; Keçeci, C. Robust and Fast Automatic Modulation Classification with CNN under Multipath Fading Channels. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020; pp. 1–6. [Google Scholar]
- O’Shea, T.J.; Corgan, J.; Clancy, T.C. Convolutional radio modulation recognition networks. In Engineering Applications of Neural Networks; Springer: Cham, Switzerland, 2016; pp. 213–226. [Google Scholar]
- Li, X.; Liu, Z.; Huang, Z. Attention-Based Radar PRI Modulation Recognition with Recurrent Neural Networks. IEEE Access 2020, 8, 57426–57436. [Google Scholar] [CrossRef]
- Zhang, M.; Zeng, Y.; Han, Z.; Gong, Y. Automatic Modulation Recognition Using Deep Learning Architectures. In Proceedings of the IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Kalamata, Greece, 25–28 June 2018; pp. 1–5. [Google Scholar]
- Liu, K.; Gao, W.; Huang, Q. Automatic Modulation Recognition Based on a DCN-BiLSTM Network. Sensors 2021, 21, 1577. [Google Scholar] [CrossRef]
- Zhang, H.; Nie, R.; Lin, M.; Wu, R.; Xian, G.; Gong, X.; Yu, Q.; Luo, R. A deep learning based algorithm with multi-level feature extraction for automatic modulation recognition. Wirel. Netw. 2021, 27, 4665–4676. [Google Scholar] [CrossRef]
- Njoku, J.N.; Morocho-Cayamcela, M.E.; Lim, W. CGDNet: Efficient Hybrid Deep Learning Model for Robust Automatic Modulation Recognition. IEEE Netw. Lett. 2021, 3, 47–51. [Google Scholar] [CrossRef]
- Ye, N.; AN, J.; Yu, J. Deep-Learning-Enhanced NOMA Transceiver Design for Massive MTC: Challenges, State of the Art, and Future Directions. IEEE Wirel. Commun. 2021, 28, 66–73. [Google Scholar] [CrossRef]
- Islam, S.M.R.; Avazov, N.; Dobre, O.A.; Kwak, K. Power-domain non-orthogonal multiple access (NOMA) in 5G systems: Potentials and challenges. IEEE Commun. Surv. Tutor. 2017, 19, 721–742. [Google Scholar] [CrossRef]
- Jayawardena, C.; Nikitopoulos, K. G-MultiSphere: Generalizing Massively Parallel Detection for Non-Orthogonal Signal Transmissions. IEEE Trans. Commun. 2019, 68, 1227–1239. [Google Scholar] [CrossRef]
- Dong, J.; Wang, A.; Ding, P.; Ye, N. Comparisons on Deep Learning Methods for NOMA Scheme Classification in Cellular Downlink. In Proceedings of the IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB), Paris, France, 27–29 October 2020; pp. 1–5. [Google Scholar]
- Norolahi, J.; Azmi, P. A Machine Learning Based Algorithm for Joint Improvement of Power Control, link adaptation, and Capacity in Beyond 5G Communication systems. arXiv 2022, arXiv:2201.07090. [Google Scholar] [CrossRef]
- Pan, Z.; Wang, B.; Zhang, R.; Wang, S.; Li, X.; Li, Y. MIML-GAN: A GAN-based Algorithm for Multi-Instance Multi-Label Learning on Overlapping Signal Waveform Recognition. IEEE Trans. Signal Process. 2023, 71, 859–872. [Google Scholar] [CrossRef]
- Ye, N.; Yu, J.; Wang, A.; Zhang, R. Help from space: Grant-free massive access for satellite-based IoT in the 6G era. Digit. Commun. Netw. 2022, 8, 215–224. [Google Scholar] [CrossRef]
- Ye, N.; Li, X.; Yu, H.; Zhao, L.; Liu, W.; Hou, X. DeepNOMA: A Unified Framework for NOMA Using Deep Multi-Task Learning. IEEE Trans. Wirel. Commun. 2020, 19, 2208–2225. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.M.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All you Need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Njoku, J.N.; Morocho-Cayamcela, M.E.; Lim, W. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Ye, N.; Li, X.; Yu, H.; Wang, A.; Liu, W.; Hou, X. Deep Learning Aided Grant-Free NOMA Toward Reliable Low-Latency Access in Tactile Internet of Things. IEEE Trans. Ind. Inform. 2019, 5, 2995–3005. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; PMLR: London, UK, 2015; pp. 448–456. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 11–18 December 2015; pp. 1026–1034. [Google Scholar]




| Name | Parameters | Activation Function | Output Data Stream | 1 |
|---|---|---|---|---|
| Input Layer | / | / | (128,2) | / |
| BiLSTM_1 | 2 | Tanh/Sigmoid | (12,256) | 140,288 |
| BiLSTM_2 | Tanh/Sigmoid | (1,128) | 164,352 | |
| FC layer | 64 | ReLU | (1,64) | 8256 |
| Output Layer | 5 | Softmax | 5 | 325 |
| Parameters Name | Parameters Value |
|---|---|
| Multiplexing Type | SCMA, MUSA, PDMA, PD-NOMA, WSMA |
| Carrier Frequency | GHz |
| Symbol Rate | MHz |
| Sampling Rate | MHz |
| 128 | |
| 6 | |
| 4 | |
| Oversampling Rate | |
| SNR Range | dB∼20 dB |
| Models | FC-DNN | LSTM | BiLSTM |
|---|---|---|---|
| Total parameters | 822,533 | 797,957 | 313,221 |
| Epochs | 50 | 30 | 30 |
| Training time (s)/epoch | 602 | 524 | 489 |
| Prediction time (s)/sample | 192 | 175 | 173 |
| FLOPS | 19,784,965 | 191,868,832 | 59,445,664 |
| Parameters Name | Parameters Value |
|---|---|
| Modulation Type | 2ASK, QPSK, 16QAM |
| Carrier Frequency | GHz |
| Symbol Rate | MHz |
| Sampling Rate | MHz |
| 128 | |
| 3 | |
| 1 | |
| Oversampling Rate | 3 |
| SNR Range | dB∼20 dB |
| Models | CNN | ResNet | STFAN |
|---|---|---|---|
| Total parameters | 8,593,563 | 4,214,922 | 23,370,448 |
| Epochs | 50 | 40 | 40 |
| Training time (s)/epoch | 631 | 598 | 721 |
| Prediction time (s)/sample | 193 | 188 | 189 |
| FLOPS | 81,259,328 | 158,353,019 | 273,799,168 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, J.; Wu, L.; Zhang, J.; Dong, J.; Wen, Z.; Zhang, Z. Deep Learning-Aided Modulation Recognition for Non-Orthogonal Signals. Sensors 2023, 23, 5234. https://doi.org/10.3390/s23115234
Fan J, Wu L, Zhang J, Dong J, Wen Z, Zhang Z. Deep Learning-Aided Modulation Recognition for Non-Orthogonal Signals. Sensors. 2023; 23(11):5234. https://doi.org/10.3390/s23115234
Chicago/Turabian StyleFan, Jiaqi, Linna Wu, Jinbo Zhang, Junwei Dong, Zhong Wen, and Zehui Zhang. 2023. "Deep Learning-Aided Modulation Recognition for Non-Orthogonal Signals" Sensors 23, no. 11: 5234. https://doi.org/10.3390/s23115234
APA StyleFan, J., Wu, L., Zhang, J., Dong, J., Wen, Z., & Zhang, Z. (2023). Deep Learning-Aided Modulation Recognition for Non-Orthogonal Signals. Sensors, 23(11), 5234. https://doi.org/10.3390/s23115234





