Abstract
This paper proposes a novel torque measurement and control technique for cycling-assisted electric bikes (E-bikes) considering various external load conditions. For assisted E-bikes, the electromagnetic torque from the permanent magnet (PM) motor can be controlled to reduce the pedaling torque generated by the human rider. However, the overall cycling torque is affected by external loads, including the cyclist’s weight, wind resistance, rolling resistance, and the road slope. With knowledge of these external loads, the motor torque can be adaptively controlled for these riding conditions. In this paper, key E-bike riding parameters are analyzed to find a suitable assisted motor torque. Four different motor torque control methods are proposed to improve the E-bike’s dynamic response with minimal variation in acceleration. It is concluded that the wheel acceleration is important to determine the E-bike’s synergetic torque performance. A comprehensive E-bike simulation environment is developed with MATLAB/Simulink to evaluate these adaptive torque control methods. In this paper, an integrated E-bike sensor hardware system is built to verify the proposed adaptive torque control.
1. Introduction
E-bikes have become popular for commuters due to the progress in AC motors and battery modules. By adding high-torque-density PM motors and lithium-ion batteries, E-bikes can provide more cycling power under the same weight. In general, electric bikes are categorized into two different systems. These are throttle-manipulated E-bikes and cycling-assisted E-bikes [1]. Considering throttle E-bikes, the motor torque output is controlled by the throttle on the handlebar. Because the throttle is directly manipulated by cyclists, safety issues can occur once the motor torque is sufficiently high. By contrast, cycling-assisted E-bikes automatically provide the motor torque, and the output value is dependent on the human pedaling torque. Compared to throttle E-bikes, cycling-assisted E-bikes have the advantage of safe riding behavior. By properly designing the motor torque, the human pedaling torque can be greatly reduced, especially under climbing and acceleration conditions.
It is not an easy task to determine suitable motor-assisted torques among all the different load conditions. In [2], a constant torque control strategy is proposed for E-bikes. Considering different road conditions, three to five different motor torque levels can be manually selected. In addition to being able to manually control the motor torque level, an electric bicycle can apply asymmetric assistance to the crank. The provision of motor torque at a specific crank angle has been proposed, which can aid patients with lower limb asymmetric function, such as post-stroke patients, so that the pedaling torque of the target leg is reduced [3]. However, this fixed torque control might not be suitable for the cyclist, considering pedaling torque variation.
In [4,5,6,7], an instantaneous pedaling torque waveform is analyzed. According to the circular motion theory, the cyclist’s pedaling torque should be a rectified sinusoidal waveform dependent on the bike pedal’s crank position. Under this effect, the motor torque can be designed as a rectified sinusoidal waveform similar to the pedaling torque. Compared to constant torque control, a smaller PM motor can be used to provide the same assisted performance. The pedaling torque might not fully contribute to the E-bike’s wheel torque. As reported in [8,9,10,11,12,13,14], an effective pedaling torque can be different depending on different crank positions.
It has been noted that cycling quality is different with respect to the different physiological factors of cyclists. The sources in [15,16,17,18,19,20,21] detail that cycling quality can be affected by various factors. These include the cyclist’s sex, purpose, cadence, speed, acceleration, vibration, experience, as well as the weather. Considering these factors, two platforms for riding performance have been derived. One is a performance index called the rating of perceived exertion (RPE), which was developed to command a suitable torque output [22], and the other makes additional use of the rider’s ability level, the E-bike’s characteristics (power, battery, weight), and the route profile (gradient and distance) to determine the output torque of the assist motor. What is unique is that the latter is built as a social platform. If the rider sets the motor’s output torque lower than the algorithm recommends, the rider will be able to earn more rewards [23].
Instead of a motor torque for pedaling torque reduction, a motor-assisted torque can also be implemented to achieve better physiological functions for the cyclist. In [24], the motor torque was manipulated with respect to the cyclist’s heart rate for a better physiological effect. However, this assisted method requires a high controller computation burden. In addition, because the E-bike frame weight is expected to be low, the cyclist’s weight and pedaling behavior might greatly affect the motor-assisted torque. In [25], the overall cycling mechanical powers were compared with two different cyclists of different weights: 95 kg and 50 kg. The resulting power consumption between the two cyclists differed by more than 50%. In [26], a comprehensive monitoring system was developed. This system integrates environmental factors [27,28], the cyclist’s heart rate [29,30] and respiratory rate [31], power consumption [32] and electromyogram [33,34] information, and journey time. Collecting data from the cloud can give the rider a reference indicator to determine the motor power of the journey in order to retain a longer battery life. The authors of [35] discuss the external load caused by the cyclist under climbing conditions. A suitable cycling performance was determined with the knowledge of various climbing-related load conditions. Instead of providing assisted torque, the recharge control can also be used to store the cyclist’s pedal power for better battery usage [36,37]. During low cyclist cadence, the stored mechanical power is returned for assisted torque to improve the cyclist’s blood oxygen and physiological stability. It is noteworthy that the feedback-based motor control can be implemented for assisted E-bike applications. The authors of [38] developed an improved feedback controller based on differential equations. In addition, a predictive feedback controller can be designed according to time-varying load conditions [39].
From a review of the existing references, key findings are summarized in Table 1. The sources in [1,2,24,38,39] aim to design suitable torque controllers for assisted E-bikes; however, no further analysis of the influence of the cyclist’s pedaling torque was addressed. By contrast, [4,5,6,7,8,9,10,11,12,13,14] investigate the cyclist’s pedaling dynamic with no motor-assisted torque assumed. Moreover, [15,16,17,18,19,20,21,22,23,25,26,27,28,29,30,31,32,33,34,35] focus on E-bike cycling performance with respect to human behaviors, including heartbeat, gender, and weight. The authors of [40,41] further evaluate recharge control for assisted motor output. Although several torque control methods have been proposed for E-bikes, a comprehensive analysis of different control methods is required with respect to various cycling load conditions.

Table 1.
Key findings of existing references.
To overcome these limitations on existing E-bike assisted torque control, this paper’s motivation is to find the best-suited assisted torque considering external loads. It is shown that the overall cycling torque is affected by external loads, including the cyclist’s weight, wind resistance, rolling resistance, and the road slope. Under these effects, the motor torque should be controlled with respect to these riding conditions. Four torque control methods are compared considering the dynamic effect on cycling torque and wheel acceleration. It is concluded that the wheel acceleration is important to determine the overall synergetic torque performance. The acceleration variation can be reduced by regulating the motor torque with the opposite phase as the human pedaling torque. All these torque control methods are evaluated with an E-bike simulation based on MATLAB/Simulink. An experimental bench is built to verify these methods.
2. E-Bike Pedaling Dynamic
This section discusses a dynamic model for an assisted E-bike. The pedaling behavior of cyclists is first discussed. After that, external disturbances’ torque loads are considered for the development of a dynamic E-bike model.
2.1. Cyclist Pedaling Behavior
Figure 1a shows cyclist pedaling behavior during bike riding. Ideally, the cyclist’s legs should be perpendicular to the horizontal ground. Under this effect, both of the cyclist’s feet are aligned with the pedal’s central axis. In this case, only the pedaling vertical force is generated. However, if the cyclist’s foot is not aligned with the pedal, the pedaling horizontal force might result in the degradation of the overall cycling performance, e.g., a reduction in pedaling torque and vibration.
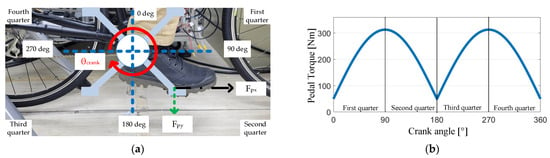
Figure 1.
Relationship between crank position and pedaling torque: (a) pedaling torque component / and crank position; (b) pedaling torque with respect to the crank position (no horizontal pedal force is assumed for simplicity).
2.2. Pedal Crank Angle Effort
Figure 1a also illustrates the relationship between the pedaling force / and the crank angle position. In general, the cyclist’s pedaling force can be categorized into four different regions depending on the crank position. In Figure 1a, the bike is assumed to move forward to the right-hand side. In this case, the pedaling force in the first and second quarters are contributed by the cyclist’s right foot.
In Figure 1b, the first quarter is defined for a pedal position between 0–90°. Ideally, at a 0° crank position, the vertical force cannot contribute to the pedaling torque . As a result, the overall should be zero at 0°, as seen in Figure 1b. By contrast, at 90°, a peak should appear, because is perpendicular to the crank. Similar cyclist pedaling behavior can be found in the second quarter.
Instead of the right foot reflecting the pedaling torque in the first and second quarters, the pedaling torque is generated by the left foot during the third and fourth quarters. Considering the third quarter for a crank position between 180–270° in Figure 1a, the corresponding pedaling torque is illustrated in Figure 1b. A similar pedaling torque can be analyzed in the fourth quarter. It is seen that the pedaling torque is equivalent to a sinusoidal waveform after the rectifier. The torque equation is formulated by:
where and are, respectively, the crank rotating radius and position. For the torque equation in (1), an ideal circular motion must be assumed, in which no horizontal force is generated by the cyclist. However, depending on different cyclist behaviors, might occur considering the external loads during cycling, resulting in a reduction in riding efficiency.
2.3. Parameters of Analyzed E-Bike
For assisted E-bikes, the total synergetic cycling torque consists of the cyclist’s pedaling torque and the motor-assisted torque. Table 2 lists the key parameters for the analyzed E-bike. In this table, the assisted motor is assumed to be installed in the rear wheel. This in-wheel motor can directly drive the wheel, avoiding torque loss due to the transmission and gear.

Table 2.
Assisted E-bike model parameters.
3. E-Bike Dynamics
This section analyzes the wheel angular speed ωw and acceleration αw of the E-bike considering different torque control methods with external loads. An analytical E-bike model in Figure 2 is developed to investigate the ωw and αw performance of the E-bike under these external loads. These external loads include the wheel friction torque Troll, the windage torque Twind, and the climbing-reflected torque Tslope. It can be shown that:
where Tdis is the summation of all external loads. In addition, the road slope angle θslope, the angular speed and acceleration ωw and αw, the tire pressure PT, the bike wheel radius R, the wind speed Vwind, the E-bike mass Me, the cyclist mass Mc, the gravitational constant g, the density of air , the aerodynamic drag coefficient , and the frontal area A are all parameters used for the calculation of external loads. The maximum climbing angle of the E-bike can also be obtained under a specific value for Tpdl and TM.
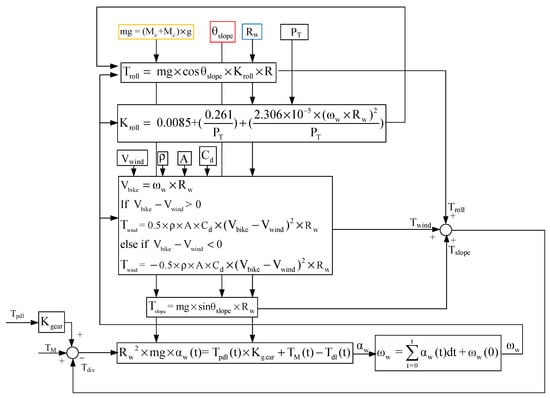
Figure 2.
Block diagram of E-bike torque management signal process.
3.1. Synergetic Torque
In this paper, a two-degree-of-freedom E-bike model is realized, in which the E-bike is assumed to move forward or backward with different climbing angles. Figure 3 illustrates the corresponding E-bike free-body diagram considering these forces and torques in Figure 2. Considering the rigid body assumption in Figure 3, the synergetic torque Ttotal combines the cyclist pedaling torque Tpdl and the motor-assisted torque TM. It can be calculated by:
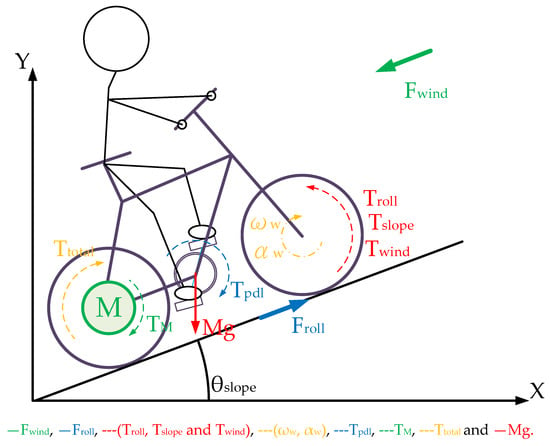
Figure 3.
Free-body diagram of E-bike system with external loads.
Ttotal is assumed to drive the rear wheel. It is noted that the pedaling torque generated by the cyclist is assumed to be a rectified sinusoidal torque, illustrated in Figure 1b. Under this effect, the synergetic Ttotal can be either the constant torque or the sinusoidal torque, depending on the manipulation of the motor torque TM.
3.2. Wheel Friction Torque
This section discusses the wheel friction-reflected torque load. Considering the wheel friction, rolling without slipping is typically assumed for the wheel’s rotation. In general, the wheel friction might result in the friction-reflected torque Troll on the overall cycling torque output. This is given by:
where mg is the equivalent mass including the cyclist and E-bike, and θslope is the road slope angle in Figure 3. In addition, R is the E-bike rolling radius in Table 2. Kroll is the resistance coefficient affected by the road’s surface shape, the tire’s structure, material, and pressure, as well as the wheel speed.
In addition, the rolling resistance coefficient Kroll is strongly influenced by tire pressure. The tire deformation is visible with considerable rolling resistance when the tire pressure is low [41,42]. In general, the resistance coefficient is calculated by:
where ωw is the wheel angular speed, and PT is the tire pressure.
Figure 4 illustrates Troll versus the wheel speed. In this simulation, a constant acceleration of 1.334 rad/s2 is assumed, in which the wheel speed is increased from 0 to 20 rad/s within 15 s. Two cyclists, weighing 70 kg and 50 kg, are compared. Although the friction torque Troll is slightly increased as the wheel speed increases, the influence of the cyclist’s weight is more visible than the wheel speed. Based on Figure 4, it can be concluded that Troll is mainly dominated by the cyclist’s weight. Thus, the motor-assisted torque TM can be manipulated depending on the current cyclist’s weight.
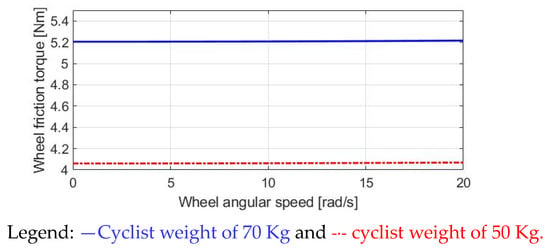
Figure 4.
Analysis of wheel friction torque in E-bike.
3.3. Windage Torque
This section explains the windage-reflected torque. Instead of the wheel friction torque, the airflow can cause aerodynamic resistance on both cyclists and E-bikes. On this basis, the airflow results in the windage torque Twind, which is shown to be:
where Vbike is calculated by the wheel angular speed, and Vwind is the corresponding wind speed depending on the airflow condition. In addition, ρ is the air density, is the aerodynamic drag coefficient, and A is the frontal area of airflow. For the analyzed E-bike in this paper, these three parameters are listed in Table 2.
Figure 5 depicts the windage torque as the E-bike’s speed increases. In this calculation, a constant 1.334 rad/s2 acceleration is assumed. Within 15 s, the wheel angular speed is increased from 0 to 20 rad/s. In the case of no wind, the windage torque is equivalent to a quadratic function proportional to . Even at zero wheel speed Vbike = 0, there is a windage Twind for the headwind with Vwind = 10 km/h. However, Twind is only 2 Nm based on the calculated parameters in Table 2. The influence of the windage Twind is relatively less than the friction torque analyzed in Figure 4.
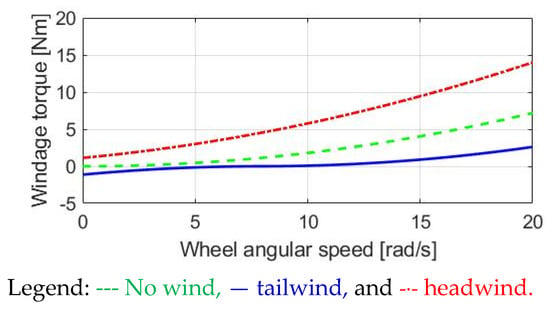
Figure 5.
Analysis of windage torque in E-bike.
In the case of a tailwind with Vwind = −10 km/h, the airflow can be used to generate an assisted torque. However, as shown in (5), once Vbike exceeds Vwind, the assisted torque is converted to resistive torque. Nevertheless, the Twind is sufficiently low during tailwind conditions.
3.4. Climbing-Reflected Torque
It is noted that an additional torque load is present in E-bikes during trekking conditions. As seen from the force diagram in Figure 3, the weight of the E-bike and cyclist lead to the climbing-reflected torque Tslope once the slope angle θslope ≠ 0. Depending on the slope angle, the Tslope can be shown to be:
Figure 6 investigates different values of the Tslope with respect to the slope angle. Different from Troll in (4) and Twind in (6), the climbing torque Tslope is only dependent on the slope angle and cyclist weight. Comparing two different cyclists of 70 kg and 50 kg on the same bike, the heavier cyclist results in a higher Tslope. However, compared to the Troll simulation in Figure 4, Tslope is mainly affected by the slope angle θslope instead of the cyclist’s weight. As a result, the motor-assisted torque should be manipulated with respect to the slope angle θslope for different E-bike trekking conditions.
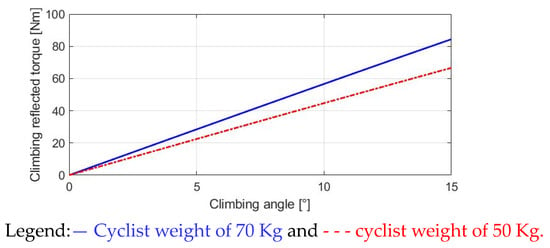
Figure 6.
Analysis of climbing-reflected torque.
3.5. E-Bike Dynamic Model
After obtaining three external torque loads analyzed in Figure 3, the actual wheel driving torque Tdrv, the wheel angular acceleration αw, and the speed ωw of the E-bike can be respectively modeled by (8) and (9):
where Jw is the corresponding wheel inertia. Considering the E-bike with different cyclist weights, Jw can be modeled by:
In (10), Me and Mc are, respectively, the weight of the E-bike and the cyclist.
For the analyzed E-bike system, the external torque loads (4)~(7) are all modeled as torque disturbances Tdis. It is noted that the torque control for this E-bike system is equivalent to an open-loop control system in this paper. As seen in Figure 7, the total torque input Ttotal consists of the cyclist pedaling torque Tpdl and the motor torque TM. In this paper, the motor torque magnitude is manually adjusted. When the external load is increased, the cyclist is expected to generate more pedaling torque as well. In this case, the overall control stability of the assisted E-bike system is only dependent on the motor torque regulation.
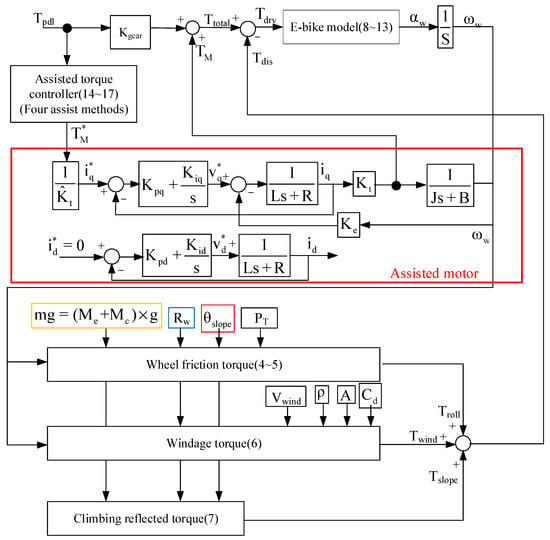
Figure 7.
Block diagram of E-bike model control process.
Figure 7 also illustrates the corresponding torque regulation. Based on the electromagnetic energy conversion, the motor torque can be modeled by (11) in the S-domain:
where id, iq are the stator current of the d- and q-axis. Vd, Vq are the stator voltage of the d- and q-axis, Kpd and Kpq are the corresponding proportional gains, and Kid and Kiq are the corresponding integral gains.
The motor torque control is achieved based on the current field-oriented control [43]. The d-axis current id is controlled to be zero, and the torque TM is directly proportional to the q-axis current iq. Regarding the torque controller design, pole/zero cancellation technology is used. PI controller gains are designed to be equal to:
where and are, respectively, the estimated motor inductance and resistance parameters. Assuming ideal parameter estimation, the resulting transfer function can be modified by:
Based on this controller design, the motor torque control can be stably maintained under external loads. In the future, a feedback-based, motor-assisted torque regulation similar to the unmanned helicopter in [44] will be investigated. Since the external friction and windage torque load are time-variant, the feedback linearization approach can be a potential solution.
4. Proposed E-Bike Torque Control
This section shows the simulation results for different torque control methods considering prior external loads including the wheel friction torque, windage torque, and climbing-reflected torque. Three key cycling performance indices are used to evaluate different motor torque controllers. These indices are the total torque output Ttotal, wheel acceleration αw, and speed ωw.
Key simulation parameters are listed in Table 2. The E-bike transmission gear ratio is 44 to 14 teeth, resulting in a gear ratio of 3:14. In the following simulation, MATLAB/Simulink was used to establish a simulation model in which the ideal cyclist pedaling torque Tpdl in Figure 1b is used. Figure 7 illustrates the control process of the E-bike model. Four motor torque-assisted methods are implemented. These four assisted methods are individually added to the original pedaling torque under the E-bike model in (3). After obtaining the total synergetic torque Ttotal, the actual torque can be obtained under the influence of three external load torques. The actual wheel driving torque Tdrv, angular acceleration αw, and speed ωw are obtained from Equations (8)–(10). It is noted that the E-bike cycling performance can be evaluated based on the E-bike wheel speed ωw and acceleration αw conditions.
4.1. No Motor-Assisted Torque (NMT)
Normal E-bike cycling without the motor-assisted torque is first analyzed. Figure 8 shows the corresponding pedaling torque based on the torque equation in (1). In this simulation, the average pedaling torque is set at 30 Nm, with a cadence per minute of 30 cpm. The average pedaling torque transmitted to the wheel is 24.60 Nm.
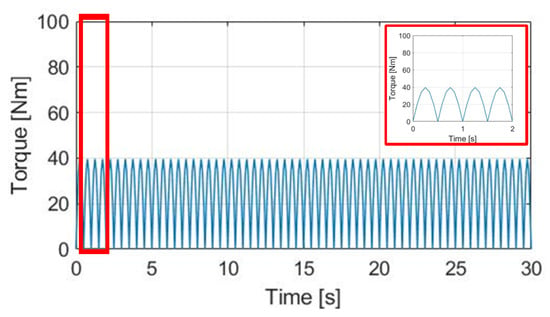
Figure 8.
Simulation of pedaling torque versus time under 30 cpm cadence.
The simulation conditions include no wind, with a 0% slope and 70 kg cyclist weight. For the wheel acceleration αw simulation in Figure 9a, the αw wheel acceleration waveform is the same as the pedaling torque Tpdl, since αw is directly proportional to Tpdl. Considering the wheel inertia Jw = 5.80 kg/ with Mc = 70 kg, the average αw is 0.48 rad/s2 with a peak-to-peak acceleration ripple of 2.38 rad/s2. By contrast, a wheel speed ωw simulation based on (8) is also analyzed in Figure 9b. The average speed is 7.69 rad/s, with a 0.28 rad/s peak-to-peak speed ripple. The corresponding αw and ωw waveforms in Figure 9 can be used as a benchmark to compare the different torque control methods listed below.
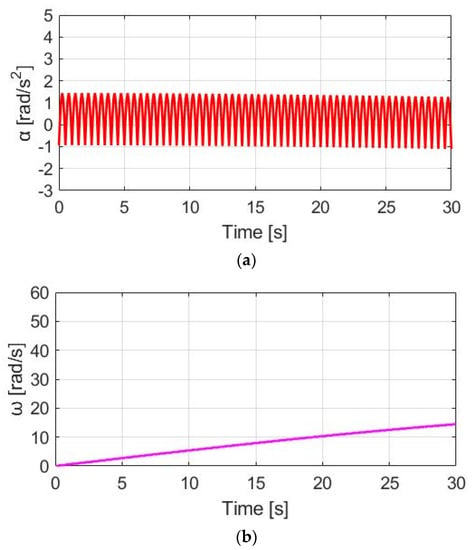
Figure 9.
Bike dynamics based on NMT: (a) wheel angular acceleration; (b) wheel angular speed.
4.2. Constant Motor-Assisted Torque (CT)
In this section, a torque control method with a constant motor torque (CT) is applied. Figure 10 compares TM, Tpdl, and Ttotal under the same 30 cpm cadence. The motor-rated torque is 45 Nm. Considering the average pedaling torque after the transmission, the ratio between TM and Tpdl is TM = 1.83 Tpdl. To easily compare different torque waveforms, a zoom-in figure is also added in Figure 10 in this simulation.
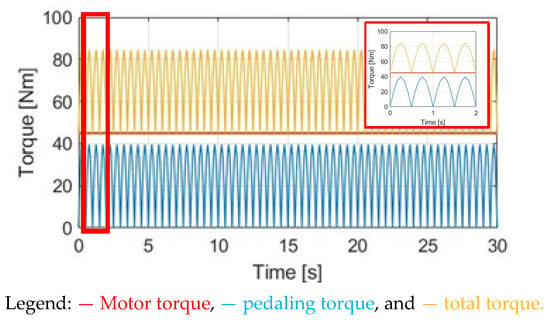
Figure 10.
Torque comparison under the CT method.
Figure 11a shows the αw for E-bike torque control with the CT method. Due to the additional constant TM, the average αw is increased from 0.48 to 1.90 rad/s2. For the speed simulation in Figure 11b, the average ωw is increased due to the additional Ttotal. It is noteworthy that the ωw ripple is increased to 0.60 rad/s compared to NMT due to the higher average αw based on (8). By applying the CT method, it is concluded that both the average αw and ωw can be increased for a better E-bike trekking performance. However, the visible ripple in ωw might degrade the cyclist’s riding experience.
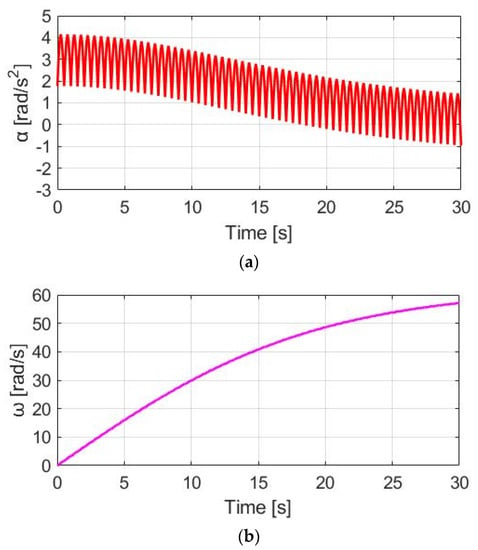
Figure 11.
Bike dynamics based on CT: (a) wheel angular acceleration; (b) wheel angular speed.
4.3. Same Phase as Pedaling Torque (SPPT)
Instead of the CT method, this section proposes a dynamic torque control method. Under these conditions, the motor torque is manipulated by the same phase as the pedaling torque (SPPT). Based on this proposed SPPT control method, the motor torque TM_SPPT is manipulated by:
where Tpdl and Tpdl_peak are, respectively, the instantaneous and peak value of the pedaling torque, depending on the pedaling torque sensor performance. Further, TM_rated is the rated motor torque.
Figure 12 demonstrates TM_SPPT, Tpdl, and Ttotal under the same 30 cpm cadence. Comparing TM_SPPT with the CT in Figure 10, it is seen that the average TM_SPPT can be smaller, leading to better battery usage. However, Figure 13a demonstrates the corresponding αw resulting from the SPPT method. Compared to αw based on the CT method in Figure 11a, the average αw is reduced from 1.90 to 1.48 rad/s2, but with the ripple increased from 2.41 to 5.09 rad/s2. For the ωw speed waveform in Figure 13b, a similar decline in performance is also observed. A detailed performance comparison between the CT and SPPT methods will be explained in Section 4.6.
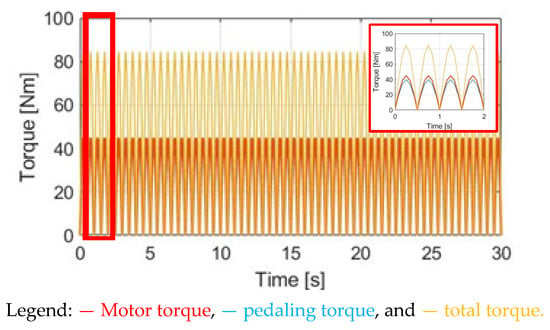
Figure 12.
Torque comparison under the SPPT method.
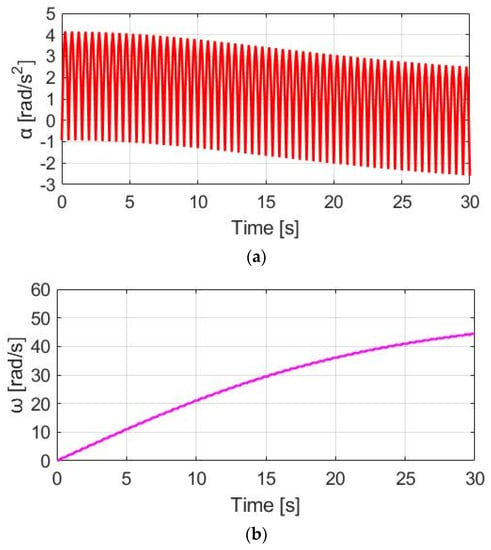
Figure 13.
Bike dynamics based on SPPT: (a) wheel angular acceleration; (b) wheel angular speed.
4.4. Delay Phase as Pedaling Torque (DPPT)
This section proposes another dynamic torque control method. On this basis, the ripple on the total torque can be reduced by manipulating the motor torque with a 90° delay phase as the pedaling torque (DPPT). Under this effect, the DPPT motor torque TM_DPPT is formulated by:
where Tpdl_d is a 90° delay torque with respect to the measured instantaneous Tpdl. For real-time implementation, Tpdl_d can be obtained by:
It is noted that Tpdl_d can only be obtained after a 90° delay of θcrank. Due to this limitation, the E-bike might not be able to provide the motor-assisted torque during the initial startup. Nevertheless, the motor torque control can be operated after one-fourth of the pedaling cycle.
Figure 14 compares TM_DPPT, Tpdl, and Ttotal under the same cadence and slope situation. Since the motor torque magnitude is the same as the SPPT method, the average total torque should be the same. More importantly, because of the lower torque ripple for Ttotal in Figure 14, peak-to-peak ripples are decreased for αw in Figure 15a and ωw in Figure 15b. It is expected that a relatively comfortable cyclist performance is achieved. However, in Figure 15, a certain amount of Ttotal ripple is still observed, because Tpdl cannot be equal to the motor TM_DPPT. The Ttotal ripple should be increased due to the increase in Tpdl under the same rated motor torque TM_rated. A detailed comparison of the performance with the SPPT method will also be explained in Section 4.6.
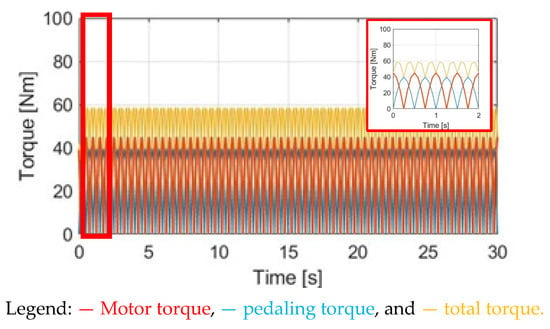
Figure 14.
Torque comparison under the DPPT method.
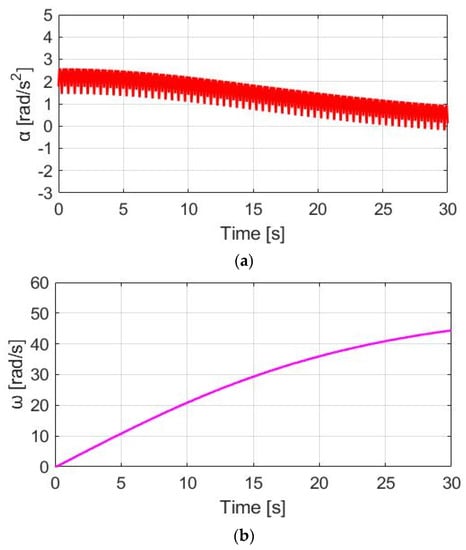
Figure 15.
Bike dynamics based on DPPT: (a) wheel angular acceleration; (b) wheel angular speed.
4.5. Compensation for the Gap in the Pedaling Torque (CGPT)
This section proposes a feedback-based dynamic torque control to improve the torque ripple on the prior DPPT method. In this case, the motor torque aims to compensate for the gap in the pedaling torque (CGPT). The corresponding CGPT motor torque TM_CGPT is derived from:
where Tref is a synergy torque reference. It can be determined by the previously mentioned external load conditions. Based on the definition in (13), the manipulated motor torque TM_CGPT is disabled when Tpdl is higher than Tref. By contrast, Ttotal can be the same as Tref once Tpdl < Tref. Figure 16 shows the torque waveform using this CGPT method. Compared to the prior torque control methods, the primary advantage is the lowest torque ripple.
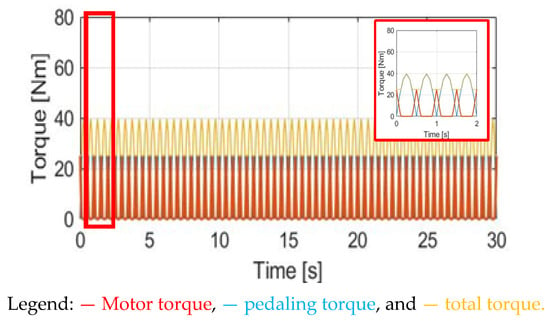
Figure 16.
Torque comparison under the CGPT method.
Figure 17a shows the corresponding acceleration based on the CGPT method under the same simulation conditions. The αw ripple is only 0.84 rad/s2, which is also smaller than 1.15 rad/s2, resulting from the prior DPPT control method. A smaller ωw ripple performance can be observed in Figure 17b. However, since TM_CGPT is generated only at a low Tpdl, a drawback is the reduced average speed in Figure 17b. Comparing CT control with the highest average ωw for trekking, CGPT control is well suited for commuter applications to maximize the E-bike’s battery usage.
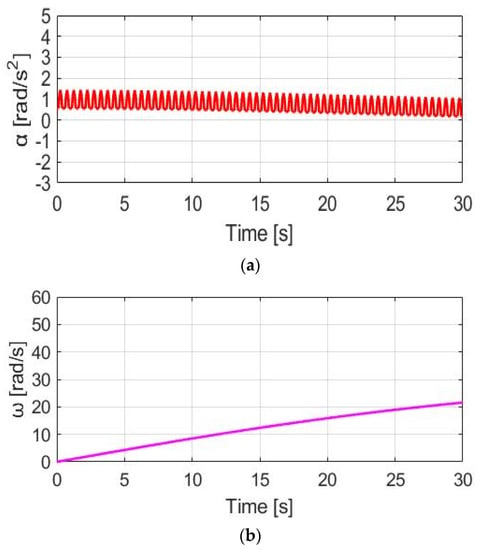
Figure 17.
Bike dynamics based on CGPT: (a) wheel angular acceleration; (b) wheel angular speed.
4.6. Performance Comparison
Table 3 compares different torque control methods with the same cycling time. These include NMT, CT, SPPT, DPPT, and CGPT. The total synergetic torque, angular acceleration, and speed with corresponding ripples are all compared. In this comparison, the cycling time is the same as 30 s, leading to the difference in the αw and ωw response. By contrast, Table 4 compares these torque control methods to reach the same final speed. In Table 4, the cycling time can be different depending on different torque methods. The key findings can be summarized as follows:

Table 3.
Comparison of different assisted methods with the same cycling time.

Table 4.
Comparison of different assisted methods to reach the same final speed.
- (1)
- CT: The CT control method results in the highest αw and ωw due to the highest motor torque output. However, the ripples in αw are also the highest. This method is well suited for trekking applications under visible external loads.
- (2)
- SPPT and DPPT: The highest αw ripple is the result of the SPPT method. When the αw ripple is much higher than in the NMT case, the cyclist may have an uncomfortable experience. By contrast, for the DPPT method, a smaller αw ripple is achieved under the same motor torque. Compared to SPPT control, the DPPT method can provide a comparable cycling experience as the original NMT. The DPPT method is well suited for standard E-bike torque management for different load conditions.
- (3)
- CGPT: Because the CGPT method generates the lowest motor torque, the resulting αw ripple can be smaller than the original NMT condition. However, the lowest motor output might degrade the E-bike’s acceleration performance. As seen in Table 4, CGPT requires 18.72 s to reach a 15 rad/s final speed. By contrast, for CT control, only 4.72 s is spent. It is concluded that the CGPT is well suited for commuting cyclists. This control results in the best battery usage at the smallest αw ripple. It is especially well suited for cyclists under a heavy daily urban traffic burden.
5. Experiment
This section describes the experimental verification. Figure 18 shows a photograph of the E-bike experimental test setup. The experiment is performed based on a 250 W 300 rpm permanent magnet (PM) AC motor. Field-oriented control (FOC) through the Hall sensor position feedback is implemented. As seen in Figure 18, the PM motor is attached to the rear wheel of the E-bike. Detailed PM motor specifications are listed in Table 5. It should be noted that the experimental test setup for the E-bike is currently under laboratory verification. At this time, power supply hardware is used for the E-bike’s power source to provide a reliable DC voltage. The E-bike analyzed is based on a standard assisted E-bike with 250 W electrical power. Considering the actual E-bike product in the future, a Li-ion battery with 7 Amp hours can be selected to provide a comparable DC voltage.

Figure 18.
E-bike experimental test setup and sensor hardware installation.

Table 5.
Specification of E-bike PM motor.
Figure 19 illustrates the hardware setup and signal process for the E-bike torque control experiment. All four different motor torque control methods are implemented on a 32-bit microcontroller, TI-TMS320F28069. The interrupt service routine is designed at 10 kHz, which is synchronous with the sampling frequency. In addition, the motor drive inverter is selected with the TI-DRV8301 evaluation kit. On this basis, the E-bike motor can be controlled through a six-switch pulse-width modulation inverter, as shown in Figure 20. Figure 21 illustrates a photograph of the test motor drive inverter, the TI-DRV8301 evaluation kit. This inverter kit can be easily integrated with the TI-TMS320F28069 microcontroller used as a motor drive system. In this case, the motor-assisted torque can be manipulated based on the desired torque command mentioned in Figure 7.
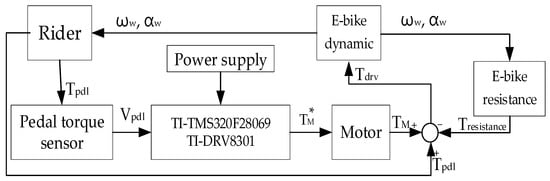
Figure 19.
Hardware setup and signal process for E-bike torque control experiment.
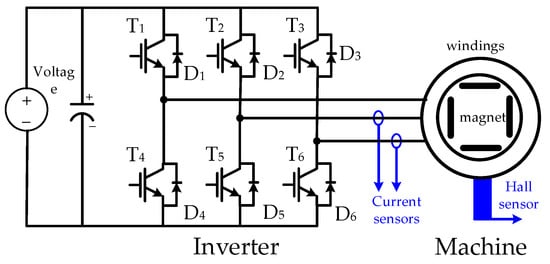
Figure 20.
Electrical circuit of six-switch motor drive inverter.

Figure 21.
Photograph of motor drive inverter.
For the PM motor control, three-phase pulse width modulation voltages are manipulated by the controller for the motor to generate the desired torque output. Because the FOC requires the instantaneous position for sinusoidal voltage control, zero-order hold (ZOH) position interpolation [45,46,47,48] is used to improve the Hall-based position-sensing resolution. As seen in (18), the position interpolation is performed every 60°:
where and are, respectively, the estimated current motor position and the last position measured by Hall sensors. Further, is the estimated speed based on prior Hall sensor position information, and and are, respectively, the current and last time interval. The estimated speed can be obtained by:
In (19), is calculated based on the two prior time steps, and . It is noted that the position interpolation is under the average speed assumption in (19) without instantaneous motor acceleration and deceleration. For E-bike applications, this assumption is still valid during normal cycling conditions.
Regarding the pedaling torque and crank cadence measurement, both the torque sensor and crank position sensor are installed inside the bracket bottom. Considering E-bike operation under different external loads, a wheel-resistive load in Figure 18 is added on the rear wheel for the load simulation. In the experiment, the pedaling torque sensor can transmit a voltage reference of between 0.7–3.3 v to the microcontroller. This voltage reference is proportional to a pedaling torque of 0–80 Nm. The experimental verification compares the cycling performance among normal NMT and the four torque control methods. However, for actual riding conditions, it is not possible for a cyclist to maintain the same pedaling torque under different load and assisted torque conditions. Under this effect, the test cyclist in these experiments was asked to maintain a wheel speed ωw of 15.88 rad/s (20 km/h). If ωw can be maintained at a more stable speed without variation, the motor torque is assumed to assist the cyclist.
5.1. NMT and CT Experiment
This section compares the time-domain waveforms of the pedaling torque, motor torque, and total synergy torque between normal NMT and the CT motor control. Since there is no assisted torque under the NMT method, the test cyclist was responsible for different E-bike load conditions. Figure 22 and Figure 23, respectively, show the pedaling torque, αw, and ωw waveforms under normal NMT. In this case, the corresponding pedaling torque condition can be used as a benchmark to compare the four different torque control methods.
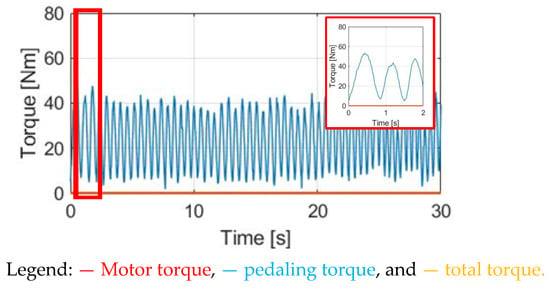
Figure 22.
Torque comparison under the NMT.
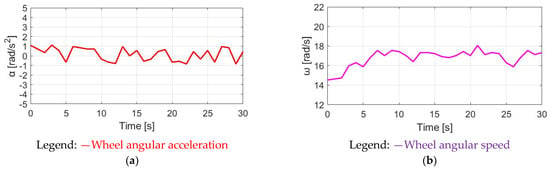
Figure 23.
NMT-reflected E-bike response: (a) wheel angular acceleration and (b) wheel angular speed.
In this experiment, a wheel resistive load was added to simulate E-bike cycling with wheel friction torque. Under a certain wheel friction load, the pedaling torque measured from the torque sensor contains a 29.81 Nm average torque with 59.92% pedaling torque variation. For all experiments in this paper, the pedaling torque variation is defined by:
where and are, respectively, the maximum and average value of the measured pedaling torque .
By contrast, considering the CT control method, Figure 24 demonstrates the time-domain waveforms of , the motor torque and the total torque . Figure 25 shows the time-domain waveforms of αw and ωw. In this control, the motor torque is controlled to maintain a 45 Nm rated torque. With additional assisted torque, the resulting average pedaling is reduced to 13.05 Nm. However, similar to the prior simulation, the pedaling variation is increased to 63.86% due to the limitation on the constant motor torque regulation. The key differences in the performance of the torque are summarized in Section 5.4.
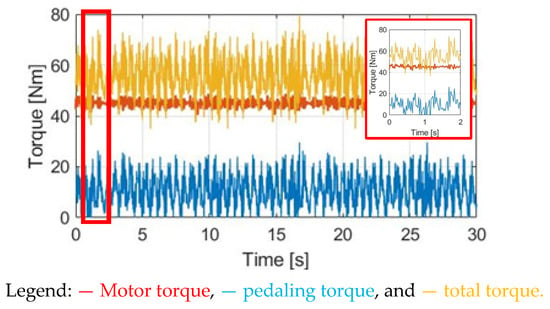
Figure 24.
Torque comparison under CT control.
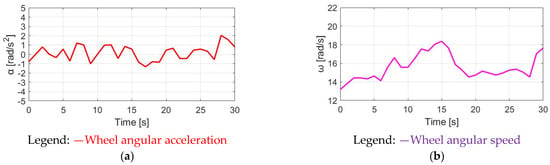
Figure 25.
CT-reflected E-bike response: (a) wheel angular acceleration and (b) wheel angular speed.
5.2. SPPT and DPPT Experiment
Figure 26 and Figure 27 depict the measurements of torque and bike dynamics, respectively, obtained under the SPPT condition. Similarly, Figure 28 and Figure 29 illustrate the corresponding measurements of torque and bike dynamics collected under the DPPT condition.
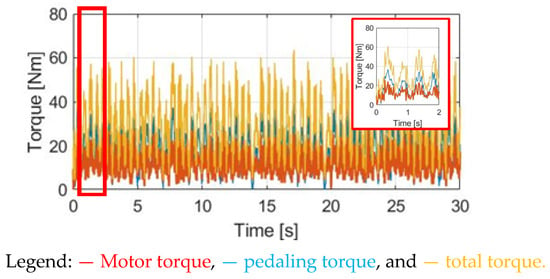
Figure 26.
Torque comparison under SPPT control method.
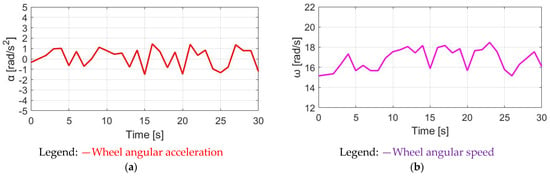
Figure 27.
SPPT-reflected E-bike response: (a) wheel angular acceleration and (b) wheel angular speed.
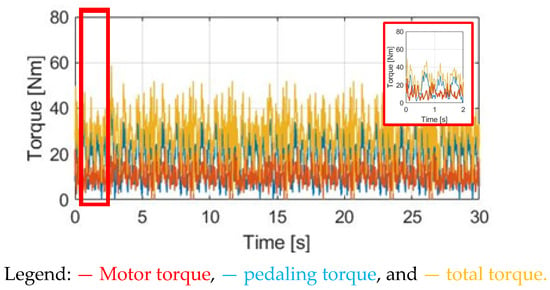
Figure 28.
Torque comparison under DPPT control method.
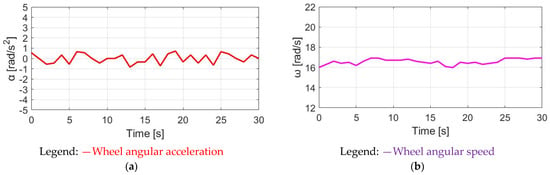
Figure 29.
DPPT-reflected E-bike response: (a) wheel angular acceleration and (b) wheel angular speed.
In addition, Figure 26 and Figure 28 compare the waveforms of the pedaling , motor and total under the dynamic SPPT and DPPT control methods, respectively. Since the motor torque is dynamically controlled under the SPPT and DPPT methods, is calculated proportionally to the measured pedaling torque for the SPPT method in (14) and the DPPT method in (15).
It is noted that for the DPPT method, the time-domain waveform of the motor torque is delayed by 90° with respect to the measured pedaling . Considering the same E-bike external load, the cyclist that is reflected by pedaling is almost the same. However, under the same average assisted torque , the total torque variation through DPPT is smaller than the variation reflected by SPPT, as listed in Table 6. Similar to the simulation comparison, it is expected that the variation in both αw and ωw are smaller, as shown in Figure 27 and Figure 29. A detailed comparison of αw and ωw will be explained in Section 5.5.
5.3. Proposed CGPT Experiment
Time-domain torque waveforms through the proposed CGPT control are shown in Figure 30. In addition, the time-domain αw and ωw waveforms are included in Figure 31. As seen in Section 4.5, the CGPT-assisted torque is determined based on (17). For the actual experiment, is determined at 25 Nm, which is the average pedaling torque on the rear wheel under normal NMT. When the pedaling torque transmission to the rear wheel is smaller than 25 Nm, should be enabled similarly to the DPPT control condition. Based on the simulation, it is expected that the average and maximum motor are the lowest among the four torque control methods. This leads to better E-bike battery usage.
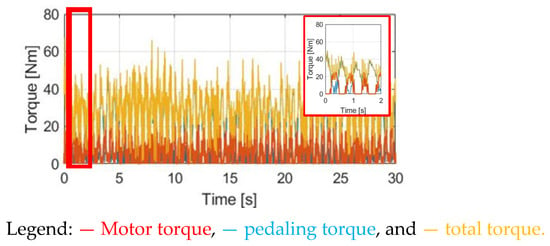
Figure 30.
Torque comparison under CGPT control method.
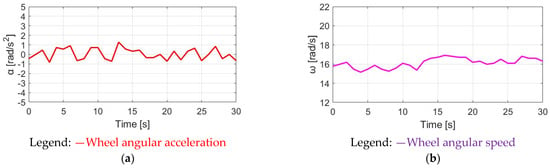
Figure 31.
CGPT-reflected E-bike response: (a) wheel angular acceleration and (b) wheel angular speed.
5.4. E-Bike Torque Performance Comparison
Table 6 summarizes the waveform conditions among the pedaling, motor, and total torque. For normal NMT, the average pedaling torque is 29.81 Nm, with 59.92% torque variation. By adding one of the four torque controls, the cyclist pedaling torque can be effectively decreased for better riding performance.

Table 6.
Motor torque comparison under different torque control methods.
Table 6.
Motor torque comparison under different torque control methods.
| Assisted Method | NMT | CT | SPPT | DPPT | CGPT | |
|---|---|---|---|---|---|---|
| Parameter | ||||||
| Average pedaling torque (Nm) | 29.81 | 13.05 | 20.83 | 21.05 | 25.63 | |
| Average motor torque (Nm) | NA | 45 | 12.01 | 11.93 | 8.24 | |
| Max pedaling torque (Nm) | 74.37 | 36.11 | 48.09 | 48.13 | 62.67 | |
| Max motor torque (Nm) | NA | 45 | 27.05 | 27.07 | 25 | |
| Pedaling torque variation (Nm) | 44.56 | 23.06 | 27.26 | 27.08 | 37.04 | |
| Variation ratio (Nm/%) | 59.92% | 63.86% | 56.69% | 56.26% | 59.10% | |
| Average total torque (Nm) | 29.81 | 58.05 | 32.84 | 32.98 | 33.87 | |
| Max total torque (Nm) | 74.37 | 81.11 | 75.14 | 75.20 | 87.67 | |
For the CT-assisted control method, the minimal average pedaling torque of 13.05 Nm is the result of the cyclist maintaining the wheel speed ωw at 15.88 rad/s (20 km/h).
The difference between SPPT and DPPT is the torque waveform’s initial phase. Under this effect, there is no visible difference in the cyclist’s reflected pedaling torque. However, the variation in αw and ωw might be different due to different peak total torques with these two control methods.
By contrast, for the proposed CGPT control method, the motor torque is efficiently manipulated. However, the required pedaling torque is the highest among these four assisted control methods. This is because, similar to the DPPT method, a smooth condition for the αw and ωw of the E-bike is expected.
5.5. E-Bike Speed and Acceleration Comparison
This section compares the performance of the E-bike acceleration αw and speed ωw in Table 7 under the different proposed torque controls. It is noted that the average value and ripple of αw and ωw are both dependent on the total torque in Table 6. Since the CT-assisted control results in the highest variation in , the highest ripples of both αw and ωw are shown in Table 7. This experimental result is consistent with the simulation in Table 3.

Table 7.
E-bike speed and acceleration comparison under different torque control methods.
Although the pedaling torque condition is similar with the SPPT and DPPT methods, the variation in the total synergy torque might be different. Under this effect, the ripples of αw and ωw for the DPPT control are smaller than those with SPPT control. Finally, for the proposed CGPT method, the corresponding αw and ωw ripple is slightly higher than those with the DPPT methos. However, compared to CT and SPPT controls, the CGPT method still results in a better αw and ωw ripple performance for E-bike torque-assisted control.
5.6. Simulation and Experiment Comparison
This section compares the results obtained by both the simulation and the experiment. Table 8 shows the corresponding comparison of the simulation and the experiment under different assisted torque control methods. The key findings are summarized as follows.

Table 8.
Comparison between simulation and experiment under different torque control methods.
First, the pedaling torque performance is compared. For the E-bike simulation, an ideal pedaling torque is assumed. Under this effect, there is no difference in the average and maximum pedaling torque among these four torque control methods. By contrast, for the experiment, the pedaling torque is directly provided by a test cyclist. Because this cyclist must maintain an overall cycling time at 30 s, the average and maximum pedaling torque are both highest under NMT control, whereas they are the smallest with CT control. From the prior conclusion in Table 6, the largest motor torque is manipulated for CT control, resulting in the lowest pedaling torque for a cyclist.
For the wheel speed and acceleration ripple comparison in Table 8, both speed and acceleration ripples can degrade the E-bike’s cycling performance. Comparing the results between the simulation and the experiment, speed/acceleration ripples are highest for the CT control method. By contrast, these ripples can be reduced based on the implementation of either DPPT or CGPT control. The proposed simulation is consistent with the experimental results.
For the average speed and acceleration comparison in Table 8, there is a difference between the simulation and the experiment. For the simulation, the average speed and acceleration are directly proportional to the average torque. By contrast, for the experiment, the average speed is almost the same under the limitation of maintaining the same cycling time. However, the average acceleration is also the highest for the CT control method, with the highest average torque.
6. Conclusions
This paper proposes a novel torque control method for assisted E-bikes considering external load conditions. For assisted E-bikes, it is shown that the overall pedaling torque can be affected by different load conditions. These include the cyclist’s weight, wind resistance, rolling resistance, and the road slope. Among them, the external loads caused by the road gradient and wind resistance are greater than those caused by the cyclist’s weight and the rolling resistance.
Figure 32 illustrates a graphical conclusion of the proposed E-bike torque control. Key E-bike cycling parameters were first identified. Four different torque control methods were developed to improve the E-bike’s dynamic response with minimal pedaling torque variation and acceleration/speed ripple. After the simulation verification from MATLAB/Simulink, an integrated E-bike sensor hardware was built to evaluate the proposed torque control. Finally, the proposed assisted torque control was verified through an experimental E-bike test bench.
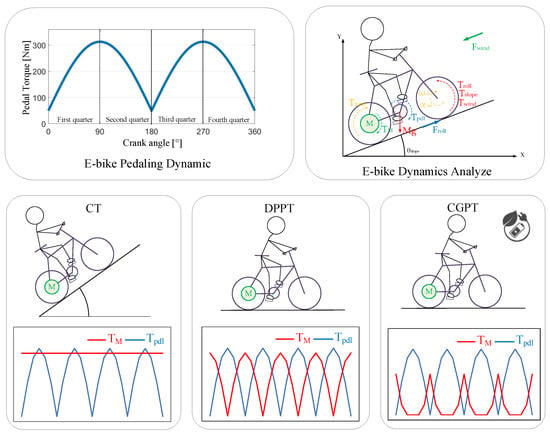
Figure 32.
Graphical conclusion of proposed E-bike torque control.
The experimental results conclude that the CT method achieves the smallest average pedaling torque. However, it results in the highest speed ripple and acceleration ripple. These ripples degrade the E-bike’s cycling performance. It is concluded that the CT control method is well suited for professional cyclists with special road conditions.
On the other hand, the proposed CGPT control resulted in the lowest motor torque output. It is especially well suited for commuting cyclists with minimal battery power consumption. By contrast, the DPPT control method can provide a comparable cycling experience to the original NMT method in terms of the wheel acceleration ripple and speed ripple. The DPPT method is well suited for standard E-bike torque management for different load conditions.
Author Contributions
Methodology, P.-J.H. and S.-C.Y.; software and hardware implementation, C.-P.Y. and Y.-J.L.; formal analysis, Y.-J.L.; writing—original draft preparation, W.-D.C. and P.-H.C.; writing—review and editing, W.-D.C., P.-H.C. and S.-C.Y.; supervision, S.-C.Y. All authors have read and agreed to the published version of the manuscript.
Funding
The authors gratefully acknowledge the financial and equipment support by the National Taiwan University, Taiwan, R.O.C. under the Grant 09HT512031.
Institutional Review Board Statement
Not applicable.
Informed Con sent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| θcrank | Crank rotating angle |
| Fpx | Pedaling horizontal force |
| Fpy | Pedaling vertical force |
| Pedaling torque | |
| TM | Motor-assisted torque |
| Ttotal | Total synergetic torque |
| Troll | Friction-reflected torque |
| Twind | Windage torque |
| Tslope | Climbing-reflected torque |
| Tdis | External disturbance torque |
| Tdrv | Actual wheel driving torque |
| Pedaling torque variation | |
| Maximum measured pedaling torque | |
| Average measured pedaling torque | |
| Crank rotating radius | |
| Me | Mass of E-bike |
| Mc | Mass of cyclist |
| Jw | Wheel inertia |
| Rw | Bike wheel radius |
| g | Gravitational constant |
| Air density | |
| Aerodynamic drag coefficient | |
| A | Frontal area |
| Transmission gear ratio | |
| T | Tire pressure |
| ωw | Wheel angular speed |
| αw | Wheel angular acceleration |
| Kroll | Wheel resistance coefficient |
| Vwind | Wind speed |
| Vbike | Bike wheel speed |
| θslope | Slope angle |
| id | Direct-axis (d-axis) motor current |
| iq | Quadrature-axis (q-axis) motor current |
| Vd | Direct-axis (d-axis) motor voltage |
| Vq | Quadrature-axis (q-axis) motor voltage |
| Kpd | Direct-axis (d-axis) proportional controller gain |
| Kpq | Quadrature-axis (q-axis) proportional controller gain |
| Kid | Direct-axis (d-axis) integral controller gain |
| Kiq | Quadrature-axis (q-axis) integral controller gain |
| Motor phase inductance | |
| Motor phase resistance | |
| Estimated motor position | |
| Last position measured by Hall sensors | |
| Estimated speed based on prior Hall sensor position |
References
- Lee, J.; Jiang, J.; Sun, Y. Design and simulation of control systems for electric-assist bikes. In Proceedings of the 2016 IEEE 11th Conference on Industrial Electronics and Applications (ICIEA), Hefei, China, 5–7 June 2016; pp. 1736–1740. [Google Scholar]
- Hunt, K.J.; Stone, B.; Negard, N.O.; Schauer, T.; Fraser, M.H.; Cathcart, A.J.; Ferrario, C.; Ward, S.A.; Grant, S. Control strategies for integration of electric motor assist and functional electrical stimulation in paraplegic cycling: Utility for exercise testing and mobile cycling. IEEE Trans. Neural Syst. Rehabil. Eng. 2004, 12, 89–101. [Google Scholar] [CrossRef] [PubMed]
- Lozinski, J.; Heidary, S.H.; Brandon, S.C.E.; Komeili, A. An Adaptive Pedaling Assistive Device for Asymmetric Torque Assistant in Cycling. Sensors 2023, 23, 2846. [Google Scholar] [CrossRef] [PubMed]
- Zaghari, B.; Stuikys, A.; Weddell, A.S.; Beeby, S. Efficient Energy Conversion in Electrically Assisted Bicycles Using a Switched Reluctance Machine Under Torque Control. IEEE Access 2020, 8, 202401–202411. [Google Scholar] [CrossRef]
- Palmieri, G.; Tiboni, M.; Legnani, G. Analysis of the Upper Limitation of the Most Convenient Cadence Range in Cycling Using an Equivalent Moment Based Cost Function. Mathematics 2020, 8, 1947. [Google Scholar] [CrossRef]
- Balbinot, A.; Milani, C.; Nascimento, J.D.S.B. A New Crank Arm-Based Load Cell for the 3D Analysis of the Force Applied by a Cyclist. Sensors 2014, 14, 22921–22939. [Google Scholar] [CrossRef]
- Böhm, H.; Siebert, S.; Walsh, M. Effects of short-term training using SmartCranks on cycle work distribution and power output during cycling. Eur. J. Appl. Physiol. 2008, 103, 225–232. [Google Scholar] [CrossRef]
- Turpin, N.A.; Watier, B. Cycling Biomechanics and Its Relationship to Performance. Appl. Sci. 2020, 10, 4112. [Google Scholar] [CrossRef]
- Caldwell, G.E.; Li, L.; McCole, S.D.; Hagberg, J.M. Pedal and Crank Kinetics in Uphill Cycling. J. Appl. Biomech. 1998, 14, 245–259. [Google Scholar] [CrossRef]
- Bini, R.; Hume, P.; Croft, J.; Kilding, A. Pedal force effectiveness in cycling: A review of constraints and training effects. J. Sci. Cycl. 2013, 2, 11–24. [Google Scholar]
- Höchtl, F.; Böhm, H.; Senner, V. Prediction of energy efficient pedal forces in cycling using musculoskeletal simulation models. Procedia Eng. 2010, 2, 3211–3215. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, D.; Wang, Y.; Yin, K.; Zhang, C.; Zou, L.; Liu, Y. Do Surface Slope and Posture Influence Lower Extremity Joint Kinetics during Cycling? Int. J. Environ. Res. Public Health 2020, 17, 2846. [Google Scholar] [CrossRef] [PubMed]
- Martín-Sosa, E.; Chaves, V.; Alvarado, I.; Mayo, J.; Ojeda, J. Design and Validation of a Device Attached to a Conventional Bicycle to Measure the Three-Dimensional Forces Applied to a Pedal. Sensors 2021, 21, 4590. [Google Scholar] [CrossRef] [PubMed]
- Mandriota, R.; Fabbri, S.; Nienhaus, M.; Grasso, E. Sensorless Pedalling Torque Estimation Based on Motor Load Torque Observation for Electrically Assisted Bicycles. Actuators 2021, 10, 88. [Google Scholar] [CrossRef]
- Avina-Bravo, E.G.; Cassirame, J.; Escriba, C.; Acco, P.; Fourniols, J.-Y.; Soto-Romero, G. Smart Electrically Assisted Bicycles as Health Monitoring Systems: A Review. Sensors 2022, 22, 468. [Google Scholar] [CrossRef]
- Evans, S.A.; James, D.A.; Rowlands, D.; Lee, J.B. Evaluation of Accelerometer-Derived Data in the Context of Cycling Cadence and Saddle Height Changes in Triathlon. Sensors 2021, 21, 871. [Google Scholar] [CrossRef]
- Murgano, E.; Caponetto, R.; Pappalardo, G.; Cafiso, S.D.; Severino, A. A Novel Acceleration Signal Processing Procedure for Cycling Safety Assessment. Sensors 2021, 21, 4183. [Google Scholar] [CrossRef]
- Hollaus, B.; Volmer, J.C.; Fleischmann, T. Cadence Detection in Road Cycling Using Saddle Tube Motion and Machine Learning. Sensors 2022, 22, 6140. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Zuriaga, A.M.; Llopis-Castelló, D.; Just-Martínez, V.; Fonseca-Cabrera, A.S.; Alonso-Troyano, C.; García, A. Implementation of a Low-Cost Data Acquisition System on an E-Scooter for Micromobility Research. Sensors 2022, 22, 8215. [Google Scholar] [CrossRef]
- Bruno, S.; Vita, L.; Loprencipe, G. Development of a GIS-Based Methodology for the Management of Stone Pavements Using Low-Cost Sensors. Sensors 2022, 22, 6560. [Google Scholar] [CrossRef]
- Pan, L.; Xia, Y.; Xing, L.; Song, Z.; Xu, Y. Exploring Use Acceptance of Electric Bicycle-Sharing Systems: An Empirical Study Based on PLS-SEM Analysis. Sensors 2022, 22, 7057. [Google Scholar] [CrossRef]
- Stilo, L.; Lugo, H.; Velandia, D.S.; Conway, P.P.; West, A.A. Personalised Controller Strategies for Next Generation Intelligent Adaptive Electric Bicycles. IEEE Trans. Intell. Transp. Syst. 2021, 22, 7814–7825. [Google Scholar] [CrossRef]
- De La Iglesia, D.H.; De Paz, J.F.; Villarrubia González, G.; Barriuso, A.L.; Bajo, J.; Corchado, J.M. Increasing the Intensity over Time of an Electric-Assist Bike Based on the User and Route: The Bike Becomes the Gym. Sensors 2018, 18, 220. [Google Scholar] [CrossRef] [PubMed]
- Meyer, D.; Körber, M.; Senner, V.; Tomizuka, M. Regulating the Heart Rate of Human–Electric Hybrid Vehicle Riders Under Energy Consumption Constraints Using an Optimal Control Approach. IEEE Trans. Control. Syst. Technol. 2019, 27, 2125–2138. [Google Scholar] [CrossRef]
- Muetze, A.; Tan, Y.C. Electric bicycles—A performance evaluation. IEEE Ind. Appl. Mag. 2007, 13, 12–21. [Google Scholar] [CrossRef]
- De La Iglesia, D.H.; Villarrubia, G.; De Paz, J.F.; Bajo, J. Multi-Sensor Information Fusion for Optimizing Electric Bicycle Routes Using a Swarm Intelligence Algorithm. Sensors 2017, 17, 2501. [Google Scholar] [CrossRef]
- Allebosch, G.; Van den Bossche, S.; Veelaert, P.; Philips, W. Camera-Based System for Drafting Detection While Cycling. Sensors 2020, 20, 1241. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Suárez, J.; Arroyo, P.; Alfonso, R.; Suárez, J.I.; Pinilla-Gil, E.; Lozano, J. A Novel Bike-Mounted Sensing Device with Cloud Connectivity for Dynamic Air-Quality Monitoring by Urban Cyclists. Sensors 2022, 22, 1272. [Google Scholar] [CrossRef]
- Królak, A.; Wiktorski, T.; Bjørkavoll-Bergseth, M.F.; Ørn, S. Artifact Correction in Short-Term HRV during Strenuous Physical Exercise. Sensors 2020, 20, 6372. [Google Scholar] [CrossRef]
- Avina-Bravo, E.G.; Sodre Ferreira de Sousa, F.A.; Escriba, C.; Acco, P.; Giraud, F.; Fourniols, J.-Y.; Soto-Romero, G. Design and Validity of a Smart Healthcare and Control System for Electric Bikes. Sensors 2023, 23, 4079. [Google Scholar] [CrossRef]
- Shahbakhti, M.; Hakimi, N.; Horschig, J.M.; Floor-Westerdijk, M.; Claassen, J.; Colier, W.N.J.M. Estimation of Respiratory Rate during Biking with a Single Sensor Functional Near-Infrared Spectroscopy (fNIRS) System. Sensors 2023, 23, 3632. [Google Scholar] [CrossRef]
- Li, X.; Liu, Z.; Gao, X.; Zhang, J. Bicycling Phase Recognition for Lower Limb Amputees Using Support Vector Machine Optimized by Particle Swarm Optimization. Sensors 2020, 20, 6533. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.-H.; Lin, C.-B.; Chen, Y.; Chen, W.; Huang, T.-S.; Hsu, C.-Y. An EMG Patch for the Real-Time Monitoring of Muscle-Fatigue Conditions During Exercise. Sensors 2019, 19, 3108. [Google Scholar] [CrossRef] [PubMed]
- Muyor, J.M.; Antequera-Vique, J.A.; Oliva-Lozano, J.M.; Arrabal-Campos, F.M. Evaluation of Dynamic Spinal Morphology and Core Muscle Activation in Cyclists—A Comparison between Standing Posture and on the Bicycle. Sensors 2022, 22, 9346. [Google Scholar] [CrossRef] [PubMed]
- Fonda, B.; Sarabon, N. Biomechanics and Energetics of Uphill Cycling: A review. Kinesiology 2012, 44, 5–17. [Google Scholar]
- Corno, M.; Berretta, D.; Spagnol, P.; Savaresi, S.M. Design, Control, and Validation of a Charge-Sustaining Parallel Hybrid Bicycle. IEEE Trans. Control. Syst. Technol. 2016, 24, 817–829. [Google Scholar] [CrossRef]
- Yang, Y.; Yeo, J.; Priya, S. Harvesting Energy from the Counterbalancing (Weaving) Movement in Bicycle Riding. Sensors 2012, 12, 10248–10258. [Google Scholar] [CrossRef]
- Martirosyan, A.V.; Ilyushin, Y.V.; Afanaseva, O.V. Development of a Distributed Mathematical Model and Control System for Reducing Pollution Risk in Mineral Water Aquifer Systems. Water 2022, 14, 151. [Google Scholar] [CrossRef]
- Mohammadzaheri, M.; Chen, L. Intelligent Predictive Control of a Model Helicopter’s Yaw Angle. Asian J. Control. 2010, 12, 667–679. [Google Scholar] [CrossRef]
- Chowdhury, H.; Alam, F.; Khan, I. An Experimental Study of Bicycle Aerodynamics. Int. J. Mech. Mater. Eng. 2011, 6, 269–274. [Google Scholar]
- Engineering ToolBox. 2008. Rolling Resistance. Available online: https://www.engineeringtoolbox.com/rolling-friction-resistance-d_1303.html (accessed on 24 March 2022).
- Roveri, N.; Pepe, G.; Mezzani, F.; Carcaterra, A.; Culla, A.; Milana, S. OPTYRE—Real Time Estimation of Rolling Resistance for Intelligent Tyres. Sensors 2019, 19, 5119. [Google Scholar] [CrossRef]
- Bojoi, R.; Lazzari, M.; Profumo, F.; Tenconi, A. Digital field oriented control for dual three-phase induction motor drives. In Proceedings of the Conference Record of the 2002 IEEE Industry Applications Conference, 37th IAS Annual Meeting, Pittsburgh, PA, USA, 13–18 October 2002; Volume 2, pp. 818–825. [Google Scholar]
- Mohammadzahri, M.; Khaleghifar, A.; Ghodsi, M.; Soltani, P.; AlSulti, S. A Discrete Approach to Feedback Linearization, Yaw Control of an Unmanned Helicopter. Unmanned Syst. 2023, 11, 57–66. [Google Scholar] [CrossRef]
- Morimoto, S.; Sanada, M.; Takeda, Y. Sinusoidal current drive system of permanent magnet synchronous motor with low resolution position sensor. In Proceedings of the IAS ‘96. Conference Record of the 1996 IEEE Industry Applications Conference Thirty-First IAS Annual Meeting, San Diego, CA, USA, 6–10 October 1996; Volume 1, pp. 9–14. [Google Scholar] [CrossRef]
- Shen, J.X.; Zhu, Z.Q.; Howe, D. PM brushless drives with low-cost and low-resolution position sensors. In Proceedings of the 4th International Power Electronics and Motion Control Conference, IPEMC, Xi’an, China, 14–16 August 2004; Volume 2, pp. 1033–1038. [Google Scholar]
- Buja, G.; Bertoluzzo, M.; Keshri, R.K. Torque Ripple-Free Operation of PM BLDC Drives with Petal-Wave Current Supply. IEEE Trans. Ind. Electron. 2015, 62, 4034–4043. [Google Scholar] [CrossRef]
- Skóra, M. Operation of PM BLDC motor drives with faulty rotor position sensor. In Proceedings of the 2017 International Symposium on Electrical Machines (SME), Naleczow, Poland, 18–21 June 2017; pp. 1–6. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).