Mixing Rules for an Exact Determination of the Dielectric Properties of Engine Soot Using the Microwave Cavity Perturbation Method and Its Application in Gasoline Particulate Filters
Abstract
1. Introduction
2. Fundamentals of the MCP and Their Application to Soot-Loaded Particulate Filters
2.1. Determination of Dielectric Properties Using the MCP
- -
- Changes in the electromagnetic field due to depolarization inside the sample.
- -
- Deviation of the field distribution in the cavity due to its non-ideal cylindrical shape.
- -
- Necessity to apply mixing rules for porous samples or samples with multiple species.
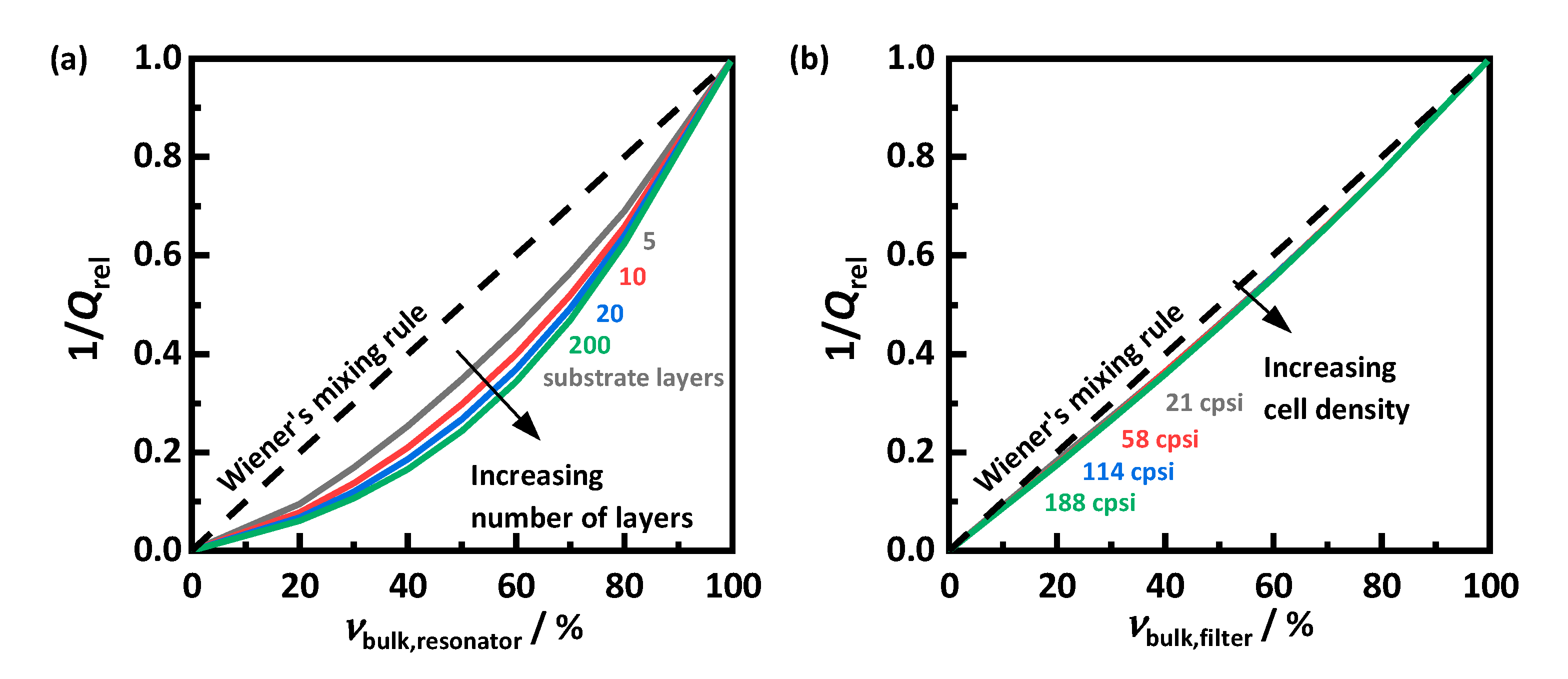
2.2. Influence of Mixing Rules on the Material Property Determination
2.3. Possible Mixing Rules for Soot-Loaded Filter
3. Determination of the Mixing Rules for Soot-Loaded Particulate Filters
3.1. Soot-Loaded Filter-Air Mixing Rule
3.2. Soot-Substrate Mixing Rule
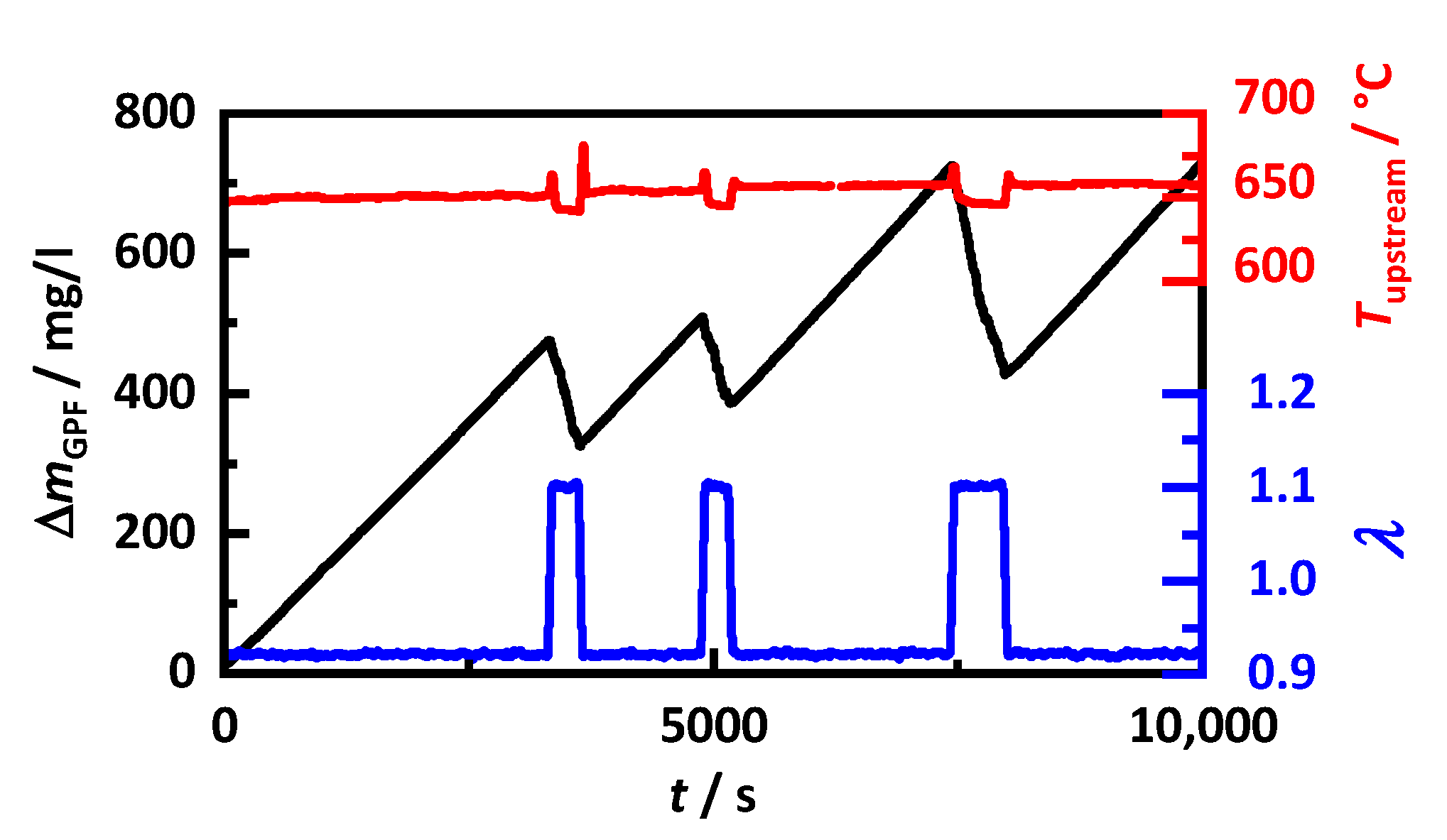
4. Validation of Mixing Rules by Engine Test Bench Measurements
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hennig, F.; Quass, U.; Hellack, B.; Küpper, M.; Kuhlbusch, T.A.J.; Stafoggia, M.; Hoffmann, B. Ultrafine and Fine Particle Number and Surface Area Concentrations and Daily Cause-Specific Mortality in the Ruhr Area, Germany, 2009–2014. Environ. Health Perspect. 2018, 126, 27008. [Google Scholar] [CrossRef] [PubMed]
- Soppa, V.J.; Shinnawi, S.; Hennig, F.; Sasse, B.; Hellack, B.; Kaminski, H.; Quass, U.; Schins, R.P.F.; Kuhlbusch, T.A.J.; Hoffmann, B. Effects of short-term exposure to fine and ultrafine particles from indoor sources on arterial stiffness—A randomized sham-controlled exposure study. Int. J. Hyg. Environ. Health 2019, 222, 1115–1132. [Google Scholar] [CrossRef] [PubMed]
- Kittelson, D.B. Engines and nanoparticles. J. Aerosol Sci. 1998, 29, 575–588. [Google Scholar] [CrossRef]
- Chen, L.; Liang, Z.; Zhang, X.; Shuai, S. Characterizing particulate matter emissions from GDI and PFI vehicles under transient and cold start conditions. Fuel 2017, 189, 131–140. [Google Scholar] [CrossRef]
- Schoenhaber, J.; Kuehn, N.; Bradler, B.; Richter, J.M.; Bauer, S.; Lenzen, B.; Beidl, C. Impact of European Real-Driving-Emissions Legislation on Exhaust Gas Aftertreatment Systems of Turbocharged Direct Injected Gasoline Vehicles. SAE Tech. Pap. 2017. [Google Scholar] [CrossRef]
- Demuynck, J.; Favre, C.; Bosteels, D.; Hamje, H.; Andersson, J. Real-World Emissions Measurements of a Gasoline Direct Injection Vehicle without and with a Gasoline Particulate Filter. SAE Tech. Pap. 2017. [Google Scholar] [CrossRef]
- Rose, D.; Boger, T. Different Approaches to Soot Estimation as Key Requirement for DPF Applications. SAE Tech. Pap. 2009. [Google Scholar] [CrossRef]
- Walter, S.; Schwanzer, P.; Hagen, G.; Haft, G.; Dietrich, M.; Rabl, H.-P.; Moos, R. Hochfrequenzsensorik zur direkten Beladungserkennung von Benzinpartikelfiltern. In Automobil-Sensorik 3; Tille, T., Ed.; Springer: Berlin, Germany, 2020; pp. 185–208. [Google Scholar] [CrossRef]
- Gaiser, G.; Mucha, P. Prediction of Pressure Drop in Diesel Particulate Filters Considering Ash Deposit and Partial Regenerations. SAE Tech. Pap. 2004. [Google Scholar] [CrossRef]
- Walter, S.; Schwanzer, P.; Hagen, G.; Haft, G.; Rabl, H.-P.; Dietrich, M.; Moos, R. Modelling the Influence of Different Soot Types on the Radio-Frequency-Based Load Detection of Gasoline Particulate Filters. Sensors 2020, 20, 2659. [Google Scholar] [CrossRef]
- Liu, X.; Chanko, T.; Lambert, C.; Maricq, M. Gasoline Particulate Filter Efficiency and Backpressure at Very Low Mileage. SAE Tech. Pap. 2018. [Google Scholar] [CrossRef]
- Lambert, C.; Chanko, T.; Dobson, D.; Liu, X.; Pakko, J. Gasoline Particle Filter Development. Emiss. Control Sci. Technol. 2017, 3, 105–111. [Google Scholar] [CrossRef]
- Saito, C.; Nakatani, T.; Miyairi, Y.; Yuuki, K.; Makino, M.; Kurachi, H.; Heuss, W.; Kuki, T.; Furuta, Y.; Kattouah, P.; et al. New Particulate Filter Concept to Reduce Particle Number Emissions. SAE Tech. Pap. 2011. [Google Scholar] [CrossRef]
- Chan, T.W.; Meloche, E.; Kubsh, J.; Rosenblatt, D.; Brezny, R.; Rideout, G. Evaluation of a Gasoline Particulate Filter to Reduce Particle Emissions from a Gasoline Direct Injection Vehicle. SAE Int. J. Fuels Lubr. 2012, 5, 1277–1290. [Google Scholar] [CrossRef]
- Wang-Hansen, C.; Ericsson, P.; Lundberg, B.; Skoglundh, M.; Carlsson, P.-A.; Andersson, B. Characterization of Particulate Matter from Direct Injected Gasoline Engines. Top. Catal. 2013, 56, 446–451. [Google Scholar] [CrossRef]
- Suresh, A.; Khan, A.; Johnson, J.H. An Experimental and Modeling Study of Cordierite Traps—Pressure Drop and Permeability of Clean and Particulate Loaded Traps. SAE Tech. Pap. 2000. [Google Scholar] [CrossRef]
- Schwanzer, P.; Mieslinger, J.; Dietrich, M.; Haft, G.; Walter, S.; Hagen, G.; Moos, R.; Gaderer, M.; Rabl, H.-P. Monitoring of a Particulate Filter for Gasoline Direct Injection Engines with a Radio-Frequency-Sensor. In Proceedings of the 11th Internationales Symposium für Abgasund Partikelemissionen, Ludwigsburg, Germany, 3–4 March 2020. [Google Scholar]
- Sethia, S.; Kubinski, D.; Nerlich, H.; Naber, J. RF Studies of Soot and Ammonia Loadings on a Combined Particulate Filter and SCR Catalyst. J. Electrochem. Soc. 2020, 167, 147516. [Google Scholar] [CrossRef]
- Moos, R. Microwave-Based Catalyst State Diagnosis—State of the Art and Future Perspectives. SAE Int. J. Engines 2015, 8, 1240–1245. [Google Scholar] [CrossRef]
- Sappok, A.; Bromberg, L.; Parks, J.E.; Prikhodko, V. Loading and Regeneration Analysis of a Diesel Particulate Filter with a Radio Frequency-Based Sensor. SAE Tech. Pap. 2010. [Google Scholar] [CrossRef]
- Sappok, A.; Bromberg, L. Radio Frequency Diesel Particulate Filter Soot and Ash Level Sensors: Enabling Adaptive Controls for Heavy-Duty Diesel Applications. SAE Int. J. Commer. Veh. 2014, 7, 468–477. [Google Scholar] [CrossRef]
- Feulner, M.; Hagen, G.; Hottner, K.; Redel, S.; Müller, A.; Moos, R. Comparative Study of Different Methods for Soot Sensing and Filter Monitoring in Diesel Exhausts. Sensors 2017, 17, 400. [Google Scholar] [CrossRef]
- Feulner, M.; Hagen, G.; Piontkowski, A.; Müller, A.; Fischerauer, G.; Brüggemann, D.; Moos, R. In-Operation Monitoring of the Soot Load of Diesel Particulate Filters: Initial Tests. Top. Catal. 2013, 56, 483–488. [Google Scholar] [CrossRef]
- Nicolin, P.; Boger, T.; Dietrich, M.; Haft, G.; Bachurina, A. Soot Load Monitoring in Gasoline Particulate Filter Applications with RF-Sensors. SAE Tech. Pap. 2020. [Google Scholar] [CrossRef]
- Dietrich, M.; Jahn, C.; Lanzerath, P.; Moos, R. Microwave-Based Oxidation State and Soot Loading Determination on Gasoline Particulate Filters with Three-Way Catalyst Coating for Homogenously Operated Gasoline Engines. Sensors 2015, 15, 21971–21988. [Google Scholar] [CrossRef] [PubMed]
- Beulertz, G.; Fritsch, M.; Fischerauer, G.; Herbst, F.; Gieshoff, J.; Votsmeier, M.; Hagen, G.; Moos, R. Microwave Cavity Perturbation as a Tool for Laboratory In Situ Measurement of the Oxidation State of Three Way Catalysts. Top. Catal. 2013, 56, 405–409. [Google Scholar] [CrossRef]
- Steiner, C.; Walter, S.; Malashchuk, V.; Hagen, G.; Kogut, I.; Fritze, H.; Moos, R. Determination of the Dielectric Properties of Storage Materials for Exhaust Gas Aftertreatment Using the Microwave Cavity Perturbation Method. Sensors 2020, 20, 6024. [Google Scholar] [CrossRef]
- Dietrich, M.; Rauch, D.; Porch, A.; Moos, R. A Laboratory Test Setup for in Situ Measurements of the Dielectric Properties of Catalyst Powder Samples under Reaction Conditions by Microwave Cavity Perturbation: Set up and Initial Tests. Sensors 2014, 14, 16856–16868. [Google Scholar] [CrossRef]
- Sihvola, A. Mixing Rules with Complex Dielectric Coefficients. Subsurf. Sens. Technol. Appl. 2000, 1, 393–415. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering, 4th ed.; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Chen, L. Microwave Electronics: Measurement and Materials Characterization; Wiley: Chichester, UK, 2005. [Google Scholar]
- Parkash, A.; Vaid, J.K.; Mansingh, A. Measurement of Dielectric Parameters at Microwave Frequencies by Cavity-Perturbation Technique. IEEE Trans. Microw. Theory Tech. 1979, 27, 791–795. [Google Scholar] [CrossRef]
- Venermo, J.; Sihvola, A. Dielectric polarizability of circular cylinder. J. Electrost. 2005, 63, 101–117. [Google Scholar] [CrossRef]
- Jylhä, L.; Sihvola, A. Equation for the effective permittivity of particle-filled composites for material design applications. J. Phys. D Appl. Phys. 2007, 40, 4966–4973. [Google Scholar] [CrossRef]
- Cheng, E.M.; Malek, M.F.b.A.; Ahmed, M.; You, K.Y.; Lee, K.Y.; Nornikman, H. The Use of Dielectric Mixture Equations to Analyze the Dielectric Properties of a Mixture of Rubber Tire Dust and Rice Husks in a Microwave Absorber. Prog. Electromagn. Res. 2012, 129, 559–578. [Google Scholar] [CrossRef][Green Version]
- Marquardt, P. Quantum-size affected conductivity of mesoscopic metal particles. Phys. Lett. A 1987, 123, 365–368. [Google Scholar] [CrossRef]
- El Bouazzaoui, S.; Achour, M.E.; Brosseau, C. Microwave effective permittivity of carbon black filled polymers: Comparison of mixing law and effective medium equation predictions. J. Appl. Phys. 2011, 110, 74105. [Google Scholar] [CrossRef]
- Jusoh, M.; Abbas, Z.; Hassan, J.; Azmi, B.; Ahmad, A. A Simple Procedure to Determine Complex Permittivity of Moist Materials Using Standard Commercial Coaxial Sensor. Meas. Sci. Rev. 2011, 11, 19–22. [Google Scholar] [CrossRef]
- Camacho Hernandez, J.N.; Link, G.; Soldatov, S.; Füssel, A.; Schubert, M.; Hampel, U. Experimental and numerical analysis of the complex permittivity of open-cell ceramic foams. Ceram. Int. 2020, 46, 26829–26840. [Google Scholar] [CrossRef]
- Camerucci, M.A.; Urretavizcaya, G.; Castro, M.S.; Cavalieri, A.L. Electrical properties and thermal expansion of cordierite and cordierite-mullite materials. J. Eur. Ceram. Soc. 2001, 21, 2917–2923. [Google Scholar] [CrossRef]
- Nelson, S.O. Density-Permittivity Relationships for Powdered and Granular Materials. IEEE Trans. Instrum. Meas. 2005, 54, 2033–2040. [Google Scholar] [CrossRef]
- Tuhkala, M.; Juuti, J.; Jantunen, H. An indirectly coupled open-ended resonator applied to characterize dielectric properties of MgTiO3–CaTiO3 powders. J. Appl. Phys. 2014, 115, 184101. [Google Scholar] [CrossRef]
- Dube, D.C. Study of Landau-Lifshitz-Looyenga’s formula for dielectric correlation between powder and bulk. J. Phys. D Appl. Phys. 1970, 3, 1648–1652. [Google Scholar] [CrossRef]
- Looyenga, H. Dielectric constants of heterogeneous mixtures. Physica 1965, 31, 401–406. [Google Scholar] [CrossRef]
- Birchak, J.R.; Gardner, C.G.; Hipp, J.E.; Victor, J.M. High dielectric constant microwave probes for sensing soil moisture. Proc. IEEE 1974, 62, 93–98. [Google Scholar] [CrossRef]
- Goncharenko, A.V. Generalizations of the Bruggeman equation and a concept of shape-distributed particle composites. Phys. Review. E Stat. Nonlinear Soft Matter Phys. 2003, 68, 41108. [Google Scholar] [CrossRef]
- Maxwell Garnett, J.C. Colours in Metal Glasses, in Metallic Films, and in Metallic Solutions. II. Philos. Trans. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1906, 205, 237–288. [Google Scholar]
- Lichtenecker, K.; Rother, K. Die Herleitung des logarithmischen Mischungsgesetzes aus allgemeinen Prinzipien der stationären Strömung. Phys. Zeitschr. 1931, 32, 255–260. [Google Scholar]
- Wiener, O. Zur Theorie der Refraktionskonstanten. Math. Phys. Kl. 1910, 62, 256–277. [Google Scholar]
- Karkkainen, K.K.; Sihvola, A.H.; Nikoskinen, K.I. Effective permittivity of mixtures: Numerical validation by the FDTD method. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1303–1308. [Google Scholar] [CrossRef]
- Seong, H.; Choi, S.; Lee, K. Examination of nanoparticles from gasoline direct-injection (GDI) engines using transmission electron microscopy (TEM). Int. J. Automot. Technol. 2014, 15, 175–181. [Google Scholar] [CrossRef]
- Boger, T.; Rose, D.; Nicolin, P.; Gunasekaran, N.; Glasson, T. Oxidation of Soot (Printex® U) in Particulate Filters Operated on Gasoline Engines. Emiss. Control Sci. Technol. 2015, 1, 49–63. [Google Scholar] [CrossRef]
- Choi, S.; Seong, H. Oxidation characteristics of gasoline direct-injection (GDI) engine soot: Catalytic effects of ash and modified kinetic correlation. Combust. Flame 2015, 162, 2371–2389. [Google Scholar] [CrossRef]


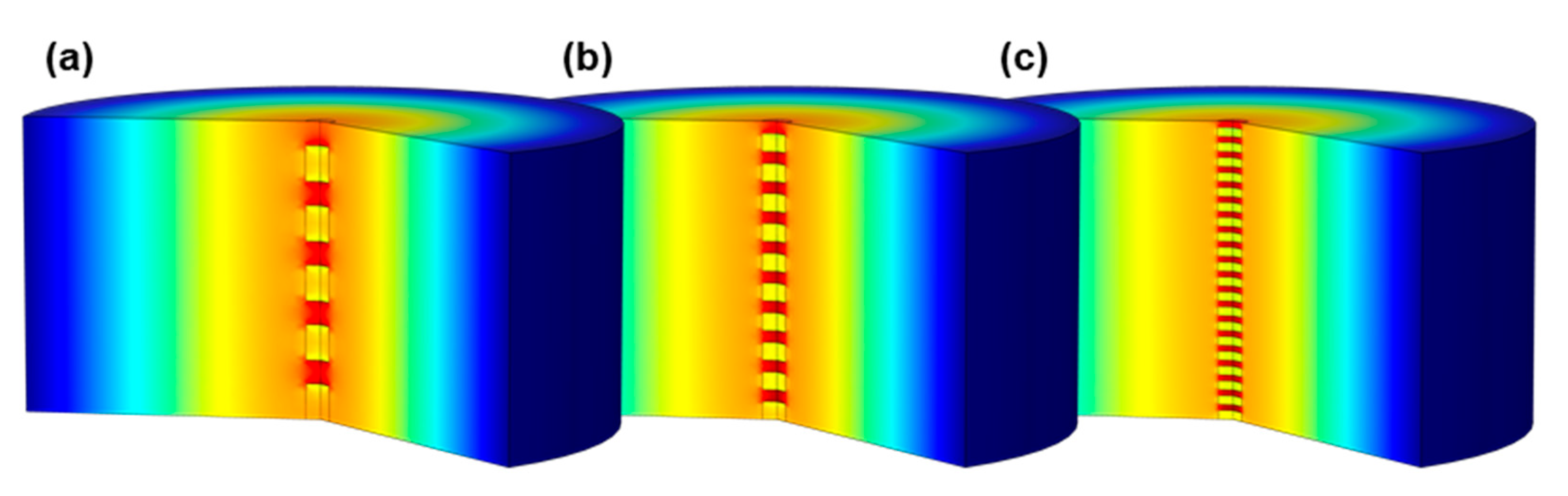








| /% | 0/20/30/40/50/60/70/80/100 |
| /mS/m | 1/10/20/40/60/80/100 |
| (a) substrate layers | 5/10/20/200 |
| (b) cell density/cpsi | 21/58/114/188 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Walter, S.; Schwanzer, P.; Steiner, C.; Hagen, G.; Rabl, H.-P.; Dietrich, M.; Moos, R. Mixing Rules for an Exact Determination of the Dielectric Properties of Engine Soot Using the Microwave Cavity Perturbation Method and Its Application in Gasoline Particulate Filters. Sensors 2022, 22, 3311. https://doi.org/10.3390/s22093311
Walter S, Schwanzer P, Steiner C, Hagen G, Rabl H-P, Dietrich M, Moos R. Mixing Rules for an Exact Determination of the Dielectric Properties of Engine Soot Using the Microwave Cavity Perturbation Method and Its Application in Gasoline Particulate Filters. Sensors. 2022; 22(9):3311. https://doi.org/10.3390/s22093311
Chicago/Turabian StyleWalter, Stefanie, Peter Schwanzer, Carsten Steiner, Gunter Hagen, Hans-Peter Rabl, Markus Dietrich, and Ralf Moos. 2022. "Mixing Rules for an Exact Determination of the Dielectric Properties of Engine Soot Using the Microwave Cavity Perturbation Method and Its Application in Gasoline Particulate Filters" Sensors 22, no. 9: 3311. https://doi.org/10.3390/s22093311
APA StyleWalter, S., Schwanzer, P., Steiner, C., Hagen, G., Rabl, H.-P., Dietrich, M., & Moos, R. (2022). Mixing Rules for an Exact Determination of the Dielectric Properties of Engine Soot Using the Microwave Cavity Perturbation Method and Its Application in Gasoline Particulate Filters. Sensors, 22(9), 3311. https://doi.org/10.3390/s22093311






