Fuzzy Gain-Scheduling PID for UAV Position and Altitude Controllers
Abstract
:1. Introduction
Main Contributions
- Proposition of a novel PID-gain schedule through the use of a fuzzy logic scheme to stabilize the position and altitude controller of a UAV;
- Devise a strategy to tune Fuzzy PID controllers, considering environmental conditions.
- Present a testing solution that can be embedded on UAV companion computers using ROS;
- Evaluate the proposed strategy in simulated and real environments.
2. Quadrotor Modeling
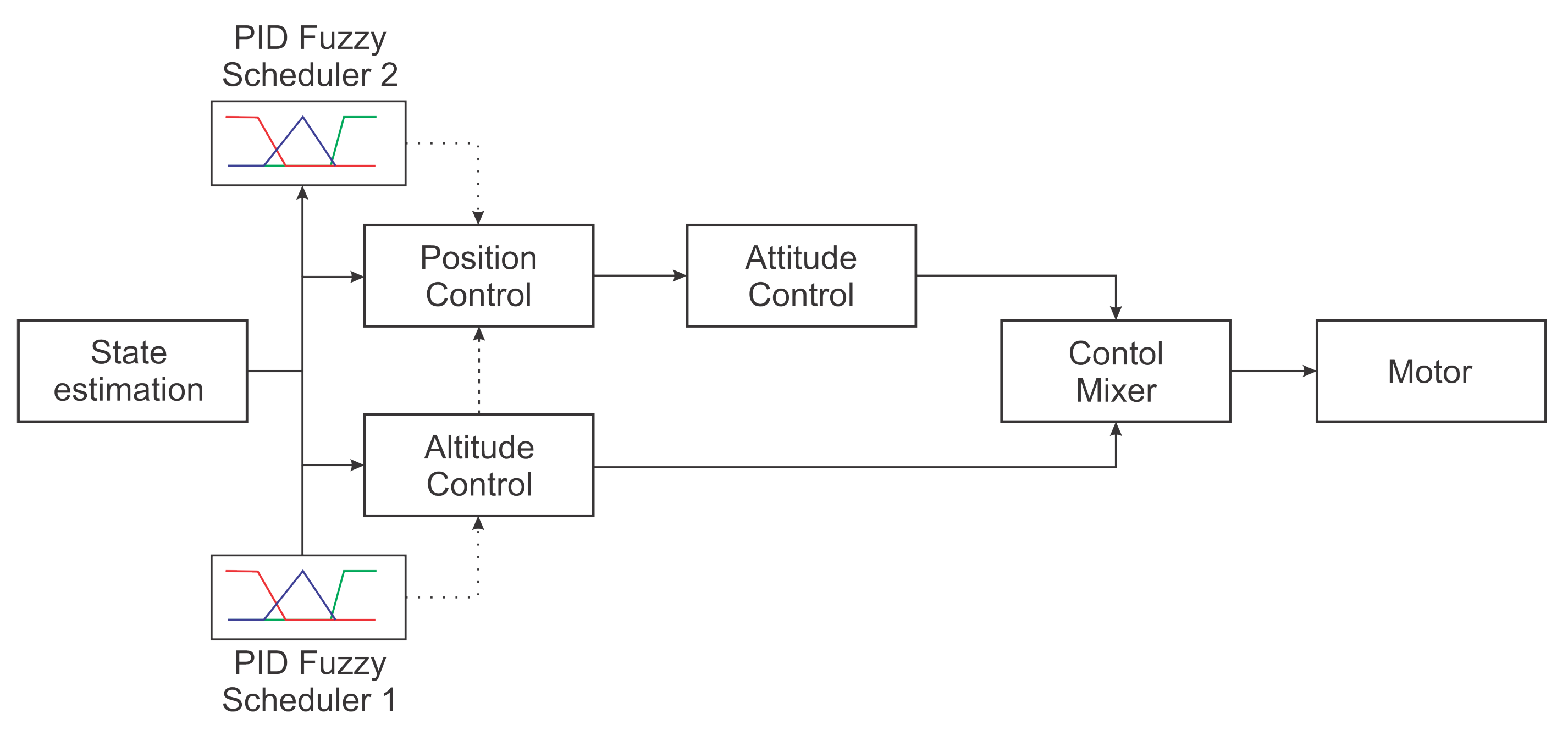
3. Control Strategy
3.1. PID Tunning
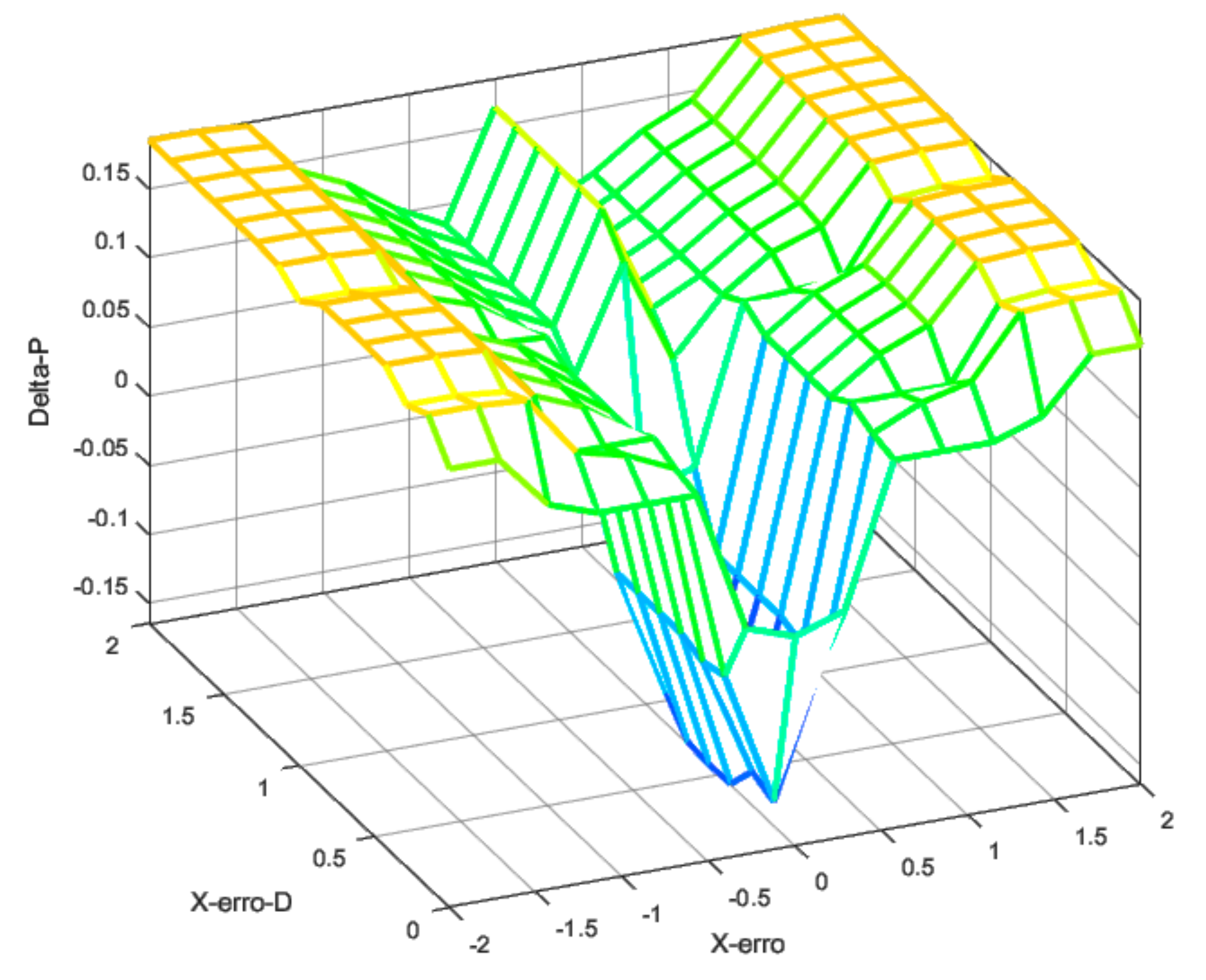
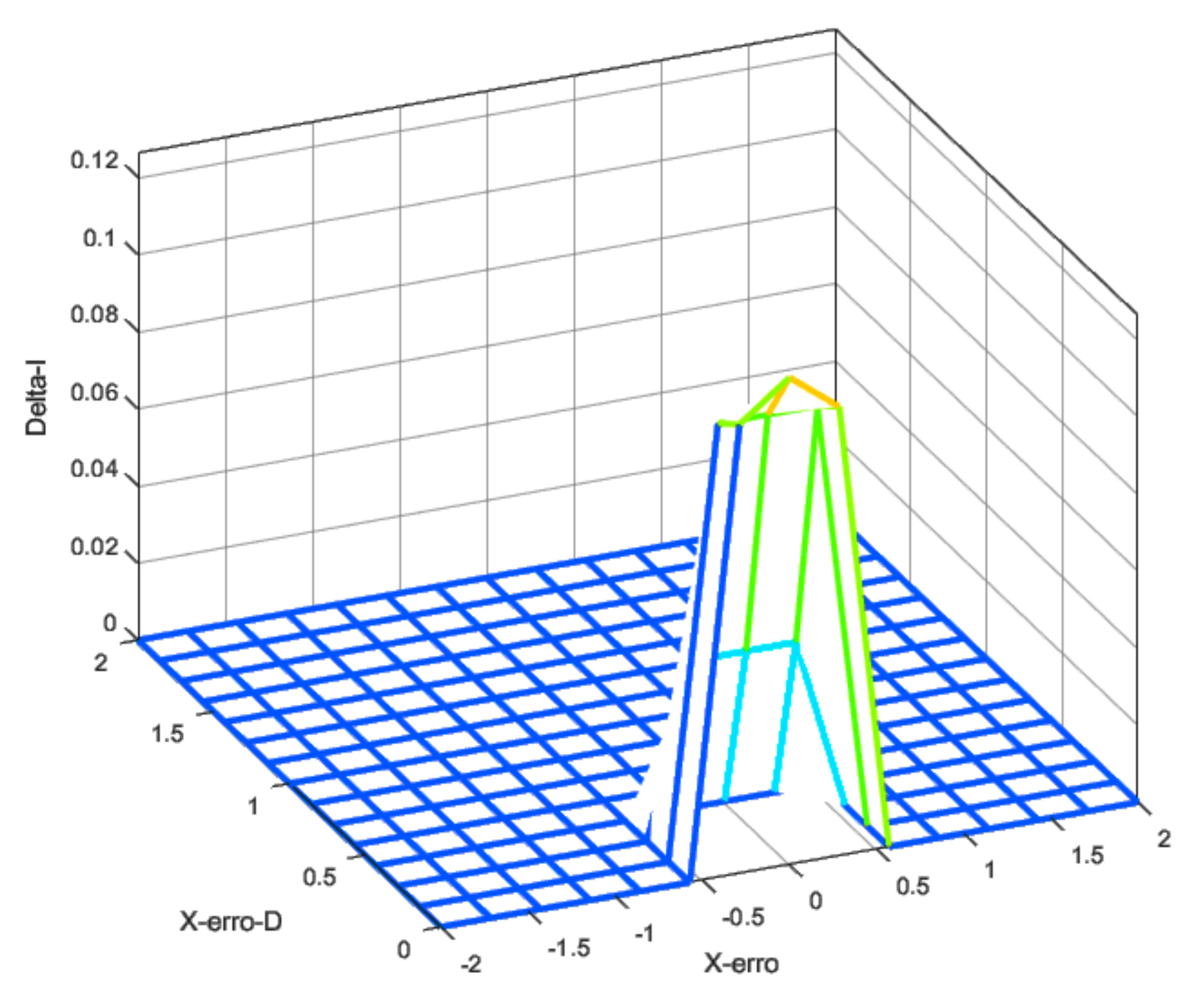
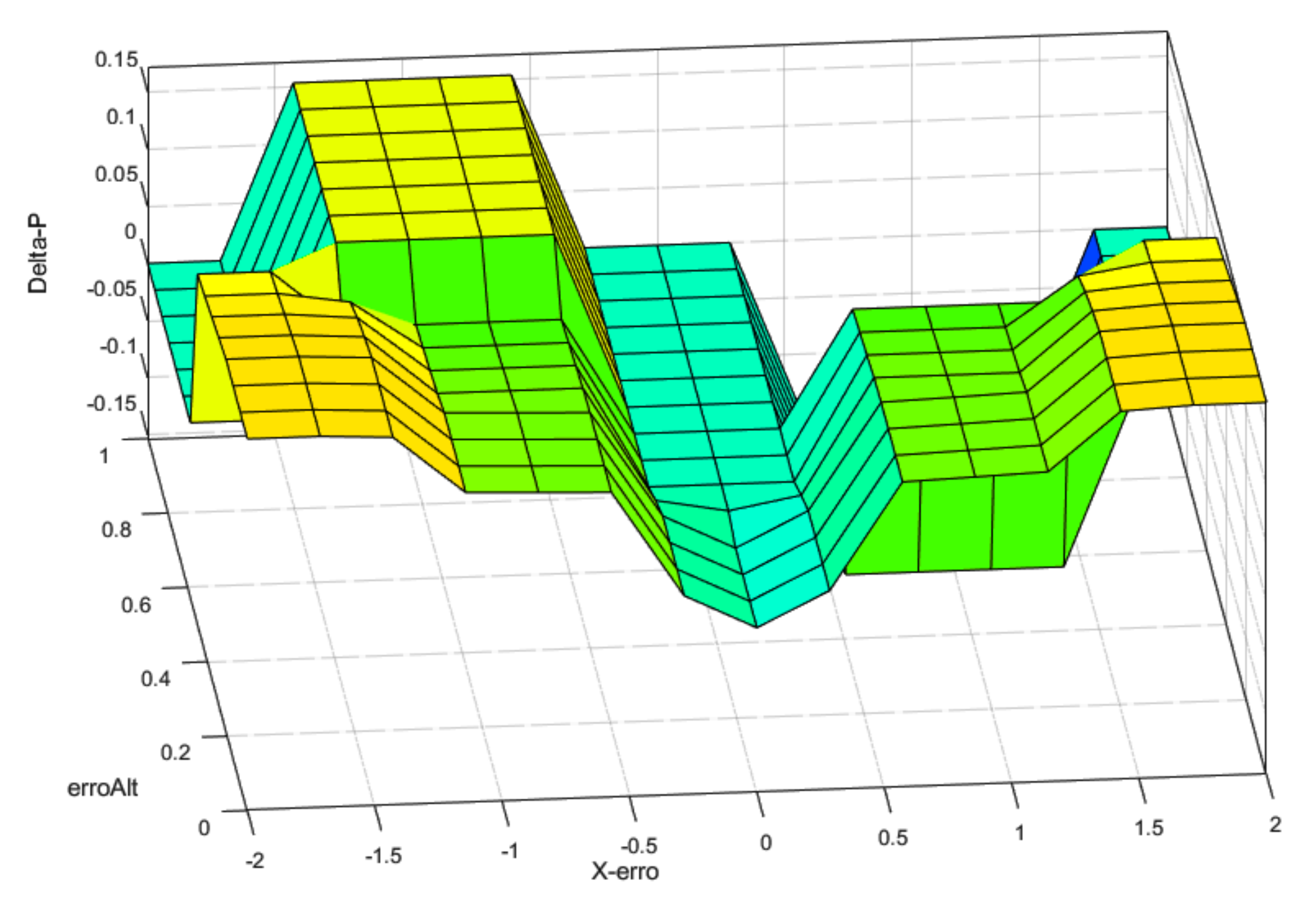
3.2. Fuzzy Gain Scheduler for Altitude Controller
3.3. Fuzzy Gain Scheduler for Position Controller
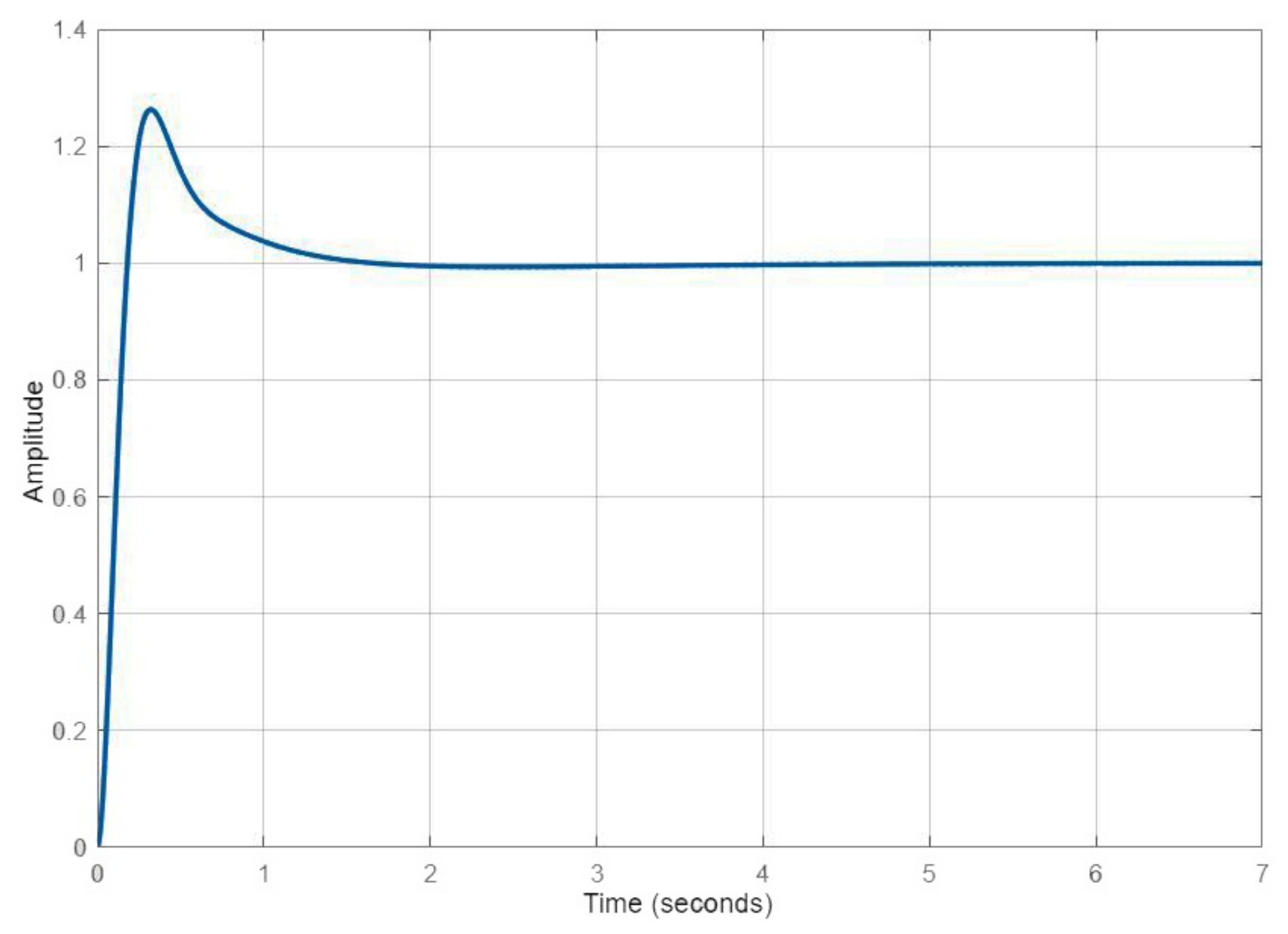
4. Results and Discussion
4.1. Results for Fuzzy Gain Scheduler for Height Controller
4.2. Results for Fuzzy Gain Scheduler for Position Controller
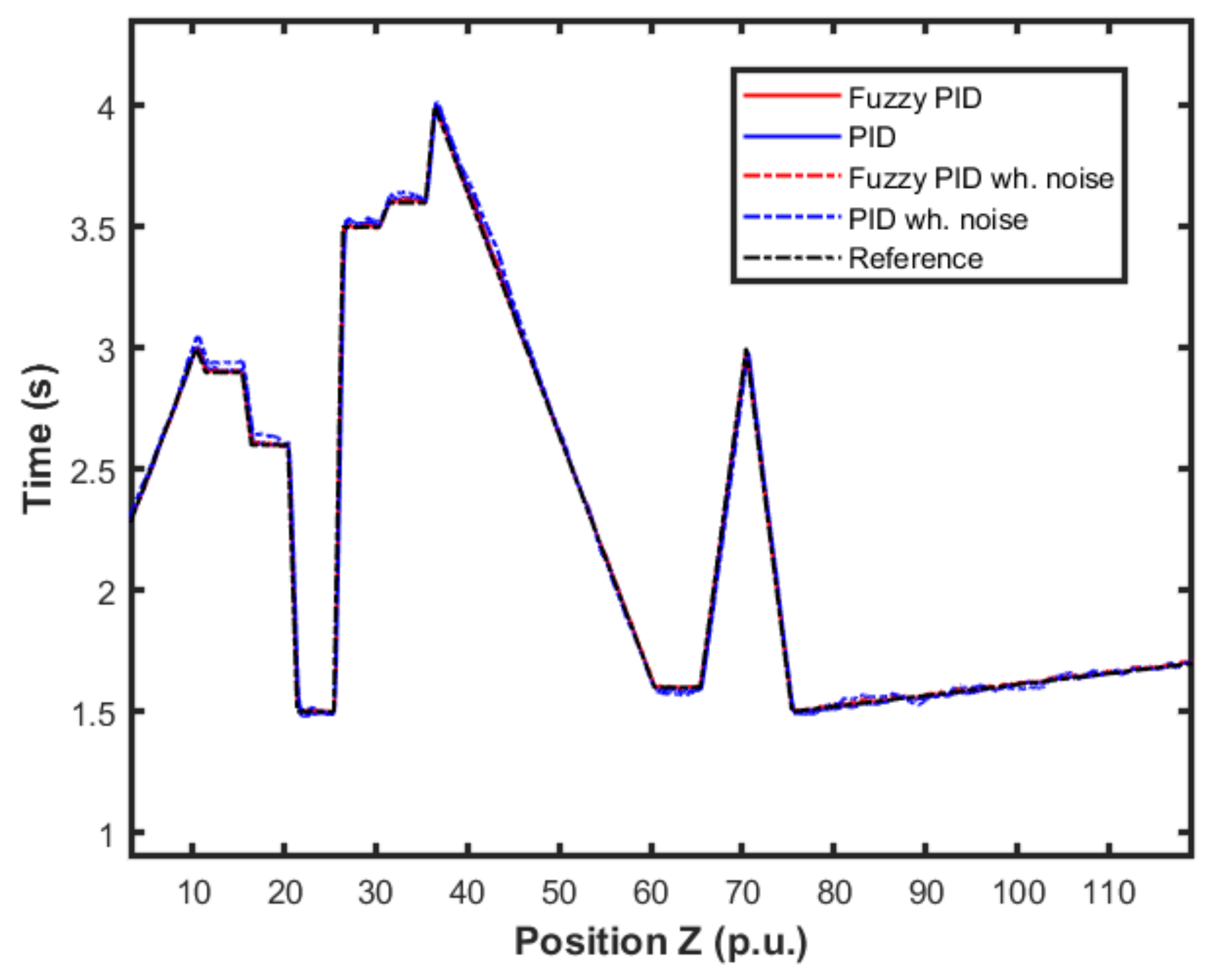
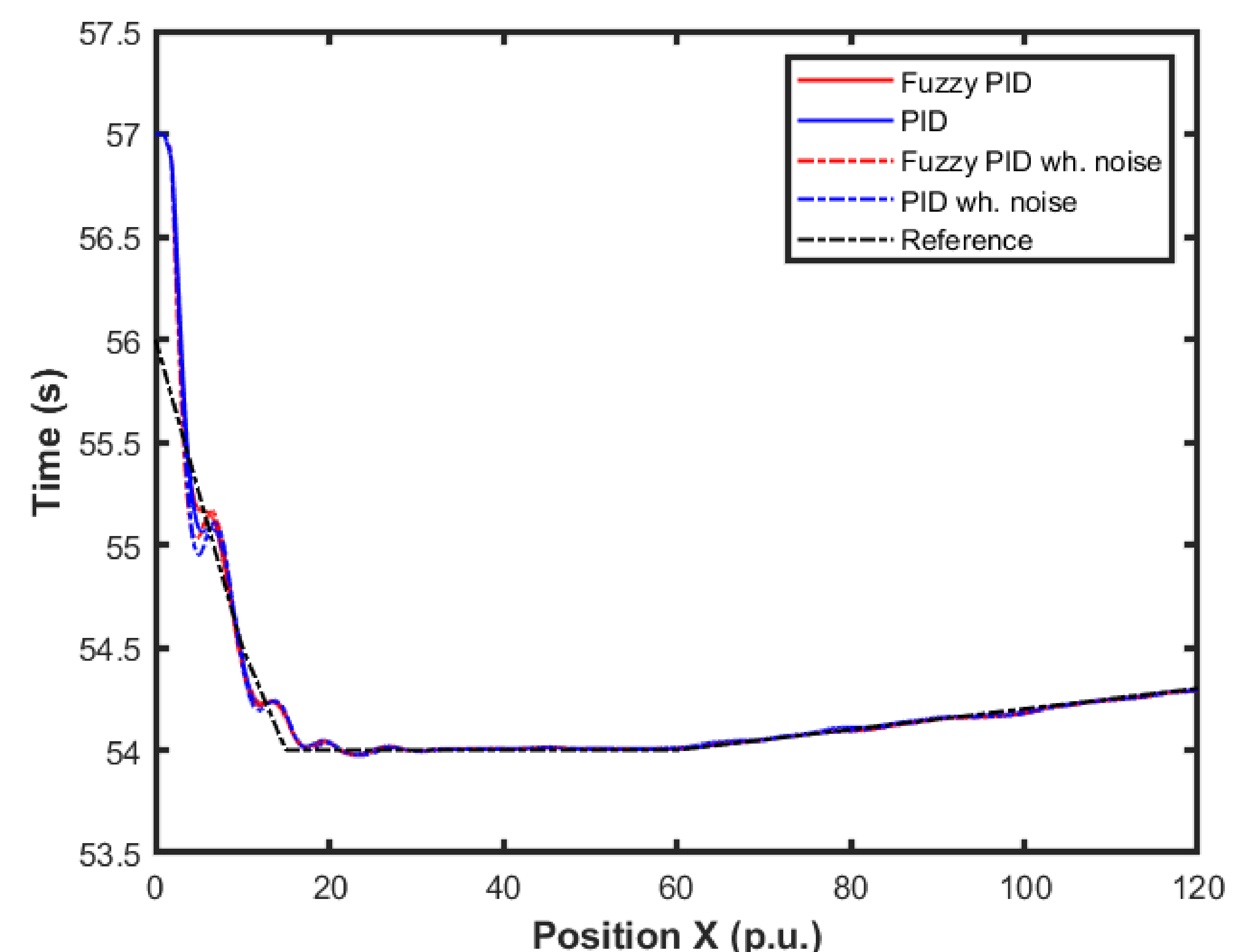
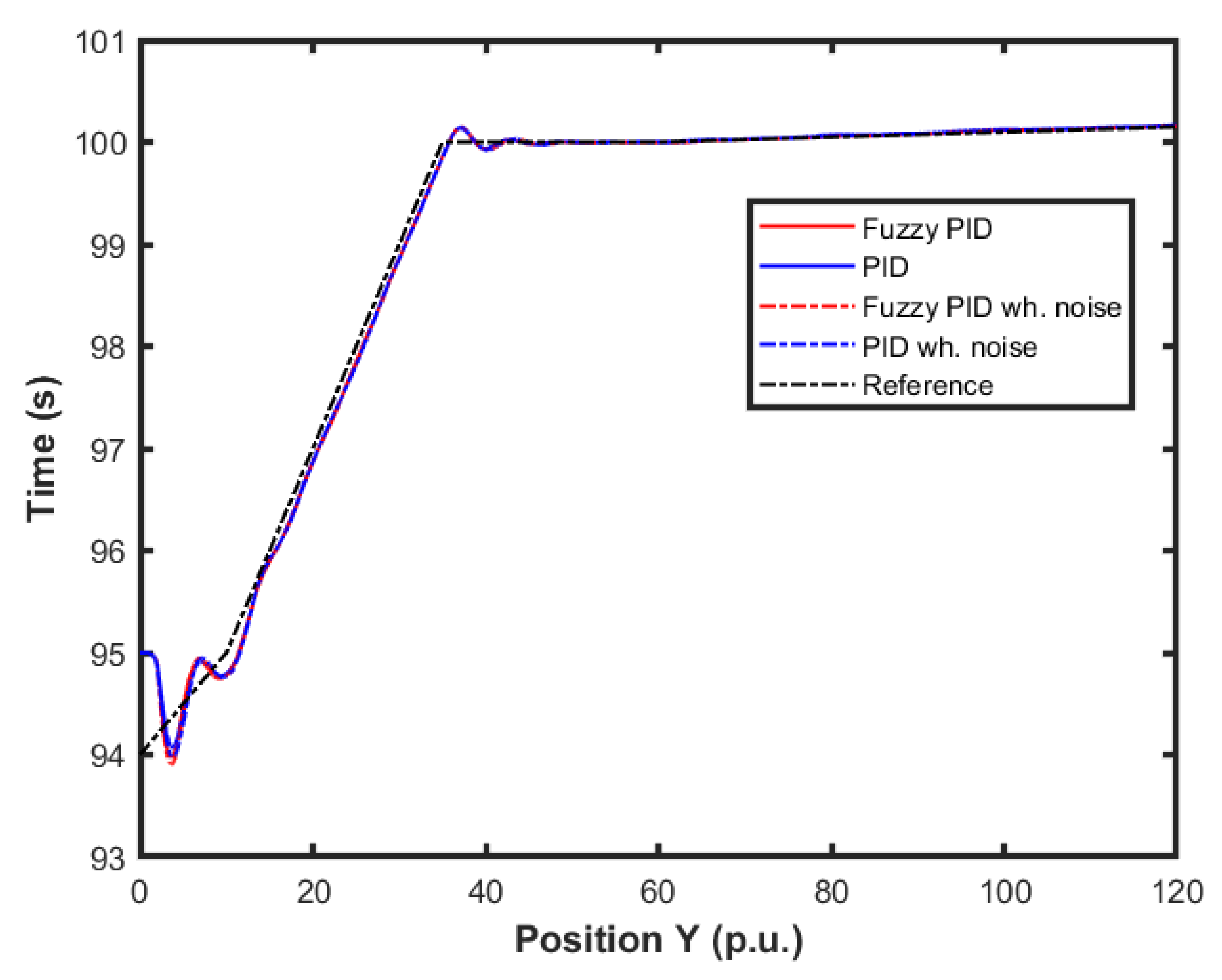
4.3. Experimental Results
4.3.1. Altitude Control
4.3.2. Control on Critical Condition
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| PD | Proportional Derivative |
| PID | Proportional Integral Derivative |
| UAV | Unmanned Aerial Vehicle |
| ROS | Robotic Operating System |
| SMC | Sliding-Mode Controller |
| PSO | Particle Swarm Optimization |
| SNA-PID | Single Neural Adaptative PID |
| ADRC | Active Disturbance Rejection Control |
References
- Pinto, M.F.; Honorio, L.M.; Melo, A.; Marcato, A.L. A Robotic Cognitive Architecture for Slope and Dam Inspections. Sensors 2020, 20, 4579. [Google Scholar] [CrossRef] [PubMed]
- Melo, A.G.; Pinto, M.F.; Honorio, L.M.; Dias, F.M.; Masson, J.E. 3D Correspondence and Point Projection Method for Structures Deformation Analysis. IEEE Access 2020, 8, 177823–177836. [Google Scholar] [CrossRef]
- Biundini, I.Z.; Melo, A.G.; Pinto, M.F.; Marins, G.M.; Marcato, A.L.; Honorio, L.M. Coverage Path Planning Optimization for Slopes and Dams Inspection. In Proceedings of the Iberian Robotics Conference; Springer: Cham, Switzerland, 2019; pp. 513–523. [Google Scholar]
- Scherer, J.; Rinner, B. Multi-UAV surveillance with minimum information idleness and latency constraints. IEEE Robot. Autom. Lett. 2020, 5, 4812–4819. [Google Scholar] [CrossRef]
- Pinto, M.F.; Melo, A.G.; Marcato, A.L.; Urdiales, C. Case-based reasoning approach applied to surveillance system using an autonomous unmanned aerial vehicle. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 9–21 June 2017; pp. 1324–1329. [Google Scholar]
- Atif, M.; Ahmad, R.; Ahmad, W.; Zhao, L.; Rodrigues, J.J. UAV-Assisted Wireless Localization for Search and Rescue. IEEE Syst. J. 2021, 15, 3261–3272. [Google Scholar] [CrossRef]
- Pinto, M.F.; Honório, L.M.; Marcato, A.L.; Dantas, M.A.; Melo, A.G.; Capretz, M.; Urdiales, C. ARCog: An Aerial Robotics Cognitive Architecture. Robotica 2021, 39, 483–502. [Google Scholar] [CrossRef]
- Villa, D.K.; Brandao, A.S.; Sarcinelli-Filho, M. A survey on load transportation using multirotor UAVs. J. Intell. Robot. Syst. 2020, 98, 267–296. [Google Scholar] [CrossRef]
- Liao, K.C.; Lu, J.H. Using UAV to Detect Solar Module Fault Conditions of a Solar Power Farm with IR and Visual Image Analysis. Appl. Sci. 2021, 11, 1835. [Google Scholar] [CrossRef]
- Sun, C.; Liu, M.; Liu, C.; Feng, X.; Wu, H. An Industrial Quadrotor UAV Control Method Based on Fuzzy Adaptive Linear Active Disturbance Rejection Control. Electronics 2021, 10, 376. [Google Scholar] [CrossRef]
- Ulus, Ş.; Eski, I. Neural network and fuzzy logic-based hybrid attitude controller designs of a fixed-wing UAV. Neural Comput. Appl. 2021, 33, 8821–8843. [Google Scholar] [CrossRef]
- Wei, J.; Zhou, J.; Du, H.; Wu, D. Flying velocity constraint control for quad-rotor system based on finite-Time control technique. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 311–316. [Google Scholar]
- Rodríguez-Abreo, O.; Rodríguez-Reséndiz, J.; Fuentes-Silva, C.; Hernández-Alvarado, R.; Falcón, M.D.C.P.T. Self-tuning neural network PID with dynamic response control. IEEE Access 2021, 9, 65206–65215. [Google Scholar] [CrossRef]
- Castillo-Zamora, J.J.; Camarillo-Gomez, K.A.; Perez-Soto, G.I.; Rodriguez-Resendiz, J. Comparison of PD, PID and sliding-mode position controllers for V–tail quadcopter stability. IEEE Access 2018, 6, 38086–38096. [Google Scholar] [CrossRef]
- Kim, H.S.; Lee, K.; Joo, Y.H. Decentralized sampled-data fuzzy controller design for a VTOL UAV. J. Frankl. Inst. 2021, 358, 1888–1914. [Google Scholar] [CrossRef]
- Carvalho, G.; Guedes, I.; Pinto, M.; Zachi, A.; Almeida, L.; Andrade, F.; Melo, A.G. Hybrid PID-Fuzzy controller for autonomous UAV stabilization. In Proceedings of the 2021 14th IEEE International Conference on Industry Applications (INDUSCON), São Paulo, Brazil, 15–18 August 2021; pp. 1296–1302. [Google Scholar]
- Eltayeb, A.; Rahmat, M.F.; Basri, M.A.M.; Eltoum, M.M.; El-Ferik, S. An Improved Design of an Adaptive Sliding Mode Controller for Chattering Attenuation and Trajectory Tracking of the Quadcopter UAV. IEEE Access 2020, 8, 205968–205979. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, T.; Zheng, L. A multilayer neural dynamic controller design method of quadrotor UAV for completing time-varying tasks. Nonlinear Dyn. 2021, 104, 3597–3616. [Google Scholar] [CrossRef]
- Chen, F.; Jiang, R.; Zhang, K.; Jiang, B.; Tao, G. Robust backstepping sliding-mode control and observer-based fault estimation for a quadrotor UAV. IEEE Trans. Ind. Electron. 2016, 63, 5044–5056. [Google Scholar] [CrossRef]
- Minervini, A.; Godio, S.; Guglieri, G.; Dovis, F.; Bici, A. Development and Validation of a LQR-Based Quadcopter Control Dynamics Simulation Model. J. Aerosp. Eng. 2021, 34, 04021095. [Google Scholar] [CrossRef]
- Lara Alabazares, D.; Rabhi, A.; Pegard, C.; Torres Garcia, F.; Romero Galvan, G. Quadrotor UAV attitude stabilization using fuzzy robust control. Trans. Inst. Meas. Control 2021, 43, 2599–2614. [Google Scholar] [CrossRef]
- Torres, F.; Rabhi, A.; Lara, D.; Romero, G.; Pégard, C. Fuzzy state feedback for attitude stabilization of quadrotor. Int. J. Adv. Robot. Syst. 2016, 13, 2. [Google Scholar] [CrossRef] [Green Version]
- Domingos, D.; Camargo, G.; Gomide, F. Autonomous fuzzy control and navigation of quadcopters. IFAC-PapersOnLine 2016, 49, 73–78. [Google Scholar] [CrossRef]
- Joyo, M.K.; Hazry, D.; Ahmed, S.F.; Tanveer, M.H.; Warsi, F.A.; Hussain, A. Altitude and horizontal motion control of quadrotor UAV in the presence of air turbulence. In Proceedings of the 2013 IEEE Conference on Systems, Process & Control (ICSPC), Kuala Lumpur, Malaysia, 13–15 December 2013; pp. 16–20. [Google Scholar]
- Tanveer, M.H.; Hazry, D.; Ahmed, S.F.; Joyo, M.K.; Warsi, F.A.; Kamaruddin, H.; Razlan, Z.M.; Wan, K.; Shahriman, A. NMPC-PID based control structure design for avoiding uncertainties in attitude and altitude tracking control of quad-rotor (UAV). In Proceedings of the 2014 IEEE 10th International Colloquium on Signal Processing and its Applications, Kuala Lumpur, Malaysia, 7–9 March 2014; pp. 117–122. [Google Scholar]
- Derrouaoui, S.H.; Bouzid, Y.; Guiatni, M. PSO Based Optimal Gain Scheduling Backstepping Flight Controller Design for a Transformable Quadrotor. J. Intell. Robot. Syst. 2021, 102, 67. [Google Scholar] [CrossRef]
- Tang, W.; Wang, L.; Gu, J.; Gu, Y. Single neural adaptive PID control for small UAV micro-turbojet engine. Sensors 2020, 20, 345. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dief, T.N.; Yoshida, S.; Abdelhady, M. Attitude and altitude stabilization of quad rotor using parameter estimation and self-tuning controller. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Dallas, TX, USA, 22–26 June 2015; p. 2392. [Google Scholar]
- Ammar, N.B.; Bouallègue, S.; Haggège, J. Fuzzy gains-scheduling of an integral sliding mode controller for a quadrotor unmanned aerial vehicle. Int. J. Adv. Comput. Sci. Appl. 2018, 9, 132–141. [Google Scholar]
- Jatsun, S.; Emelyanova, O.; Leon, A.S.M.; Stykanyova, S. Control fligth of a UAV type tricopter with fuzzy logic controller. In Proceedings of the 2017 Dynamics of Systems, Mechanisms and Machines (Dynamics), Omsk, Russia, 14–16 November 2017; pp. 1–5. [Google Scholar]
- Dong, J.; He, B. Novel fuzzy PID-type iterative learning control for quadrotor UAV. Sensors 2019, 19, 24. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Andrade, F.A.; Guedes, I.P.; Carvalho, G.F.; Zachi, A.R.; Haddad, D.B.; Almeida, L.F.; de Melo, A.G.; Pinto, M.F. Unmanned Aerial Vehicles Motion Control with Fuzzy Tuning of Cascaded-PID Gains. Machines 2022, 10, 12. [Google Scholar] [CrossRef]
- Ramos, G.S.; Pinto, M.F.; Coelho, F.O.; Honório, L.M.; Haddad, D.B. Hybrid methodology based on computational vision and sensor fusion for assisting autonomous UAV on offshore messenger cable transfer operation. Robotica 2022, 1–29. [Google Scholar] [CrossRef]
- Fernández, R.A.S.; Dominguez, S.; Campoy, P. L1 adaptive control for wind gust rejection in quad-rotor uav wind turbine inspection. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 1840–1849. [Google Scholar]
- Zou, Y.; Yin, Y.; Song, J. Flight control of a flying-wing UAV based on active disturbance rejection control. In Proceedings of the 2017 3rd IEEE International Conference on Control Science and Systems Engineering (ICCSSE), Beijing, China, 17–19 August 2017; pp. 50–55. [Google Scholar]
- Talha, M.; Asghar, F.; Rohan, A.; Rabah, M.; Kim, S.H. Fuzzy logic-based robust and autonomous safe landing for UAV quadcopter. Arab. J. Sci. Eng. 2019, 44, 2627–2639. [Google Scholar] [CrossRef]
- Amoozgar, M.H.; Chamseddine, A.; Zhang, Y. Fault-tolerant fuzzy gain-scheduled PID for a quadrotor helicopter testbed in the presence of actuator faults. IFAC Proc. Vol. 2012, 45, 282–287. [Google Scholar] [CrossRef] [Green Version]
- Erginer, B.; Altuğ, E. Design and implementation of a hybrid fuzzy logic controller for a quadrotor VTOL vehicle. Int. J. Control. Autom. Syst. 2012, 10, 61–70. [Google Scholar] [CrossRef]
- Sharma, A.; Barve, A. Controlling of quad-rotor uav using pid controller and fuzzy logic controller. Int. J. Electr. Electron. Comput. Eng. 2012, 1, 38–41. [Google Scholar]
- Demir, B.E.; Bayir, R.; Duran, F. Real-time trajectory tracking of an unmanned aerial vehicle using a self-tuning fuzzy proportional integral derivative controller. Int. J. Micro Air Veh. 2016, 8, 252–268. [Google Scholar] [CrossRef] [Green Version]
- Prayitno, A.; Indrawati, V.; Trusulaw, I.I. Fuzzy gain scheduling PID control for position of the AR. Drone. Int. J. Electr. Comput. Eng. (IJECE) 2018, 8, 1939–1946. [Google Scholar] [CrossRef]
- Rabah, M.; Rohan, A.; Mohamed, S.A.; Kim, S.H. Autonomous moving target-tracking for a UAV quadcopter based on fuzzy-PI. IEEE Access 2019, 7, 38407–38419. [Google Scholar] [CrossRef]
- Sarhan, A.; Qin, S. Adaptive PID control of UAV altitude dynamics based on parameter optimization with fuzzy inference. Int. J. Model. Optim. 2016, 6, 246. [Google Scholar] [CrossRef] [Green Version]
- El Hamidi, K.; Mjahed, M.; El Kari, A.; Ayad, H. Neural network and fuzzy-logic-based self-tuning PID control for quadcopter path tracking. Stud. Inform. Control 2019, 28, 401–412. [Google Scholar] [CrossRef]
- Kaplan, M.R.; Eraslan, A.; Beke, A.; Kumbasar, T. Altitude and position control of parrot mambo minidrone with PID and fuzzy PID controllers. In Proceedings of the 2019 11th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 28–30 November 2019; pp. 785–789. [Google Scholar]
- Castillo-Effen, M.; Castillo, C.; Moreno, W.; Valavanis, K. Control fundamentals of small/miniature helicopters—A survey. In Advances in Unmanned Aerial Vehicles; Springer: Dordrecht, The Netherlands, 2007; pp. 73–118. [Google Scholar]
- Idrissi, M.; Salami, M.; Annaz, F. A Review of Quadrotor Unmanned Aerial Vehicles: Applications, Architectural Design and Control Algorithms. J. Intell. Robot. Syst. 2022, 104, 22. [Google Scholar] [CrossRef]
- González, J.A.C.; Salas-Peña, O.; De León-Morales, J. Observer-based super twisting design: A comparative study on quadrotor altitude control. ISA Trans. 2021, 109, 307–314. [Google Scholar] [CrossRef]
- Sakti, I. Methodology of fuzzy logic with mamdani fuzzy models applied to the microcontroller. In Proceedings of the 2014 The 1st International Conference on Information Technology Computer, and Electrical Engineering, Semarang, Indonesia, 8 November 2014; pp. 93–98. [Google Scholar]








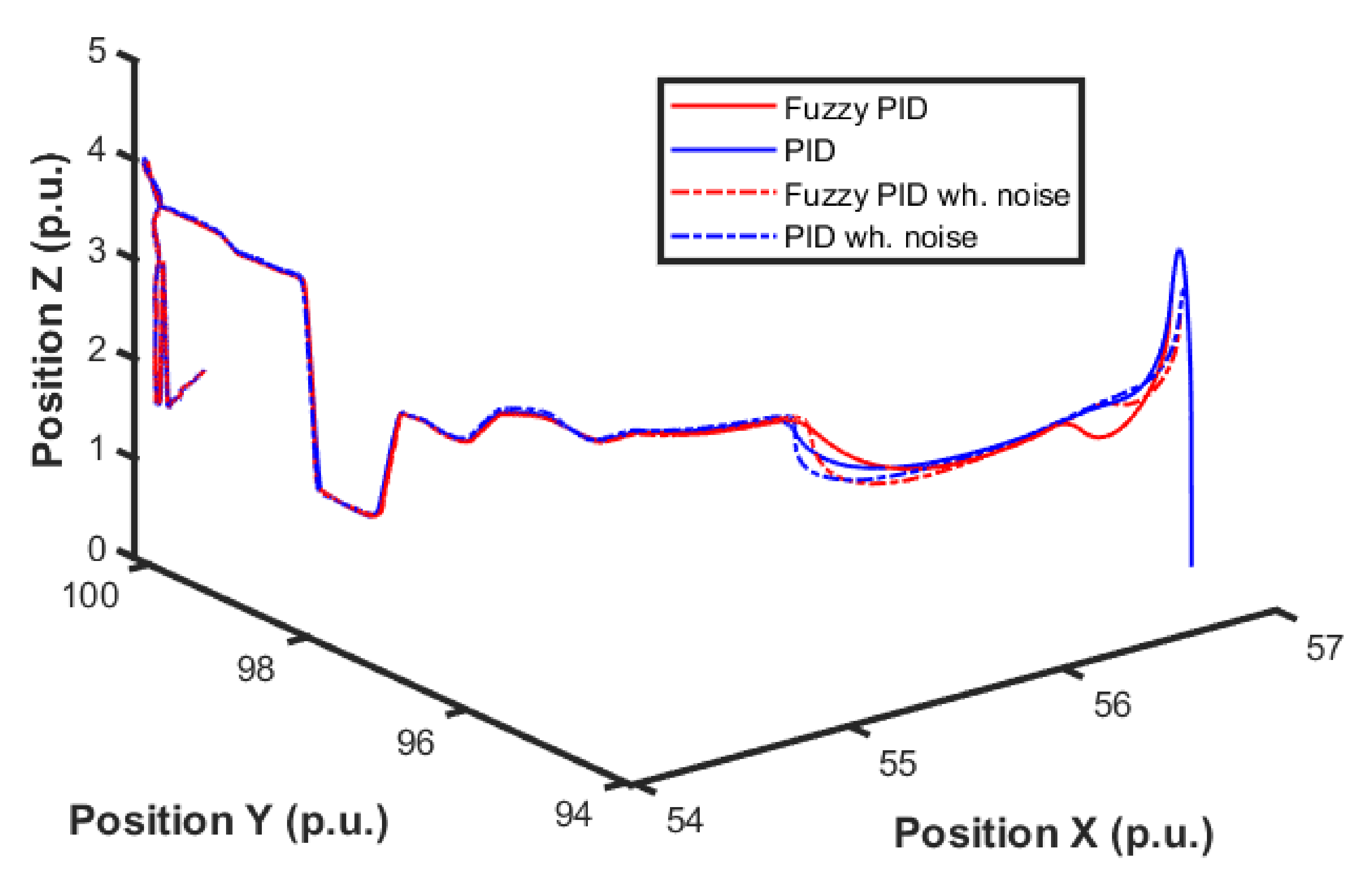

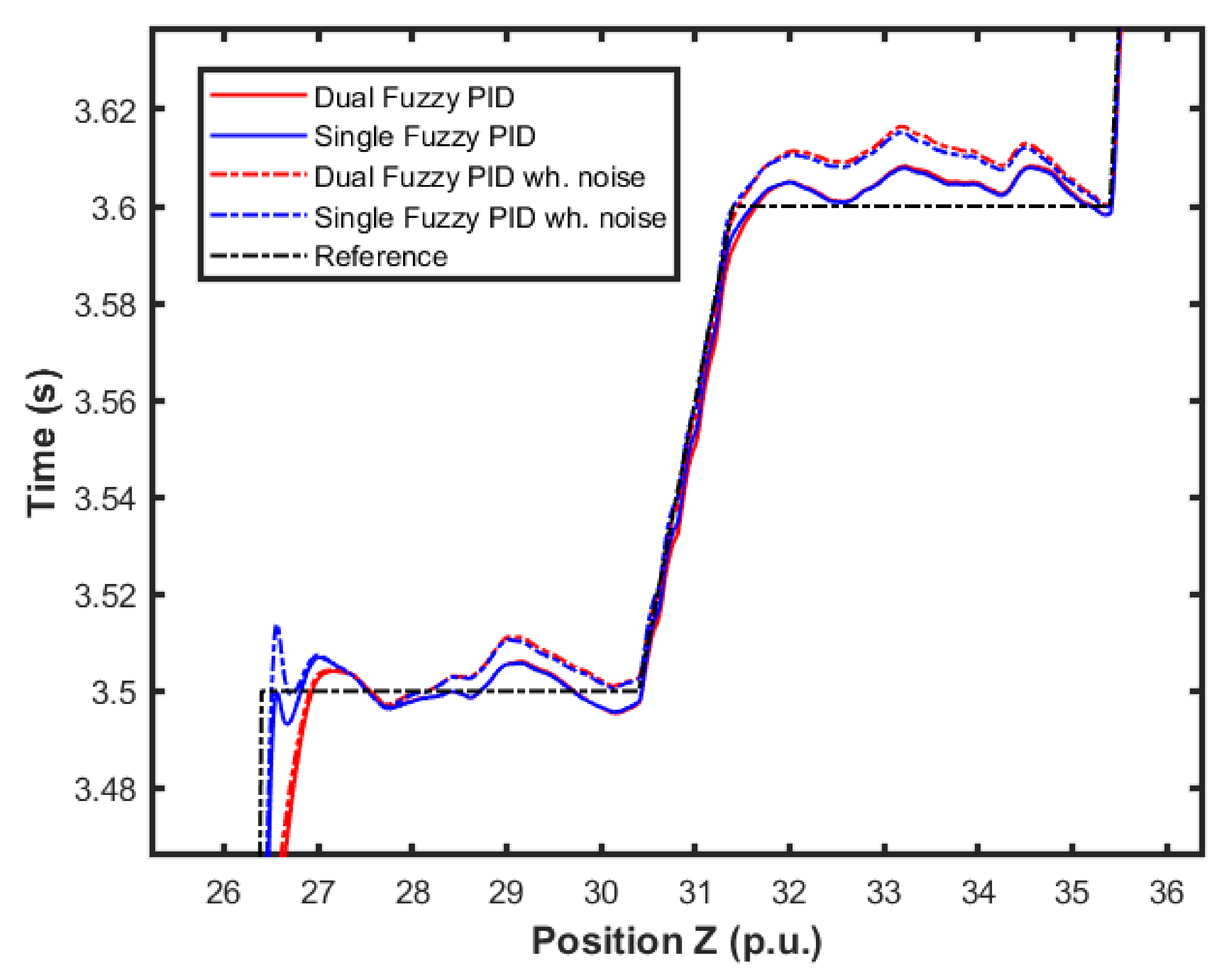



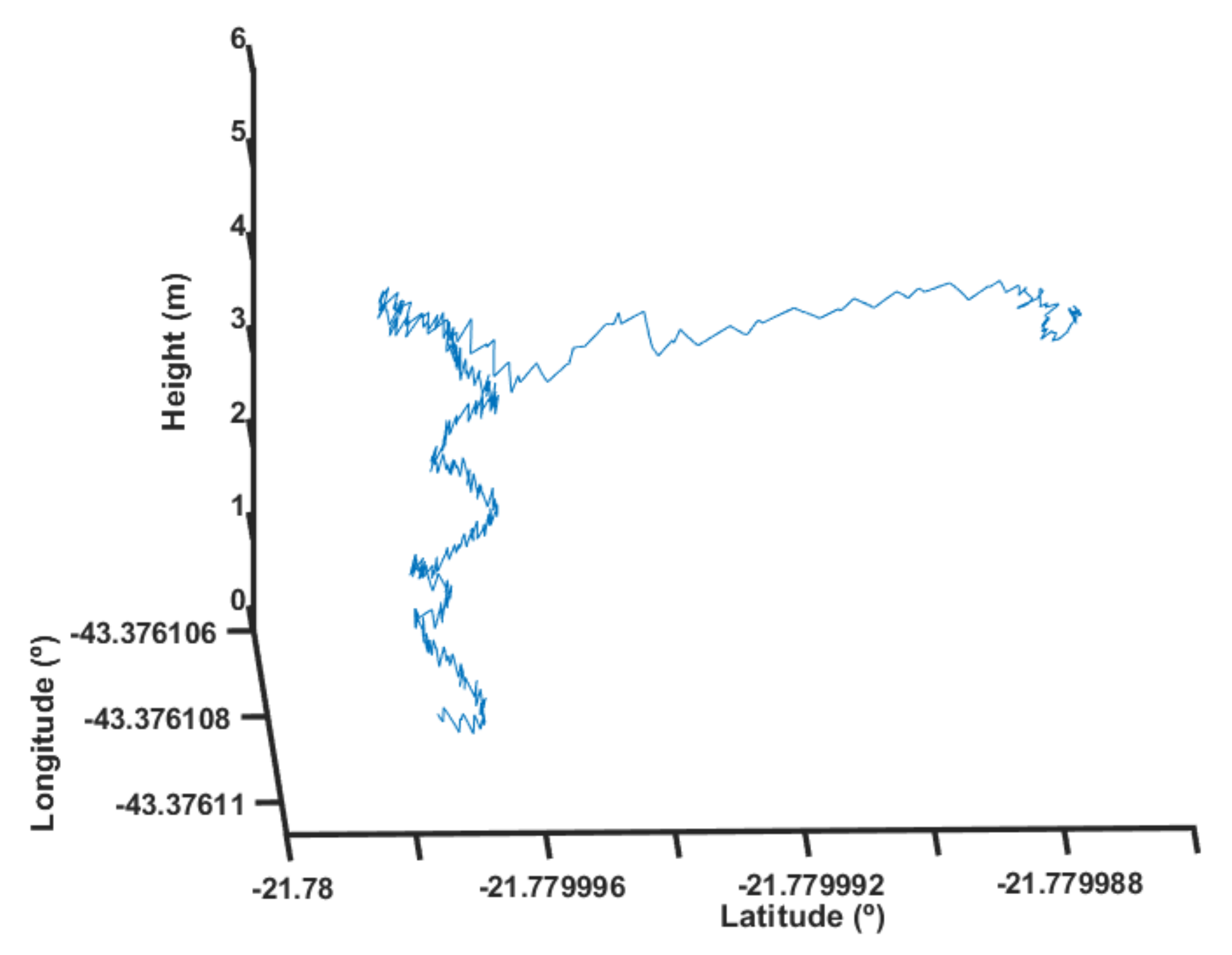

| Gain | ||
|---|---|---|
| Control Law 1 | Control Law 2 | |
| P | 1.7 | 0.16 |
| I | 0 | 0.009 |
| D | 0.6 | 0.6 |
| Control Law 1 | Control Law 2 | |
|---|---|---|
| Rise time | 0.12 | 0.2 |
| Setting time | 1.0 | 1.6 |
| Overshoot | 20% | 2% |
| Gain | ||
|---|---|---|
| Control Law 1 | Control Law 2 | |
| P | 0.24 | 0.07 |
| I | 0 | 0 |
| D | 0.1 | 0.05 |
| Original | Fuzzy | |
|---|---|---|
| Rise Time | 0.1 s | 0.1 s |
| Settling Time | 0.1 s | 0.2 s |
| Overshoot | 13% | 1% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melo, A.G.; Andrade, F.A.A.; Guedes, I.P.; Carvalho, G.F.; Zachi, A.R.L.; Pinto, M.F. Fuzzy Gain-Scheduling PID for UAV Position and Altitude Controllers. Sensors 2022, 22, 2173. https://doi.org/10.3390/s22062173
Melo AG, Andrade FAA, Guedes IP, Carvalho GF, Zachi ARL, Pinto MF. Fuzzy Gain-Scheduling PID for UAV Position and Altitude Controllers. Sensors. 2022; 22(6):2173. https://doi.org/10.3390/s22062173
Chicago/Turabian StyleMelo, Aurelio G., Fabio A. A. Andrade, Ihannah P. Guedes, Guilherme F. Carvalho, Alessandro R. L. Zachi, and Milena F. Pinto. 2022. "Fuzzy Gain-Scheduling PID for UAV Position and Altitude Controllers" Sensors 22, no. 6: 2173. https://doi.org/10.3390/s22062173
APA StyleMelo, A. G., Andrade, F. A. A., Guedes, I. P., Carvalho, G. F., Zachi, A. R. L., & Pinto, M. F. (2022). Fuzzy Gain-Scheduling PID for UAV Position and Altitude Controllers. Sensors, 22(6), 2173. https://doi.org/10.3390/s22062173








