Oligoclonal Band Straightening Based on Optimized Hierarchical Warping for Multiple Sclerosis Diagnosis
Abstract
:1. Introduction
1.1. Clinical Context
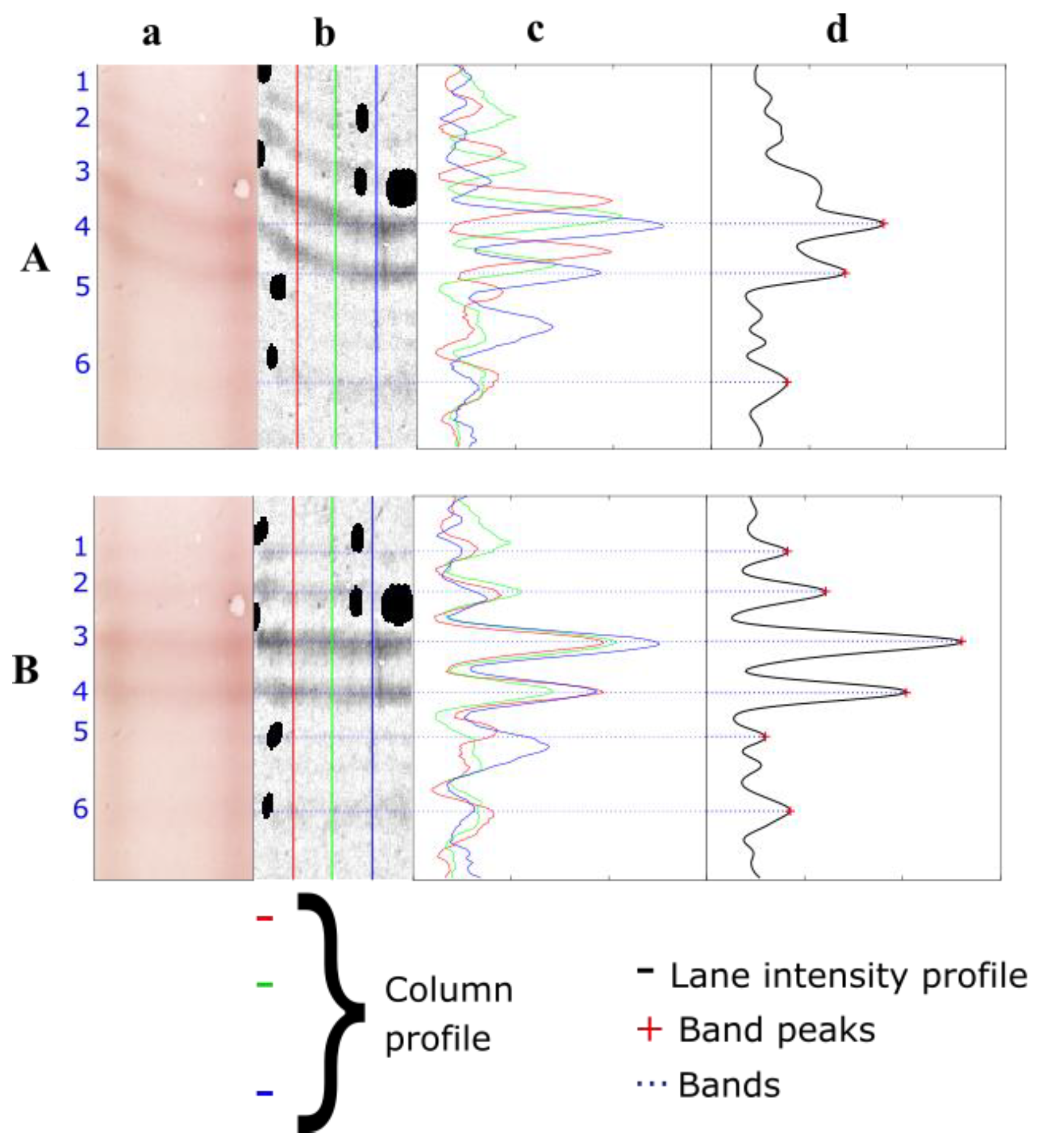
1.2. The Automatic Analysis of IEF Membranes
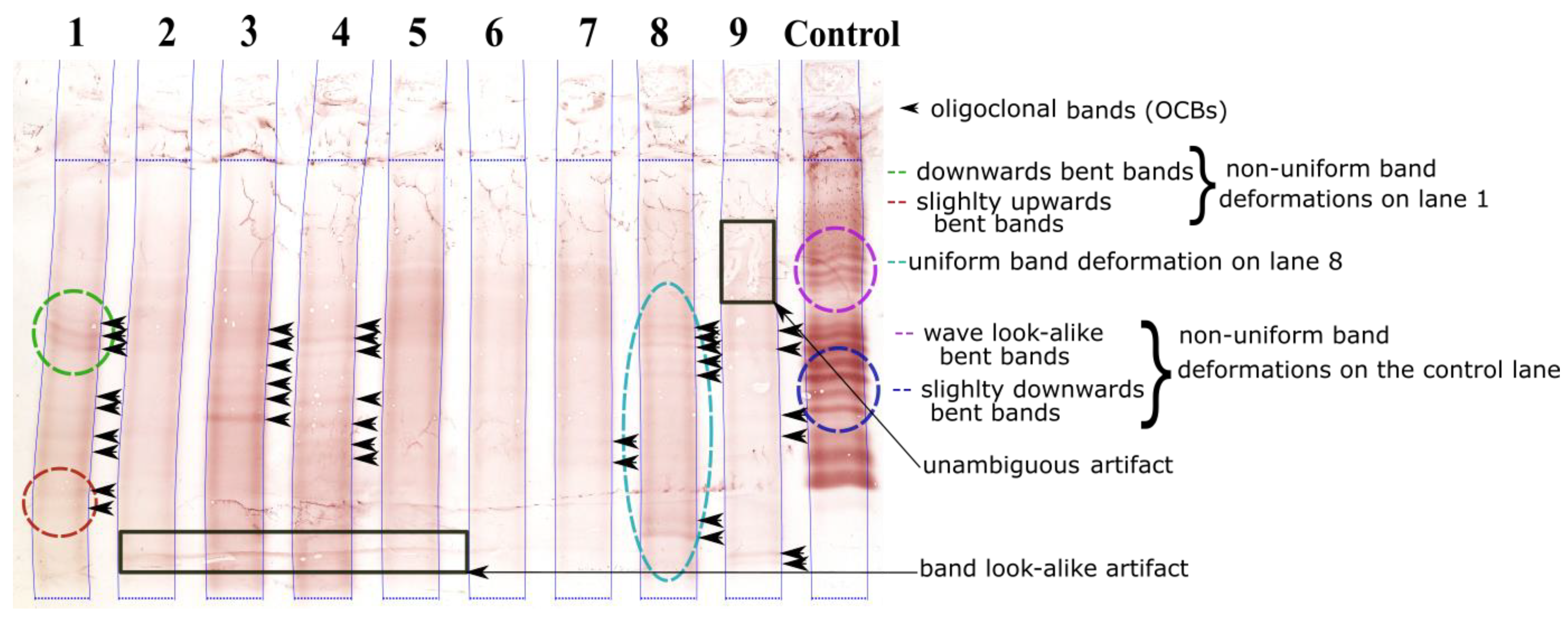
1.3. Geometric Band Distortions in IEF Images
1.4. Related Research on Band Straightening
2. Materials and Methods
2.1. Description of the Datasets
2.1.1. IEF Image Acquisition and Pre-Processing
2.1.2. The Real IEF Dataset
2.1.3. The Synthetic Dataset
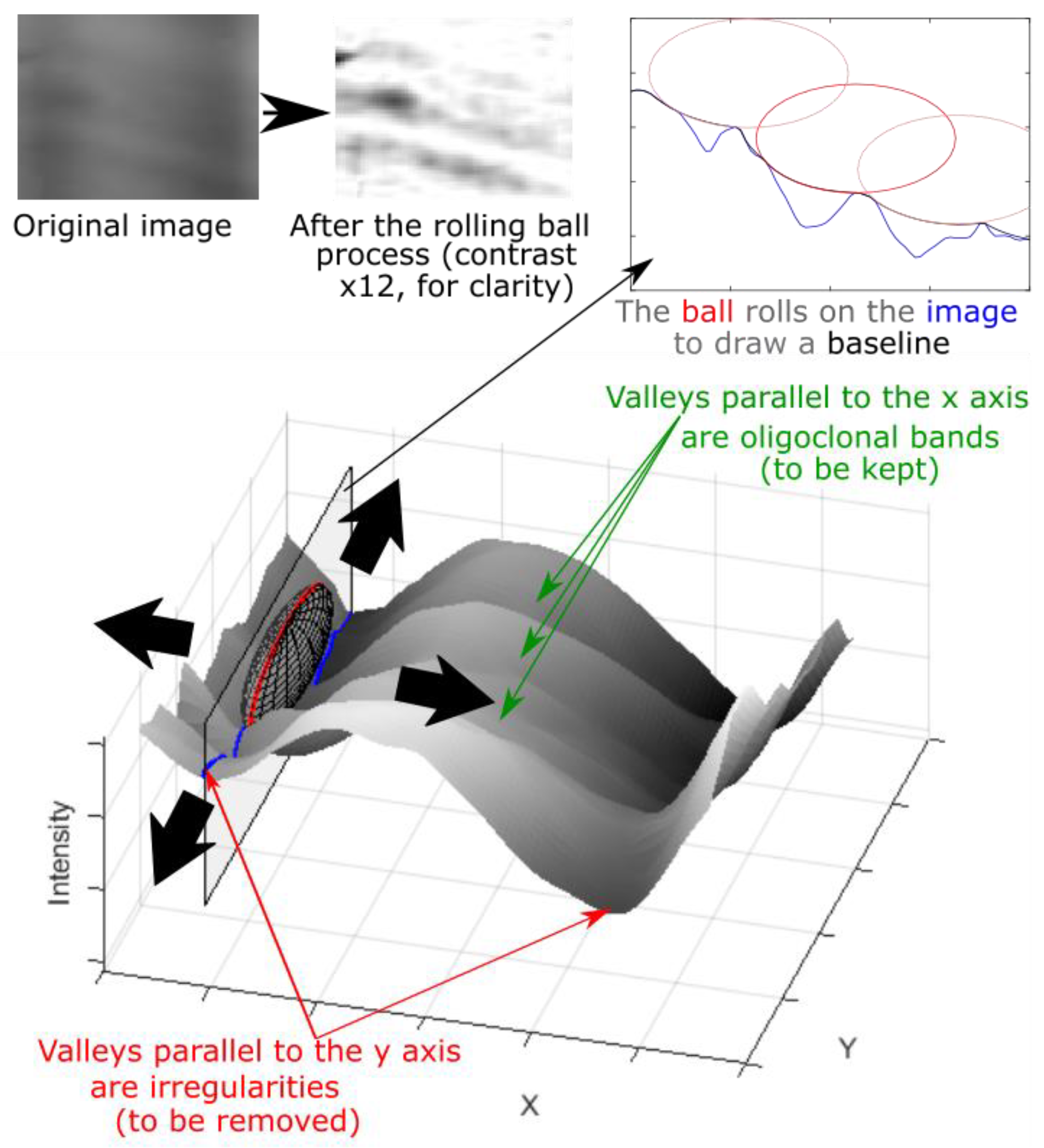
2.2. Background Removal
2.3. Correlation-Based Image Warping
2.3.1. The Energy Minimization Approach for Image Warping
- External energy
- b.
- Internal energy
- c.
- The deformation constraint
2.3.2. The Transformation Hierarchy
2.3.3. Coupling of a Hierarchy of Image Resolutions to a Hierarchy of Transformations
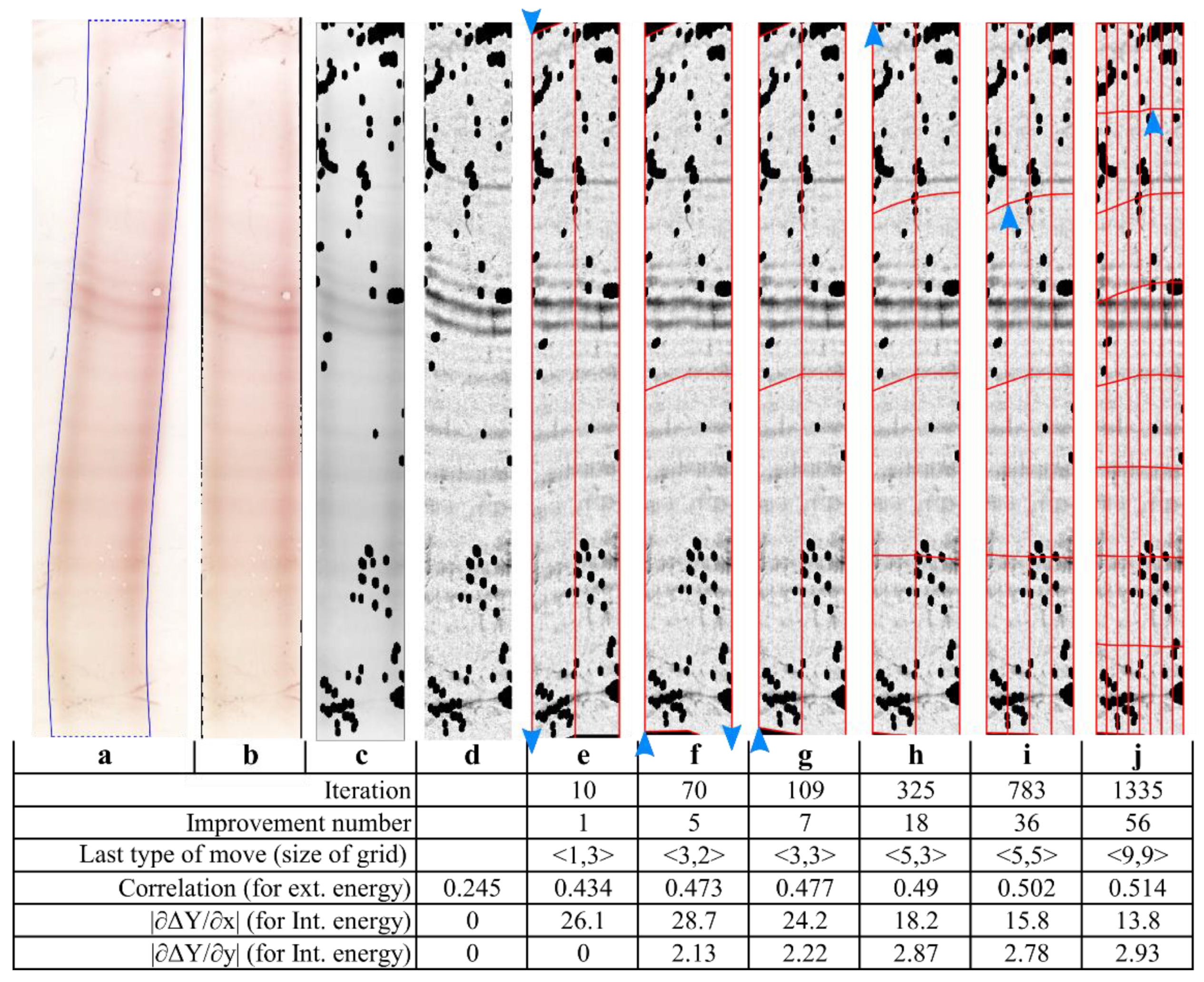
2.3.4. The Band-Straightening Algorithm
- Downsample the original lane image with the corresponding scale factors ( (Section 2.3.3)
- Apply the deformation to obtain the current image:
- For each type of move ( being a list of types of move specific for each hierarchical step ) corresponding to a grid size :
- Choose a random permutation of the set of the grid points
- For each grid point in with coordinates and for each possible sign of the shift (−1 being down, and 1 being up):
- Move vertically with
- Adjust the position of grid points on the same row as , to comply with the band-straightening algorithm’s constraint (Section 2.3.2)
- Linearly interpolate between grid points to obtain the warped lane image
- If ):
- (a)
- Put the 4-neighbor grid points of at the end of (except when is located at border)
- (b)
- Move with a smaller shift (equal to ) and a larger shift (equal to ) and repeat steps 2 and 3 to obtain and
- (c)
- Set
2.3.5. The Algorithm’s Settings
2.3.6. Optimization of the Band-Straightening Algorithm
2.4. Evaluation Methods
2.4.1. Real IEF Dataset
- (i)
- SD 2 pixels correspond to a negligibly to-strongly deformed band.
- (ii)
- SD 3 pixels correspond to a weakly to-strongly deformed band.
- (iii)
- SD corresponds to a moderately-to-strongly deformed band.
- (iv)
- SD 5 pixels correspond to a strongly deformed band.
2.4.2. Synthetic Dataset
3. Results and Discussion
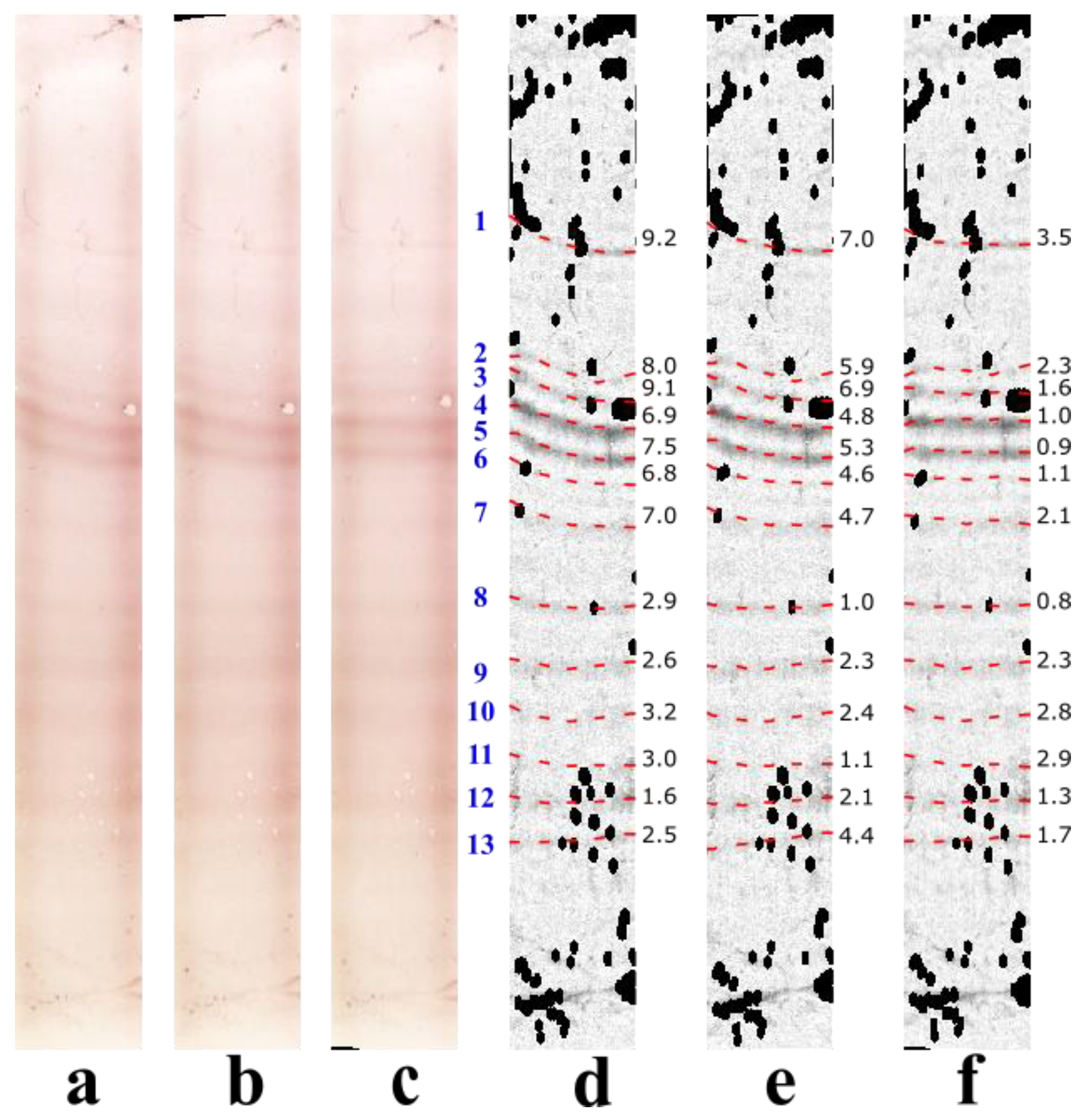
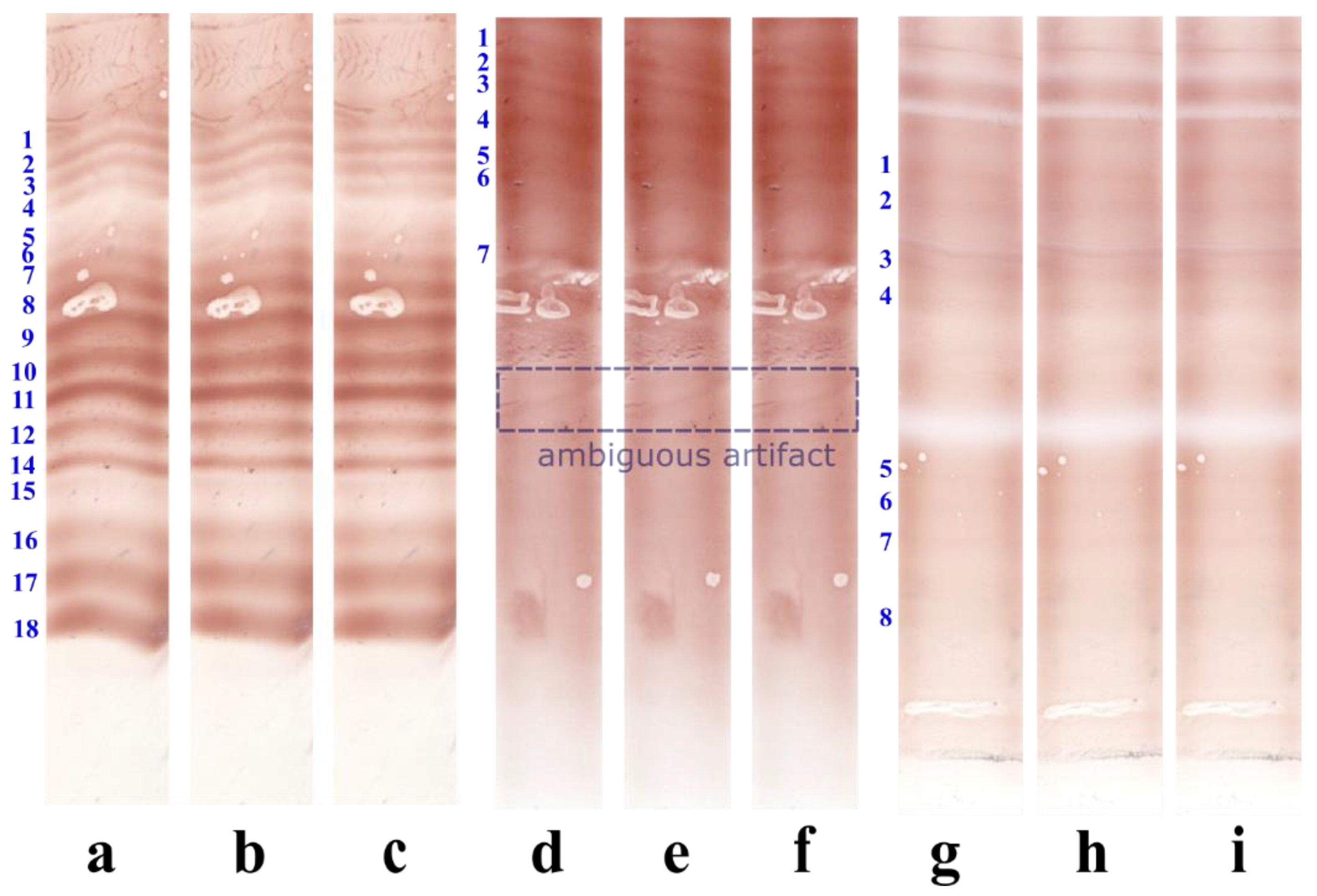
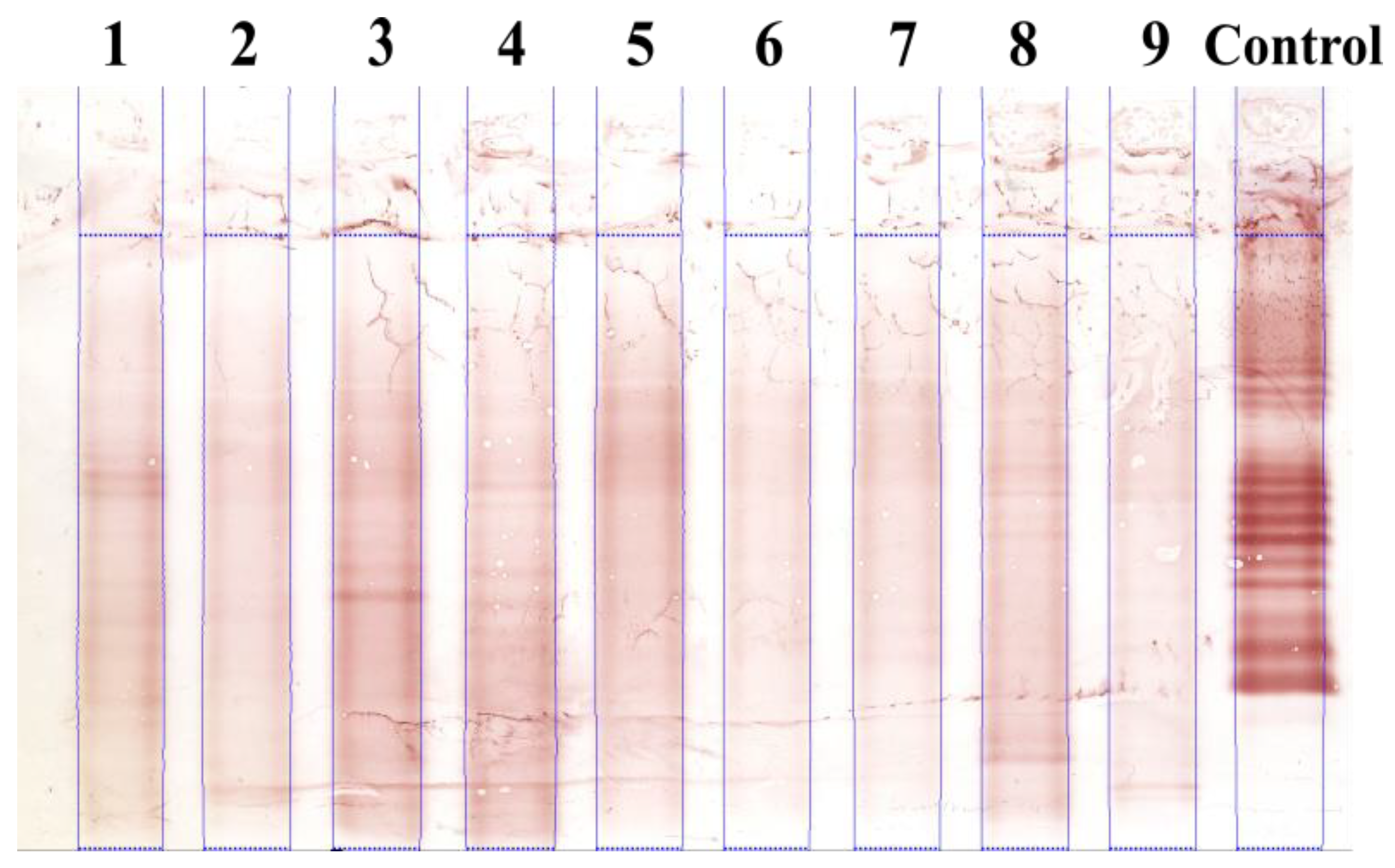
3.1. Illustrative Results
3.1.1. Results with the Real IEF Dataset
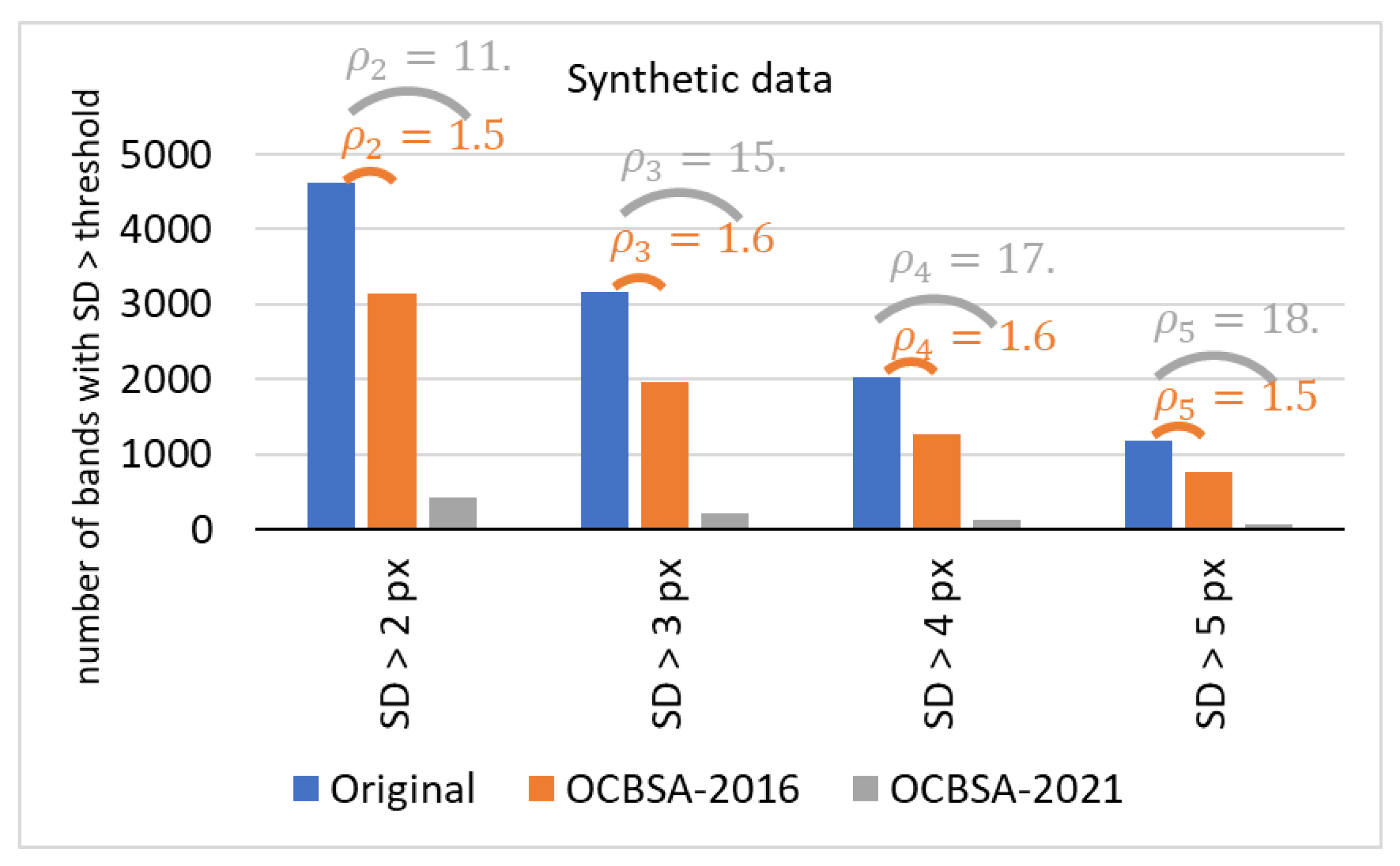
3.1.2. Results with the Synthetic Dataset
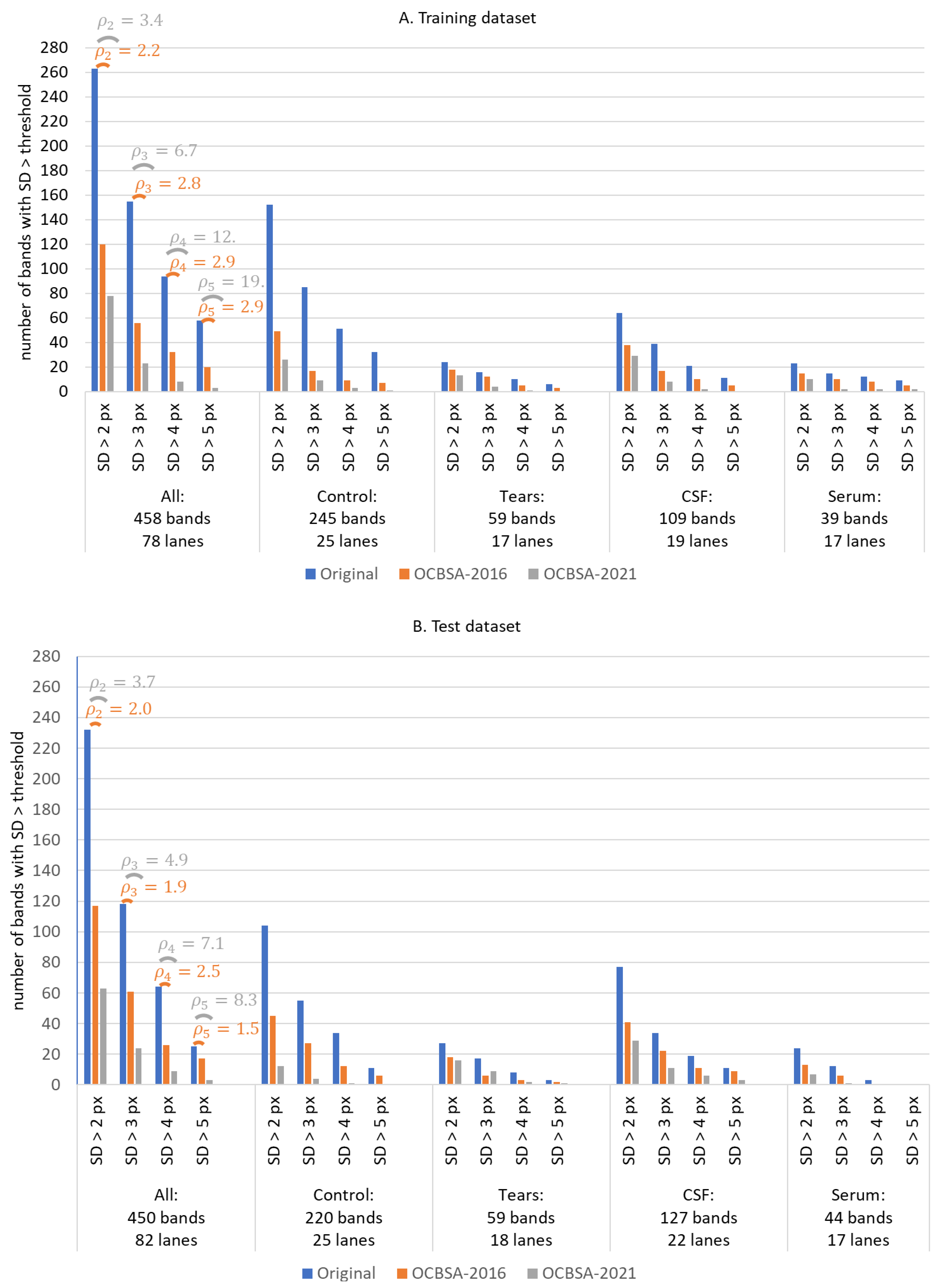
3.2. Statistical Evaluation of the Algorithm’s Performance with Real and Synthetic Data
3.3. OCBSA-2021’s Contribution to OCB Detection
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Poser, C.M.; Paty, D.W.; Scheinberg, L.; McDonald, W.I.; Davis, F.A.; Ebers, G.C.; Johnson, K.P.; Sibley, W.A.; Silberberg, D.H.; Tourtellotte, W.W. New diagnostic criteria for multiple sclerosis: Guidelines for research protocols. Ann. Neurol. 1983, 13, 227–231. [Google Scholar] [CrossRef] [PubMed]
- Freedman, M.S.; Thompson, E.J.; Deisenhammer, F.; Giovannoni, G.; Grimsley, G.; Keir, G.; Öhman, S.; Racke, M.K.; Sharief, M.; Sindic, C.J.M.; et al. Recommended Standard of Cerebrospinal Fluid Analysis in the Diagnosis of Multiple Sclerosis: A Consensus Statement. Arch. Neurol. 2005, 62, 865–870. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thompson, A.J.; Banwell, B.L.; Barkhof, F.; Carroll, W.M.; Coetzee, T.; Comi, G.; Correale, J.; Fazekas, F.; Filippi, M.; Freedman, M.S.; et al. Diagnosis of multiple sclerosis: 2017 revisions of the McDonald criteria. Lancet Neurol. 2018, 17, 162–173. [Google Scholar] [CrossRef]
- Calais, G.; Forzy, G.; Crinquette, C.; Mackowiak, A.; de Seze, J.; Blanc, F.; Lebrun, C.; Heinzlef, O.; Clavelou, P.; Moreau, T.; et al. Tear analysis in clinically isolated syndrome as new multiple sclerosis criterion. Mult. Scler. J. 2010, 16, 87–92. [Google Scholar] [CrossRef]
- Lebrun, C.; Forzy, G.; Collongues, N.; Cohen, M.; de Seze, J.; Hautecoeur, P. Tear analysis as a tool to detect oligoclonal bands in radiologically isolated syndrome. Rev. Neurol. 2015, 171, 390–393. [Google Scholar] [CrossRef]
- Franciotta, D.; Lolli, F. Interlaboratory Reproducibility of Isoelectric Focusing in Oligoclonal Band Detection. Clin. Chem. 2007, 53, 1557–1558. [Google Scholar] [CrossRef]
- Bajla, I.; Holländer, I.; Minichmayr, M.; Gmeiner, G.; Reichel, C. GASepo—A software solution for quantitative analysis of digital images in Epo doping control. Comput. Methods Progr. Biomed. 2005, 80, 246–270. [Google Scholar] [CrossRef]
- Štolc, S.; Bajla, I. Improvement of band segmentation in Epo images via column shift transformation with cost functions. Med. Biol. Eng. Comput. 2006, 44, 257–274. [Google Scholar] [CrossRef]
- Boudet, S.; Peyrodie, L.; Wang, Z.; Forzy, G. Semi-automated image analysis of gel electrophoresis of cerebrospinal fluid for oligoclonal band detection. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; IEEE: Manhattan, NY, USA, 2016; pp. 744–747. [Google Scholar]
- Forzy, G.; Peyrodie, L.; Boudet, S.; Wang, Z.; Vinclair, A.; Chieux, V. Evaluation of semi-automatic image analysis tools for cerebrospinal fluid electrophoresis of IgG oligoclonal bands. Pract. Lab. Med. 2018, 10, 1–9. [Google Scholar] [CrossRef]
- Haddad, F.; Boudet, S.; Peyrodie, L.; Vandenbroucke, N.; Hautecoeur, P.; Forzy, G. Toward an automatic tool for oligoclonal band detection in cerebrospinal fluid and tears for multiple sclerosis diagnosis: Lane segmentation based on a ribbon univariate open active contour. Med. Biol. Eng. Comput. 2020, 58, 967–976. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, N.-P.V.; Carstensen, J.M.; Smedsgaard, J. Aligning of single and multiple wavelength chromatographic profiles for chemometric data analysis using correlation optimised warping. J. Chromatogr. A 1998, 805, 17–35. [Google Scholar] [CrossRef]
- Skov, T.; van den Berg, F.; Tomasi, G.; Bro, R. Automated alignment of chromatographic data. J. Chemom. 2006, 20, 484–497. [Google Scholar] [CrossRef]
- Moreira, B.M.; Sousa, A.V.; Mendonça, A.M.; Campilho, A. Correction of Geometrical Distortions in Bands of Chromatography Images. In Image Analysis and Recognition; Kamel, M., Campilho, A., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7950, pp. 274–281. ISBN 978-3-642-39093-7. [Google Scholar]
- Vauterin, L.; Vauterin, P. Integrated Databasing and Analysis. In Molecular Identification, Systematics, and Population Structure of Prokaryotes; Stackebrandt, E., Ed.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 141–217. ISBN 978-3-540-23155-4. [Google Scholar]
- Bailey, D.G.; Christie, C.B. Processing of DNA and Protein Electrophoresis Gels by Image Analysis; Massey University: Palmerston North, New Zealand, 1994; pp. 221–228. [Google Scholar]
- Das, R. SAFA: Semi-automated footprinting analysis software for high-throughput quantification of nucleic acid footprinting experiments. RNA 2005, 11, 344–354. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mitov, M.I.; Greaser, M.L.; Campbell, K.S. GelBandFitter—A computer program for analysis of closely spaced electrophoretic and immunoblotted bands. Electrophoresis 2009, 30, 848–851. [Google Scholar] [CrossRef]
- Heras, J.; Domínguez, C.; Mata, E.; Pascual, V.; Lozano, C.; Torres, C.; Zarazaga, M. GelJ—A tool for analyzing DNA fingerprint gel images. BMC Bioinform. 2015, 16, 270. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cai, F.; Verbeek, F.J. Dam-based rolling ball with fuzzy-rough constraints, a new background subtraction algorithm for image analysis in microscopy. In Proceedings of the 2015 International Conference on Image Processing Theory, Tools and Applications (IPTA), Orleans, France, 10–13 November 2015; IEEE: Mahattan, NY, USA, 2015; pp. 298–303. [Google Scholar]
- Glasbey, C.A.; Mardia, K.V. A review of image-warping methods. J. Appl. Stat. 1998, 25, 155–171. [Google Scholar] [CrossRef] [Green Version]
- Sorzano, C.O.S.; Thevenaz, P.; Unser, M. Elastic Registration of Biological Images Using Vector-Spline Regularization. IEEE Trans. Biomed. Eng. 2005, 52, 652–663. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wensch, J.; Gerisch, A.; Posch, S. Optimised coupling of hierarchies in image registration. Image Vis. Comput. 2008, 26, 1000–1011. [Google Scholar] [CrossRef]
- Potra, F.A.; Liu, X.; Seillier-Moiseiwitsch, F.; Roy, A.; Hang, Y.; Marten, M.R.; Raman, B.; Whisnant, C. Protein image alignment via piecewise affine transformations. J. Comput. Biol. 2006, 13, 614–630. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salmi, J.; Aittokallio, T.; Westerholm, J.; Griese, M.; Rosengren, A.; Nyman, T.A.; Lahesmaa, R.; Nevalainen, O. Hierarchical grid transformation for image warping in the analysis of two-dimensional electrophoresis gels. Proteomics 2002, 2, 1504–1515. [Google Scholar] [CrossRef]
- Glasbey, C.A.; Mardia, K.V. A penalized likelihood approach to image warping. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2001, 63, 465–492. [Google Scholar] [CrossRef]
- Knight, P.A. Fast rectangular matrix multiplication and QR decomposition. Linear Algebra Appl. 1995, 221, 69–81. [Google Scholar] [CrossRef] [Green Version]

| Band-Straightening Algorithm | ||
|---|---|---|
| Training—All (22 lanes) | OCBSA-2016 | 1.214 |
| OCBSA-2021 | 0.976 | |
| Test—All (18 lanes) | OCBSA-2016 | 1.416 |
| OCBSA-2021 | 1.043 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haddad, F.; Boudet, S.; Peyrodie, L.; Vandenbroucke, N.; Poupart, J.; Hautecoeur, P.; Chieux, V.; Forzy, G. Oligoclonal Band Straightening Based on Optimized Hierarchical Warping for Multiple Sclerosis Diagnosis. Sensors 2022, 22, 724. https://doi.org/10.3390/s22030724
Haddad F, Boudet S, Peyrodie L, Vandenbroucke N, Poupart J, Hautecoeur P, Chieux V, Forzy G. Oligoclonal Band Straightening Based on Optimized Hierarchical Warping for Multiple Sclerosis Diagnosis. Sensors. 2022; 22(3):724. https://doi.org/10.3390/s22030724
Chicago/Turabian StyleHaddad, Farah, Samuel Boudet, Laurent Peyrodie, Nicolas Vandenbroucke, Julien Poupart, Patrick Hautecoeur, Vincent Chieux, and Gérard Forzy. 2022. "Oligoclonal Band Straightening Based on Optimized Hierarchical Warping for Multiple Sclerosis Diagnosis" Sensors 22, no. 3: 724. https://doi.org/10.3390/s22030724
APA StyleHaddad, F., Boudet, S., Peyrodie, L., Vandenbroucke, N., Poupart, J., Hautecoeur, P., Chieux, V., & Forzy, G. (2022). Oligoclonal Band Straightening Based on Optimized Hierarchical Warping for Multiple Sclerosis Diagnosis. Sensors, 22(3), 724. https://doi.org/10.3390/s22030724








