A Self-Calibrating Localization Solution for Sport Applications with UWB Technology
Abstract
1. Introduction
1.1. Related Works
1.2. Study Contributions
- Time of Flight (TOF) measurements among APs are used to reconstruct the network geometry in the SL procedure. An algorithm based on GN is used to handle the errors due to antenna delays in the TOF estimate. The algorithm relies on an iterative procedure for estimating the antenna delay by minimizing the difference between the true and estimated TOF at each UWB node. Compared with other methods such as [34], the proposed method converges to the optimal solution and can be applied to conventional ranging schemes, avoiding the definition of custom messages as in [37].
- Outlier identification and removal is here addressed by proposing a modified IFA. Compared with the standard IFA [45], the proposed algorithm can tackle a very-low-dimensional set of measurements while achieving high accuracy in detecting outliers. This method was designed due to the low number of TOF measurements available for anchors’ SL.
- For anchors’ SL, we developed an iterative algorithm that exploits the filtered TOF measurements to reconstruct the system geometry. The algorithm, inspired by [26], iteratively searches for an AP configuration that minimizes the residual error between the TOF measurements provided by the UWB system and the distances extracted from the positioned anchors. Rather than relying on complex optimization procedures, such as the ones proposed in [31], the developed algorithm relies on GN algorithm which is computationally efficient.
- Tag localization is achieved by multilateration of TDOA measurements. To compensate for the TDOA antenna delay at the anchors, we statistically modeled the TDOA measurements and extracted the corresponding delay through an inversion operation. Compared with the other approaches available in the literature, the proposed approach does not require any training procedure, as opposed to [40] or complex optimization procedures as in [39].
2. System and Measurement Models
2.1. Measurements for AP Network Localization
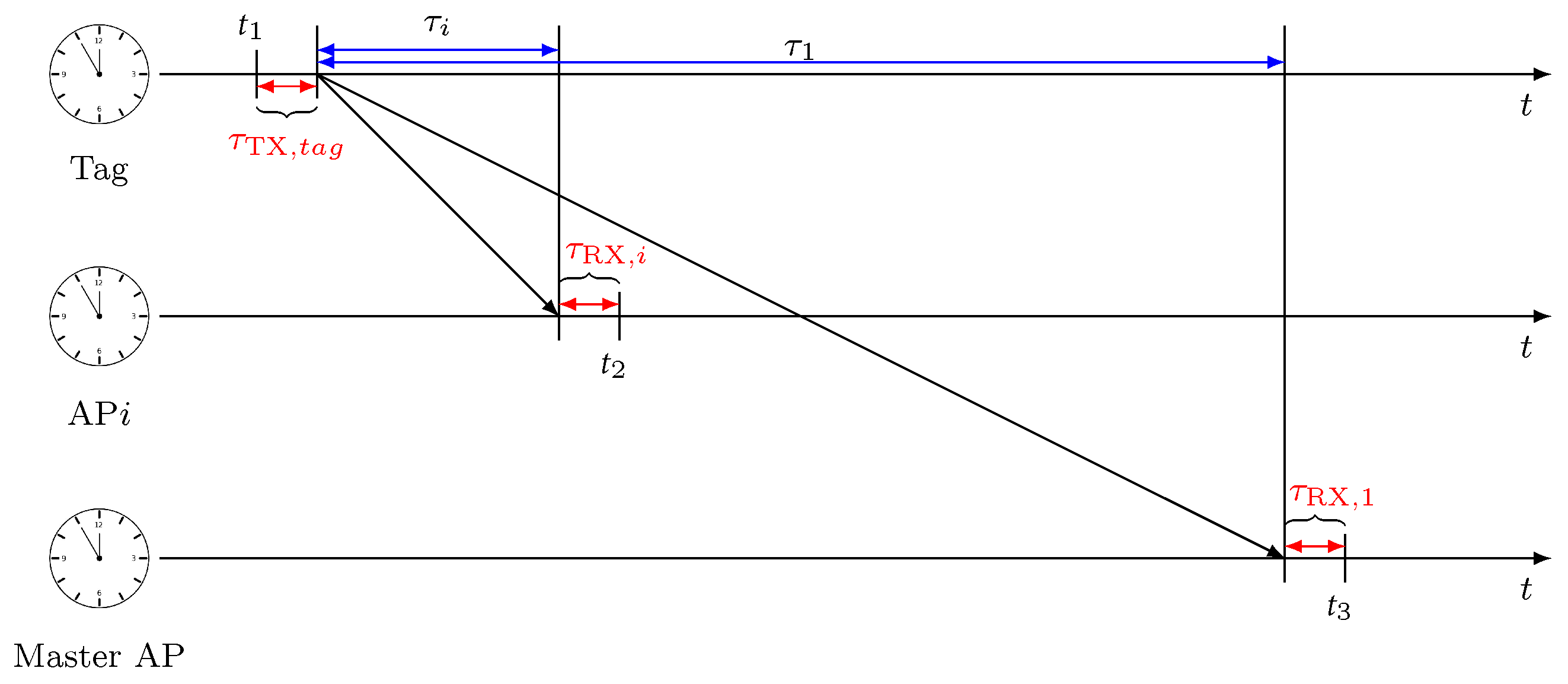
2.2. Measurements for Tag Localization
3. Antenna Delay Calibration
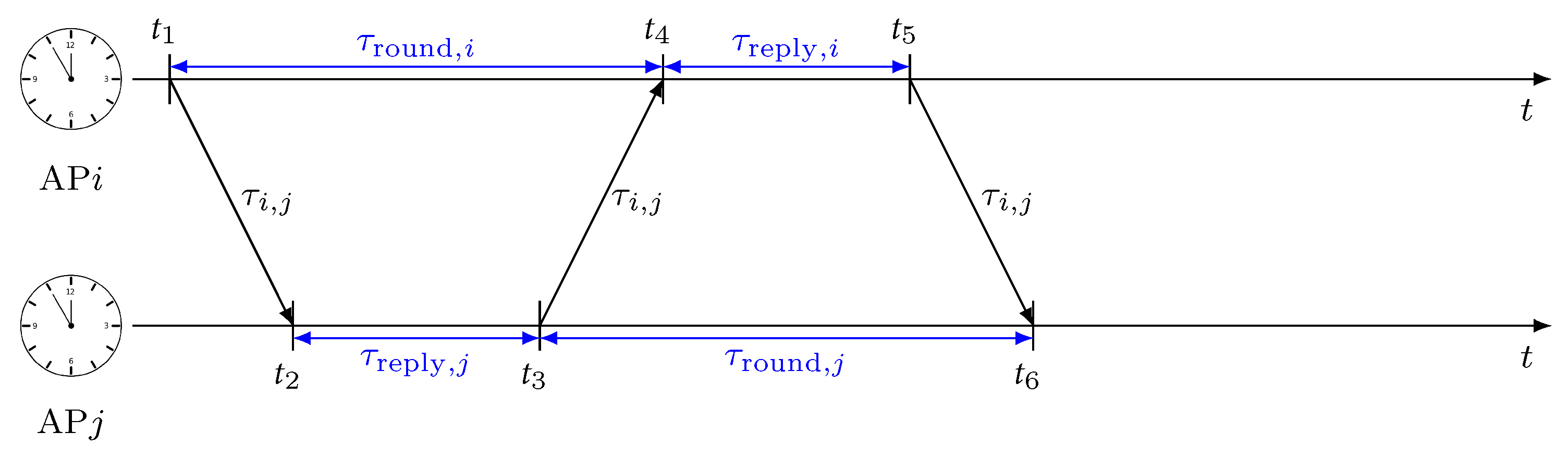
3.1. ADS-TWR Antenna Delay Calibration
3.2. TDOA Antenna Delay Calibration
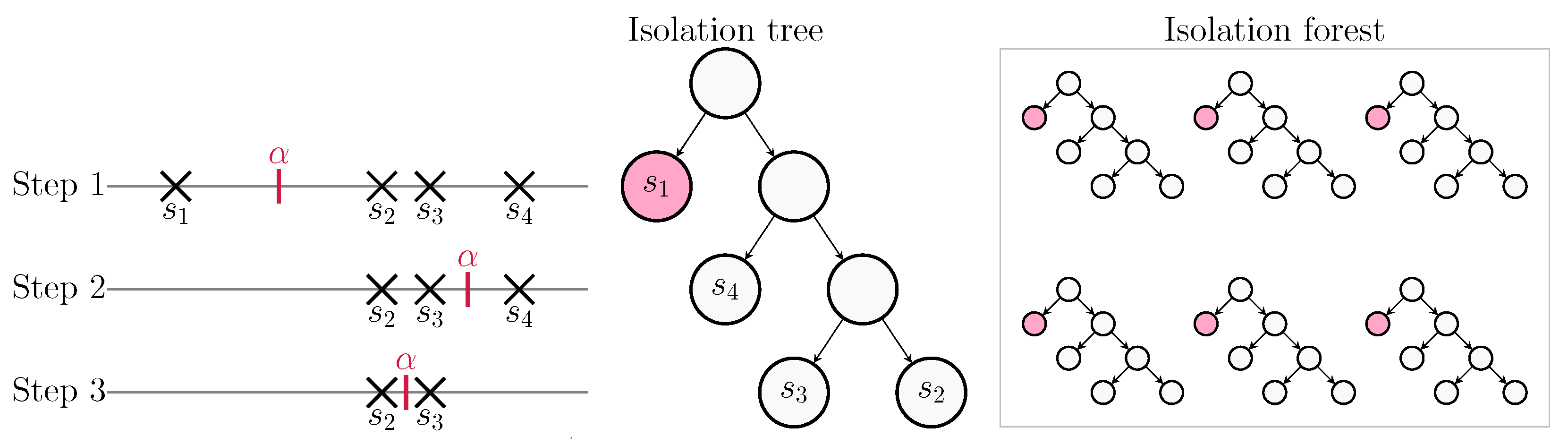
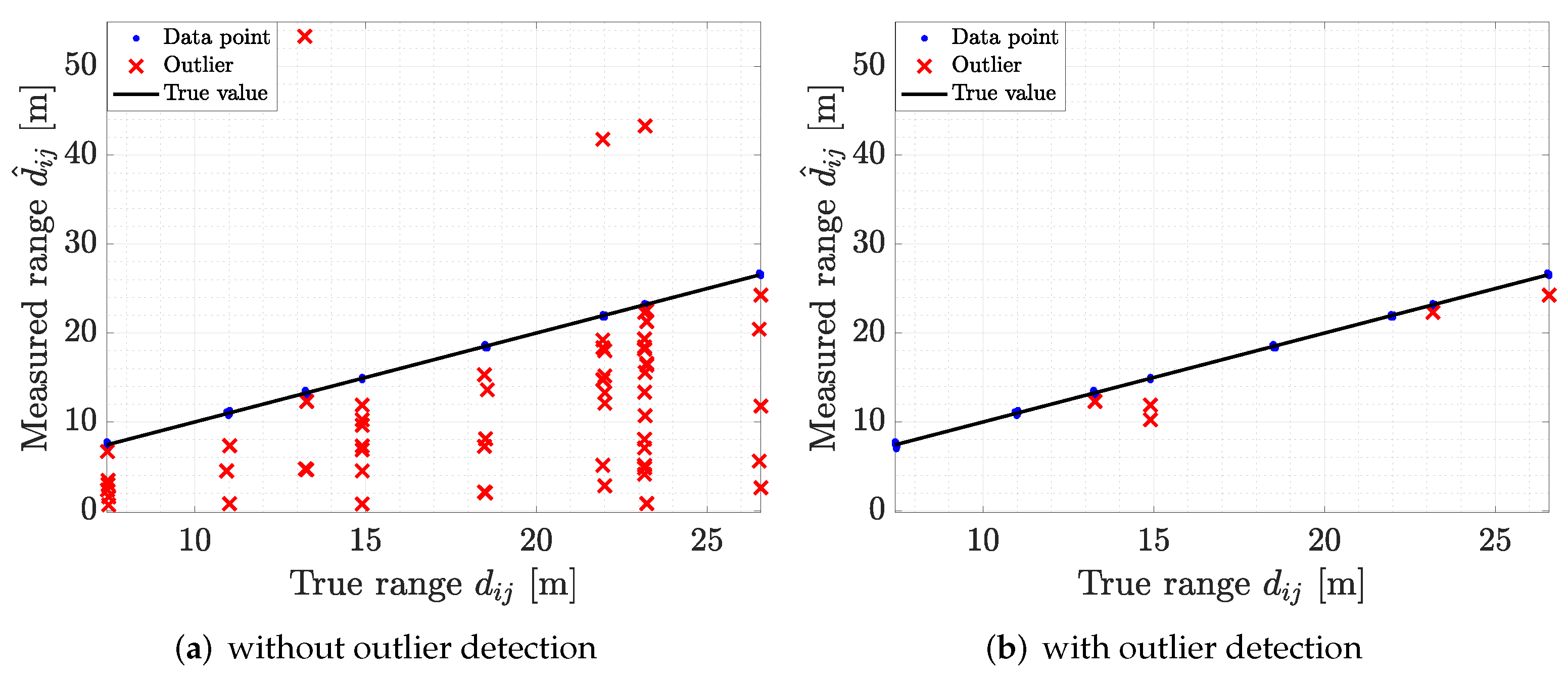
4. Modified 1D IFA for Outlier Removal
- Isolation Tree (iTree): It is a binary tree, where each node has either zero or two child nodes. Nodes can be either external or internal depending on their position into the tree. An internal node is denoted as , where and are the left and right child nodes, respectively; and is the split value that defines the separation between data and data. An external node is denoted as , being thus defined on the set of data points belonging to the extNode and its cardinality.
- Path length is denoted as ; it measures the depth of the data point in the iTree. Outliers typically have shorter path lengths because they are more likely to be isolated.
- Isolation forest: It is a set composed by a fixed number of iTrees that are generated on the same set of data .
| Algorithm 1: iTree(, n, ) |
 |
5. Localization Methods
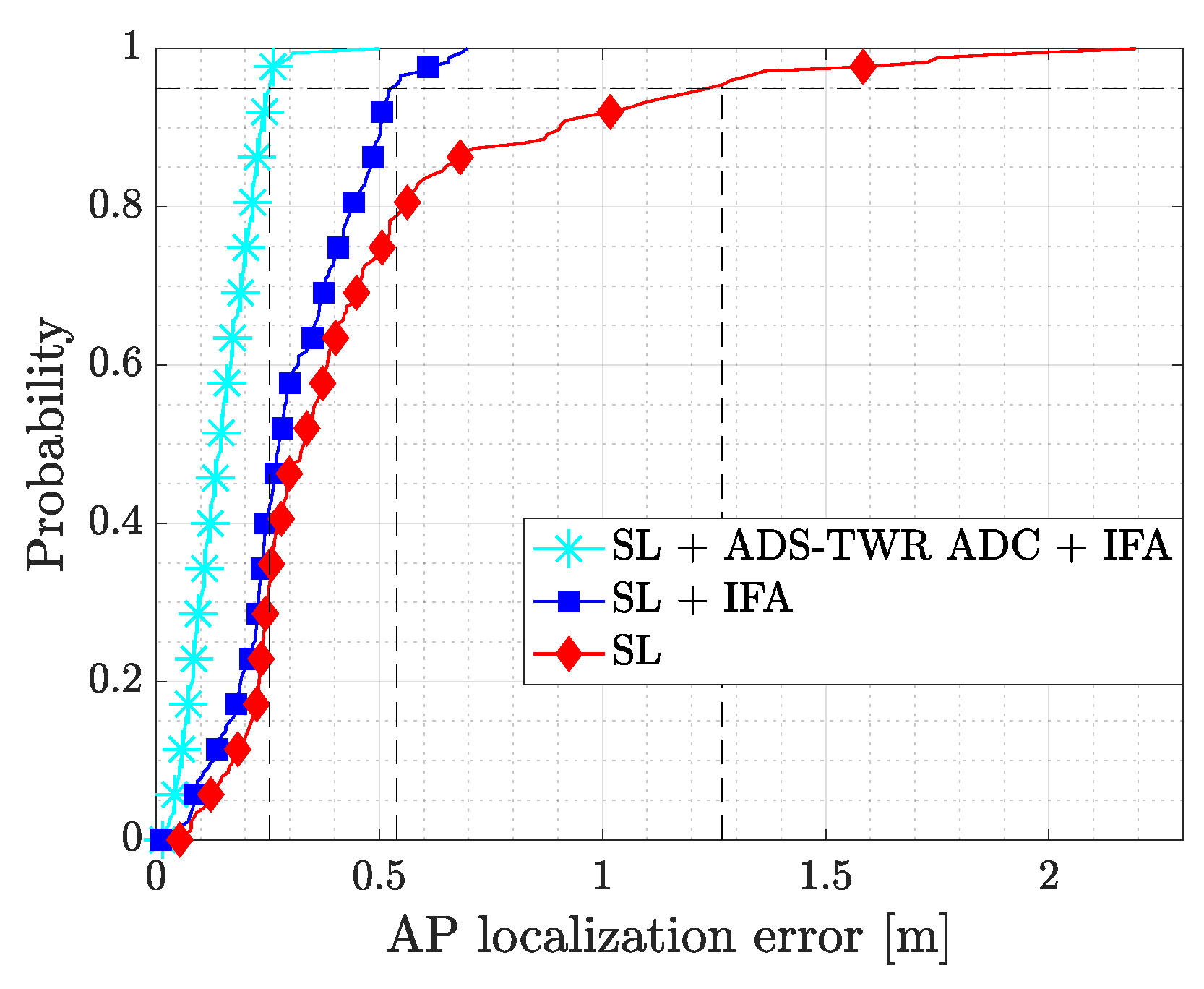
5.1. Anchors Self-Localization
| Algorithm 2:Autolocalization() |
 |
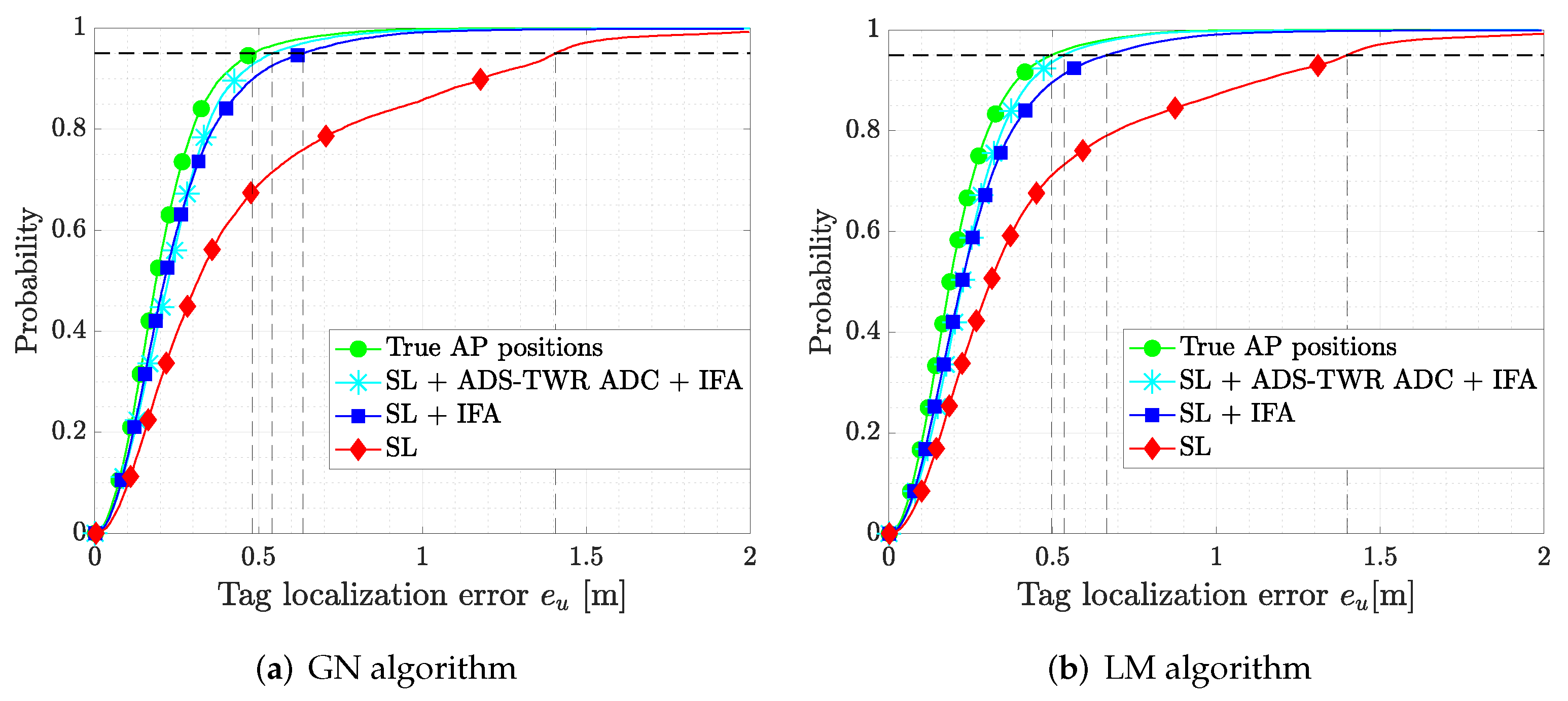
5.2. Tag Localization
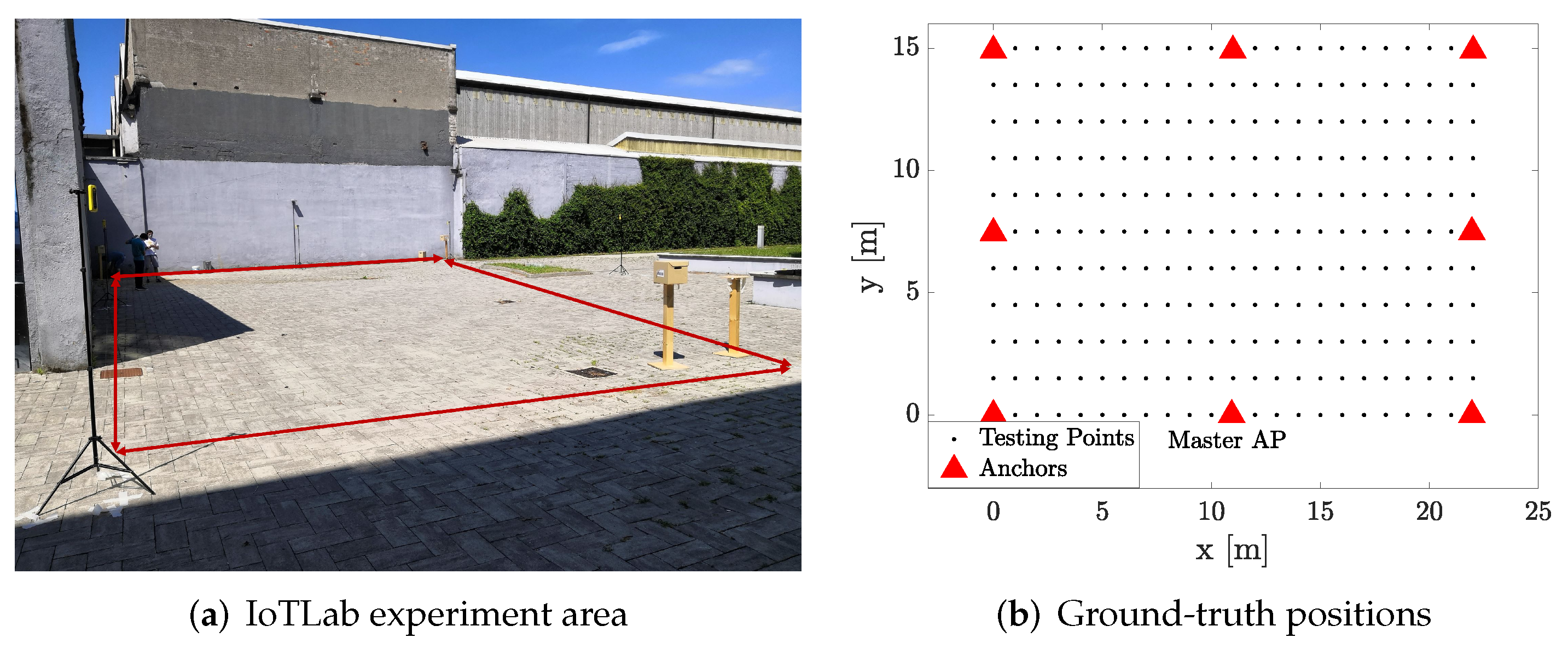
6. Experimental Setup and Performance Metrics
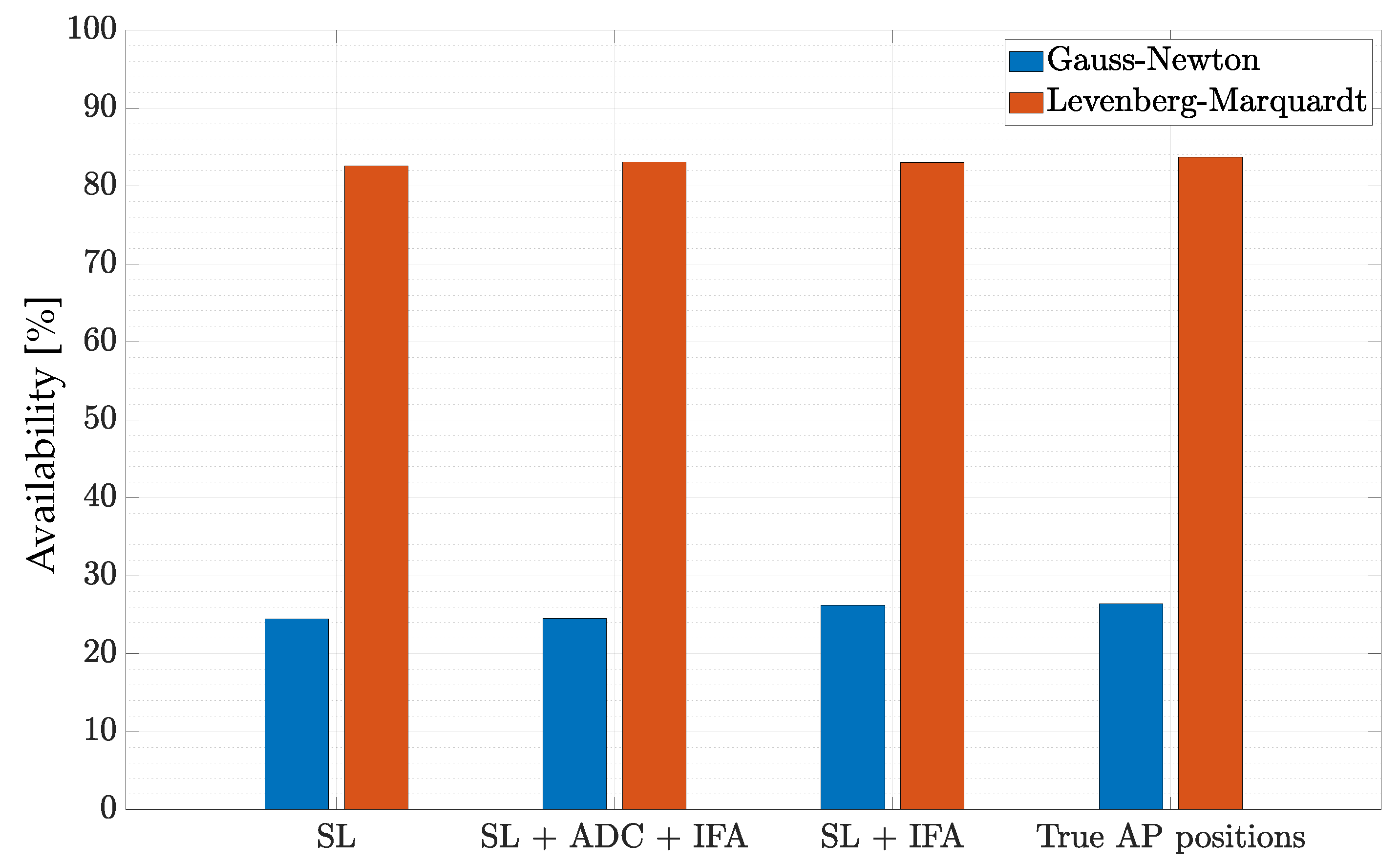
7. Results and Discussion
8. Conclusions and Future Studies
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Definition |
| ADC | Antenna Delay Calibration |
| ADS-TWR | Asymmetric Double-Sided Two-Way Ranging |
| AOA | Angle of Arrival |
| AP | Access Point |
| CEP | Circular Error Probable |
| CDF | Cumulative Distribution Function |
| GN | Gauss–Newton |
| GNSS | Global Navigation Satellite System |
| IFA | Isolation Forest Algorithm |
| IoT | Internet of Things |
| LM | Levenberg–Marquardt |
| LS | Least Square |
| PSO | Particle Swarm Optimization |
| RMSE | Root Mean Square Error |
| RSS | Received Signal Strength |
| RTT | Round Trip Time |
| SL | Self-Localization |
| TDMA | Time Division Multiple Access |
| TDOA | Time Difference of Arrival |
| TOA | Time of Arrival |
| TOF | Time of Flight |
| TWR | Two-Way Ranging |
| UWB | Ultrawide-Band |
| WSN | Wireless Sensor Network |
References
- Xu, L.D.; He, W.; Li, S. Internet of Things in Industries: A Survey. IEEE Trans. Ind. Inform. 2014, 10, 2233–2243. [Google Scholar] [CrossRef]
- Islam, S.M.R.; Kwak, D.; Kabir, M.H.; Hossain, M.; Kwak, K.S. The Internet of Things for Health Care: A Comprehensive Survey. IEEE Access 2015, 3, 678–708. [Google Scholar] [CrossRef]
- Qadri, Y.A.; Nauman, A.; Zikria, Y.B.; Vasilakos, A.V.; Kim, S.W. The Future of Healthcare Internet of Things: A Survey of Emerging Technologies. IEEE Commun. Surv. Tutor. 2020, 22, 1121–1167. [Google Scholar] [CrossRef]
- Gaikwad, P.P.; Gabhane, J.P.; Golait, S.S. A Survey Based on Smart Homes System Using Internet-of-Things. In Proceedings of the 2015 International Conference on Computation of Power, Energy, Information and Communication (ICCPEIC), Melmaruvathur, India, 22–23 April 2015; pp. 0330–0335. [Google Scholar] [CrossRef]
- Dian, F.J.; Vahidnia, R.; Rahmati, A. Wearables and the Internet of Things (IoT), Applications, Opportunities, and Challenges: A Survey. IEEE Access 2020, 8, 69200–69211. [Google Scholar] [CrossRef]
- Zafari, F.; Gkelias, A.; Leung, K.K. A Survey of Indoor Localization Systems and Technologies. IEEE Commun. Surv. Tutor. 2019, 21, 2568–2599. [Google Scholar] [CrossRef]
- Farahsari, P.S.; Farahzadi, A.; Rezazadeh, J.; Bagheri, A. A Survey on Indoor Positioning Systems for IoT-Based Applications. IEEE Internet Things J. 2022, 9, 7680–7699. [Google Scholar] [CrossRef]
- Leser, R.; Baca, A.; Ogris, G. Local Positioning Systems in (Game) Sports. Sensors 2011, 11, 9778–9797. [Google Scholar] [CrossRef]
- Gustafsson, F.; Gunnarsson, F. Mobile Positioning Using Wireless Networks: Possibilities and Fundamental Limitations Based on Available Wireless Network Measurements. IEEE Signal Process. Mag. 2005, 22, 41–53. [Google Scholar] [CrossRef]
- Gu, Y.; Lo, A.; Niemegeers, I. A Survey of Indoor Positioning Systems for Wireless Personal Networks. IEEE Commun. Surv. Tutor. 2009, 11, 13–32. [Google Scholar] [CrossRef]
- Khelifi, F.; Bradai, A.; Benslimane, A.; Rawat, P.; Atri, M. A Survey of Localization Systems in Internet of Things. Mob. Netw. Appl. 2019, 24, 761–785. [Google Scholar] [CrossRef]
- Win, M.Z.; Scholtz, R.A. Impulse Radio: How it Works. IEEE Commun. Lett. 1998, 2, 36–38. [Google Scholar] [CrossRef]
- Porcino, D.; Hirt, W. Ultra-Wideband Radio Technology: Potential and Challenges Ahead. IEEE Commun. Mag. 2003, 41, 66–74. [Google Scholar] [CrossRef]
- Gungor, V.C.; Hancke, G.P. Industrial Wireless Sensor Networks: Challenges, Design Principles, and Technical Approaches. IEEE Trans. Ind. Electron. 2009, 56, 4258–4265. [Google Scholar] [CrossRef]
- Barbieri, L.; Brambilla, M.; Pitic, R.; Trabattoni, A.; Mervic, S.; Nicoli, M. UWB Real-Time Location Systems for Smart Factory: Augmentation Methods and Experiments. In Proceedings of the 2020 IEEE 31st Annual International Symposium on Personal, Indoor and Mobile Radio Communications, London, UK, 31 August–3 September 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Malajner, M.; Planinšič, P.; Gleich, D. UWB Ranging Accuracy. In Proceedings of the 2015 International Conference on Systems, Signals and Image Processing (IWSSIP), London, UK, 10–12 September 2015; pp. 61–64. [Google Scholar] [CrossRef]
- Zhang, F.; Yang, L.; Liu, Y.; Ding, Y.; Yang, S.H.; Li, H. Design and Implementation of Real-Time Localization System (RTLS) Based on UWB and TDoA Algorithm. Sensors 2022, 22, 4353. [Google Scholar] [CrossRef] [PubMed]
- Buccella, C.; Feliziani, M.; Manzi, G. Penetration of Ultra-WideBand (UWB) Communication Signals through Walls. In Ultra-Wideband, Short-Pulse Electromagnetics 7; Springer: New York, NY, USA, 2007; p. 784. ISBN 978-0-387-37728-5. [Google Scholar] [CrossRef]
- Win, M.; Scholtz, R. On the Energy Capture of Ultrawide Bandwidth Signals in Dense Multipath Environments. IEEE Commun. Lett. 1998, 2, 245–247. [Google Scholar] [CrossRef]
- Win, M.; Scholtz, R. On the Robustness of Ultra-wide Bandwidth Signals in Dense Multipath Environments. IEEE Commun. Lett. 1998, 2, 51–53. [Google Scholar] [CrossRef]
- Dardari, D.; Conti, A.; Ferner, U.; Giorgetti, A.; Win, M.Z. Ranging with Ultrawide Bandwidth Signals in Multipath Environments. Proc. IEEE 2009, 97, 404–426. [Google Scholar] [CrossRef]
- Gezici, S.; Tian, Z.; Giannakis, G.B.; Kobayashi, H.; Molisch, A.F.; Poor, H.V.; Sahinoglu, Z. Localization via Ultra-Wideband radios: A Look at Positioning Aspects for Future Sensor Networks. IEEE Signal Process. Mag. 2005, 22, 70–84. [Google Scholar] [CrossRef]
- Alarifi, A.; Al-Salman, A.; Alsaleh, M.; Alnafessah, A.; Alhadhrami, S.; Al-Ammar, M.; Al-Khalifa, H. Ultra Wideband Indoor Positioning Technologies: Analysis and Recent Advances. Sensors 2016, 16, 707. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, W.; She, X.; Li, X. 2-D Indoor Passive Real-Time Location System Based on Ultrawideband Technology. IEEE Trans. Instrum. Meas. 2022, 71, 9510017. [Google Scholar] [CrossRef]
- Laadung, T.; Ulp, S.; Alam, M.M.; Moullec, Y.L. Novel Active-Passive Two-Way Ranging Protocols for UWB Positioning Systems. IEEE Sens. J. 2022, 22, 5223–5237. [Google Scholar] [CrossRef]
- Pelka, M.; Goronzy, G.; Hellbrück, H. Iterative Approach for Anchor Configuration of Positioning Systems. ICT Express 2016, 2, 1–4. [Google Scholar] [CrossRef][Green Version]
- Niculescu, D.; Nath, B. Ad Hoc Positioning System APS Using AOA. In Proceedings of the IEEE INFOCOM 2003. Twenty-Second Annual Joint Conference of the IEEE Computer and Communications Societies, San Francisco, CA, USA, 30 March–3 April 2003; Volume 3, pp. 1734–1743. [Google Scholar] [CrossRef]
- Shi, Q.; Zhao, S.; Cui, X.; Lu, M.; Jia, M. Anchor Self-localization Algorithm Based on UWB Ranging and Inertial Measurements. Tsinghua Sci. Technol. 2019, 24, 728–737. [Google Scholar] [CrossRef]
- Krapež, P.; Munih, M. Anchor Calibration for Real-Time-Measurement Localization Systems. IEEE Trans. Instrum. Meas. 2020, 69, 9907–9917. [Google Scholar] [CrossRef]
- Shang, Y.; Rumi, W.; Zhang, Y.; Fromherz, M. Localization from Connectivity in Sensor Networks. IEEE Trans. Parallel Distrib. Syst. 2004, 15, 961–974. [Google Scholar] [CrossRef]
- Drusvyatskiy, D.; Krislock, N.; Voronin, Y.L.; Wolkowicz, H. Noisy Euclidean Distance Realization: Robust Facial Reduction and the Pareto Frontier. SIAM J. Optim. 2017, 27, 2301–2331. [Google Scholar] [CrossRef]
- Goldenberg, D.K.; Bihler, P.; Cao, M.; Fang, J.; Anderson, B.D.O.; Morse, A.S.; Yang, Y.R. Localization in Sparse Networks Using Sweeps. In Proceedings of the MobiCom ’06, Los Angeles, CA, USA, 23–29 September 2006; Association for Computing Machinery: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- Müller, M.; Lategahn, J.; Telle, L.; Röhrig, C. Automatic Anchor Calibration in IEEE 802.15.4a Networks. In Proceedings of the 2011 8th Workshop on Positioning, Navigation and Communication, Dresden, Germany, 7–8 April 2011; pp. 67–71. [Google Scholar] [CrossRef]
- Gui, X.; Guo, S.; Chen, Q.; Han, L. A New Calibration Method of UWB Antenna Delay Based on the ADS-TWR. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 7364–7369. [Google Scholar] [CrossRef]
- Haggenmiller, A.; Krogius, M.; Olson, E. Non-parametric Error Modeling for Ultra-wideband Localization Networks. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 2568–2574. [Google Scholar] [CrossRef]
- Decawave. APS014 Application Notes: Antenna Delay Calibration of DW1000-Based Products and Systems; Decawave: Dublin, Ireland, 2018. [Google Scholar]
- Shah, S.; Chaiwong, K.; Kovavisaruch, L.O.; Kaemarungsi, K.; Demeechai, T. Antenna Delay Calibration of UWB Nodes. IEEE Access 2021, 9, 63294–63305. [Google Scholar] [CrossRef]
- Wang, Y.; Ho, K.C. TDOA Source Localization in the Presence of Synchronization Clock Bias and Sensor Position Errors. IEEE Trans. Signal Process. 2013, 61, 4532–4544. [Google Scholar] [CrossRef]
- Zou, Y.; Liu, H. Semidefinite Programming Methods for Alleviating Clock Synchronization Bias and Sensor Position Errors in TDOA Localization. IEEE Signal Process. Lett. 2020, 27, 241–245. [Google Scholar] [CrossRef]
- Zhao, W.; Panerati, J.; Schoellig, A.P. Learning-Based Bias Correction for Time Difference of Arrival Ultra-Wideband Localization of Resource-Constrained Mobile Robots. IEEE Robot. Autom. Lett. 2021, 6, 3639–3646. [Google Scholar] [CrossRef]
- Hawkins, S.; He, H.; Williams, G.; Baxter, R. Outlier Detection Using Replicator Neural Networks. In Data Warehousing and Knowledge Discovery; Kambayashi, Y., Winiwarter, W., Arikawa, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 170–180. [Google Scholar] [CrossRef]
- Lamrini, B.; Gjini, A.; Daudin, S.; Armando, F.; Pratmarty, P.; Travé-Massuyès, L. Anomaly Detection Using Similarity-based One-Class SVM for Network Traffic Characterization. In Proceedings of the 29th International Workshop on Principles of Diagnosis, Warsaw, Poland, 27–30 August 2018. [Google Scholar]
- Dang, T.T.; Ngan, H.Y.; Liu, W. Distance-Based K-Nearest Neighbors Outlier Detection Method in Large-Scale Traffic Data. In Proceedings of the 2015 IEEE International Conference on Digital Signal Processing (DSP), Singapore, 21–24 July 2015; pp. 507–510. [Google Scholar] [CrossRef]
- Breunig, M.M.; Kriegel, H.P.; Ng, R.T.; Sander, J. LOF: Identifying Density-Based Local Outliers. SIGMOD Rec. 2000, 29, 93–104. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation Forest. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 413–422. [Google Scholar] [CrossRef]
- Qinghua, L.; Sicheng, L.; Yipeng, Y.; Chunyu, J.; Xiaozhen, Y. An Accurate Maximum Likelihood Location Method Based on UWB Platform. In Proceedings of the 2019 14th IEEE International Conference on Electronic Measurement Instruments (ICEMI), Changsha, China, 1–3 November 2019; pp. 515–521. [Google Scholar] [CrossRef]
- Mensing, C.; Plass, S. Positioning Algorithms for Cellular Networks Using TDOA. In Proceedings of the 2006 IEEE International Conference on Acoustics Speech and Signal Processing, Toulouse, France, 14–19 May 2006; Volume 4, p. IV. [Google Scholar] [CrossRef]
- Alraih, S.; Alhammadi, A.; Shayea, I.; Al-Samman, A.M. Improving Accuracy in Indoor Localization System Using Fingerprinting Technique. In Proceedings of the 2017 International Conference on Information and Communication Technology Convergence (ICTC), Jeju, Republic of Korea, 18–20 October 2017; pp. 274–277. [Google Scholar] [CrossRef]
- Alhammadi, A.; Alraih, S.; Hashim, F.; Rasid, M.F.A. Robust 3D Indoor Positioning System Based on Radio Map Using Bayesian Network. In Proceedings of the 2019 IEEE 5th World Forum on Internet of Things (WF-IoT), Limerick, Ireland, 15–18 April 2019; pp. 107–110. [Google Scholar] [CrossRef]
- Barbieri, L.; Brambilla, M.; Trabattoni, A.; Mervic, S.; Nicoli, M. UWB Localization in a Smart Factory: Augmentation Methods and Experimental Assessment. IEEE Trans. Instrum. Meas. 2021, 70, 1–18. [Google Scholar] [CrossRef]
- Suski, W.; Banerjee, S.; Hoover, A. Using a Map of Measurement Noise to Improve UWB Indoor Position Tracking. IEEE Trans. Instrum. Meas. 2013, 62, 2228–2236. [Google Scholar] [CrossRef]
- Zhu, X.; Yi, J.; Cheng, J.; He, L. Adapted Error Map Based Mobile Robot UWB Indoor Positioning. IEEE Trans. Instrum. Meas. 2020, 69, 6336–6350. [Google Scholar] [CrossRef]
- Tian, Q.; Wang, K.I.; Salcic, Z. A Resetting Approach for INS and UWB Sensor Fusion Using Particle Filter for Pedestrian Tracking. IEEE Trans. Instrum. Meas. 2020, 69, 5914–5921. [Google Scholar] [CrossRef]
- Hol, J.D.; Dijkstra, F.; Luinge, H.; Schon, T.B. Tightly Coupled UWB/IMU Pose Estimation. In Proceedings of the 2009 IEEE International Conference on Ultra-Wideband, Vancouver, BC, Canada, 9–1 September 2009; pp. 688–692. [Google Scholar] [CrossRef]
- Kim, D.H.; Farhad, A.; Pyun, J.Y. UWB Positioning System Based on LSTM Classification with Mitigated NLOS Effects. IEEE Internet Things J. 2022, 1. [Google Scholar] [CrossRef]
- Piavanini, M.; Barbieri, L.; Brambilla, M.; Cerutti, M.; Ercoli, S.; Agili, A.; Nicoli, M. A Calibration Method for Antenna Delay Estimation and Anchor Self-Localization in UWB Systems. In Proceedings of the 2022 IEEE International Workshop on Metrology for Industry 4.0&IoT (MetroInd4.0&IoT), Trento, Italy, 7–9 June 2022; pp. 173–177. [Google Scholar] [CrossRef]
- Decawave. APS013 Application Notes: The Implementation of Two-Way Ranging with DW1000; Decawave: Dublin, Ireland, 2014. [Google Scholar]
- Jiang, Y.; Leung, V.C. An Asymmetric Double Sided Two-Way Ranging for Crystal Offset. In Proceedings of the 2007 International Symposium on Signals, Systems and Electronics, Montreal, QC, Canada, 30 July–2 August 2007; pp. 525–528. [Google Scholar] [CrossRef]
- IEEE Std 802.15.4-2011; IEEE Standard for Local and Metropolitan Area Networks–Part 15.4: Low-Rate Wireless Personal Area Networks (LR-WPANs). (Revision of IEEE Std 802.15.4-2006). Institute of Electrical and Electronics Engineers IEEE: Piscataway, NJ, USA, 2011; pp. 1–314.
- Ranganathan, A. The Levenberg-Marquardt Algorithm. Tutor. LM Algorithm 2004, 11, 101–110. [Google Scholar]




| RMSE (m) | CEP 95 (m) | Mean Error (m) | |
|---|---|---|---|
| SL | 0.6154 | 1.3068 | 0.4708 |
| SL + IFA | 0.3365 | 0.5223 | 0.3056 |
| SL + ADS-TWR ADC + IFA | 0.1626 | 0.2482 | 0.1463 |
| RMSE (m) | CEP 95 (m) | Mean Error (m) | |
|---|---|---|---|
| GN with true AP positions | 0.3509 | 0.6887 | 0.2817 |
| GN with true AP position + TDOA ADC | 0.2817 | 0.4875 | 0.2181 |
| LM with true AP positions | 0.3654 | 0.7208 | 0.2959 |
| LM with true AP positions + TDOA ADC | 0.2617 | 0.4965 | 0.2176 |
| RMSE (m) | CEP 95 (m) | Mean Error (m) | |
|---|---|---|---|
| GN with true AP positions | 0.2817 | 0.4875 | 0.2181 |
| GN with SL | 0.6316 | 1.4089 | 0.4842 |
| GN with SL + IFA | 0.3447 | 0.6381 | 0.2660 |
| GN with SL + ADS-TWR ADC + IFA | 0.3072 | 0.5584 | 0.2487 |
| LM with true AP positions | 0.2617 | 0.4965 | 0.2176 |
| LM with SL | 0.6606 | 1.3991 | 0.4635 |
| LM with SL + IFA | 0.3447 | 0.6887 | 0.2770 |
| LM with SL + ADS-TWR ADC + IFA | 0.2993 | 0.5335 | 0.2494 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piavanini, M.; Barbieri, L.; Brambilla, M.; Cerutti, M.; Ercoli, S.; Agili, A.; Nicoli, M. A Self-Calibrating Localization Solution for Sport Applications with UWB Technology. Sensors 2022, 22, 9363. https://doi.org/10.3390/s22239363
Piavanini M, Barbieri L, Brambilla M, Cerutti M, Ercoli S, Agili A, Nicoli M. A Self-Calibrating Localization Solution for Sport Applications with UWB Technology. Sensors. 2022; 22(23):9363. https://doi.org/10.3390/s22239363
Chicago/Turabian StylePiavanini, Marco, Luca Barbieri, Mattia Brambilla, Mattia Cerutti, Simone Ercoli, Andrea Agili, and Monica Nicoli. 2022. "A Self-Calibrating Localization Solution for Sport Applications with UWB Technology" Sensors 22, no. 23: 9363. https://doi.org/10.3390/s22239363
APA StylePiavanini, M., Barbieri, L., Brambilla, M., Cerutti, M., Ercoli, S., Agili, A., & Nicoli, M. (2022). A Self-Calibrating Localization Solution for Sport Applications with UWB Technology. Sensors, 22(23), 9363. https://doi.org/10.3390/s22239363






