Analysis and Accuracy Improvement of UWB-TDoA-Based Indoor Positioning System
Abstract
1. Introduction
- (i)
- A theoretical study of the precision of the position estimates is performed based on a CRLB analysis for round-robin scheduling and an anisotropic representation of the signal-to-noise ratio function of the 3D radiation pattern of the anchor antennas.
- (ii)
- A geometrical study of the 2D IPS domain is carried out, defining bifurcation envelopes that bound the areas where the IPS is predicted to fail. This complements the CRLB analysis, which does not predict regions of failure. Together, they define the so-called flyable area in which positioning is reliable.
- (iii)
- Experiments using an existing IPS with four anchors and a static tagged object are used to validate the precision and failure predictions and to estimate the bias (inaccuracy).
- (iv)
- A debiasing filter is developed to increase the accuracy of the static position estimates, which is then tested for both static and moving tagged objects.
2. Theoretical Study of Precision and Failure
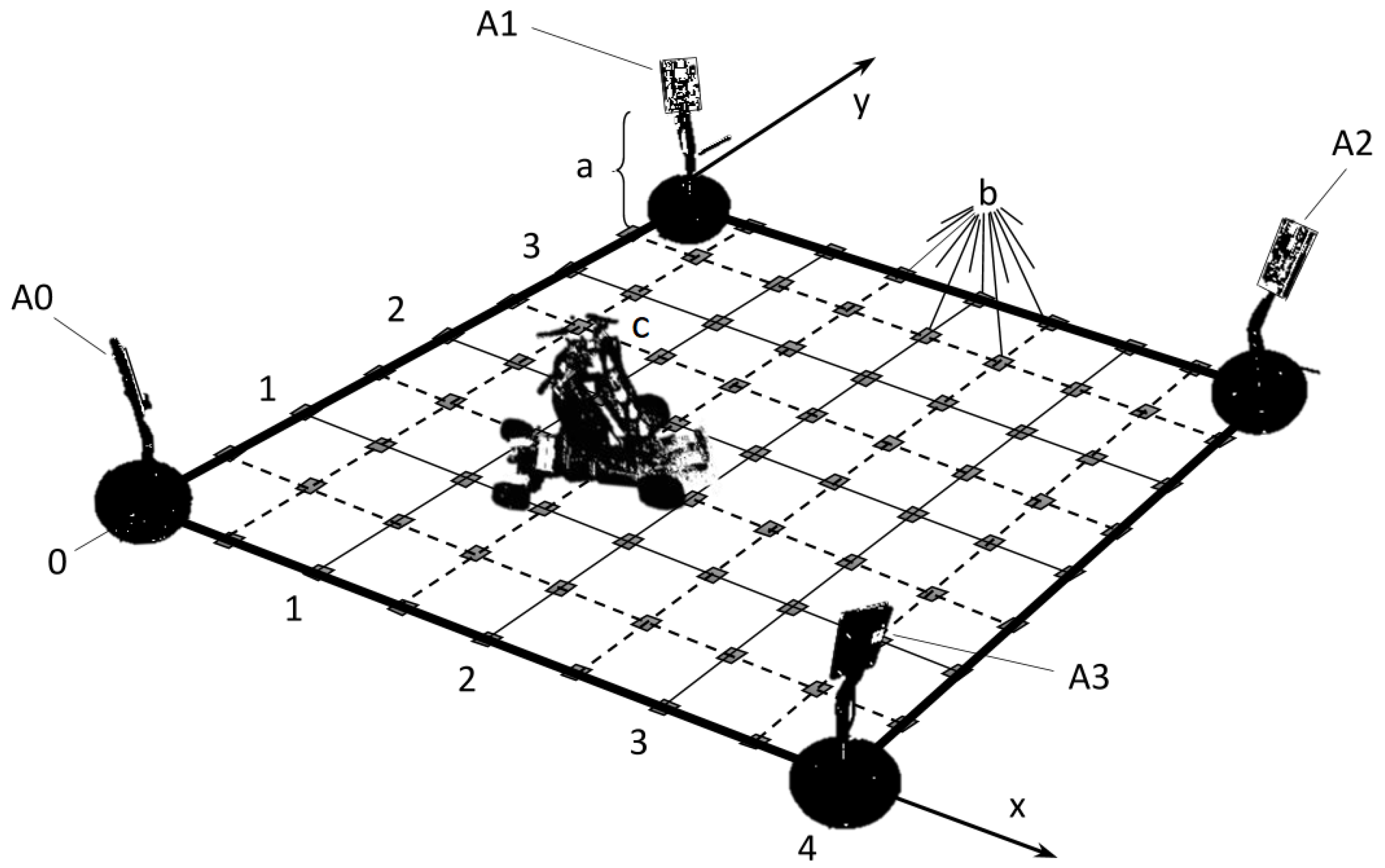
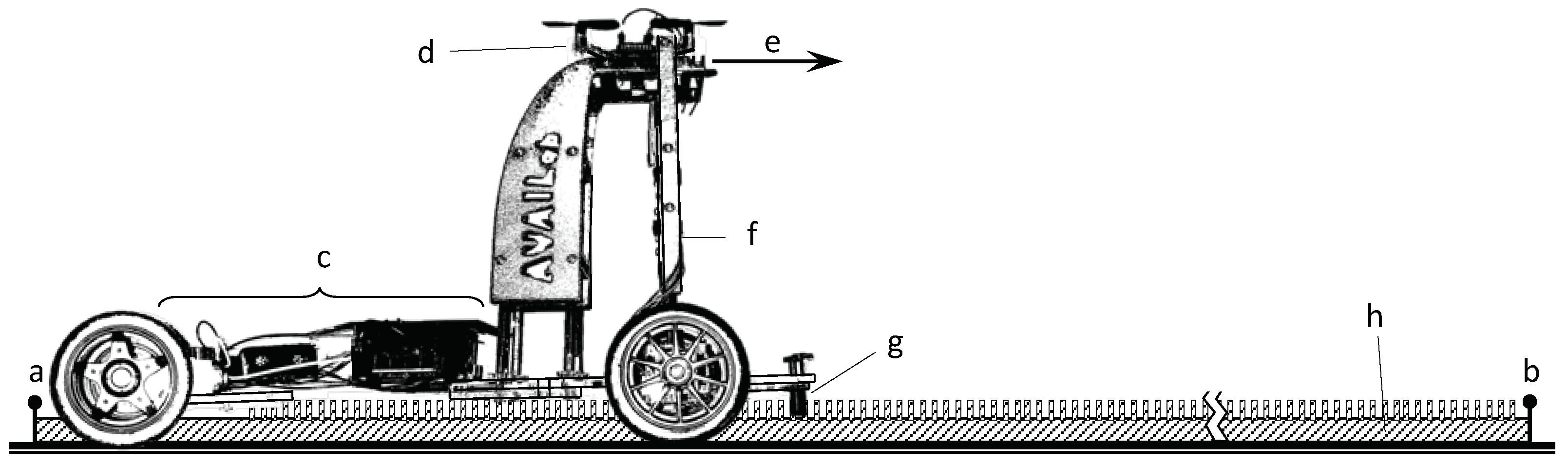
2.1. IPS under Study
2.2. CRLB Analysis for Pseudo-Range Multilateration with Round-Robin Scheduling
2.2.1. Signal-to-Noise Ratio Formulation
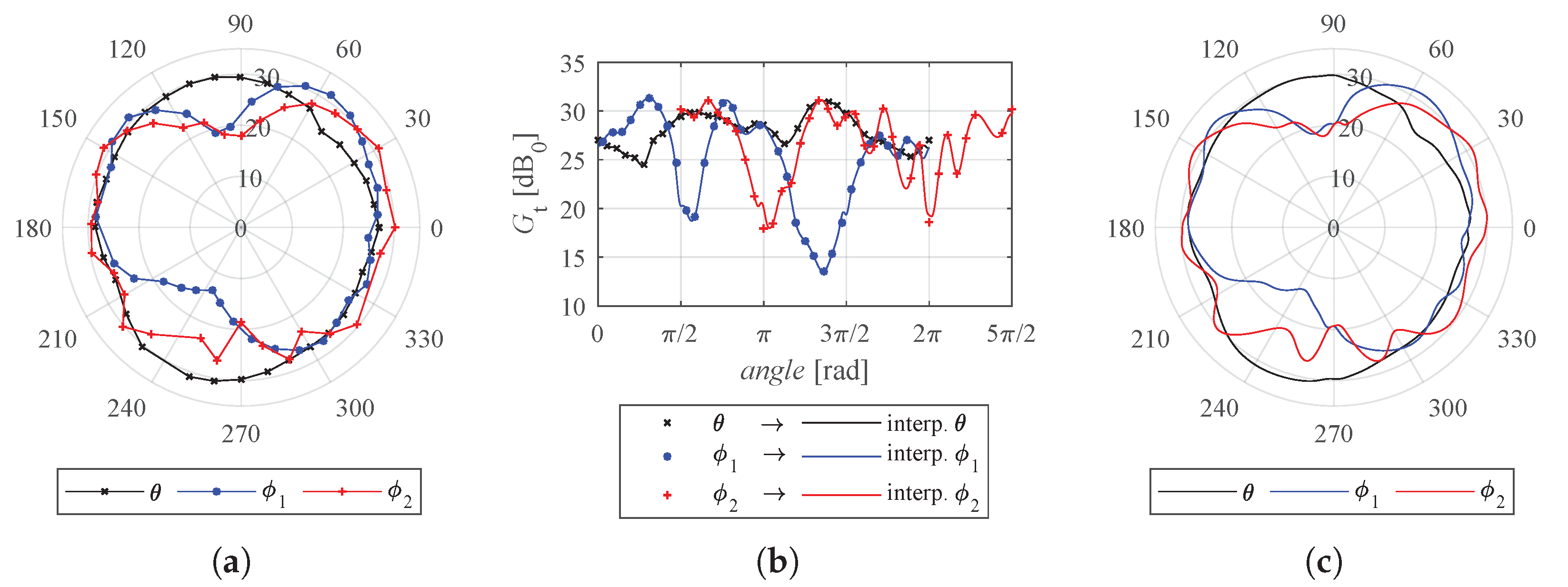
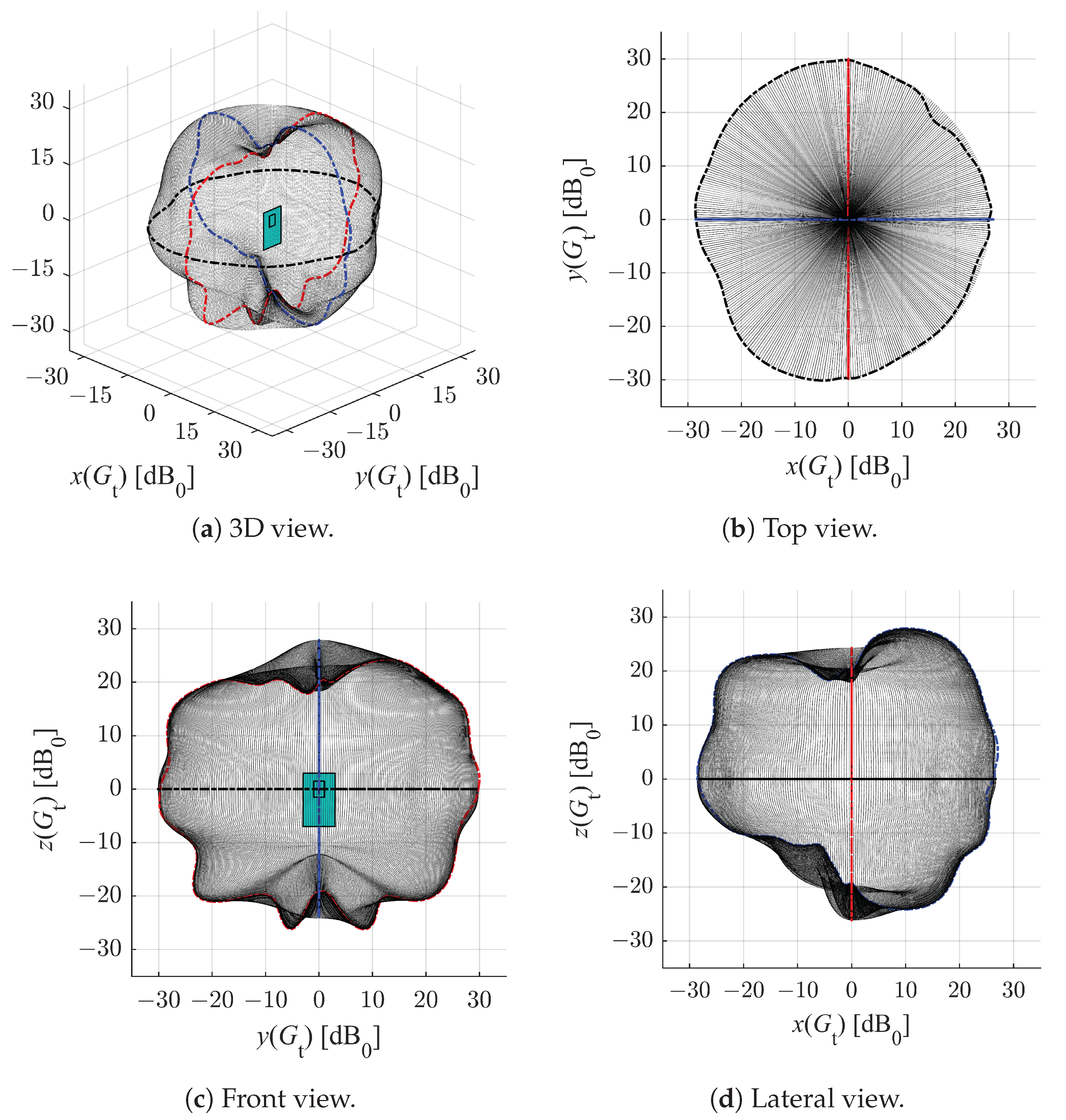
2.2.2. Radiation Pattern of the DW1000 Anchor Antenna
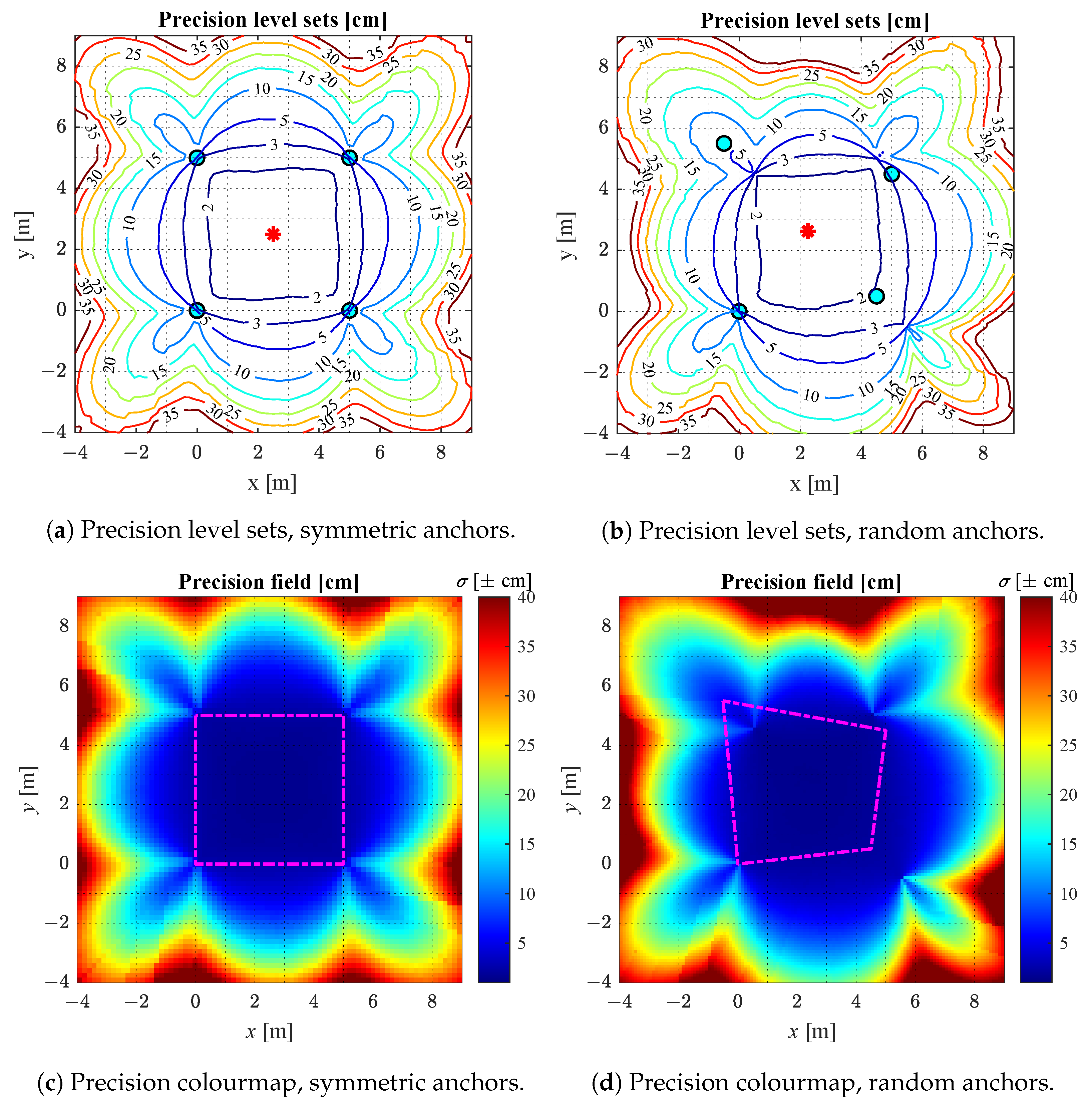
2.2.3. Analytical Results of CRLB Analysis
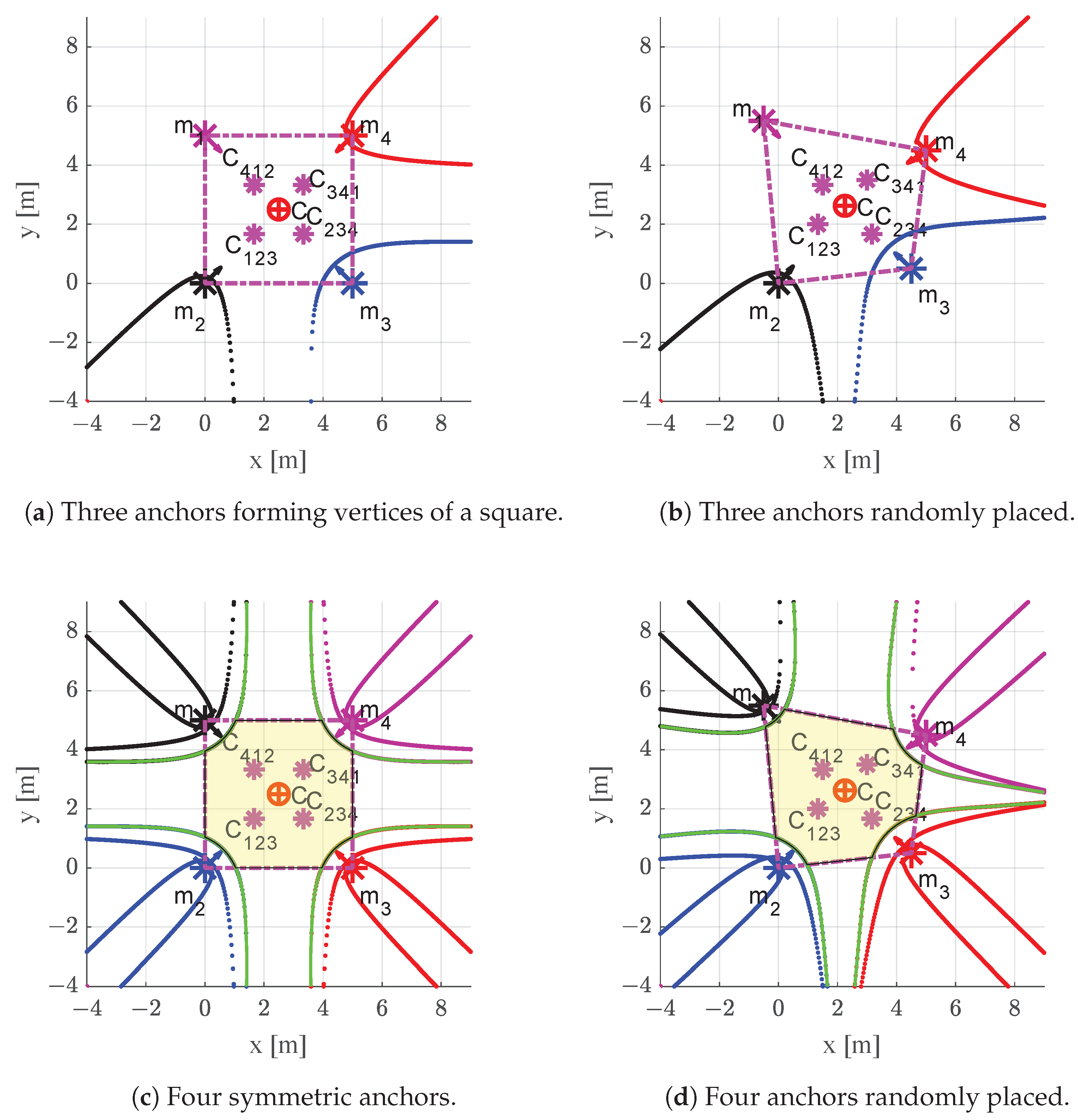
2.3. Bifurcation Envelope Analysis
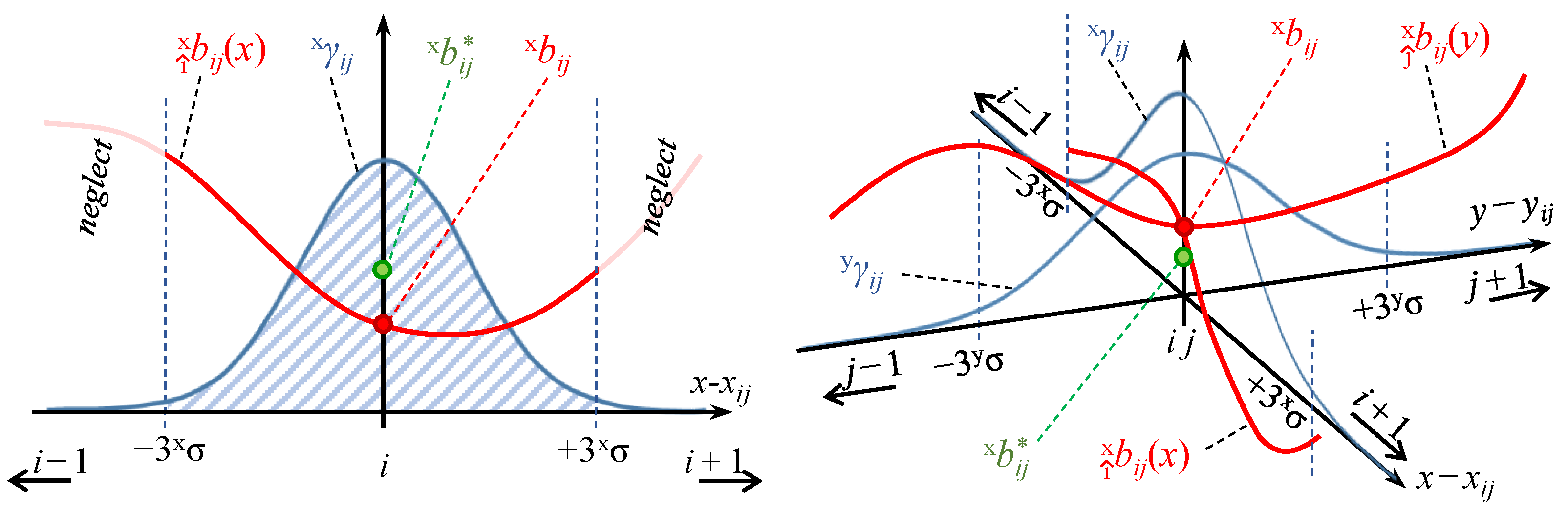
2.3.1. Bifurcation Curve
2.3.2. Bifurcation Envelope
- 1.
- The unique-solution area, defined as the intersection of all concave areas outside each green bifurcation envelope (i.e., not including anchors).
- 2.
- The region with acceptable precision returned by the CRLB analysis (the convex hull).
3. Filter Design
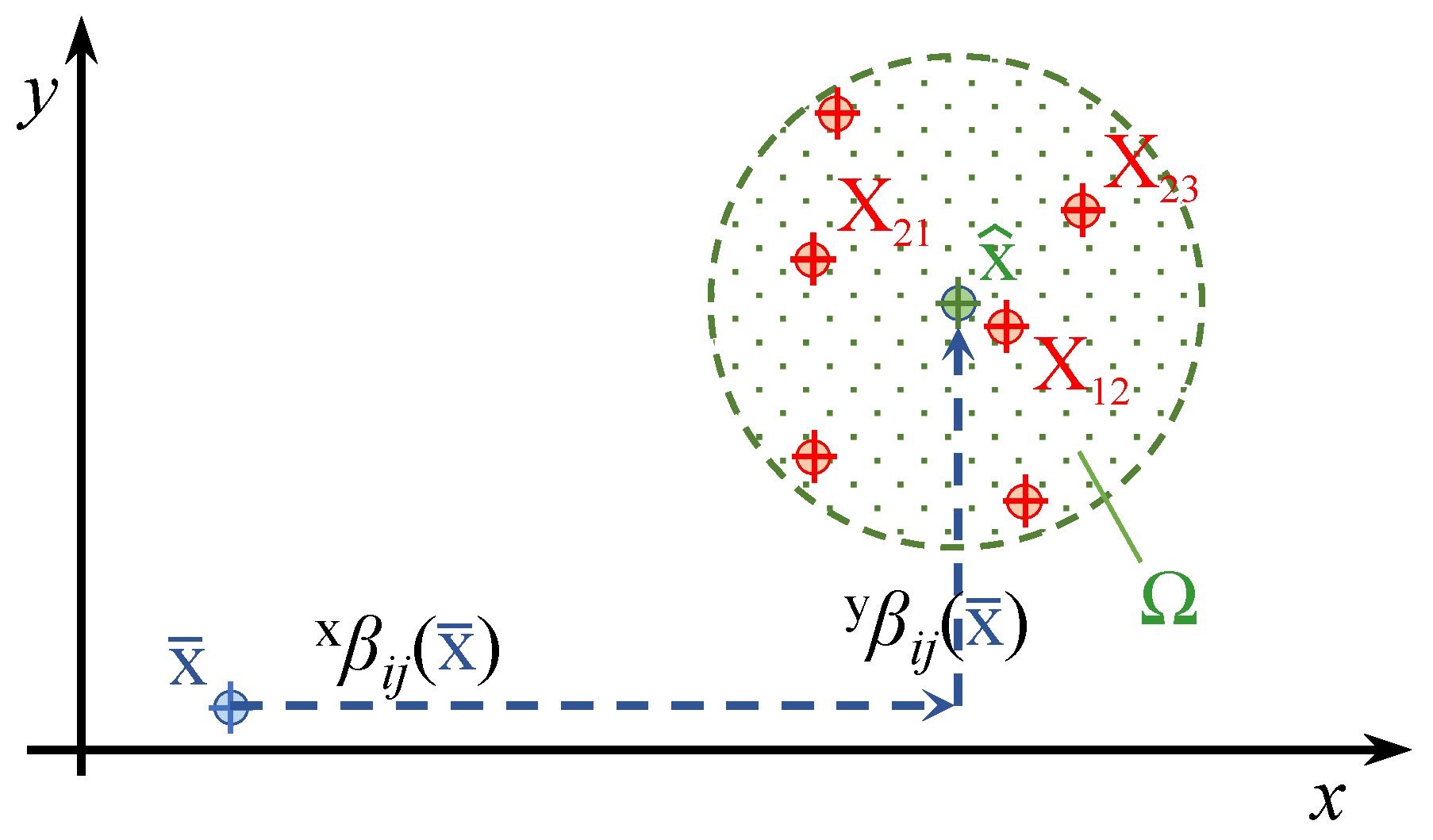
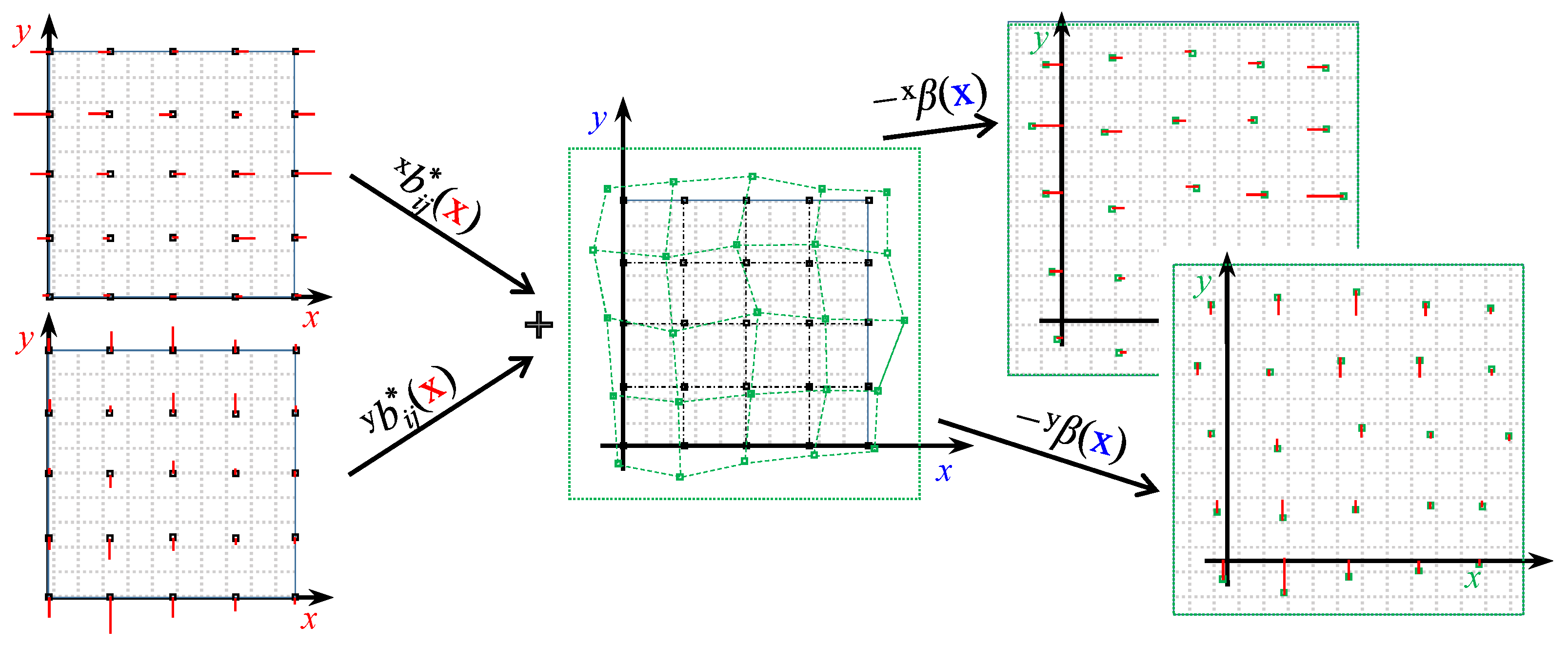
3.1. Proposed Filter Design
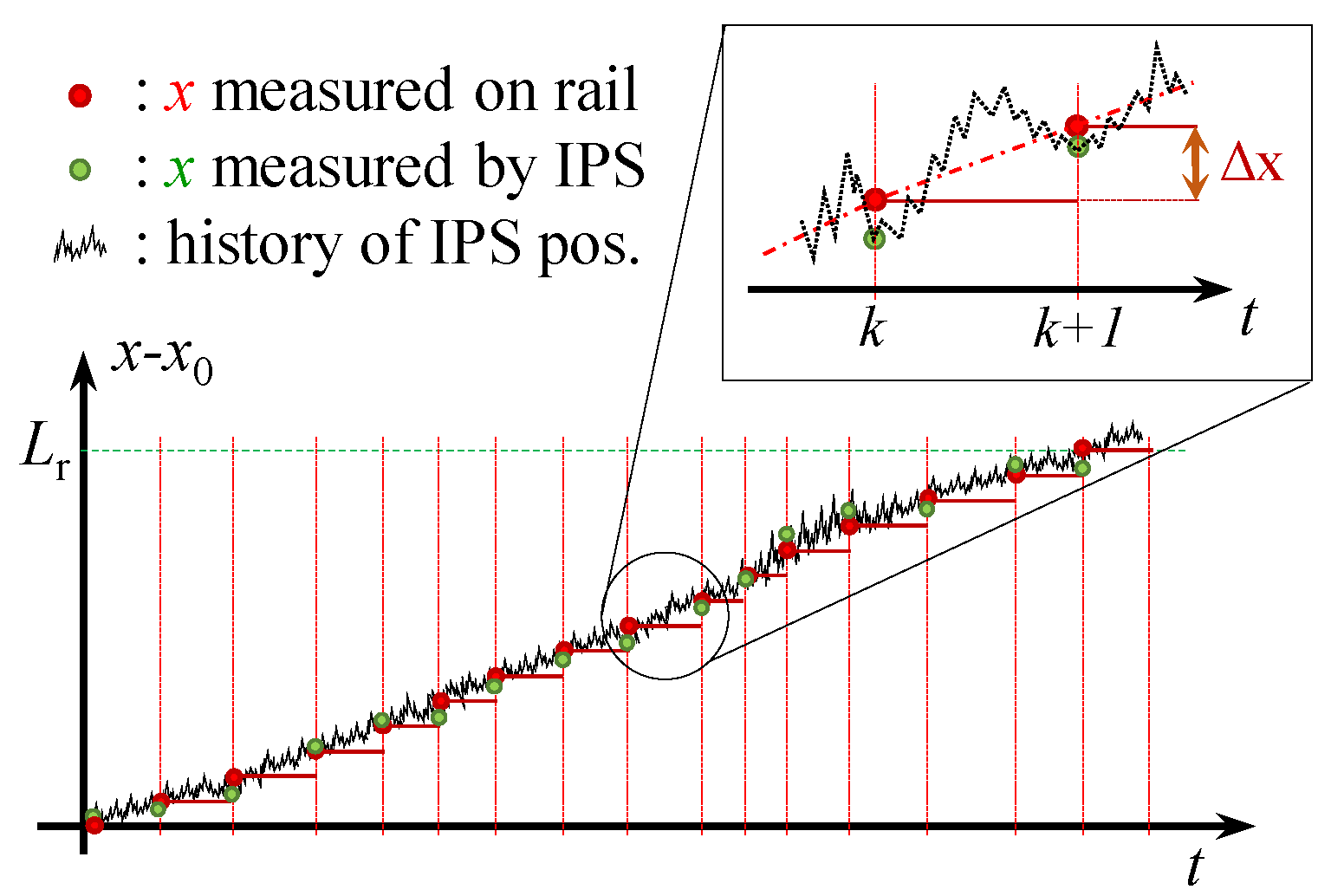
3.2. Debiasing Filter
- 1.
- The bias values are available only at a limited set of points, and therefore they need to be interpolated to cover the continuous domain.
- 2.
- The bias to be subtracted from a measured position to obtain the actual one is a function of the actual position itself.
4. Design of Experiments
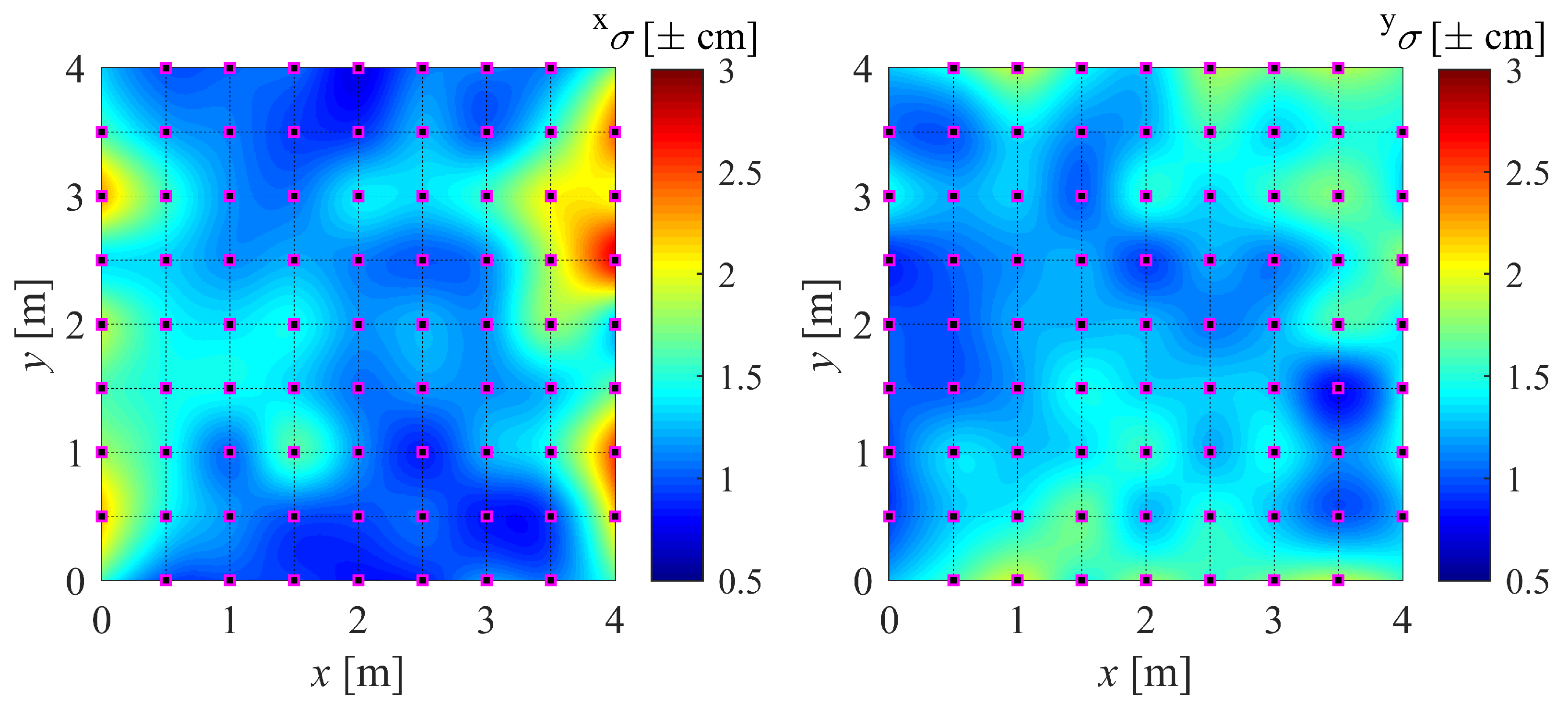
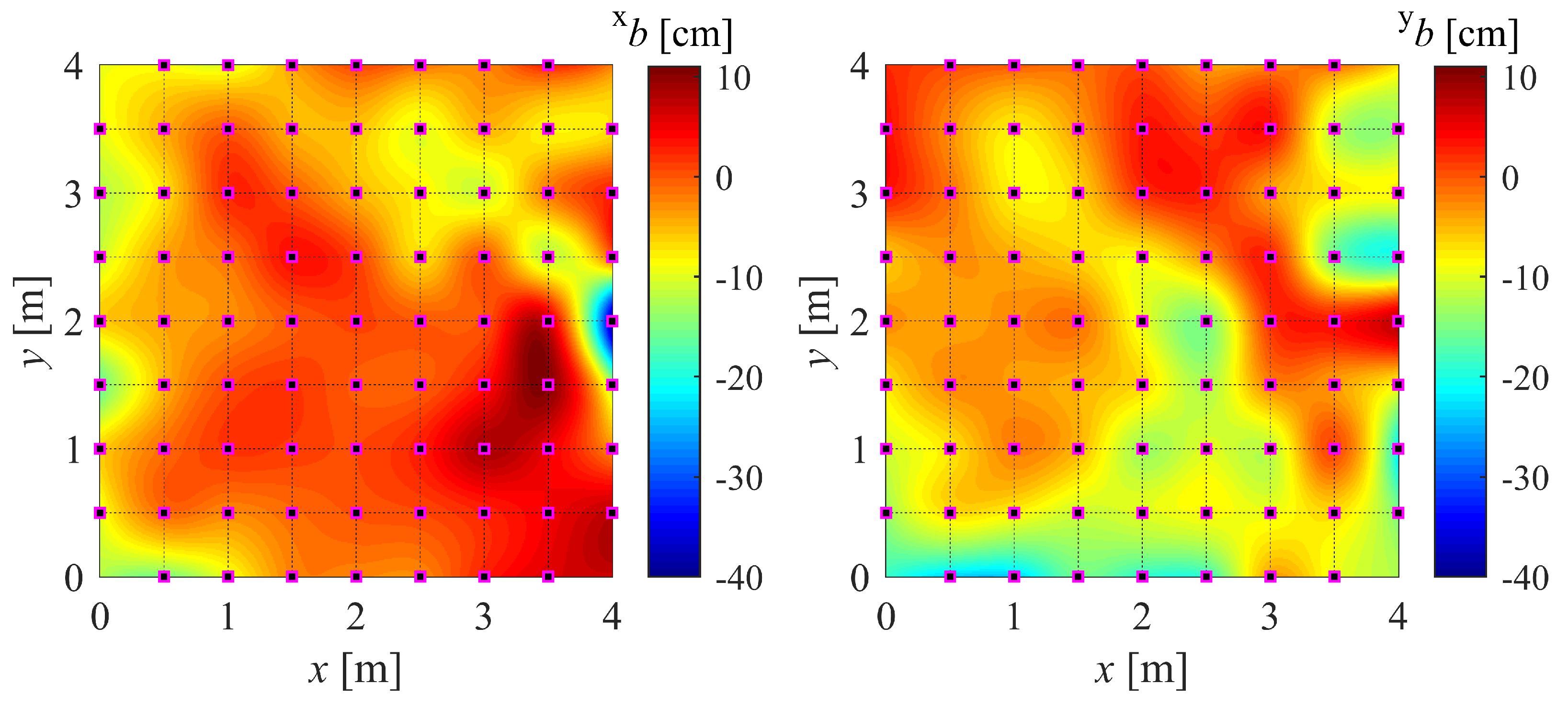
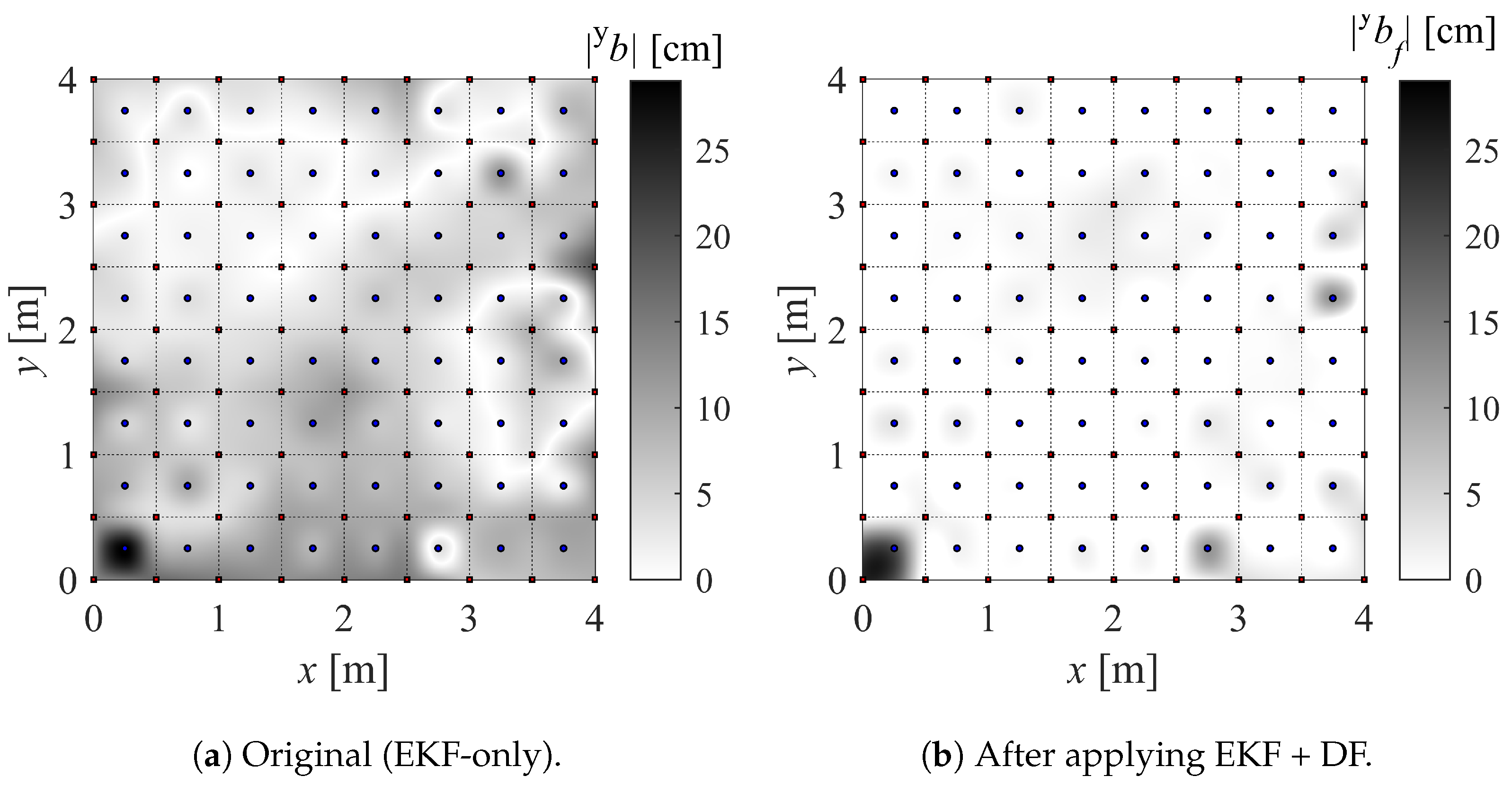
4.1. IPS Bias Map Generation
4.2. DF Calibration and Validation Setup
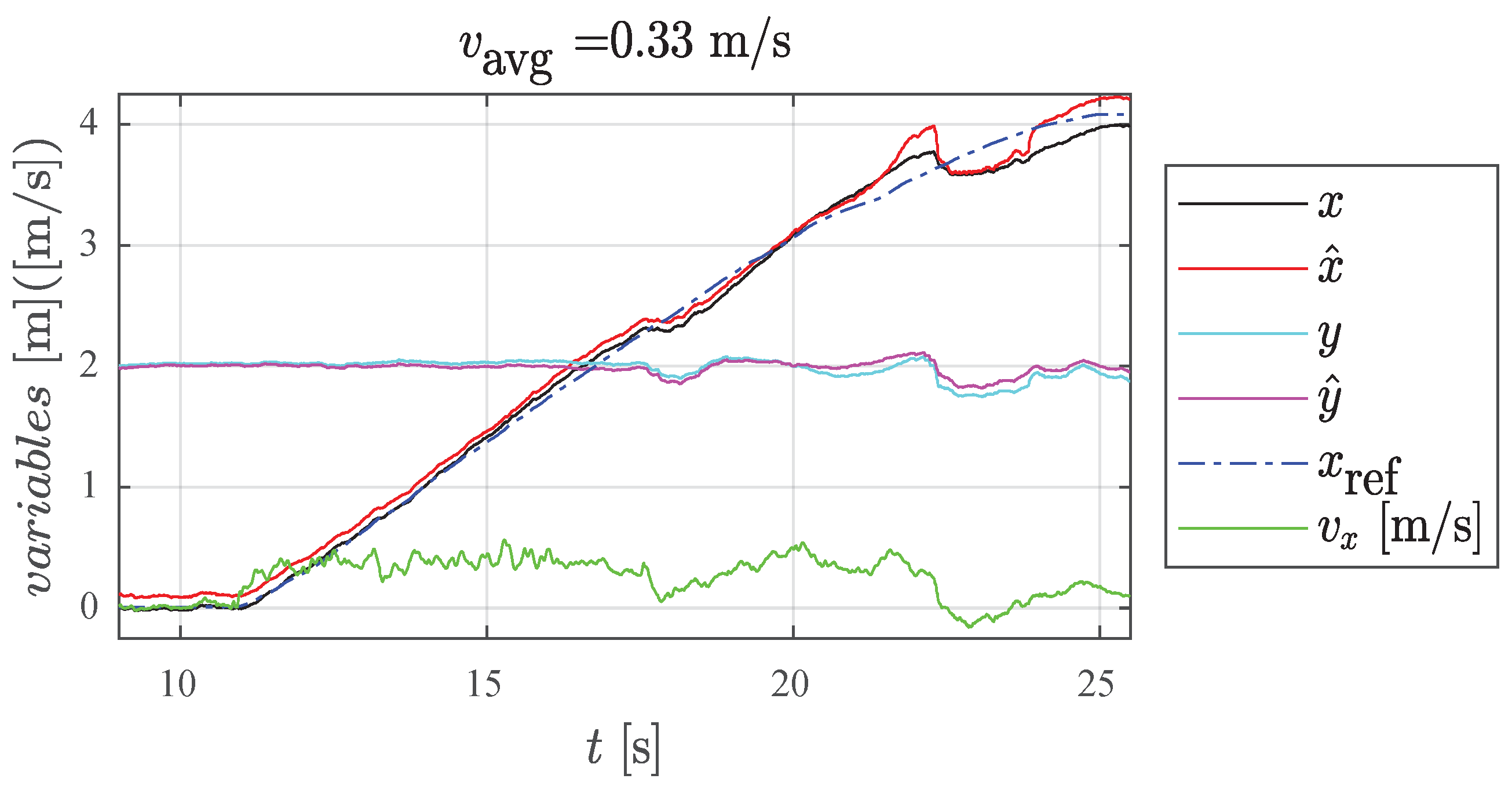
4.3. DF Validation under Dynamic Setup Conditions
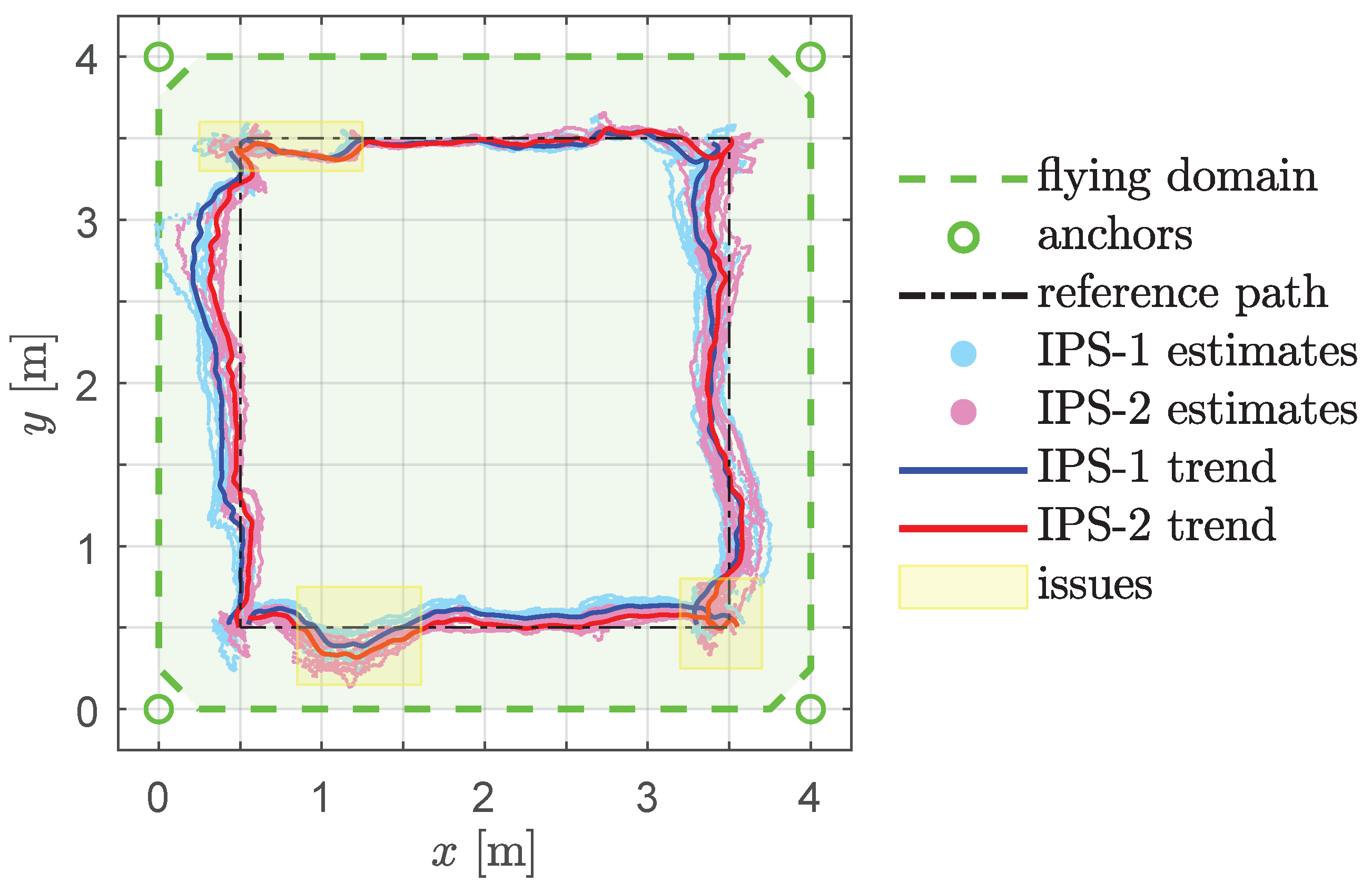
4.4. Square Path Experiment Setup
5. Results and Discussion
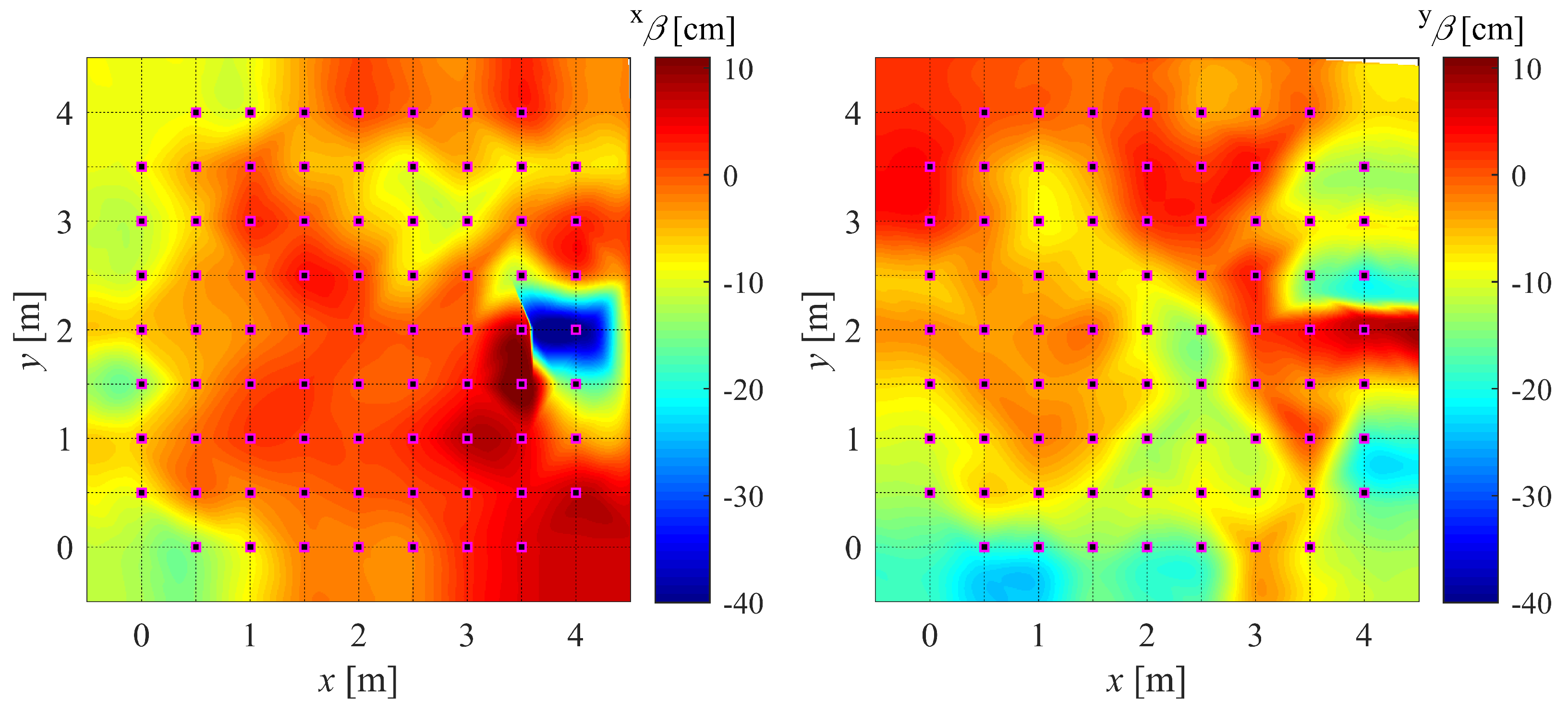
5.1. Proof of Accuracy Improvement
5.2. Dynamic Validation of Debiasing
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| IPS | Indoor Positioning System |
| ToA | Time of Arrival |
| TDoA | Time Difference of Arrival |
| UWB | Ultra-Wideband |
| CRLB | Cramér–Rao Lower Bound |
| GNSS | Global Navigation Satellite System |
| GDoP | Geometric Dilution of Precision |
| CRLB | Cramér–Rao Lower Bound |
| EKF | Extended Kalman Filter |
| DF | Debiasing filter |
Appendix A. Radial Basis Function Network Implementation
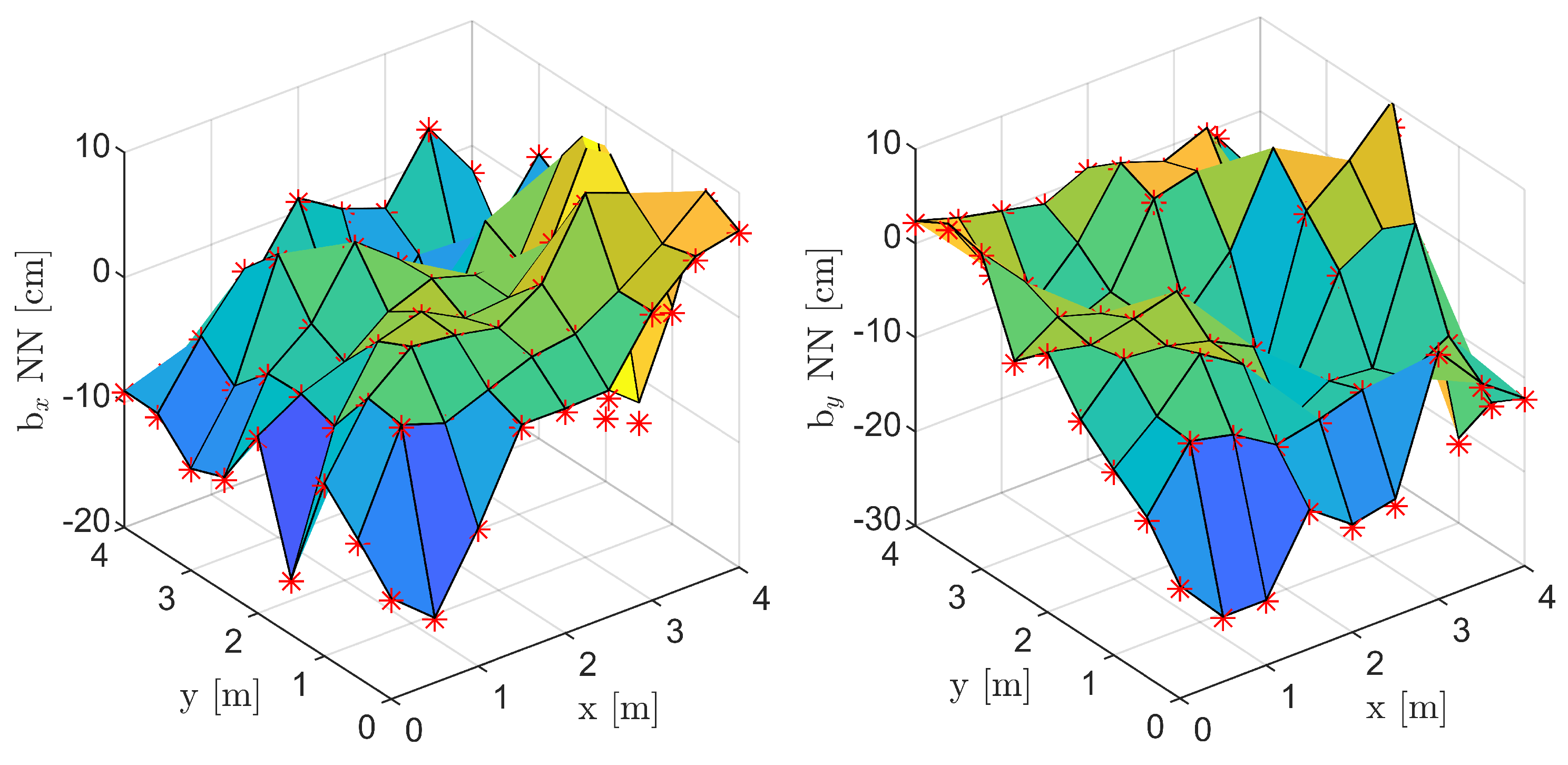

Appendix B. Reference CRLB Analysis
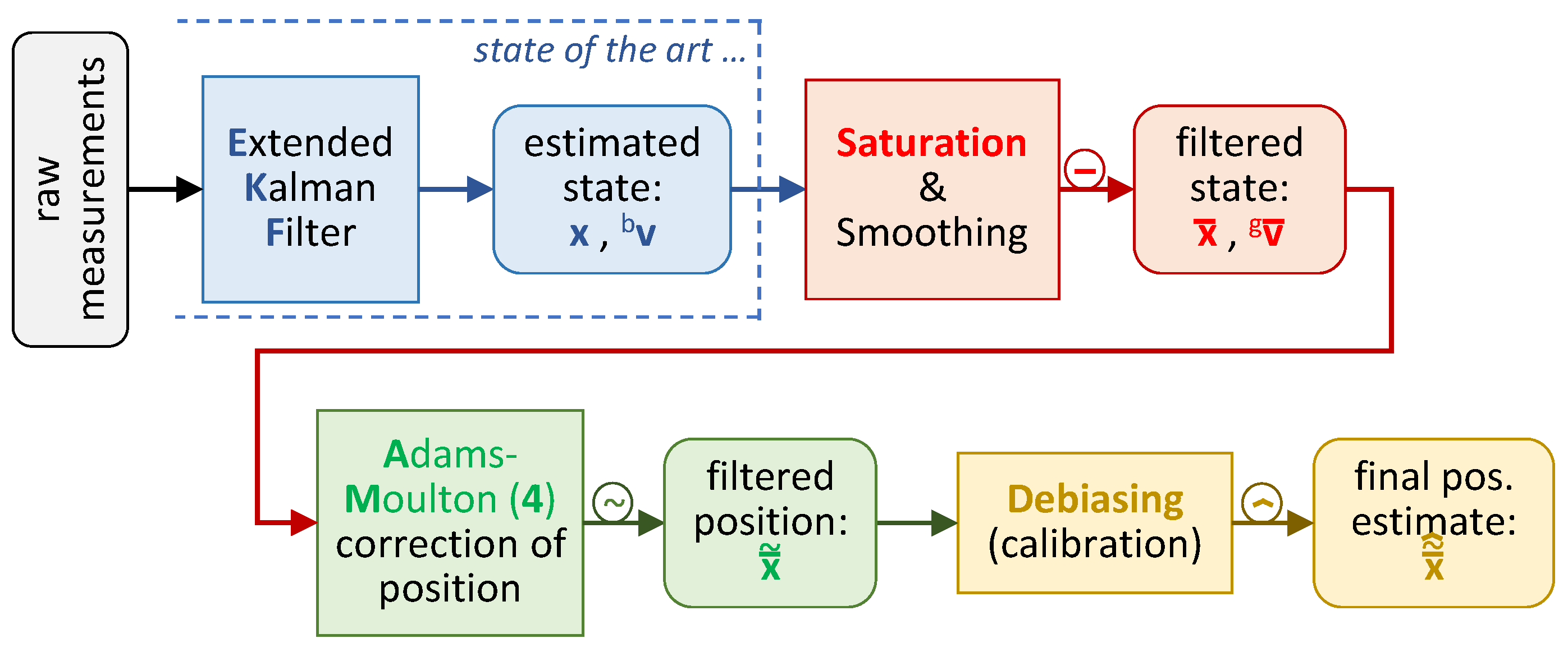
Appendix C. Initial Filter Design
- 1.
- Extended Kalman Filter
- 2.
- Saturation (and artificial smoothing)
- 3.
- Correction of position via fourth-order Adams–Moulton (AM4) method
- 4.
- Debiasing filter
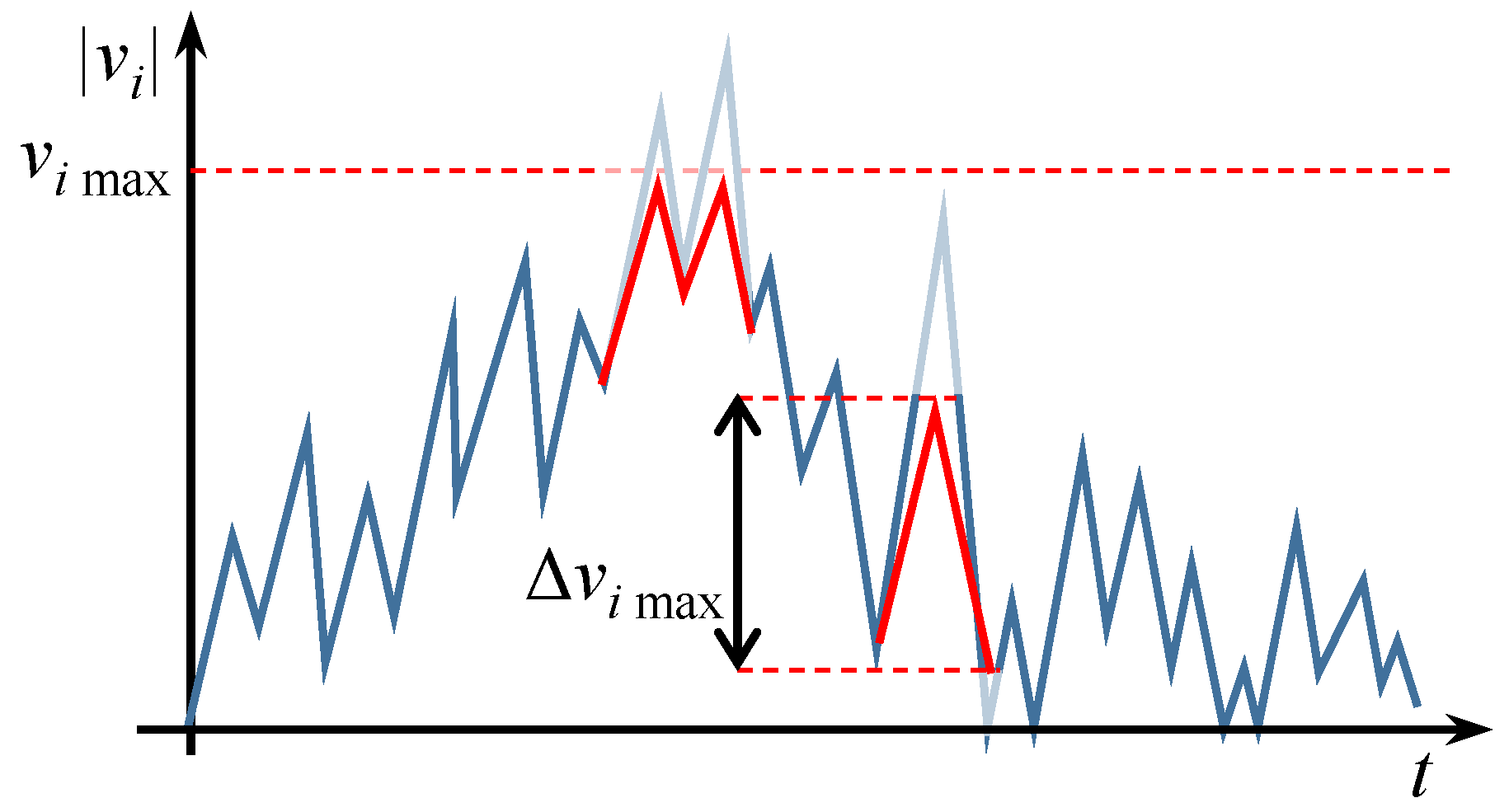
Appendix C.1. Saturation and Smoothing Filter
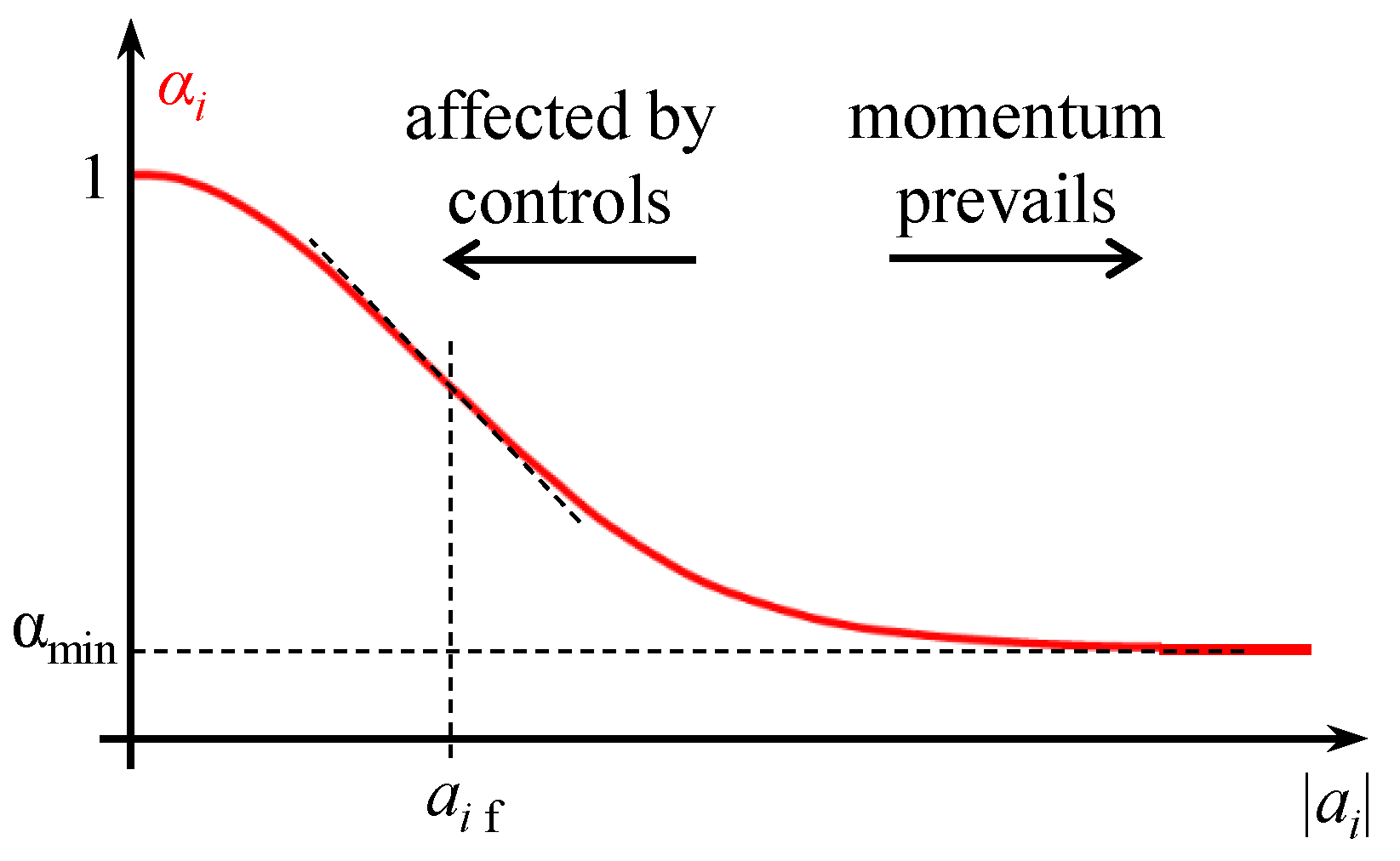
Appendix C.2. Adams–Moulton Filter
References
- Elsanhoury, M.; Makela, P.; Koljonen, J.; Valisuo, P.; Shamsuzzoha, A.; Mantere, T.; Elmusrati, M.; Kuusniemi, H. Precision Positioning for Smart Logistics Using Ultra-Wideband Technology-Based Indoor Navigation: A Review. IEEE Access 2022, 10, 44413–44445. [Google Scholar] [CrossRef]
- Roy, P.; Chowdhury, C. A Survey of Machine Learning Techniques for Indoor Localization and Navigation Systems. J. Intell. Robot. Syst. 2021, 101, 63. [Google Scholar] [CrossRef]
- Chen, D.; Neusypin, K.; Selezneva, M.; Mu, Z. New Algorithms for Autonomous Inertial Navigation Systems Correction with Precession Angle Sensors in Aircrafts. Sensors 2019, 19, 5016. [Google Scholar] [CrossRef] [PubMed]
- Rong, H.; Gao, Y.; Guan, L.; Zhang, Q.; Zhang, F.; Li, N. GAM-Based Mooring Alignment for SINS Based on An Improved CEEMD Denoising Method. Sensors 2019, 19, 3564. [Google Scholar] [CrossRef]
- Widodo, S.; Shiigi, T.; Hayashi, N.; Kikuchi, H.; Yanagida, K.; Nakatsuchi, Y.; Ogawa, Y.; Kondo, N. Moving Object Localization Using Sound-Based Positioning System with Doppler Shift Compensation. Robotics 2013, 2, 36–53. [Google Scholar] [CrossRef]
- Schott, D.J.; Saphala, A.; Fischer, G.; Xiong, W.; Gabbrielli, A.; Bordoy, J.; Höflinger, F.; Fischer, K.; Schindelhauer, C.; Rupitsch, S.J. Comparison of Direct Intersection and Sonogram Methods for Acoustic Indoor Localization of Persons. Sensors 2021, 21, 4465. [Google Scholar] [CrossRef] [PubMed]
- Arbula, D.; Ljubic, S. Indoor Localization Based on Infrared Angle of Arrival Sensor Network. Sensors 2020, 20, 6278. [Google Scholar] [CrossRef]
- Mahmoud, A.A.; Ahmad, Z.U.; Haas, O.C.; Rajbhandari, S. Precision indoor three-dimensional visible light positioning using receiver diversity and multi-layer perceptron neural network. IET Optoelectron. 2020, 14, 440–446. [Google Scholar] [CrossRef]
- Alarifi, A.; Al-Salman, A.; Alsaleh, M.; Alnafessah, A.; Al-Hadhrami, S.; Al-Ammar, M.; Al-Khalifa, H. Ultra Wideband Indoor Positioning Technologies: Analysis and Recent Advances. Sensors 2016, 16, 707. [Google Scholar] [CrossRef] [PubMed]
- Tsang, Y.P.; Wu, C.H.; Ip, W.; Ho, G.; Tse, M. A Bluetooth-based Indoor Positioning System: A Simple and Rapid Approach. Annu. J. IIE 2015, 35, 11–26. [Google Scholar]
- Zhao, X.; Xiao, Z.; Markham, A.; Trigoni, N.; Ren, Y. Does BTLE measure up against WiFi? A comparison of indoor location performance. In Proceedings of the European Wireless 2014; 20th European Wireless Conference, Barcelona, Spain, 14–16 May 2014; pp. 1–6. [Google Scholar]
- Ezhumalai, B.; Song, M.; Park, K. An Efficient Indoor Positioning Method Based on Wi-Fi RSS Fingerprint and Classification Algorithm. Sensors 2021, 21, 3418. [Google Scholar] [CrossRef] [PubMed]
- Abusara, A.; Hassan, M.S.; Ismail, M.H. Reduced-complexity fingerprinting in WLAN-based indoor positioning. Telecommun. Syst. 2016, 65, 407–417. [Google Scholar] [CrossRef]
- Sahota, H.; Kumar, R. Sensor Localization Using Time of Arrival Measurements in a Multi-Media and Multi-Path Application of In-Situ Wireless Soil Sensing. Inventions 2021, 6, 16. [Google Scholar] [CrossRef]
- Sakpere, W.; Oshin, M.A.; Mlitwa, N.B. A State-of-the-Art Survey of Indoor Positioning and Navigation Systems and Technologies. S. Afr. Comput. J. 2017, 29, 145–197. [Google Scholar] [CrossRef]
- Hernandez, L.A.M.; Arteaga, S.P.; Perez, G.S.; Orozco, A.L.S.; Villalba, L.J.G. Outdoor Location of Mobile Devices Using Trilateration Algorithms for Emergency Services. IEEE Access 2019, 7, 52052–52059. [Google Scholar] [CrossRef]
- Mosleh, M.F.; Zaiter, M.J.; Hashim, A.H. Position Estimation Using Trilateration based on ToA/RSS and AoA Measurement. J. Phys. Conf. Ser. 2021, 1773, 012002. [Google Scholar] [CrossRef]
- Neirynck, D.; Luk, E.; McLaughlin, M. An alternative double-sided two-way ranging method. In Proceedings of the 2016 13th Workshop on Positioning, Navigation and Communications (WPNC), Bremen, Germany, 19–20 October 2016. [Google Scholar] [CrossRef]
- Jamil, F.; Iqbal, N.; Ahmad, S.; Kim, D.H. Toward Accurate Position Estimation Using Learning to Prediction Algorithm in Indoor Navigation. Sensors 2020, 20, 4410. [Google Scholar] [CrossRef] [PubMed]
- Mahida, P.; Shahrestani, S.; Cheung, H. Deep Learning-Based Positioning of Visually Impaired People in Indoor Environments. Sensors 2020, 20, 6238. [Google Scholar] [CrossRef] [PubMed]
- Alraih, S.; Alhammadi, A.; Shayea, I.; Al-Samman, A.M. Improving accuracy in indoor localization system using fingerprinting technique. In Proceedings of the 2017 International Conference on Information and Communication Technology Convergence (ICTC), Jeju, Republic of Korea, 18–20 October 2017. [Google Scholar] [CrossRef]
- Alhammadi, A.; Alraih, S.; Hashim, F.; Rasid, M.F.A. Robust 3D Indoor Positioning System Based on Radio Map Using Bayesian Network. In Proceedings of the 2019 IEEE 5th World Forum on Internet of Things (WF-IoT), Limerick, Ireland, 15–18 April 2019. [Google Scholar] [CrossRef]
- Alhammadi, A.; Hashim, F.; Rasid, M.F.A.; Alraih, S. A three-dimensional pattern recognition localization system based on a Bayesian graphical model. Int. J. Distrib. Sens. Netw. 2020, 16, 155014771988489. [Google Scholar] [CrossRef]
- European Union Agency for the Space Programme. Galileo Initial Services. 2021. Available online: https://www.euspa.europa.eu/european-space/galileo/services/initial-services (accessed on 18 August 2021).
- Yeh, S.C.; Hsu, W.H.; Su, M.Y.; Chen, C.H.; Liu, K.H. A study on outdoor positioning technology using GPS and WiFi networks. In Proceedings of the 2009 International Conference on Networking, Sensing and Control, Okayama, Japan, 26–29 March 2009. [Google Scholar] [CrossRef]
- Ghavami, M.; Michael, L.; Kohno, R. Ultra Wideband Signals and Systems in Communication Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Innocente, M.S.; Grasso, P. Self-organising swarms of firefighting drones: Harnessing the power of collective intelligence in decentralised multi-robot systems. J. Comput. Sci. 2019, 34, 80–101. [Google Scholar] [CrossRef]
- Bezas, K.; Tsoumanis, G.; Angelis, C.T.; Oikonomou, K. Coverage Path Planning and Point-of-Interest Detection Using Autonomous Drone Swarms. Sensors 2022, 22, 7551. [Google Scholar] [CrossRef] [PubMed]
- Cramér, H. Mathematical Methods of Statistics (PMS-9); Princeton University Press: Princeton, NJ, USA, 1999; Volume 9. [Google Scholar]
- Chen, C.S.; Chiu, Y.J.; Lee, C.T.; Lin, J.M. Calculation of Weighted Geometric Dilution of Precision. J. Appl. Math. 2013, 2013, 953048. [Google Scholar] [CrossRef]
- Sieskul, B.; Kaiser, T. Cramer-Rao Bound for TOA Estimations in UWB Positioning Systems. In Proceedings of the 2005 IEEE International Conference on Ultra-Wideband, Zurich, Switzerland, 5–8 September 2005. [Google Scholar] [CrossRef]
- Amigo, A.G.; Closas, P.; Mallat, A.; Vandendorpe, L. Cramér-Rao Bound analysis of UWB based Localization Approaches. In Proceedings of the 2014 IEEE International Conference on Ultra-WideBand (ICUWB), Paris, France, 1–3 September 2014. [Google Scholar] [CrossRef]
- Zhang, J.; Kennedy, R.A.; Abhayapala, T.D. Cramér-Rao Lower Bounds for the Synchronization of UWB Signals. EURASIP J. Adv. Signal Process. 2005, 2005, 293649. [Google Scholar] [CrossRef][Green Version]
- Alhakim, R.; Raoof, K.; Simeu, E.; Serrestou, Y. Cramer–Rao lower bounds and maximum likelihood timing synchronization for dirty template UWB communications. Signal Image Video Process. 2011, 7, 741–757. [Google Scholar] [CrossRef]
- D’Amico, A.A.; Mengali, U.; Taponecco, L. Cramer-Rao Bound for Clock Drift in UWB Ranging Systems. IEEE Wirel. Commun. Lett. 2013, 2, 591–594. [Google Scholar] [CrossRef]
- Mallat, A.; Louveaux, J.; Vandendorpe, L. UWB based positioning: Cramer Rao bound for Angle of Arrival and comparison with Time of Arrival. In Proceedings of the 2006 Symposium on Communications and Vehicular Technology, Liege, Belgium, 23 November 2006. [Google Scholar] [CrossRef]
- Silva, B.; Pang, Z.; Akerberg, J.; Neander, J.; Hancke, G. Experimental study of UWB-based high precision localization for industrial applications. In Proceedings of the 2014 IEEE International Conference on Ultra-WideBand (ICUWB), Paris, France, 1–3 September 2014. [Google Scholar] [CrossRef]
- Grasso, P.; Innocente, M.S. Theoretical study of signal and geometrical properties of Two-dimensional UWB-based Indoor Positioning Systems using TDoA. In Proceedings of the 2020 6th International Conference on Mechatronics and Robotics Engineering (ICMRE), Barcelona, Spain, 12–15 February 2020. [Google Scholar] [CrossRef]
- Compagnoni, M.; Notari, R.; Antonacci, F.; Sarti, A. A comprehensive analysis of the geometry of TDOA maps in localization problems. Inverse Probl. 2014, 30, 035004. [Google Scholar] [CrossRef]
- Dulman, S.O.; Baggio, A.; Havinga, P.J.; Langendoen, K.G. A geometrical perspective on localization. In Proceedings of the First ACM International Workshop on Mobile Entity Localization and Tracking in GPS-Less Environments—MELT ’08, San Francisco, CA, USA, 19 September 2008. [Google Scholar] [CrossRef]
- Park, K.; Kang, J.; Arjmandi, Z.; Shahbazi, M.; Sohn, G. Multilateration under Flip Ambiguity for UAV Positioning Using Ultrawide-Band. ISPRS Ann. Photogramm. Remote. Sens. Spat. Inf. Sci. 2020, V-1-2020, 317–323. [Google Scholar] [CrossRef]
- Li, Y.L.; Shao, W.; You, L.; Wang, B.Z. An Improved PSO Algorithm and Its Application to UWB Antenna Design. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 1236–1239. [Google Scholar] [CrossRef]
- Lim, K.S.; Nagalingam, M.; Tan, C.P. Design and construction of microstrip UWB antenna with time domain analysis. Prog. Electromagn. Res. M 2008, 3, 153–164. [Google Scholar] [CrossRef]
- Chahat, N.; Zhadobov, M.; Sauleau, R.; Ito, K. A Compact UWB Antenna for On-Body Applications. IEEE Trans. Antennas Propag. 2011, 59, 1123–1131. [Google Scholar] [CrossRef]
- Chen, Z.N. UWB antennas: Design and application. In Proceedings of the 2007 6th International Conference on Information, Communications & Signal Processing, Singapore, 10–13 December 2007. [Google Scholar] [CrossRef]
- Compagnoni, M.; Pini, A.; Canclini, A.; Bestagini, P.; Antonacci, F.; Tubaro, S.; Sarti, A. A Geometrical–Statistical Approach to Outlier Removal for TDOA Measurements. IEEE Trans. Signal Process. 2017, 65, 3960–3975. [Google Scholar] [CrossRef]
- Compagnoni, M.; Notari, R. TDOA-based Localization in Two Dimensions: The Bifurcation Curve. Fundam. Inform. 2014, 135, 199–210. [Google Scholar] [CrossRef]
- Kaune, R.; Horst, J.; Koch, W. Accuracy Analysis for TDOA Localization in Sensor Networks. In Proceedings of the 14th International Conference on Information Fusion, Chicago, IL, USA, 5–8 July 2011. [Google Scholar]
- Kaune, R. Accuracy studies for TDOA and TOA localization. In Proceedings of the 2012 15th International Conference on Information Fusion, Singapore, 9–12 July 2012; pp. 408–415. [Google Scholar]
- Grasso, P.; Innocente, M.S. Debiasing of position estimations of UWB-based TDoA indoor positioning system. In Proceedings of the UKRAS20 Conference: “Robots into the Real World” Proceedings, Lincoln, UK, 14–17 April 2020. [Google Scholar] [CrossRef]
- Bitcraze. Loco Positioning System: TDOA Principles. 2020. Available online: http://www.bitcraze.io/documentation/repository/lps-node-firmware/2020.09/functional-areas/tdoa_principles/ (accessed on 18 August 2021).
- Kay, S.M. Fundamentals of Statistical Processing; Prentice Hall: Hoboken, NJ, USA, 1993; Volume I. [Google Scholar]
- Bitcraze. Loco Positioning System: TDOA2 vs. TDOA3. 2020. Available online: http://www.bitcraze.io/documentation/repository/lps-node-firmware/2020.09/functional-areas/tdoa2-vs-tdoa3/ (accessed on 18 August 2021).
- DW1000 IEEE802.15.4-2011 UWB Transceiver—Datasheet v2.09. 2015.
- DWM1000 IEEE 802.15.4-2011 UWB Transceiver Module—Datasheet v1.3. 2015.
- Bitcraze. Getting Started with the Loco Positioning System. 2022. Available online: https://www.bitcraze.io/documentation/tutorials/getting-started-with-loco-positioning-system/ (accessed on 14 November 2022).
- Mueller, M.W.; Hamer, M.; D’Andrea, R. Fusing ultra-wideband range measurements with accelerometers and rate gyroscopes for quadrocopter state estimation. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015. [Google Scholar] [CrossRef]
- Mueller, M.W.; Hehn, M.; D’Andrea, R. Covariance Correction Step for Kalman Filtering with an Attitude. J. Guid. Control. Dyn. 2017, 40, 2301–2306. [Google Scholar] [CrossRef]


| RMSEx,avg [cm] | RMSEy,avg [cm] | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| dir. | [m] | y[m] | IPS-1 | IPS-2 | IPS-1 | IPS-2 | |||
| hor. | [0, 4] | 1 | 12.7 | 6.8 | 5.9 | 10.0 | 7.9 | 2.1 | 0.58 |
| hor. | [0, 4] | 2 | 12.0 | 8.1 | 3.9 | 6.7 | 4.3 | 2.4 | 0.44 |
| hor. | [0, 4] | 3 | 12.6 | 8.0 | 4.6 | 9.3 | 8.0 | 1.3 | 0.43 |
| ver. | 1 | [4, 0] | 15.6 | 10.3 | 5.4 | 9.4 | 6.8 | 2.7 | 0.58 |
| ver. | 2 | [4, 0] | 10.3 | 8.0 | 2.3 | 15.8 | 10.1 | 5.7 | 0.51 |
| ver. | 3 | [4, 0] | 11.4 | 9.4 | 2.0 | 15.3 | 12.2 | 3.1 | 0.42 |
| RMSEIPS-1 [cm] | RMSEIPS-2 [cm] | |||||||
|---|---|---|---|---|---|---|---|---|
| Edge | dir. | x[m] | y[m] | Raw | sel. | Raw | sel. | [cm] |
| bot | hor. | [0.5, 3.5] | 0.5 | 9.2 | 9.5 | 7.5 | 4.7 | 4.8 |
| right | ver. | 3.5 | [0.5, 3.5] | 12.6 | 12.5 | 9.0 | 8.3 | 4.2 |
| top | hor. | [3.5, 0.5] | 3.5 | 6.0 | 5.5 | 5.7 | 4.6 | 0.9 |
| left | ver. | 0.5 | [3.5, 0.5] | 15.8 | 15.2 | 8.8 | 6.7 | 8.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grasso, P.; Innocente, M.S.; Tai, J.J.; Haas, O.; Dizqah, A.M. Analysis and Accuracy Improvement of UWB-TDoA-Based Indoor Positioning System. Sensors 2022, 22, 9136. https://doi.org/10.3390/s22239136
Grasso P, Innocente MS, Tai JJ, Haas O, Dizqah AM. Analysis and Accuracy Improvement of UWB-TDoA-Based Indoor Positioning System. Sensors. 2022; 22(23):9136. https://doi.org/10.3390/s22239136
Chicago/Turabian StyleGrasso, Paolo, Mauro S. Innocente, Jun Jet Tai, Olivier Haas, and Arash M. Dizqah. 2022. "Analysis and Accuracy Improvement of UWB-TDoA-Based Indoor Positioning System" Sensors 22, no. 23: 9136. https://doi.org/10.3390/s22239136
APA StyleGrasso, P., Innocente, M. S., Tai, J. J., Haas, O., & Dizqah, A. M. (2022). Analysis and Accuracy Improvement of UWB-TDoA-Based Indoor Positioning System. Sensors, 22(23), 9136. https://doi.org/10.3390/s22239136








