Optimal Greedy Control in Reinforcement Learning
Abstract
:1. Introduction and Related Works
2. Theoretical Description
3. Case Studies
3.1. Inverted Double Pendulum
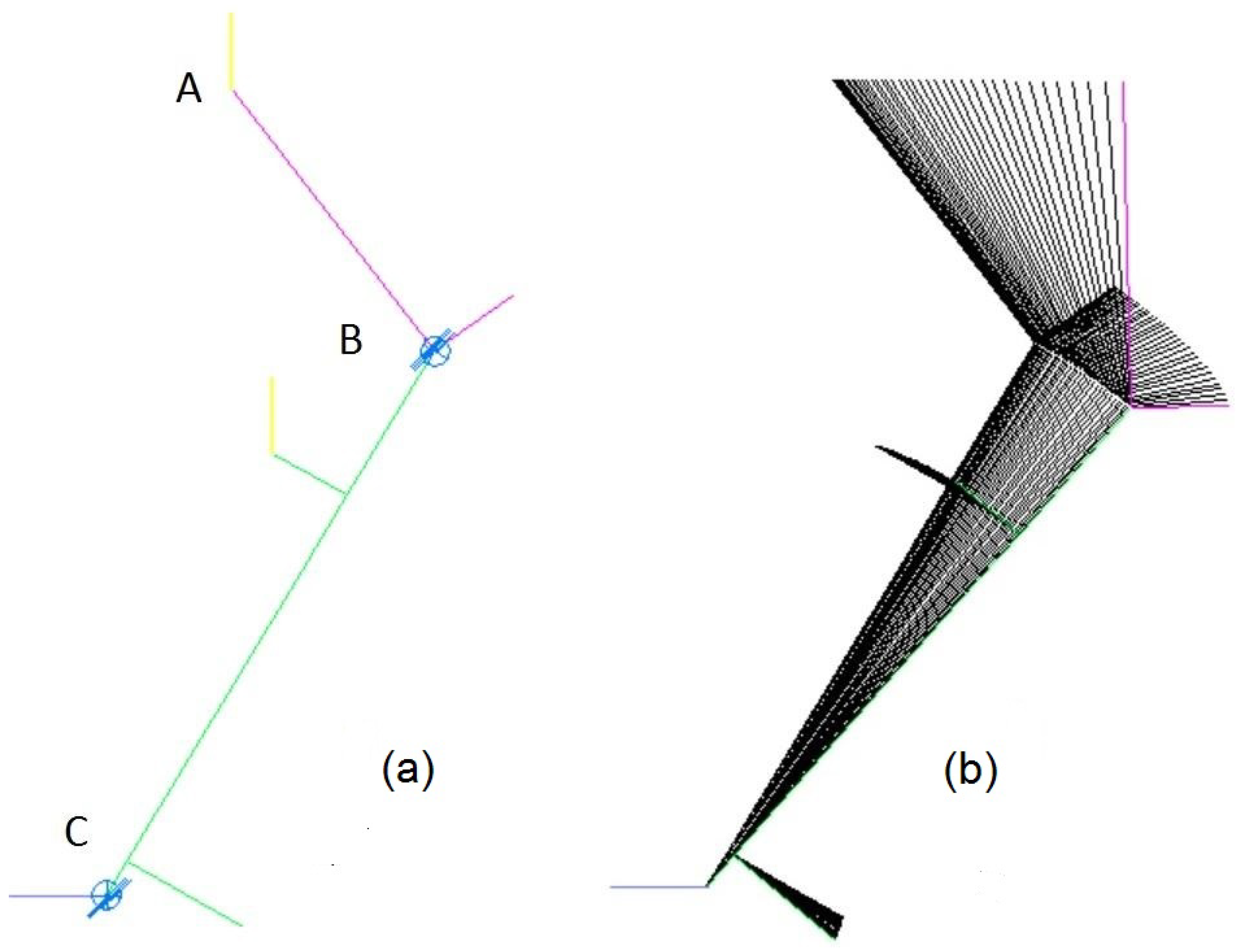
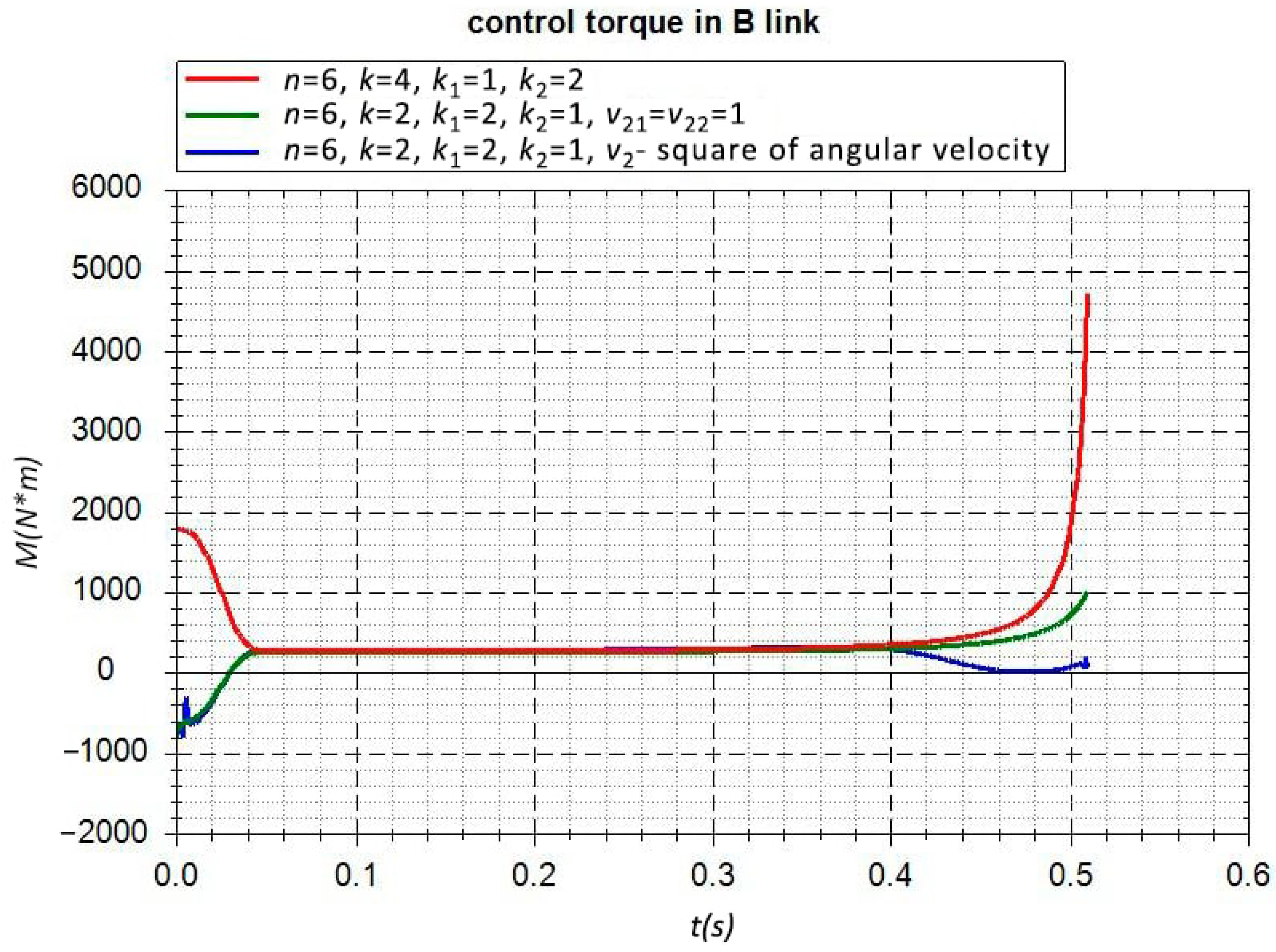
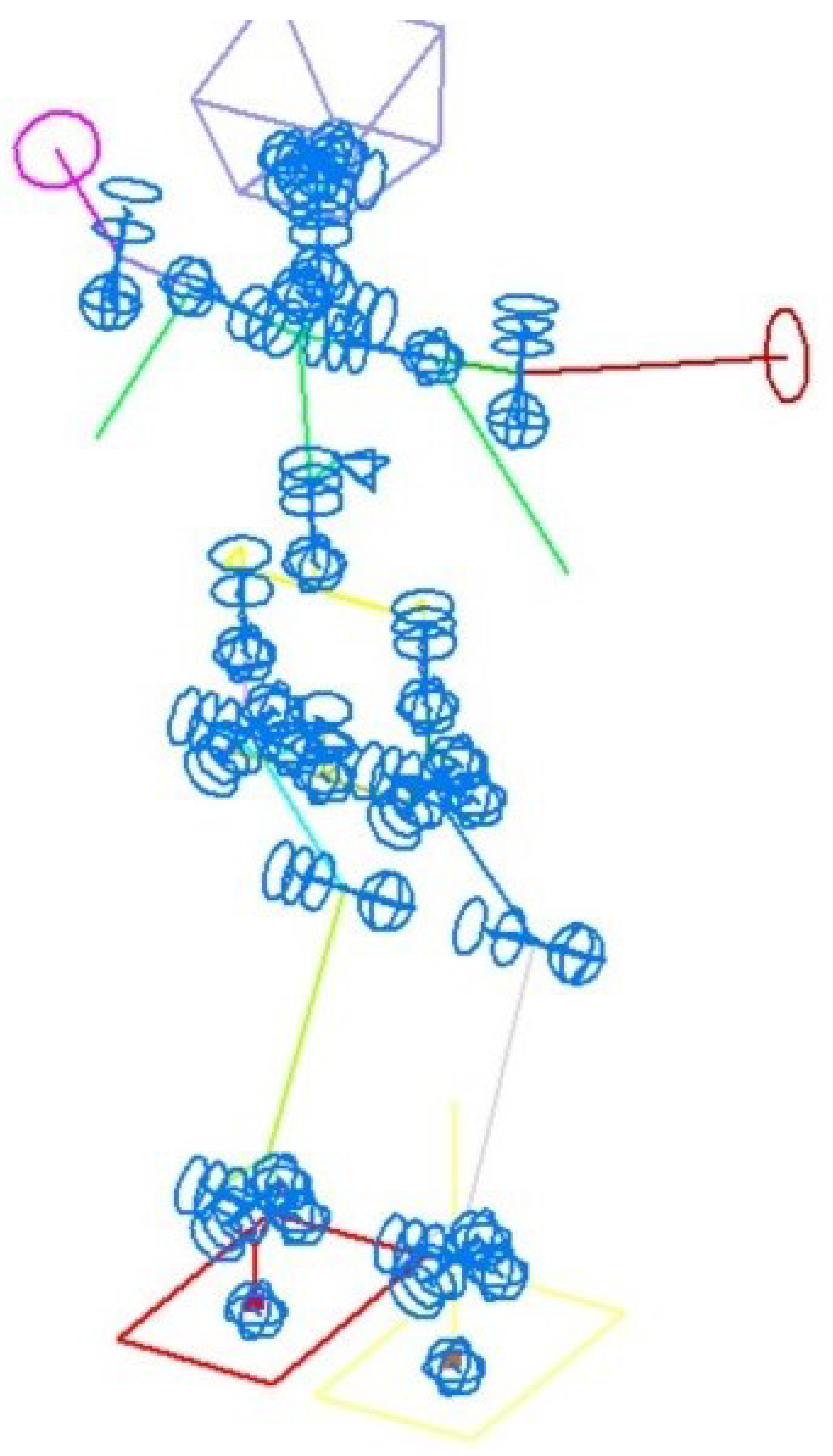
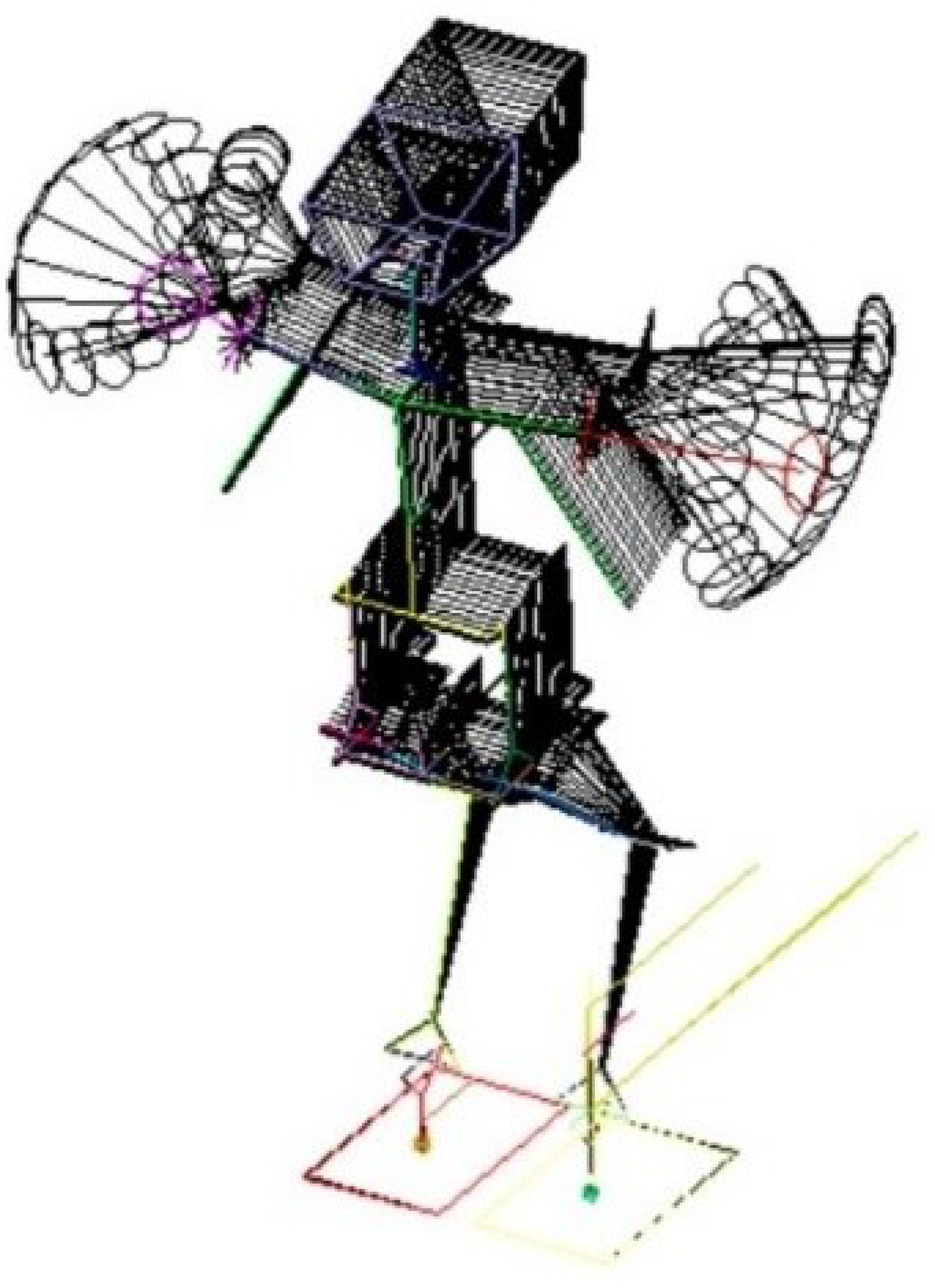
3.2. Spatial Model of Android
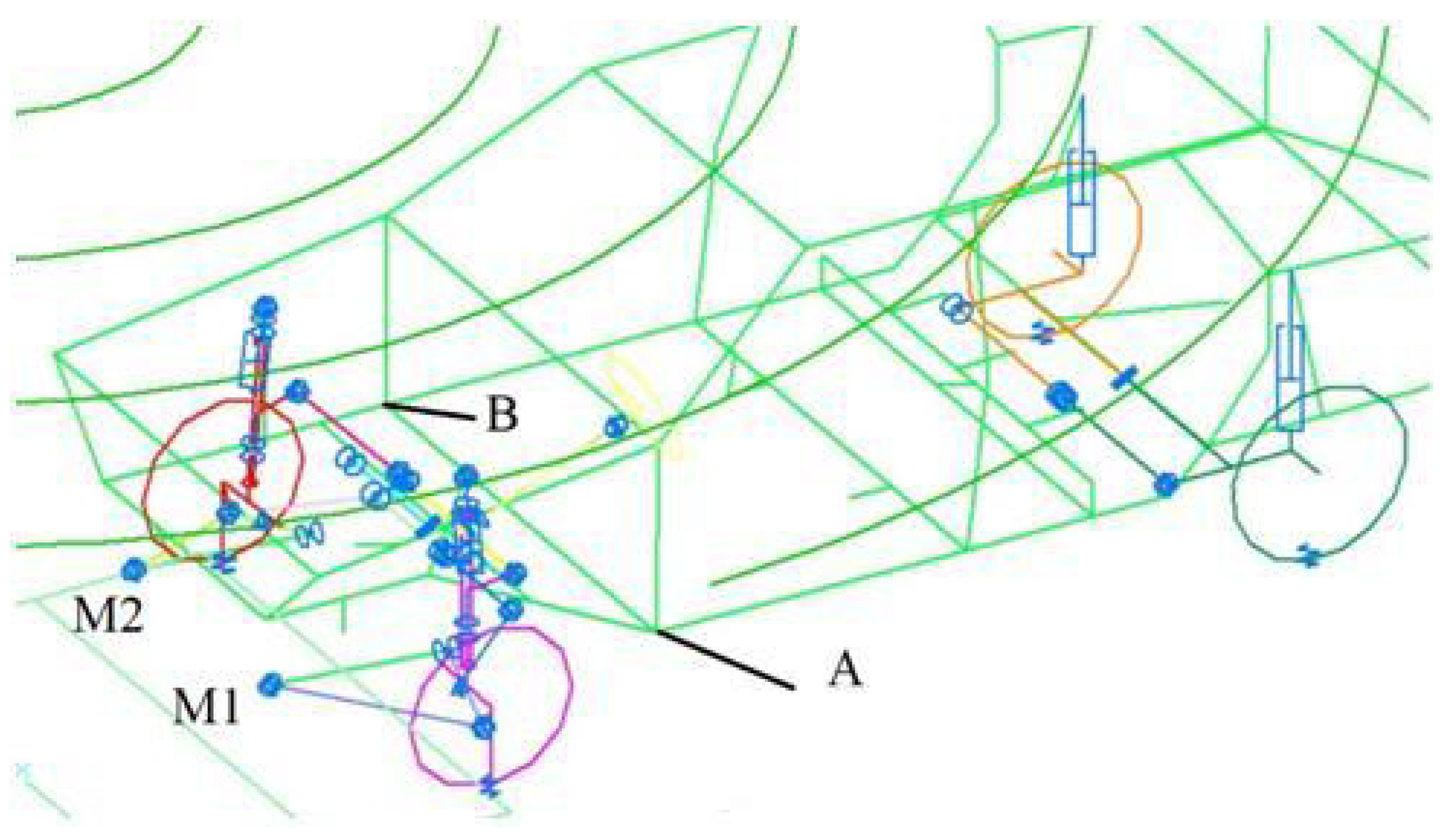
3.3. Optimal Control Problems in the Example of Car Vibrations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DAE | differential-algebraic equations |
| MBS | multibody system |
| KKT | Karush–Kuhn–Tucker method |
References
- Bellman, R. Dynamic Programming; Princeton Landmarks in Mathematics and Physics; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Pontryagin, L. Mathematical Theory of Optimal Processes; Classics of Soviet Mathematics; Taylor & Francis: Abingdon, England, 1987. [Google Scholar]
- Heess, N.; Dhruva, T.; Sriram, S.; Lemmon, J.; Merel, J.; Wayne, G.; Tassa, Y.; Erez, T.; Wang, Z.; Eslami, S.M.A.; et al. Emergence of Locomotion Behaviours in Rich Environments. arXiv 2017, arXiv:1707.02286. [Google Scholar]
- Tassa, Y.; Erez, T.; Todorov, E. Synthesis and stabilization of complex behaviors through online trajectory optimization. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, IROS 2012, Vilamoura, Algarve, Portugal, 7–12 October 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 4906–4913. [Google Scholar] [CrossRef]
- Schulman, J.; Moritz, P.; Levine, S.; Jordan, M.I.; Abbeel, P. High-Dimensional Continuous Control Using Generalized Advantage Estimation. In Proceedings of the 4th International Conference on Learning Representations, ICLR 2016, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Schulman, J.; Levine, S.; Moritz, P.; Jordan, M.I.; Abbeel, P. Trust Region Policy Optimization. arXiv 2015, arXiv:1502.05477. [Google Scholar]
- Duan, Y.; Chen, X.; Houthooft, R.; Schulman, J.; Abbeel, P. Benchmarking Deep Reinforcement Learning for Continuous Control. In JMLR Workshop and Conference Proceedings, Proceedings of the 33nd International Conference on Machine Learning, ICML 2016, New York, NY, USA, 19–24 June 2016; JMLR.org, Balcan, M., Weinberger, K.Q., Eds.; Microtome Publishing: Brookline, MA, USA, 2016; Volume 48, pp. 1329–1338. [Google Scholar]
- Tulshyan, R.; Arora, R.; Deb, K.; Dutta, J. Investigating EA solutions for approximate KKT conditions in smooth problems. In Proceedings of the Genetic and Evolutionary Computation Conference, GECCO 2010, Portland, OR, USA, 7–11 July 2010; Pelikan, M., Branke, J., Eds.; ACM: New York, NY, USA, 2010; pp. 689–696. [Google Scholar] [CrossRef]
- Fu, J.; Li, C.; Teng, X.; Luo, F.; Li, B. Compound Heuristic Information Guided Policy Improvement for Robot Motor Skill Acquisition. Appl. Sci. 2020, 10, 5346. [Google Scholar] [CrossRef]
- Cho, N.J.; Lee, S.H.; Kim, J.B.; Suh, I.H. Learning, Improving, and Generalizing Motor Skills for the Peg-in-Hole Tasks Based on Imitation Learning and Self-Learning. Appl. Sci. 2020, 10, 2719. [Google Scholar] [CrossRef] [Green Version]
- Peters, J.; Schaal, S. Reinforcement learning of motor skills with policy gradients. Neural Netw. 2008, 21, 682–697. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wen, G.; Ge, S.S.; Chen, C.L.P.; Tu, F.; Wang, S. Adaptive Tracking Control of Surface Vessel Using Optimized Backstepping Technique. IEEE Trans. Cybern. 2019, 49, 3420–3431. [Google Scholar] [CrossRef] [PubMed]
- Tu Vu, V.; Pham, T.L.; Dao, P.N. Disturbance observer-based adaptive reinforcement learning for perturbed uncertain surface vessels. ISA Trans. 2022, 130, 277–292. [Google Scholar] [CrossRef] [PubMed]
- Sutton, R.; Barto, A.G. Reinforcement Learning; MIT Press: Cambidge, MA, USA, 2020; p. 547. [Google Scholar]
- Gorobtsov, A.S.; Karcov, S.K.; Pletnev, A.E.; Polyakov, Y.A. Komp’yuternye Metody Postroeniya i Issledovaniya Matematicheskih Modelej Dinamiki Konstrukcij Avtomobilej; Nauchno-Tekhnicheskoe Izdatel’stvo “Mashinostroenie”: Moscow, Russia, 2011; p. 462. (In Russian) [Google Scholar]
- Pogorelov, D. Differential–algebraic equations in multibody system modeling. newblock Numerical Algorithms 1998, 19, 183–194. [Google Scholar] [CrossRef]
- Wittenburg, J. Dynamics of Systems of Rigid Bodies; Leitfäden der Angewandten Mathematik und Mechanik; Vieweg+Teubner Verlag: Wiesbaden, Germany, 1977. [Google Scholar]
- Gorobtsov, A.S.; Skorikov, A.V.; Tarasov, P.S.; Markov, A.; Dianskij, A. Metod sinteza programmnogo dvizheniya robotov s uchetom zadannyh ogranichenij reakcij v svyazyah. In Proceedings of the XIII Vserosijskaia Nauchno Tekhnicheskaia Konferencia s Mezhdunarodnym Uchastiem “Robototekhnika i Iskusstvennyj Intellekt”, Krasnoyarsk, Russia, 27 November 2021; pp. 199–203. (In Russian). [Google Scholar]
- Mamedov, S.; Khusainov, R.; Gusev, S.; Klimchik, A.; Maloletov, A.; Shiriaev, A. Underactuated mechanical systems: Whether orbital stabilization is an adequate assignment for a controller design? IFAC-PapersOnLine 2020, 53, 9262–9269. [Google Scholar] [CrossRef]
- FRUND—A System for Solving Non-Linear Dynamic Equations. Available online: http://frund.vstu.ru/ (accessed on 24 October 2022).
- Raibert, M.H. Legged Robots. Commun. ACM 1986, 29, 499–514. [Google Scholar] [CrossRef]
- Kim, J.Y.; Park, I.W.; Oh, J.H. Experimental realization of dynamic walking of the biped humanoid robot KHR-2 using zero moment point feedback and inertial measurement. Adv. Robot. 2006, 20, 707–736. [Google Scholar] [CrossRef] [Green Version]
- Gorobtsov, A.; Andreev, A.; Markov, A.; Skorikov, A.; Tarasov, P. Features of solving the inverse dynamic method equations for the synthesis of stable walking robots controlled motion. Inform. Autom. 2019, 18, 85–122. (In Russian) [Google Scholar] [CrossRef]
- Englsberger, J.; Werner, A.; Ott, C.; Henze, B.; Roa, M.A.; Garofalo, G.; Burger, R.; Beyer, A.; Eiberger, O.; Schmid, K.; et al. Overview of the torque-controlled humanoid robot TORO. In Proceedings of the 14th IEEE-RAS International Conference on Humanoid Robots, Humanoids 2014, Madrid, Spain, 18–20 November 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 916–923. [Google Scholar] [CrossRef] [Green Version]
- Englsberger, J.; Ott, C.; Albu-Schäffer, A. Three-dimensional bipedal walking control using Divergent Component of Motion. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 2600–2607. [Google Scholar] [CrossRef] [Green Version]
- Pratt, J.E.; Carff, J.; Drakunov, S.V.; Goswami, A. Capture Point: A Step toward Humanoid Push Recovery. In Proceedings of the 2006 6th IEEE-RAS International Conference on Humanoid Robots, Genova, Italy, 4–6 December 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 200–207. [Google Scholar] [CrossRef] [Green Version]
- Englsberger, J.; Koolen, T.; Bertrand, S.; Pratt, J.E.; Ott, C.; Albu-Schäffer, A. Trajectory generation for continuous leg forces during double support and heel-to-toe shift based on divergent component of motion. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 4022–4029. [Google Scholar] [CrossRef] [Green Version]
- Khusainov, R.; Klimchik, A.; Magid, E. Swing Leg Trajectory Optimization for a Humanoid Robot Locomotion. In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016), Lisbon, Portugal, 29–31 July 2016; Gusikhin, O., Peaucelle, D., Madani, K., Eds.; SciTePress: Setúbal, Portugal, 2016; Volume 2, pp. 130–141. [Google Scholar] [CrossRef]
- Khusainov, R.; Shimchik, I.; Afanasyev, I.; Magid, E. Toward a Human-like Locomotion: Modelling Dynamically Stable Locomotion of an Anthropomorphic Robot in Simulink Environment. In Proceedings of the ICINCO 2015—12th International Conference on Informatics in Control, Automation and Robotics, Colmar, Alsace, France, 21–23 July 2015; Filipe, J., Madani, K., Gusikhin, O.Y., Sasiadek, J.Z., Eds.; SciTePress: Setúbal, Portugal, 2015; Volume 2, pp. 141–148. [Google Scholar] [CrossRef]
- Khusainov, R.; Afanasyev, I.; Sabirova, L.; Magid, E. Bipedal robot locomotion modelling with virtual height inverted pendulum and preview control approaches in Simulink environment. J. Robot. Netw. Artif. Life 2016, 3, 182–187. [Google Scholar] [CrossRef] [Green Version]
- Khusainov, R.; Afanasyev, I.; Magid, E. Anthropomorphic robot modelling with virtual height inverted pendulum approach in Simulink: Step length and robot height influence on walking stability. In Proceedings of the ICAROB 2016—International Conference on Artificial Life and Robotics, Okinawa Convention Center, Ginowan, Japan, 29 January 2016; Volume 21, pp. 208–211. [Google Scholar] [CrossRef]
- Liu, C.; Wang, D.; Chen, Q. Central Pattern Generator Inspired Control for Adaptive Walking of Biped Robots. IEEE Trans. Syst. Man Cybern. Syst. 2013, 43, 1206–1215. [Google Scholar] [CrossRef]
- Glazunov, V. Mekhanizmy Parallel’noj Struktury i ih Primenenie: Robototekhnicheskie, Tekhnologicheskie. Medicinskie, Obuchayushchie Sistemy; Izhevskij Institut Komp’yuternyh Issledovanij: Izhevsk, Russia, 2018. (In Russian) [Google Scholar]
- Ganiev, R.F.; Glazunov, V.A. Manipulyacionnye mekhanizmy parallel’noj struktury i ih prilozheniya v sovremennoj tekhnike. Dokl. Akad. Nauk. 2014, 459, 428. (In Russian) [Google Scholar] [CrossRef]
- Glazunov, V.A. Mekhanizmy Perspektivnyh Robototekhnicheskih Sistem; Tekhnosfera: Moskva, Russia, 2020; p. 296. (In Russian) [Google Scholar]
- Qi, Q.; Lin, W.; Guo, B.; Chen, J.; Deng, C.; Lin, G.; Sun, X.; Chen, Y. Augmented Lagrangian-Based Reinforcement Learning for Network Slicing in IIoT. Electronics 2022, 11, 3385. [Google Scholar] [CrossRef]
- Kamikokuryo, K.; Haga, T.; Venture, G.; Hernandez, V. Adversarial Autoencoder and Multi-Armed Bandit for Dynamic Difficulty Adjustment in Immersive Virtual Reality for Rehabilitation: Application to Hand Movement. Sensors 2022, 22, 4499. [Google Scholar] [CrossRef] [PubMed]
- Pontryagin, L.S.; Boltyanskij, V.G.; Gamkrelidze, R.V.; Mishchenko, E.F. Matematicheskaya Teoriya Optimalnih Processov; Fizmatgiz: Moscow, Russia, 1961; p. 391. (In Russian) [Google Scholar]
- Bellman, R. Dynamic Programming, 1st ed.; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Kolesnikov, A.A.; Kolesnikov, A.A.; Kuz’menko, A.A. Metody AKAR i AKOR v zadachah sinteza nelinejnyh sistem upravleniya. Mekhatronika Avtomatizaciya Upravlenie 2016, 17, 657–669. (In Russian) [Google Scholar] [CrossRef]
- Frolov, K. Umen’shenie amplitudy kolebanij rezonansnyh sistem putem upravlyaemogo izmeneniya parametrov. Mashinovedenie 1965, 3, 38–42. (In Russian) [Google Scholar]
- Dmitriev, A.A. Teoriya i Raschet Nelinejnyh Sistem Podressorivaniya Gusenichnyh Mashin; Mashinostroenie: Moscow, Russia, 1976. (In Russian) [Google Scholar]
- Gorobtsov, A. Issledovanie vozmozhnostej sistemy vibrozashchity so stupenchato izmenyayushchimisya parametrami. In Proceedings of the IV Vsesoyuz. Simpozium Vliyanie Vibracii na Organizm Cheloveka i Problemy Vibrozashchity, Moscow, Russia, 18–20 July 1982; pp. 74–75. (In Russian). [Google Scholar]
- Karnopp, D.; Rosenberg, R. Analysis and Simulation of Multiport Systems: The Bond Graph Approach to Physical System Dynamics; MIT Press: Cambidge, MA, USA, 1968; p. 220. [Google Scholar]
- Vukobratovic, M.; Stokić, D.; Kirćanski, N. Non-Adaptive and Adaptive Control of Manipulation Robots; Communications and Control Engineering Series; Springer: Berlin, Germany, 1985. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gorobtsov, A.; Sychev, O.; Orlova, Y.; Smirnov, E.; Grigoreva, O.; Bochkin, A.; Andreeva, M. Optimal Greedy Control in Reinforcement Learning. Sensors 2022, 22, 8920. https://doi.org/10.3390/s22228920
Gorobtsov A, Sychev O, Orlova Y, Smirnov E, Grigoreva O, Bochkin A, Andreeva M. Optimal Greedy Control in Reinforcement Learning. Sensors. 2022; 22(22):8920. https://doi.org/10.3390/s22228920
Chicago/Turabian StyleGorobtsov, Alexander, Oleg Sychev, Yulia Orlova, Evgeniy Smirnov, Olga Grigoreva, Alexander Bochkin, and Marina Andreeva. 2022. "Optimal Greedy Control in Reinforcement Learning" Sensors 22, no. 22: 8920. https://doi.org/10.3390/s22228920
APA StyleGorobtsov, A., Sychev, O., Orlova, Y., Smirnov, E., Grigoreva, O., Bochkin, A., & Andreeva, M. (2022). Optimal Greedy Control in Reinforcement Learning. Sensors, 22(22), 8920. https://doi.org/10.3390/s22228920






