Real-Time Adaptive Traffic Signal Control in a Connected and Automated Vehicle Environment: Optimisation of Signal Planning with Reinforcement Learning under Vehicle Speed Guidance
Abstract
1. Introduction
2. Related Work
2.1. Traffic Signal Control under CAVs
2.2. Closed-Loop Signal Control
2.2.1. Non-Learning-Based Approach
2.2.2. Learning-Based Approach (Reinforcement Learning)
3. Methods
3.1. Reinforcement Learning (RL)
- a vector encoding the current queue lengths on all incoming lanes,
- a one-hot vector encoding of the last chosen signal phase at time t − 1,
- the elapsed time since the last signal phase change,
- for each signal phase, the elapsed time since it was last active.
3.2. Simulation Platform
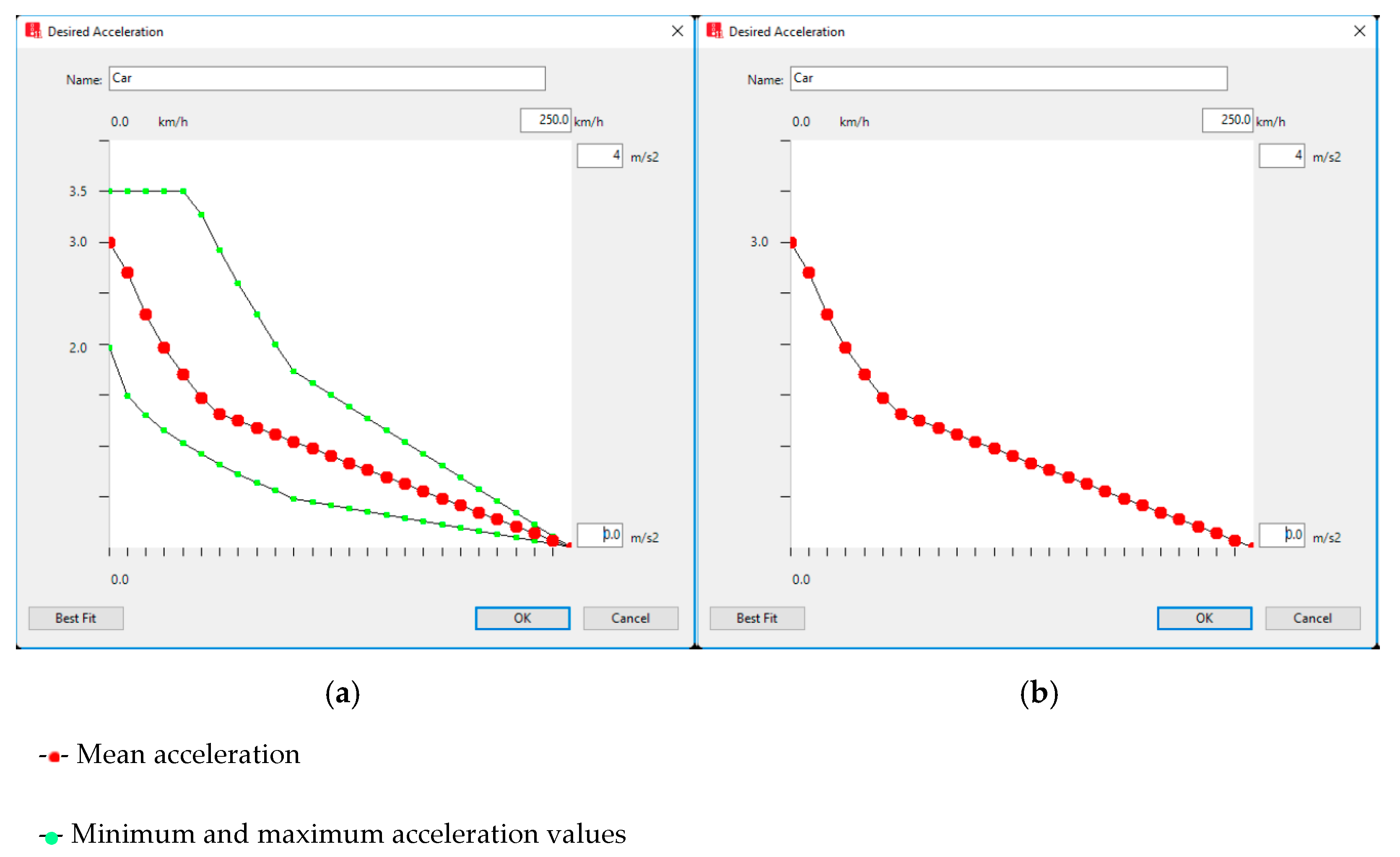
3.3. Driving Behaviours
- (1)
- Conventional vehicles: This type of vehicle has typical characteristics of a human-driven car. The default VISSIM car-following model (Wiedemann 74) was used. Furthermore, the uniform distribution with a minimum value of 45 km per hour and the maximum value of 55 km per hour was utilised to generate the speed of conventional vehicles.
- (2)
- Connected and automated vehicles (CAVs): driving behaviour for this vehicle class consists of two major components, autonomous behaviour and connected behaviour, which will be explained below.
3.3.1. Autonomous Behaviour
3.3.2. Connected Behaviour
- Step 1. The first question that should be asked of all vehicles entering the network is if the car is able to receive signal data or not. Therefore, conventional vehicles will proceed with movement at their desired speed (the speed at which the driver wants to drive). However, if the vehicle is connected, Step 2 is executed.
- Step 2. The vehicle will continue with its current speed if it passes the intersection or no signal controller can be found ahead of this vehicle; otherwise, Step 3 must be performed.
- Step 3. In this step, the following question should be answered. “Is the signal at its green phase?”. If the response is negative and the signal controller is at its red phase, the vehicle speed must be adjusted (5). Otherwise, go to Step 4.Vopt = max(min(Vmax for green start, Vdes) − Vdiff, Vmin)
- Step 4. If Vmin for a green end (a minimum speed required to arrive at the intersection during the current green) is lower than the desired speed of the vehicle, then Vopt should be equal to Vdes. Conversely, Step 5 is executed. Vmin for a green end can be calculated by (7).
- Step 5. If Vmax for a green start is greater than the desired speed of the vehicle, then Vopt should be equal to Vdes. Otherwise, Vopt = Vmax for a green start. Therefore, the optimal speed of all CAVs in the network can be calculated through this procedure.
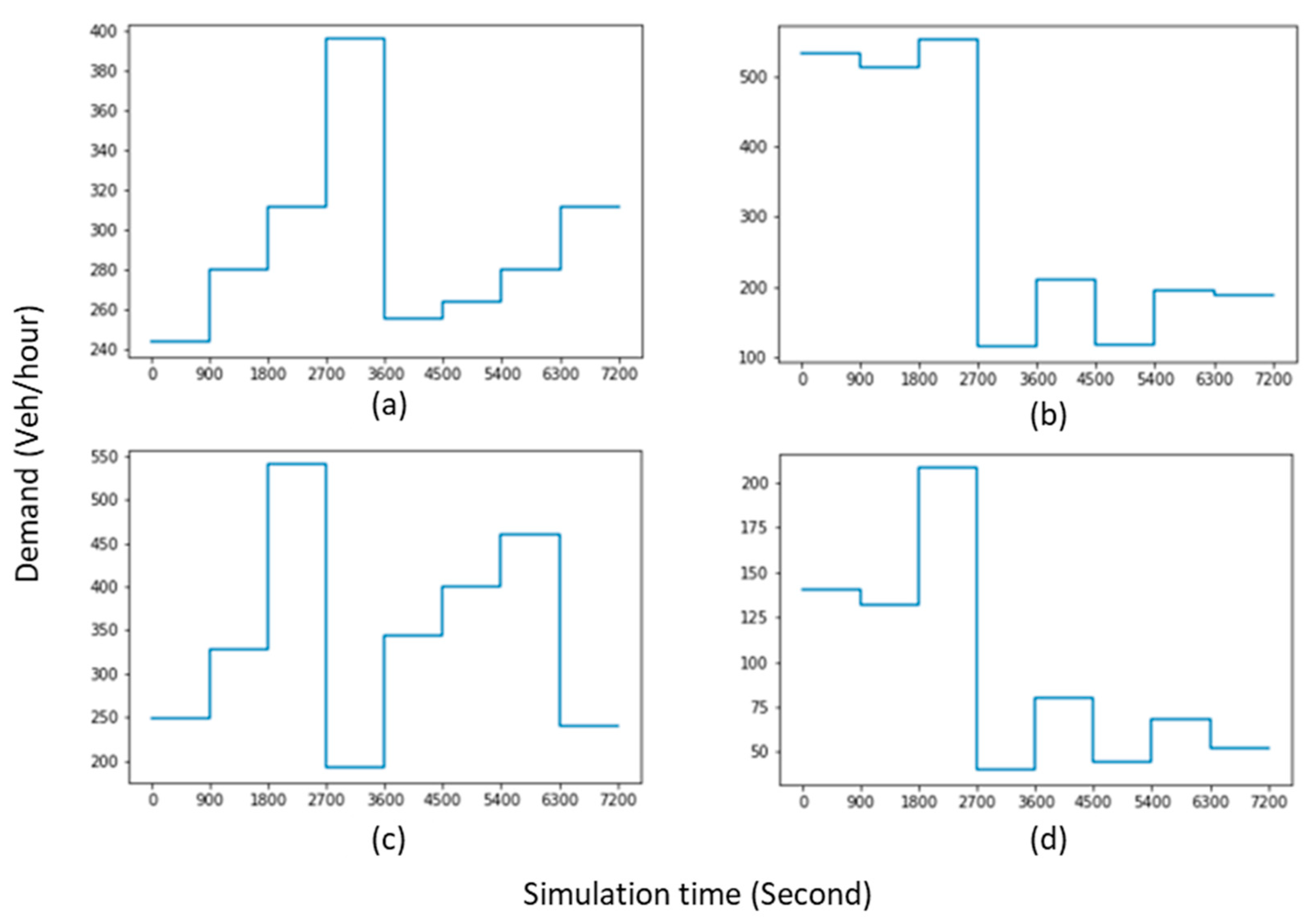
3.4. Simulation Scenarios
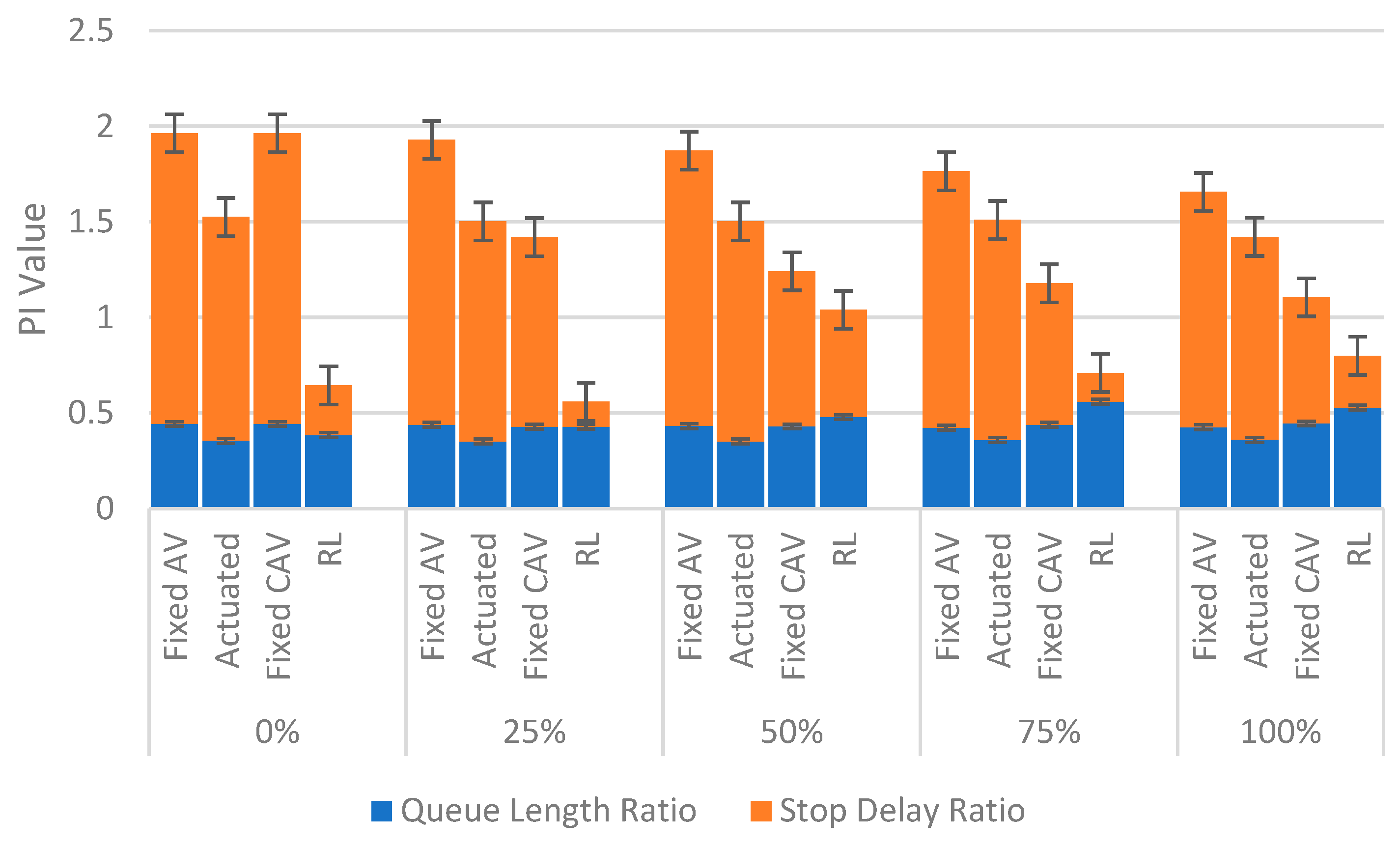
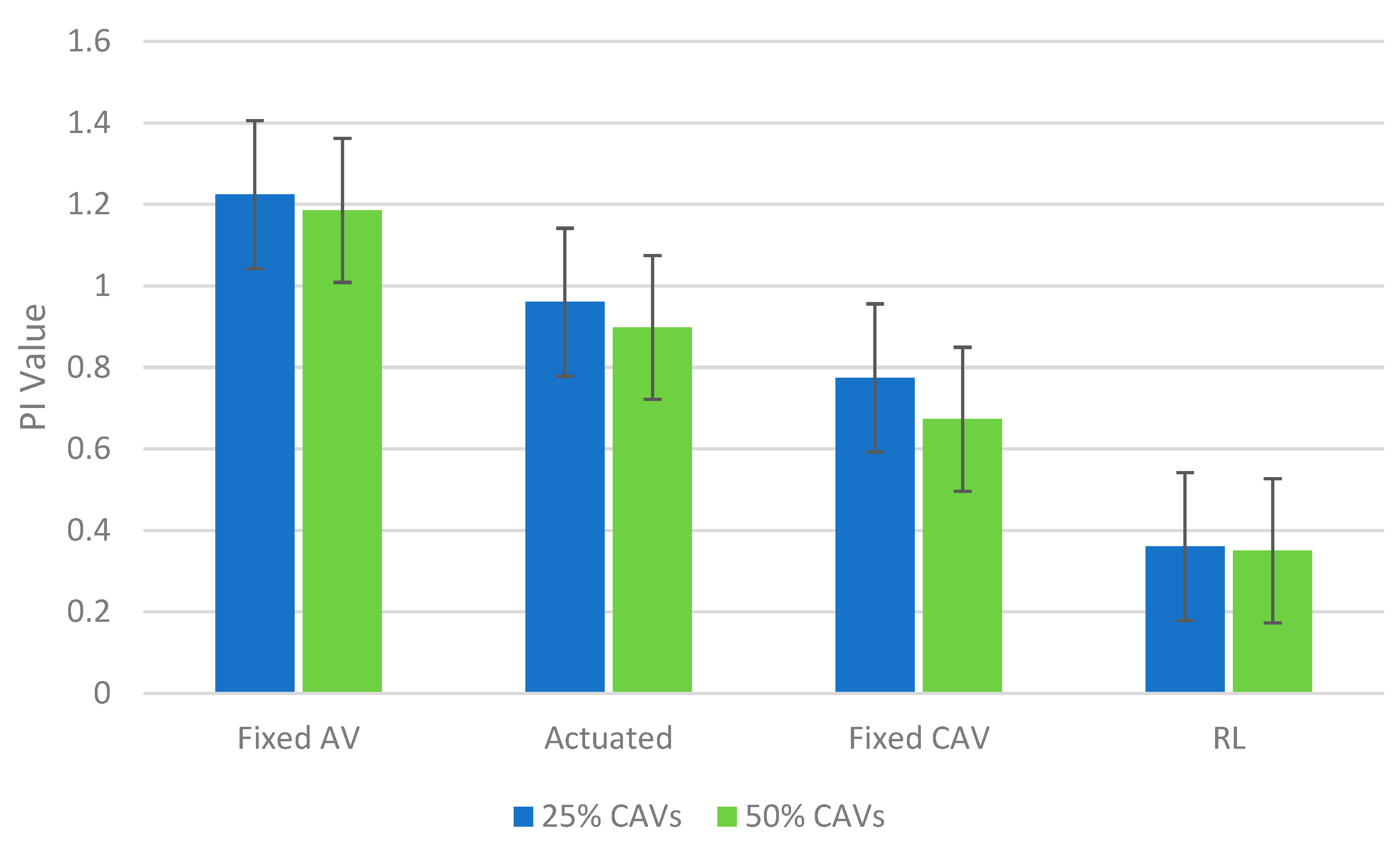
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Institute of Economic Affairs (IEA) Discussion Paper, No.68, 2016. SEEING RED Traffic Controls and the Economy. Available online: https://iea.org.uk/wpcontent/uploads/2016/07/IEA%20Seeing%20Red%20%20Traffic%20Controls%20and%20the%20Economy.pdf (accessed on 11 January 2021).
- Gartner, N.H. OPAC: A demand-responsive strategy for traffic signal control. Transp. Res. Rec. J. Transp. Res. Board 1983, 906, 75–81. [Google Scholar]
- Head, K.L.; Mirchandani, P.B.; Sheppard, D. Hierarchical framework for real-time traffic control. Transp. Res. Rec. 1992, 1360, 82–88. [Google Scholar]
- Luyanda, F.; Gettman, D.; Head, L.; Shelby, S.; Bullock, D.; Mirchandani, P. ACS-Lite algorithmic architecture: Applying adaptive control system technology to closed-loop traffic signal control systems. Transp. Res. Record 2003, 1856, 175–184. [Google Scholar] [CrossRef]
- Mirchandani, P.; Head, L. A real-time traffic signal control system: Architecture, algorithms, and analysis. Transp. Res. Part C Emerg. Technol. 2001, 9, 415–432. [Google Scholar] [CrossRef]
- Ran, Q.; Yang, J. A novel closed-loop feedback traffic signal control strategy at an isolated intersection. In Proceedings of the 2012 IEEE International Conference on Information Science and Technology, ICIST, Wuhan, China, 23–25 March 2012. [Google Scholar] [CrossRef]
- Fagnant, D.J.; Kockelman, K. Preparing a nation for autonomous vehicles: Opportunities, barriers and policy recommendations. Transp. Res. Part A Policy Pract. 2015, 77, 167–181. [Google Scholar] [CrossRef]
- Kockelman, K.; Boyles, S. Smart Transport for Cities & Nations: The Rise of Self-Driving & Connected Vehicles. The University of Texas at Austin, 2018. Available online: https://bit.ly/3gDpEaa (accessed on 15 March 2021).
- Elliott, D.; Keen, W.; Miao, L. Recent advances in connected and automated vehicles. J. Traffic Transp. Eng. 2019, 6, 109–131. [Google Scholar] [CrossRef]
- Feng, Y.; Head, K.L.; Khoshmagham, S.; Zamanipour, M. A real-time adaptive signal control in a connected vehicle environment. Transp. Res. Part C Emerg. Technol. 2015, 55, 460–473. [Google Scholar] [CrossRef]
- Yao, H.; Jin, Y.; Jiang, H.; Hu, L.; Jiang, Y. CTM-based traffic signal optimisation of mixed traffic flow with connected automated vehicles and human-driven vehicles. Phys. A: Stat. Mech. Its Appl. 2022, 603, 127708. [Google Scholar] [CrossRef]
- Yao, Z.; Shen, L.; Liu, R.; Jiang, Y.; Yang, X. A Dynamic Predictive Traffic Signal Control Framework in a Cross-Sectional Vehicle Infrastructure Integration Environment. Proc. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1455–1466. [Google Scholar] [CrossRef]
- Saldivar-Carranza, E.; Li, H.; Mathew, J.; Fisher, C.; Bullock, D. Signalized Corridor Timing Plan Change Assessment Using Connected Vehicle Data. J. Transp. Technol. 2022, 12, 310–322. [Google Scholar] [CrossRef]
- Yao, Z.; Jiang, Y.; Zhao, B.; Luo, X.; Peng, B. A dynamic optimization method for adaptive signal control in a connected vehicle environment, Journal of Intelligent Transportation. Systems 2020, 24, 184–200. [Google Scholar] [CrossRef]
- Guo, Q.; Li, L.; Ban, X. Urban traffic signal control with connected and automated vehicles: A survey. Transp. Res. Part C Emerg. Technol. 2019, 101, 313–334. [Google Scholar] [CrossRef]
- Mintsis, E.; Vlahogianni, E.I.; Mitsakis, E.; Ozkul, S. Enhanced speed advice for connected vehicles in the proximity of signalized intersections. Eur. Transp. Res. Rev. 2021, 13, 2. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhao, B.; Liu, M.; Yao, Z. A Two-Level Model for Traffic Signal Timing and Trajectories Planning of Multiple CAVs in a Random Environment. J. Adv. Transp. 2021, 2021, 9945398. [Google Scholar] [CrossRef]
- He, X.; Liu, H.X.; Liu, X. Optimal vehicle speed trajectory on a signalised arterial with consideration of queue. Transp. Res. Part C Emerg. Technol. 2015, 61, 106–120. [Google Scholar] [CrossRef]
- Wang, M.; Daamen, W.; Hoogendoorn, S.P.; van Arem, B. Rolling horizon control framework for driver assistance systems. Part I: Mathematical formulation and non-cooperative systems. Transp. Res. Part C Emerg. Technol. 2014, 40, 271–289. [Google Scholar] [CrossRef]
- Wu, X.; He, X.; Yu, G.; Harmandayan, A.; Wang, Y. Energy-optimal speed control for electric vehicles on signalised arterials. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2786–2796. [Google Scholar] [CrossRef]
- Wang, P.; Chan, C.Y.; de La, F.A. A reinforcement learning-based approach for automated lane change maneuvers. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu/Suzhou, China, 26–30 June 2018; pp. 1379–1384. [Google Scholar]
- Abdulhai, B.; Kattan, L. Reinforcement learning: Introduction to theory and potential for transport applications. Can. J. Civ. Eng. 2003, 30, 981–991. [Google Scholar] [CrossRef]
- Shatnawi, I.; Yi, P.; Khliefat, I. Automated intersection delay estimation using the input-output principle and turning movement data. Int. J. Transp. Sci. Technol. 2018, 7, 137–150. [Google Scholar] [CrossRef]
- Traffic Analysis Toolbox Volume III: Guidelines for Applying Traffic Microsimulation Modeling Software. US Department of Transportation, 2010. Available online: https://ops.fhwa.dot.gov/trafficanalysistools/tat_vol3/vol3_guidelines.pdf (accessed on 16 March 2021).
- Hunt, P.B.; Robertson, D.I.; Bretherton, R.D. The SCOOT online traffic signal optimisation technique (Glasgow). Traffic Eng. Control. 1982, 23, 190–192. [Google Scholar]
- Sims, A.G.; Dobinson, K.W. The Sydney Coordinated Adaptive Traffic (SCAT) System Philosophy and Benefits. IEEE Trans. Veh. Technol. 1980, 29, 130–137. [Google Scholar] [CrossRef]
- Athmaraman, N.; Soundararajan, S. Adaptive predictive traffic timer control algorithm. In Proceedings of the 2005 Mid-Continent Transportation Research Symposium, Ames, IA, USA, 18–19 August 2005; Available online: https://www.cs.uic.edu/~nathmara/AthmaramanTraffic.pdf (accessed on 1 March 2021).
- Wang, Y.; Yang, X.; Liang, H.; Liu, Y. A Review of the Self-Adaptive Traffic Signal Control System Based on Future Traffic Environment. J. Adv. Transp. 2018, 2018, 1096123. [Google Scholar] [CrossRef]
- Ke-Zhao, B.; Rui-Xiong, C.; Mu-ren, L.; Ling-Jiang, K.; Rong-sen, Z. Study of the grade roundabout crossing. Comput. Sci. 2009. [Google Scholar] [CrossRef]
- El-tantawy, S.; Member, S.; Abdulhai, B.; Abdelgawad, H. Multiagent Reinforcement Learning for Integrated Network of Adaptive Traffic Signal Controllers Application on Downtown Toronto. IEEE Trans. Intell. Transp. Syst. 2013, 14, 1140–1150. [Google Scholar] [CrossRef]
- Jing, P.; Huang, H.; Chen, L. An Adaptive Traffic Signal Control in a Connected Vehicle Environment: A Systematic Review. Information 2017, 8, 101. [Google Scholar] [CrossRef]
- Wu, W.; Huang, L.; Du, R. Simultaneous Optimization of Vehicle Arrival Time and Signal Timings within a Connected Vehicle Environment. Sensors 2020, 20, 191. [Google Scholar] [CrossRef] [PubMed]
- Katsaros, K.; Kernchen, R.; Dianati, M.; Rieck, D. Performance study of a Green Light Optimized Speed Advisory (GLOSA) application using an integrated cooperative ITS simulation platform. In Proceedings of the IWCMC 2011 7th International Wireless Communications and Mobile Computing Conference, Istanbul, Turkey, 4–8 July 2011. [Google Scholar] [CrossRef]
- Tang, T.Q.; Yi, Z.Y.; Zhang, J.; Wang, T.; Leng, J.Q. A speed guidance strategy for multiple signalised intersections based on car-following model. Phys. A: Stat. Mech. Its Appl. 2018, 496, 399–409. [Google Scholar] [CrossRef]
- Beak, B.; Larry Head, K.; Feng, Y. Adaptive coordination based on connected vehicle technology. Transp. Res. Rec. 2017, 2619, 1–12. [Google Scholar] [CrossRef]
- Pandit, K.; Ghosal, D.; Zhang, H.M.; Chuah, C.N. Adaptive traffic signal control with vehicular Ad Hoc networks. IEEE Trans. Veh. Technol. 2013, 62, 1459–1471. [Google Scholar] [CrossRef]
- Yu, C.; Feng, Y.; Liu, H.X.; Ma, W.; Yang, X. Integrated optimisation of traffic signals and vehicle trajectories at isolated urban intersections. Transp. Res. Part B Methodol. 2018, 112, 89–112. [Google Scholar] [CrossRef]
- Lämmer, S.; Helbing, D. Self-control of traffic lights and vehicle flows in urban road networks. J. Stat. Mech. Theory Exp. 2008, 2008, P04019. [Google Scholar] [CrossRef]
- Carlson, R.C.; Papamichail, I.; Papageorgiou, M. Local feedback-based mainstream traffic flow control on motorways using variable speed limits. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1261–1276. [Google Scholar] [CrossRef]
- Diakaki, C.; Papageorgiou, M.; Aboudolas, K. A multivariable regulator approach to traffic-responsive network—Wide signal control. Control Eng. Pract. 2002, 10, 183–195. [Google Scholar] [CrossRef]
- Chin, Y.K.; Lee, L.K.; Yang, S.S.; Tze, K.; Teo, K. Exploring Q-Learning Optimisation in Traffic Signal Timing Plan Management. In Proceedings of the 2011 Third International Conference on Computational Intelligence, Communication Systems and Networks, Bali, Indonesia, 26–28 July 2011; pp. 269–274. [Google Scholar] [CrossRef]
- Chu, T.; Wang, J.; Codecà, L.; Li, Z. Multi-agent deep reinforcement learning for large-scale traffic signal control. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1086–1095. [Google Scholar] [CrossRef]
- Kim, D.; Jeong, O. Cooperative Traffic Signal Control with Traffic Flow Prediction in Multi-Intersection. Sensors 2019, 20, 137. [Google Scholar] [CrossRef]
- Yang, K.; Tan, I.; Menendez, M. A reinforcement learning-based traffic signal control algorithm in a connected vehicle environment. In Proceedings of the 17th Swiss Transport Research Conference (STRC 2017), Ascona, Switzerland, 17–19 May 2017. [Google Scholar]
- Aslani, M.; Seipel, S.; Saadi, M.; Wiering, M. Advanced Engineering Informatics Traffic signal optimisation through discrete and continuous reinforcement learning with robustness analysis in downtown Tehran. Adv. Eng. Inform. 2018, 38, 639–655. [Google Scholar] [CrossRef]
- Prabuchandran, K.J.; Hemanth Kumar, A.N.; Bhatnagar, S. Decentralised Learning for Traffic Signal Control. In Proceedings of the Intelligent Transportation System Workshop, COMSNETS, Bangalore, India, 6–10 January 2015. [Google Scholar] [CrossRef]
- Chen, J.; Xue, Z.; Fan, D. Deep Reinforcement Learning Based Left-Turn Connected and Automated Vehicle Control at Signalized Intersection in Vehicle-to-Infrastructure Environment. Information 2020, 11, 77. [Google Scholar] [CrossRef]
- Liu, W.; Qin, G.; He, Y.; Jiang, F. Distributed Cooperative Reinforcement Learning-Based Traffic Signal Control That Integrates V2X Networks’ Dynamic Clustering. Proc. IEEE Trans. Veh. Technol. 2017, 66, 8667–8681. [Google Scholar] [CrossRef]
- Mousavi, S.S.; Schukat, M.; Howley, E. Traffic light control using deep policy- gradient and value-function-based reinforcement learning. IET Intell. Transp. Syst. 2017, 11, 417–423. [Google Scholar] [CrossRef]
- van der Pol, E.; Oliehoek, F.A. Coordinated deep reinforcement learners for traffic light control. In Proceedings of the 30th Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Nishi, T.; Otaki, K.; Hayakawa, K.; Yoshimura, T. Traffic Signal Control Based on Reinforcement Learning with Graph Convolutional Neural Nets. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 877–883. [Google Scholar] [CrossRef]
- Zhao, J.; Li, W.; Wang, J.; Ban, X. Dynamic traffic signal timing optimisation strategy incorporating various vehicle fuel consumption characteristics. IEEE Trans. Veh. Technol. 2015, 65, 3874–3887. [Google Scholar] [CrossRef]
- Aria, E.; Olstam, J.; Schwietering, C. Investigation of Automated Vehicle Effects on Driver’s Behavior and Traffic Performance. Transp. Res. Procedia 2016, 15, 761–770. [Google Scholar] [CrossRef]
- ATKINS. Research on the Impacts of Connected and Autonomous Vehicles (CAVs) on Traffic Flow. 2016. [Google Scholar]
- Stanek, D.; Huang, E.; Milam, R.T. Measuring Autonomous Vehicle Impacts on Congested Networks Using Simulation. In Proceedings of the Transportation Research Board 97th Annual Meeting, Washington, DC, USA, 7–11 January 2018. [Google Scholar]
- Asadi, F.E.; Anwar, A.K.; Miles, J.C. Investigating the potential transportation impacts of connected and autonomous vehicles. In Proceedings of the 2019 8th IEEE International Conference on Connected Vehicles and Expo, ICCVE, Graz, Austria, 4–8 November 2019. [Google Scholar] [CrossRef]
- Zeidler, V.; Buck, S.; Kautzsch, L.; Vortisch, P.; Weyland, C. Simulation of Autonomous Vehicles Based on Wiedemann’s Car Following Model in PTV Vissim. In Proceedings of the Transportation Research Board 98th Annual Meeting, Washington, DC, USA, 13–17 January 2019. [Google Scholar]
- PTV Group. PTV Vissim 10 User Manual. Ptv Ag. Available online: https://usermanual.wiki/Document/Vissim20102020Manual.1098038624.pdf (accessed on 1 March 2021).
- CoEXist. Working towards a Shared Road Network. 2020. Available online: https://www.h2020-coexist.eu/ (accessed on 12 January 2020).
- Council, N.R. TRB. Highway Capacity Manual; National Research Council: Washington, DC, USA, 2000. [Google Scholar]
- Marler, R.T.; Arora, J.S. Function-transformation methods for multi-objective optimisation. Eng. Optim. 2005, 37, 551–570. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maadi, S.; Stein, S.; Hong, J.; Murray-Smith, R. Real-Time Adaptive Traffic Signal Control in a Connected and Automated Vehicle Environment: Optimisation of Signal Planning with Reinforcement Learning under Vehicle Speed Guidance. Sensors 2022, 22, 7501. https://doi.org/10.3390/s22197501
Maadi S, Stein S, Hong J, Murray-Smith R. Real-Time Adaptive Traffic Signal Control in a Connected and Automated Vehicle Environment: Optimisation of Signal Planning with Reinforcement Learning under Vehicle Speed Guidance. Sensors. 2022; 22(19):7501. https://doi.org/10.3390/s22197501
Chicago/Turabian StyleMaadi, Saeed, Sebastian Stein, Jinhyun Hong, and Roderick Murray-Smith. 2022. "Real-Time Adaptive Traffic Signal Control in a Connected and Automated Vehicle Environment: Optimisation of Signal Planning with Reinforcement Learning under Vehicle Speed Guidance" Sensors 22, no. 19: 7501. https://doi.org/10.3390/s22197501
APA StyleMaadi, S., Stein, S., Hong, J., & Murray-Smith, R. (2022). Real-Time Adaptive Traffic Signal Control in a Connected and Automated Vehicle Environment: Optimisation of Signal Planning with Reinforcement Learning under Vehicle Speed Guidance. Sensors, 22(19), 7501. https://doi.org/10.3390/s22197501






