Adaptive Scheme for Detecting Induction Motor Incipient Broken Bar Faults at Various Load and Inertia Conditions
Abstract
1. Introduction
- ▪
- Proposing a novel scheme based on an analytical approach to detect and diagnose BBFs. Hence, the results are easy to interpret. Furthermore, no training process is required.
- ▪
- The proposed scheme does not need any settings instead; it employs an adaptive threshold to discriminate between healthy and faulty cases under different operating conditions.
- ▪
- The proposed scheme can effectively detect incipient BBFs and non-adjacent BBFs, representing a stumbling block to many other methods in the literature.
- ▪
- The proposed scheme can precisely detect BBFs under variable loading and different inertia conditions.
- ▪
- The proposed scheme is immune to high-level noise and independent from motor parameters.
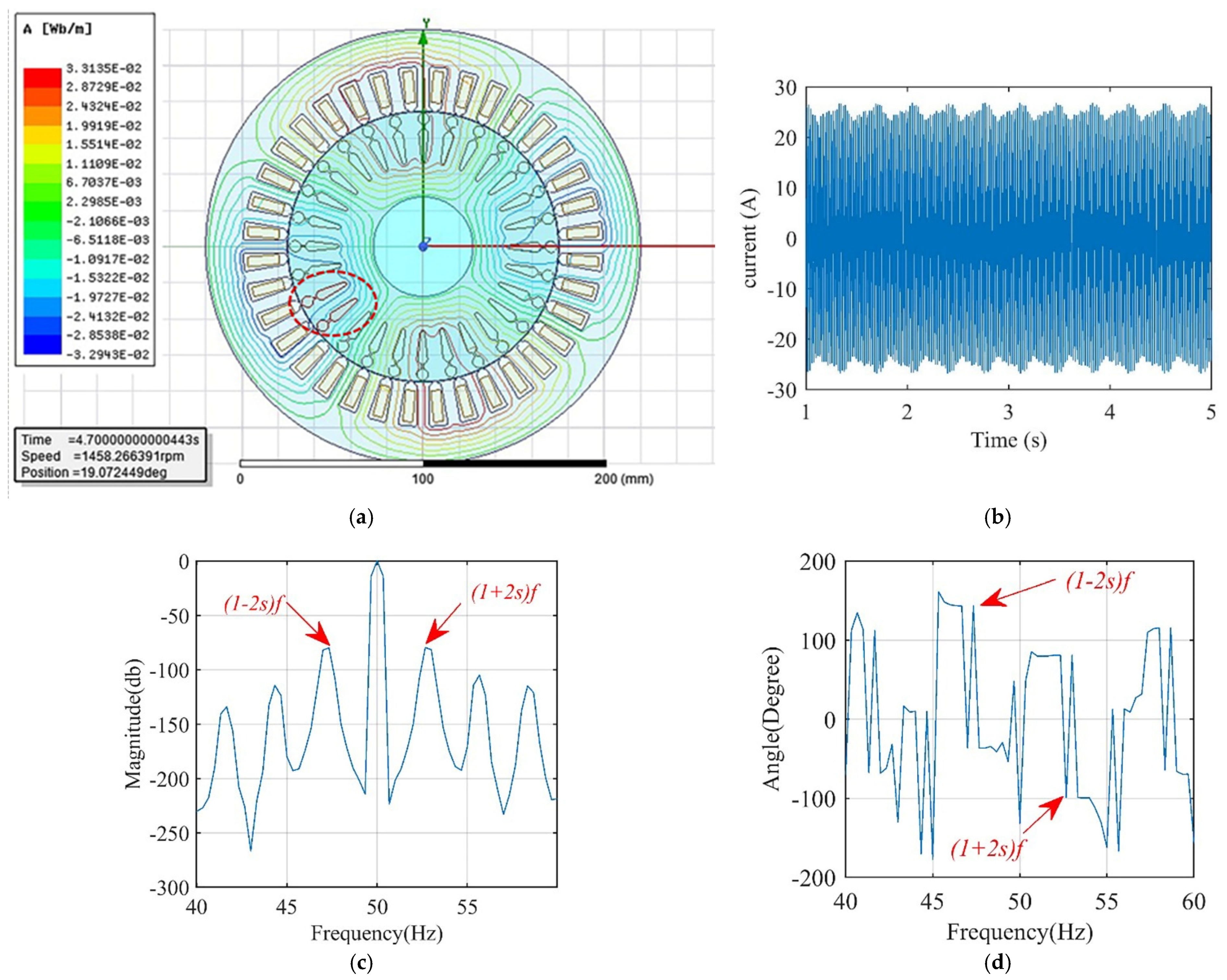
2. Simulating Broken Bar Faults in Induction Motor
3. Methodology of the Proposed Scheme
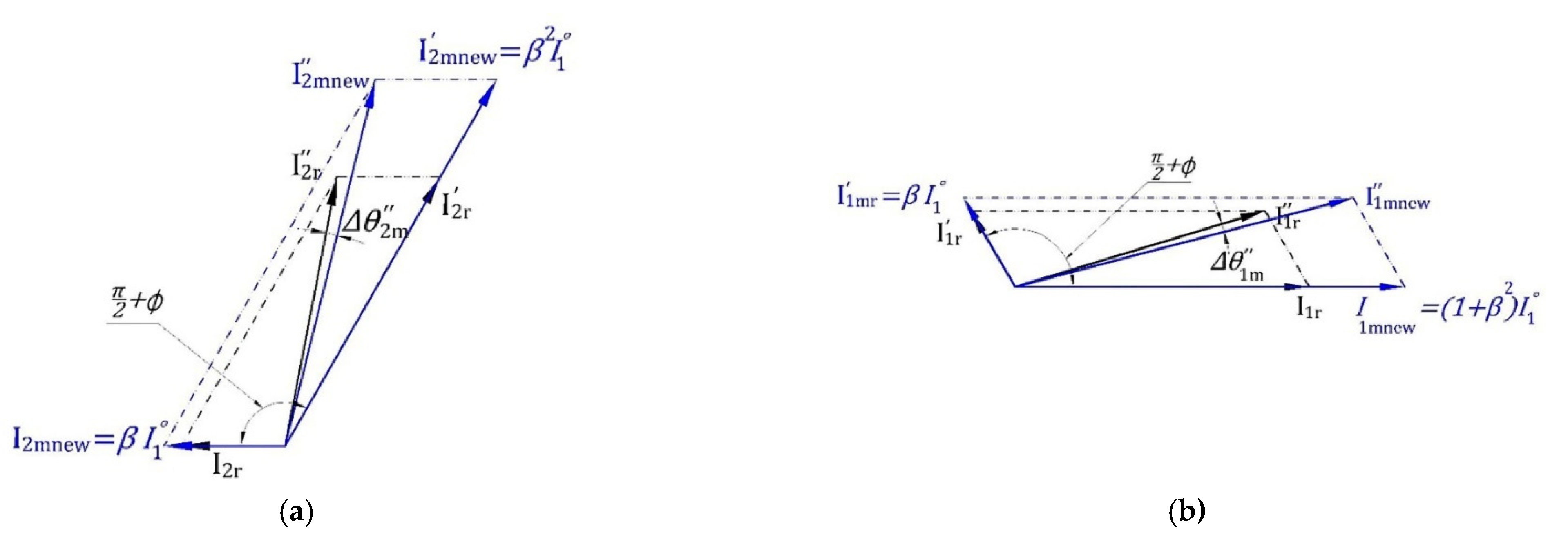
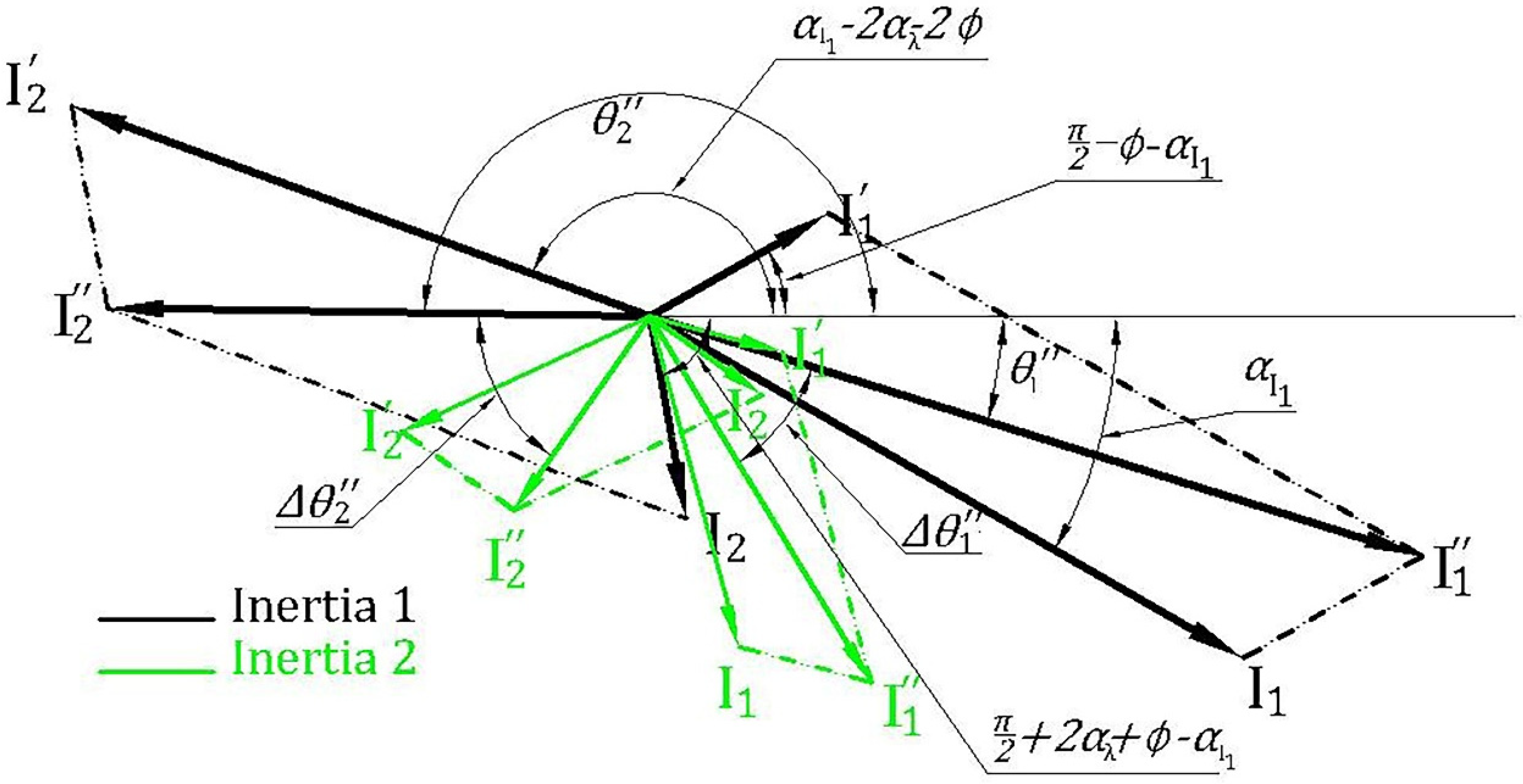
4. Analyzing the Variation of Main Sideband Phase Angle under Different Conditions
4.1. Main Sideband Phase Angle Variation under Healthy Conditions
4.1.1. Under Inertia Changing
4.1.2. Under Load Changing
4.2. Main Sideband Phase Angle Variation under Fault Conditions
5. Implementation of the Proposed Scheme
- ▪
- Data acquisition stage: It includes the sampling process of the current and voltage signal and storing samples to reach the required frequency resolutions.
- ▪
- Data processing stage: It includes data windowing block, FFT block, and localization of the main sideband component block to obtain the magnitude and angle of these sideband components.
- ▪
- Adaptive threshold determination and fault detection stage: It includes a method for adaptive threshold calculation to differentiate between healthy and BBFs conditions.
- ▪
- Severity index calculation stage: It provides a severity index to designate the severity of the fault.
5.1. Data Acquisition Stage
5.2. Data Processing Stage
5.2.1. Signal Windowing Block
5.2.2. Fast Fourier Transformer Block
5.2.3. Localization of Main Side Band Components
- Step 1:
- Determine the current power frequency components that have the maximum magnitude and its associated frequency from the two arrays, and .
- Step 2:
- Determine the frequency searching zone for the main side band components, which is limited by and where is the maximum slip at which the motor can operate and its associated magnitude .
- Step 3:
- Search for the local maxima in the magnitudes of the searching zone such that and then arrange them in descending order inand their associated frequencies in .
- Step 4:
- Ensure that the frequency of the first and the second greatest local maxima is symmetrical around the power frequency otherwise; take the third greatest local maxima instead of the second one and check for this condition.
- Step 5:
- When the condition in Step 4 is fulfilled, set the following:
5.3. Adaptive Threshold Determination and Fault Detection Stage
- Calculate at a reference healthy condition for the motor to be monitored using FFT at any inertia and under any loading conditions.
- Calculate the reference values and from Equations (12) and (14). Only positive and real values of them will be accepted.
- The previous two steps are carried out once for the healthy motor in the commissioning phase.
- Calculate for the new current samples using FFT.
- Calculate the value of from Equations (12) and (14). Using , which has been obtained from Step (2) to limit the variation to be in only. The value of that has the largest deviation from will be selected to provide a safety margin to avoid false diagnosis.
- Calculate the magnitudes of using Equations (7), (5), (8) and (6), respectively, with the values of and
- To study the magnitude variation effect of current components calculated in Step (5) on , the model introduced in Figure 2 is used to calculate using the data obtained from Step (5).
- Calculate threshold value using Equation (15).
- For checking BBFs occurrence, calculate the angle difference using Equation (16).
- If the condition is satisfied, the healthy condition is confirmed otherwise a broken bar fault is detected.
5.4. Severity Index Calculation Stage
- Calculate the values of from Equations (12) and (14) using value, which has been obtained from Step (2) in the threshold determination module.
- Calculate the average of values.
- Calculate the corrected current as follows, as is directly proportional to :
- Calculate the severity index:
6. Testing Results for Proposed Scheme Performance
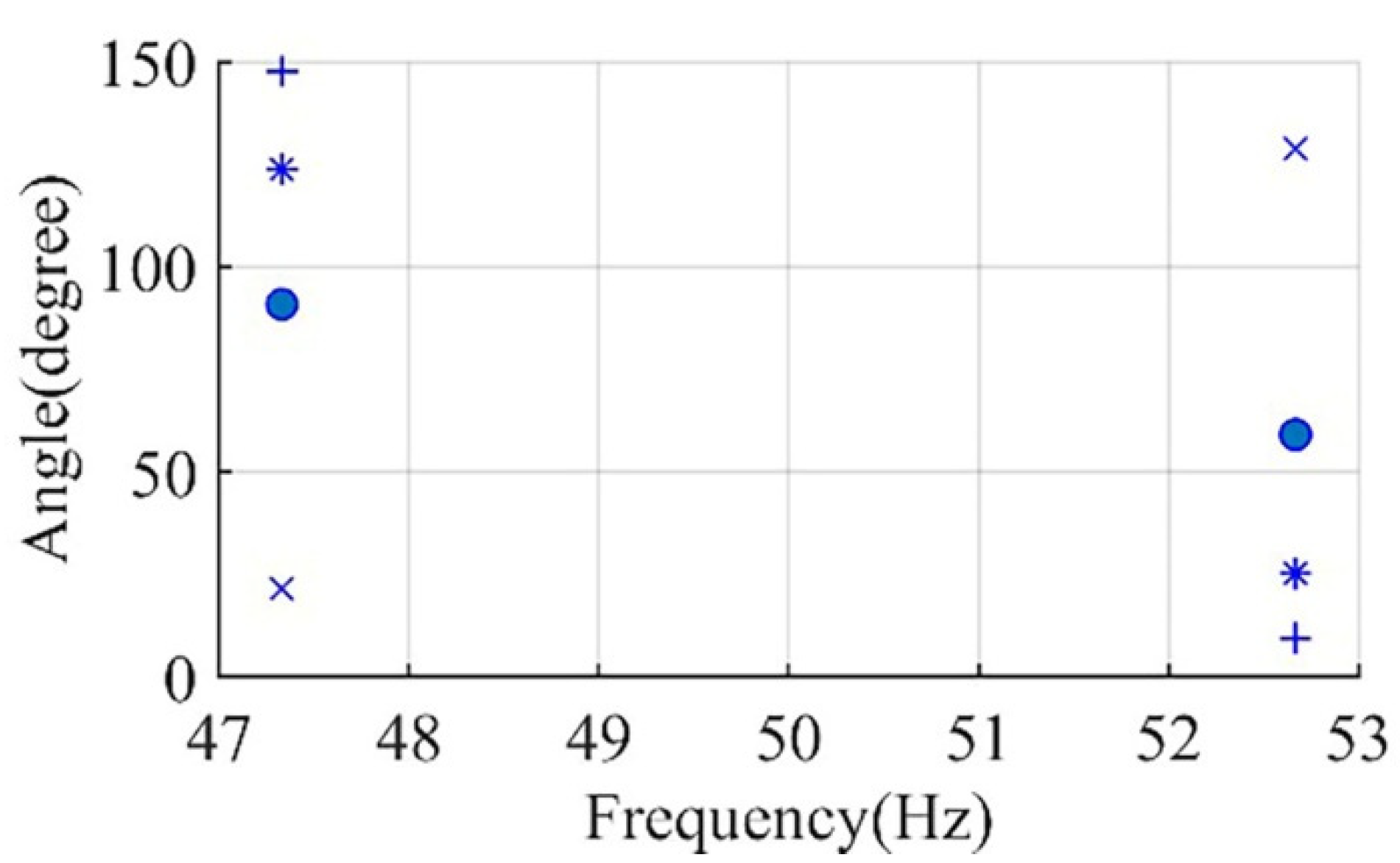
6.1. Under Different System Inertia
6.2. Under Different Loading Conditions
6.3. Under Different Fault Severity
6.4. In a Noisy Environment
6.5. Faulty Severity Determination
6.6. Validation of the Proposed Scheme Using Real Experimental Dataset
- -
- Healthy;
- -
- One bar with 3 mm diameter hole;
- -
- One bar with two 3 mm diameter holes each;
- -
- One bar with two 4 mm diameter holes each (as illustrated in Figure 13a);
- -
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Definition |
| AI | Artificial Intelligence |
| BBF | Broken Bar Fault |
| BBR | Broken Bar |
| EMD | Empirical Mode Decomposition |
| EMF | Electromotive Forces |
| ESPRIT | Estimation of Signal Parameters via Rotational Invariance Techniques |
| FC | Fundamental Current Component |
| FEM | Finite Element Method |
| FFT | Fast Fourier Transform |
| HBBR | Half-Broken Bar |
| HHT | Hilbert–Huang transform |
| MCSA | Motor Current Signature Analysis |
| MUSIC | Multiple Signal Classification |
| NEMA | National Electrical Manufacturers Association |
| RLSH | Left-Side Harmonic |
| RMS | Root Mean Square |
| RSH | Right Sideband Harmonic |
| SNR | Signal To Noise Ratio |
| WT | Wavelet Transform |
| and | The RMS of electromotive force of the LSH and RSH respectively |
| The instantaneous of electromotive force of the LSH and RSH respectively | |
| The supply frequency | |
| Rotor frequency component | |
| The stator current | |
| System inertia | |
| and | The RMS of fundamental current, LSH and RSH components respectively |
| and | Notations for different current components, where subscript (1) and (2) indicate components related to LSH and RSH respectively |
| Initial left sideband current | |
| The corrected values of | |
| Number of poles | |
| Motor slip | |
| Synchronous speed | |
| and | The circuit impedance for LSH and RSH respectively |
| and | The magnitude and the angle of the equivalent circuit impedance at supply frequency |
| and | The phase angles of FC, LSH, and RSH |
| The angle of the fundamental flux linkage | |
| A parameter equals | |
| and | The phase angle of the current components , respectively |
| The change in the angle | |
| The RMS value of the fundamental flux linkage | |
| The instantaneous value of the fundamental flux linkage | |
| The subscript denotes reference cases | |
| The subscript denotes new cases | |
| indicates the new case current components calculated using the model in Figure 2 | |
| The subscript (m) indicates the model indicates the model |
References
- Atta, M.E.E.-D.; Ibrahim, D.K.; Gilany, M.I. Broken Bar Faults Detection Under Induction Motor Starting Conditions Using the Optimized Stockwell Transform and Adaptive Time–Frequency Filter. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Park, Y.; Choi, H.; Shin, J.; Park, J.; Bin Lee, S.; Jo, H. Airgap Flux Based Detection and Classification of Induction Motor Rotor and Load Defects During the Starting Transient. IEEE Trans. Ind. Electron. 2020, 67, 10075–10084. [Google Scholar] [CrossRef]
- Valtierra-Rodriguez, M.; Rivera-Guillen, J.R.; Basurto-Hurtado, J.A.; De-Santiago-Perez, J.J.; Granados-Lieberman, D.; Amezquita-Sanchez, J.P. Convolutional Neural Network and Motor Current Signature Analysis during the Transient State for Detection of Broken Rotor Bars in Induction Motors. Sensors 2020, 20, 3721. [Google Scholar] [CrossRef]
- Faiz, J.; Ghorbanian, V.; Joksimovic, G. Fault Diagnosis of Induction Motors; Institution of Engineering and Technology: London, UK, 2017; pp. 71–167. [Google Scholar]
- Thompson, W.T.; Culbert, I. MCSA Industrial Case Histories—Diagnosis of Cage Winding Defects in SCIMs Driving Steady Loads. In Current Signature Analysis for Condition Monitoring of Cage Induction Motors; Wiley: Hoboken, NJ, USA, 2017; pp. 119–145. [Google Scholar]
- Concari, C.; Franceschini, G.; Tassoni, C.; Toscani, A. Validation of a Faulted Rotor Induction Machine Model With an Insightful Geometrical Interpretation of Physical Quantities. IEEE Trans. Ind. Electron. 2012, 60, 4074–4083. [Google Scholar] [CrossRef]
- Kral, C.; Pirker, F.; Pascoli, G. The Impact of Inertia on Rotor Fault Effects—Theoretical Aspects of the Vienna Monitoring Method. IEEE Trans. Power Electron. 2008, 23, 2136–2142. [Google Scholar] [CrossRef]
- Da Silva, A.M.; Povinelli, R.J.; Demerdash, N.A.O. Induction Machine Broken Bar and Stator Short-Circuit Fault Diagnostics Based on Three-Phase Stator Current Envelopes. IEEE Trans. Ind. Electron. 2008, 55, 1310–1318. [Google Scholar] [CrossRef]
- Sapena-Baño, A.; Pineda-Sanchez, M.; Puche-Panadero, R.; Martinez-Roman, J.; Kanović, Ž. Low-Cost Diagnosis of Rotor Asymmetries in Induction Machines Working at a Very Low Slip Using the Reduced Envelope of the Stator Current. IEEE Trans. Energy Convers. 2015, 30, 1409–1419. [Google Scholar] [CrossRef]
- Sridhar, S.; Rao, K.U.; Jade, S. Detection of broken rotor bar fault in induction motor at various load conditions using wavelet transforms. In Proceedings of the 2015 International Conference on Recent Developments in Control, Automation and Power Engineering (RDCAPE), Noida, India, 12–13 March 2015; pp. 77–82. [Google Scholar]
- Hassan, O.E.; Amer, M.; Abdelsalam, A.K.; Williams, B.W. Induction motor broken rotor bar fault detection techniques based on fault signature analysis—A review. IET Electr. Power Appl. 2018, 12, 895–907. [Google Scholar] [CrossRef]
- Abd-El-Malek, M.; Abdelsalam, A.K.; Hassan, O. Induction motor broken rotor bar fault location detection through envelope analysis of start-up current using Hilbert transform. Mech. Syst. Signal Process. 2017, 93, 332–350. [Google Scholar] [CrossRef]
- Liu, Y.; Bazzi, A.M. A review and comparison of fault detection and diagnosis methods for squirrel-cage induction motors: State of the art. ISA Trans. 2017, 70, 400–409. [Google Scholar] [CrossRef]
- Gyftakis, K.N.; Cardoso, A.J.M.; Antonino-Daviu, J.A. Introducing the Filtered Park’s and Filtered Extended Park’s Vector Approach to detect broken rotor bars in induction motors independently from the rotor slots number. Mech. Syst. Signal Process. 2017, 93, 30–50. [Google Scholar] [CrossRef]
- Díaz, I.M.; Morinigo-Sotelo, D.; Duque-Perez, O.; Arredondo-Delgado, P.; Camarena-Martinez, D.; Romero-Troncoso, R. Analysis of various inverters feeding induction motors with incipient rotor fault using high-resolution spectral analysis. Electr. Power Syst. Res. 2017, 152, 18–26. [Google Scholar] [CrossRef]
- Romero-Troncoso, R.; Garcia-Perez, A.; Morinigo-Sotelo, D.; Duque-Perez, O.; Osornio-Rios, R.A.; Ibarra-Manzano, M.-A. Rotor unbalance and broken rotor bar detection in inverter-fed induction motors at start-up and steady-state regimes by high-resolution spectral analysis. Electr. Power Syst. Res. 2016, 133, 142–148. [Google Scholar] [CrossRef]
- Xu, B.; Sun, L.; Xu, L.; Xu, G. An ESPRIT-SAA-Based Detection Method for Broken Rotor Bar Fault in Induction Motors. IEEE Trans. Energy Convers. 2012, 27, 654–660. [Google Scholar] [CrossRef]
- Samanta, A.K.; Naha, A.; Routray, A.; Deb, A.K. Fast and accurate spectral estimation for online detection of partial broken bar in induction motors. Mech. Syst. Signal Process. 2018, 98, 63–77. [Google Scholar] [CrossRef]
- Aydin, I.; Karakose, M.; Akin, E. An approach for automated fault diagnosis based on a fuzzy decision tree and boundary analysis of a reconstructed phase space. ISA Trans. 2014, 53, 220–229. [Google Scholar] [CrossRef]
- Bacha, K.; Ben Salem, S.; Chaari, A. An improved combination of Hilbert and Park transforms for fault detection and identification in three-phase induction motors. Int. J. Electr. Power Energy Syst. 2012, 43, 1006–1016. [Google Scholar] [CrossRef]
- Godoy, W.F.; da Silva, I.N.; Goedtel, A.; Palácios, R.H.C.; Lopes, T.D. Application of intelligent tools to detect and classify broken rotor bars in three-phase induction motors fed by an inverter. IET Electr. Power Appl. 2016, 10, 430–439. [Google Scholar] [CrossRef]
- Ferrucho-Alvarez, E.R.; Martinez-Herrera, A.L.; Cabal-Yepez, E.; Rodriguez-Donate, C.; Lopez-Ramirez, M.; Mata-Chavez, R.I. Broken Rotor Bar Detection in Induction Motors through Contrast Estimation. Sensors 2021, 21, 7446. [Google Scholar] [CrossRef]
- Pezzani, C.; Donolo, P.; Bossio, G.; Donolo, M.; Guzmán, A.; Zocholl, S.E. Detecting Broken Rotor Bars with Zero-Setting Protection. IEEE Trans. Ind. Appl. 2014, 50, 1373–1384. [Google Scholar] [CrossRef]
- Panagiotou, P.A.; Arvanitakis, I.; Lophitis, N.; Antonino-Daviu, J.A.; Gyftakis, K.N. A New Approach for Broken Rotor Bar Detection in Induction Motors Using Frequency Extraction in Stray Flux Signals. IEEE Trans. Ind. Appl. 2019, 55, 3501–3511. [Google Scholar] [CrossRef]
- Park, Y.; Choi, H.; Lee, S.B.; Gyftakis, K.N. Search Coil-based Detection of Non-adjacent Rotor Bar Damage in Squirrel Cage Induction Motors. IEEE Trans. Ind. Appl. 2020, 56, 4748–4757. [Google Scholar] [CrossRef]
- Antonino-Daviu, J.A.; Gyftakis, K.N.; Garcia-Hernandez, R.; Razik, H.; Cardoso, A.J.M. Comparative influence of adjacent and non-adjacent broken rotor bars on the induction motor diagnosis through MCSA and ZSC methods. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 001680–001685. [Google Scholar]
- Naha, A.; Samanta, A.K.; Routray, A.; Deb, A.K. A Method for Detecting Half-Broken Rotor Bar in Lightly Loaded Induction Motors Using Current. IEEE Trans. Instrum. Meas. 2016, 65, 1614–1625. [Google Scholar] [CrossRef]
- Singh, G.; Naikan, V. Detection of half broken rotor bar fault in VFD driven induction motor drive using motor square current MUSIC analysis. Mech. Syst. Signal Process. 2018, 110, 333–348. [Google Scholar] [CrossRef]
- Morales-Perez, C.; Rangel-Magdaleno, J.; Peregrina-Barreto, H.; Amezquita-Sanchez, J.P.; Valtierra-Rodriguez, M. Incipient Broken Rotor Bar Detection in Induction Motors Using Vibration Signals and the Orthogonal Matching Pursuit Algorithm. IEEE Trans. Instrum. Meas. 2018, 67, 2058–2068. [Google Scholar] [CrossRef]
- Garcia-Bracamonte, J.E.; Ramirez-Cortes, J.M.; Rangel-Magdaleno, J.D.J.; Gomez-Gil, P.; Peregrina-Barreto, H.; Alarcon-Aquino, V. An Approach on MCSA-Based Fault Detection Using Independent Component Analysis and Neural Networks. IEEE Trans. Instrum. Meas. 2019, 68, 1353–1361. [Google Scholar] [CrossRef]
- Filippetti, F.; Franceschini, G.; Tassoni, C.; Vas, P. AI techniques in induction machines diagnosis including the speed ripple effect. IEEE Trans. Ind. Appl. 1998, 34, 98–108. [Google Scholar] [CrossRef]
- Tan, L.; Jiang, J. (Eds.) Chapter 4—Discrete Fourier Transform and Signal Spectrum. In Digital Signal Processing, 3rd ed.; Academic Press: Cambridge, MA, USA, 2019; pp. 91–142. [Google Scholar]
- Jing, H.; Yang, L. Research on Window Function Selection in Phase Estimation of Digital Signal; Atlantis Press: Paris, France, 2017; pp. 1162–1165. [Google Scholar]
- Climente Alarcon, V.; Riera-Guasp, M. Rotor Bar Breakage Data Obtained from Fatigue Test [Dataset]; Universitat Politècnica de València: Valencia, Spain, 2019. [Google Scholar] [CrossRef]
- Kim, Y.-H.; Youn, Y.-W.; Hwang, D.-H.; Sun, J.-H.; Kang, D.-S. High-Resolution Parameter Estimation Method to Identify Broken Rotor Bar Faults in Induction Motors. IEEE Trans. Ind. Electron. 2012, 60, 4103–4117. [Google Scholar] [CrossRef]
- Cabanas, M.F.; Pedrayes, F.; Rojas-Garcia, C.H.; Melero, M.G.; Norniella, J.G.; Orcajo, G.A.; Cano, J.M.; Nuno, F.; Fuentes, D.R. A New Portable, Self-Powered, and Wireless Instrument for the Early Detection of Broken Rotor Bars in Induction Motors. IEEE Trans. Ind. Electron. 2011, 58, 4917–4930. [Google Scholar] [CrossRef]
- Moussa, M.A.; Boucherma, M.; Khezzar, A. A Detection Method for Induction Motor Bar Fault Using Sidelobes Leakage Phenomenon of the Sliding Discrete Fourier Transform. IEEE Trans. Power Electron. 2016, 32, 5560–5572. [Google Scholar] [CrossRef]
- Puche-Panadero, R.; Pineda-Sanchez, M.; Riera-Guasp, M.; Roger-Folch, J.; Hurtado-Perez, E.; Perez-Cruz, J. Improved Resolution of the MCSA Method Via Hilbert Transform, Enabling the Diagnosis of Rotor Asymmetries at Very Low Slip. IEEE Trans. Energy Convers. 2009, 24, 52–59. [Google Scholar] [CrossRef]
- Climente-Alarcon, V.; Nair, D.; Sundaria, R.; Antonino-Daviu, J.A.; Arkkio, A. Combined Model for Simulating the Effect of Transients on a Damaged Rotor Cage. IEEE Trans. Ind. Appl. 2017, 53, 3528–3537. [Google Scholar] [CrossRef][Green Version]
- Climente-Alarcon, V.; Antonino-Daviu, J.A.; Riera-Guasp, M.; Vlcek, M. Induction Motor Diagnosis by Advanced Notch FIR Filters and the Wigner–Ville Distribution. IEEE Trans. Ind. Electron. 2014, 61, 4217–4227. [Google Scholar] [CrossRef]
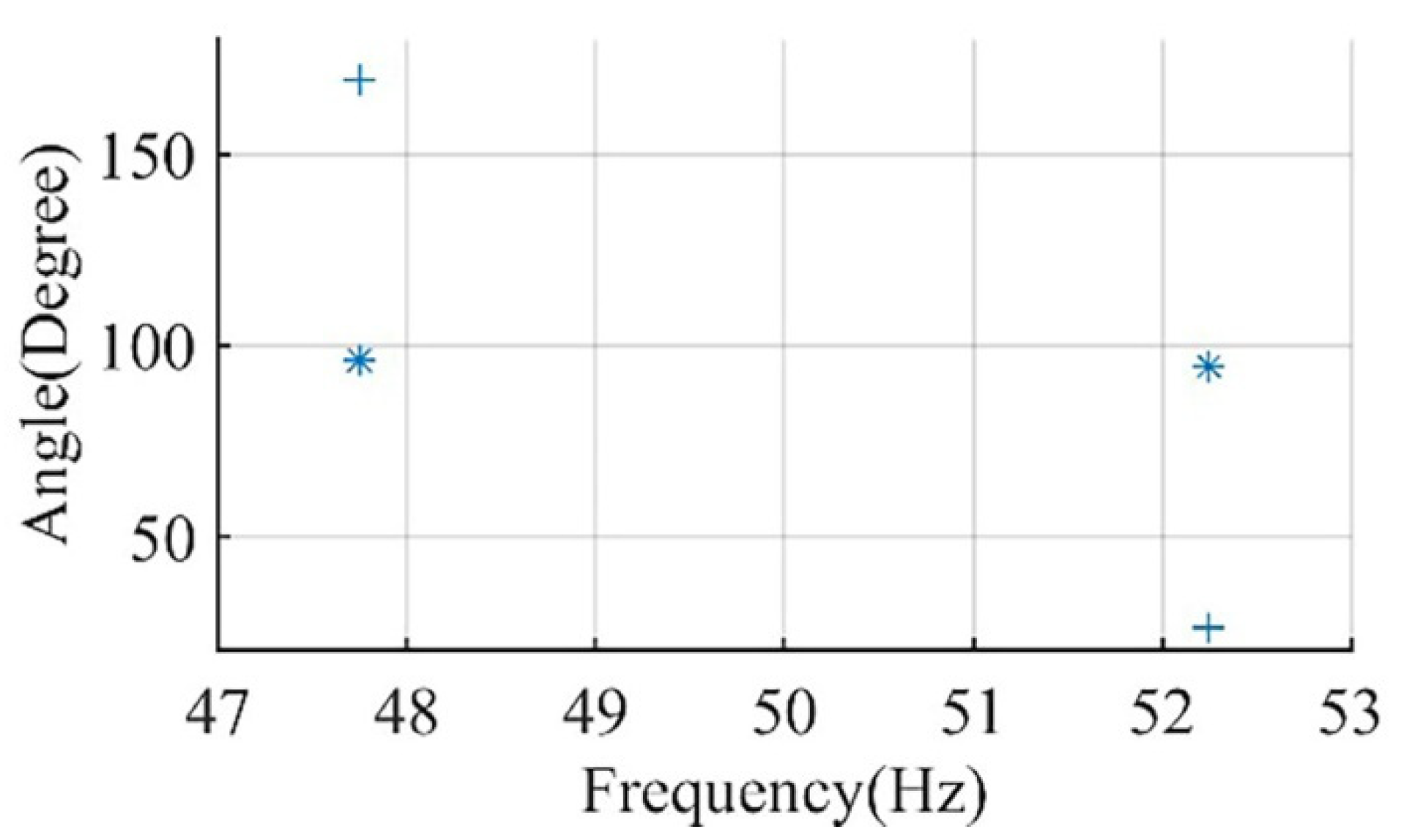
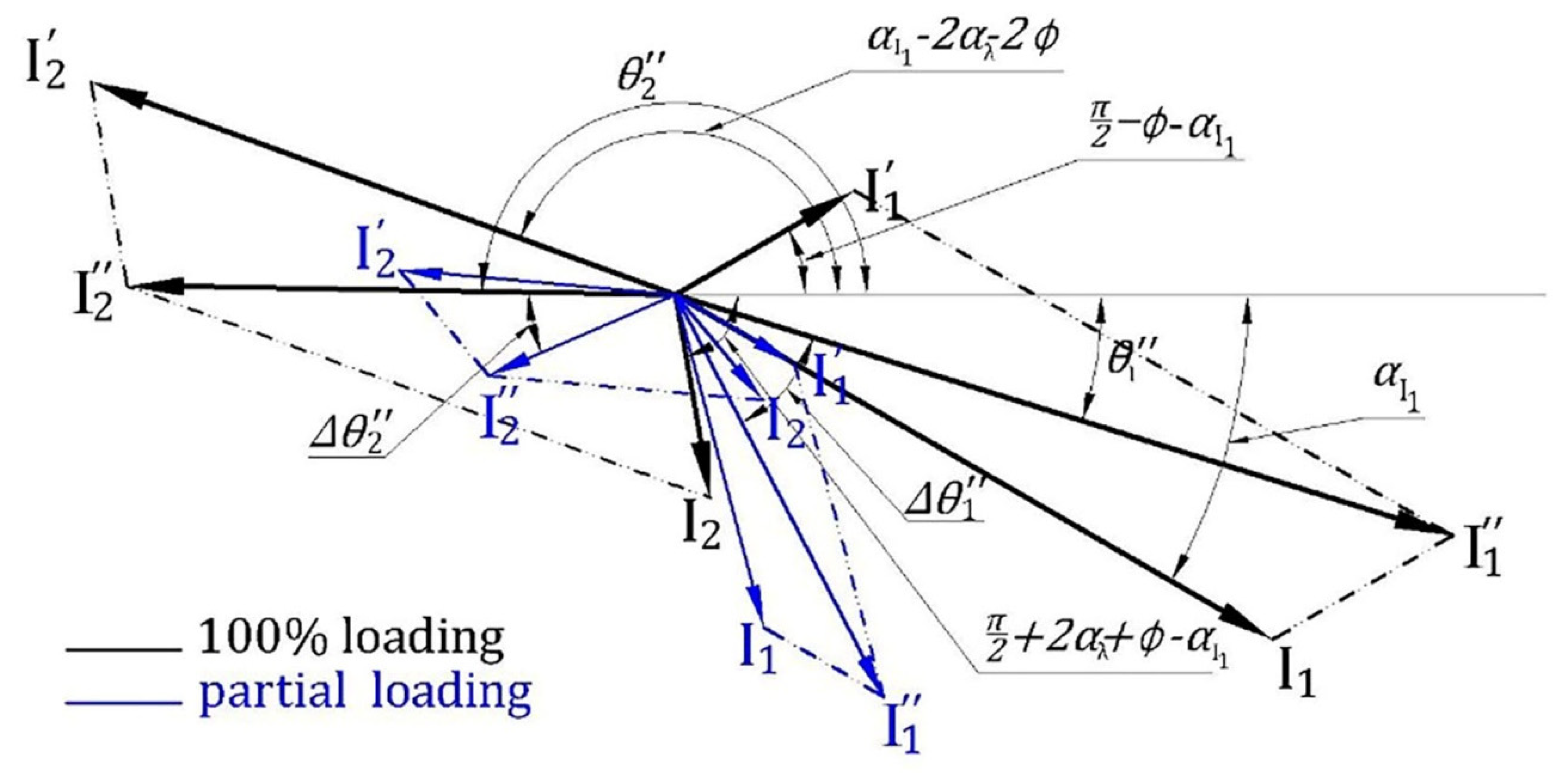
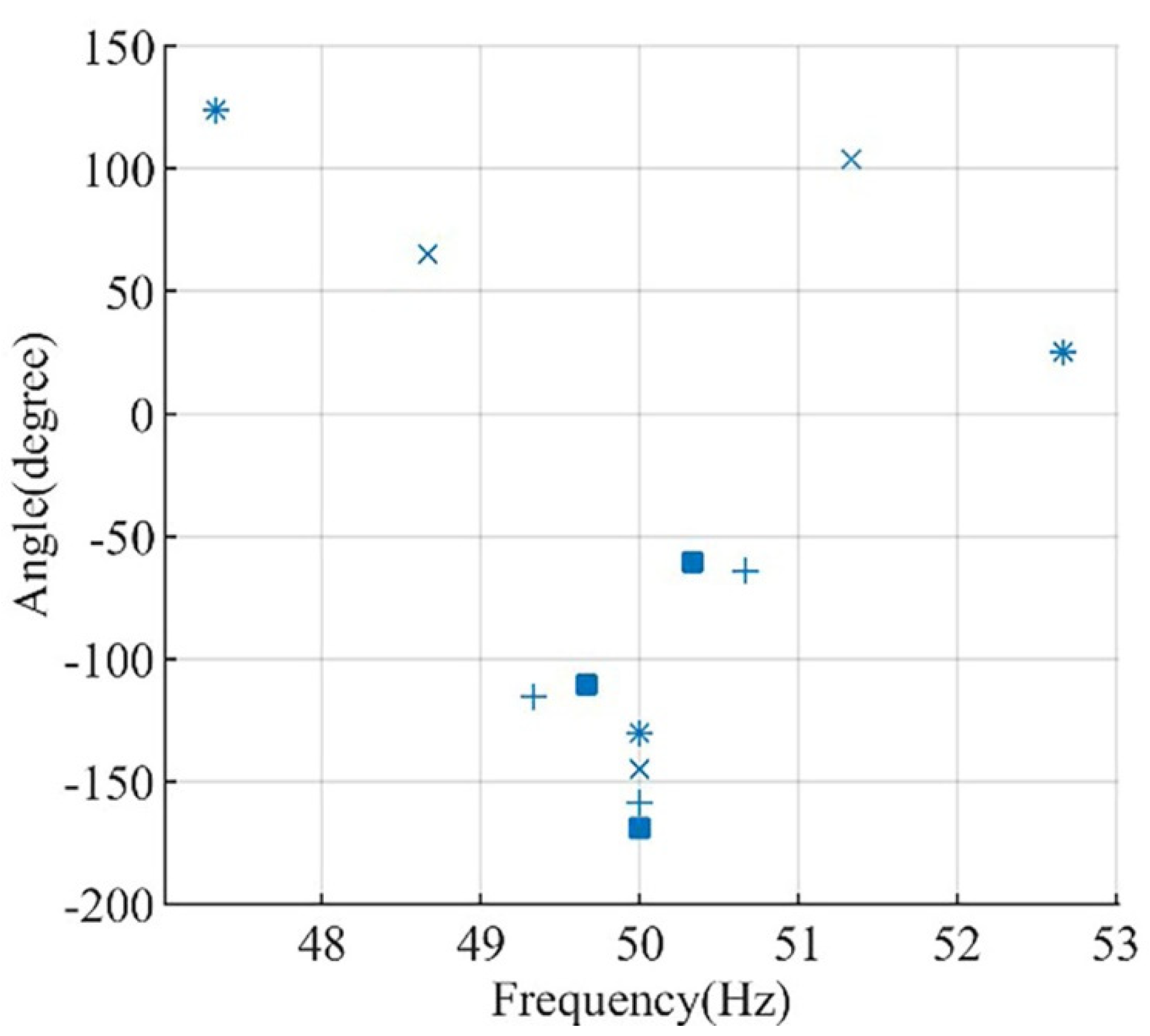
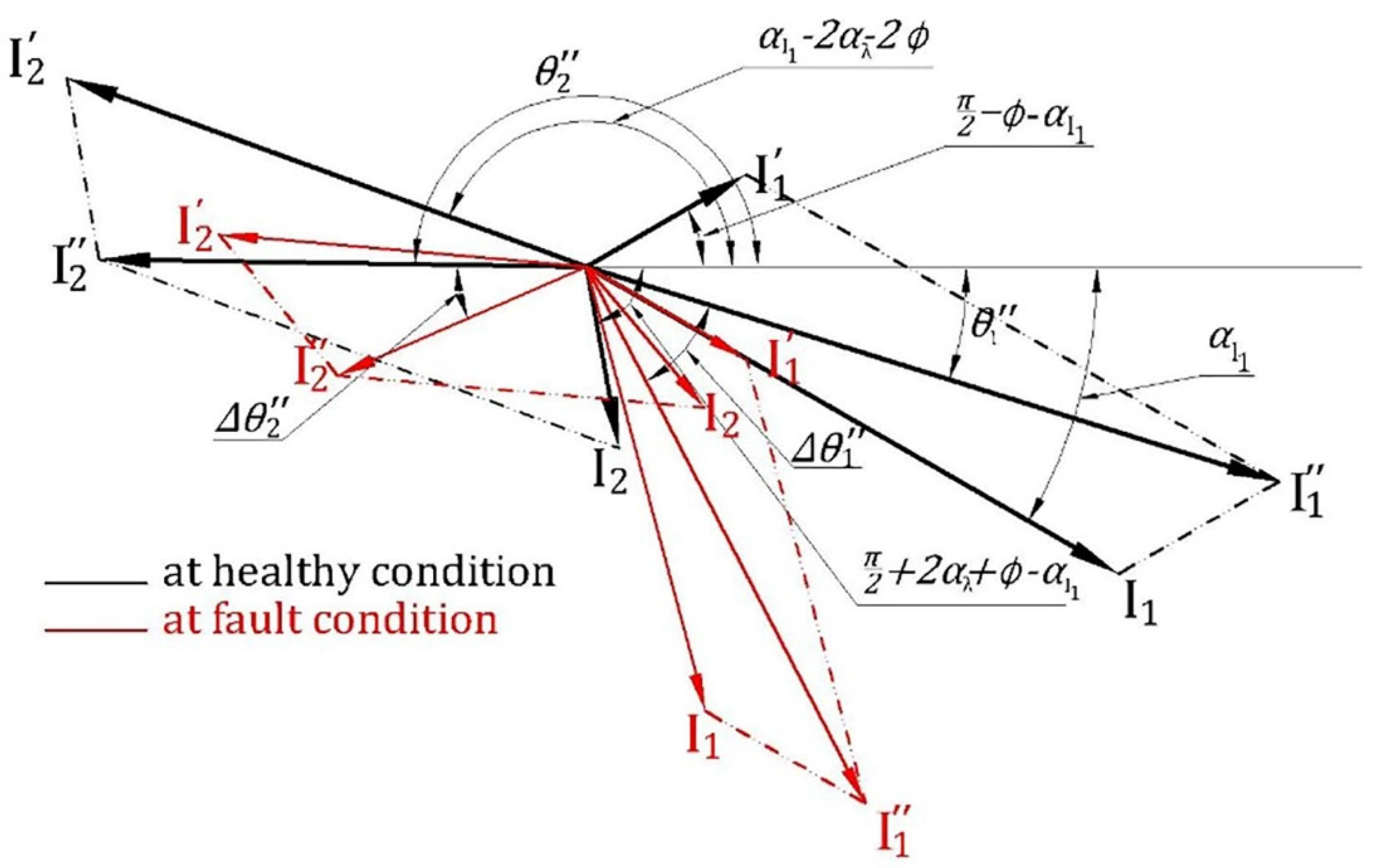

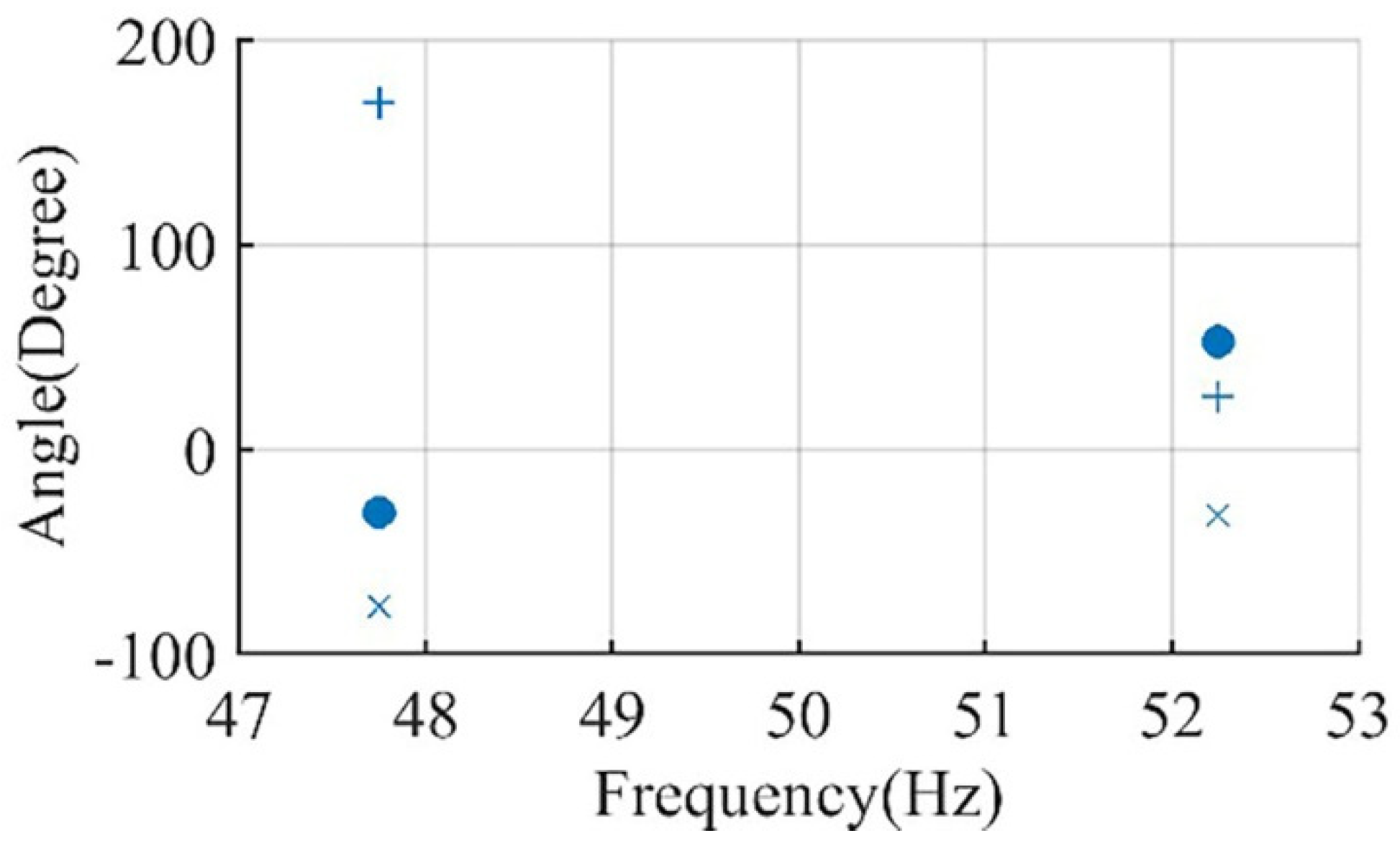

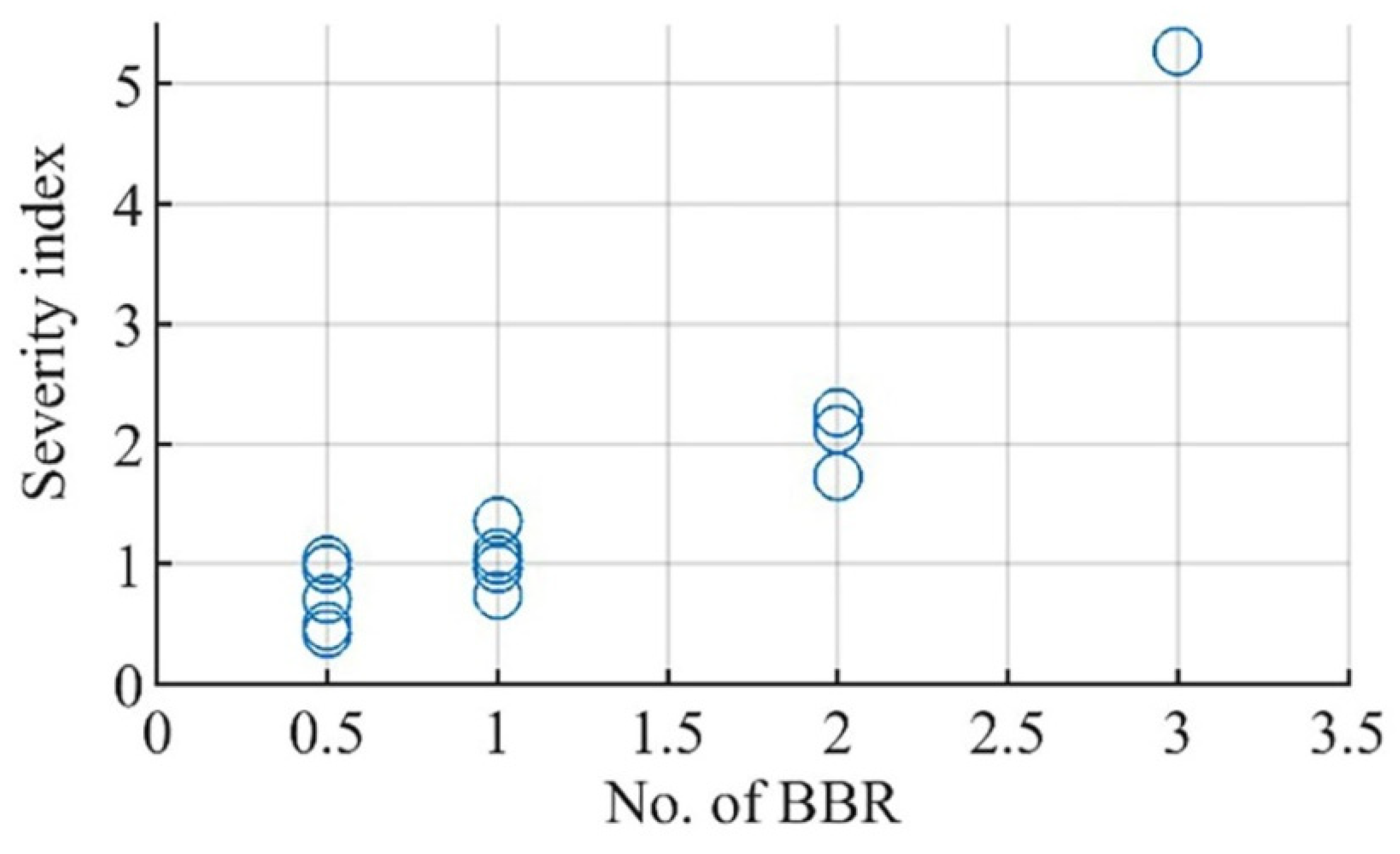
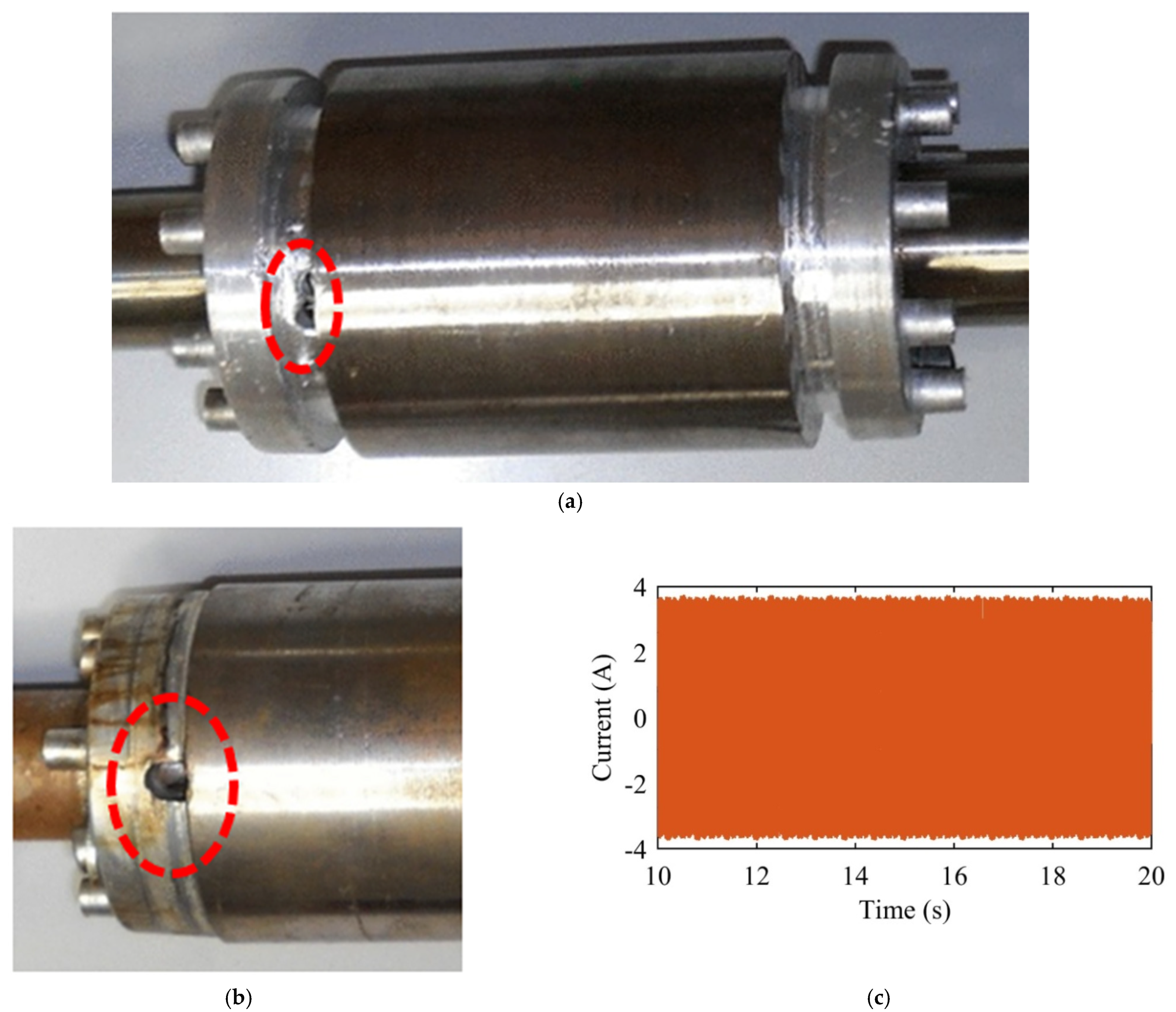
| Data | Motor I [4] | Motor II |
|---|---|---|
| Power | 11 kW | 11 kW |
| Voltage (rms) | 380 V | 380 V |
| No. of poles | 4 | 6 |
| Rated slip | 2.9% | 2.3% |
| Number of stator slots | 36 | 72 |
| Number of rotor bars | 28 | 58 |
| Number of turns | 27 | 6 |
| Silicon steel material | M19_29G | M19_24G |
| Case No. | Case Description | Performance of the Proposed Scheme | |||||
|---|---|---|---|---|---|---|---|
| Healthy/BBFs | Loading Condition (%) | Inertial Condition (kg·m2) | Estimated Threshold (°) | Calculated Phase Angle Difference (°) | Status | Severity Index | |
| 1 | Healthy | Full load | 5.7 | 49.97 | 8.62 | Healthy | -------- |
| 2 | BBR | Full load | 5.7 | 52.09 | 120 | Fault | 0.965 |
| 3 | Half BBR | Full load | 5.7 | 56.28 | 132.5 | Fault | 0.418 |
| 4 | Healthy | Full load | 0.625 | 22.58 | 0.91 | Healthy | -------- |
| 5 | Non-adjacent 2 BBR | Full load | 0.625 | 20.72 | 170.1 | Fault | 1.73 |
| 6 | 2 BBR | Full load | 0.625 | 23.27 | 155.1 | Fault | 2.126 |
| 7 | BBR | Full load | 0.625 | 23.74 | 145.30 | Fault | 1.034 |
| 8 | Healthy | Full load | 0.925 | 23.59 | 1.43 | Healthy | -------- |
| 9 | 3 BBR | Full load | 0.925 | 19.2085 | 104.5312 | Fault | 5.27 |
| 10 | Non-adjacent 2 BBR | Full load | 0.0625 | 19.99 | 141.4 | Fault | 2.26 |
| 11 | BBR | 50% | 0.0625 | 22.23 | 60.9 | Fault | 1.36 |
| 12 | Half BBR | 50% | 0.0625 | 24.56 | 43.44 | Fault | 1.030 |
| 13 | Healthy | 25% | 0.0625 | 26.42 | 2.72 | Healthy | -------- |
| 14 | BBR | 25% | 0.0625 | 24.16 | 50.6 | Fault | 1.09 |
| 15 | Half BBR | 25% | 0.0625 | 26.09 | 28.94 | Fault | 0.96 |
| 16 | Healthy | 10% | 0.0625 | 29.00 | 0.71 | Healthy | -------- |
| 17 | BBR | 10% | 0.0625 | 26.19 | 154.6 | Fault | 0.736 |
| 18 | Half BBR | 10% | 0.0625 | 27.81 | 102.38 | Fault | 0.708 |
| 19 | Healthy + 20 db Noise | Full load | 0.0625 | 21.2 | 9.75 | Healthy | -------- |
| 20 | Half BBR + 20 db Noise | Full load | 5.7 | 36.9 | 76.03 | Fault | 0.484 |
| 21 | Half BBR + 18.5 db Noise | 25% | 0.0625 | 20.67 | 34.74 | Fault | 1.96 |
| Case No. | Case Description | Performance of the Proposed Scheme | ||||
|---|---|---|---|---|---|---|
| Healthy/BBFs | Loading Condition (%) | Inertial Condition (kg·m2) | Estimated Threshold (°) | Calculated Difference (°) | Status | |
| 1 | Healthy | Full load | 0.0410 | 64.08 | 5.85 | Healthy |
| 2 | Half BBR | Full load | 0.0410 | 48.49 | 169.67 | Fault |
| 3 | Half BBR | Full load | 16.84 | 48.56 | 60.58 | Fault |
| 4 | Healthy | 90% loading | 0.0410 | 49.57 | 3.13 | Healthy |
| Case No. | Case Description | Performance of the Proposed Scheme | |||||
|---|---|---|---|---|---|---|---|
| Healthy/BBFs | Loading Condition (%) | Inertial Condition (kg·m2) | Estimated Threshold (°) | Calculated Phase Angle Difference (°) | Status | Severity Index | |
| 1 | Healthy | Full load | 0.11 | 13.015 | 3.2 | Healthy | -------- |
| 2 | Healthy | Full load | 0.11 | 14.5 | 3.4 | Healthy | -------- |
| 3 | A bar with one 3 mm diameter hole | Full load | 0.11 | 18.5 | 77.94 | Fault | 0.78 |
| 4 | One bar with two 3 mm diameter holes each | Full load | 0.11 | 18.069 | 93.836 | Fault | 4.17 |
| 5 | One bar with two 4 mm diameter holes each | Full load | 0.11 | 18.071 | 160.78 | Fault | 5.02 |
| 6 | One full broken bar | Full load | 0.11 | 13.5 | 166.49 | Fault | 7.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atta, M.E.E.-D.; Ibrahim, D.K.; Gilany, M.; Zobaa, A.F. Adaptive Scheme for Detecting Induction Motor Incipient Broken Bar Faults at Various Load and Inertia Conditions. Sensors 2022, 22, 365. https://doi.org/10.3390/s22010365
Atta MEE-D, Ibrahim DK, Gilany M, Zobaa AF. Adaptive Scheme for Detecting Induction Motor Incipient Broken Bar Faults at Various Load and Inertia Conditions. Sensors. 2022; 22(1):365. https://doi.org/10.3390/s22010365
Chicago/Turabian StyleAtta, Mohamed Esam El-Dine, Doaa Khalil Ibrahim, Mahmoud Gilany, and Ahmed F. Zobaa. 2022. "Adaptive Scheme for Detecting Induction Motor Incipient Broken Bar Faults at Various Load and Inertia Conditions" Sensors 22, no. 1: 365. https://doi.org/10.3390/s22010365
APA StyleAtta, M. E. E.-D., Ibrahim, D. K., Gilany, M., & Zobaa, A. F. (2022). Adaptive Scheme for Detecting Induction Motor Incipient Broken Bar Faults at Various Load and Inertia Conditions. Sensors, 22(1), 365. https://doi.org/10.3390/s22010365







