Advanced Network Sampling with Heterogeneous Multiple Chains
Abstract
1. Introduction
- We propose the concept of a network sampling method with heterogeneous multiple Markov chains, which can traverse the entire target space on a database with network-structured data.
- We apply advanced non-reversible random walk on edge space as an augmented state to obtain better unbiased sampling results.
- Experiments on synthetic or real–world databases with scale–free network properties demonstrate that the proposed method can preserve the statistical characteristics of the original network-structured data.
2. Related Work
2.1. Network (Graph) Sampling
2.2. Sampling under Restricted Access
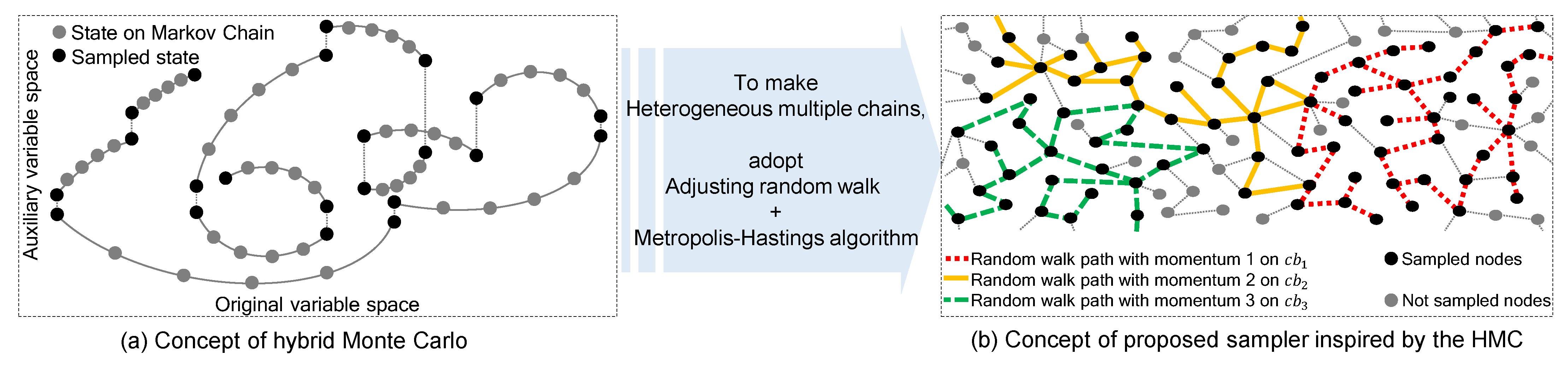
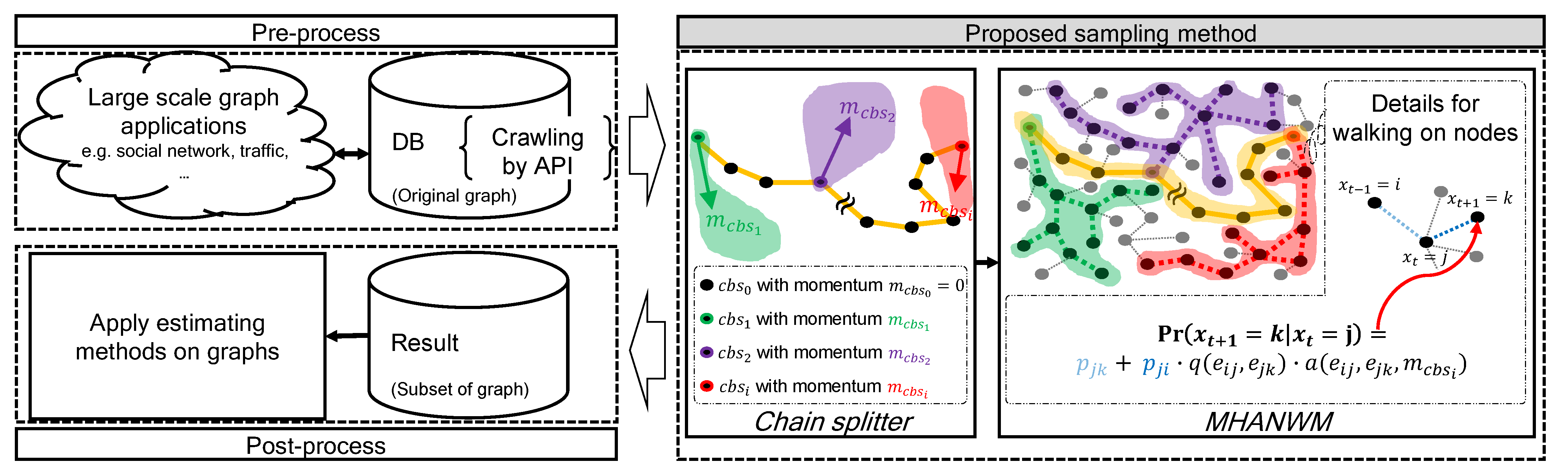
3. Proposed Method
3.1. Chain Splitter
3.2. MHANWM (Metropolis–Hastings Advanced Non-Reversible Walk with Momentum)
| Algorithm 1: Network sampling at xt |
 |
4. Experimental Evaluation
4.1. Evaluation Methodology
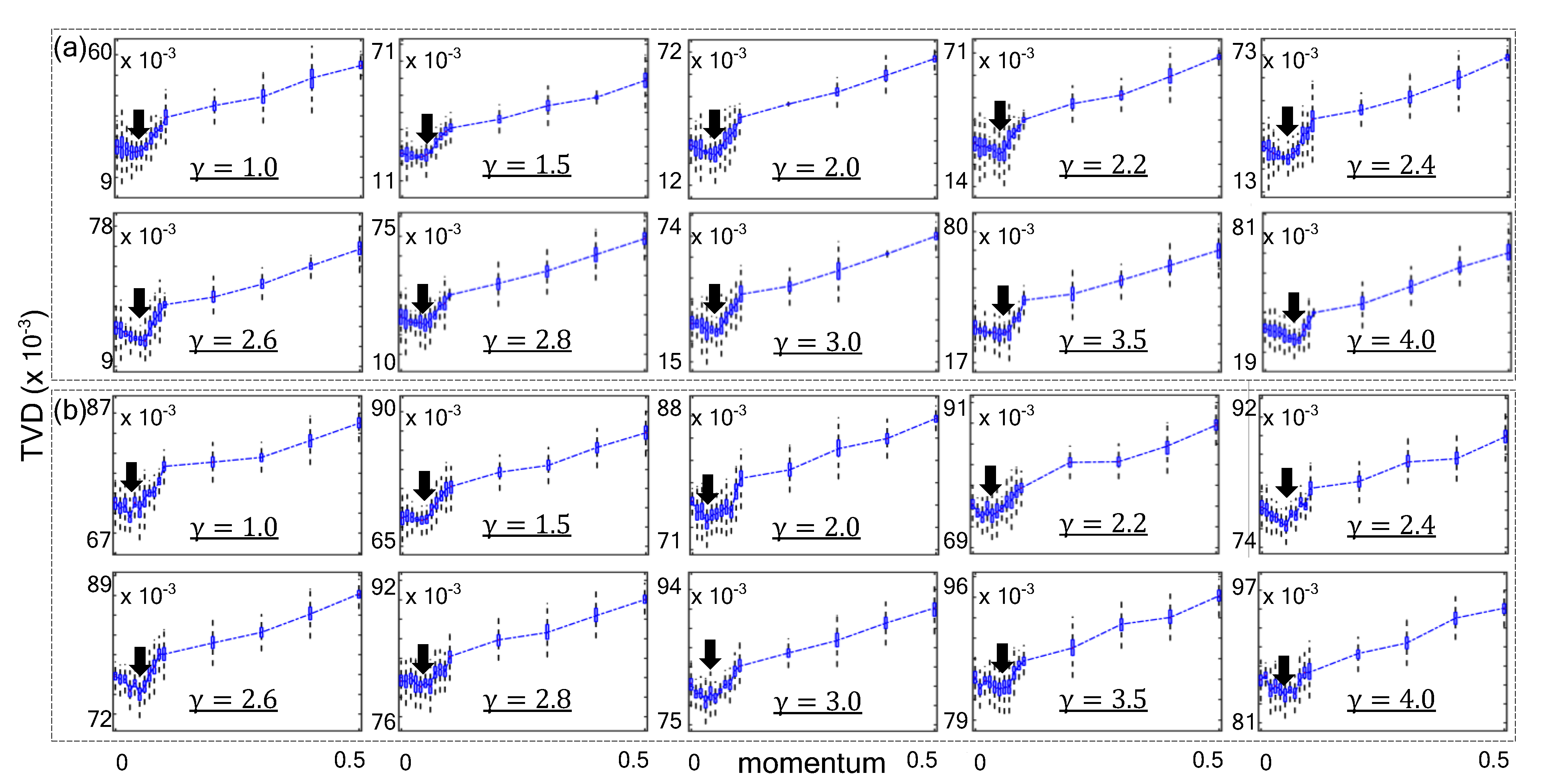
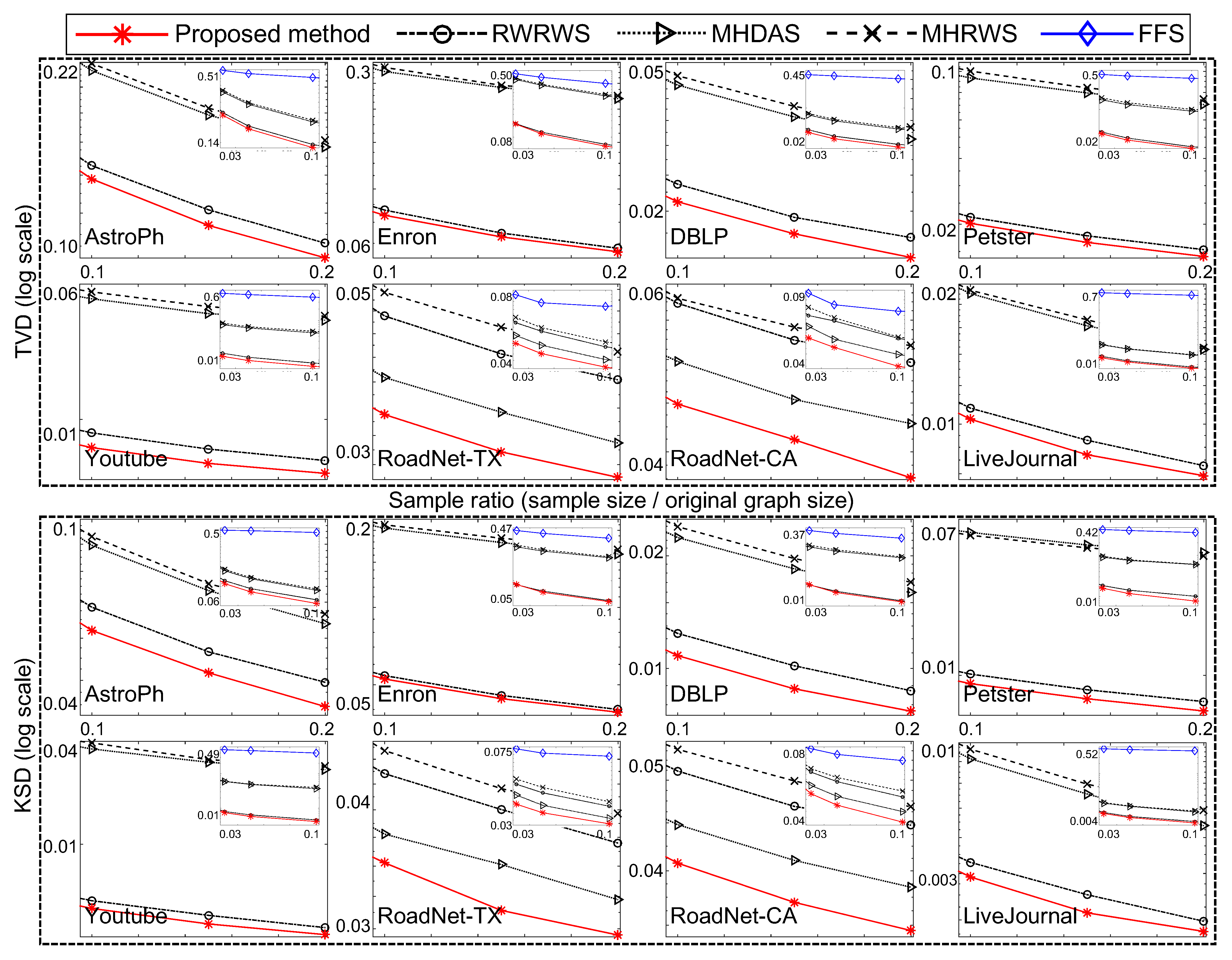
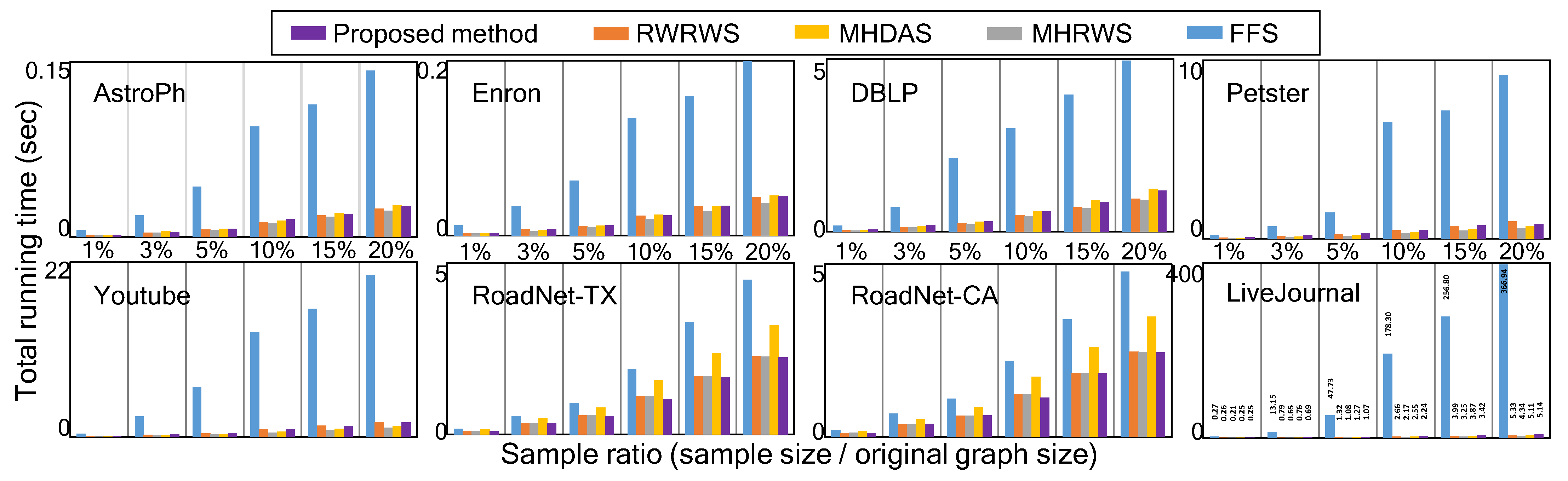
4.2. Experimental Results
4.3. Discussion
| Algorithm 2: Parallelization |
 |
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Facebook Reports Second Quarter 2020 Results. 2020. Available online: https://investor.fb.com/investor-news/press-release-details/2020/Facebook-Reports-Second-Quarter-2020-Results/default.aspx (accessed on 30 July 2020).
- How Big Is the Internet of Things? How Big Will It Get? 2020. Available online: https://paxtechnica.org/?page_id=738 (accessed on 30 July 2020).
- Krishnamachari, B.; Estrin, D.; Wicker, S. The impact of data aggregation in wireless sensor networks. In Proceedings of the 22nd International Conference on Distributed Computing Systems Workshops, Vienna, Austria, 2–5 July 2002; pp. 575–578. [Google Scholar]
- Jeong, H.; Tombor, B.; Albert, R.; Oltvai, Z.N.; Barabási, A.L. The large-scale organization of metabolic networks. Nature 2000, 407, 651–654. [Google Scholar] [CrossRef] [PubMed]
- Krishnamurthy, V.; Faloutsos, M.; Chrobak, M.; Lao, L.; Cui, J.H.; Percus, A.G. Reducing large internet topologies for faster simulations. In Networking 2005. Networking Technologies, Services, and Protocols; Springer: Berlin/Heidelberg, Germany, 2005; pp. 328–341. [Google Scholar]
- Sharan, R.; Ideker, T.; Kelley, B.; Shamir, R.; Karp, R.M. Identification of protein complexes by comparative analysis of yeast and bacterial protein interaction data. J. Comput. Biol. 2005, 12, 835–846. [Google Scholar] [CrossRef] [PubMed]
- Leskovec, J.; McGlohon, M.; Faloutsos, C.; Glance, N.S.; Hurst, M. Patterns of Cascading behavior in large blog graphs. In Proceedings of the 2007 SIAM International Conference on Data Mining, Minneapolis, MN, USA, 26–28 April 2007; Volume 7, pp. 551–556. [Google Scholar]
- Liu, Y.; Ning, P.; Reiter, M.K. False data injection attacks against state estimation in electric power grids. ACM Trans. Inf. Syst. Secur. 2011, 14, 13. [Google Scholar] [CrossRef]
- Agmon, N.; Shabtai, A.; Puzis, R. Deployment optimization of IoT devices through attack graph analysis. In Proceedings of the 12th Conference on Security and Privacy in Wireless and Mobile Networks, New York, NY, USA, 15–17 May 2019; pp. 192–202. [Google Scholar]
- Newman, M.E. Spread of epidemic disease on networks. Phys. Rev. E 2002, 66, 016128. [Google Scholar] [CrossRef] [PubMed]
- Girvan, M.; Newman, M.E. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed]
- Page, L.; Brin, S.; Motwani, R.; Winograd, T. The PageRank Citation Ranking: Bringing Order to the Web; Stanford InfoLab.: Stanford, CA, USA, 1999. [Google Scholar]
- Pržulj, N. Biological network comparison using graphlet degree distribution. Bioinformatics 2007, 23, e177–e183. [Google Scholar] [CrossRef] [PubMed]
- Malewicz, G.; Austern, M.H.; Bik, A.J.; Dehnert, J.C.; Horn, I.; Leiser, N.; Czajkowski, G. Pregel: A system for large-scale graph processing. In Proceedings of the 2010 ACM SIGMOD International Conference on Management of Data, Indianapolis, IN, USA, 6–10 June 2010; pp. 135–146. [Google Scholar]
- Low, Y.; Bickson, D.; Gonzalez, J.; Guestrin, C.; Kyrola, A.; Hellerstein, J.M. Distributed GraphLab: A framework for machine learning and data mining in the cloud. Proc. VLDB Endow. 2012, 5, 716–727. [Google Scholar] [CrossRef]
- Xin, R.S.; Gonzalez, J.E.; Franklin, M.J.; Stoica, I. Graphx: A resilient distributed graph system on spark. In Proceedings of the First International Workshop on Graph Data Management Experiences and Systems, New York, NY, USA, 24 June 2013; p. 2. [Google Scholar]
- Duane, S.; Kennedy, A.D.; Pendleton, B.J.; Roweth, D. Hybrid monte carlo. Phys. Lett. B 1987, 195, 216–222. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin, Germany, 2006. [Google Scholar]
- Neal, R.M. MCMC using Hamiltonian dynamics. In Handbook of Markov Chain Monte Carlo; CRC press: Boca Raton, FL, USA, 2011; Volume 2. [Google Scholar]
- Hu, P.; Lau, W.C. A survey and taxonomy of graph sampling. arXiv 2013, arXiv:1308.5865. [Google Scholar]
- Leskovec, J.; Faloutsos, C. Sampling from large graphs. In Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Philadelphia, PA, USA, 20–23 August 2006; pp. 631–636. [Google Scholar]
- Cormen, T.H. Introduction to Algorithms; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Goodman, L.A. Snowball sampling. Ann. Math. Stat. 1961, 32, 148–170. [Google Scholar] [CrossRef]
- Rasti, A.H.; Torkjazi, M.; Rejaie, R.; Duffield, N.; Willinger, W.; Stutzbach, D. Respondent-driven sampling for characterizing unstructured overlays. In Proceedings of the IEEE INFOCOM 2009, Rio de Janeiro, Brazil, 19–25 April 2009; pp. 2701–2705. [Google Scholar]
- Gjoka, M.; Kurant, M.; Butts, C.T.; Markopoulou, A. Walking in Facebook: A case study of unbiased sampling of OSNs. In Proceedings of the 2010 Proceedings IEEE INFOCOM, San Diego, CA, USA, 14–19 March 2010; pp. 1–9. [Google Scholar]
- Mira, A. On Metropolis-Hastings algorithms with delayed rejection. Metron 2001, 59, 231–241. [Google Scholar]
- Lee, C.H.; Xu, X.; Eun, D.Y. Beyond random walk and metropolis-hastings samplers: Why you should not backtrack for unbiased graph sampling. In Proceedings of the ACM SIGMETRICS Performance Evaluation Review, London, UK, 11–15 June 2012; Volume 40, pp. 319–330. [Google Scholar]
- Avrachenkov, K.; Ribeiro, B.; Towsley, D. Improving random walk estimation accuracy with uniform restarts. In Algorithms and Models for the Web-Graph; Springer: Berlin, Germany, 2010; pp. 98–109. [Google Scholar]
- Cheng, K. Sampling from Large Graphs with a Reservoir. In Proceedings of the 2014 17th International Conference on NBiS, Salerno, Italy, 10–12 September 2014; pp. 347–354. [Google Scholar]
- Aldous, D.; Fill, J. Reversible Markov Chains and Random Walks on Graphs; University of California: Berkeley, CA, USA, 2014. [Google Scholar]
- Alon, N.; Benjamini, I.; Lubetzky, E.; Sodin, S. Non-backtracking random walks mix faster. Commun. Contemp. Math. 2007, 9, 585–603. [Google Scholar] [CrossRef]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47. [Google Scholar] [CrossRef]
- Onnela, J.P.; Saramäki, J.; Hyvönen, J.; Szabó, G.; Lazer, D.; Kaski, K.; Kertész, J.; Barabási, A.L. Structure and tie strengths in mobile communication networks. Proc. Natl. Acad. Sci. USA 2007, 104, 7332–7336. [Google Scholar] [CrossRef] [PubMed]
- Choromański, K.; Matuszak, M.; Miȩkisz, J. Scale-free graph with preferential attachment and evolving internal vertex structure. J. Stat. Phys. 2013, 151, 1175–1183. [Google Scholar] [CrossRef]
- Mira, A.; Geyer, C.J. On non-reversible Markov chains. In Monte Carlo Methods; Fields Institute/AMS: Toronto, ON, Canada, 2000; pp. 95–110. [Google Scholar]
- Roberts, G.O.; Rosenthal, J.S. General state space Markov chains and MCMC algorithms. Probab. Surv. 2004, 1, 20–71. [Google Scholar] [CrossRef]
- Leskovec, J.; Krevl, A. SNAP Datasets: Stanford Large Network Dataset Collection. 2014. Available online: http://snap.stanford.edu/data (accessed on 3 October 2020).
- Kunegis, J. Konect: The koblenz network collection. In Proceedings of the 22nd International Conference on World Wide Web Companion, Rio de Janeiro, Brazil, 13–17 May 2013; pp. 1343–1350. [Google Scholar]
- Ahmed, N.K.; Duffield, N.; Neville, J.; Kompella, R. Graph sample and hold: A framework for big-graph analytics. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 1446–1455. [Google Scholar]
- Ribeiro, B.; Towsley, D. Estimating and sampling graphs with multidimensional random walks. In Proceedings of the 10th ACM SIGCOMM Conference on Internet Measurement, Melbourne, Australia, 1–3 November 2010; pp. 390–403. [Google Scholar]
- Bar-Yossef, Z.; Gurevich, M. Random sampling from a search engine’s index. J. ACM 2008, 55, 24. [Google Scholar] [CrossRef]
- Daniel, W.W. Applied Nonparametric Statistics; PWS-Kent: Boston, MA, USA, 1990. [Google Scholar]




| Notation | Definition |
|---|---|
| g | graph or network |
| n | node |
| number of nodes | |
| e, | edge, edge between node i and node j |
| number of edges | |
| degree of node i | |
| neighbors of node i | |
| s | sample set |
| size of total sample set | |
| w | weight vector |
| length of weight vector | |
| chain block subset of total sample | |
| number of chain block | |
| N | original state-space |
| E | augmented state-space |
| x | original state (variable) |
| augmented state (variable) | |
| momentum of chain block | |
| mean of the momentum distribution | |
| variance of the momentum distribution | |
| probability | |
| q | proposal probability distribution |
| a | acceptance probability |
| stationary distribution | |
| transition matrix with elements | |
| transition probability from state to state , | |
| transition matrix of augmented state-space |
| Access Types | Sampling Approaches | Algorithms |
|---|---|---|
| Full | Node | Random Node Sampling (RNS) [20,21] |
| Random Degree Node Sampling (RDNS) [21] | ||
| Edge | Edge Random Edge Sampling (RES) [20,21] | |
| Node-Edge | Random Node-Edge Sampling (RNES) [21] | |
| Full or Restricted | Traversal | Breadth First Sampling (BFS) [22] |
| Depth First Sampling (DFS) [22] | ||
| Snowball Sampling (SBS) [23] | ||
| Forest Fire Sampling (FFS) [21] | ||
| Random Walk | Basic Random-Walk Sampling (RWS) [21] | |
| Re-Weighted Random-Walk Sampling (RWRWS) [24,25] | ||
| Metropolis–Hastings Random-Walk Sampling (MHRWS) [24,25] | ||
| Metropolis–Hastings Random-Walk with Delay acceptance Sampling (MHDAS) [26,27] | ||
| Random Walk with Restart Sampling (RWRS) [21] | ||
| Random Walk with Random Jump Sampling (RWRJS) [21,28] | ||
| Stream | Online | Random Reservoir Sampling (RRS) [29] |
| in LWCC | ACC | |||||
|---|---|---|---|---|---|---|
| AstroPh | 14 | |||||
| Enron | 11 | |||||
| DBLP | 21 | |||||
| Petster | 15 | |||||
| YouTube | 20 | |||||
| RoadNet-TX | 1054 | |||||
| RoadNet-CA | 849 | |||||
| LiveJournal | 17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Yoon, M.; Noh, S. Advanced Network Sampling with Heterogeneous Multiple Chains. Sensors 2021, 21, 1905. https://doi.org/10.3390/s21051905
Lee J, Yoon M, Noh S. Advanced Network Sampling with Heterogeneous Multiple Chains. Sensors. 2021; 21(5):1905. https://doi.org/10.3390/s21051905
Chicago/Turabian StyleLee, Jaekoo, MyungKeun Yoon, and Song Noh. 2021. "Advanced Network Sampling with Heterogeneous Multiple Chains" Sensors 21, no. 5: 1905. https://doi.org/10.3390/s21051905
APA StyleLee, J., Yoon, M., & Noh, S. (2021). Advanced Network Sampling with Heterogeneous Multiple Chains. Sensors, 21(5), 1905. https://doi.org/10.3390/s21051905






