An Intraocular Pressure Measurement Technique Based on Acoustic Radiation Force Using an Ultrasound Transducer: A Feasibility Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Acoustic Radiation Force
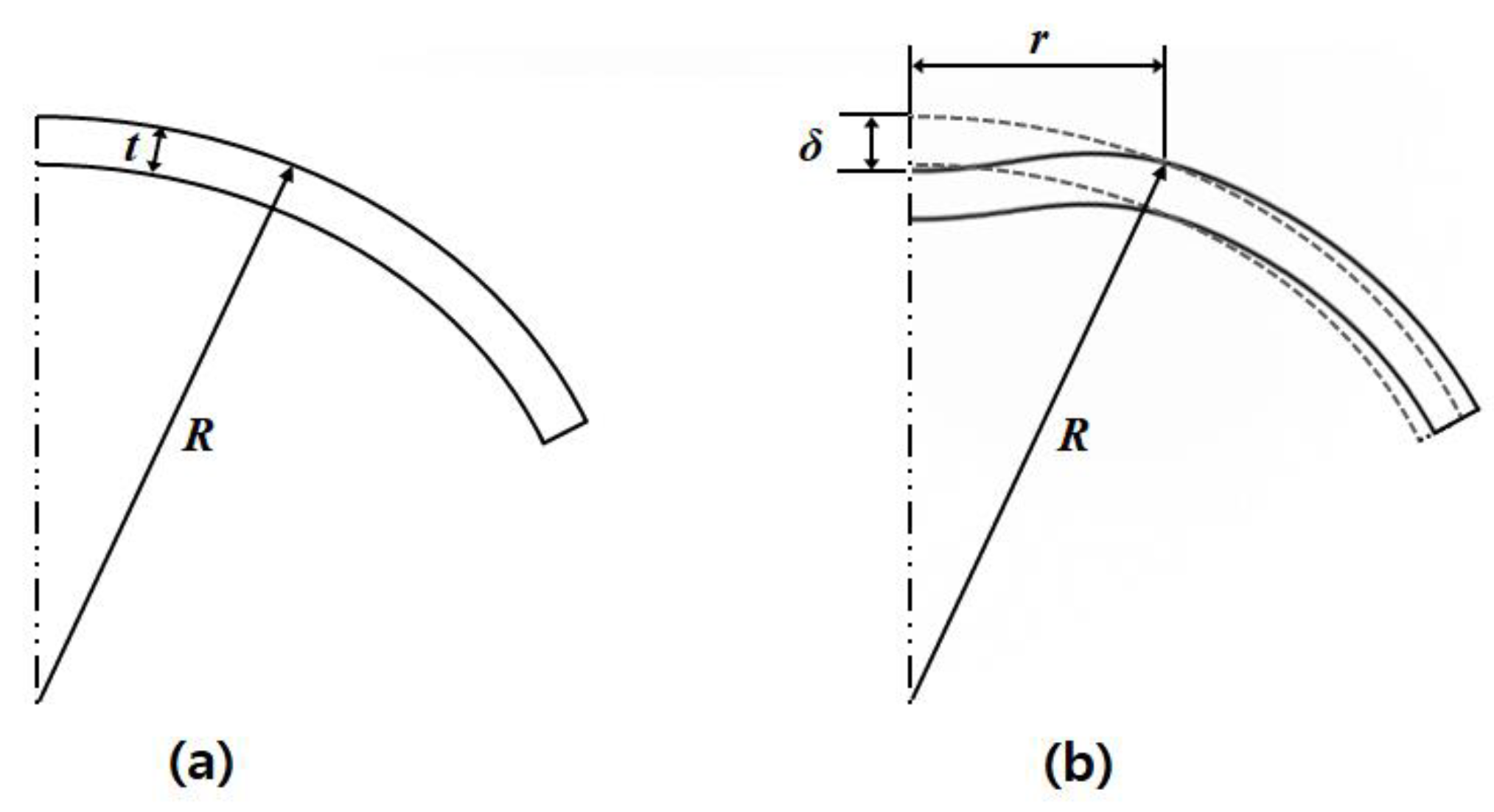
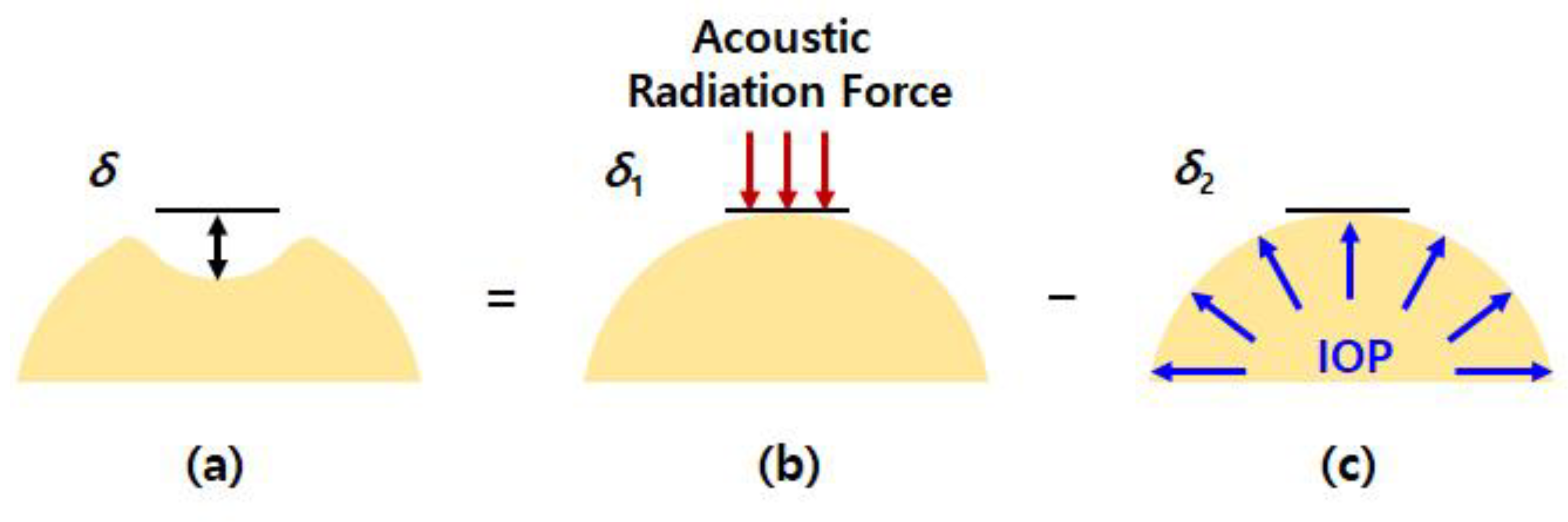
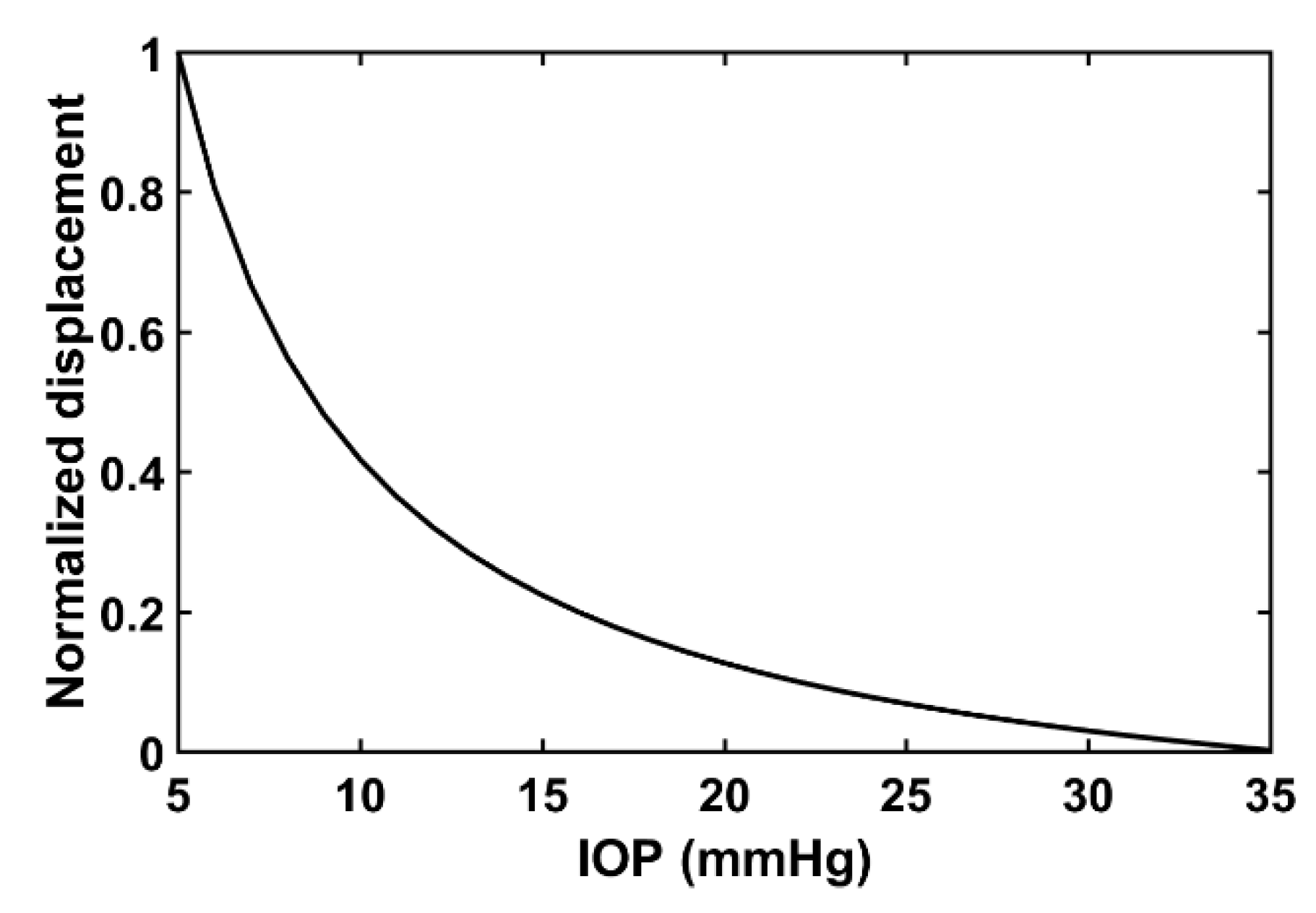
2.2. Relationship between Acoustic Radiation Force Induced Displacement and Internal Pressure
3. Experimental Validation
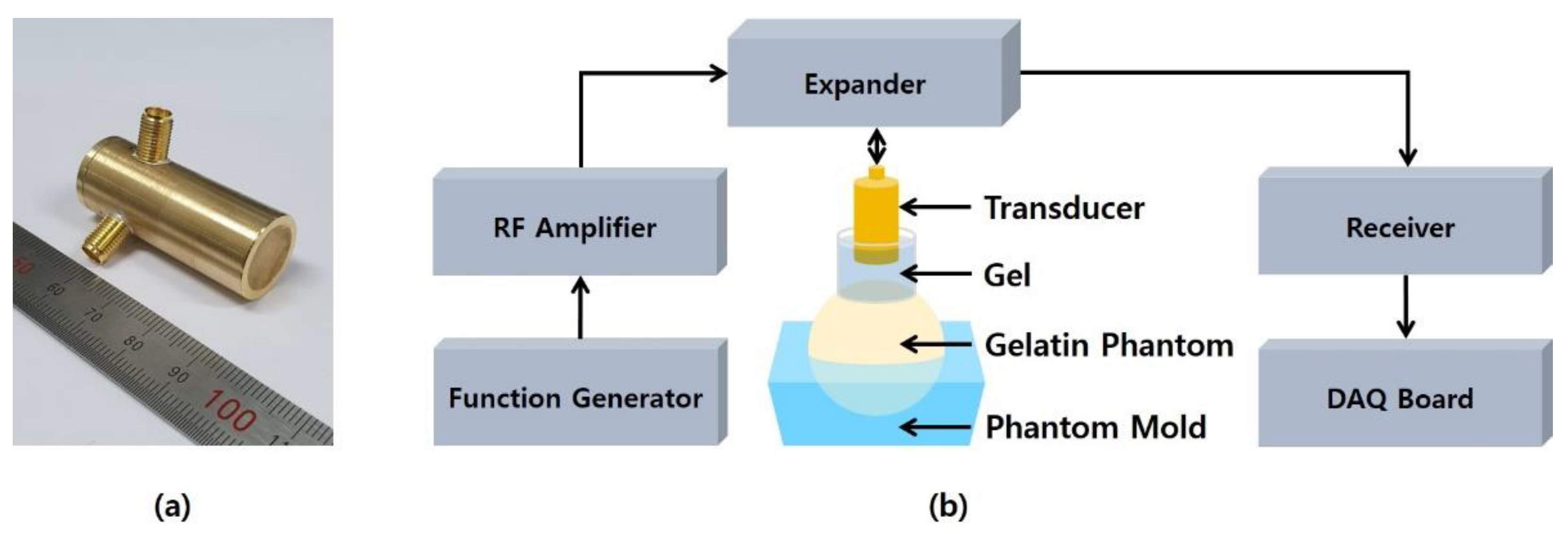
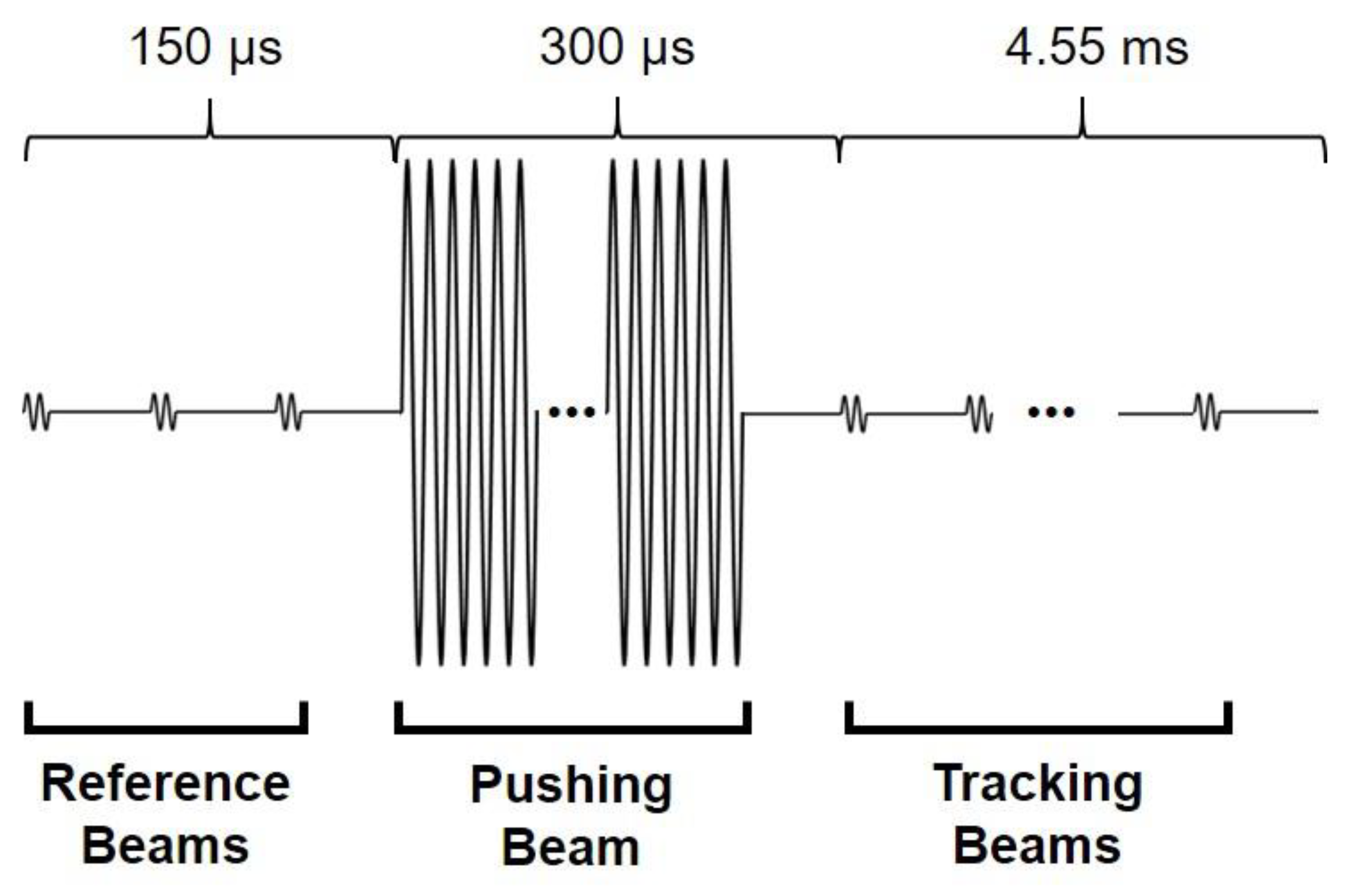
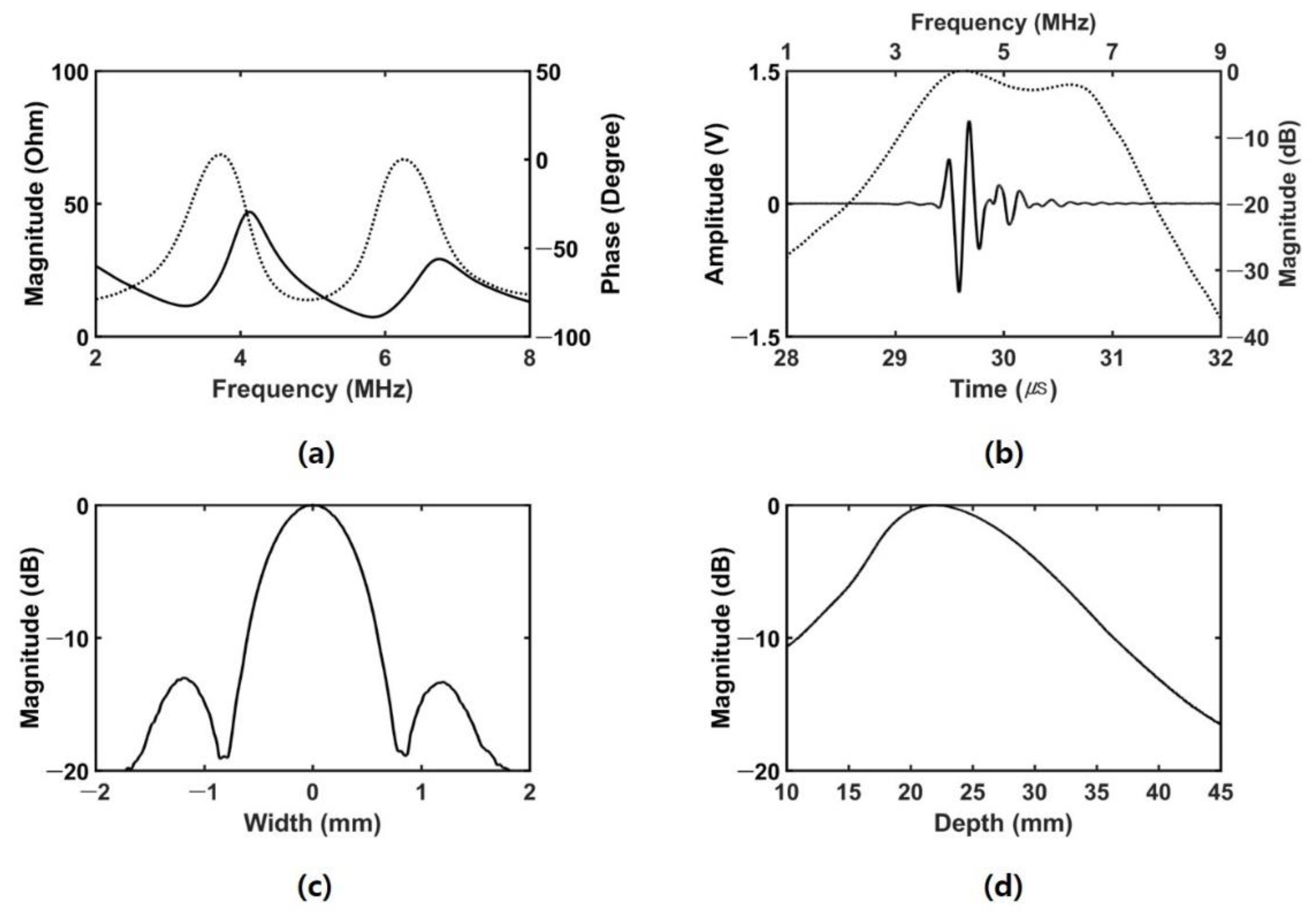
3.1. Experimental Setup
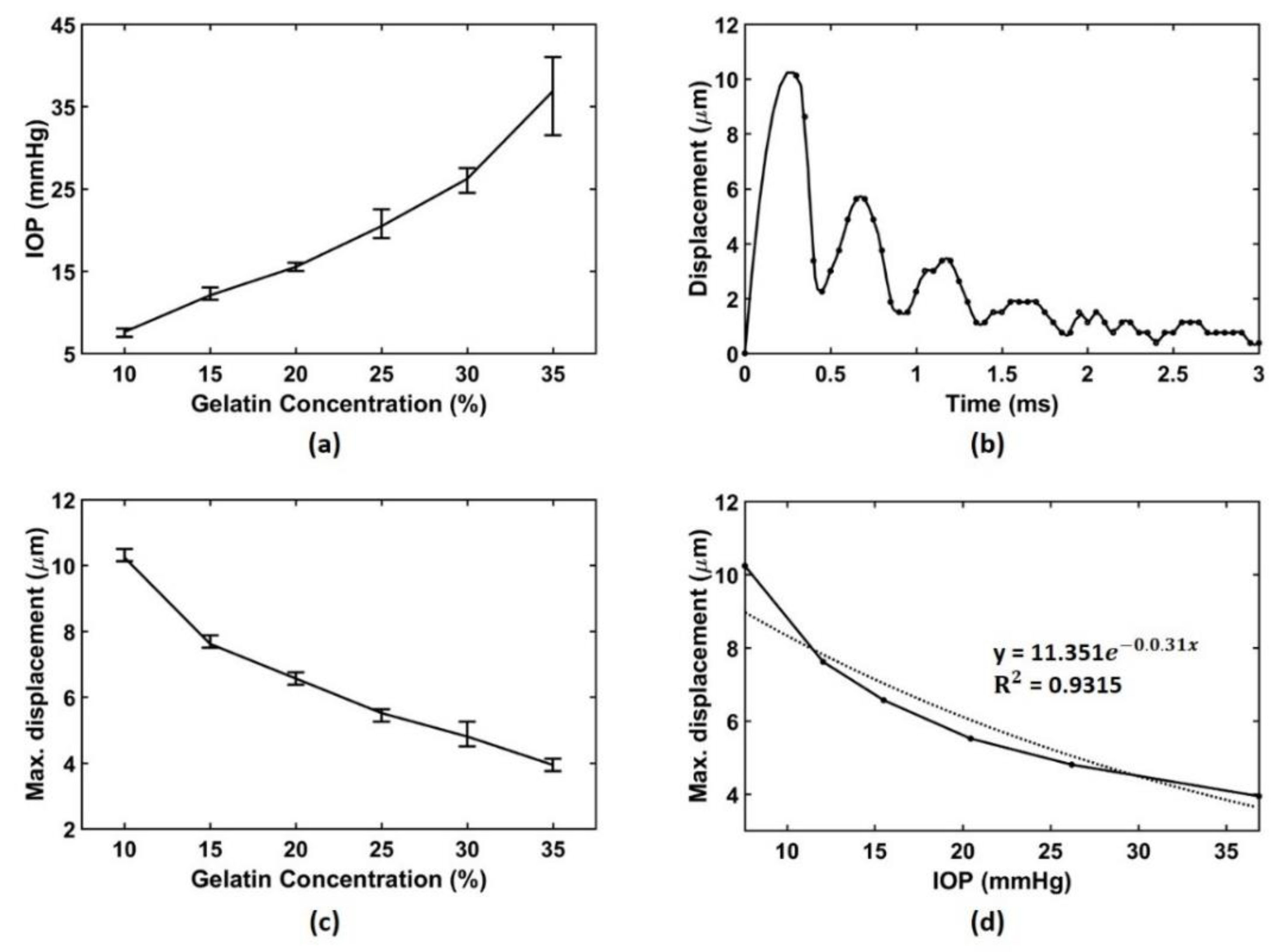
3.2. Experimental Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Quigley, H.A. Number of people with glaucoma worldwide. Br. J. Ophthalmol. 1996, 80, 389–393. [Google Scholar] [CrossRef] [PubMed]
- Kingman, S. Glaucoma is second leading cause of blindness globally. Bull. World Health Organ. 2004, 82, 887–888. [Google Scholar] [PubMed]
- Quigley, H.A. Neuronal death in glaucoma. Prog. Retin. Eye Res. 1999, 18, 39–57. [Google Scholar] [CrossRef]
- Weinreb, R.N.; Khaw, P.T. Primary open-angle glaucoma. Lancet 2004, 363, 1711–1720. [Google Scholar] [CrossRef]
- van der Valk, R.; Webers, C.A.; Schouten, J.S.; Zeegers, M.P.; Hendrikse, F.; Prins, M.H. Intraocular pressure–lowering effects of all commonly used glaucoma drugs: A meta-analysis of randomized clinical trials. Ophthalmology 2005, 112, 1177–1185. [Google Scholar] [CrossRef] [PubMed]
- Nemesure, B.; Honkanen, R.; Hennis, A.; Wu, S.; Leske, M.C. Incident open-angle glaucoma and intraocular pressure. Ophthalmology 2007, 114, 1810–1815. [Google Scholar] [CrossRef] [PubMed]
- Quigley, H.A. Reappraising the risks and benefits of aggressive glaucoma therapy. Ophthalmology 1997, 104, 1985–1986. [Google Scholar] [CrossRef]
- Hughes, E.; Spry, P.; Diamond, J. 24-hour monitoring of intraocular pressure in glaucoma management: A retrospective review. J. Glaucoma 2003, 12, 232–236. [Google Scholar] [CrossRef] [PubMed]
- Goldmann, H.; Schmidt, T. Über applanationstonometrie. Ophthalmologica 1957, 134, 221–242. [Google Scholar] [CrossRef]
- Whitacre, M.M.; Stein, R. Sources of error with use of Goldmann-type tonometers. Surv. Ophthalmol. 1993, 38, 1–30. [Google Scholar] [CrossRef]
- Poostchi, A.; Mitchell, R.; Nicholas, S.; Purdie, G.; Wells, A. The iCare rebound tonometer: Comparisons with Goldmann tonometry, and influence of central corneal thickness. Clin. Exp. Ophthalmol. 2009, 37, 687–691. [Google Scholar] [CrossRef] [PubMed]
- Iliev, M.E.; Goldblum, D.; Katsoulis, K.; Amstutz, C.; Frueh, B. Comparison of rebound tonometry with Goldmann applanation tonometry and correlation with central corneal thickness. Br. J. Ophthalmol. 2006, 90, 833–835. [Google Scholar] [CrossRef]
- Kass, M.A. Standardizing the measurement of intraocular pressure for clinical research: Guidelines from the Eye Care Technology Forum. Ophthalmology 1996, 103, 183–185. [Google Scholar] [CrossRef]
- Kaufmann, C.; Bachmann, L.M.; Thiel, M.A. Comparison of dynamic contour tonometry with Goldmann applanation tonometry. Investig. Ophthalmol. Vis. Sci. 2004, 45, 3118–3121. [Google Scholar] [CrossRef] [PubMed]
- Kontiola, A. A new electromechanical method for measuring intraocular pressure. Doc. Ophthalmol. 1997, 93, 265–276. [Google Scholar] [CrossRef] [PubMed]
- Davies, L.N.; Bartlett, H.; Mallen, E.A.; Wolffsohn, J.S. Clinical evaluation of rebound tonometer. Acta Ophthalmol. Scand. 2006, 84, 206–209. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, P.; Díaz-Rey, J.A.; Queiros, A.; Gonzalez-Meijome, J.M.; Jorge, J. Comparison of the ICare® rebound tonometer with the Goldmann tonometer in a normal population. Ophthalmic Physiol. Opt. 2005, 25, 436–440. [Google Scholar] [CrossRef]
- Abraham, L.M.; Epasinghe, N.C.R.; Selva, D.; Casson, R. Comparison of the ICares rebound tonometer with the Goldmann applanation tonometer by experienced and inexperienced tonometrists. Eye 2008, 22, 503–506. [Google Scholar] [CrossRef]
- Pakrou, N.; Gray, T.; Mills, R.; Landers, J.; Craig, J. Clinical comparison of the Icare tonometer and Goldmann applanation tonometry. J. Glaucoma 2008, 17, 43–47. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, M.; Darhad, U.; Tatsumi, Y.; Fujioka, M.; Kusuhara, A.; Maeda, H.; Negi, A. Agreement of rebound tonometer in measuring intraocular pressure with three types of applanation tonometers. Am. J. Ophthalmol. 2006, 142, 332–334. [Google Scholar] [CrossRef] [PubMed]
- Brusini, P.; Salvetat, M.L.; Zeppieri, M.; Tosoni, C.; Parisi, L. Comparison of ICare tonometer with Goldmann applanation tonometer in glaucoma patients. J. Glaucoma 2006, 15, 213–217. [Google Scholar] [CrossRef]
- Shields, M.B. The non-contact tonometer. Its value and limitations. Surv. Ophthalmol. 1980, 24, 211–219. [Google Scholar] [CrossRef]
- Ogbuehi, K.C. Assessment of the accuracy and reliability of the Topcon CT80 non-contact tonometer. Clin. Exp. Ophthalmol. 2006, 89, 310–314. [Google Scholar] [CrossRef] [PubMed]
- Moseley, M.J.; Thompson, J.R.; Deutsch, J.; Misson, G.P.; Naylor, G.; Tan-Yee, A.; Taylor, R.H.; Fielder, A.R. Comparison of the Keeler Pulsair 2000 non-contact tonometer with Goldmann applanation. Eye 1993, 7, 127–130. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Grolman, B. A new tonometer system. Optom. Vis. Sci. 1972, 49, 646–660. [Google Scholar] [CrossRef]
- Tonnu, P.; Ho, T.; Newson, T.; El Sheikh, A.; Sharma, K.; White, E.; Bunce, C.; Garway-Heath, D. The influence of central corneal thickness and age on intraocular pressure measured by pneumotonometry, non-contact tonometry, the Tono-Pen XL, and Goldmann applanation tonometry. Br. J. Ophthalmol. 2005, 89, 851–854. [Google Scholar] [CrossRef]
- Matsumoto, T.; Makino, H.; Uozato, H.; Saishin, M.; Miyamoto, S. The influence of corneal thickness and curvature on the difference between intraocular pressure measurements obtained with a non-contact tonometer and those with a Goldmann applanation tonometer. Jpn. J. Ophthalmol. 2000, 44, 691. [Google Scholar] [CrossRef]
- Nightingale, K.; Soo, M.S.; Nightingale, R.; Trahey, G. Acoustic radiation force impulse imaging: In vivo demonstration of clinical feasibility. Ultrasound Med. Biol. 2002, 28, 227–235. [Google Scholar] [CrossRef]
- Palmeri, M.L.; Sharma, A.C.; Bouchard, R.R.; Nightingale, R.W.; Nightingale, K.R. A finite-element method model of soft tissue response to impulsive acoustic radiation force. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 1699–1712. [Google Scholar] [CrossRef] [PubMed]
- Shiina, T.; Nightingale, K.R.; Palmeri, M.L.; Hall, T.J.; Bamber, J.C.; Barr, R.G.; Castera, L.; Choi, B.I.; Chou, Y.-H.; Cosgrove, D. WFUMB guidelines and recommendations for clinical use of ultrasound elastography: Part 1: Basic principles and terminology. Ultrasound Med. Biol. 2015, 41, 1126–1147. [Google Scholar] [CrossRef] [PubMed]
- Palmeri, M.L. Imaging the Mechanical Properties of Tissue with Ultrasound: An Investigation of the Response of Soft Tissue to Acoustic Radiation Force; Duke University: Durham, NC, USA, 2005. [Google Scholar]
- McAleavey, S.A.; Nightingale, K.R.; Trahey, G.E. Estimates of echo correlation and measurement bias in acoustic radiation force impulse imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2003, 50, 631–641. [Google Scholar] [CrossRef] [PubMed]
- Pinton, G.F.; Dahl, J.J.; Trahey, G.E. Rapid tracking of small displacements with ultrasound. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2006, 53, 1103–1117. [Google Scholar] [CrossRef] [PubMed]
- Nightingale, K.R.; Palmeri, M.; Trahey, G. Analysis of contrast in images generated with transient acoustic radiation force. Ultrasound Med. Biol. 2006, 32, 61–72. [Google Scholar] [CrossRef] [PubMed]
- Nightingale, K.R.; Nightingale, R.W.; Palmeri, M.L.; Trahey, G.E. A finite element model of remote palpation of breast lesions using radiation force: Factors affecting tissue displacement. Ultrason. Imaging 2000, 22, 35–54. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; He, X.; Chen, Z. Acoustic radiation force optical coherence elastography for elasticity assessment of soft tissues. Appl. Spectrosc. Rev. 2019, 54, 457–481. [Google Scholar] [CrossRef]
- Qu, Y.; Ma, T.; He, Y.; Zhu, J.; Dai, C.; Yu, M.; Huang, S.; Lu, F.; Shung, K.K.; Zhou, Q.; et al. Acoustic Radiation Force Optical Coherence Elastography of Corneal Tissue. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 288–294. [Google Scholar] [CrossRef]
- Kennedy, B.F.; Kennedy, K.M.; Sampson, D.D. A Review of Optical Coherence Elastography: Fundamentals, Techniques and Prospects. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 272–288. [Google Scholar] [CrossRef]
- Wang, S.; Larin, K.V. Optical coherence elastography for tissue characterization: A review. J. Biophotonics 2015, 8, 279–302. [Google Scholar] [CrossRef]
- Qu, Y.Q.; He, Y.N.; Saidi, A.; Xin, Y.H.; Zhou, Y.X.; Zhu, J.; Ma, T.; Silverman, R.H.; Minckler, D.S.; Zhou, Q.F.; et al. In Vivo Elasticity Mapping of Posterior Ocular Layers Using Acoustic Radiation Force Optical Coherence Elastography. Investig. Ophthalmol. Vis. Sci. 2018, 59, 455–461. [Google Scholar] [CrossRef] [PubMed]
- Nightingale, K.R.; Palmeri, M.L.; Nightingale, R.W.; Trahey, G.E. On the feasibility of remote palpation using acoustic radiation force. J. Acoust. Soc. Am. 2001, 110, 625–634. [Google Scholar] [CrossRef] [PubMed]
- Torr, G.R. The acoustic radiation force. Am. J. Phys. 1984, 52, 402–408. [Google Scholar] [CrossRef]
- Young, W.C.; Budynas, R.G. Roark’s Formulas for Stress and Strain, 7th ed.; McGraw-Hill Publication: New York, NY, USA, 2002. [Google Scholar]
- Orssengo, G.J.; Pye, D.C. Determination of the true intraocular pressure and modulus of elasticity of the human cornea in vivo. Bull. Math. Biol. 1999, 61, 551–572. [Google Scholar] [CrossRef]
- Liu, J.; Roberts, C.J. Influence of corneal biomechanical properties on intraocular pressure measurement: Quantitative analysis. J. Cataract Refract. Surg. 2005, 31, 146–155. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, A.S.; Woo, S.L.; Lawrence, C.; Schlegel, W.A. Analysis of the corneo-scleral shell by the method of direct stiffness. J. Biomech. 1971, 4, 323–330. [Google Scholar] [CrossRef]
- Eysteinsson, T.; Jonasson, F.; Sasaki, H.; Arnarsson, A.; Sverrisson, T.; Sasaki, K.; Stefansson, E.; Reykjavik Eye Study Group. Central corneal thickness, radius of the corneal curvature and intraocular pressure in normal subjects using non-contact techniques: Reykjavik Eye Study. Acta Ophthalmol. Scand. 2002, 80, 11–15. [Google Scholar] [CrossRef]
- Herndon, L.W.; Choudhri, S.A.; Cox, T.; Damji, K.F.; Shields, M.B.; Allingham, R.R. Central corneal thickness in normal, glaucomatous, and ocular hypertensive eyes. Arch. Ophthalmol. 1997, 115, 1137–1141. [Google Scholar] [CrossRef] [PubMed]
- Wolfs, R.C.; Klaver, C.C.; Vingerling, J.R.; Grobbee, D.E.; Hofman, A.; de Jong, P.T. Distribution of central corneal thickness and its association with intraocular pressure: The Rotterdam Study. Am. J. Ophthalmol. 1997, 123, 767–772. [Google Scholar] [CrossRef]
- Reissner, E. Stresses and small displacements of shallow spherical shells. II. J. Math. Phys. 1946, 25, 80–85. [Google Scholar] [CrossRef]
- Jeong, E.Y.; Sung, J.H.; Jeong, J.S. Improved acoustic radiation force impulse imaging using split-focused ultrasound transducer with phase inversion technique. IEEE Sens. J. 2021, 21, 1395–1402. [Google Scholar] [CrossRef]
- Li, J.S.; Wang, S.; Manapuram, R.K.; Singh, M.; Menodiado, F.M.; Aglyamov, S.; Emelianov, S.; Twa, M.D.; Larin, K.V. Dynamic optical coherence tomography measurements of elastic wave propagation in tissue-mimicking phantoms and mouse cornea in vivo. J. Biomed. Opt. 2013, 18, 121503. [Google Scholar] [CrossRef]
- Li, J.S.; Han, Z.L.; Singh, M.; Twa, M.D.; Larin, K.V. Differentiating untreated and cross-linked porcine corneas of the same measured stiffness with optical coherence elastography. J. Biomed. Opt. 2014, 19, 110502. [Google Scholar] [CrossRef] [PubMed]
- Zvietcovich, F.; Pongchalee, P.; Meemon, P.; Rolland, J.P.; Parker, K.J. Reverberant 3D optical coherence elastography maps the elasticity of individual corneal layers. Nat. Commun. 2019, 10, 4895. [Google Scholar] [CrossRef] [PubMed]
| μ | 0 | 0.1 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 |
| β | 0.433 | 0.431 | 0.425 | 0.408 | 0.386 | 0.362 | 0.337 | 0.311 | 0.286 |
| Phantom #1 | Phantom #2 | Phantom #3 | Phantom #4 | Phantom #5 | Phantom #6 | |
|---|---|---|---|---|---|---|
| Gelatin (g) | 7 | 10.5 | 14 | 17.5 | 21 | 24.5 |
| Water (mL) | 70 | 70 | 70 | 70 | 70 | 70 |
| Concentration (%) | 10 | 15 | 20 | 25 | 30 | 35 |
| Concentration | Mean (mmHg) | * SD (mmHg) | Min–Max (mmHg) |
|---|---|---|---|
| Phantom #1 (10%) | 7.6 | 3.4 | 7–8 |
| Phantom #2 (15%) | 12.1 | 1.8 | 11.5–13 |
| Phantom #3 (20%) | 15.5 | 3.9 | 15–16 |
| Phantom #4 (25%) | 20.5 | 3.4 | 19–22.5 |
| Phantom #5 (30%) | 26.2 | 5.4 | 24.5–27.5 |
| Phantom #6 (35%) | 36.9 | 7.5 | 31.5–41 |
| Concentration | Mean (μm) | * SD (μm) | Min–Max (μm) |
|---|---|---|---|
| Phantom #1 (10%) | 10.2 | 0.2 | 10.1–10.5 |
| Phantom #2 (15%) | 7.6 | 0.2 | 7.5–7.9 |
| Phantom #3 (20%) | 6.6 | 0.2 | 6.4–6.8 |
| Phantom #4 (25%) | 5.5 | 0.2 | 5.3–5.6 |
| Phantom #5 (30%) | 4.8 | 0.2 | 4.5–5.3 |
| Phantom #6 (35%) | 3.9 | 0.2 | 3.8–4.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.S.; Jeong, E.Y.; Sung, J.H.; Choi, B.E.; Jeong, J.S. An Intraocular Pressure Measurement Technique Based on Acoustic Radiation Force Using an Ultrasound Transducer: A Feasibility Study. Sensors 2021, 21, 1857. https://doi.org/10.3390/s21051857
Lee HS, Jeong EY, Sung JH, Choi BE, Jeong JS. An Intraocular Pressure Measurement Technique Based on Acoustic Radiation Force Using an Ultrasound Transducer: A Feasibility Study. Sensors. 2021; 21(5):1857. https://doi.org/10.3390/s21051857
Chicago/Turabian StyleLee, Hee Su, Eun Young Jeong, Jin Ho Sung, Bo Eun Choi, and Jong Seob Jeong. 2021. "An Intraocular Pressure Measurement Technique Based on Acoustic Radiation Force Using an Ultrasound Transducer: A Feasibility Study" Sensors 21, no. 5: 1857. https://doi.org/10.3390/s21051857
APA StyleLee, H. S., Jeong, E. Y., Sung, J. H., Choi, B. E., & Jeong, J. S. (2021). An Intraocular Pressure Measurement Technique Based on Acoustic Radiation Force Using an Ultrasound Transducer: A Feasibility Study. Sensors, 21(5), 1857. https://doi.org/10.3390/s21051857





