A Sensitive and Fast Fiber Bragg Grating-Based Investigation of the Biomechanical Dynamics of In Vitro Spinal Cord Injuries
Abstract
1. Introduction
2. Model and Theory
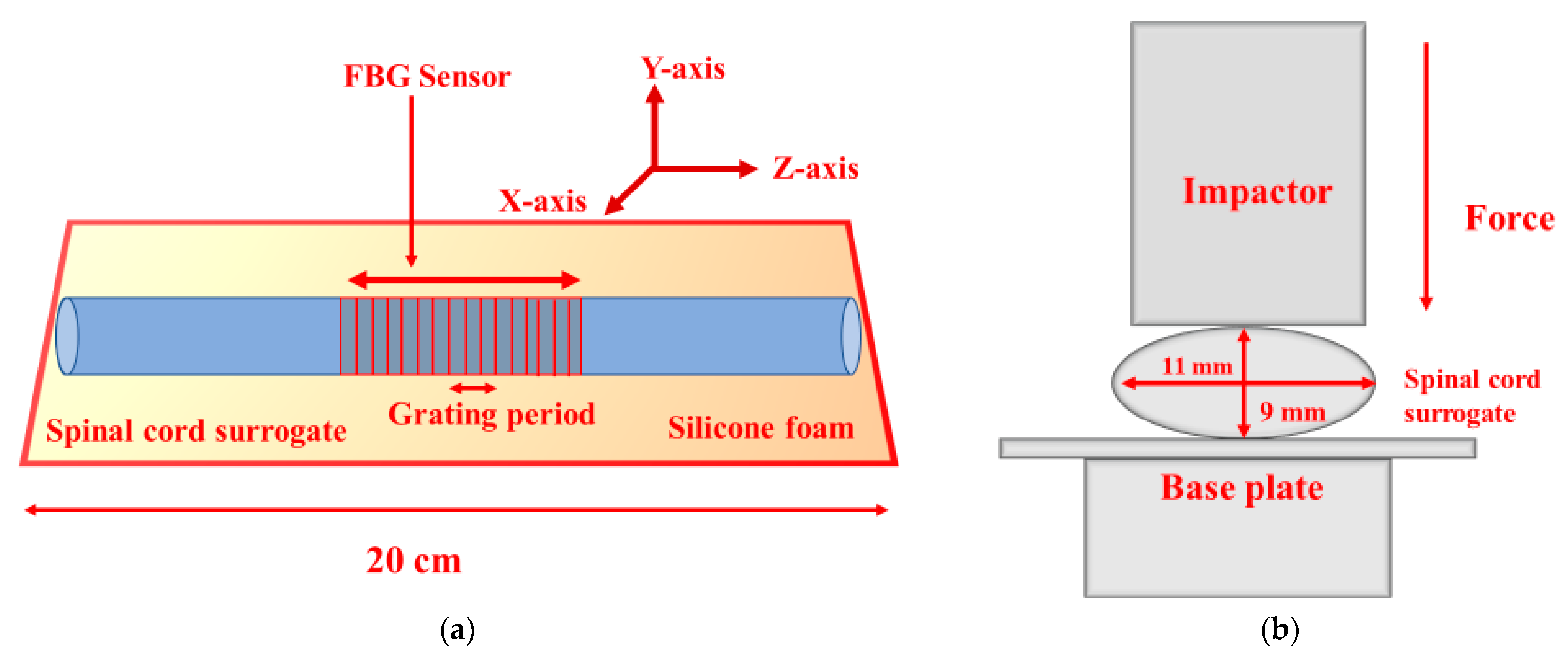
2.1. Physical Spinal Cord Surrogate
2.2. FBG Fiber Sensor Theory
3. Results
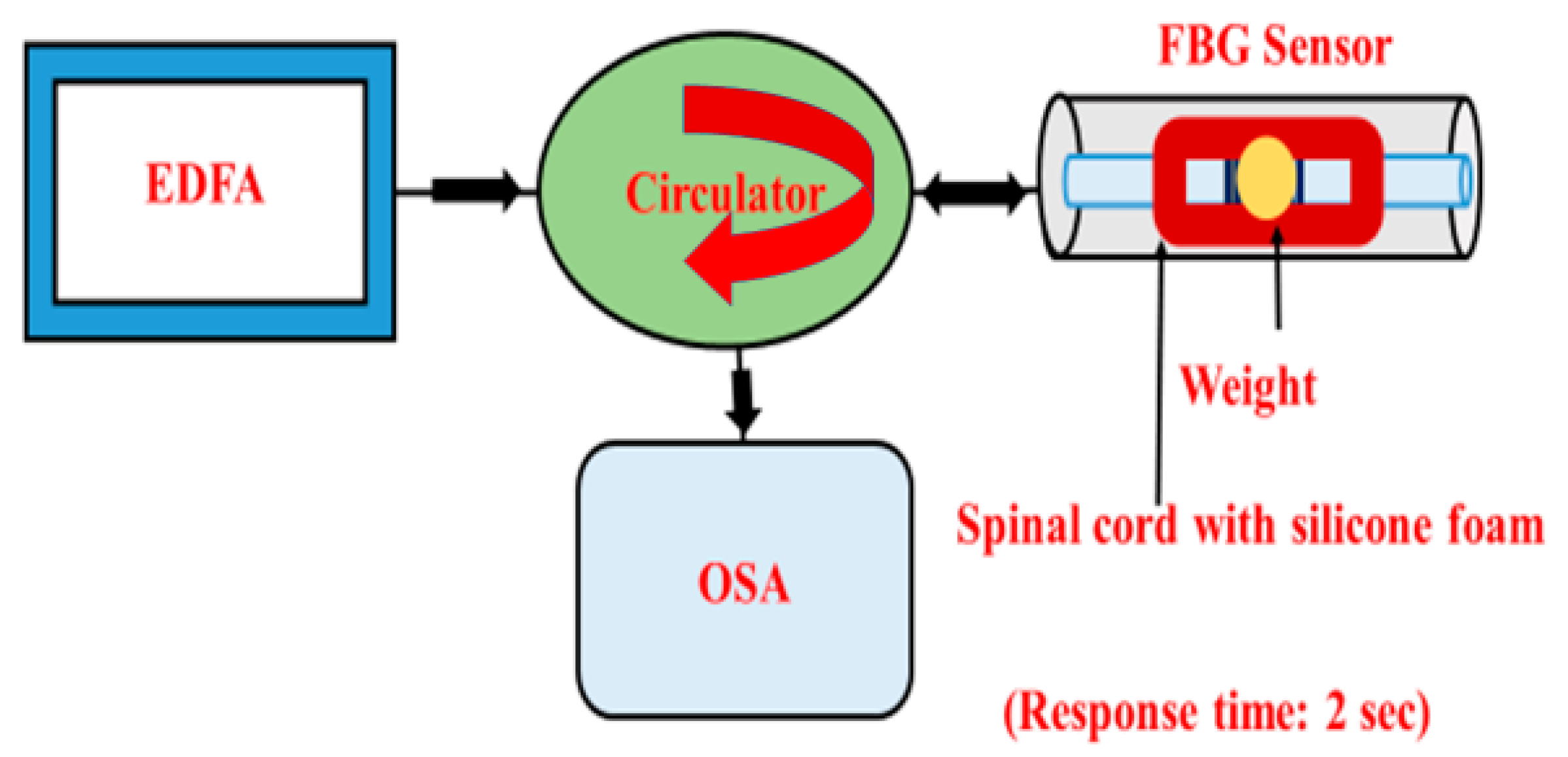
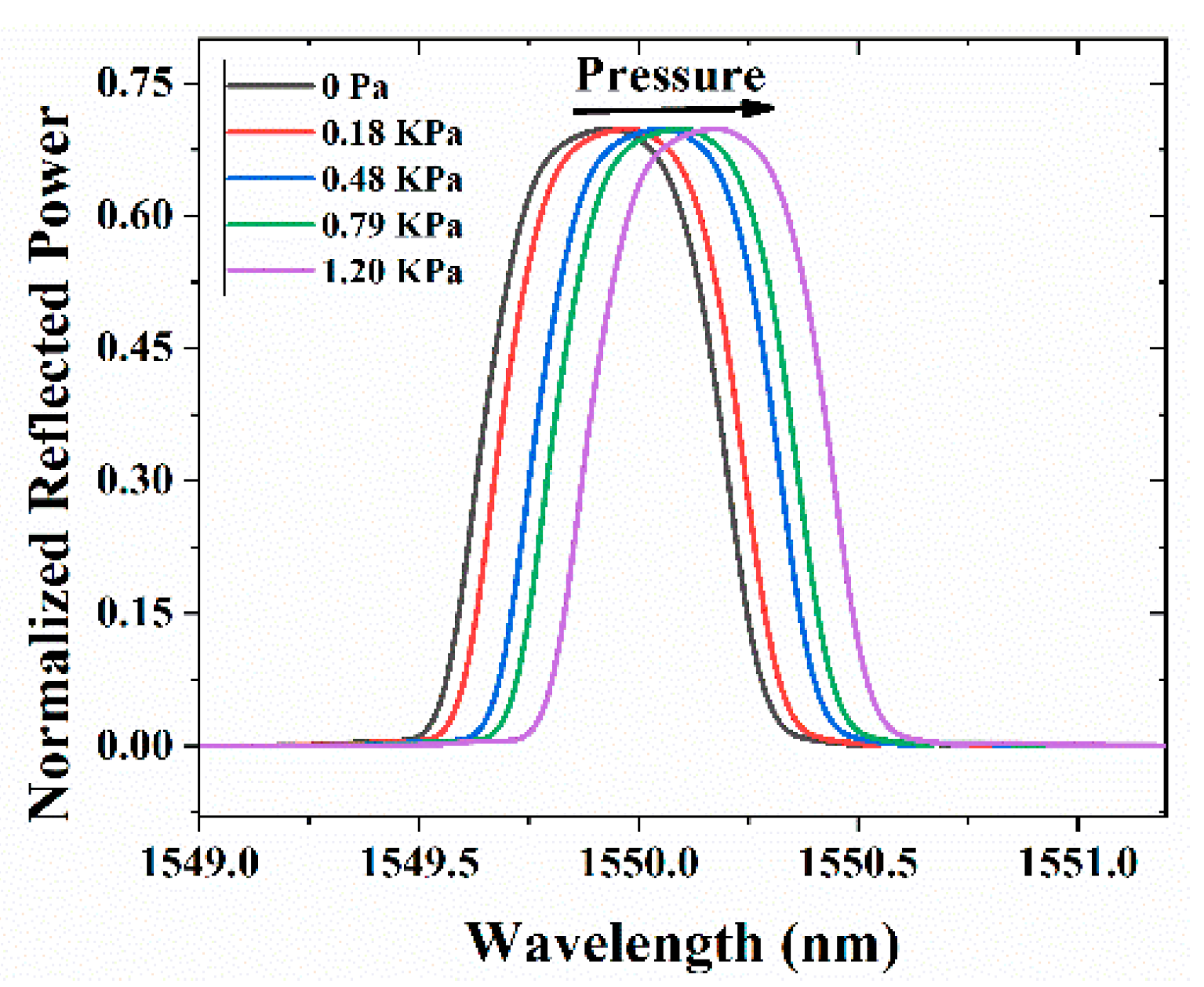
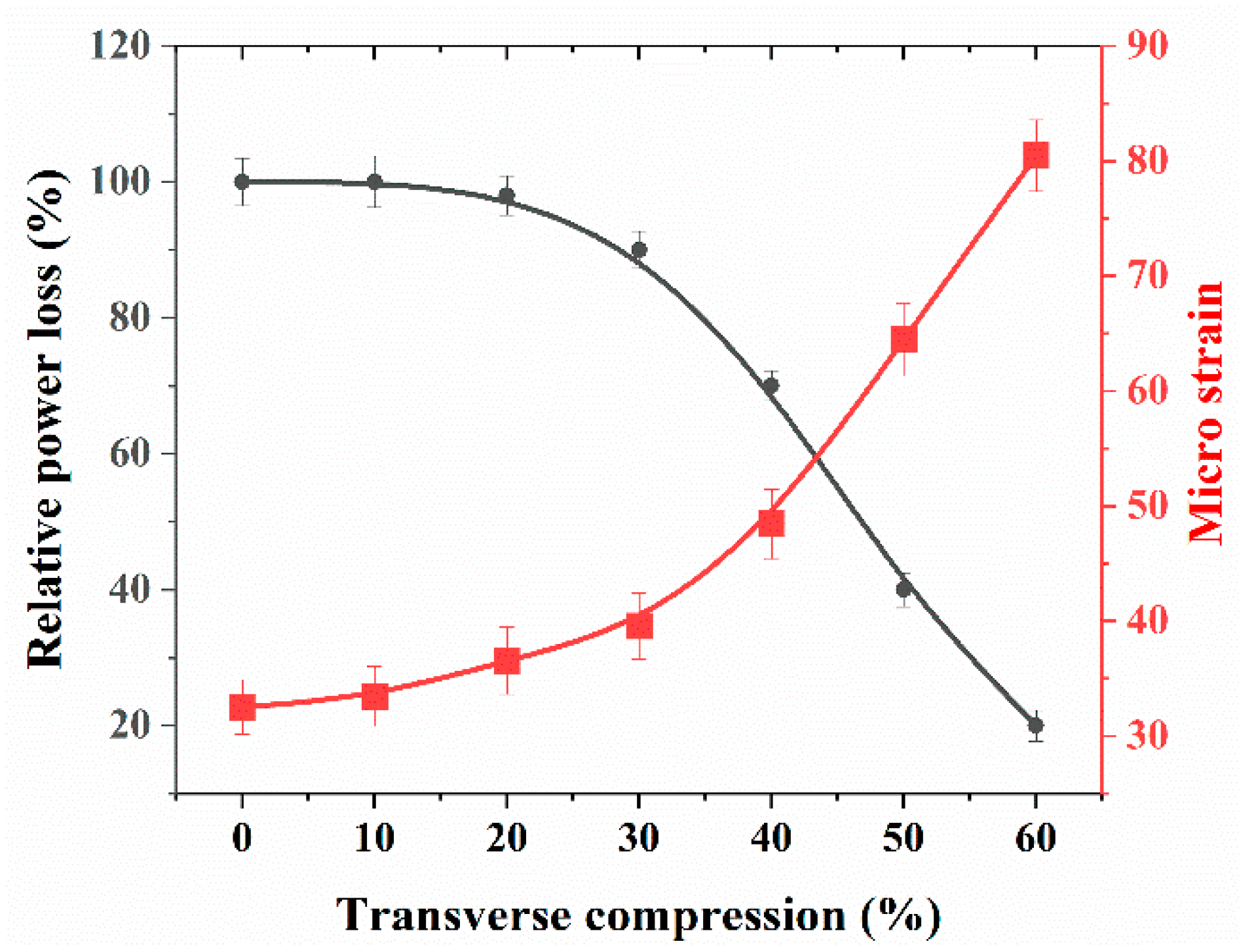
3.1. Characterization of FBG Sensor with OSA
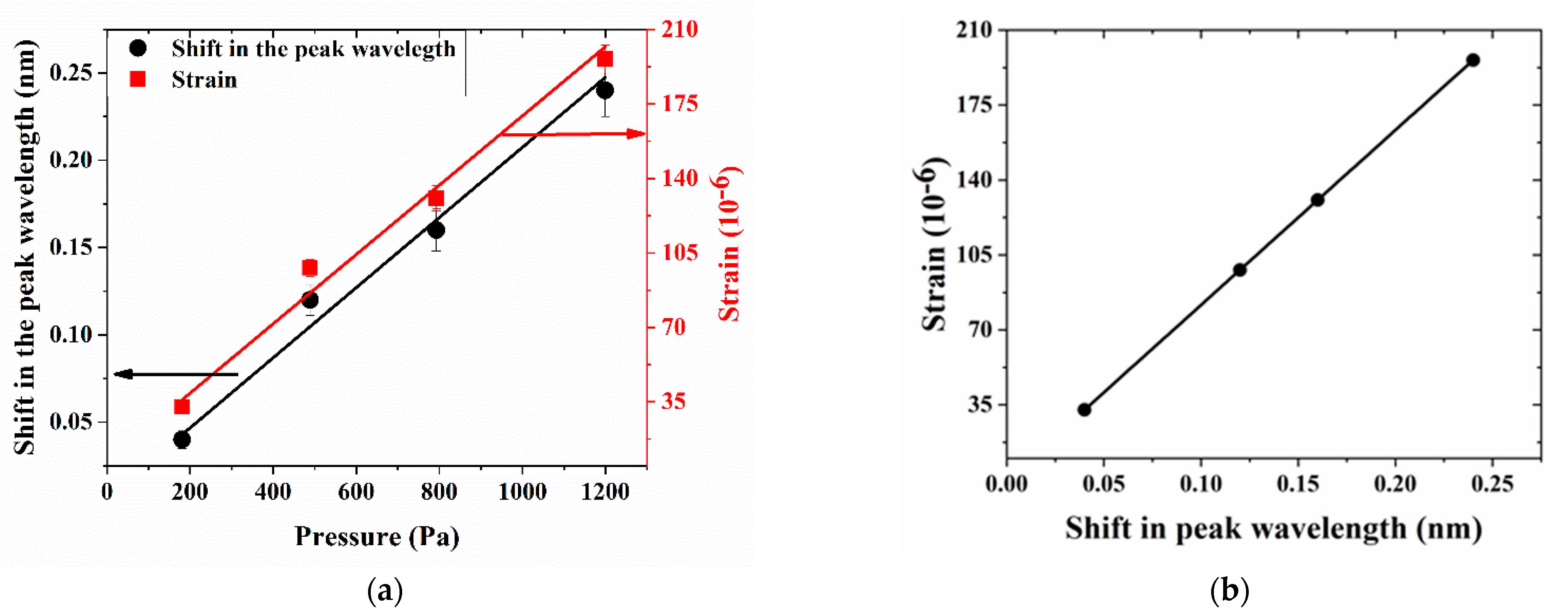
3.2. Calibration of Compression Sensing Capability of Spinal Cord
3.3. Fast Transverse Compression Measurement Using a Narrow-Band-Pass Filter and Power Meter
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rao, A.; Pandya, S. Engineering approaches for characterizing soft tissue mechanical properties: A review. Clin. Biomech. (Bristol. Avon.) 2019, 69, 127–140. [Google Scholar]
- Griffin, M.; Premakumar, Y.; Seifalian, A.; Butler, P.E.; Szarko, M. Biomechanical characterization of human soft tissues using indentation and tensile testing. J. Vis. 2016, 54872. [Google Scholar] [CrossRef]
- Westwood, J.D. Medicine Meets Virtual Reality 2001: Outer Space, Inner Space, Virtual Space; IOS Press: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Westwood, J.D. Medicine Meets Virtual Reality 02/10: Digital Upgrades, Applying Moore’s Law to Health; IOS Press: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Westwood, J.D. Medicine Meets Virtual Reality 11: NextMed: Health Horizon; IOS Press: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Henize, S.; Echtermeyer, T.A. A Running Reference Analysis Method to Greatly Improve Optical Backscatter Reflectometry Strain Data from the Inside of Hardening and Shrinking Materials. Appl. Sci. 2018, 8, 1137. [Google Scholar] [CrossRef]
- Tian, Z.B.; Yam, S.S.H.; Loock, H.P. Single-mode fiber refractive index sensor based on core-offset attenuators. IEEE Photonics Technol. Lett. 2008, 20, 1387–1389. [Google Scholar] [CrossRef]
- Tian, Z.B.; Yam, S.S.H. In-line single-mode optical fiber interferometric refractive index sensors. J. Lightwave Technol. 2009, 27, 2296–2306. [Google Scholar] [CrossRef]
- Qian, Y.; Zhao, Y.; Wu, Q.; Yang, Y. Review of salinity measurement technology based on optical fiber sensor. Sens. Actuators B Chem. 2018, 260, 86–105. [Google Scholar] [CrossRef]
- Fukano, H.; Watanabe, D.; Taue, S. Sensitivity characteristics of multimode-interference optical-fiber temperature-sensor with solid cladding material. IEEE Sens. J. 2016, 16, 8921–8927. [Google Scholar] [CrossRef]
- Lecheng, L.; Li, X.; Zhenhai, X.; Liangning, H.; Binbin, S.; Deming, L. In-line fiber Mach-Zehnder interferometer for simultaneous measurement of refractive index and temperature based on thinned fiber. Sens. Actuators A Phys. 2012, 180, 19–24. [Google Scholar]
- Qian, W.W.; Zhao, C.L.; He, S.L.; Dong, X.Y.; Zhang, S.Q.; Zhang, Z.X.; Jin, S.Z.; Guo, J.T.; Wei, H.F. High-sensitivity temperature sensor based on an alcohol-filled photonic crystal fiber loop mirror. Opt. Lett. 2011, 36, 1548–1550. [Google Scholar] [CrossRef] [PubMed]
- Sun, G.Y.; Moon, D.S.; Chuang, Y. Simultaneous temperature and strain measurement using two types of high-birefringence fibers in Sagnac loop mirror. IEEE Photonics Technol. Lett. 2007, 19, 2027–2029. [Google Scholar] [CrossRef]
- Fernande, L.A.; Becker, O.; Frazao, K.; Schuster, J.; Kobelke, M.; Rothjhardt, H.; Bartelt, J.L.; Santos, P.V. Temperature and strain sensing with femtosecond laser written Bragg gratings in defect and non-defect suspended-silica-core fibers. IEEE Photonics Technol. Lett. 2012, 24, 554–556. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, M.Q.; Lv, R.Q.; Xia, F. In-fiber rectangular air Fabry-Perot strain sensor based on high-precision fiber cutting platform. Opt. Commun. 2017, 384, 107–110. [Google Scholar] [CrossRef]
- Ren, K.L.; Ren, R.Y.; Liang, J.; Kong, X.D.; Ju, H.J.; Wu, X.J. Highly strain and bending sensitive micro tapered long-period fiber gratings. IEEE Photonics Technol. Lett. 2017, 29, 1085–1088. [Google Scholar] [CrossRef]
- Zhang, X.P.; Peng, W. Bent fiber interferometer. J. Lightwave Technol. 2015, 33, 3351–3356. [Google Scholar] [CrossRef]
- Campanella, C.E.; Cuccovillo, A.; Campanella, C.; Yurt, A.; Passaro, V.M.N. Fibre Bragg Grating Based Strain Sensors: Review of Technology and Applications. Sensors 2018, 18, 3115. [Google Scholar] [CrossRef] [PubMed]
- Kwon, B.K.; Hillyer, J.; Tetzlaff, W. Translational research in spinal cord injury: A survey of opinion from the SCI community. J. Neurotrauma 2010, 48, 13–15. [Google Scholar] [CrossRef]
- Czyz, M.; Scigala, K.; Beidzinski, R. the biomechanical analysis of the traumatic cervical spinal cord injury using finite element approach. Acta Bioeng. Biomech. 2008, 10, 43–54. [Google Scholar] [PubMed]
- Carter, J.W.; Mirza, S.K.; Tencer, A.F.; Ching, R.P.C. Canal geometry changes associated with axial compression cervical spine fracture. Spine 2000, 25, 46–54. [Google Scholar] [CrossRef]
- Ching, R.P.; Watson, N.A.; Carter, J.W.; Tencer, A.F. the effect of post-injury spinal position on canal occlusion in a cervical spine burst fracture model. Spine 1997, 22, 1710–1715. [Google Scholar] [CrossRef]
- Kroeker, S.G.; Morley, P.L.; Jones, C.F.; Bilston, L.E.; Cripton, P.A. The development of an improved physical surrogate model of the human spinal cord-tension and transverse compression. J. Biomech. 2007, 42, 878–883. [Google Scholar] [CrossRef]
- Saari, A.; Itshek, E.; Cripton, P.A. Spinal cord deformation during simulated head- first impact injuries. J. Biomech. 2011, 44, 2565–2571. [Google Scholar] [CrossRef]
- Lucas, E.; Whyte, T.; Liu, J.; Russell, C.; Tetzlaff, W.; Cripton, P.A. High-speed fluoroscopy to measure dynamic spinal cord deformation in an vivo Rat model. J. Neurotrauma 2018, 35, 2572–2580. [Google Scholar] [CrossRef] [PubMed]
- Bhatanagar, T.; Liu, J.; Yung, A.; Cripton, P.A.; Kozlowski, P.; Oxland, T. In vivo measurement of cervical spinal cord deformation during traumatic spinal cord injury in a Rodent model. Ann. Biomed. Eng. 2016, 44, 1285–1298. [Google Scholar] [CrossRef]
- Chang, D.G.; Tencer, A.F.; Ching, R.P.; Treece, B.; Senft, D.; Anderson, P.A. Geometric changes in the cervical spinal canal during impact. Spine 1994, 19, 973–980. [Google Scholar] [CrossRef]
- Facchinello, Y.; Wagnac, E.; Ung, B.; Petit, Y.; Pradhan, P.; Peyrache, L.M.; Thiong, J.M.M. Development of an instrumented spinal cord surrogate using optical fibers: A feasibility study. Med. Eng. Phys. 2017, 48, 212–216. [Google Scholar] [CrossRef] [PubMed]
- Diotalevi, L.; Petit, Y.; Peyrache, L.-M.; Facchinello, Y.; Mac-Thiong, J.M.; Wagnac, E. A novel spinal cord surrogate for the study of compressive traumatic spinal cord injuries. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019. [Google Scholar]
- Marco, L.; Karaelkas, D.; Botsis, J. On the Effects of the Lateral Strains on the Fiber Bragg Grating Response. Sensors 2013, 13, 2631–2644. [Google Scholar]
- Wilcox, R.K.; Allen, D.J.; Hall, R.M.; Limb, D.; Barton, D.C.; Dickson, R.A. A dynamic investigations of the burst fracture process using a combined experimental and finite element approach. Eur. Spine J. 2004, 13, 481–488. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mishra, S.K.; Mac-Thiong, J.-M.; Wagnac, É.; Petit, Y.; Ung, B. A Sensitive and Fast Fiber Bragg Grating-Based Investigation of the Biomechanical Dynamics of In Vitro Spinal Cord Injuries. Sensors 2021, 21, 1671. https://doi.org/10.3390/s21051671
Mishra SK, Mac-Thiong J-M, Wagnac É, Petit Y, Ung B. A Sensitive and Fast Fiber Bragg Grating-Based Investigation of the Biomechanical Dynamics of In Vitro Spinal Cord Injuries. Sensors. 2021; 21(5):1671. https://doi.org/10.3390/s21051671
Chicago/Turabian StyleMishra, Satyendra Kumar, Jean-Marc Mac-Thiong, Éric Wagnac, Yvan Petit, and Bora Ung. 2021. "A Sensitive and Fast Fiber Bragg Grating-Based Investigation of the Biomechanical Dynamics of In Vitro Spinal Cord Injuries" Sensors 21, no. 5: 1671. https://doi.org/10.3390/s21051671
APA StyleMishra, S. K., Mac-Thiong, J.-M., Wagnac, É., Petit, Y., & Ung, B. (2021). A Sensitive and Fast Fiber Bragg Grating-Based Investigation of the Biomechanical Dynamics of In Vitro Spinal Cord Injuries. Sensors, 21(5), 1671. https://doi.org/10.3390/s21051671






