Robust Filtering Techniques for RTK Positioning in Harsh Propagation Environments
Abstract
1. Introduction
2. Background on GNSS RTK Precise Positioning
- and are the code and phase observations (m), respectively;
- and are the positions of the ith satellite and the GNSS receiver, respectively;
- is the ionospheric error (m);
- is the tropospheric error (m);
- c is the speed of light ();
- and are the satellite and receiver clock offsets (s), respectively;
- is the carrier phase wavelength (m);
- is an unknown number of cycles between the receiver and the satellite; and
- and are the remaining unmodelled errors for the code and phase observations, respectively.
2.1. A Least-Squares Approach
2.2. A Kalman Filter Approach
3. Robust Kalman Filtering Approaches
3.1. Robust Statistics-Based Filtering
- Robust Information Filters (RIF). The information filter (IF) is an algebraically equivalent form of the KF, where instead of the state vector and covariance matrix, the filter propagates the so-called information vector, , and information matrix, . Instead of the standard IF recursion [45,46], the framework of RIF iteratively performs the following procedure until the convergence is reached:This formulation is particularly interesting in the context of robust filtering. Indeed, the use of redescending loss functions (where the weight functions go to zero), may cause numerical issues within the standard robust regression KF (i.e., the weight functions must be inverted). Using the IF formulation, it is possible to avoid these numerical issues and to exploit redescending cost functions. The generic robust information filter (RIF) formulation for nonlinear/Gaussian state-space models was proposed in [44]. During Section 4. Four representative robust functions are used as RIFs: (i) a RIF using a Huber function, (ii) a RIF using a Tukey function, (iii) a RIF using IGG weighting, and iv) a RIF using a simple rejection rule ([43] Chapter 7).
- Generalized M-estimator KF (GMKF). The LS form of the KF correction in (20) and (21) is exploited by the GMKF to offer robustness against outlying observations and innovation outliers from the prediction step. For RIF, GMKF consists of an iterative process until convergence of the solution is reached:where is estimated using Equation (27) over the augmented vector of observations . Once the convergence is reached, the covariance matrix of the associated estimate isUnlike RIF, GMKF involves realizing the inverse operations over the weighting matrix, leading to potential numerical issues upon the use of redescending functions. Moreover, since more “observations” (the actual observations and the predicted state estimate) are weighted, the search space for the robust mechanism grows and leads to a slight poorer performance for the case when outliers are present only during the correction stage. A case disregarded in this work relates to protection against structural errors (i.e., wrong observation and/or prediction models), for which a similar GMKF was introduced in [47].
3.2. Variational-Based Filtering
- Scalar VB Kalman filter (S-VKF): a scalar outlier indicator is used for all observations gathered in [50]. In the problem at hand, this may have strong implications because, if a single outlier is detected, then the complete set of observations is disregarded. The following model is considered:where is an outlier indicator that assists in detecting and mitigating the impact of outliers. Particularly, when , the model assumes that there are no outliers and that the measurements are Gaussian distributed; if , the outliers are considered and the correction step is not realized. In practice, the outliers might differently affect the elements in , which motivates the use of the second solution.
- Independent indicator VB Kalman filter (I-VKF): a complete vector is considered, such that for each measurement an independent indicator is assigned [29,30]. Then, the model iswhere is an indicator for each code or carrier-phase observation. For the complete derivation and implementation details, refer to [29,30].
4. Validation and Experimentation
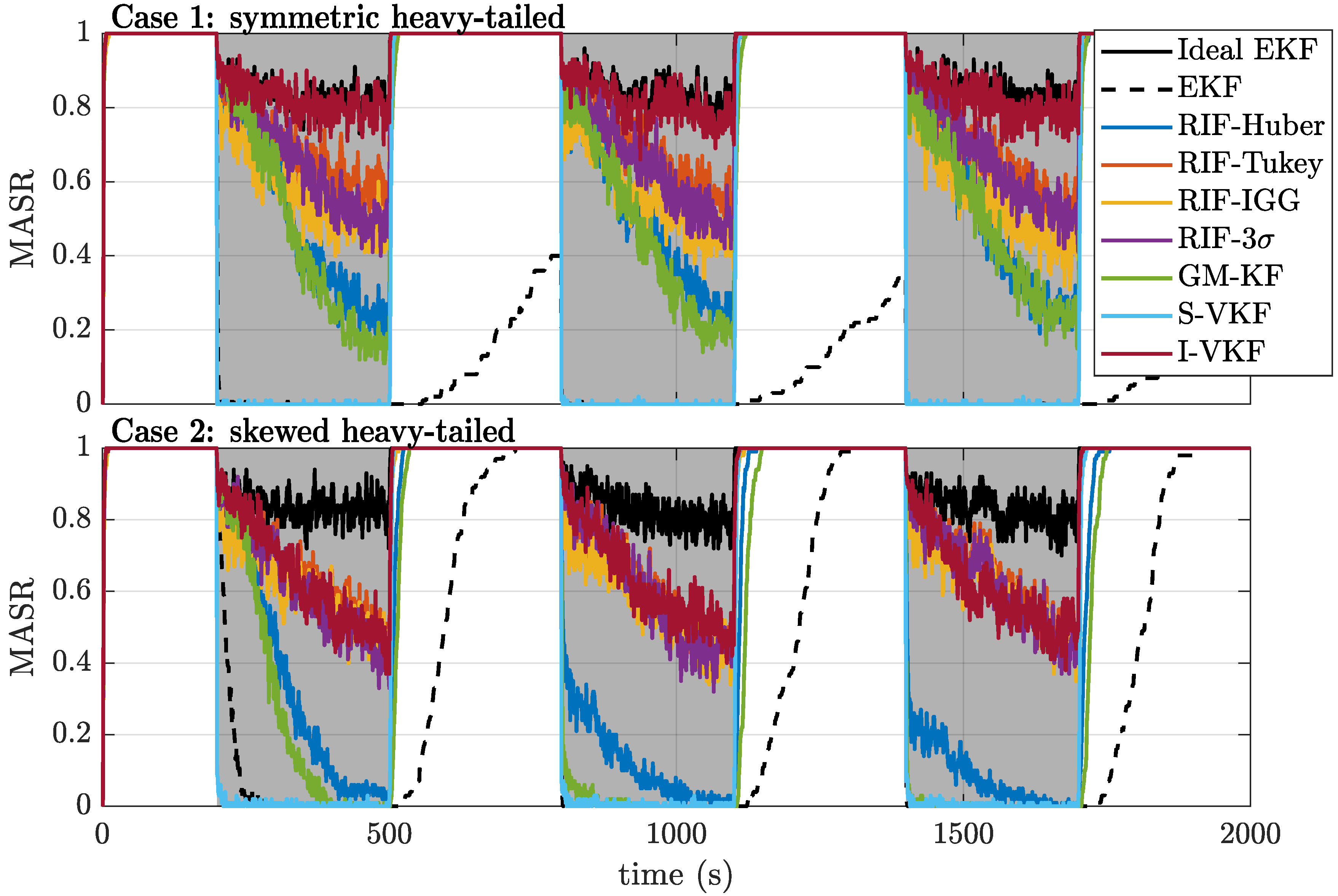
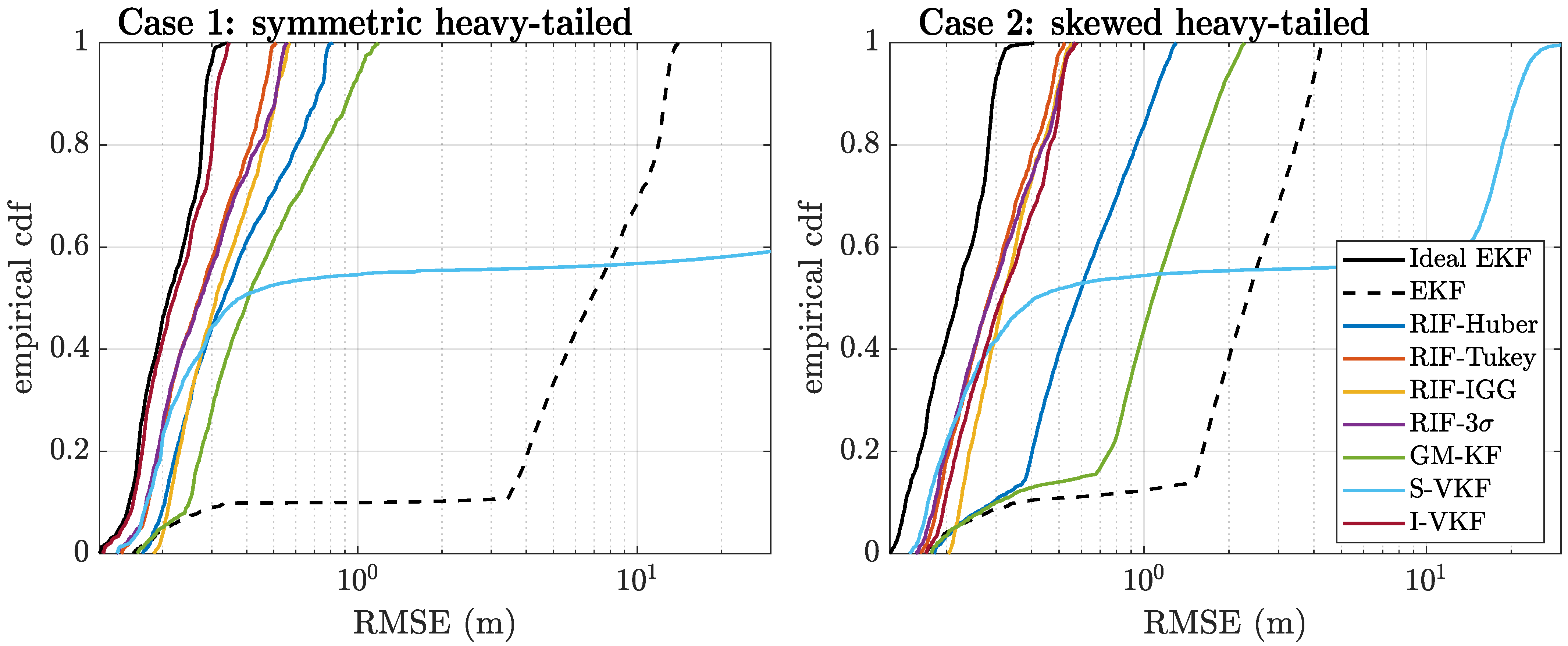
4.1. Simulation Results
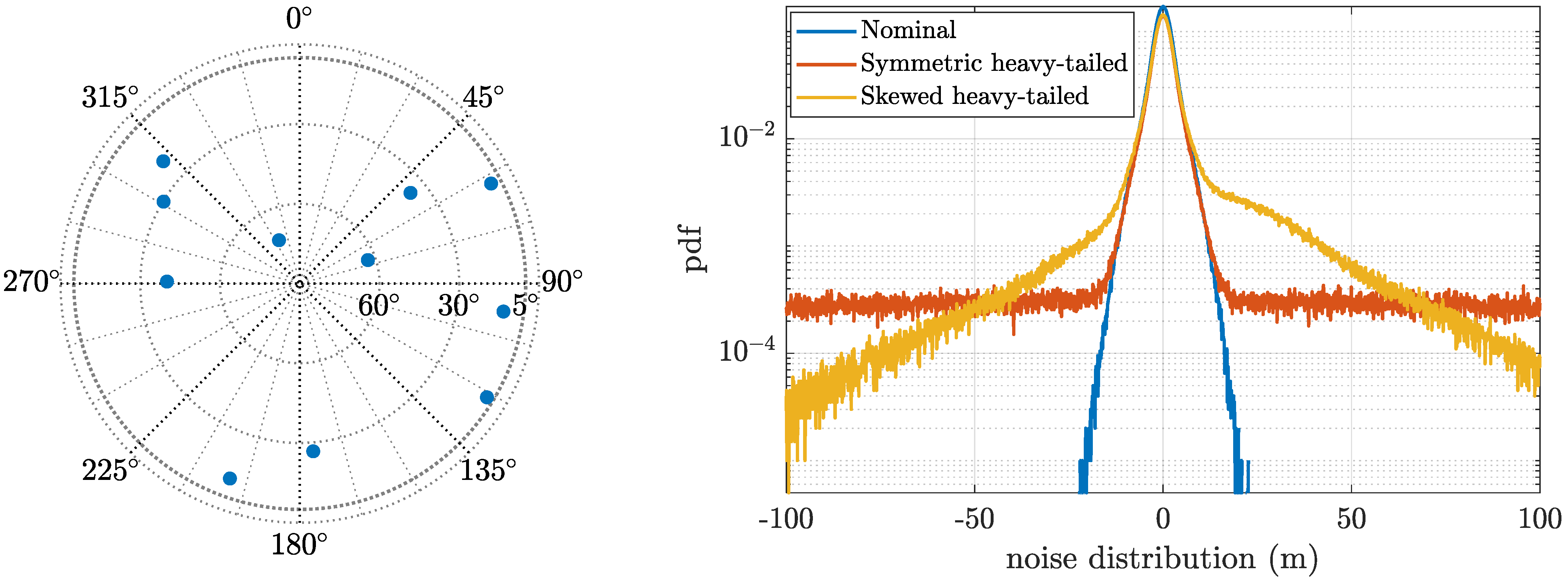
- Case 0: Nominal. The noise distribution corresponds to the nominal case, for whichwith as the ith satellite elevation.
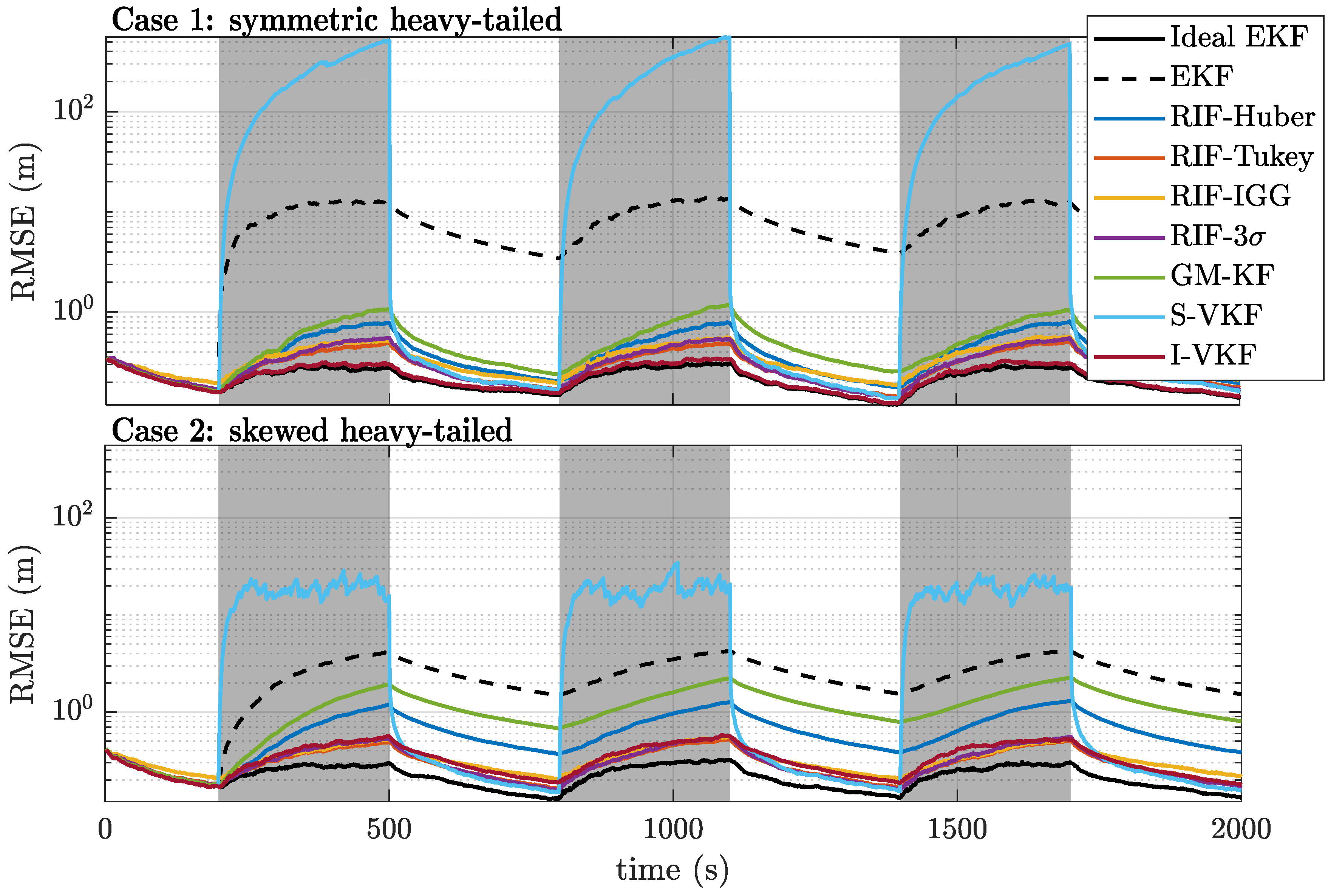
- Case 1: Symmetric heavy-tailed. In this case, the noise distribution for the observations is described bywhich corresponds to a symmetric heavy-tailed noise scenario.
- Case 2: Skewed heavy-tailed. During the “corrupted” time periods, the noise distribution is as follows:This corresponds to a skewed heavy-tailed noise scenario, where the second term has a positive mean and accounts for possible multipath conditions.
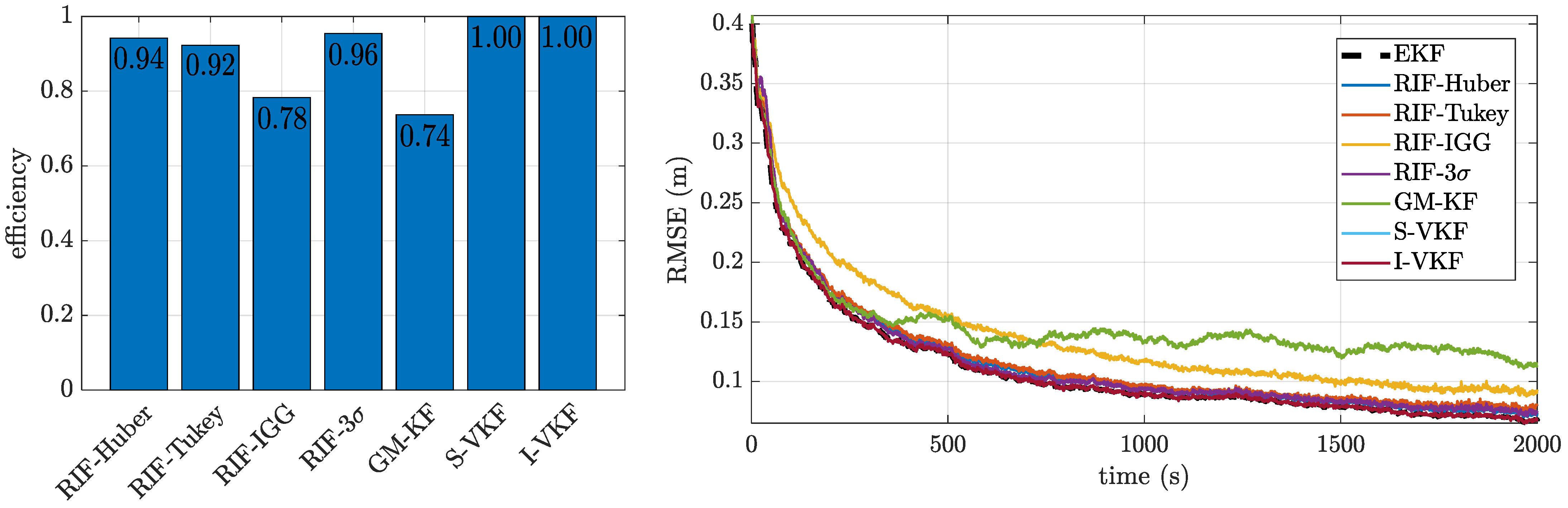
4.1.1. Case 0: Nominal Gaussian Scenario
4.1.2. Heavy-Tailed Noise Scenarios
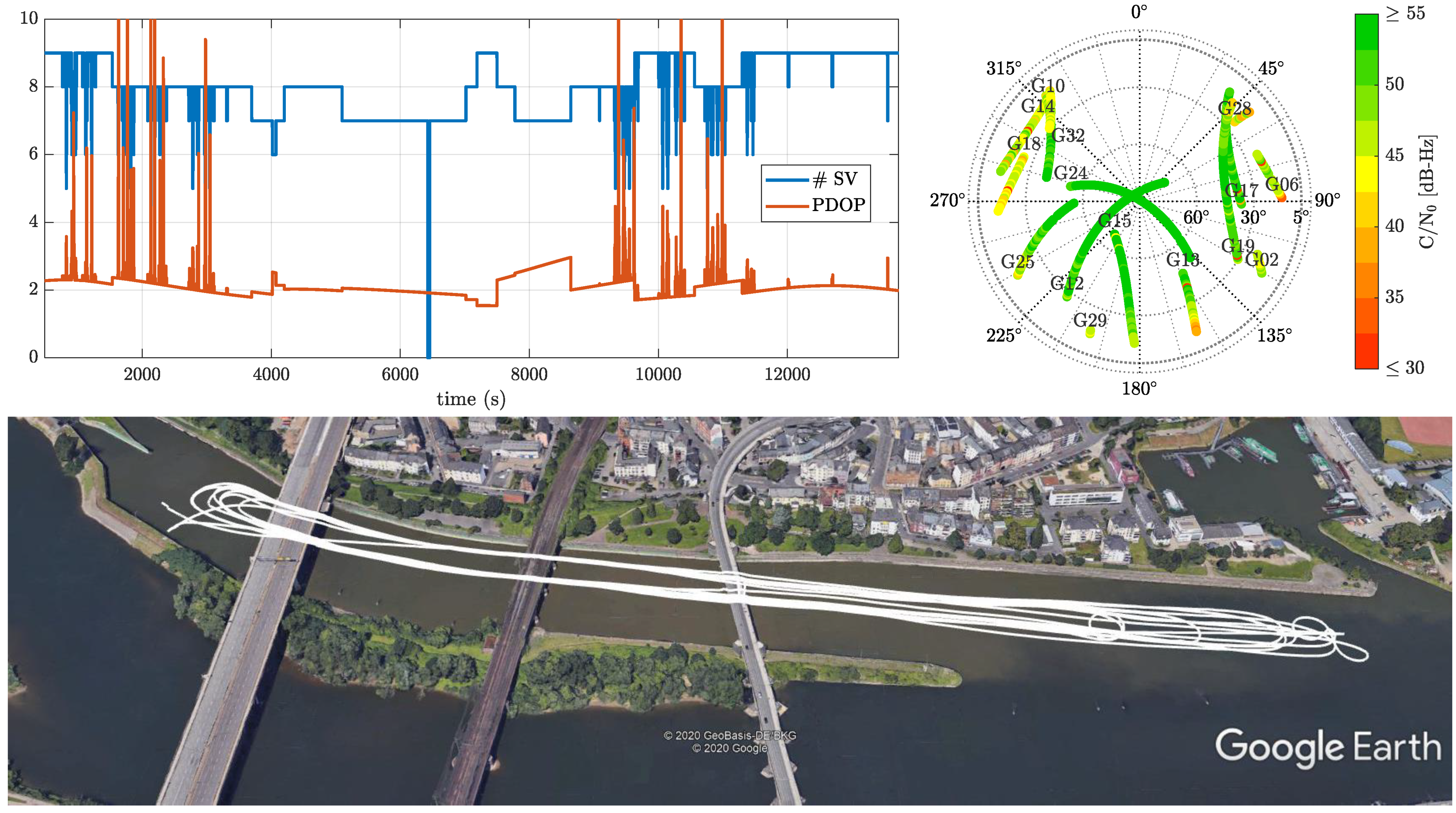
4.2. Real Data Experimentation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dardari, D.; Falletti, E.; Luise, M. Satellite and Terrestrial Radio Positioning Techniques: A Signal Processing Perspective; Academic Press: Oxford, UK, 2011. [Google Scholar]
- Amin, M.G.; Closas, P.; Broumandan, A.; Volakis, J.L. Vulnerabilities, threats, and authentication in satellite-based navigation systems [scanning the issue]. Proc. IEEE 2016, 104, 1169–1173. [Google Scholar] [CrossRef]
- Dardari, D.; Closas, P.; Djurić, P.M. Indoor tracking: Theory, methods, and technologies. IEEE Trans. Veh. Technol. 2015, 64, 1263–1278. [Google Scholar] [CrossRef]
- Morton, Y.J.; van Diggelen, F.; Spilker, J.J., Jr.; Parkinson, B.W.; Lo, S.; Gao, G. Position, Navigation, and Timing Technologies in the 21st Century, Volumes 1 and 2: Integrated Satellite Navigation, Sensor Systems, and Civil Applications, Set; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Langley, R.B. RTK GPS. GPS World 1998, 9, 70–76. [Google Scholar]
- Hesselbarth, A.; Medina, D.; Ziebold, R.; Sandler, M.; Hoppe, M.; Uhlemann, M. Enabling Assistance Functions for the Safe Navigation of Inland Waterways. IEEE Intell. Transp. Syst. Mag. 2020, 12, 123–135. [Google Scholar] [CrossRef]
- Duník, J.; Biswas, S.K.; Dempster, A.G.; Pany, T.; Closas, P. State Estimation Methods in Navigation: Overview and Application. IEEE Aerosp. Electron. Syst. Mag. 2020, 35, 16–31. [Google Scholar] [CrossRef]
- Teunissen, P.J. Least-squares estimation of the integer GPS ambiguities. In Invited Lecture, Section IV Theory and Methodology, IAG General Meeting; Beijing, China, 1993. [Google Scholar]
- Medina, D.; Ortega, L.; Vilà-Valls, J.; Closas, P.; Vincent, F.; Chaumette, E. Compact CRB for Delay, Doppler and Phase Estimation—Application to GNSS SPP & RTK Performance Characterization. IET Radar Sonar Navig. 2020, 14, 1537–1549. [Google Scholar]
- Borio, D. Robust signal processing for GNSS. In Proceedings of the 2017 European Navigation Conference (ENC), Lausanne, Switzerland, 9–12 May 2017; pp. 150–158. [Google Scholar]
- Borio, D. Myriad non-linearity for GNSS robust signal processing. IET Radar Sonar Navig. 2017, 11, 1467–1476. [Google Scholar] [CrossRef]
- Borio, D.; Li, H.; Closas, P. Huber’s non-linearity for GNSS interference mitigation. Sensors 2018, 18, 2217. [Google Scholar] [CrossRef]
- Borio, D.; Closas, P. Robust transform domain signal processing for GNSS. Navig. J. Inst. Navig. 2019, 66, 305–323. [Google Scholar] [CrossRef]
- Chang, X.W.; Guo, Y. Huber’s M-estimation in relative GPS positioning: Computational aspects. J. Geod. 2005, 79, 351–362. [Google Scholar] [CrossRef]
- Knight, N.L.; Wang, J. A comparison of outlier detection procedures and robust estimation methods in GPS positioning. J. Navig. 2009, 62, 699. [Google Scholar] [CrossRef]
- Lass, C.; Arias Medina, D.; Herrera Pinzón, I.D.; Ziebold, R. Methods of robust snapshot positioning in Multi-Antenna systems for inland water applications. In Proceedings of the European Navigation Conference 2016, Helsinki, Finnland, 30 May–2 June 2016. [Google Scholar]
- Medina, D.; Li, H.; Vilà-Valls, J.; Closas, P. Robust Statistics for GNSS Positioning under Harsh Conditions: A Useful Tool? Sensors 2019, 19, 5402. [Google Scholar] [CrossRef] [PubMed]
- Crespillo, O.G.; Andreetti, A.; Grosch, A. Design and Evaluation of Robust M-Estimators for GNSS Positioning in Urban Environments. In Proceedings of the 2020 International Technical Meeting of The Institute of Navigation, San Diego, CA, USA, 21–24 January 2020. [Google Scholar]
- Medina, D.; Romanovas, M.; Herrera-Pinzón, I.; Ziebold, R. Robust position and velocity estimation methods in integrated navigation systems for inland water applications. In Proceedings of the 2016 IEEE/ION Position, Location and Navigation Symposium (PLANS), Savannah, GA, USA, 11–14 April 2016; pp. 491–501. [Google Scholar]
- Crespillo, O.G.; Medina, D.; Skaloud, J.; Meurer, M. Tightly Coupled GNSS/INS Integration Based on Robust M-estimators. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018. [Google Scholar]
- Lesouple, J.; Robert, T.; Sahmoudi, M.; Tourneret, J.Y.; Vigneau, W. Multipath mitigation for GNSS positioning in an urban environment using sparse estimation. IEEE Trans. Intell. Transp. Syst. 2018, 20, 1316–1328. [Google Scholar] [CrossRef]
- Li, Z.; Yao, Y.; Wang, J.; Gao, J. Application of improved robust Kalman filter in data fusion for PPP/INS tightly coupled positioning system. Metrol. Meas. Syst. 2017, 24. [Google Scholar] [CrossRef]
- Gao, Z.; Li, Y.; Zhuang, Y.; Yang, H.; Pan, Y.; Zhang, H. Robust Kalman filter aided GEO/IGSO/GPS raw-PPP/INS tight integration. Sensors 2019, 19, 417. [Google Scholar] [CrossRef]
- Bidon, S.; Roche, S. Variational Bayes phase tracking for correlated dual-frequency measurements with slow dynamics. Signal Process. 2015, 113, 182–194. [Google Scholar] [CrossRef]
- Fabozzi, F.; Bidon, S.; Roche, S.; Priot, B. Robust GNSS phase tracking in case of slow dynamics using variational Bayes inference. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 1189–1195. [Google Scholar]
- Watson, R.M.; Gross, J.N. Robust navigation in GNSS degraded environment using graph optimization. In Proceedings of the 30th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2017), Portland, OR, USA, 25–29 September 2017; pp. 2906–2918. [Google Scholar]
- Pfeifer, T.; Protzel, P. Incrementally learned Mixture Models for GNSS Localization. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; IEEE: New York, NY, USA, 2019; pp. 1131–1138. [Google Scholar]
- Li, H.; Medina, D.; Vilà-Valls, J.; Closas, P. Robust Kalman Filter for RTK Positioning Under Signal-Degraded Scenarios. In Proceedings of the International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+), Miami, FL, USA, 16–20 September 2019. [Google Scholar]
- Li, H.; Medina, D.; Vila-Valls, J.; Closas, P. Robust Variational-based Kalman Filter for Outlier Rejection with Correlated Measurements. IEEE Trans. Signal Process. 2020, 69, 357–369. [Google Scholar] [CrossRef]
- Verhagen, S.; Teunissen, P.J. The ratio test for future GNSS ambiguity resolution. GPS Solut. 2013, 17, 535–548. [Google Scholar] [CrossRef]
- Kuusniemi, H.; Wieser, A.; Lachapelle, G.; Takala, J. User-level reliability monitoring in urban personal satellite-navigation. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1305–1318. [Google Scholar] [CrossRef]
- Medina, D.; Gibson, K.; Ziebold, R.; Closas, P. Determination of pseudorange error models and multipath characterization under signal-degraded scenarios. In Proceedings of the 31st International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2018), Miami, FL, USA, 24–28 September 2018; pp. 3446–3456. [Google Scholar]
- Teunissen, P.J. An optimality property of the integer least-squares estimator. J. Geod. 1999, 73, 587–593. [Google Scholar] [CrossRef]
- Teunissen, P. Theory of integer equivariant estimation with application to GNSS. J. Geod. 2003, 77, 402–410. [Google Scholar] [CrossRef]
- Medina, D.; Vilà-Valls, J.; Chaumette, E.; Vincent, F.; Closas, P. Cramér-Rao bound for a mixture of real-and integer-valued parameter vectors and its application to the linear regression model. Signal Process. 2020, 179, 107792. [Google Scholar] [CrossRef]
- Verhagen, S. The GNSS Integer Ambiguities: Estimation and Validation. Ph.D. Thesis, Technische Universiteit Delft, Delft, The Netherlands, 2005. [Google Scholar]
- Teunissen, P. Integer aperture GNSS ambiguity resolution. Artif. Satell. 2003, 38, 79–88. [Google Scholar]
- Bar-Shalom, Y.; Willett, P.K.; Tian, X. Tracking and Data Fusion; YBS: Storrs, CT, USA, 2011; Volume 11. [Google Scholar]
- Van Der Merwe, R.; others. Sigma-Point Kalman Filters for Probabilistic Inference in Dynamic State-Space Models. Ph.D. Thesis, OGI School of Science & Engineering at OHSU, Portland, OR, USA, 2004. [Google Scholar]
- Huber, P.J. Robust Statistics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1981. [Google Scholar]
- Hampel, F.R.; Ronchetti, E.M.; Rousseeuw, P.J.; Stahel, W.A. Robust Statistics: The Approach Based on Influence Functions; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 196. [Google Scholar]
- Zoubir, A.M.; Koivunen, V.; Ollila, E.; Muma, M. Robust Statistics for Signal Processing; Cambridge University Press: London, UK, 2018. [Google Scholar]
- Chang, L.; Li, K. Unified form for the robust Gaussian information filtering based on M-estimate. IEEE Signal Process. Lett. 2017, 24, 412–416. [Google Scholar] [CrossRef]
- Vercauteren, T.; Wang, X. Decentralized Sigma-Point Information Filters for Target Tracking in Collaborative Sensor Networks. IEEE Trans. Sig. Process. 2005, 53, 2997–3009. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Chandra, K. Multisensor Data Fusion: From Algorithms and Architectural Design to Applications; Chapter Cubature Information Filters: Theory and Applications to Multisensor Fusion; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Gandhi, M.A.; Mili, L. Robust Kalman filter based on a generalized maximum-likelihood-type estimator. IEEE Trans. Signal Process. 2009, 58, 2509–2520. [Google Scholar] [CrossRef]
- Hoffman, M.D.; Blei, D.M.; Wang, C.; Paisley, J. Stochastic Variational Inference. J. Mach. Learn. Res. 2013, 14, 1303–1347. [Google Scholar]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Wang, H.; Li, H.; Fang, J.; Wang, H. Robust Gaussian Kalman Filter With Outlier Detection. IEEE Signal Process. Lett. 2018, 25, 1236–1240. [Google Scholar] [CrossRef]
- Huber, P.J. Robust regression: Asymptotics, conjectures and Monte Carlo. Ann. Stat. 1973, 1, 799–821. [Google Scholar] [CrossRef]

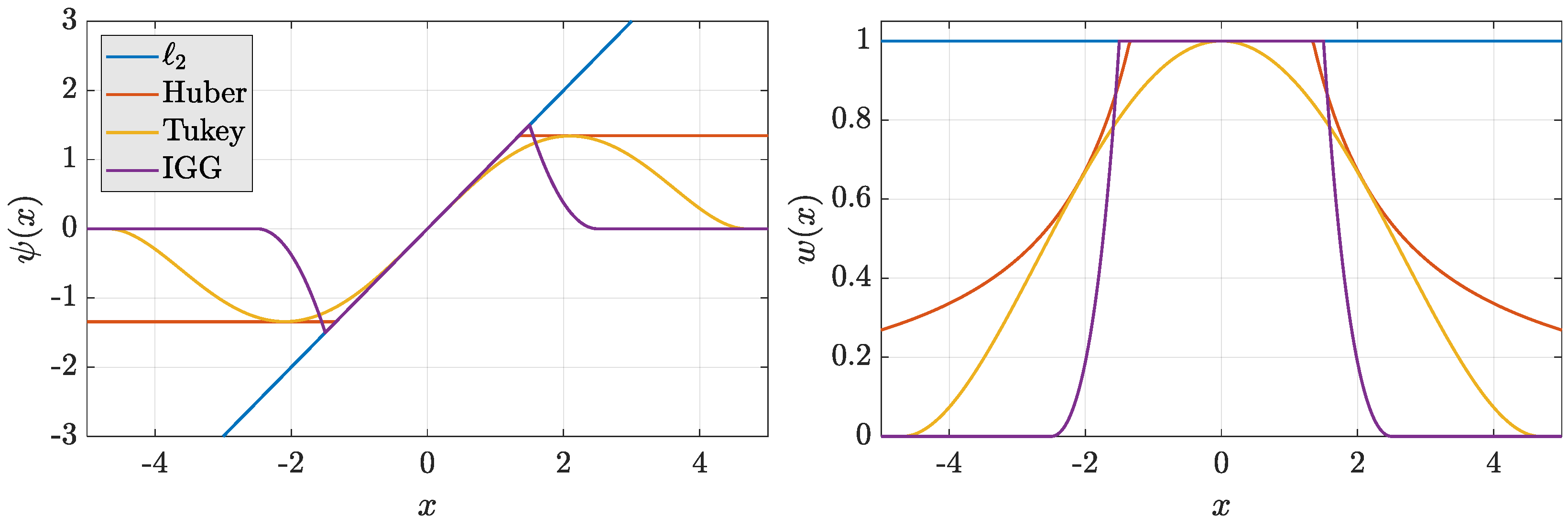

| Framework | Processing stage | Application | References |
|---|---|---|---|
| Robust Statistics | Baseband processing | Interference mitigation | [11,12,13,14] |
| PVT processing | Snapshot code-based positioning | [15,16,17,18,19] | |
| Recursive code-based positioning | [20,21,22] | ||
| Recursive RTK/PPP | [23,24] | ||
| Variational Inference | Baseband processing | Adaptive phase tracking | [25,26] |
| PVT processing | Recursive code-based positioning | [27,28] | |
| Recursive RTK/PPP | [29,30] |
| Conventional EKF | Robust Statistics-Based | Variational-Based | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Ideal EKF | EKF | RIF-Huber | RIF-Tukey | RIF-IGG | RIF-3 | GM-KF | S-VKF | I-VKF | |
| Case 0 | 99.96 | 99.96 | 99.96 | 99.96 | 99.96 | 99.96 | 99.96 | 99.96 | 99.96 |
| Case 1 | 92.74 | 16.20 | 76.63 | 85.42 | 80.41 | 84.19 | 75.38 | 54.46 | 91.82 |
| Case 2 | 92.47 | 39.89 | 61.42 | 83.62 | 81.47 | 82.45 | 56.31 | 54.60 | 83.22 |
| Estimator | ||||
|---|---|---|---|---|
| EKF | RIF-Tukey | GM-KF | I-VKF | |
| Fix ratio (%) | 53.22 | 46.74 | 58.27 | 53.46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medina, D.; Li, H.; Vilà-Valls, J.; Closas, P. Robust Filtering Techniques for RTK Positioning in Harsh Propagation Environments. Sensors 2021, 21, 1250. https://doi.org/10.3390/s21041250
Medina D, Li H, Vilà-Valls J, Closas P. Robust Filtering Techniques for RTK Positioning in Harsh Propagation Environments. Sensors. 2021; 21(4):1250. https://doi.org/10.3390/s21041250
Chicago/Turabian StyleMedina, Daniel, Haoqing Li, Jordi Vilà-Valls, and Pau Closas. 2021. "Robust Filtering Techniques for RTK Positioning in Harsh Propagation Environments" Sensors 21, no. 4: 1250. https://doi.org/10.3390/s21041250
APA StyleMedina, D., Li, H., Vilà-Valls, J., & Closas, P. (2021). Robust Filtering Techniques for RTK Positioning in Harsh Propagation Environments. Sensors, 21(4), 1250. https://doi.org/10.3390/s21041250









