A New Dynamical Method for Bearing Fault Diagnosis Based on Optimal Regulation of Resonant Behaviors in a Fluctuating-Mass-Induced Linear Oscillator
Abstract
1. Introduction
2. System Model
2.1. GST Based FMLO System
2.2. System Stationary Response
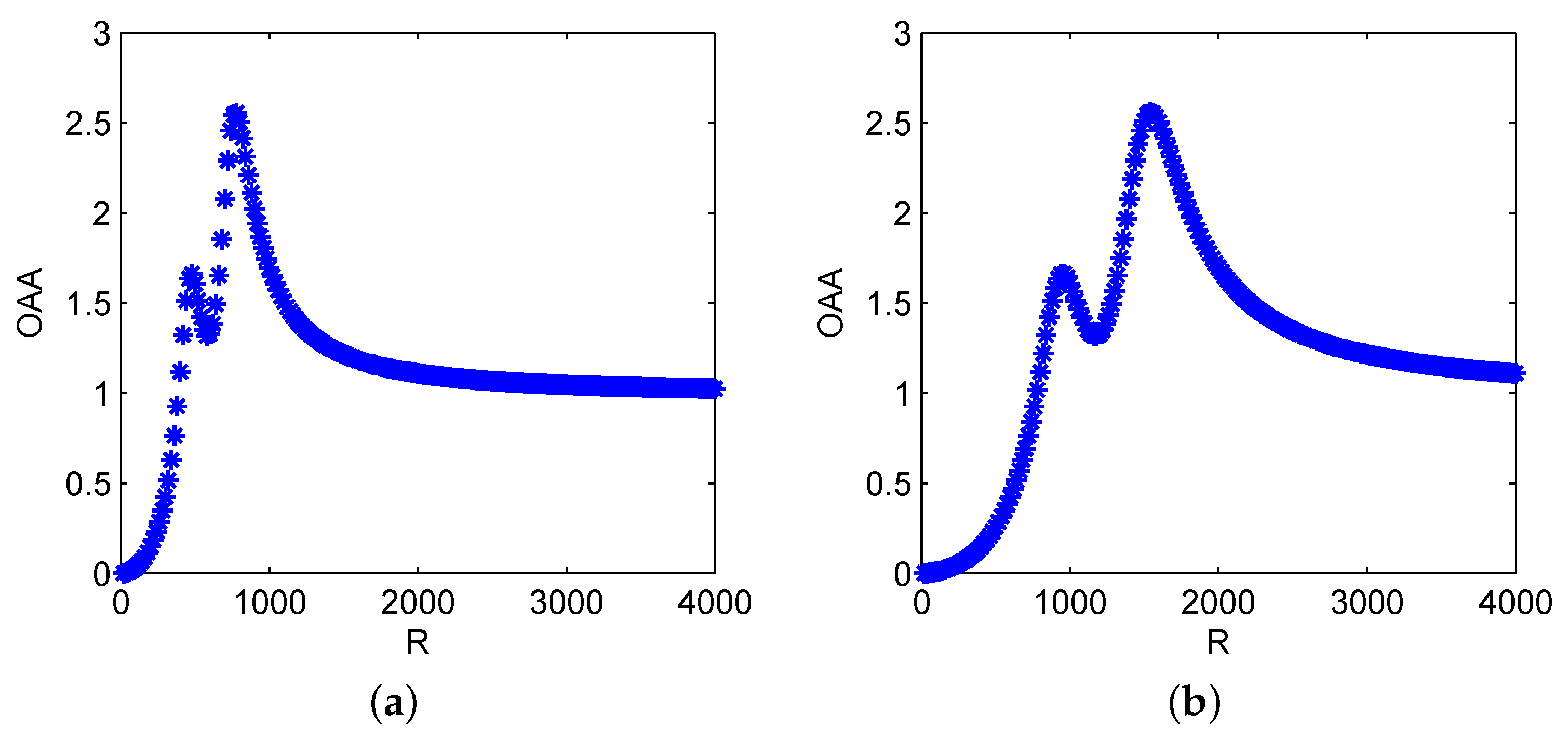
2.3. Multi-Parameter Induced GSR Behaviors
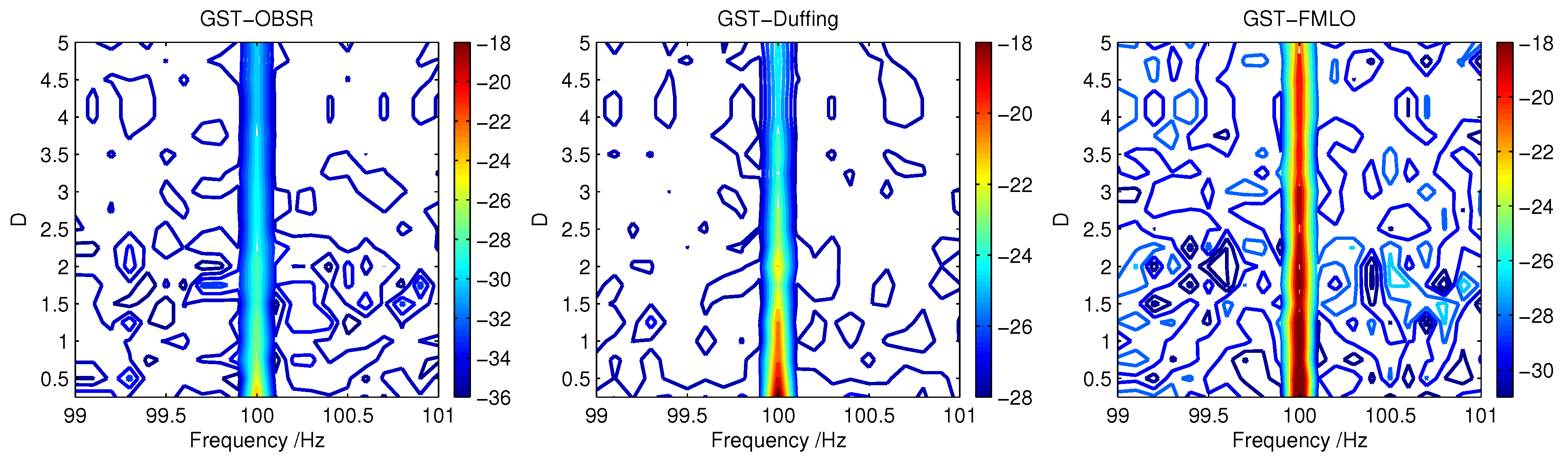
3. Numerical Performance Based on Multi-Parameter Optimization
3.1. Numerical Implementation
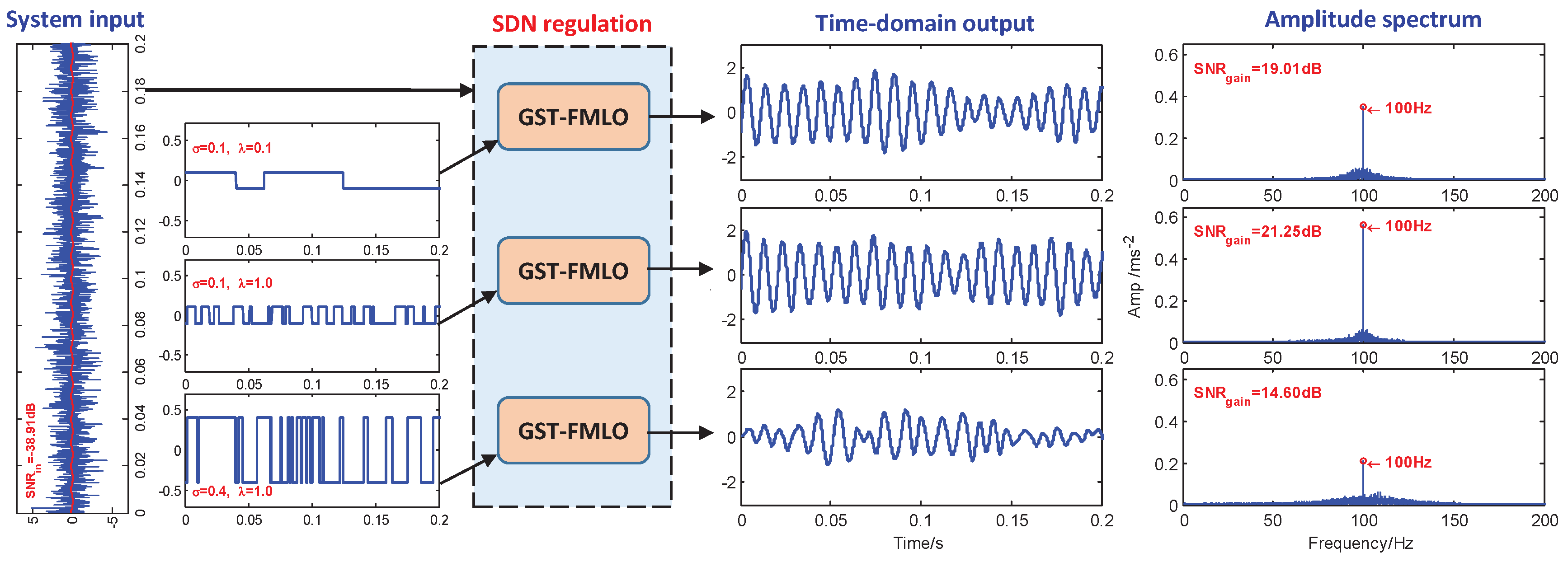
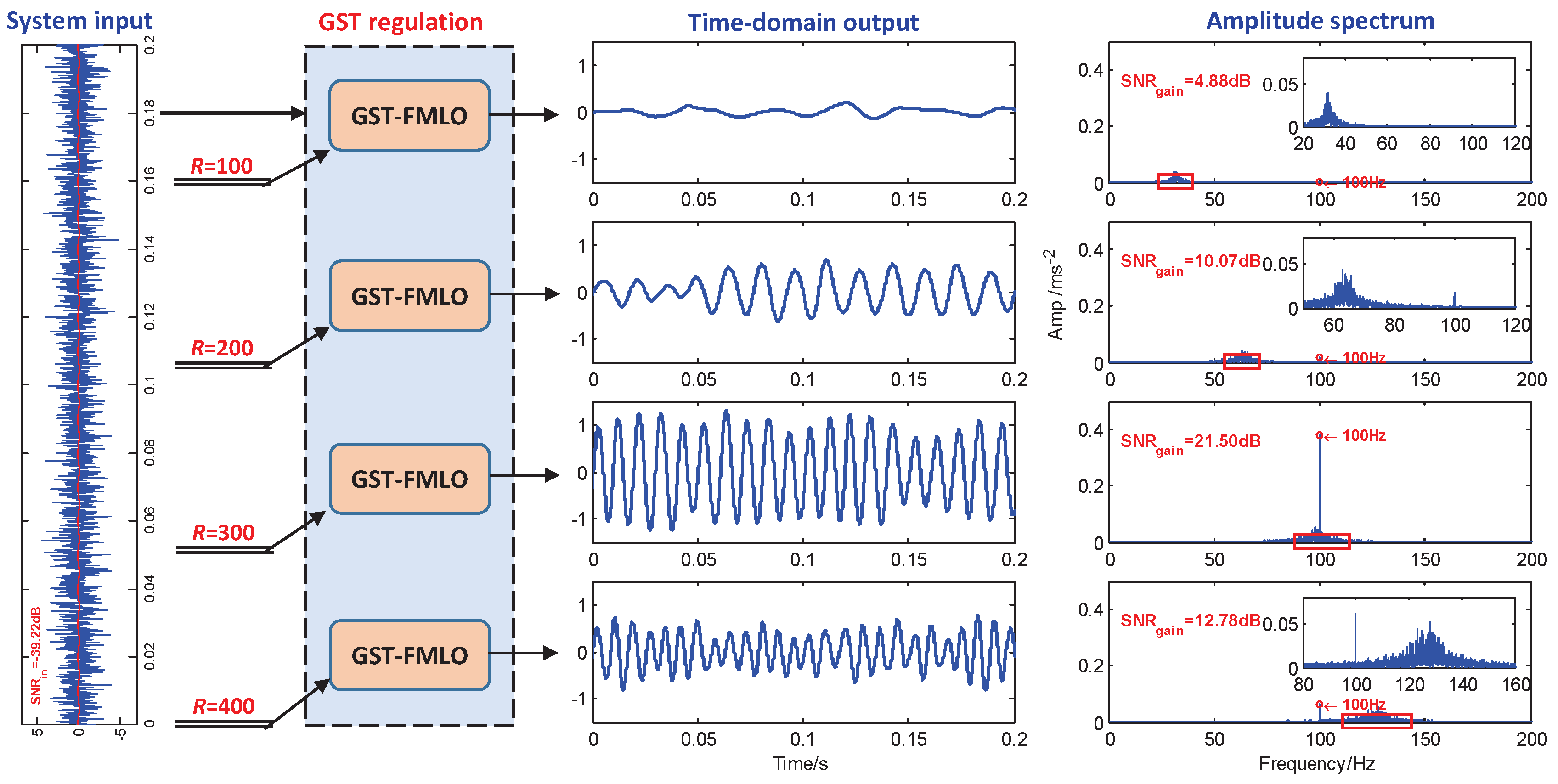
3.2. System Regulation Mechanism
- -
- Damping Regulation
- -
- Inherent Frequency Regulation
- -
- SDN Regulation
- -
- GST Regulation
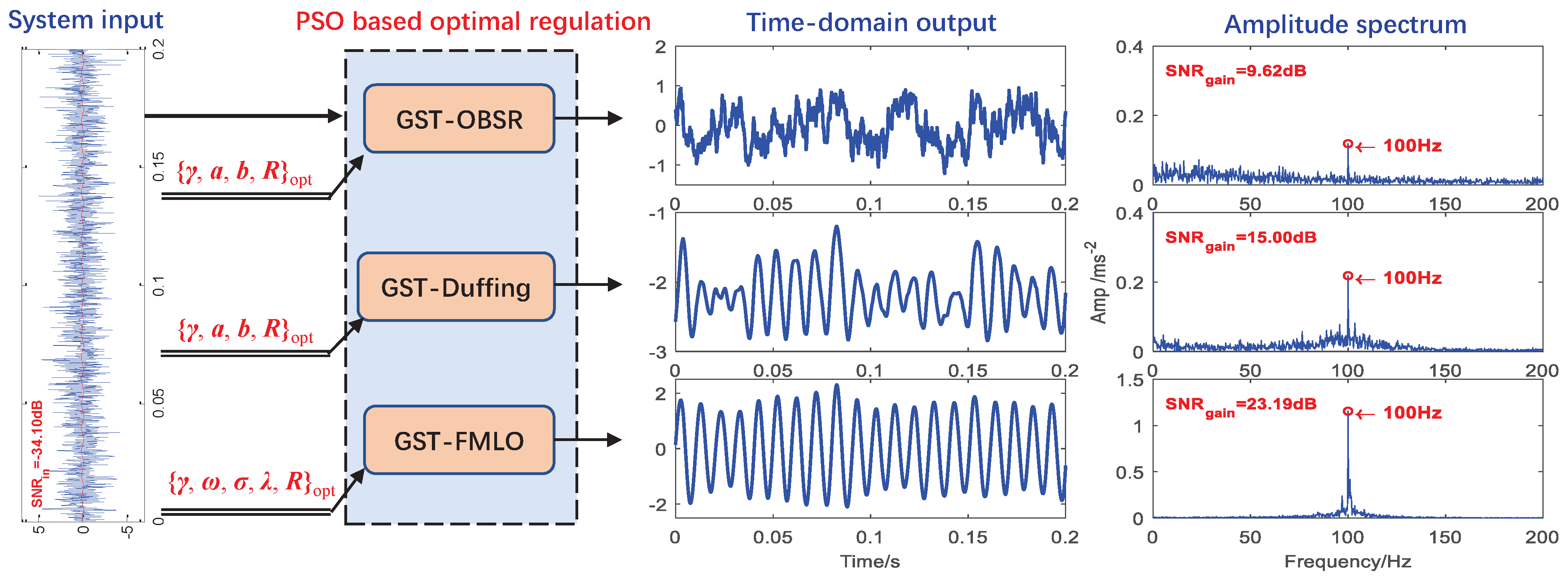
3.3. PSO Based Multi-Parameter Regulation
- overdamped bistable SR system (GST-OBSR)with four parameters: , a, b, R;
- underdamped Duffing oscillator (GST-Duffing)with four parameters: , a, b, R;
- our proposed GST-FMLO system Equation (5) with five parameters: , , , , R.It is noted that, all the parameters in GST-OBSR and GST-Duffing systems are also optimized by the previously mentioned PSO algorithm with the objective function . In practical applications, the actual input driving frequency may be known, or unknown and should be estimated. Thus, in the following simulations, we focus on the performance of two cases, respectively with known and unknown driving frequency.
- -
- Performance with Known Driving Frequency
- -
- Adaptive Performance with Unknown Driving Frequency
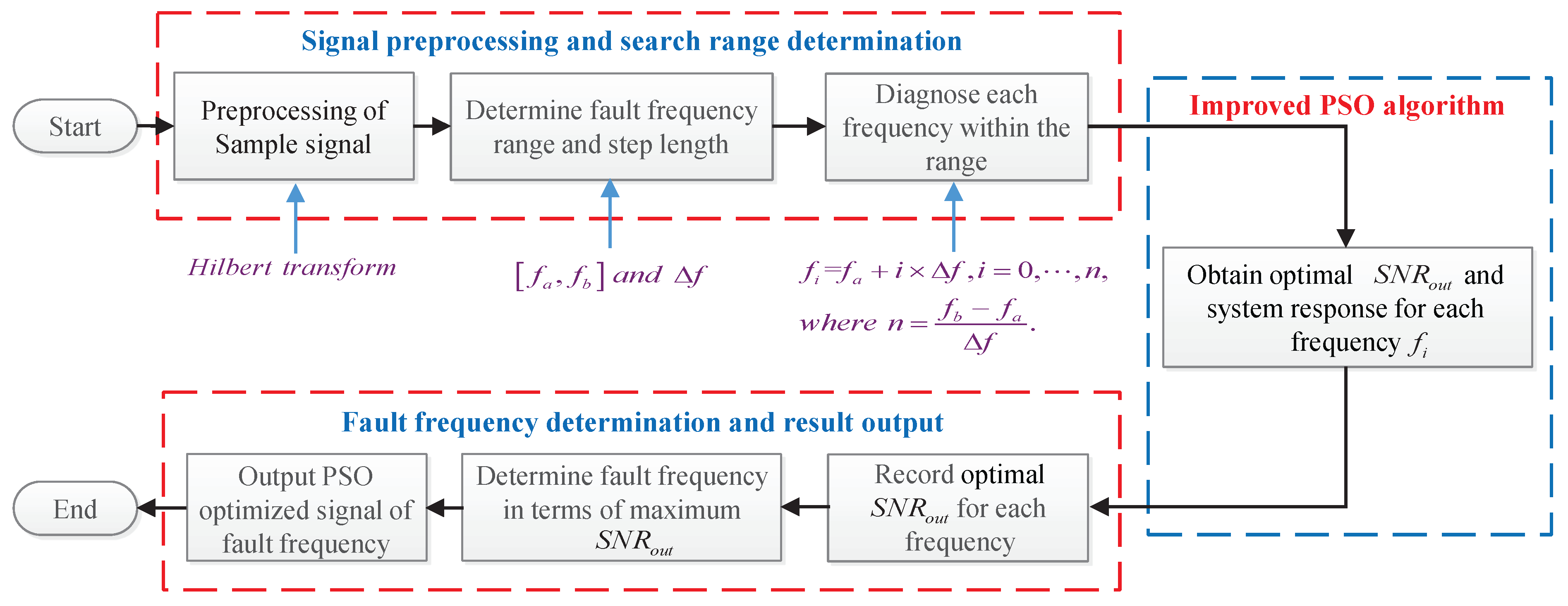
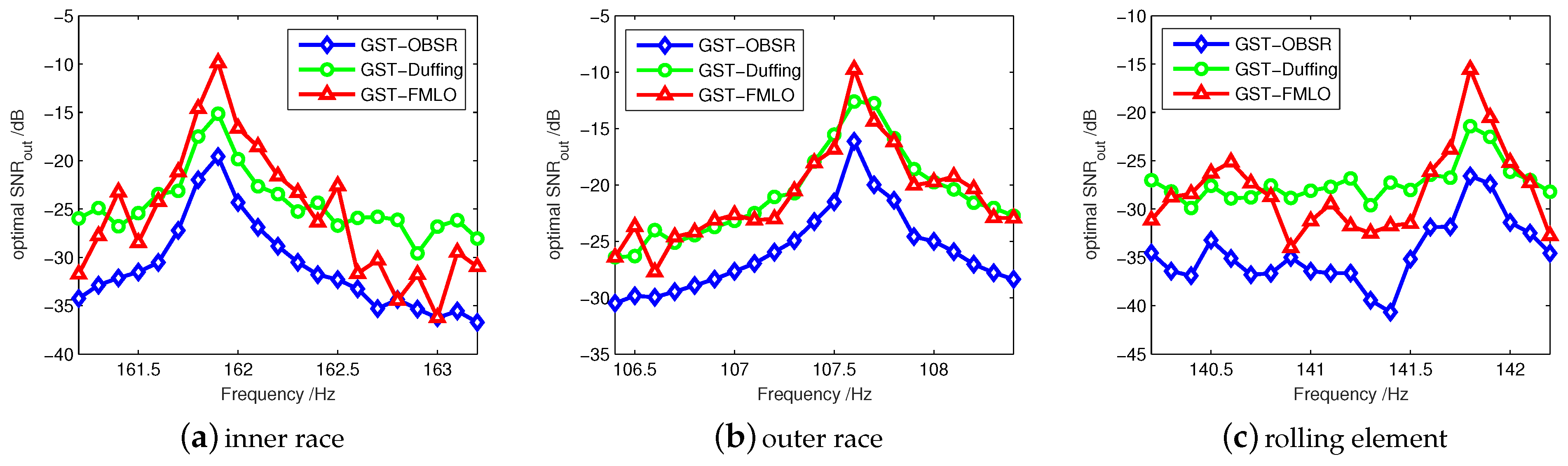
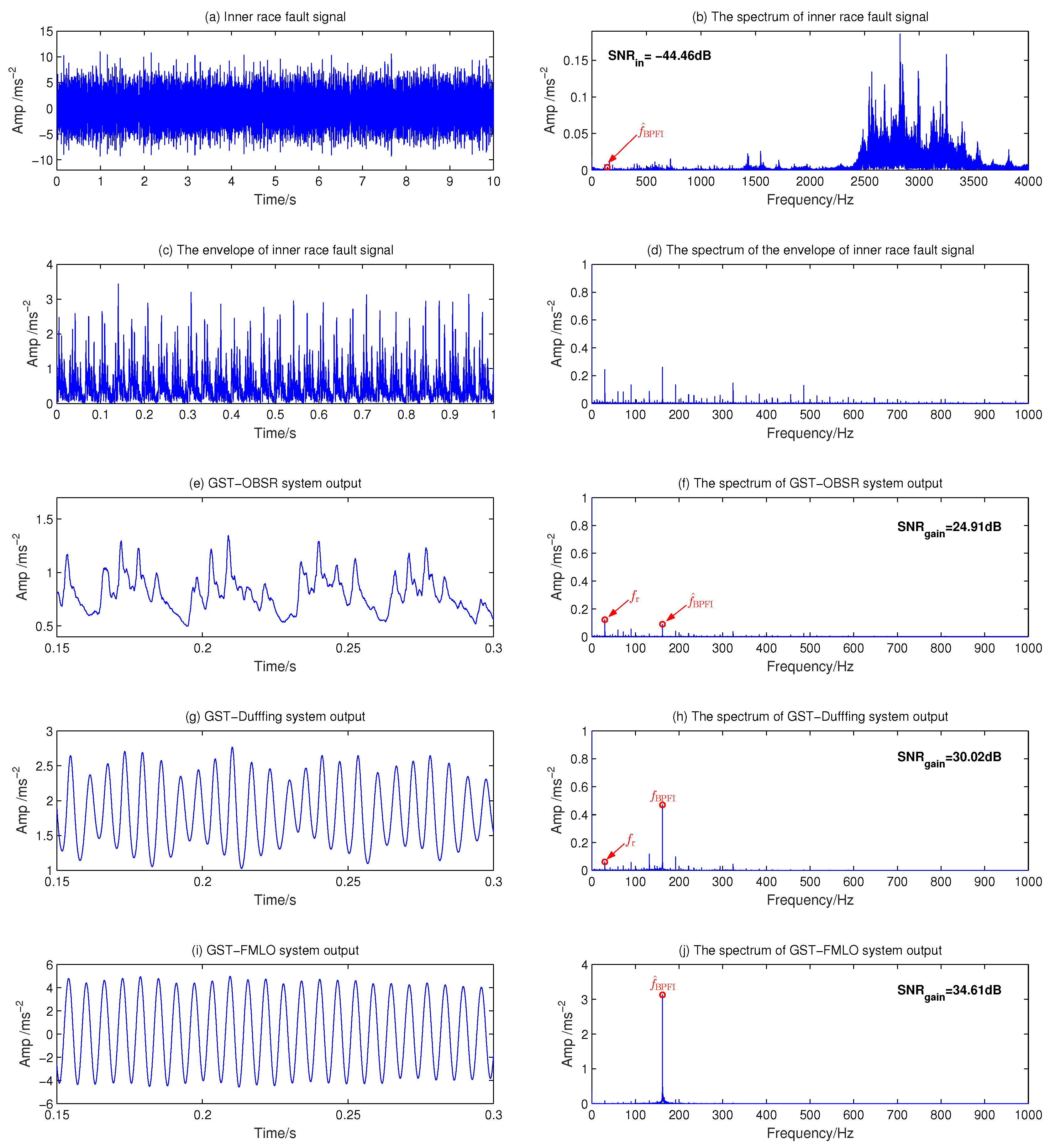
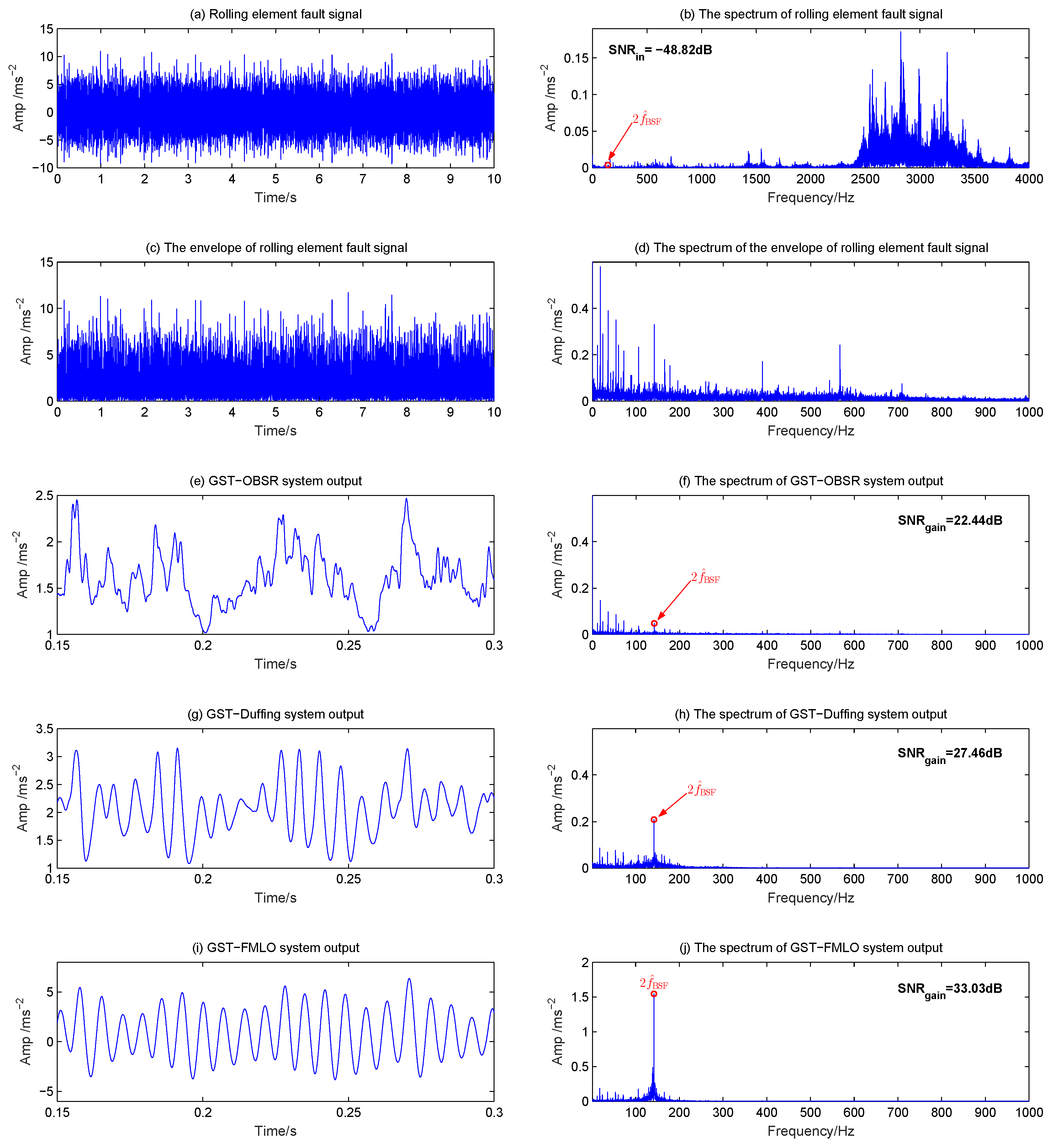
4. Experimental Applications
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Randall, R.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Ibarra-Zarate, D.; Tamayo-Pazos, O.; Vallejo-Guevara, A. Bearing fault diagnosis in rotating machinery based on cepstrum pre-whitening of vibration and acoustic emission. Int. J. Adv. Manuf. Technol. 2019, 104, 4155–4168. [Google Scholar] [CrossRef]
- Urreta, H.; Aguirre, G.; Kuzhir, P.; Norberto, L. Seals based on magnetic fluids for high precision spindles of machine tools. Int. J. Precis. Eng. Manuf. 2018, 19, 495–503. [Google Scholar] [CrossRef]
- Urreta, H.; Aguirre, G.; Kuzhir, P.; Norberto, L. Actively lubricated hybrid journal bearings based on magnetic fluids for high-precision spindles of machine tools. J. Intell. Mater. Syst. Struct. 2019, 30, 2257–2271. [Google Scholar] [CrossRef]
- He, M.; He, D. A deep learning based approach for bearing fault diagnosis. IEEE Trans. Ind. Appl. 2017, 53, 3057–3065. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.; Shan, H.; Lin, J. Early fault diagnosis of bearings using an improved spectral kurtosis by maximum correlated kurtosis deconvolution. Sensors 2015, 15, 29363–29377. [Google Scholar] [CrossRef]
- Wang, Y.; Xiang, J.; Markert, R.; Liang, M. Spectral kurtosis for fault detection, diagnosis and prognostics of rotating machines: A review with applications. Mech. Syst. Signal Process. 2016, 66, 679–698. [Google Scholar] [CrossRef]
- Georgoulas, G.; Loutas, T.; Stylios, C.D.; Kostopoulos, V. Bearing fault detection based on hybrid ensemble detector and empirical mode decomposition. Mech. Syst. Signal Process. 2013, 41, 510–525. [Google Scholar] [CrossRef]
- Kedadouche, M.; Liu, Z.; Vu, V. A new approach based on OMA-empirical wavelet transforms for bearing fault diagnosis. Measurement 2016, 90, 292–308. [Google Scholar] [CrossRef]
- Yau, H.; Wu, S.; Chen, C.; Li, Y. Fractional-order chaotic self-synchronization-based tracking faults diagnosis of ball bearing systems. IEEE Trans. Ind. Electron. 2016, 63, 3824–3833. [Google Scholar] [CrossRef]
- Zhou, P.; Lu, S.; Liu, F.; Liu, Y.; Li, G.; Zhao, J. Novel synthetic index-based adaptive stochastic resonance method and its application in bearing fault diagnosis. J. Sound Vib. 2017, 391, 194–210. [Google Scholar] [CrossRef]
- Lu, S.; He, Q.; Wang, J. A review of stochastic resonance in rotating machine fault detection. Mech. Syst. Signal Process. 2019, 116, 502–535. [Google Scholar] [CrossRef]
- Qiao, Z.; Lei, Y.; Li, N. Applications of stochastic resonance to machinery fault detection: A review and tutorial. Mech. Syst. Signal Process. 2019, 122, 230–260. [Google Scholar] [CrossRef]
- Gao, J.; Yang, J.; Huang, D.; Liu, H.; Liu, S. Experimental application of vibrational resonance on bearing fault diagnosis. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 1–13. [Google Scholar] [CrossRef]
- Jia, P.; Wu, C.; Yang, J.; Sanjuán, M.; Liu, G. Improving the weak aperiodic signal by three kinds of vibrational resonance. Nonlinear Dyn. 2018, 91, 2699–2713. [Google Scholar] [CrossRef]
- Li, S.; Gu, K.; Huang, S. A chaotic system-based signal identification Technology: Fault-diagnosis of industrial bearing system. Measurement 2020, 171, 108832. [Google Scholar] [CrossRef]
- Li, S.; Gu, K. Smart fault-detection machine for ball-bearing system with chaotic mapping strategy. Sensors 2019, 19, 2178. [Google Scholar] [CrossRef]
- Shi, J.; Liang, M.; Guan, Y. Bearing fault diagnosis under variable rotational speed via the joint application of windowed fractal dimension transform and generalized demodulation: A method free from prefiltering and resampling. Mech. Syst. Signal Process. 2016, 68, 15–33. [Google Scholar] [CrossRef]
- Wang, X.; Liu, C.; Bi, F.; Bi, X.; Shao, K. Fault diagnosis of diesel engine based on adaptive wavelet packets and EEMD-fractal dimension. Mech. Syst. Signal Process. 2013, 41, 581–597. [Google Scholar] [CrossRef]
- Mba, C.; Marchesiello, S.; Fasana, A.; Garibaldi, L. Gearbox damage identification and quantification using stochastic resonance. Mech. Ind. 2017, 18, 805. [Google Scholar] [CrossRef][Green Version]
- Liu, X.; Liu, H.; Yang, J.; Litak, G.; Cheng, G.; Han, S. Improving the bearing fault diagnosis efficiency by the adaptive stochastic resonance in a new nonlinear system adaptive stochastic resonance in a new nonlinear system. Mech. Syst. Signal Process. 2017, 96, 58–76. [Google Scholar] [CrossRef]
- Gammaitoni, L.; Hanggi, P.; Jung, P.; Marchesoni, F. Stochastic resonance. Rev. Mod. Phys. 1998, 70, 223–287. [Google Scholar] [CrossRef]
- Leng, Y.; Wang, T. Numerical analysis and engineering application of large parameter stochastic resonance. J. Sound Vib. 2006, 292, 788–801. [Google Scholar] [CrossRef]
- Lai, Z.; Leng, Y. Weak-signal detection based on the stochastic resonance of bistable duffing oscillator and its application in incipient fault diagnosis. Mech. Syst. Signal Process. 2016, 81, 60–74. [Google Scholar] [CrossRef]
- Huang, D.; Yang, J.; Zhang, J.; Liu, H. An improved adaptive stochastic resonance method for improving the efficiency of bearing faults diagnosis. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 232, 2352–2368. [Google Scholar] [CrossRef]
- Liu, J.; Leng, Y.; Lai, Z.; Fan, S. Multi-frequency signal detection based on frequency exchange and re-scaling stochastic resonance and its application to weak fault diagnosis. Sensors 2018, 18, 1325. [Google Scholar] [CrossRef]
- Ma, Q.; Huang, D.; Yang, J. Adaptive stochastic resonance in second-order system with general scale transformation for weak feature extraction and its application in bearing fault diagnosis. Fluct. Noise Lett. 2018, 17, 185009. [Google Scholar] [CrossRef]
- Lu, Z.; Yang, T.; Zhu, M. Study of the method of multi-frequency signal detection based on the adaptive stochastic resonance. Abstr. Appl. Anal. 2013, 2013, 1–10. [Google Scholar] [CrossRef]
- Li, J.; Chen, X.; He, Z. Adaptive stochastic resonance method for impact signal detection based on sliding window. Mech. Syst. Signal Process. 2013, 36, 240–255. [Google Scholar] [CrossRef]
- Huang, Z.; Guo, F. Stochastic resonance in a fractional linear oscillator subject to random viscous damping and signal-modulated noise. Chin. J. Phys. 2016, 54, 69–76. [Google Scholar] [CrossRef]
- He, G.; Tian, Y.; Wang, Y. Stochastic resonance in a fractional oscillator with random damping strength and random spring stiffness. J. Stat. Mech. Theory Exp. 2013, 2013, P09026. [Google Scholar] [CrossRef]
- Zhong, S.; Zhang, L.; Wang, H.; Ma, H.; Luno, M. Nonlinear effect of time delay on the generalized stochastic resonance in a fractional oscillator with multiplicative polynomial noise. Nonlinear Dyn. 2017, 89, 1327–1340. [Google Scholar] [CrossRef]
- Mankin, R.; Kekker, A. Memory-enhanced energetic stability for a fractional oscillator with fluctuating frequency. Phys. Rev. E 2010, 81, 041122. [Google Scholar] [CrossRef] [PubMed]
- Lin, L.; Chen, C.; Wang, H. Trichotomous noise induced stochastic resonance in a fractional oscillator with random damping and random frequency. J. Stat. Mech. Theory Exp. 2016, 2016, 023201. [Google Scholar] [CrossRef]
- Sauga, A.; Mankin, R.; Ainsaar, A. Resonant behavior of a fractional oscillator with fluctuating mass. Phys. Rev. E 2010, 81, 011141. [Google Scholar]
- Zhong, S.; Yang, J.; Zhang, L.; Ma, H.; Luo, M. Resonant behavior of a harmonic oscillator with fluctuating mass driven by a Mittag-Leffler noise. J. Stat. Mech. Theory Exp. 2017, 2017, 023211. [Google Scholar] [CrossRef]
- Burov, S.; Gitterman, M. Noisy oscillator: Random mass and random damping. Phys. Rev. E 2016, 94, 052144. [Google Scholar] [CrossRef]
- Tong, L.; Li, X.; Hu, J.; Ren, L. A PSO optimization scale-transformation stochastic-resonance algorithm with stability mutation operator. IEEE Access 2017, 1167–1176. [Google Scholar] [CrossRef]
- Shapiro, V.; Loginov, V. “Formulae of differentiation” and their use for solving stochastic equations. Physica A 1978, 91, 563–574. [Google Scholar] [CrossRef]
- Laas, K.; Mankin, R.; Reiter, E. Influence of memory time on the resonant behavior of an oscillatory system described by a generalized langevin equation. Int. J. Math. Model. Methods Appl. Sci. 2011, 5, 280–289. [Google Scholar]
- Yu, L.; Wang, H.; Lin, L.; Zhong, S. The incentive effect of venture capital in bilateral partnership systems with the bias mono-stable Cobb-Douglas utility. Nonlinear Dyn. 2019, 95, 3127–3147. [Google Scholar] [CrossRef]
- Smith, W.; Randall, R. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study. Mech. Syst. Signal Process. 2015, 64, 100–131. [Google Scholar] [CrossRef]
- Download a Data File. Available online: https://csegroups.case.edu/bearingdatacenter/pages/download-data-file (accessed on 18 August 2020).






| Method | Optimal System Parameters (osp) | Detection Performance | ||||||
|---|---|---|---|---|---|---|---|---|
| osp-1 | osp-2 | osp-3 | osp-4 | |||||
| GST-OBSR | 0.4680 | 0.0025 | 0.8440 | - | dB | dB | dB | |
| GST-Duffing | 0.2224 | 1.2144 | 0.2384 | - | dB | dB | dB | |
| GST-FMLO | 0.0407 | 1.5839 | 0.0812 | 0.7088 | dB | dB | dB | |
| Method | Optimal System Parameters (osp) | Diagnosis Performance | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Inner race fault with Hz | |||||||||
| osp-1 | osp-2 | osp-3 | osp-4 | R | |||||
| GST-OBSR | 1.7930 | 0.0036 | 0.8986 | - | dB | dB | dB | 6.60 | |
| GST-Duffing | 0.2345 | 1.8715 | 0.5370 | - | dB | dB | dB | 6.74 | |
| GST-FMLO | 0.0205 | 1.7558 | 0.0272 | 0.6580 | dB | dB | dB | 1.00 | |
| Outer race fault with Hz | |||||||||
| osp-1 | osp-2 | osp-3 | osp-4 | R | |||||
| GST-OBSR | 1.6615 | 0.0096 | 1.0263 | - | dB | dB | dB | 6.58 | |
| GST-Duffing | 0.5250 | 0.0878 | 1.4789 | - | dB | dB | dB | 6.72 | |
| GST-FMLO | 0.1196 | 1.7923 | 0.0071 | 0.9982 | dB | dB | dB | 1.00 | |
| Rolling element fault with Hz | |||||||||
| osp-1 | osp-2 | osp-3 | osp-4 | R | |||||
| GST-OBSR | 1.6864 | 0.0537 | 0.5879 | - | dB | dB | dB | 6.51 | |
| GST-Duffing | 0.4721 | 1.7500 | 0.6105 | - | dB | dB | dB | 7.02 | |
| GST-FMLO | 0.0817 | 1.7770 | 0.0305 | 0.8001 | dB | dB | dB | 1.00 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, K.; Lu, Y.; Lin, L.; Wang, H. A New Dynamical Method for Bearing Fault Diagnosis Based on Optimal Regulation of Resonant Behaviors in a Fluctuating-Mass-Induced Linear Oscillator. Sensors 2021, 21, 707. https://doi.org/10.3390/s21030707
Chen K, Lu Y, Lin L, Wang H. A New Dynamical Method for Bearing Fault Diagnosis Based on Optimal Regulation of Resonant Behaviors in a Fluctuating-Mass-Induced Linear Oscillator. Sensors. 2021; 21(3):707. https://doi.org/10.3390/s21030707
Chicago/Turabian StyleChen, Kehan, Yuting Lu, Lifeng Lin, and Huiqi Wang. 2021. "A New Dynamical Method for Bearing Fault Diagnosis Based on Optimal Regulation of Resonant Behaviors in a Fluctuating-Mass-Induced Linear Oscillator" Sensors 21, no. 3: 707. https://doi.org/10.3390/s21030707
APA StyleChen, K., Lu, Y., Lin, L., & Wang, H. (2021). A New Dynamical Method for Bearing Fault Diagnosis Based on Optimal Regulation of Resonant Behaviors in a Fluctuating-Mass-Induced Linear Oscillator. Sensors, 21(3), 707. https://doi.org/10.3390/s21030707





