A Quality Control Check to Ensure Comparability of Stereophotogrammetric Data between Sessions and Systems
Abstract
1. Introduction
2. Materials and Methods
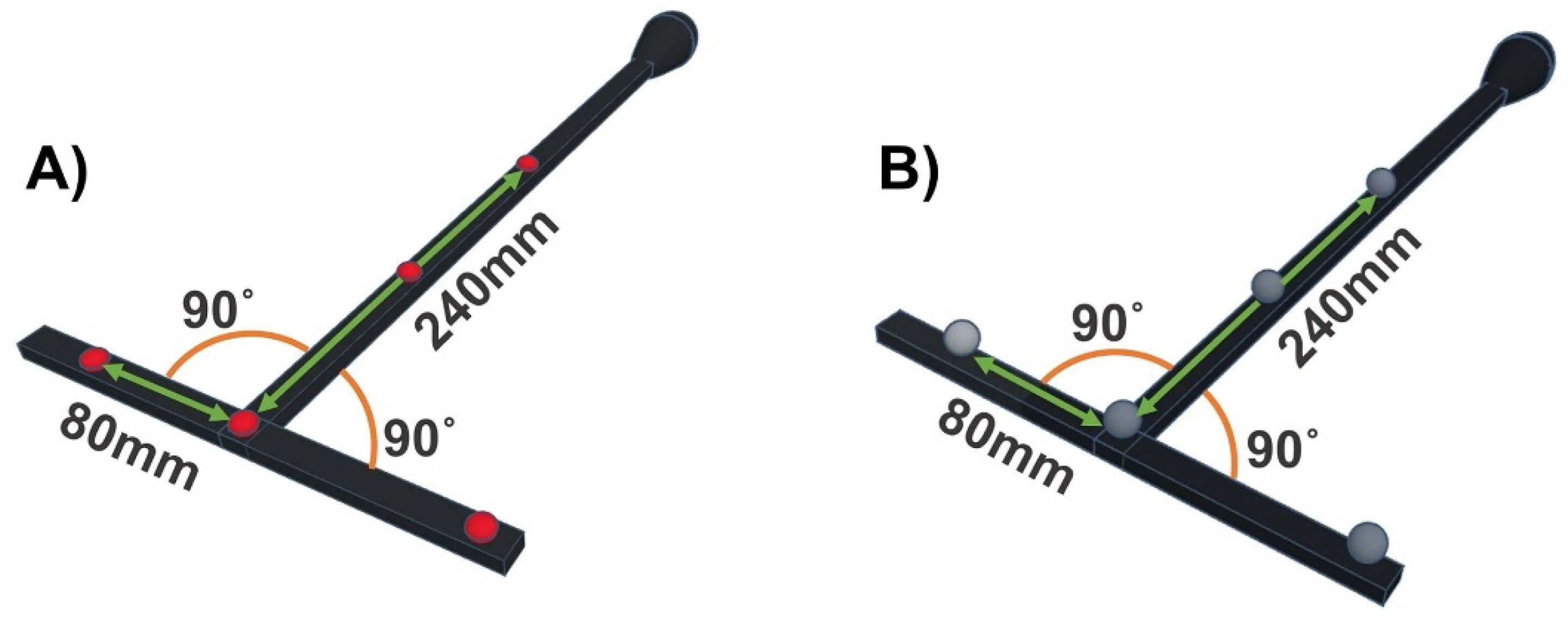
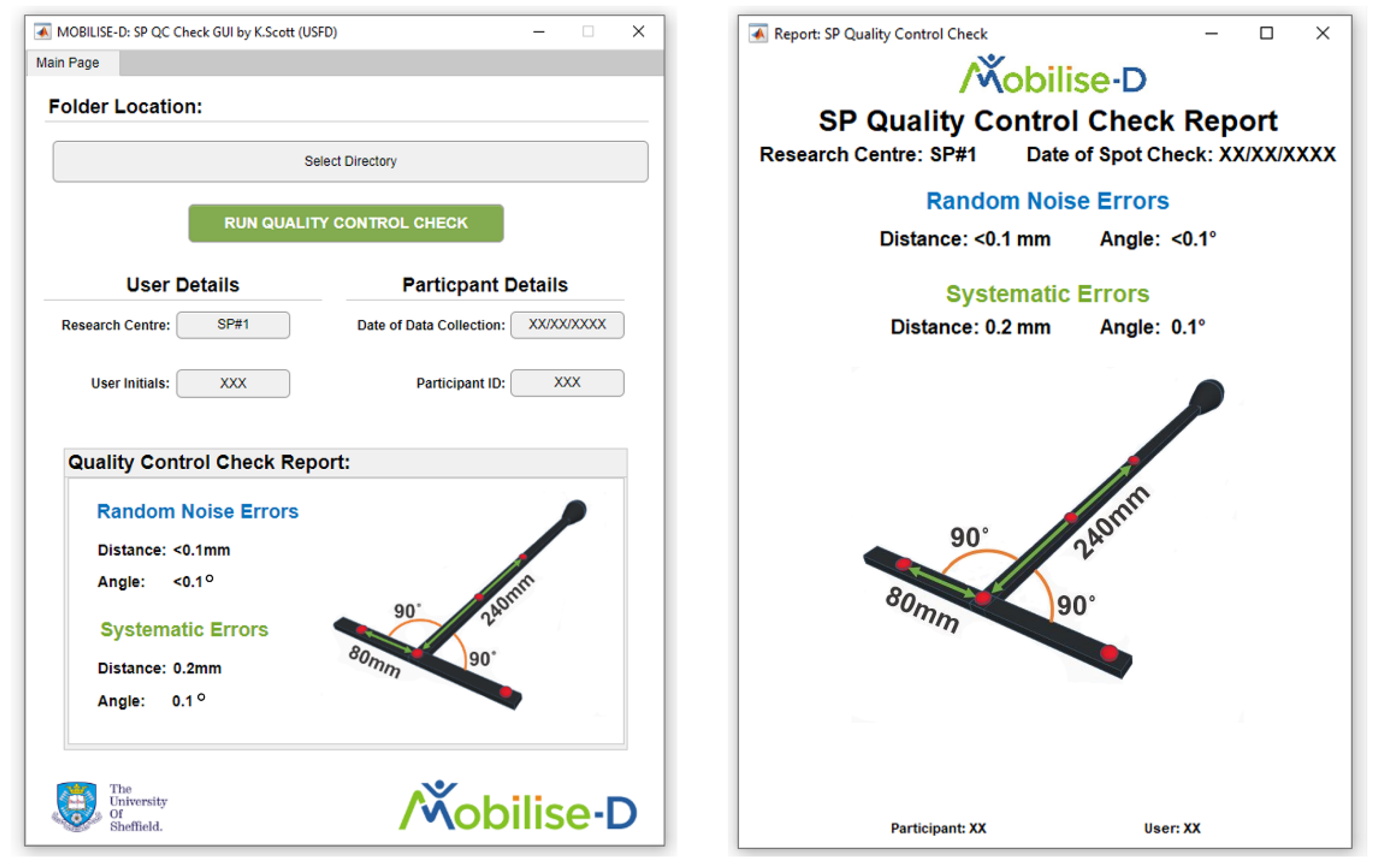
2.1. The Quality Control (QC) Check
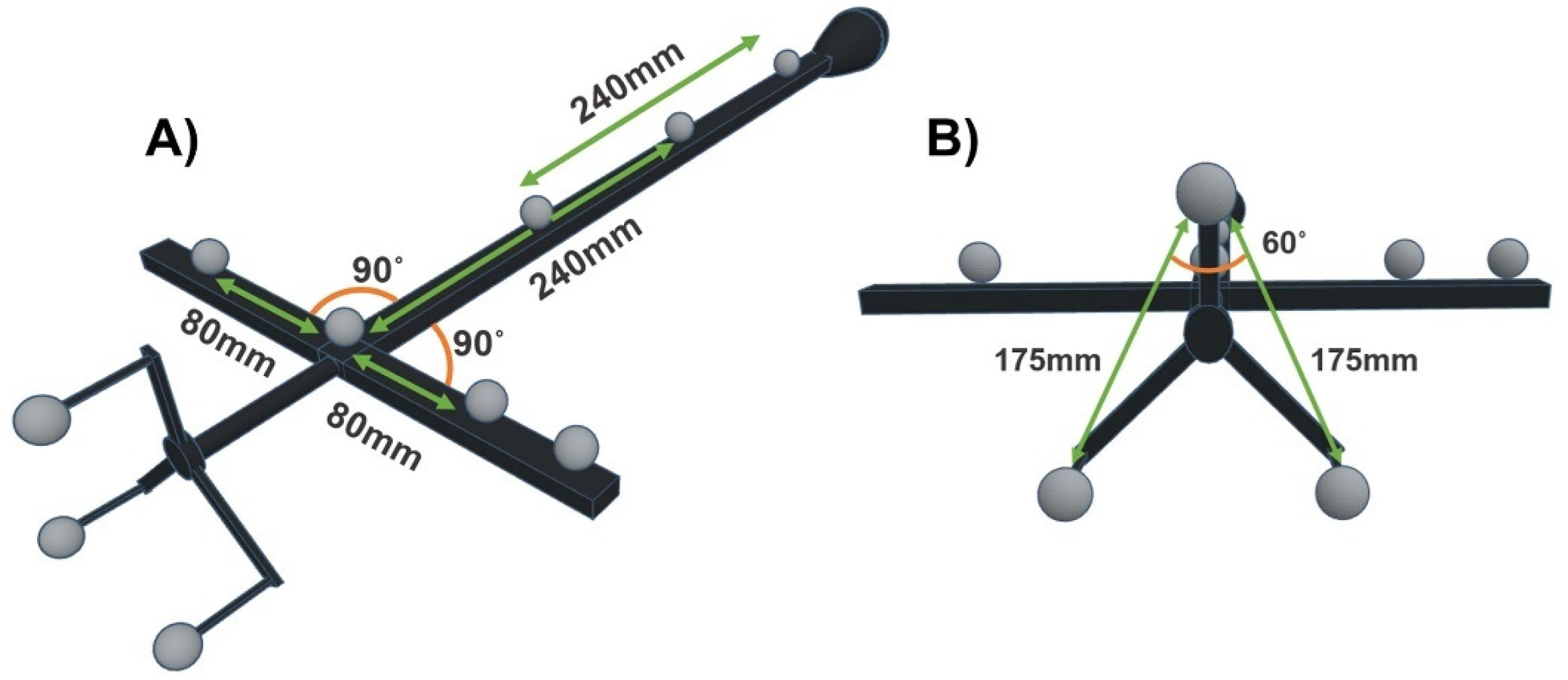
2.2. Validation
Static Trial: “Please place the calibration object level on the floor in the middle of the capture volume and record a trial of the object in this position for 5 s.”Dynamic Trial: “Please move the calibration object at a velocity comparable with the one you would use in the system calibration procedure for at least 20 s. Please make sure to exploit the full volume of the desired capture area.”
2.3. Multicentric Deployment
2.4. Data Processing and Analysis
3. Results
3.1. Validation
3.2. Multicentric Deployment
4. Discussion
4.1. Validation
4.2. Multicentric Deployment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baker, R.; Leboeuf, F.; Reay, J.; Sangeux, M. The Conventional Gait Model—Success and Limitations. In Handbook of Human Motion; Springer: Berlin/Heidelberg, Germany, 2018; pp. 489–508. [Google Scholar]
- States, R.A.; Krzak, J.J.; Salem, Y.; Godwin, E.M.; Bodkin, A.W.; McMulkin, M.L. Instrumented gait analysis for management of gait disorders in children with cerebral palsy: A scoping review. Gait Posture 2021, 90, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Shanahan, C.J.; Boonstra, F.M.C.; Lizama, L.E.C.; Strik, M.; Moffat, B.A.; Khan, F.; Kilpatrick, T.J.; Van Der Walt, A.; Galea, M.P.; Kolbe, S.C. Technologies for Advanced Gait and Balance Assessments in People with Multiple Sclerosis. Front. Neurol. 2018, 8, 708. [Google Scholar] [CrossRef]
- Richards, R.E.; Noort, J.C.V.D.; van der Esch, M.; Booij, M.J.; Harlaar, J. Effect of real-time biofeedback on peak knee adduction moment in patients with medial knee osteoarthritis: Is direct feedback effective? Clin. Biomech. 2018, 57, 150–158. [Google Scholar] [CrossRef] [PubMed]
- Pham, M.H.; Elshehabi, M.; Haertner, L.; Del Din, S.; Srulijes, K.; Heger, T.; Synofzik, M.; Hobert, M.A.; Faber, G.S.; Hansen, C.; et al. Validation of a Step Detection Algorithm during Straight Walking and Turning in Patients with Parkinson’s Disease and Older Adults Using an Inertial Measurement Unit at the Lower Back. Front. Neurol. 2017, 8, 457. [Google Scholar] [CrossRef]
- Köse, A.; Cereatti, A.; Della Croce, U. Bilateral step length estimation using a single inertial measurement unit attached to the pelvis. J. Neuroeng. Rehabil. 2012, 9, 9. [Google Scholar] [CrossRef]
- Bertuletti, S.; Della Croce, U.; Cereatti, A. A wearable solution for accurate step detection based on the direct measurement of the inter-foot distance. J. Biomech. 2018, 84, 274–277. [Google Scholar] [CrossRef]
- Kanko, R.M.; Laende, E.K.; Davis, E.M.; Selbie, W.S.; Deluzio, K.J. Concurrent assessment of gait kinematics using marker-based and markerless motion capture. J. Biomech. 2021, 127, 110665. [Google Scholar] [CrossRef] [PubMed]
- Van Der Kruk, E.; Reijne, M.M. Accuracy of human motion capture systems for sport applications; state-of-the-art review. Eur. J. Sport Sci. 2018, 18, 806–819. [Google Scholar] [CrossRef]
- Chiari, L.; Della Croce, U.; Leardini, A.; Cappozzo, A. Human movement analysis using stereophotogrammetry: Part 2: Instrumental errors. Gait Posture 2005, 21, 197–211. [Google Scholar] [CrossRef]
- DeLuzio, K.J.; Wyss, U.P.; Li, J.; Costigan, P.A. A procedure to validate three-dimensional motion assessment systems. J. Biomech. 1993, 26, 753–759. [Google Scholar] [CrossRef][Green Version]
- Richards, J.G. The measurement of human motion: A comparison of commercially available systems. Hum. Mov. Sci. 1999, 18, 589–602. [Google Scholar] [CrossRef]
- Merriaux, P.; Dupuis, Y.; Boutteau, R.; Vasseur, P.; Savatier, X. A Study of Vicon System Positioning Performance. Sensors 2017, 17, 1591. [Google Scholar] [CrossRef] [PubMed]
- Aurand, A.M.; Dufour, J.S.; Marras, W.S. Accuracy map of an optical motion capture system with 42 or 21 cameras in a large measurement volume. J. Biomech. 2017, 58, 237–240. [Google Scholar] [CrossRef]
- Della Croce, U.; Cappozzo, A. A spot check for estimating stereophotogrammetric errors. Med. Biol. Eng. Comput. 2000, 38, 260–266. [Google Scholar] [CrossRef]
- Diaz Novo, C.; Alharbi, S.; Fox, M.; Ouellette, E.; Biden, E.; Tingley, M.; Chester, V. The impact of technical parameters such as video sensor technology, system configuration, marker size and speed on the accuracy of motion analysis systems. Ing. Mecánica Tecnol. Desarro. 2014, 5, 265–271. [Google Scholar]
- Miller, C.; Mulavara, A.; Bloomberg, J. A quasi-static method for determining the characteristics of a motion capture camera system in a “split-volume” configuration. Gait Posture 2002, 16, 283–287. [Google Scholar] [CrossRef]
- Everaert, D.G.; Spaepen, A.J.; Wouters, M.J.; Stappaerts, K.H.; Oostendorp, R.A. Measuring small linear displacements with a three-dimensional video motion analysis system: Determining its accuracy and precision. Arch. Phys. Med. Rehabil. 1999, 80, 1082–1089. [Google Scholar] [CrossRef]
- Windolf, M.; Götzen, N.; Morlock, M. Systematic accuracy and precision analysis of video motion capturing systems—exemplified on the Vicon-460 system. J. Biomech. 2008, 41, 2776–2780. [Google Scholar] [CrossRef]
- Eichelberger, P.; Ferraro, M.; Minder, U.; Denton, T.; Blasimann, A.; Krause, F.; Baur, H. Analysis of accuracy in optical motion capture—A protocol for laboratory setup evaluation. J. Biomech. 2016, 49, 2085–2088. [Google Scholar] [CrossRef]
- Di Marco, R.; Rossi, S.; Castelli, E.; Patanè, F.; Mazzà, C.; Cappa, P. Effects of the calibration procedure on the metrological performances of stereophotogrammetric systems for human movement analysis. Measurement 2017, 101, 265–271. [Google Scholar] [CrossRef]
- Mazzà, C.; Alcock, L.; Aminian, K.; Becker, C.; Bertuletti, S.; Bonci, T.; Brown, P.; Brogzol, M.; Buckley, E.; Carsin, A.; et al. Technical Validation of real-world monitoring of gait: A multicentric observational study. BMJ Open 2021, 11, e050785. [Google Scholar] [CrossRef]
- Maletsky, L.P.; Sun, J.; Morton, N.A. Accuracy of an optical active-marker system to track the relative motion of rigid bodies. J. Biomech. 2007, 40, 682–685. [Google Scholar] [CrossRef] [PubMed]


| RMSE | ||||
|---|---|---|---|---|
| CO1 | CO2 | |||
| Measure | Active Markers | Passive Markers | 2D Configuration | 3D Configuration |
| Distance (mm) | 0.2 | 0.5 | 0.6 | 0.8 |
| Angle (deg) | 0.1 | 0.3 | 0.5 | 0.4 |
| RMSE | |||
|---|---|---|---|
| Measure | Intra-Operator Intra-Session | Intra-Operator Inter-Session | Inter-Operator Intra-Session |
| Distance (mm) | 0.2 ± 0.1 | 0.3 ± 0.1 | 1.0 ± 0.1 |
| Angle (deg) | 0.1 ± 0.1 | 0.1 ± 0.1 | 0.4 ± 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scott, K.; Bonci, T.; Alcock, L.; Buckley, E.; Hansen, C.; Gazit, E.; Schwickert, L.; Cereatti, A.; Mazzà, C.; on behalf of the Mobilise-D Consortium. A Quality Control Check to Ensure Comparability of Stereophotogrammetric Data between Sessions and Systems. Sensors 2021, 21, 8223. https://doi.org/10.3390/s21248223
Scott K, Bonci T, Alcock L, Buckley E, Hansen C, Gazit E, Schwickert L, Cereatti A, Mazzà C, on behalf of the Mobilise-D Consortium. A Quality Control Check to Ensure Comparability of Stereophotogrammetric Data between Sessions and Systems. Sensors. 2021; 21(24):8223. https://doi.org/10.3390/s21248223
Chicago/Turabian StyleScott, Kirsty, Tecla Bonci, Lisa Alcock, Ellen Buckley, Clint Hansen, Eran Gazit, Lars Schwickert, Andrea Cereatti, Claudia Mazzà, and on behalf of the Mobilise-D Consortium. 2021. "A Quality Control Check to Ensure Comparability of Stereophotogrammetric Data between Sessions and Systems" Sensors 21, no. 24: 8223. https://doi.org/10.3390/s21248223
APA StyleScott, K., Bonci, T., Alcock, L., Buckley, E., Hansen, C., Gazit, E., Schwickert, L., Cereatti, A., Mazzà, C., & on behalf of the Mobilise-D Consortium. (2021). A Quality Control Check to Ensure Comparability of Stereophotogrammetric Data between Sessions and Systems. Sensors, 21(24), 8223. https://doi.org/10.3390/s21248223










