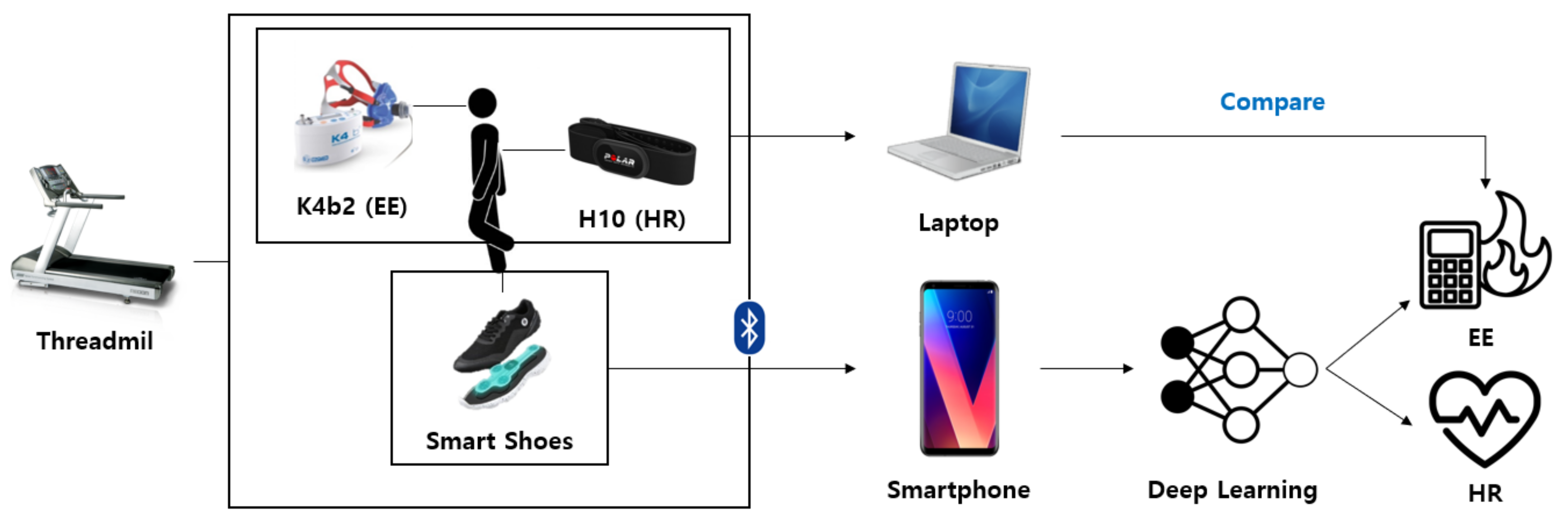
1. Introduction
Wearable technologies have been continuously developed to improve the quality of human life and facilitate mobility and connectivity among users due to the rapid development of the Internet of Things (IoT). Its global demand is increasing every year [
1,
2,
3]. Recently, several wearable devices, including wrist bands, watches, glasses, and shoes, have started enabling the continuous monitoring of an individual’s health, wellness, and fitness [
4]. In particular, the coronavirus disease (COVID-19) pandemic highlighted the importance of remote healthcare delivery, resulting in further expansion of the wearable technology market [
3,
5]. This is because wearable devices could continuously collect and analyze the movement and physiological data of a user and provide appropriate feedback in function of users’ exercise information and health status.
The shoe is a useful wearable device that is easy to use, unobtrusive, lightweight, and easily available when doing outdoor activities [
6,
7,
8,
9]. Previous studies on shoes include gait type classification [
9,
10,
11], step count [
8,
12,
13], and energy expenditure (EE) estimation [
14]. Three types of sensors (i.e., pressure, accelerometer, and gyroscope sensors) were equipped in the shoes to realize these tasks. These relatively low-cost sensors could be mounted in an unconstrained and convenient manner and record the movement information of users to estimate their physical behaviors.
The EE estimation was associated with physical activity (PA) which could influence an individual’s health conditions [
15]. The PA level, which can be quantitatively assessed, is highly correlated with the risk of developing cardiovascular diseases, diabetes, and obesity [
16,
17]. In addition, there are only a few studies conducted on EE estimation using shoes compared to those on gait type classification and step counting. In addition, the accelerometer is one of the most commonly used sensors in shoes and other various devices for estimating EE [
18,
19,
20,
21,
22].
In a previous study, a regression model was designed to estimate personal characteristics such as age, gender, height, weight, and BMI using accelerometer sensor data [
18,
20]. On the other hand, Vathsangam et al. used an accelerometer and a gyroscope sensor together to estimate EE, showing the improvement of the EE estimation by utilizing both sensor data [
23]. In addition, a pressure sensor can also provide significant information to estimate EE. In a study conducted by Ngueleu et al., they predicted the number of steps taken by users using pressure sensors that were equipped to their shoes [
13]. The results show that there was a high correlation between the number of steps and EE conducted by Nielson et al. [
19]. Moreover, the pressure sensor could also be used along with the accelerometer sensor to improve the EE estimation. In [
22], EE was estimated using barometric pressure and triaxial accelerometer sensors in various states such as sitting, lying, and walking. Additionally, Sazonova et al. estimated EE using the data from the triaxial accelerometer and five pressure sensors which were measured whilst the participants performed various activities such as sitting, standing, walking, and cycling [
14].
The World Health Organization (WHO) reported that more than 30% of fatalities worldwide are caused by cardiovascular diseases (CVDs) [
24]. The heart rate variability (HRV) is known as an important risk index for CVDs [
25]. Accordingly, in recent years, various types of wearable devices have been developed (e.g., a watch-type device mounting electrocardiogram (ECG) or photoplethysmogram (PPG) sensors) to conveniently measure heart rate (HR). However, in an exercise environment, ECG is inconvenient to measure and PPG is affected by severe noise due to the movement. Instead of measuring the direct cardiac response, Lee et al. estimated HR from the activity information measured using an accelerometer and gyroscope sensors attached to the chest [
26,
27].
In recent years, advanced deep learning algorithms have been developed with the help of increasing computing power and a sufficient big dataset. There have been studies on the application of the deep learning approach to the wearable technology [
28,
29,
30], where the algorithm performed well in regression and classification problems using physiological sensor data [
21,
31,
32]. Staudenmayer et al. reported that an artificial neural network (ANN) model can predict the EE information using the accelerometer signals [
21]. However, they extracted hand-crafted features from the signals and fed them into the ANN model, which are challenging to extract and suboptimal in distinguishing sophisticated patterns in the signal due to its fixed model-based approach. Zhu et al. successfully improved the accuracy of the EE estimation using convolutional neural network (CNN) by extracting subtle patterns from the accelerometer and heart rate signals [
33].
In the studies [
23,
33], the multichannel data from the accelerometer and gyroscope sensors were simultaneously analyzed to estimate EE and HR, which could have been improved by considering the significance of each channel data. It is important to investigate which channel’s data are the most significant when multivariate input data can be obtained from multichannel sensors to derive the target variable. In recent studies, a method to determine the weight for each input channel to a neural network was suggested using the channel-wise attention based on deep learning techniques [
34,
35,
36].
This study investigated the novel approach in estimating EE and HR using wearable sensors. A smart shoes system was selected for the convenience of users rather than the direct cardiac response measurement system, owing to its unobtrusive and natural manner of measuring the activities of users in their daily life. Conventionally, smart shoes are equipped with three types of sensors (i.e., pressure, accelerometer, and gyroscope) to produce multichannel data. Moreover, a deep neural network model was designed to infer EE and HR information from the multichannel data without using model-based hand-crafted feature extraction methods, and the attention mechanism provides appropriate weights to the input channels of the networks to improve the inference performance. Additionally, the weights decided by the attention algorithm provide the importance of three different sensors and their channels to the estimation of the physiological variations, EE, and HR. This could also enhance our understanding of the designed deep neural network structure, also known as explainable artificial intelligence [
37].
The rest of this study is organized as follows.
Section 2 discusses the design and data collection process of the experiment.
Section 3 introduces the structure and the learning process of the proposed deep learning model. In addition,
Section 4 discusses the results of HR and EE estimations using the proposed model and statistical analysis of the attention weights of sensors used as inputs. The results presented in
Section 4 are discussed in
Section 5 using the existing related studies. Finally, this study is concluded in
Section 6.
3. Proposed Model
Figure 7 shows the overall structure of the model proposed in this study. The channel-wise attention layer, which is described in
Section 3.1, provides weights to the significant channels of the sensors mounted on the shoes to accurately estimate HR and EE. The weighted signals by the attention layer pass using DenseNet [
39], which is a CNN-based model known to be excellent in extracting key features from input data and generating spatial feature vectors that are discussed in
Section 3.2. The bidirectional gated recurrent unit (GRU) [
40] models the temporal relationship among the feature vectors, enabling an intuitive and efficient learning by observing the variations of input data over time (described in
Section 3.3). Furthermore, the global average pooling (GAP) [
41] layer compresses the information of the spatiotemporal features vectors and output values of HR and EE (described in
Section 3.4). The advantages of the proposed model are as follows:
The manual feature extraction process is not necessary since a fully automated end-to-end deep learning model was applied;
The spatiotemporal characteristics of the multivariate time-series data that is complex to process could be effectively extracted using DenseNet and bidirectional GRU (Bi-GRU);
The importance of each channel in estimating HR and EE could be quantified using the channel-wise attention method, and it can explain the optimal sensors for the task.
Figure 7.
Structure of the proposed model. The shoe data from 20 channel sensors are fed into the input of the model and the channel-wise attention layer increases the intensity of the significant channels. The spatial features from the multi-channel data are extracted using DenseNet, and the temporal features are produced through Bi-GRU. Finally, HR and EE are estimated after the global average pooling (GAP) layer.
Figure 7.
Structure of the proposed model. The shoe data from 20 channel sensors are fed into the input of the model and the channel-wise attention layer increases the intensity of the significant channels. The spatial features from the multi-channel data are extracted using DenseNet, and the temporal features are produced through Bi-GRU. Finally, HR and EE are estimated after the global average pooling (GAP) layer.
3.1. Channel-Wise Attention
It is difficult to extract the key features corresponding to HR and EE from the complex multivariate show data consisting of 20 channels. The conventional deep learning models train all input data with equal weights. This could deteriorate the learning efficiency of the model owing to the unnecessary and redundant information. However, the deep learning model could be efficiently trained by minimizing the unnecessary information in the input data and maximizing the significant information to the task. The attention mechanism is an optimized way of making this possible. In this study, we aimed to find and verify the optimal sensors for the estimation of HR and EE using the channel-wise attention expressed as follows:
where
O is calculated with the 20 channel signal
, a trainable weight matrix
, a bias
, and a non-linear activation function
. In addition,
t is the time length of a sample and
i the number of channels. A sigmoid function [
42] was chosen in this study for the activation function.
represents the attention weights, which is calculated by the average of
O across the time axis using the
function. Finally, the signal
is derived by multiplying
and
element-wise operation, which is expressed as ⊗.
3.2. DenseNet
DenseNet has yielded excellent performance in various image classification tasks [
43,
44,
45,
46]. Moreover, it avoids information dilution unlike other CNN-based models by concatenating the feature map output and input data in each convolutional layer. In addition, this method achieved higher performance with fewer parameters than that of the other models [
39]. Therefore, DenseNet was used as a feature extractor in this study. The convolution layer was changed from two-dimensional (2D) to one-dimensional (1D), as shown in the
Figure 8, since the shoe data are time-series data. In addition, the GAP layer was removed from its connection with the Bi-GRU layer in the last layer. The input to DenseNet
is produced from the channel-wise attention layer. The output is represented as follows:
The final output vector is , where T is the time length compressed by the pooling layer and is the number of output of the last convolution layer, because the DenseNet used in this study has no GAP in the last layer.
3.3. Bidirectional Gated Recurrent Unit
In the proposed model, the temporal features are extracted from the output of DenseNet,
, using the Bi-GRU layer defined in Equation (
5). GRU is one of RNN models with powerful modeling capabilities for long-term dependencies. On the other hand, long short-term memory (LSTM) [
47] is another popular RNN model. Between the two, GRU has a more efficient structure with fewer parameters [
40]:
The hidden vector of Bi-GRU,
, was obtained from
, where
is the size of the hidden unit of the GRU, as shown in
Figure 9. Moreover, the internal structure of the GRU cell is shown in
Figure 10. The operation is elaborated as follows:
In Equations (
6)–(
9),
and
are the update gate and the reset gate vectors for an arbitrary time point
, respectively. The update gate determines how much information from the past and the present will be used to generate new information. The reset gate specifies which information to retain from the past information at the time
. Moreover,
is a candidate state, which decides the amount of current information to be learned using the result of the reset gate.
,
, and
are the trainable weight vectors of each gate. In addition,
and
are the sigmoid and hyperbolic tangential functions, respectively. Furthermore, * denotes the element-wise multiplication.
Bi-GRU could simultaneously utilize both the past and future information, creating more useful features than unidirectional GRU. This is implemented as a forward and backward layer, as shown in
Figure 9. The final output
of Bi-GRU is determined by the concatenation of the two vectors when the forward and backward hidden vectors are represented as
and
, respectively:
3.4. Global Average Pooling
In the proposed model, the GAP layer was designed in the last layer instead of the fully connected (FC) layer, which tends to overfit on the training data. This could degrade the generalization performance of the networks. On the other hand, no additional parameters were required since the GAP layer only calculates the average across the final output vectors of the network, reducing the overall network size and preventing overfitting. The final predicted target variables (i.e., HR and EE) using GAP are calculated as follows:
3.5. Model Training Environment
The proposed model uses leave-one-subject-out (LOSO) cross-validation to evaluate the robustness and generalizability in an inter-subject analysis. The data of 9 subjects out of 10 subjects were used as the training set and the data of the remaining 1 subject were used as the testing set, which was repeated for all subjects. The mean and standard deviation of performance for each subject were calculated and described in
Section 4. The Adam [
48] optimization (learning rate =
) was used to train the model, and the batch size was empirically set to 16. The initial weights of the networks were set at random and the loss function was designed based on the mean squared error (MSE). An early stopping method was applied to find the optimal model when there is no significant improvement in the validation loss of 20 epochs in a total of 150 training epochs. Furthermore, 4.2 GHz Intel Core i7 processor (Intel, Santa Clara, CA, USA) and NVIDIA GeForce RTX 2080Ti (NVIDIA corporation, Santa Clara, CA, USA) (with 11 GB VRAM), which are the computing environment for network training, were used. The model was implemented in Keras deep learning framework with TensorFlow backend.
5. Discussion
In this study, it was shown that the proposed model could estimate the EE and HR using physical sensors such as accelerometer, gyroscope, and pressure sensors that can be equipped in smart shoes. In particular, the accuracy was improved with adaptively assigning weights to the sensors through the channel-wise attention, which is the core of the model to select the optimal sensors, making important contributions to the EE and HR estimations.
The proposed model shows that the z axis sensors in the accelerometer and gyroscope have higher contributions to the EE estimation than the others, as shown in
Table 3 and
Table 8. Among the previous EE estimation studies, Vathsangam et al. [
23] calculated the EE in the treadmill while walking using an accelerometer sensor and a gyroscope sensor. They claimed that the x axis sensor in the accelerometer (y axis in this study) was aligned with the movement direction of the foot, indicating that its contribution to the EE estimation could be high. On the other hand, Javed et al. [
51] found that the y and z axis features of the accelerometer were important to recognize walking and jogging activities. In another related study, Smith et al. [
52] calculated the ratio of the triaxial to uniaxial (vertical) number in the accelerometer for various activities using an accelerometer sensor on the wrist. The results show that activities such as running are greatly affected by vertical movement. Moreover, we found that the average attention weight of the z axis was high corresponding to the running activity, which is largely affected by vertical activity. The findings of the significance of the z axis monitoring the vertical movement are consistent with the results of Javed et al. [
51] and Smith et al. [
52] since our study was conducted on a treadmill under similar conditions to the jogging activity.
In the HR estimation, the contributions of the z axis sensors in the accelerometer and gyroscope were high, which is similar to the results of EE estimation. In various previous EE estimation studies, the EE was directly calculated using the HR level [
53]. However, in this study, the EE estimation was carried out separately from the HR estimation. As a result, large attention weights in the z axis in the proposed model seem to be significant considering the high correlation between HR and EE.
As an additional analysis, we performed ANOVA and post hoc analysis to verify whether there is a significant difference in attention weights among the x, y, and z axis sensors in the accelerometer and gyroscope.
Figure 15 shows the average attention weight for each axis to predict the EE and HR levels. As a result, there was a significant difference between the x and z axes and between the y and z axes
, although there was no statistical difference between the x and y axes.
6. Conclusions
In this study, the efficient HR and EE estimation models from multivariate raw signals including pressure, accelerometer, and gyroscope sensor data were designed using a deep learning architecture in an end-to-end manner. In addition, significant channels of the sensors were investigated using the channel-wise attention mechanism to estimate HR and EE, which found that the effects of the z axis sensors of the accelerometer and the gyroscope were significant in walking and running conditions. This is consistent with the previous study demonstrating that a general running activity is greatly affected by a vertical movement in the z axis direction [
51,
52]. This study also demonstrated the possibility of estimating HR and EE using the sensors mounted on shoes and suggests an effective and cost-efficient design of a wearable shoe-based device with selecting the optimal sensors. Furthermore, using the channel-wise attention, HR and EE were effectively estimated even when the individual left and right foot movements were not constant the during exercise. A limitation of this study is the small size of the training dataset and the individual characteristics of the participants with small deviations. Whilst the predictions might be a little unstable for datasets obtained under various conditions, the proposed model is trained and validated through the inter-subject analysis using LOSO, which could guarantee the generalizability of the proposed model if being adaptively retrained for each individual datum. Another limitation is that the computational load is large compared with the conventional approaches to estimate the HR and EE using a wrist band-typed photoplethysmogram (PPG) sensor (deep learning model size: approximately 70 mb, testing time: a few seconds). However, the existing HR and EE measurement devices have disadvantages when worn on a wrist, as some users feel uncomfortable to wear. In addition, they are too sensitive to noise, resulting in poor SNR. On the other hand, the proposed shoe sensor could be more natural for use to wear compared to the wrist-typed sensor.
For the future research, it would be possible to improve the generalization performance using more diverse datasets and adding personal information (gender, BMI, foot size, etc.) to the model input. It will also include the investigation of the sensor-specific functions corresponding to the variations in HR and EE values.