A Novel Interference Avoidance Based on a Distributed Deep Learning Model for 5G-Enabled IoT
Abstract
:1. Introduction
- The proposed approach developed an efficient method to enhance the overall system performance in terms of system throughput and energy efficiency.
- An optimization problem using an analytical and deep learning model was formulated to ascertain the reliability and efficiency of communication among 5G and IoTs.
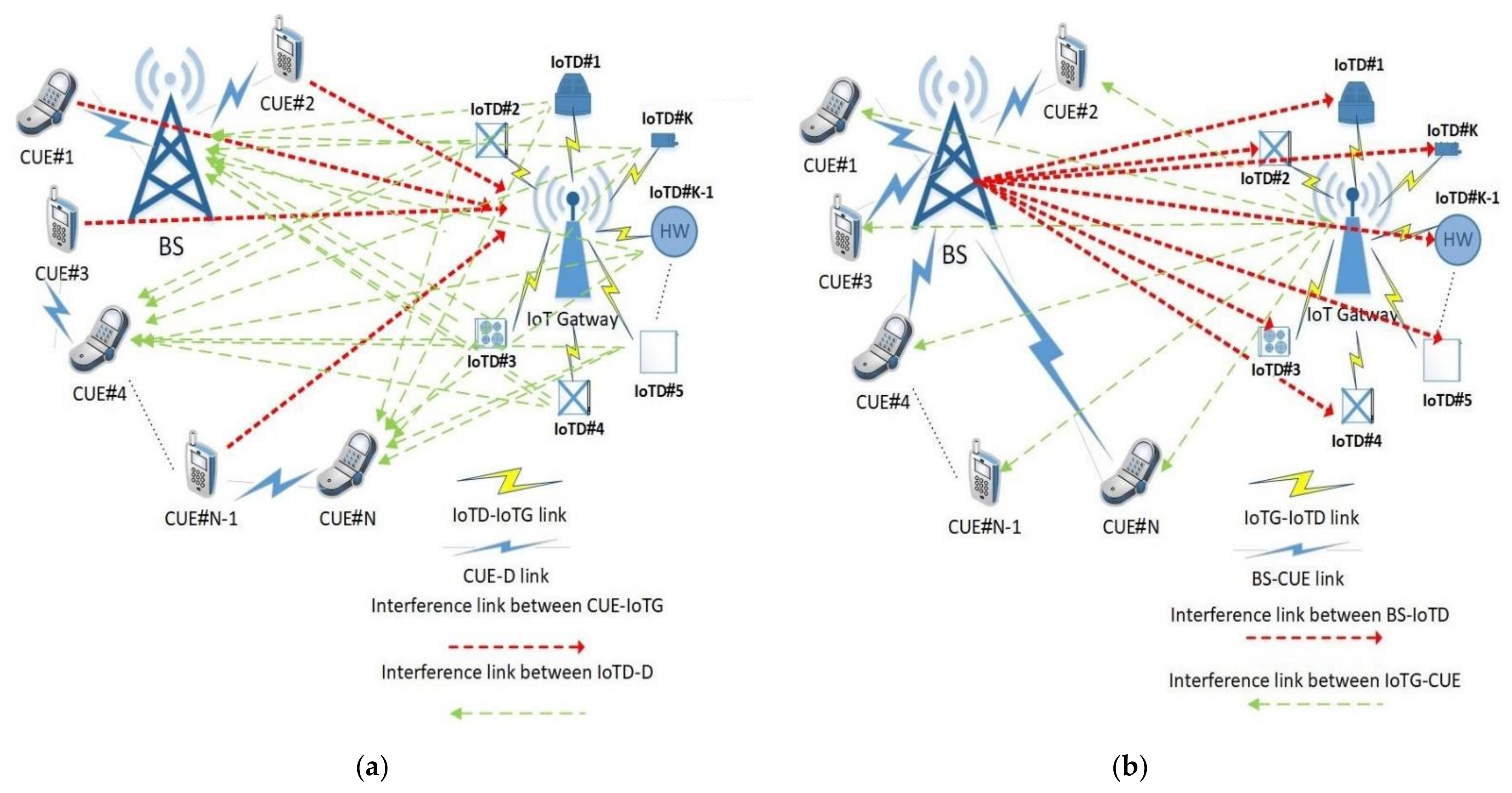
- The proposed approach aims to decrease or eliminate the interference in 5G networks and IoT systems. This was achieved through determining the optimum distance between CUE-IoTG and IoTD-D for the uplink (UL) data communication and between BS-IoTD and IoTG-CUE for the downlink (DL) data communication. This can be achieved based on different parameters, which affect the system performance such as transmission power, distance between CUE-D and IoTD-IoTG, path loss and signal-to-interference-plus-noise ratio (SINRth).
- The proposed approach allowed the transmission of CUE and IoTD, using a deep learning model, to predict the suitable acceptable distance between CUE-IoTG and IoTD-D (uplink) and between BS-IoTD and IoTG-CUE (downlink) thus avoiding severe interference.
- The proposed deep learning model was compared to state-of-the-art benchmark methods and it provided a marked improvement in the results.
- The proposed model can be used in the design phase for interference prediction and circumvention.
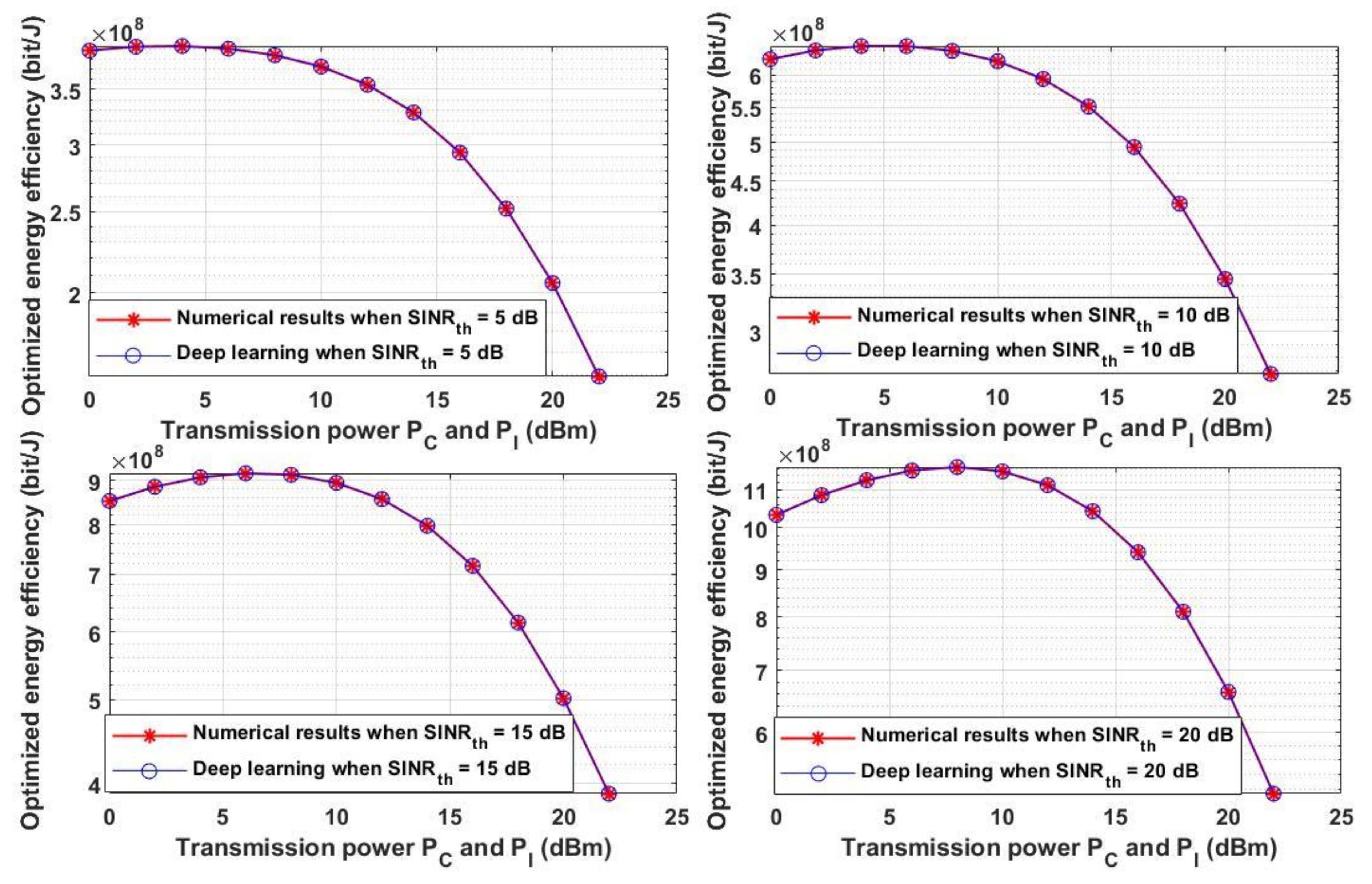
- The proposed approach was investigated in terms of overall system throughput and energy efficiency under different conditions, such as the path loss exponent, transmission power, different SINRth values, and different transmission ranges. The whole network can be optimized by these findings in a vibrant environment.
2. Related Work
3. Proposed Model
3.1. System Model and Problem Formulation
3.1.1. Uplink Data Communication
3.1.2. Downlink Data Communication
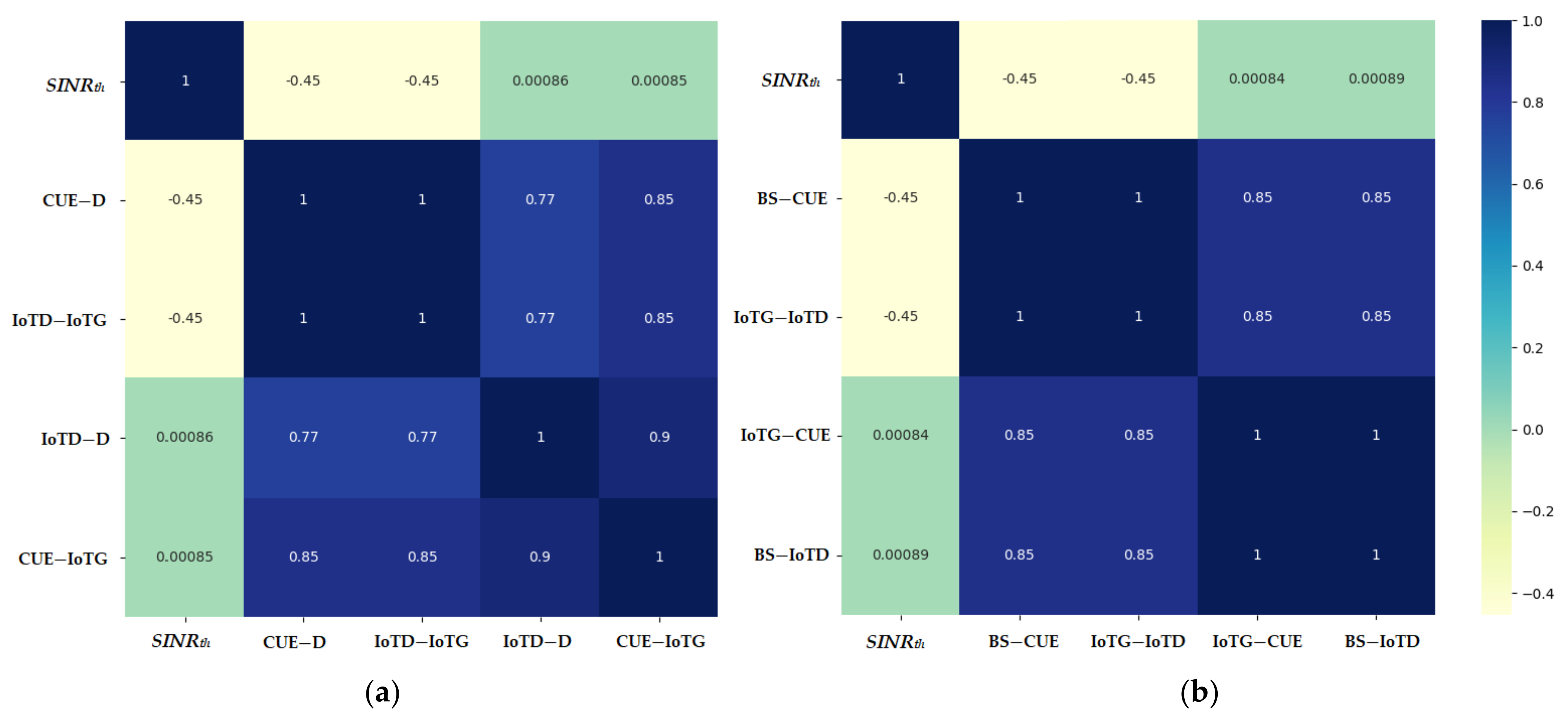
3.2. Dataset Generation
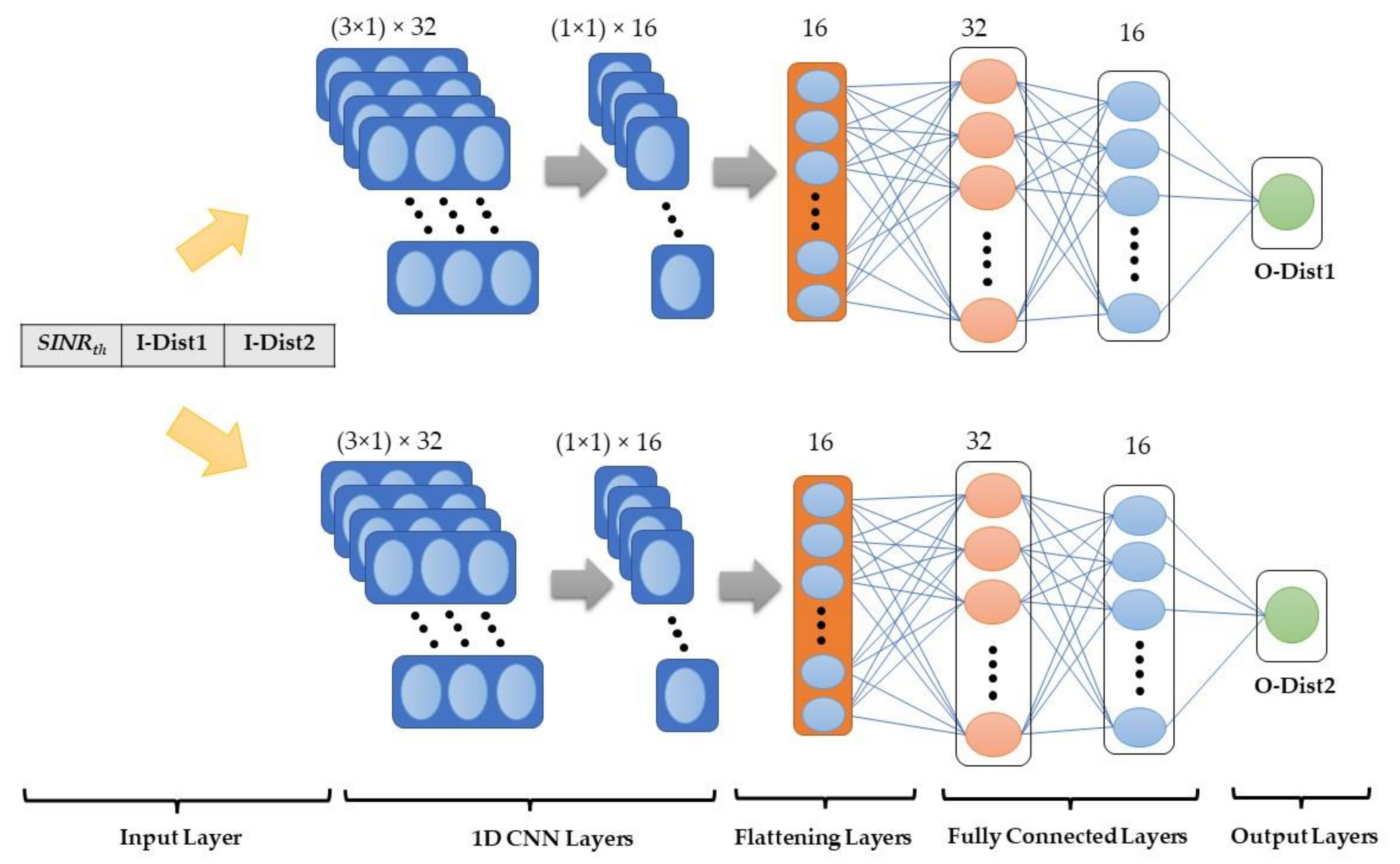
3.3. Proposed Deep Learning Model
3.3.1. Network Structure
- An abstract input layer that takes the current values of the input and passes it to the 1D-CNN layers
- The first 1D-CNN is 3 × 1 having 32 filters, with a kernel size of 3
- The second 1D-CNN is 1 × 1 having 16 filters, with a kernel size of 1
- A flattening layer to reshape the 1D CNN can be input to the fully connected layers
- A 32-neuron fully connected layer
- A 16-neuron fully connected layer
- An output layer to produce the regression distance result
3.3.2. Data Scaling
3.3.3. Activation Function
3.3.4. Optimization Function
3.3.5. Parameter Optimization
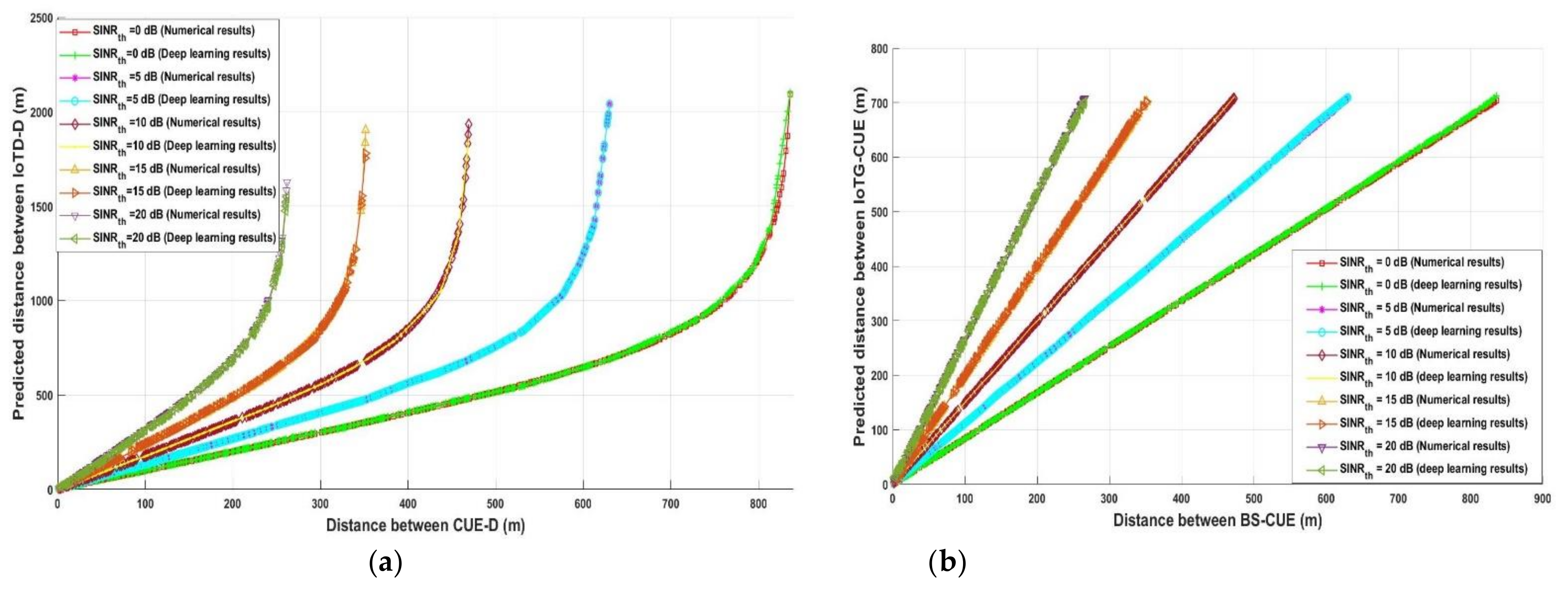
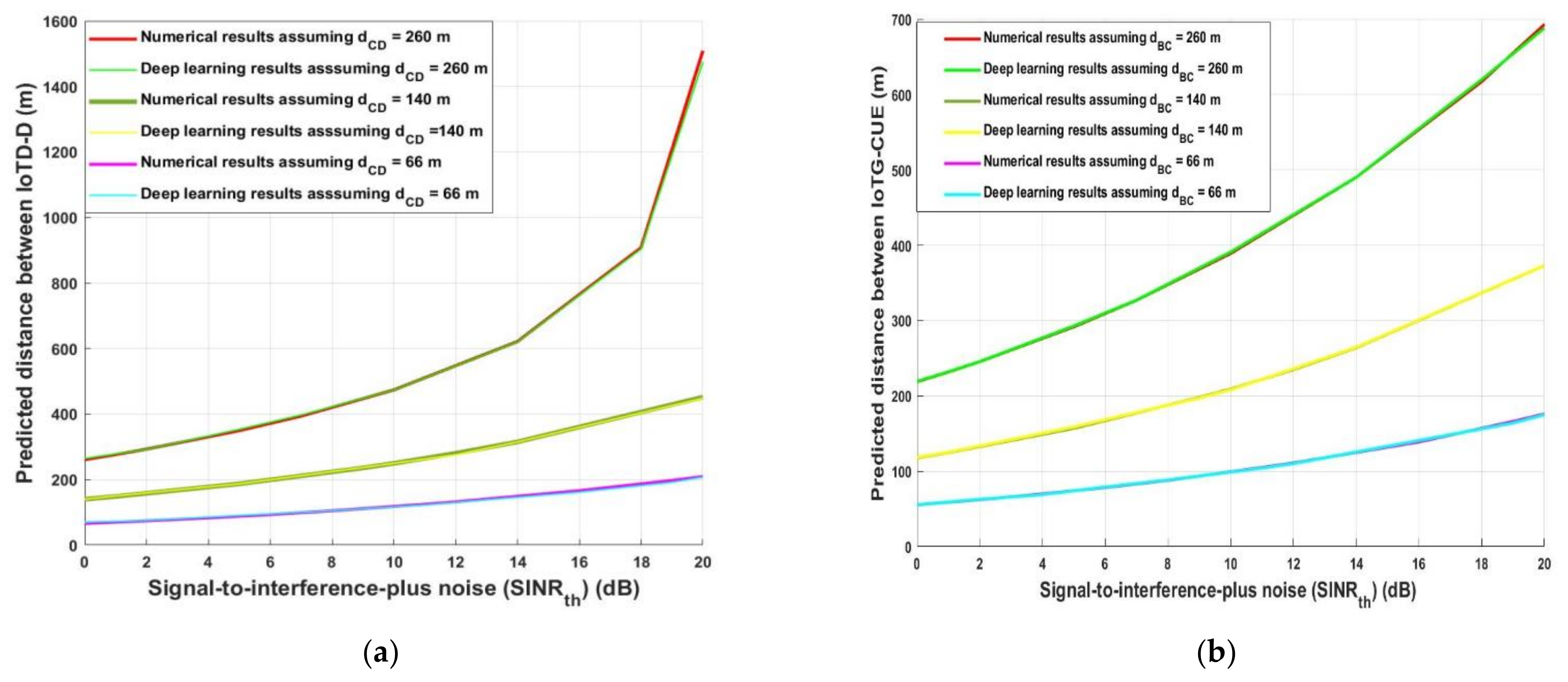
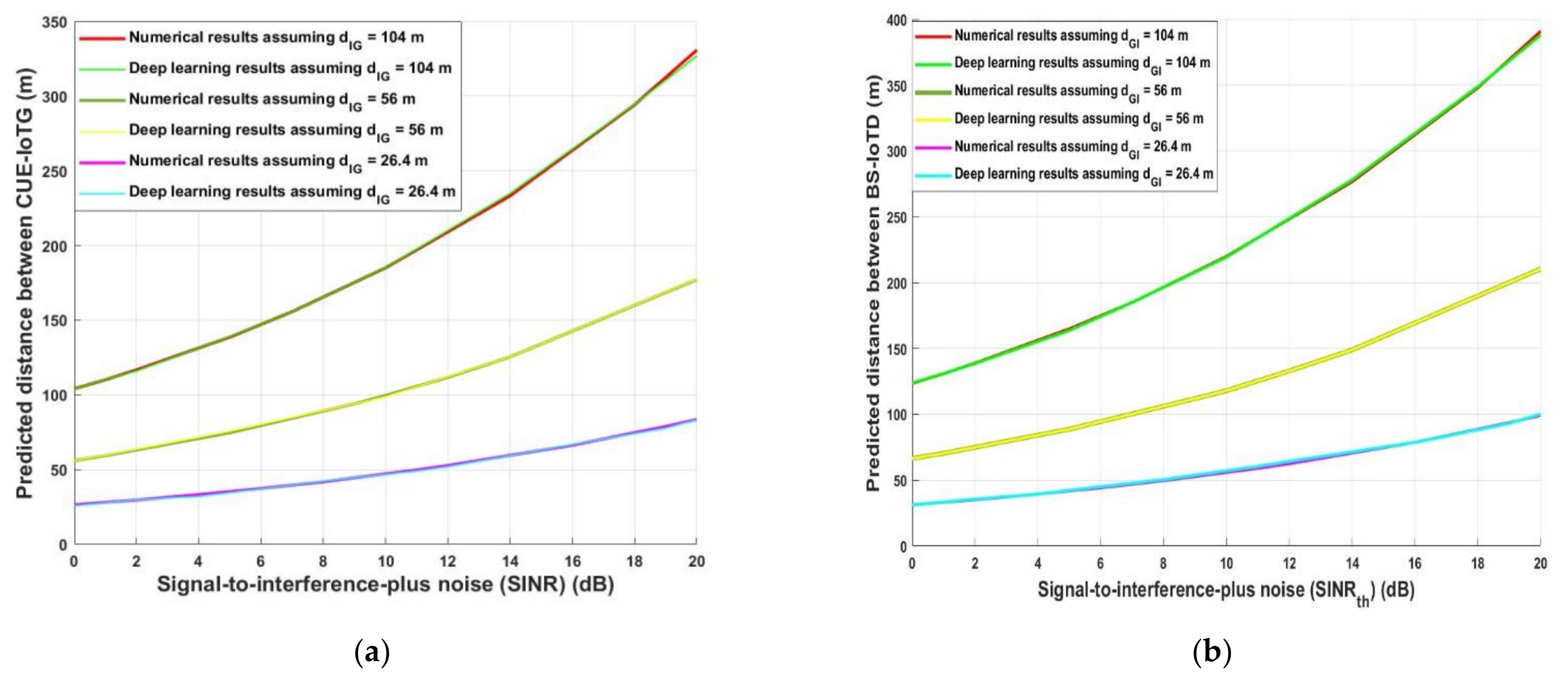
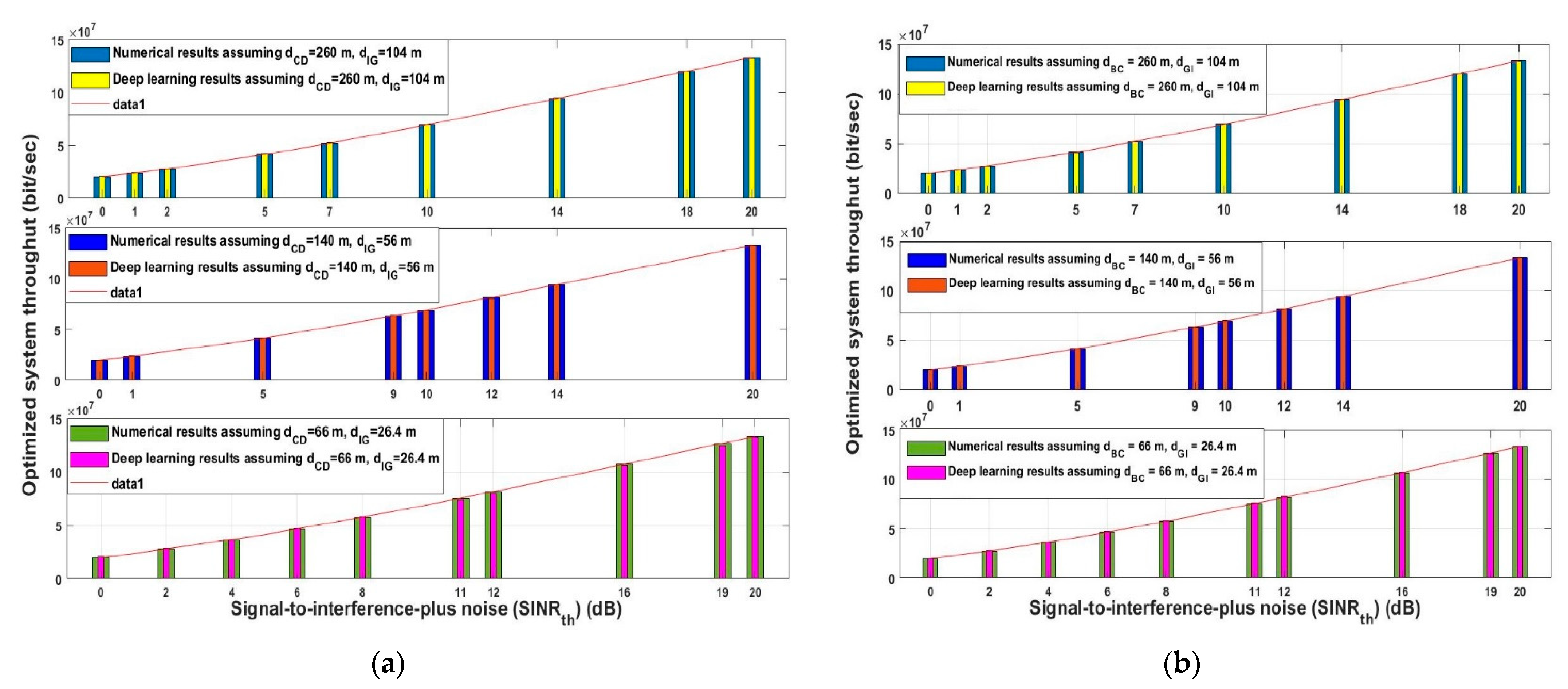
4. Results and Discussion
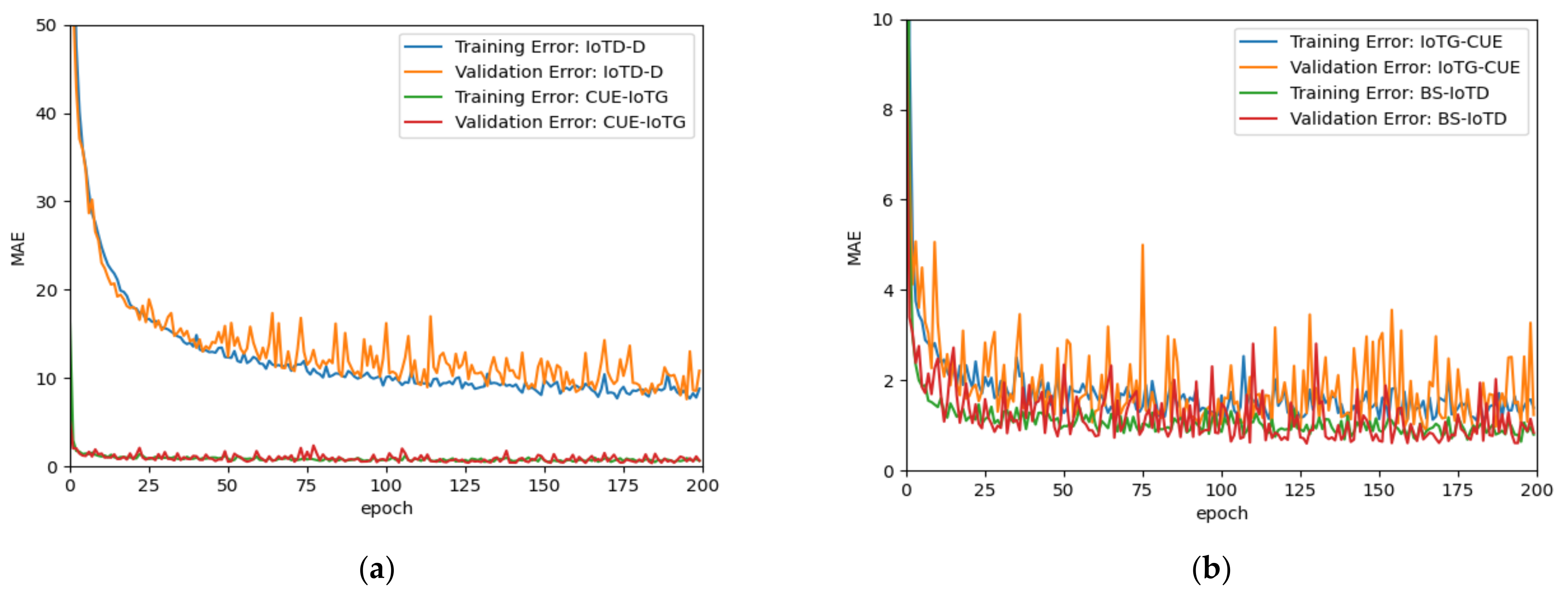
4.1. Deep Learning Model Results Evaluation
- Mean Absolute Error (MAE), which measures the average differences between actual and predicted values.
- Root Mean Squared Error, which calculates the square root of the average of the squared differences between actual and predicted values as
4.2. Analytical Evaluation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, H.; Xiong, D.; Wang, P.; Liu, Y. A Lightweight XMPP Publish/Subscribe Scheme for Resource-Constrained IoT Devices. IEEE Access 2017, 5, 16393–16405. [Google Scholar] [CrossRef]
- Ahmad, I.; Kumar, T.; Liyanage, M.; Okwuibe, J.; Ylianttila, M.; Gurtov, A. Overview of 5G Security Challenges and Solutions. IEEE Commun. Stand. Mag. 2018, 2, 36–43. [Google Scholar] [CrossRef] [Green Version]
- Wazid, M.; Das, A.K.; Shetty, S.; Gope, P.; Rodrigues, J.J.P.C. Security in 5G-Enabled Internet of Things Communication: Issues, Challenges, and Future Research Roadmap. IEEE Access 2021, 9, 4466–4489. [Google Scholar] [CrossRef]
- Luong, N.C.; Hoang, D.T.; Wang, P.; Niyato, D.; Kim, D.I.; Han, Z. Data Collection and Wireless Communication in Internet of Things (IoT) Using Economic Analysis and Pricing Models: A Survey. IEEE Commun. Surv. Tutorials 2016, 18, 2546–2590. [Google Scholar] [CrossRef] [Green Version]
- Chettri, L.; Bera, R. A Comprehensive Survey on Internet of Things (IoT) Toward 5G Wireless Systems. IEEE Internet Things J. 2020, 7, 16–32. [Google Scholar] [CrossRef]
- Alhajri, M.I.; Ali, N.T.; Shubair, R.M. Classification of Indoor Environments for IoT Applications: A Machine Learning Approach. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 2164–2168. [Google Scholar] [CrossRef]
- Abbasi, M.; Shahraki, A.; Taherkordi, A. Deep Learning for Network Traffic Monitoring and Analysis (NTMA): A Survey. Comput. Commun. 2021, 170, 19–41. [Google Scholar] [CrossRef]
- Hansen, E.B.; Bøgh, S. Artificial intelligence and internet of things in small and medium-sized enterprises: A survey. J. Manuf. Syst. 2021, 58, 362–372. [Google Scholar] [CrossRef]
- Hattab, G.; Cabric, D. Energy-Efficient Massive IoT Shared Spectrum Access Over UAV-Enabled Cellular Networks. IEEE Trans. Commun. 2020, 68, 5633–5648. [Google Scholar] [CrossRef]
- Seo, J.-B.; Jung, B.C.; Jin, H. Online Backoff Control for NOMA-Enabled Random Access Procedure for Cellular Networks. IEEE Wirel. Commun. Lett. 2021, 10, 1158–1162. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, K.; Han, J.; Zhu, L.; Xiao, Z.; Xia, X.-G. Resource Allocation and 3-D Placement for UAV-Enabled Energy-Efficient IoT Communications. IEEE Internet Things J. 2021, 8, 1322–1333. [Google Scholar] [CrossRef]
- Kolawole, O.Y.; Biswas, S.; Singh, K.; Ratnarajah, T. Transceiver Design for Energy-Efficiency Maximization in mmWave MIMO IoT Networks. IEEE Trans. Green Commun. Netw. 2019, 4, 109–123. [Google Scholar] [CrossRef]
- Khodakhah, F.; Mahmood, A.; Österberg, P.; Gidlund, M. Multiple Access-Enabled Relaying with Piece-Wise and Forward NOMA: Rate Optimization under Reliability Constraints. Sensors 2021, 21, 4783. [Google Scholar] [CrossRef] [PubMed]
- Osman, R.A.; Zaki, A.I. Energy-Efficient and Reliable Internet of Things for 5G: A Framework for Interference Control. Electron. 2020, 9, 2165. [Google Scholar] [CrossRef]
- Budhiraja, I.; Kumar, N.; Tyagi, S. Deep-Reinforcement-Learning-Based Proportional Fair Scheduling Control Scheme for Underlay D2D Communication. IEEE Internet Things J. 2021, 8, 3143–3156. [Google Scholar] [CrossRef]
- Sakib, S.; Tazrin, T.; Fouda, M.M.; Fadlullah, Z.M.; Nasser, N. An Efficient and Lightweight Predictive Channel Assignment Scheme for Multiband B5G-Enabled Massive IoT: A Deep Learning Approach. IEEE Internet Things J. 2021, 8, 5285–5297. [Google Scholar] [CrossRef]
- Xiao, L.; Zhang, H.; Xiao, Y.; Wan, X.; Liu, S.; Wang, L.-C.; Poor, H.V. Reinforcement Learning-Based Downlink Interference Control for Ultra-Dense Small Cells. IEEE Trans. Wirel. Commun. 2019, 19, 423–434. [Google Scholar] [CrossRef]
- Gu, B.; Zhang, X.; Lin, Z.; Alazab, M. Deep Multiagent Reinforcement-Learning-Based Resource Allocation for Internet of Controllable Things. IEEE Internet Things J. 2021, 8, 3066–3074. [Google Scholar] [CrossRef]
- Kim, J.; Park, J.; Noh, J.; Cho, S. Autonomous Power Allocation Based on Distributed Deep Learning for Device-to-Device Communication Underlaying Cellular Network. IEEE Access 2020, 8, 107853–107864. [Google Scholar] [CrossRef]
- Xiao, Y.; Niu, G.; Xiao, L.; Ding, Y.; Liu, S.; Fan, Y. Reinforcement learning based energy-efficient internet-of-things video transmission. Intell. Converg. Netw. 2020, 1, 258–270. [Google Scholar] [CrossRef]
- Azari, A.; Masoudi, M. Interference management for coexisting Internet of Things networks over unlicensed spectrum. Ad Hoc Networks 2021, 120, 102539. [Google Scholar] [CrossRef]
- Babich, F.; Buttazzoni, G.; Vatta, F.; Comisso, M. Energy-Constrained Design of Joint NOMA-Diversity Schemes with Imperfect Interference Cancellation. Sensors 2021, 21, 4194. [Google Scholar] [CrossRef]
- Alexandre, L.C.; De Souza Filho, A.L.; Sodré, A.C. Indoor Coexistence Analysis Among 5G New Radio, LTE-A and NB-IoT in the 700 MHz Band. IEEE Access 2020, 8, 135000–135010. [Google Scholar] [CrossRef]
- Li, Y.; Liang, Y.; Liu, Q.; Wang, H. Resources Allocation in Multicell D2D Communications for Internet of Things. IEEE Internet Things J. 2018, 5, 4100–4108. [Google Scholar] [CrossRef]
- Fu, S.; Su, Z.; Jia, Y.; Zhou, H.; Jin, Y.; Ren, J.; Wu, B.; Huq, K.M.S. Interference Cooperation via Distributed Game in 5G Networks. IEEE Internet Things J. 2017, 6, 311–320. [Google Scholar] [CrossRef]
- Siddiqui, M.U.A.; Qamar, F.; Ahmed, F.; Nguyen, Q.N.; Hassan, R. Interference Management in 5G and Beyond Network: Requirements, Challenges and Future Directions. IEEE Access 2021, 9, 68932–68965. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, L.; Liang, Y.-C.; Kam, P.-Y. Backscatter-NOMA: A Symbiotic System of Cellular and Internet-of-Things Networks. IEEE Access 2019, 7, 20000–20013. [Google Scholar] [CrossRef]
- Abrardo, A.; Moretti, M. Distributed Power Allocation for D2D Communications Underlaying/Overlaying OFDMA Cellular Networks. IEEE Trans. Wirel. Commun. 2017, 16, 1466–1479. [Google Scholar] [CrossRef] [Green Version]
- Fan, B.; Tian, H.; Jiang, L.; Vasilakos, A.V. A Social-Aware Virtual MAC Protocol for Energy-Efficient D2D Communications Underlying Heterogeneous Cellular Networks. IEEE Trans. Veh. Technol. 2018, 67, 8372–8385. [Google Scholar] [CrossRef]
- Elhalawany, B.M.; Ruby, R.; Wu, K. D2D Communication for Enabling Internet-of-Things: Outage Probability Analysis. IEEE Trans. Veh. Technol. 2019, 68, 2332–2345. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, M.; Liu, Y. Energy-Efficient SWIPT in IoT Distributed Antenna Systems. IEEE Internet Things J. 2018, 5, 2646–2656. [Google Scholar] [CrossRef] [Green Version]
- Chae, S.H.; Jeon, S.-W.; Jeong, C. Efficient Resource Allocation for IoT Cellular Networks in the Presence of Inter-Band Interference. IEEE Trans. Commun. 2019, 67, 4299–4308. [Google Scholar] [CrossRef]
- Liu, C.-H.; Shen, Y.-H.; Lee, C.-H. Energy-Efficient Activation and Uplink Transmission for Cellular IoT. IEEE Internet Things J. 2020, 7, 906–921. [Google Scholar] [CrossRef] [Green Version]
- Staniec, K.; Kucharzak, M.; Jóskiewicz, Z.; Chowański, B. Measurement-Based Investigations of the NB-IoT Downlink Performance in Fading Channels. IEEE Wirel. Commun. Lett. 2021, 10, 1780–1784. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Ince, T.; Hamila, R.; Gabbouj, M. Convolutional Neural Networks for patient-specific ECG classification. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 2608–2611. [Google Scholar]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the International Conference on Computer Vision (ICCV), Las Condes, Chile, 11–18 December 2015; pp. 1026–1034. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]



| Parameters | Value |
|---|---|
| 174 dBm [31] | |
| B | 10 MHz |
| SINRth | 20 dB [32] |
| Pc | 23 dBm [32] |
| PI | 23 dBm [32] |
| PB | 46 dBm [9,25] |
| PG | 43 dBm [33,34] |
| α | 4 |
| γo | 10−1 [32] |
| fc | 2 GHz |
| SINRth | CUE-D | IoTD-IoTG | IoTD-D | CUE-IoTG | |
|---|---|---|---|---|---|
| Number of records | 21,055 | 21,055 | 21,055 | 21,055 | 21,055 |
| Minimum | 0.00 | 1.00 | 0.40 | 1.00 | 0.40 |
| Maximum | 20.00 | 840.00 | 336.00 | 4644.00 | 338.65 |
| Mean | 7.94 | 281.23 | 112.49 | 501.97 | 168.77 |
| Standard Deviation | 5.84 | 190.82 | 76.33 | 395.39 | 97.39 |
| SINRth | BS-CUE | IoTG-IoTD | IoTG-CUE | BS-IoTD | |
|---|---|---|---|---|---|
| Number of records | 21,055 | 21,055 | 21,055 | 21,055 | 21,055 |
| Minimum | 0 | 1 | 0.4 | 0.84 | 0.48 |
| Maximum | 20 | 840 | 336 | 709 | 400 |
| Mean | 7.94 | 281.23 | 112.49 | 354.39 | 200.15 |
| Standard Deviation | 5.84 | 190.82 | 76.33 | 204.09 | 115.22 |
| Benchmarks | IoTG-CUE | BS-IoTD |
|---|---|---|
| Support vector regressor | kernel = ‘rbf’, C = 220, gamma = 40 | Kernel = ‘rbf’, C = 200, gamma = 50 |
| Random forest regressor | max_depth = 100, max_features = 3, min_samples_leaf = 3, min_samples_split = 8, n_estimators = 1000 | max_depth = 90, max_features = 3, min_samples_leaf = 3, min_samples_split = 8, n_estimators = 1000 |
| Adaboost regressor | learning_rate = 0.01, loss = ‘Linear’, n_estimators = 150 | learning_rate = 1, loss = ‘linear’, n_estimators = 150 |
| Multilayer perceptron | activation = ‘tanh’, alpha = 0.05, solver = ‘sgd’, hidden_layer_sizes = (300,), learning_rate = ‘adaptive’ | activation = ‘tanh’, alpha = 0.05, solver = ‘sgd’, hidden_layer_sizes = (300,), learning_rate = ‘adaptive’ |
| Benchmarks | IoTG-CUE | BS-IoTD |
|---|---|---|
| Support vector regressor | kernel = ‘rbf’, C = 220, gamma = 40 | Kernel = ‘rbf’, C = 200, gamma = 50 |
| Random forest regressor | max_depth = 100, max_features = 3, min_samples_leaf = 3, min_samples_split = 8, n_estimators = 1000 | max_depth = 90, max_features = 3, min_samples_leaf = 3, min_samples_split = 8, n_estimators = 1000 |
| Adaboost regressor | learning_rate = 0.1, loss = ‘square’, n_estimators = 100 | learning_rate = 1, loss = ‘linear’, n_estimators = 100 |
| Multilayer perceptron | activation = ‘tanh’, alpha = 0.05, solver = ‘sgd’, hidden_layer_sizes = (100,), learning_rate = ‘adaptive’ | activation = ‘tanh’, alpha = 0.05, solver = sgd, hidden_layer_sizes = (100,), learning_rate = ‘adaptive‘ |
| IoTD-D | CUE-IoTG | |||||||
|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | |||||
| Benchmarks | Train | Test | Train | Test | Train | Test | Train | Test |
| Support vector regressor | 12.83 | 15.14 | 96.29 | 94.28 | 0.07 | 0.75 | 0.07 | 1.14 |
| Random forest regressor | 2.52 | 11.63 | 35.32 | 64.84 | 0.11 | 0.83 | 0.18 | 1.16 |
| Adaboost regressor | 128.06 | 129.21 | 215.24 | 216.70 | 18.13 | 18.36 | 21.69 | 21.90 |
| Multilayer perceptron | 21.86 | 24.64 | 77.00 | 80.97 | 0.16 | 0.78 | 0.26 | 1.16 |
| Proposed model | 9.59 | 9.84 | 66.09 | 63.43 | 0.77 | 0.77 | 1.01 | 1.06 |
| IoTG-CUE | BS-IoTD | |||||||
|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | |||||
| Benchmarks | Train | Test | Train | Test | Train | Test | Train | Test |
| Support vector regressor | 0.17 | 1.56 | 0.24 | 2.37 | 0.14 | 0.89 | 0.20 | 1.34 |
| Random forest regressor | 0.26 | 1.74 | 0.39 | 2.43 | 0.16 | 0.98 | 0.24 | 1.38 |
| Adaboost regressor | 40.39 | 40.75 | 49.66 | 50.16 | 21.36 | 21.69 | 25.52 | 25.83 |
| Multilayer perceptron | 0.59 | 1.73 | 0.84 | 2.50 | 0.29 | 0.93 | 0.42 | 1.38 |
| Proposed model | 1.64 | 1.47 | 2.16 | 2.06 | 0.94 | 0.89 | 1.25 | 1.24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Osman, R.A.; Saleh, S.N.; Saleh, Y.N.M. A Novel Interference Avoidance Based on a Distributed Deep Learning Model for 5G-Enabled IoT. Sensors 2021, 21, 6555. https://doi.org/10.3390/s21196555
Osman RA, Saleh SN, Saleh YNM. A Novel Interference Avoidance Based on a Distributed Deep Learning Model for 5G-Enabled IoT. Sensors. 2021; 21(19):6555. https://doi.org/10.3390/s21196555
Chicago/Turabian StyleOsman, Radwa Ahmed, Sherine Nagy Saleh, and Yasmine N. M. Saleh. 2021. "A Novel Interference Avoidance Based on a Distributed Deep Learning Model for 5G-Enabled IoT" Sensors 21, no. 19: 6555. https://doi.org/10.3390/s21196555
APA StyleOsman, R. A., Saleh, S. N., & Saleh, Y. N. M. (2021). A Novel Interference Avoidance Based on a Distributed Deep Learning Model for 5G-Enabled IoT. Sensors, 21(19), 6555. https://doi.org/10.3390/s21196555






