Opportunistic Large Array Propagation Models: A Comprehensive Survey
Abstract
1. Introduction
2. Continuum Model with Deterministic Channel Assumption
3. One-Dimensional Propagation Models of OLA-Based Networks
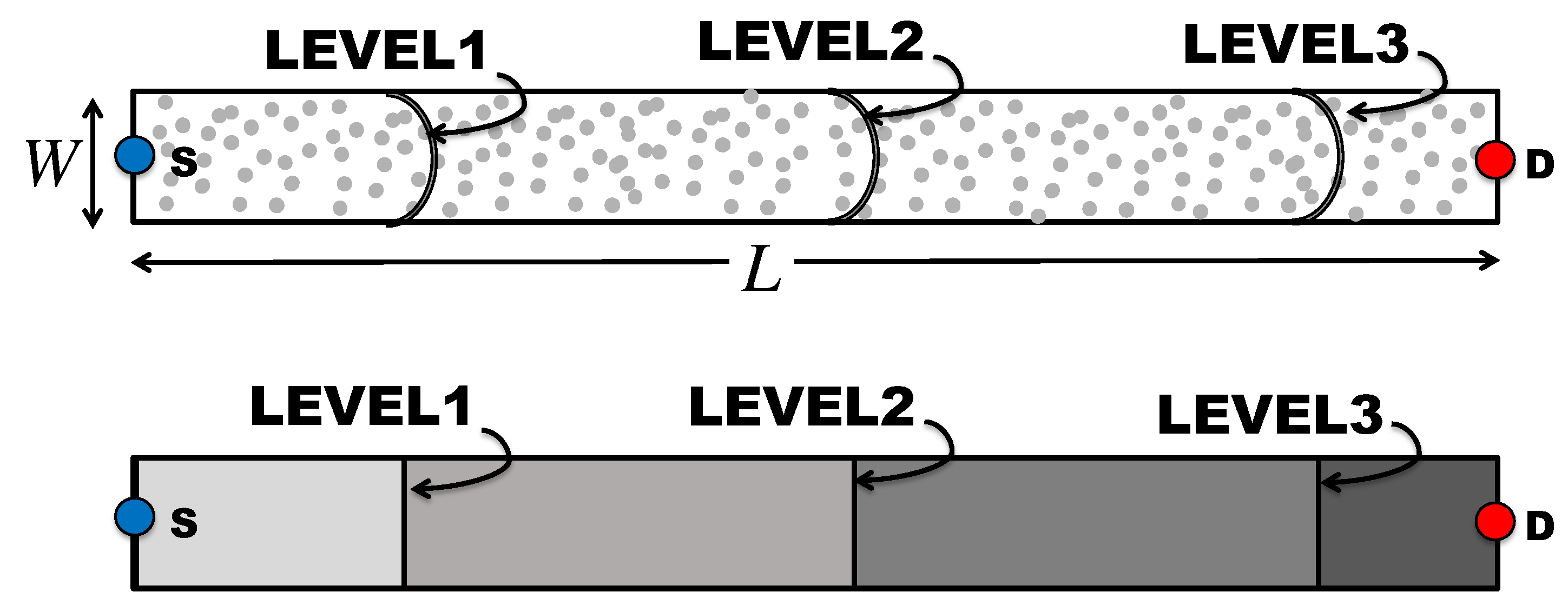
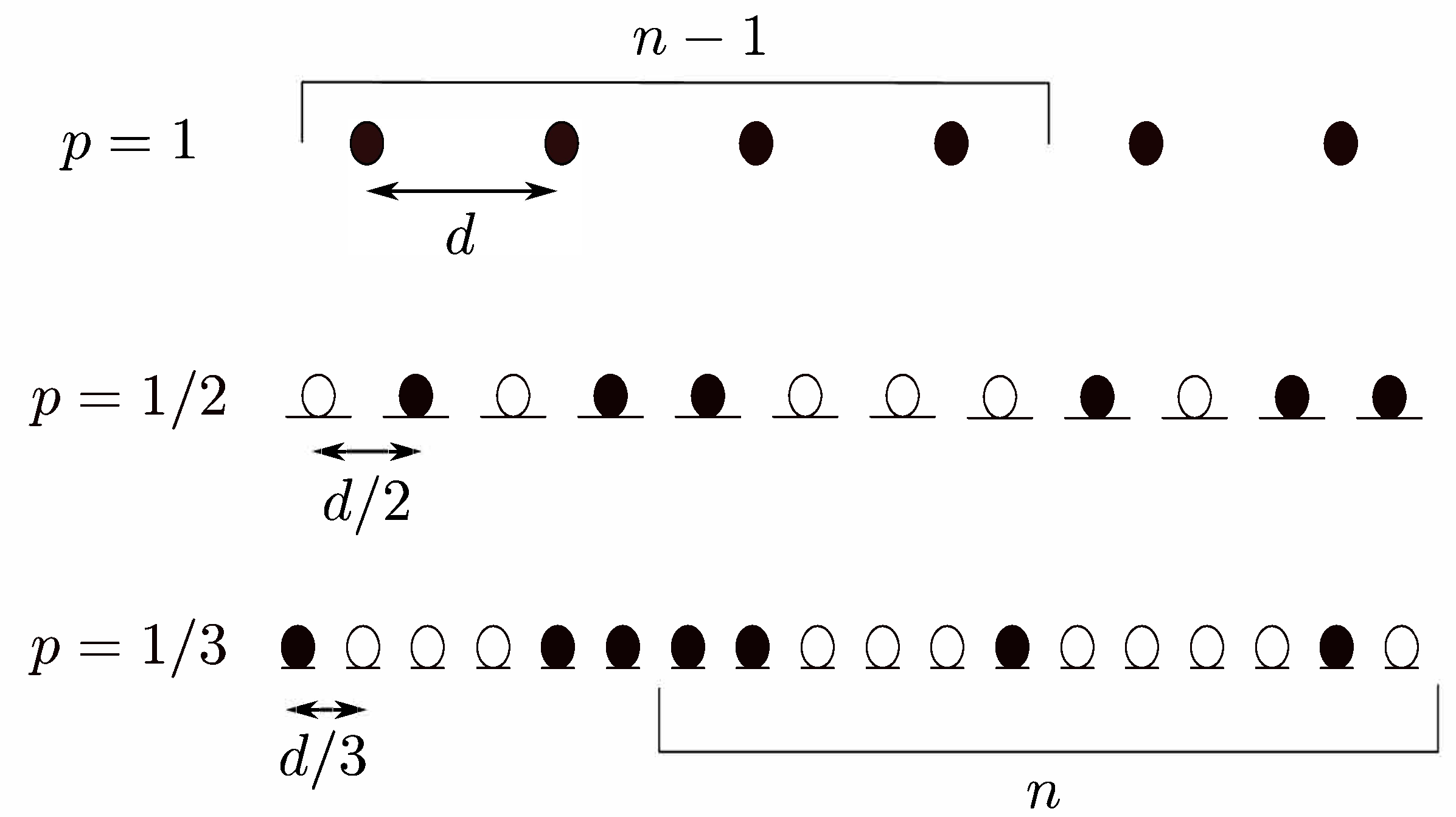
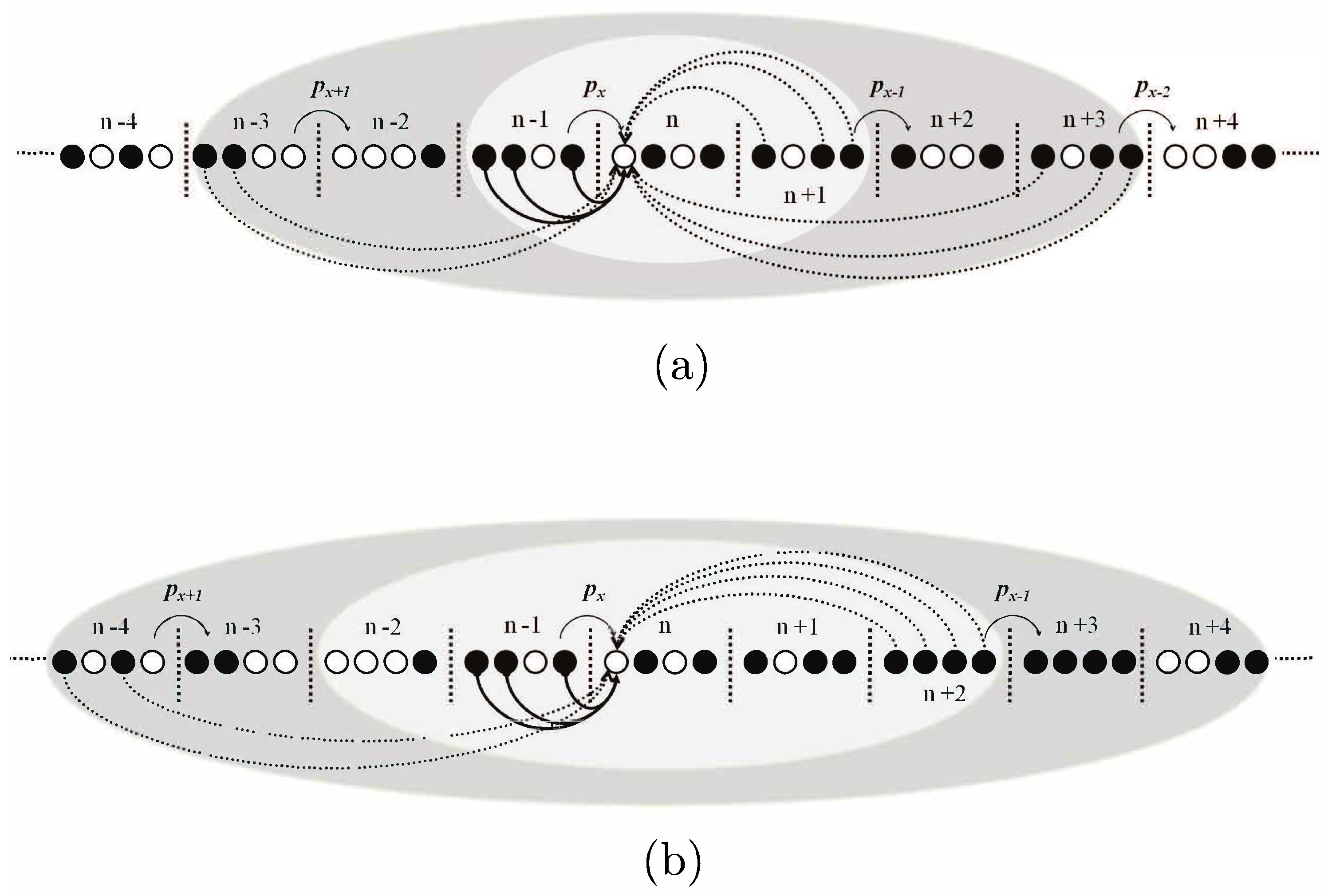
3.1. Non-Overlapping 1D OLA Network
3.2. Overlapping 1D OLA Network
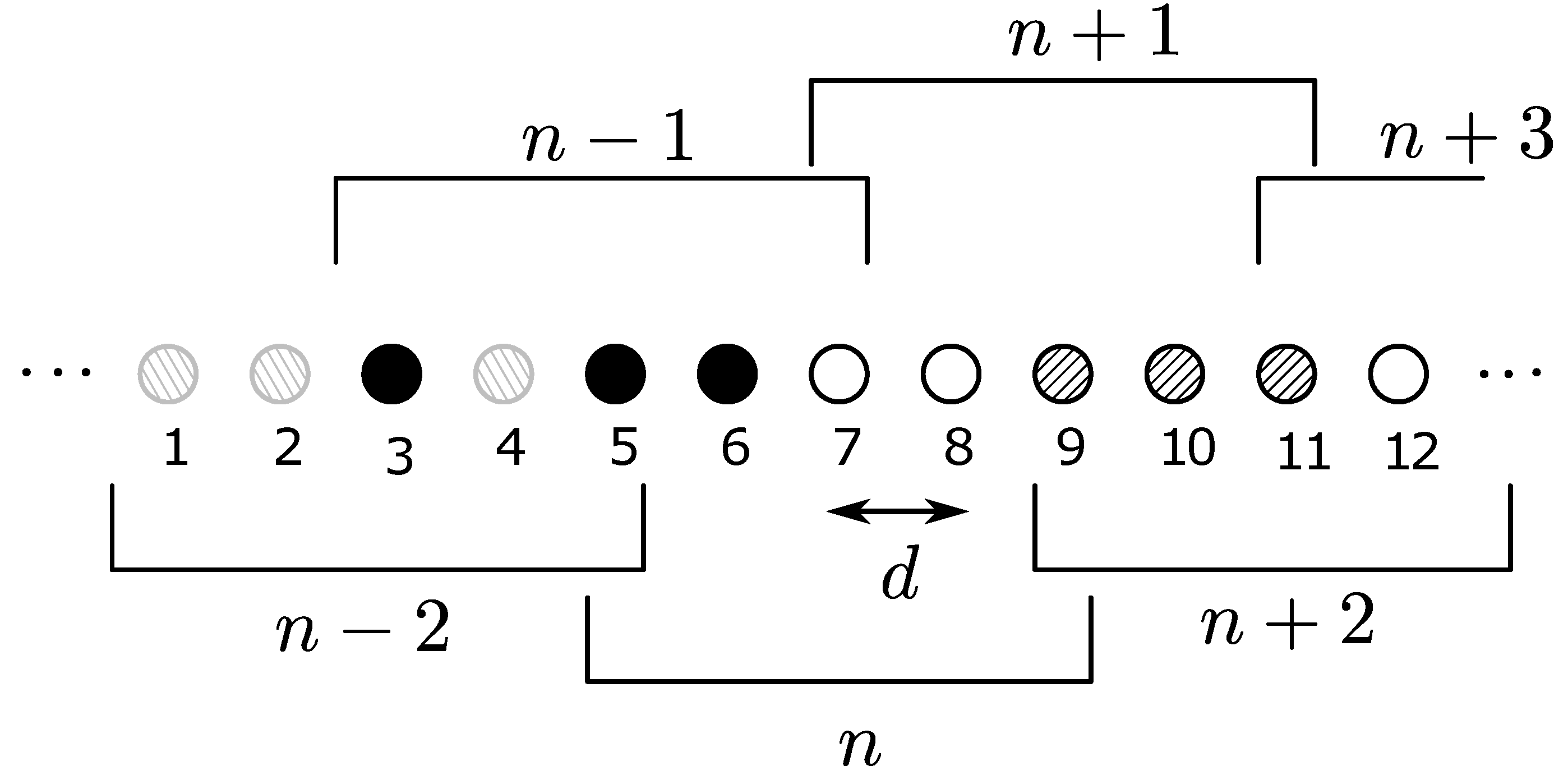
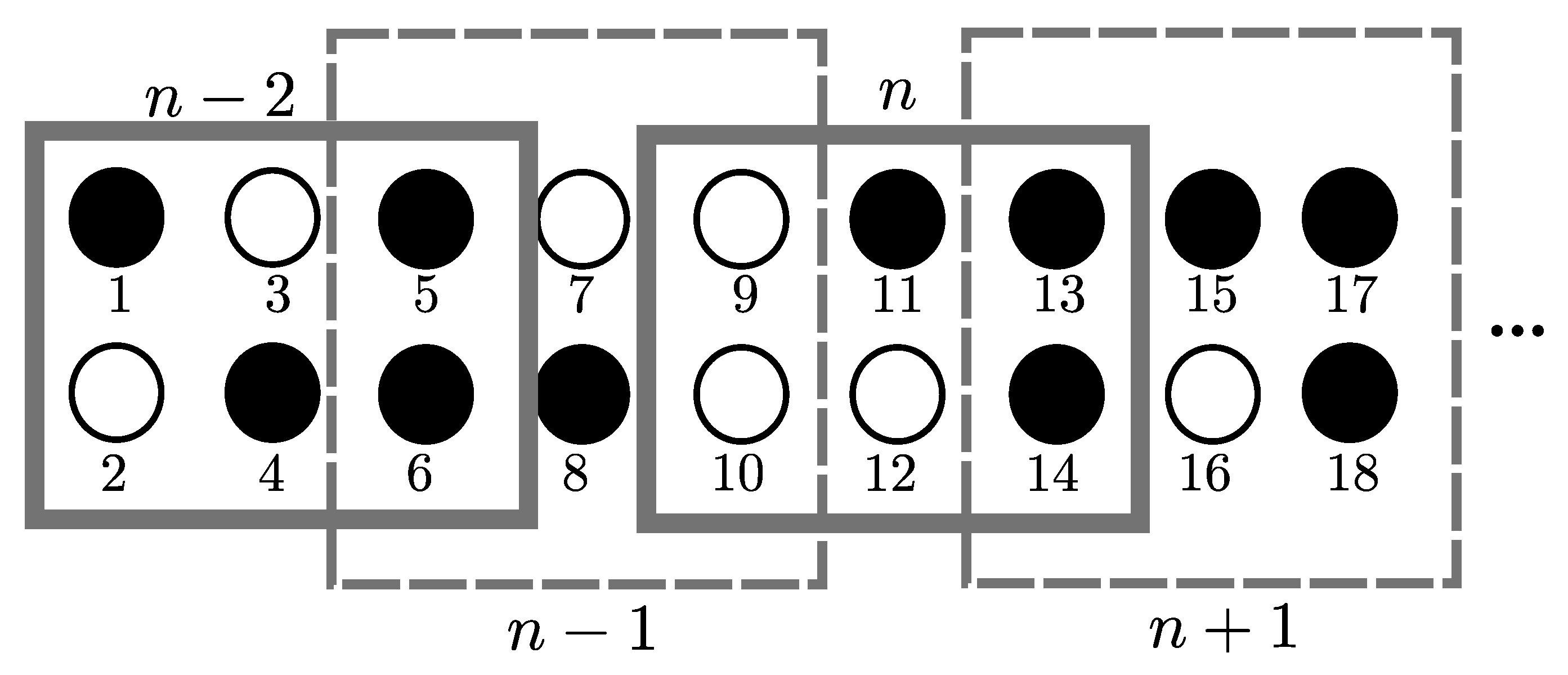
3.3. 1D OLA Network with Co-Locating Groups of Nodes
3.4. Randomly Deployed 1D OLA Network
4. Two-Dimensional Propagation Models of OLA-Based Networks
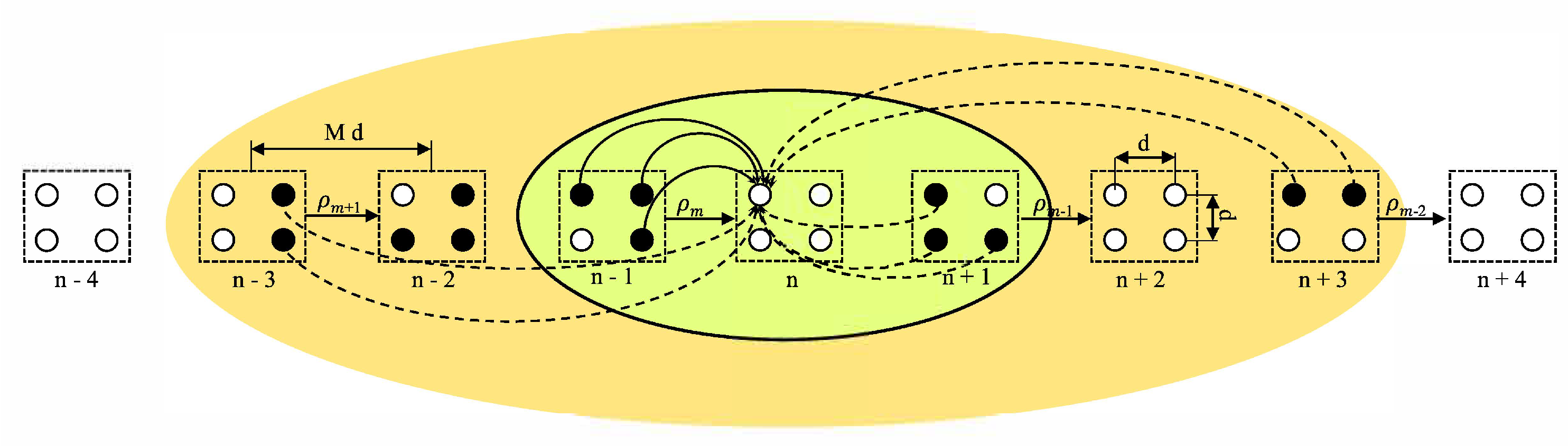
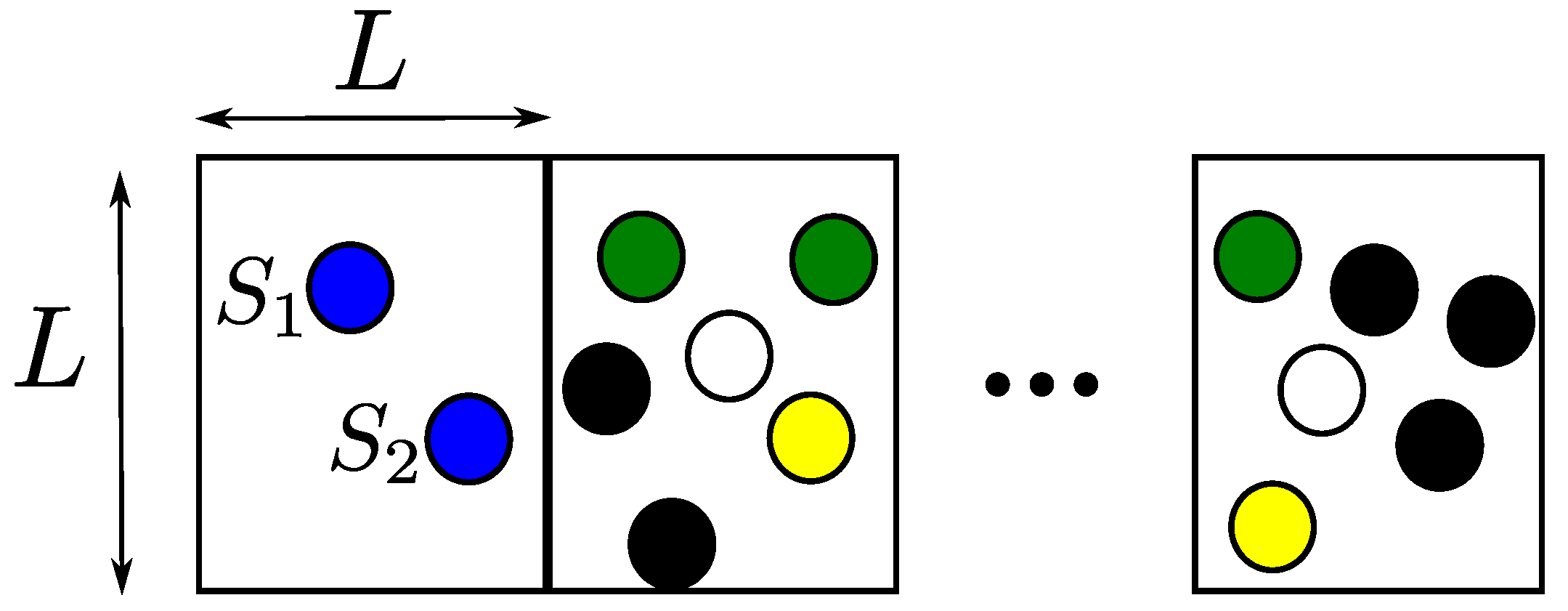
4.1. Overlapping 2D OLA Network
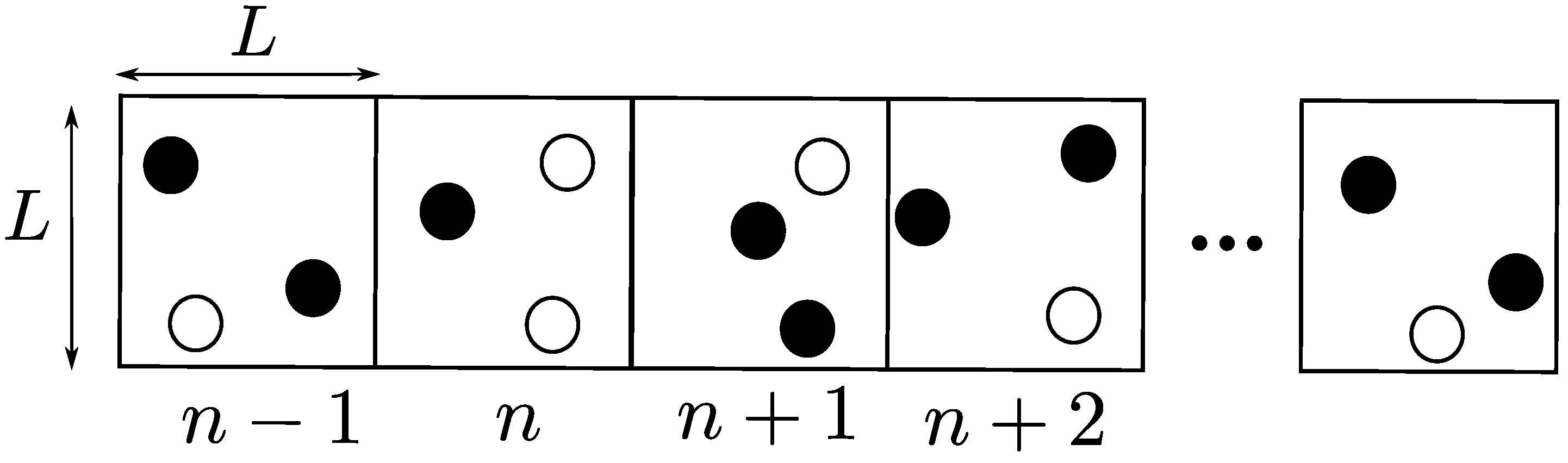
4.2. Non-Overlapping Fixed Boundary 2D OLA Network with a Fixed Number of Nodes at Arbitrary Locations
4.3. Non-Overlapping Fixed Boundary 2D OLA Network with a Random Number of Nodes with Arbitrary Locations
4.4. Large-Scale 2D OLA Network with Random Boundaries
5. Multi-Packet OLA Transmission Networks
5.1. 1D Multi-Packet OLA Network
5.2. 2D Multi-Packet OLA Network
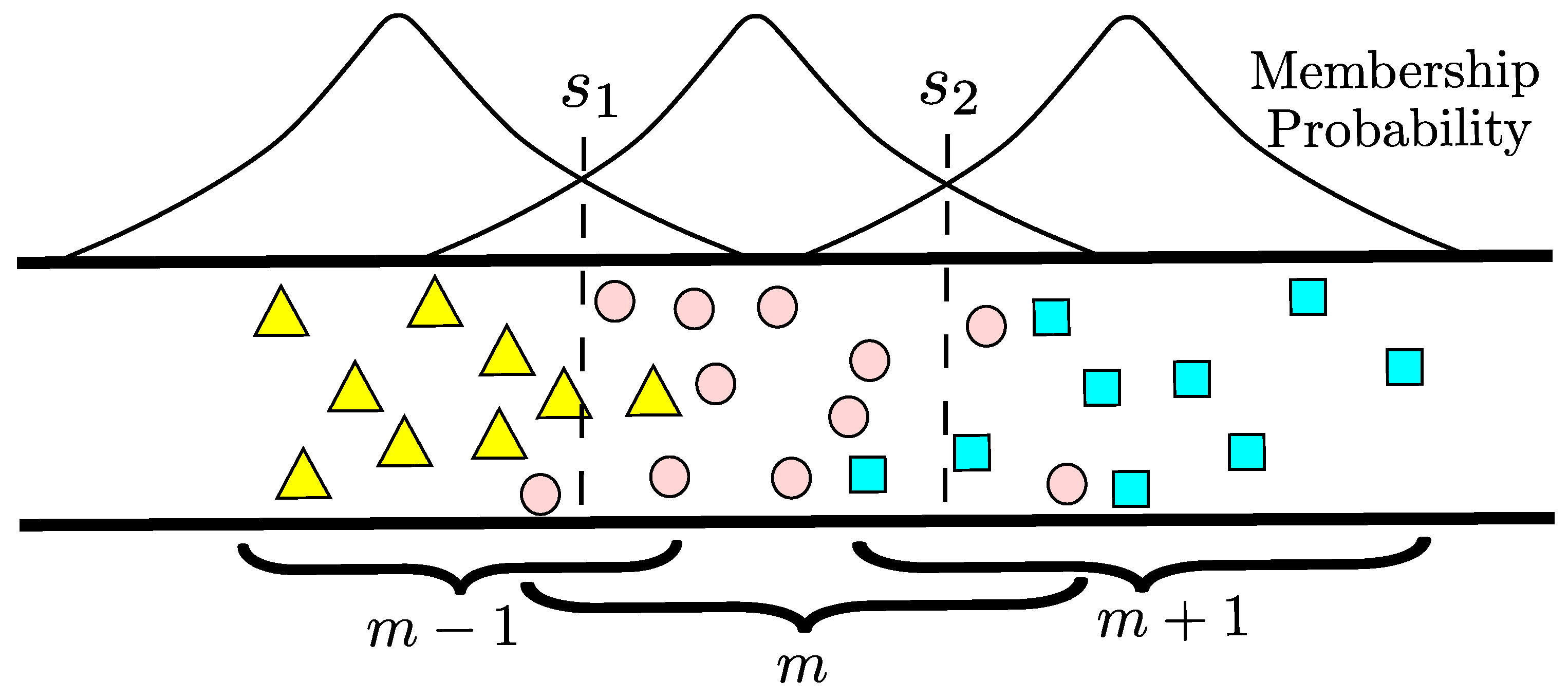
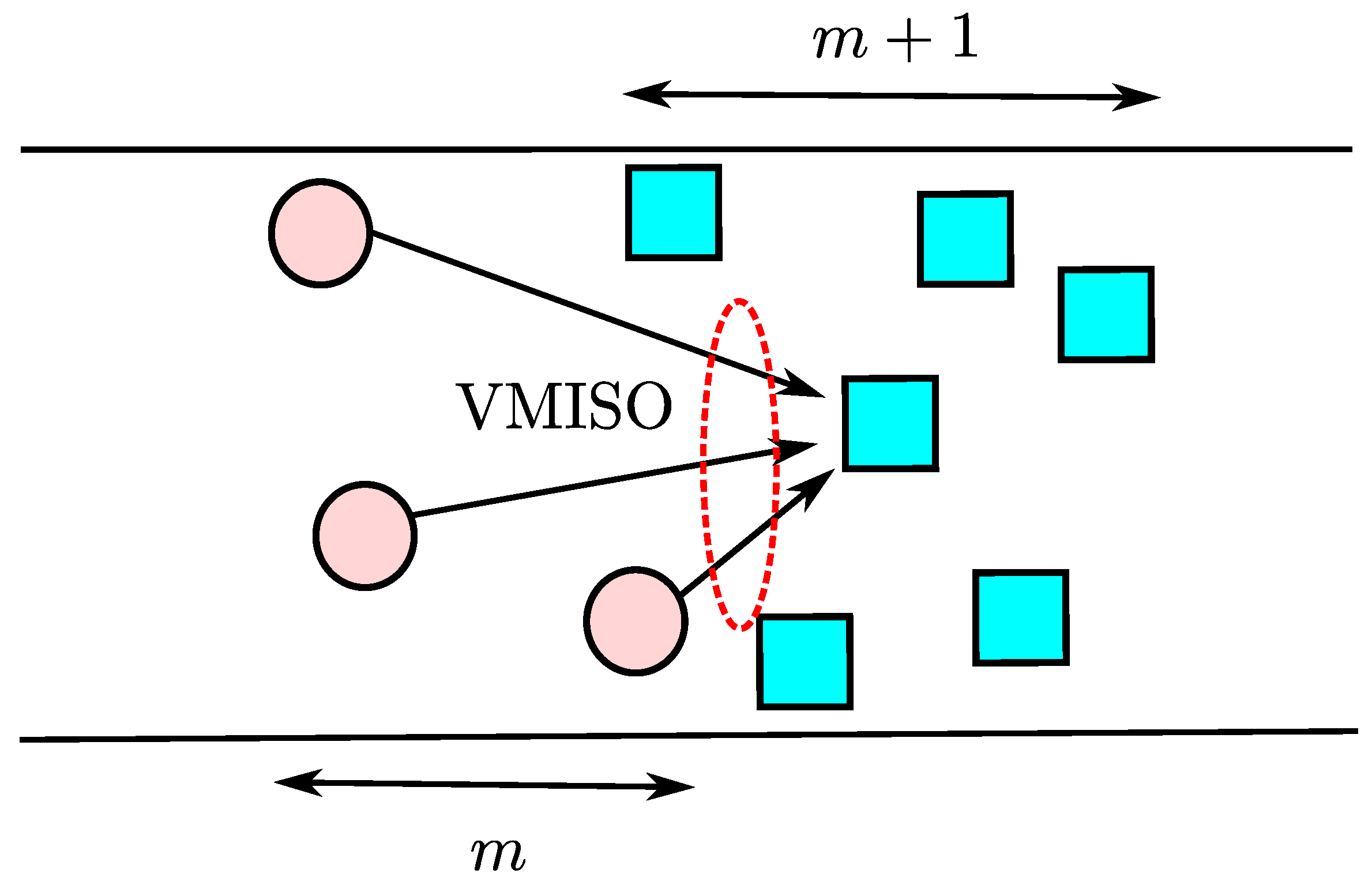
5.3. 2D OLA Network with Multiple Sources
6. Energy-Efficient OLA Protocols
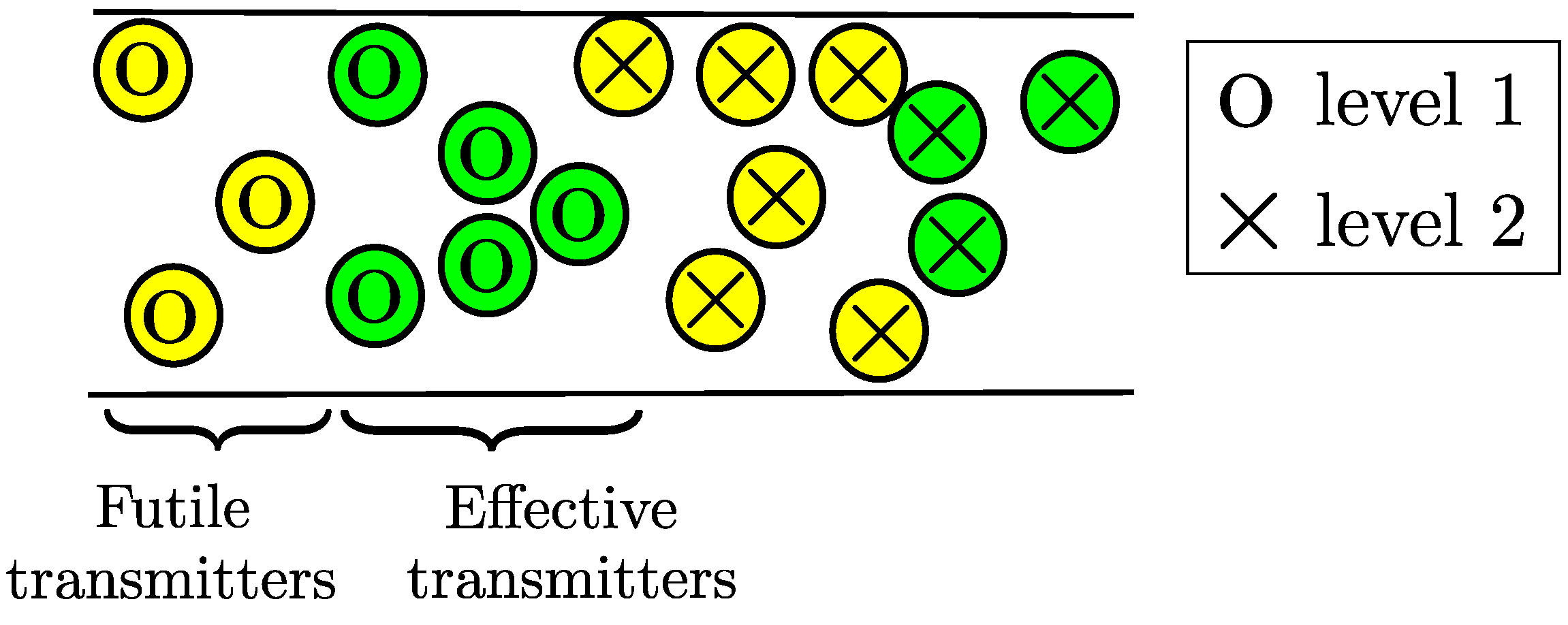
6.1. OLA with Transmission Threshold (OLA-T)
6.2. Alternating OLA-T (A-OLA-T)
6.3. OLA Concentric Routing Algorithm (OLACRA)
6.4. OLA Concentric Routing Algorithm with Threshold (OLACRA-T)
7. Future Directions
7.1. Scheduling in OLA Networks with Multiple Routes
7.2. OLA and Cooperative Routing for Underwater Sensor Networks
7.3. Machine Learning and Deep Learning-Based Relay Selections in OLA Cooperative Networks
7.4. Cooperation and Wireless-Powered Networks
7.5. Backscatter-Aided Cooperative Transmissions
7.6. Security for OLA Networks
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| 5G | Fifth Generation |
| B5G | Beyond Fifth Generation |
| IoT | Internet-of-Things |
| mMTC | massive machine-type communication |
| CT | Cooperative Transmission |
| OLA | Opportunistic Large Array |
| IoT | Internet-of-Things |
| mMTC | massive machine-type communication |
| eMBB | enhanced mobile broadband |
| D2D | Device-to-Device |
| VMISO | Virtual Multiple-Input-Single-Output |
| MISO | Multiple-Input-Single-Output |
| SISO | Single-Input–Single-Output |
| DF | Decode-and-Forward |
| AF | Amplify-and-Forward |
| MRC | Maximum Ratio Combining |
| EGC | Equal Gain Combining |
| SC | Selective Combining |
| MAC | Medium Access Control |
| 1D | One-Dimensional |
| 2D | Two-Dimensional |
| SDR | Software-Defined Radio |
| SNR | Signal-to-Noise-Ratio |
| PIR | Packet Insertion Rate |
| UWSN | Underwater Sensor Network |
| ML | Machine Learning |
| DL | Deep learning |
| BackCom | Backscatter Communication |
References
- Ijaz, A.; Zhang, L.; Grau, M.; Mohamed, A.; Vural, S.; Quddus, A.U.; Imran, M.A.; Foh, C.H.; Tafazolli, R. Enabling Massive IoT in 5G and Beyond Systems: PHY Radio Frame Design Considerations. IEEE Access 2016, 4, 3322–3339. [Google Scholar] [CrossRef]
- Guo, F.; Yu, F.R.; Zhang, H.; Li, X.; Ji, H.; Leung, V.C.M. Enabling Massive IoT Toward 6G: A Comprehensive Survey. IEEE Internet Things J. 2021. [Google Scholar] [CrossRef]
- Akhta, M.W.; Hassan, S.A.; Ghaffar, R.; Jung, H.; Garg, S.; Hossain, M.S. The shift to 6G communications: Vision and requirements. Hum. Centric Comput. Inf. Sci. 2020, 10, 1–27. [Google Scholar]
- Verma, S.; Kawamoto, Y.; Fadlullah, Z.M.; Nishiyama, H.; Kato, N. A Survey on Network Methodologies for Real-Time Analytics of Massive IoT Data and Open Research Issues. IEEE Commun. Surv. Tutor. 2017, 19, 1457–1477. [Google Scholar] [CrossRef]
- Ge, Y.; Liang, X.; Zhou, Y.C.; Pan, Z.; Zhao, G.T.; Zheng, Y.L. Adaptive Analytic Service for Real-Time Internet of Things Applications. In Proceedings of the 2016 IEEE International Conference on Web Services (ICWS), San Francisco, CA, USA, 27 June–2 July 2016; pp. 484–491. [Google Scholar] [CrossRef]
- Lianghai, J.; Han, B.; Liu, M.; Schotten, H.D. Applying Device-to-Device Communication to Enhance IoT Services. IEEE Commun. Stand. Mag. 2017, 1, 85–91. [Google Scholar] [CrossRef][Green Version]
- Elouafadi, R.; Benjillali, M. Cooperative NOMA-based D2D communications: A survey in the 5G/IoT context. In Proceedings of the 2018 19th IEEE Mediterranean Electrotechnical Conference (MELECON), Marrakech, Morocco, 2–7 May 2018; pp. 132–137. [Google Scholar] [CrossRef]
- ElHalawany, B.M.; Ruby, R.; Wu, K. D2D Communication for Enabling Internet-of-Things: Outage Probability Analysis. IEEE Trans. Veh. Technol. 2019, 68, 2332–2345. [Google Scholar] [CrossRef]
- Nawaz, F.; Hassan, S.A.; Hashmi, A.J.; Jung, H. A Physical-Layer Scheduling Approach in Large-Scale Cooperative Networks. IEEE Access 2019, 7, 134338–134347. [Google Scholar] [CrossRef]
- Jung, H.; Ko, S.W.; Lee, I.H. Secure Transmission Using Linearly Distributed Virtual Antenna Array with Element Position Perturbations. IEEE Trans. Veh. Technol. 2021, 70, 474–489. [Google Scholar] [CrossRef]
- Akhtar, M.W.; Hassan, S.A.; Saleem, S.; Jung, H. STBC-Aided Cooperative NOMA with Timing Offsets, Imperfect Successive Interference Cancellation, and Imperfect Channel State Information. IEEE Trans. Veh. Technol. 2020, 69, 11712–11727. [Google Scholar] [CrossRef]
- Jung, H.; Chang, Y.; Ingram, M.A. Experimental Range Extension of Concurrent Cooperative Transmission in Indoor Environments at 2.4 GHz. In Proceedings of the IEEE MILCOM, San Jose, CA, USA, 31 October–3 November 2010. [Google Scholar]
- Jamal, M.N.; Hassan, S.A.; Jayakody, D.N.K.; Rodrigues, J.J.P.C. Efficient Nonorthogonal Multiple Access: Cooperative Use of Distributed Space-Time Block Coding. IEEE Veh. Technol. Mag. 2018, 13, 70–77. [Google Scholar] [CrossRef]
- Scaglione, A.; Hong, Y.W. Opportunistic large arrays: Cooperative transmission in wireless multihop ad hoc networks to reach far distances. IEEE Trans. Signal Proc. 2003, 51, 2082–2092. [Google Scholar] [CrossRef]
- Laneman, J.; Tse, D.; Wornell, G. Cooperative diversity in wireless networks: Efficient protocols and outage behavior. IEEE Trans. Inf. Theory 2004, 50, 3062–3080. [Google Scholar] [CrossRef]
- Chang, Y.J.; Ingram, M. Convergence Property of Transmit Time Pre-Synchronization for Concurrent Cooperative Communication. In Proceedings of the IEEE GLOBECOM, Miami, FL, USA, 6–10 December 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Sirkeci-Mergen, B.; Scaglione, A. On the power efficiency of cooperative broadcast in dense wireless networks. IEEE J. Sel. Areas Commun. 2007, 25, 497–507. [Google Scholar] [CrossRef]
- Thanayankizil, L.; Kailas, A.; Ingram, M.A. Routing for Wireless Sensor Networks with an Opportunistic Large Array (OLA) Physical Layer. Ad Hoc Sens. Wirel. Netw. 2009, 8, 79–117. [Google Scholar]
- Jung, H.; Weitnauer, M.A. Multi-packet Interference in Opportunistic Large Array Broadcasts over Disk Networks. IEEE Trans. Wirel. Commun. 2013, 12, 5631–5645. [Google Scholar] [CrossRef]
- Kailas, A.; Ingram, M.A. Analysis of a Simple Recruiting Method for Cooperative Routes and Strip Networks. IEEE Trans. Wirel. Commun. 2010, 9, 2415–2419. [Google Scholar] [CrossRef]
- Kailas, A.; Ingram, M.A. Alternating opportunistic large arrays in broadcasting for network lifetime extension. IEEE Trans. Wirel. Commun. 2009, 8, 2831–2835. [Google Scholar] [CrossRef]
- Rohokale, V.; Kulkarni, N.; Prasad, N.; Cornean, H. Cooperative opportunistic large array approach for cognitive radio networks. In Proceedings of the 2010 8th International Conference on Communications, Bucharest, Romania, 10–12 June 2010; pp. 513–516. [Google Scholar] [CrossRef]
- Chowdhuri, S.; Das, S.K.; Roy, P.; Chakraborty, S.; Maji, M.; Dey, N. Implementation of a new packet broadcasting algorithm for MIMO equipped Mobile ad hoc network. In Proceedings of the International Conference on Circuits, Communication, Control and Computing, Bangalore, India, 21–22 November 2014; pp. 372–376. [Google Scholar] [CrossRef]
- Ansel, V.P.; Aboothahir, M.A.; Smritilakshmi, A.S.; Jose, B.R. Secure opportunistic large array for Internet of Things. In Proceedings of the 2016 Sixth International Symposium on Embedded Computing and System Design (ISED), Patna, India, 15–17 December 2016; pp. 201–204. [Google Scholar] [CrossRef]
- Rohokale, V.M.; Prasad, N.R.; Prasad, R. A cooperative Internet of Things (IoT) for rural healthcare monitoring and control. In Proceedings of the 2011 2nd International Conference on Wireless Communication, Vehicular Technology, Information Theory and Aerospace Electronic Systems Technology (Wireless VITAE), Chennai, India, 28 Febuary–3 March 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Ud Din, I.; Almogren, A.; Guizani, M.; Zuair, M. A Decade of Internet of Things: Analysis in the Light of Healthcare Applications. IEEE Access 2019, 7, 89967–89979. [Google Scholar] [CrossRef]
- Biagioni, E.S. Algorithms for Communication in Wireless multi-hop ad hoc Networks using Broadcasts in Opportunistic Large Arrays (OLA). In Proceedings of the 2007 16th International Conference on Computer Communications and Networks, Honolulu, HI, USA, 13–16 August 2007; pp. 1111–1116. [Google Scholar] [CrossRef]
- Scaglione, A.; Goeckel, D.; Laneman, J. Cooperative communications in mobile ad hoc networks. IEEE Signal Proc. Mag. 2006, 23, 18–29. [Google Scholar] [CrossRef]
- Hong, Y.W.; Scaglione, A. Energy-efficient broadcasting with cooperative transmissions in wireless sensor networks. IEEE Trans. Wirel. Commun. 2006, 5, 2844–2855. [Google Scholar] [CrossRef]
- Kailas, A.; Ingram, M.A. OLA with transmission threshold for strip networks. In Proceedings of the MILCOM 2009—2009 IEEE Military Communications Conference, Boston, MA, USA, 18–21 October 2009; pp. 1–7. [Google Scholar] [CrossRef]
- Thanayankizil, L.; Ingram, M. Reactive Routing for Multi-Hop Dynamic Ad Hoc Networks Based on Opportunistic Large Arrays. In Proceedings of the IEEE GLOBECOM, New Orleans, LA, USA, 30 November–4 December 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Thanayankizil, L.; Ingram, M. Reactive Robust Routing with Opportunistic Large Arrays. In Proceedings of the IEEE ICC, Dresden, Germany, 14–18 June 2009; pp. 1–5. [Google Scholar] [CrossRef]
- Kailas, A. On the Performance of Alternating Concurrent Cooperative Transmissions in the High Path-Loss Attenuation Regime. Int. J. Netw. Protoc. Algorithms 2012, 4, 68–81. [Google Scholar] [CrossRef]
- Jung, H.; Weitnauer, M. Multi-Packet Opportunistic Large Array Transmission on Strip-Shaped Cooperative Routes or Networks. IEEE Trans. Wirel. Commun. 2014, 13, 144–158. [Google Scholar] [CrossRef]
- Chang, Y.J.; Jung, H.; Ingram, M.A. Demonstration of an OLA-based Cooperative Routing Protocol in an Indoor Environment. In Proceedings of the IEEE European Wireless, Vienna, Austria, 27–29 April 2011; pp. 1–8. [Google Scholar]
- Chang, Y.; Jung, H.; Ingram, M.A. Demonstration of a New Degree of Freedom in Wireless Routing: Concurrent Cooperative Transmission. In Proceedings of the HotEMNETS 2010 Workshop on Hot Topics in Embedded Networked Sensors, Killarney, Ireland, 28–29 June 2010. [Google Scholar] [CrossRef]
- Hassan, S.A.; Ingram, M.A. Modeling of a Cooperative One-Dimensional Multi-Hop Network Using Quasi-Stationary Markov Chains. In Proceedings of the IEEE GLOBECOM, Miami, FL, USA, 6–10 December 2010; pp. 1–5. [Google Scholar]
- Lin, J.; Jung, H.; Chang, Y.J.; Jung, J.W.; Weitnauer, M.A. On cooperative transmission range extension in multi-hop wireless ad hoc and sensor networks: A review. Ad Hoc Netw. 2015, 29, 117–134. [Google Scholar] [CrossRef]
- Hassan, S.A.; Ingram, M.A. A Quasi-Stationary Markov Chain Model of a Cooperative Multi-Hop Linear Network. IEEE Trans. Wirel. Commun. 2011, 10, 2306–2315. [Google Scholar] [CrossRef]
- Hassan, S.A.; Ingram, M.A. The Benefit of Co-Locating Groups of Nodes in Cooperative Line Networks. IEEE Commun. Lett. 2012, 16, 234–237. [Google Scholar] [CrossRef]
- Hassan, S.A.; Ingram, M.A. On the modeling of randomized distributed cooperation for linear multi-hop networks. In Proceedings of the IEEE International Conference on Communications (ICC), On the Modeling of Randomized Distributed Cooperation for Linear Multi-Hop Networks, Ottawa, ON, Canada, 10–15 June 2012; pp. 366–370. [Google Scholar] [CrossRef]
- Hassan, S.A. Performance Analysis of Cooperative Multi-hop Strip Networks. Wirel. Pers. Commun. 2014, 74, 391–400. [Google Scholar] [CrossRef]
- Afzal, A.; Hassan, S.A. Stochastic Modeling of Cooperative Multi-Hop Strip Networks with Fixed Hop Boundaries. IEEE Trans. Wirel. Commun. 2014, 13, 4146–4155. [Google Scholar] [CrossRef]
- Ahsen, M.; Hassan, S.A. A poisson point process model for coverage analysis of multi-hop cooperative networks. In Proceedings of the IEEE International Wireless Communications and Mobile Computing Conference (IWCMC), Dubrovnik, Croatia, 24–28 August 2015; pp. 442–447. [Google Scholar] [CrossRef]
- Ahsen, M.; Hassan, S.A.; Jayakody, D.N.K. Propagation Modeling in Large-Scale Cooperative Multi-Hop Ad Hoc Networks. IEEE Access 2016, 4, 8925–8937. [Google Scholar] [CrossRef]
- Shafi, Q.; Hassan, S.A. Interference analysis in cooperative multi-hop networks subject to multiple flows. In Proceedings of the IEEE IFIP Wireless Days (WD), Rio de Janeiro, Brazil, 12–14 November 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Hussain, M.; Hassan, S.A. Impact of Intra-Flow Interference on the Performance of 2-D Multi-Hop Cooperative Network. IEEE Commun. Lett. 2017, 21, 869–872. [Google Scholar] [CrossRef]
- Aslam, M.A.; Hassan, S.A. Analysis of Multi-Source Multi-Hop Cooperative Networks Employing Network Coding. In Proceedings of the IEEE VTC, Glasgow, UK, 11–14 May 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Narsani, H.K.; Raut, P.; Dev, K.; Singh, K.; Li, C.P. Interference Limited Network for Factory Automation with Multiple Packets Transmissions. In Proceedings of the 2021 IEEE 18th Annual Consumer Communications Networking Conference (CCNC), Las Vegas, NV, USA, 9–12 January 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Marcus, K.; Nilsson, J.; Suri, N.; Hansson, A.; Breedy, M.; Fronteddu, R.; Cramer, E. Emulating Synchronized Cooperative Broadcast in the Anglova Scenario and EMANE. In Proceedings of the 2020 Military Communications and Information Systems Conference (MilCIS), Canberra, ACT, Australia, 10–12 November 2020; pp. 1–9. [Google Scholar] [CrossRef]
- Shukla, R.K.; Prakash, V.; Pandey, S. A Perspective on Internet of Things: Challenges Applications. In Proceedings of the 2020 9th International Conference System Modeling and Advancement in Research Trends (SMART), Moradabad, India, 4–5 December 2020; pp. 184–189. [Google Scholar] [CrossRef]
- Tarek, D.; Benslimane, A.; Darwish, M.; Kotb, A.M. Cognitive Radio Networks Channel State Estimation Using Machine Learning Techniques. In Proceedings of the 2019 15th International Wireless Communications Mobile Computing Conference (IWCMC), Tangier, Morocco, 24–28 June 2019; pp. 342–347. [Google Scholar] [CrossRef]
- Gopi, R.; Jayanthi, J.; Pandiyan, S. A guaranteed data transmission system for wireless ad hoc networks. Trans. Emerg. Telecommun. Technol. 2020, 31, e4005. [Google Scholar] [CrossRef]
- Sirkeci-Mergen, B.; Moballegh, S. Broadcasting in dense linear networks: To cooperate or not to cooperate? Ad Hoc Netw. 2019, 83, 182–197. [Google Scholar] [CrossRef]
- Bader, A.; Alouini, M.S. Autonomous Cooperative Routing for Mission-Critical Applications. In Mission-Oriented Sensor Networks and Systems: Art and Science: Volume 2: Advances; Ammari, H.M., Ed.; Springer International Publishing: Cham, Switzerland, 2019; pp. 11–54. [Google Scholar] [CrossRef]
- Jung, H.; Weitnauer, M.A. Characterization of Path-Loss Disparity in Virtual Multiple-Input-Single-Output Links. Int. J. Antennas Propag. 2014, 2014. [Google Scholar] [CrossRef]
- Jung, H.; Weitnauer, M.A. SNR Penalty from the Path-loss Disparity in Virtual Multiple-Input-Single-Output (VMISO) Link. In Proceedings of the IEEE ICC, Budapest, Hungary, 9–13 June 2013. [Google Scholar]
- Talarico, S.; Valenti, M.C.; Halford, T.R. Unicast Barrage Relay Networks: Outage Analysis and Optimization. In Proceedings of the 2014 IEEE Military Communications Conference, Baltimore, MD, USA, 6–8 October 2014; pp. 537–543. [Google Scholar] [CrossRef]
- Na, Q.; Xuebing, W.; Yantao, L. Simulation Studies on Barrage Relay Networks. In Proceedings of the 2019 34rd Youth Academic Annual Conference of Chinese Association of Automation (YAC), Jinzhou, China, 6–8 June 2019; pp. 189–194. [Google Scholar] [CrossRef]
- Halford, T.R.; Courtade, T.A.; Turck, K.A. The user capacity of barrage relay networks. In Proceedings of the MILCOM 2012—2012 IEEE Military Communications Conference, Orlando, FL, USA, 29 October–1 November 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Yan, J.; Tian, C.; Liu, W.; Tu, L.; Huang, B. Multi-source Broadcast Scheduling Algorithm of Barrage Relay Network in Tactical MANET. In Proceedings of the 2014 IEEE 11th International Conference on Ubiquitous Intelligence and Computing and 2014 IEEE 11th International Conference on Autonomic and Trusted Computing and 2014 IEEE 14th International Conference on Scalable Computing and Communications and Its Associated Workshops, Bali, Indonesia, 9–12 December 2014; pp. 268–275. [Google Scholar] [CrossRef]
- Blair, A.; Brown, T.; Chugg, K.M.; Halford, T.R.; Johnson, M. Barrage relay networks for cooperative transport in tactical MANETs. In Proceedings of the MILCOM 2008—2008 IEEE Military Communications Conference, San Diego, CA, USA, 16–19 November 2008; pp. 1–7. [Google Scholar] [CrossRef]
- Halford, T.R.; Chugg, K.M.; Polydoros, A. Barrage relay networks: System protocol design. In Proceedings of the 21st Annual IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, Istanbul, Turkey, 26–30 September 2010; pp. 1133–1138. [Google Scholar] [CrossRef]
- Narsani, H.K.; Hassan, S.A.; Saleem, S. An Energy-Efficient Approach for Large Scale Opportunistic Networks. In Proceedings of the 2018 IEEE 88th Vehicular Technology Conference (VTC-Fall), Chicago, IL, USA, 27–30 August 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Thanayankizil, L.V.; Kailas, A.; Ingram, M.A. Two Energy-Saving Schemes for Cooperative Transmission with Opportunistic Large Arrays. In Proceedings of the IEEE GLOBECOM 2007—IEEE Global Telecommunications Conference, Washington, DC, USA, 26–30 November 2007; pp. 1038–1042. [Google Scholar] [CrossRef]
- Kailas, A.; Thanayankizil, L.; Ingram, M.A. A simple cooperative transmission protocol for energy-efficient broadcasting over multi-hop wireless networks. J. Commun. Netw. 2008, 10, 213–220. [Google Scholar] [CrossRef]
- Kailas, A.; Ingram, M.A. Alternating Cooperative Transmission for Energy-Efficient Broadcasting. In Proceedings of the IEEE GLOBECOM 2008—2008 IEEE Global Telecommunications Conference, New Orleans, LA, USA, 30 November–4 December 2008; pp. 1–5. [Google Scholar] [CrossRef]
- Kailas, A.; Ingram, M.A. Alternating cooperative transmissions for a strip-shaped sensor network. In Proceedings of the 2010 44th Annual Conference on Information Sciences and Systems (CISS), Princeton, NJ, USA, 17–19 March 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Thanayankizil, L.; Kailas, A.; Ingram, M.A. Opportunistic Large Array Concentric Routing Algorithm (OLACRA) for Upstream Routing in Wireless Sensor Networks. Ad Hoc Netw. 2011, 8, 79–117. [Google Scholar] [CrossRef]
- Thanayankizil, L.V.; Kailas, A.; Ingram, M.A. Energy-Efficient Strategies for Cooperative Communications in Wireless Sensor Networks. In Proceedings of the 2007 International Conference on Sensor Technologies and Applications (SENSORCOMM 2007), Valencia, Spain, 14–20 October 2007; pp. 541–546. [Google Scholar] [CrossRef]
- Yan, H.; Shi, Z.J.; Cui, J.H. DBR: Depth-based routing for underwater sensor networks. In Proceedings of the International Conference on Research in Networking, San Francisco, CA, USA, 14–19 September 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 72–86. [Google Scholar]
- Hwang, D.; Kim, D. DFR: Directional flooding-based routing protocol for underwater sensor networks. In Proceedings of the IEEE OCEANS 2008, Quebec City, QC, Canada, 15–18 September 2008; pp. 1–7. [Google Scholar]
- Jornet, J.M.; Stojanovic, M.; Zorzi, M. Focused Beam Routing Protocol for Underwater Acoustic Networks. In Proceedings of the Third ACM International Workshop on Underwater Networks, San Francisco, CA, USA, 15 September 2008; pp. 75–82. [Google Scholar] [CrossRef]
- Ahmed, S.; Javaid, N.; Khan, F.A.; Durrani, M.Y.; Ali, A.; Shaukat, A.; Sandhu, M.M.; Khan, Z.A.; Qasim, U. Co-UWSN: Cooperative energy-efficient protocol for underwater WSNs. Int. J. Distrib. Sens. Netw. 2015, 11, 891410. [Google Scholar] [CrossRef]
- Nasir, H.; Javaid, N.; Ashraf, H.; Manzoor, S.; Khan, Z.A.; Qasim, U.; Sher, M. CoDBR: Cooperative depth based routing for underwater wireless sensor networks. In Proceedings of the IEEE 2014 Ninth International Conference on Broadband and Wireless Computing, Communication and Applications, Guangdong, China, 8–10 November 2014; pp. 52–57. [Google Scholar]
- Umar, A.; Akbar, M.; Iqbal, Z.; Khan, Z.A.; Qasim, U.; Javaid, N. Cooperative partner nodes selection criteria for cooperative routing in underwater WSNs. In Proceedings of the IEEE 2015 5th National Symposium on Information Technology: Towards New Smart World (NSITNSW), Riyadh, Saudi Arabia, 17–19 February 2015; pp. 1–7. [Google Scholar]
- Jiang, W.; Schotten, H.D. A Simple Cooperative Diversity Method Based on Deep-Learning-Aided Relay Selection. IEEE Trans. Veh. Technol. 2021. [Google Scholar] [CrossRef]
- Jiang, W.; Schotten, H.D. A Deep Learning Method to Predict Fading Channel in Multi-Antenna Systems. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Jiang, W.; Schotten, H.D. Deep Learning for Fading Channel Prediction. IEEE Open J. Commun. Soc. 2020, 1, 320–332. [Google Scholar] [CrossRef]
- Jiang, W.; Schotten, H.D. Predictive Relay Selection: A Cooperative Diversity Scheme Using Deep Learning. In Proceedings of the 2021 IEEE Wireless Communications and Networking Conference (WCNC), Nanjing, China, 29 March–1 April 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Z. Outage Analysis and Learning-Based Relay Selection for Opportunistic Lossy Forwarding Relaying Systems. IEEE Access 2020, 8, 104386–104395. [Google Scholar] [CrossRef]
- Jeong, C.; Son, H. Cooperative Transmission of Energy-Constrained IoT Devices in Wireless-Powered Communication Networks. IEEE Internet Things J. 2021, 8, 3972–3982. [Google Scholar] [CrossRef]
- Shan, F.; Luo, J.; Wu, W.; Dong, F.; Shen, X. Throughput Maximization for the Wireless Powered Communication in Green Cities. IEEE Trans. Ind. Inform. 2018, 14, 2560–2569. [Google Scholar] [CrossRef]
- Kim, S.H.; Park, S.Y.; Choi, K.W.; Lee, T.J.; Kim, D.I. Backscatter-Aided Cooperative Transmission in Wireless-Powered Heterogeneous Networks. IEEE Trans. Wirel. Commun. 2020, 19, 7309–7323. [Google Scholar] [CrossRef]
- Lyu, B.; Hoang, D.T.; Yang, Z. User Cooperation in Wireless-Powered Backscatter Communication Networks. IEEE Wirel. Commun. Lett. 2019, 8, 632–635. [Google Scholar] [CrossRef]
- Chen, W.; Liu, W.; Gao, L.; Gong, S.; Li, C.; Zhu, K. Backscatter-Aided Relay Communications in Wireless Powered Hybrid Radio Networks. In Proceedings of the 2019 IEEE Wireless Communications and Networking Conference (WCNC), Marrakesh, Morocco, 15–18 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Lu, X.; Niyato, D.; Jiang, H.; Hossain, E.; Wang, P. Ambient Backscatter-Assisted Wireless-Powered Relaying. IEEE Trans. Green Commun. Netw. 2019, 3, 1087–1105. [Google Scholar] [CrossRef]
- Mao, Y.; Wu, M. Tracing Malicious Relays in Cooperative Wireless Communications. IEEE Trans. Inf. Forensics Secur. 2007, 2, 198–212. [Google Scholar] [CrossRef]
- Makda, S.; Choudhary, A.; Raman, N.; Korakis, T.; Tao, Z.; Panwar, S. Security Implications of Cooperative Communications in Wireless Networks. In Proceedings of the 2008 IEEE Sarnoff Symposium, Princeton, NJ, USA, 28–30 April 2008; pp. 1–6. [Google Scholar] [CrossRef]


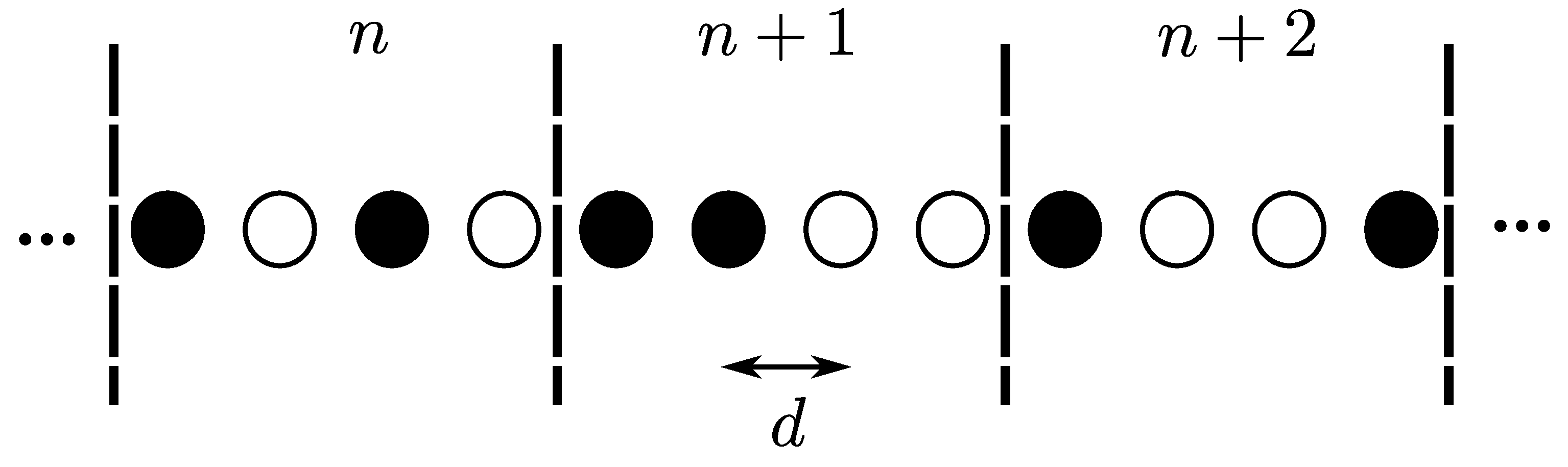
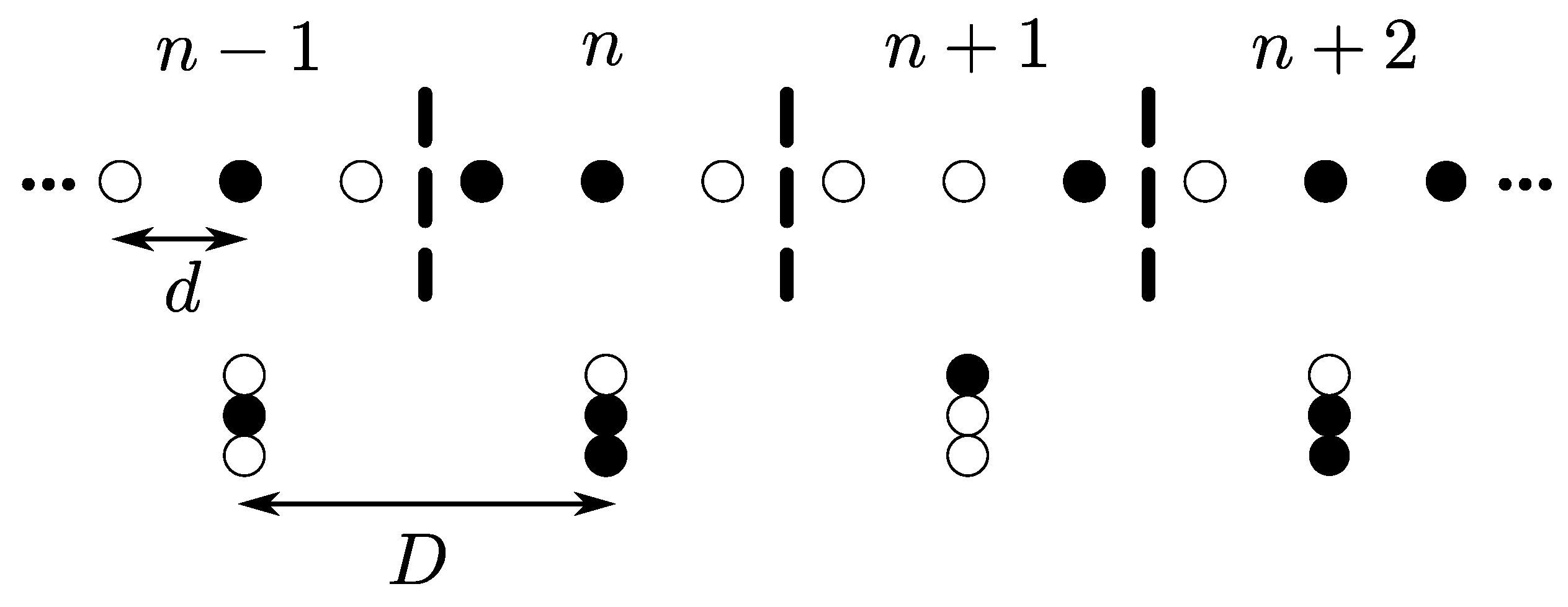

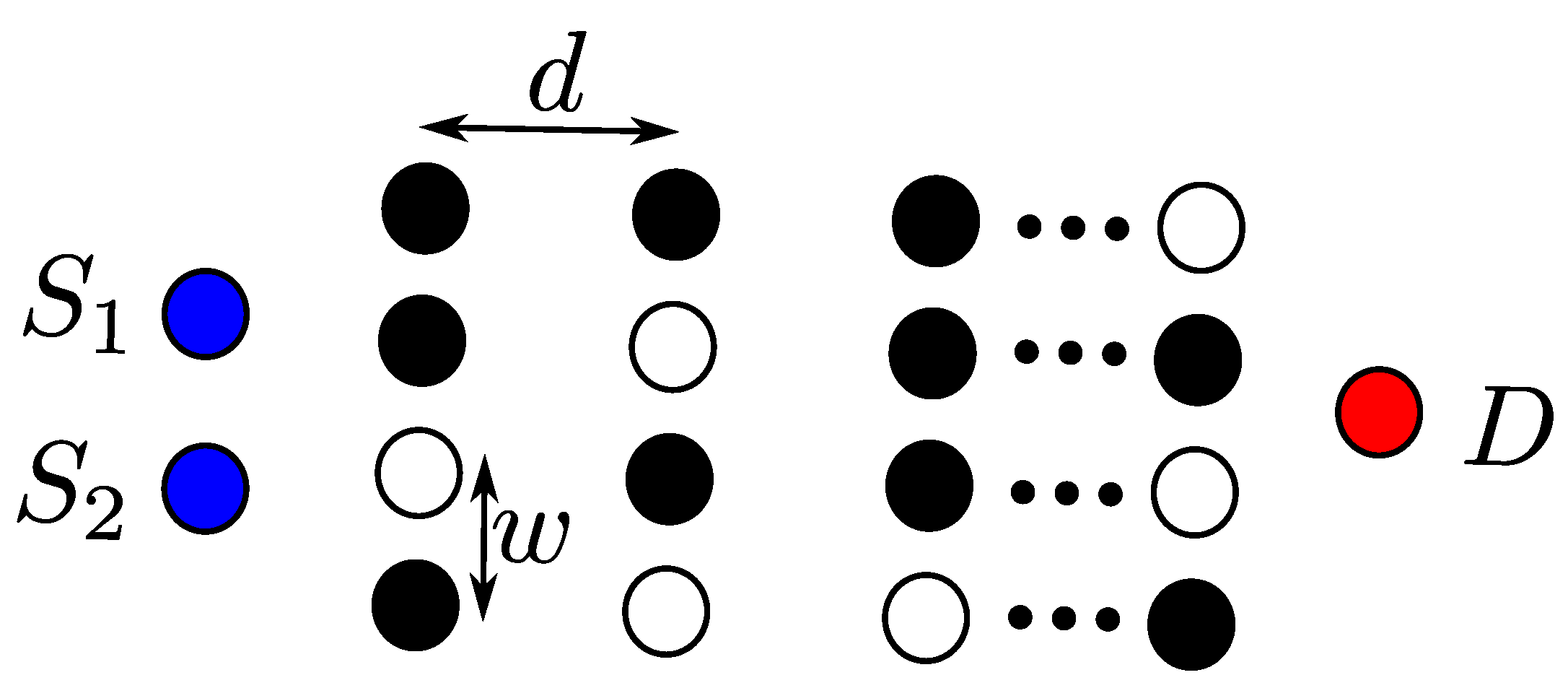
| Reference | Shape | Density | Node Locations | Set Boundary |
|---|---|---|---|---|
| [20] | Strip (2D) | Infinite | Fixed | Deterministic |
| [14] | Disk (2D) | Infinite | Fixed | Deterministic |
| [37] | Linear (1D) | Finite | Fixed | Non-overlapping |
| [39] | Linear (1D) | Finite | Fixed | Overlapping |
| [40] | Linear (1D) | Finite | Fixed (collocated) | Non-overlapping |
| [41] | Linear (1D) | Finite | Random | Overlapping |
| [42] | Strip (2D) | Finite | Fixed | Overlapping |
| [43] | Strip (2D) | Finite | Random (fixed number) | Non-overlapping |
| [44] | Strip (2D) | Finite | Random (random number) | Non-overlapping |
| [45] | Strip (2D) | Finite | Random (random number) | Overlapping |
| Reference | Shape | Density | Node Locations | Set Boundary | Sources |
|---|---|---|---|---|---|
| [19] | Strip (2D) | Infinite | Fixed | Deterministic | 1 |
| [34] | Disk (2D) | Infinite | Fixed | Deterministic | 1 |
| [46] | Linear (1D) | Finite | Fixed | Non-overlapping | 1 |
| [47] | Strip (2D) | Finite | Fixed | Non-overlapping | 1 |
| [48] | Strip (2D) | Finite | Fixed | Non-overlapping | 2 or more |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nawaz, F.; Kumar, H.; Hassan, S.A.; Jung, H. Opportunistic Large Array Propagation Models: A Comprehensive Survey. Sensors 2021, 21, 4206. https://doi.org/10.3390/s21124206
Nawaz F, Kumar H, Hassan SA, Jung H. Opportunistic Large Array Propagation Models: A Comprehensive Survey. Sensors. 2021; 21(12):4206. https://doi.org/10.3390/s21124206
Chicago/Turabian StyleNawaz, Farhan, Hemant Kumar, Syed Ali Hassan, and Haejoon Jung. 2021. "Opportunistic Large Array Propagation Models: A Comprehensive Survey" Sensors 21, no. 12: 4206. https://doi.org/10.3390/s21124206
APA StyleNawaz, F., Kumar, H., Hassan, S. A., & Jung, H. (2021). Opportunistic Large Array Propagation Models: A Comprehensive Survey. Sensors, 21(12), 4206. https://doi.org/10.3390/s21124206








