Adaptive and Robust Operation with Active Fuzzy Harvester under Nonstationary and Random Disturbance Conditions
Abstract
1. Introduction
2. Materials and Methods
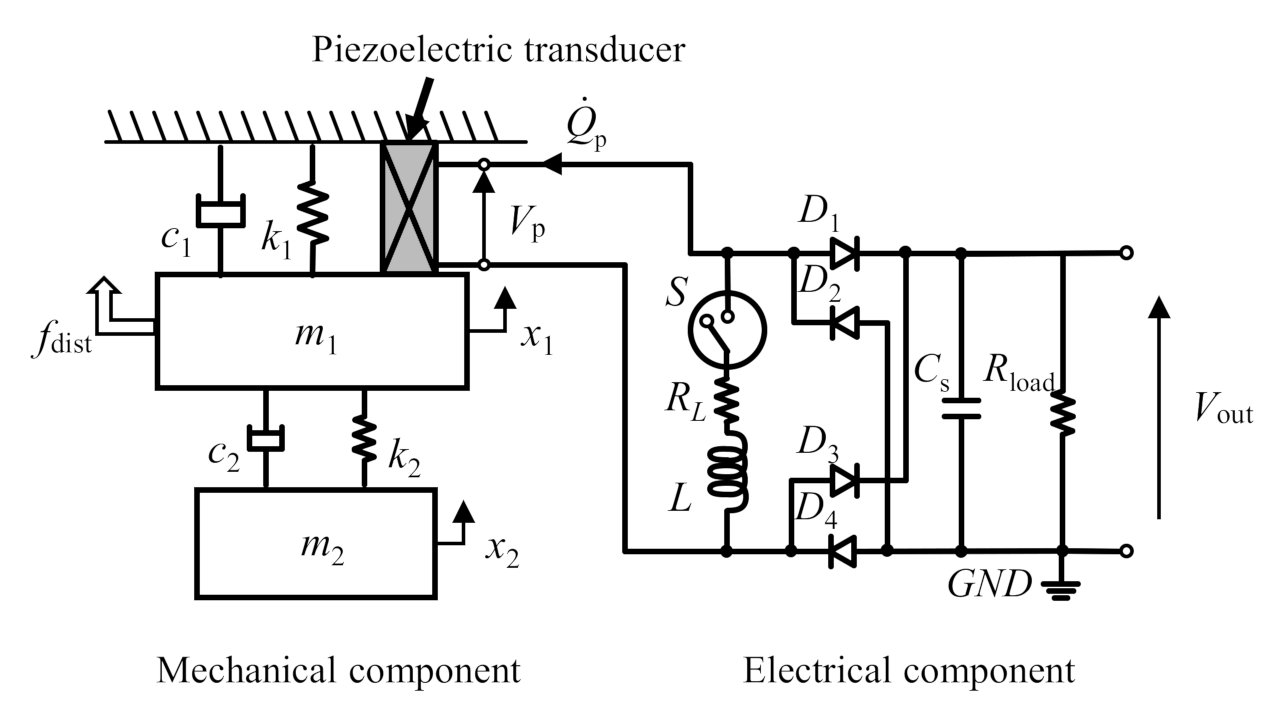
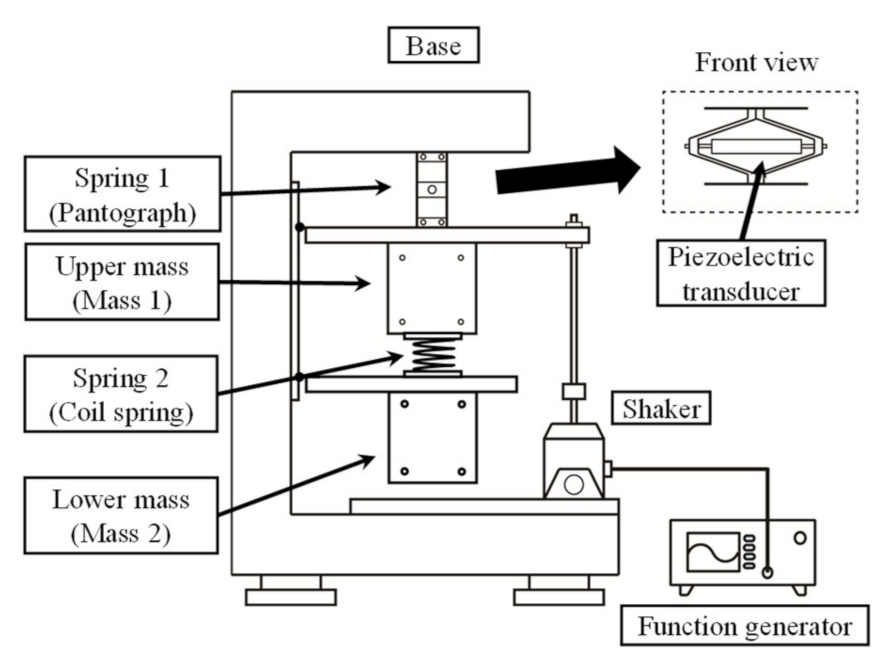
2.1. Harvester Model
- The mechanical components are composed of two masses connected in series by two springs. This system is modeled as a linear 2-DOF structure and has two vibration modes.
- The piezoelectric transducer mechanically deforms only in one direction. Both direct and inverse piezoelectric effects are discussed for a range of small deformations and do not consider hysteresis properties. The transducer is installed between the first vibrating mass and the fixed base. The deformation of the transducer corresponds to the displacement of the first mass.
- The electrical components are modeled using only passive components. Semiconductor elements in the electric circuit are modeled linearly as either open or closed electrical conditions. Because the forward voltage in diode elements is sufficiently small compared to the piezoelectric voltage, the forward voltage of the diodes is neglected.
2.2. Mechanism of Charge Inversion Circuit and Switching Action
- A switching action should be performed when the signs between the displacement and charge are opposite.
- A switching action should be performed when the magnitude of displacement is sufficiently larger than the right term depending on the piezoelectric charge in inequality (6).
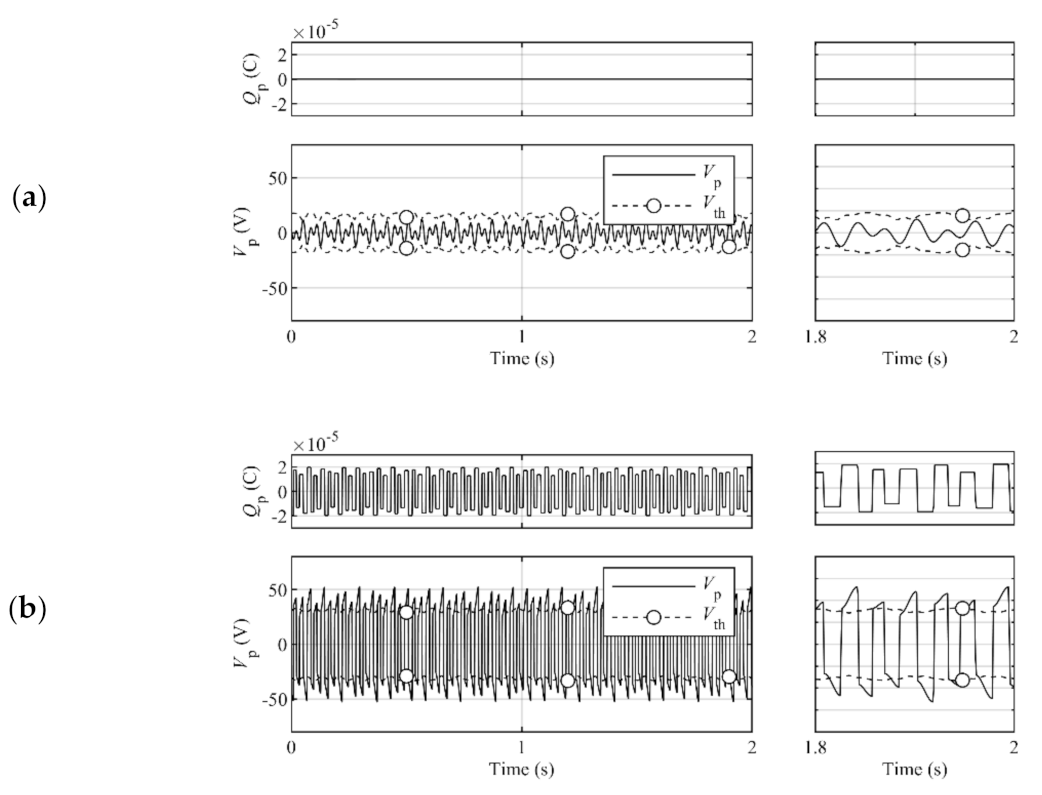
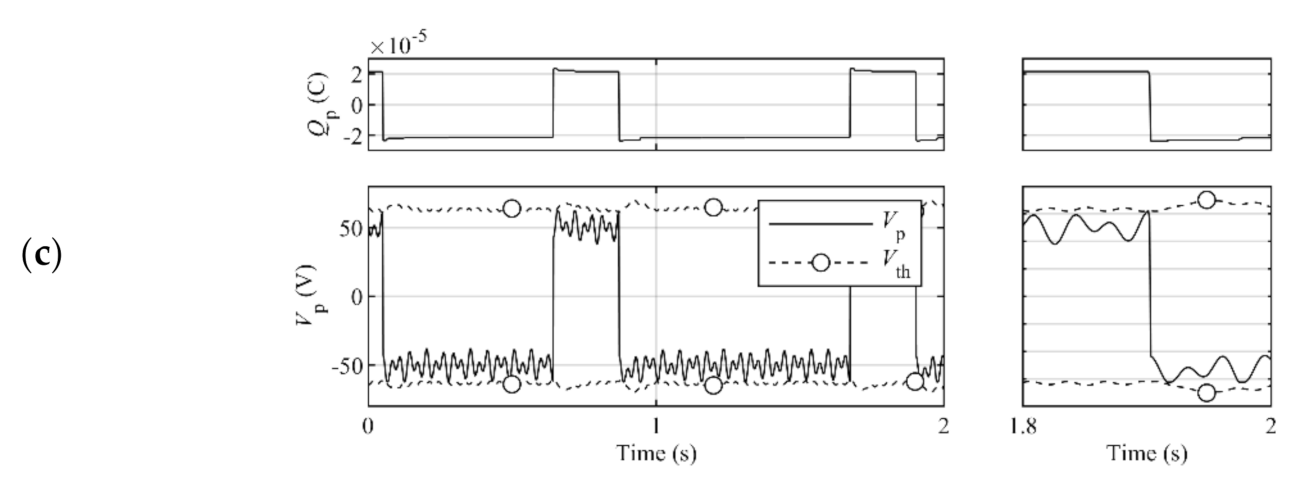
2.3. Threshold-Based Switching Strategy for Complex Vibration
- The STDH control type, which occurs by the exceedingly large threshold coefficient magnitude, does not perform switching actions in the harvesting process. This type relinquishes the opportunities of the increment of the piezoelectric charge by switching actions and should be avoided by decreasing the threshold magnitude.
- The SSHI control type, which occurs because of the exceedingly small threshold coefficient magnitude, performs switching actions, including both desirable and undesirable actions. This type leads to the attenuation of the piezoelectric charge because of the undesirable switching actions and should be avoided by increasing the threshold magnitude.
- The SCVS control type, which occurs because of the adequate threshold coefficient magnitude, accomplishes appropriate intermittent switching actions for effective harvesting. The present threshold design is aimed at this type.
3. Experiment
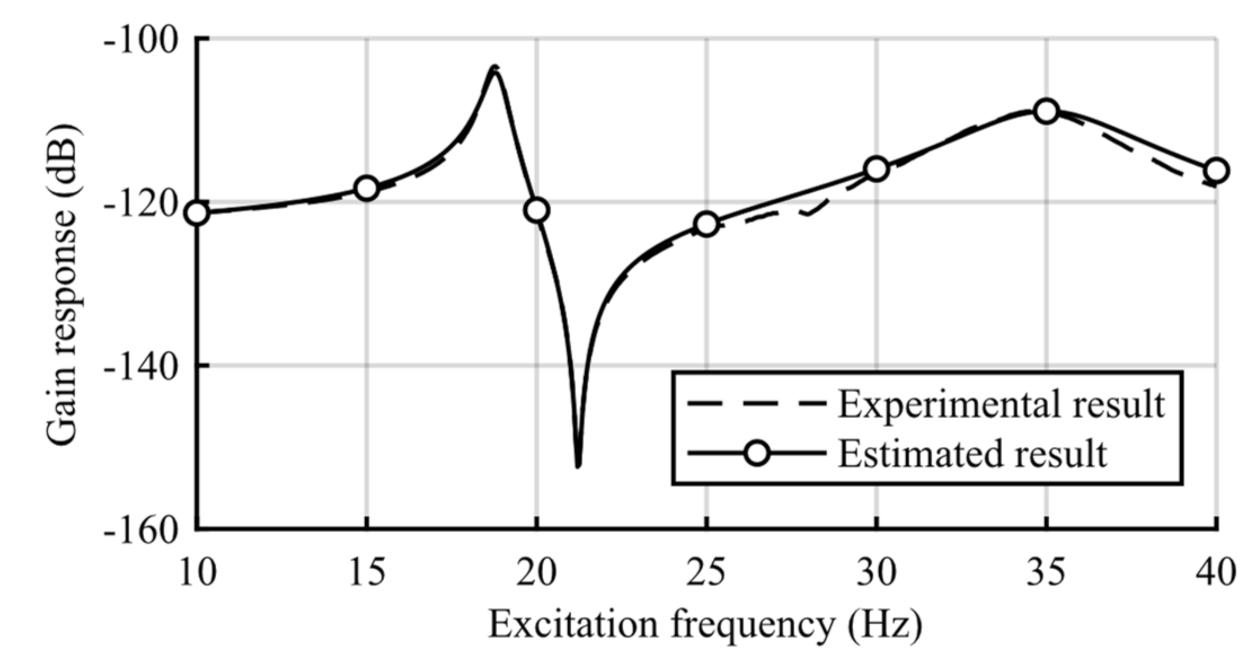
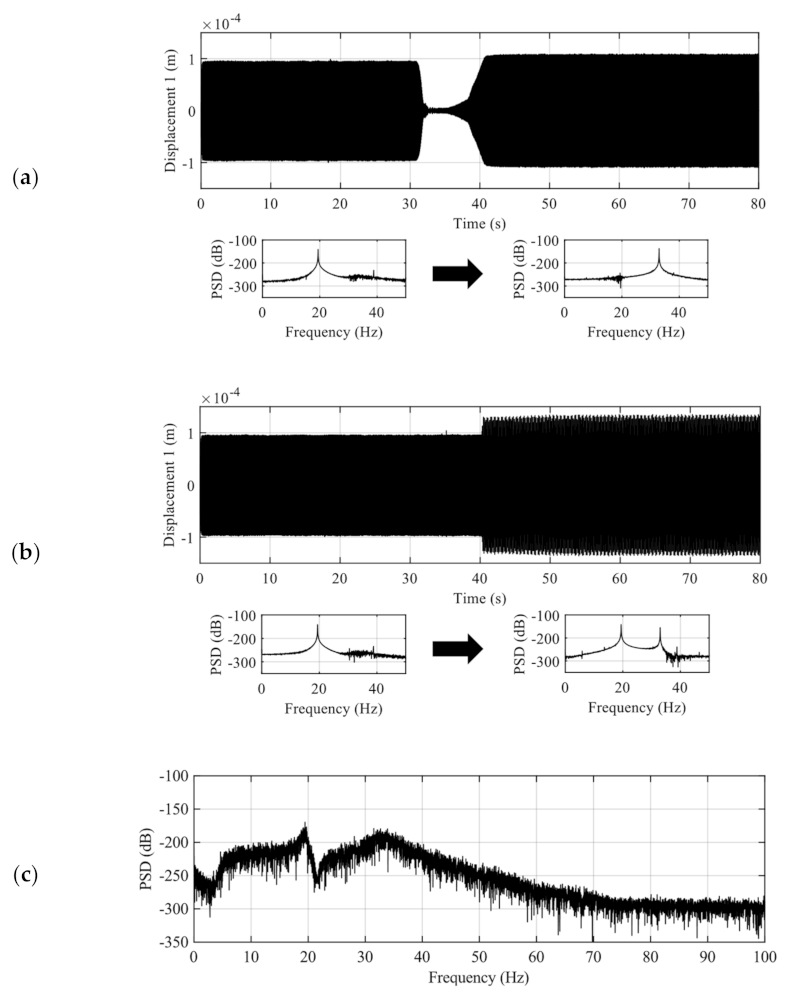
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
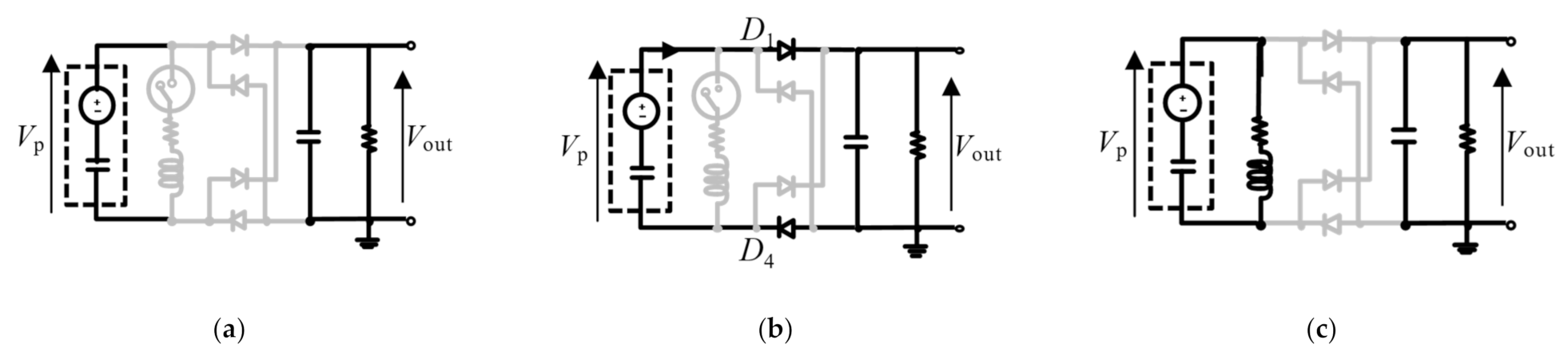
Appendix A
- The first circuit connection indicates that the switch element and rectifier are open and nonconductive. The piezoelectric charge does not change during this process because the piezoelectric transducer is an open circuit. In contrast, the storage charge Qs in the smoothing capacitor is consumed during this process by the resistor assumed as an electric device.
- The second circuit equation indicates that the switch element and the rectifier are open and conductive. The piezoelectric charge stored in the transducer flows out to the smoothing capacitor and the resistor. Because of the rectifies functions, the sign of the circuit equations is changed depending on the polarity of the piezoelectric voltage.
- The third circuit equation, which is a unique connection on an active harvester, is that the switch element and rectifier are closed and nonconductive. The piezoelectric charge vibrates because of the LC series resonance.
References
- Jia, Y.; Li, S.; Shi, Y. An Analytical and Numerical Study of Magnetic Spring Suspension with Energy Recovery Capabilities. Energies 2018, 11, 3126. [Google Scholar] [CrossRef]
- Jia, Y.; Wei, X.; Pu, J.; Xie, P.; Wen, T.; Wang, C.; Lian, P.; Xue, S.; Shi, Y. A Numerical Feasibility Study of Kinetic Energy Harvesting from Lower Limb Prosthetics. Energies 2019, 12, 3824. [Google Scholar] [CrossRef]
- Wen, T.; Ratner, A.; Jia, Y.; Shi, Y. Parametric Study of Environmental Conditions on The Energy Harvesting Efficiency for The Multifunctional Composite Structures. Compos. Struct. 2021, 255, 112979. [Google Scholar] [CrossRef]
- Ye, Z.; Chen, Z. Self-Sensing of Dielectric Elastomer Actuator Enhanced by Artificial Neural Network. Smart Mater. Struct. 2017, 26, 095056. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Y.; Zheng, Y.; Li, Z.; Fan, J.; Wang, L.; Liu, X.; Liu, J.; Shou, W. Enhanced Energy Harvesting Ability of ZnO/PAN Hybrid Piezoelectric Nanogenerators. ACS Appl. Mater. Interfaces 2020, 12, 54936–54945. [Google Scholar] [CrossRef]
- Sugiura, K.; Sawada, R.; Nemoto, Y.; Haraguchi, R.; Asai, T. Wave Flume Testing of an Oscillating-Body Wave Energy Converter with a Tuned Inerter. Appl. Ocean Res. 2020, 98, 102127. [Google Scholar] [CrossRef]
- Haraguchi, R.; Asai, T. Enhanced Power Absorption of a Point Absorber Wave Energy Converter Using a Tuned Inertial mass. Energy 2020, 202, 117740. [Google Scholar] [CrossRef]
- Sebald, G.; Nakano, M.; Lallart, M.; Tian, T.; Diguet, G.; Cavaille, J.-Y. Energy Conversion in Magneto-Rheological Elastomers. Sci. Technol. Adv. Mater. 2017, 18, 766–778. [Google Scholar] [CrossRef]
- Tang, Y.; Khaligh, A. A Multiinput Bridgeless Resonant AC–DC Converter for Electromagnetic Energy Harvesting. IEEE Trans. Power Electron. 2015, 31, 2254–2263. [Google Scholar] [CrossRef]
- Phan, T.N.; Bader, S.; Oelmann, B. Performance of An Electromagnetic Energy Harvester with Linear and Nonlinear Springs under Real Vibrations. Sensors 2020, 20, 5456. [Google Scholar] [CrossRef]
- Asanuma, H.; Oguchi, H.; Hara, M.; Yoshida, R.; Kuwano, H. Ferroelectric Dipole Electrets for Output Power Enhancement in Electrostatic Vibration Energy Harvesters. Appl. Phys. Lett. 2013, 103, 162901. [Google Scholar] [CrossRef]
- Asanuma, H.; Hara, M.; Oguchi, H.; Kuwano, H. Nonlinear Restoring Force of Spring with Stopper for Ferroelectric Dipole Electret-Based Electrostatic Vibration Energy Harvesters. AIP Adv. 2016, 6, 075206. [Google Scholar] [CrossRef]
- Yang, Z.; Onodera, R.; Tayama, T.; Watanabe, M.; Narita, F. Magnetomechanical Design and Power Generation of Magnetostrictive Clad Plate Cantilever. Appl. Phys. Lett. 2019, 115, 243504. [Google Scholar] [CrossRef]
- Kurita, H.; Katabira, K.; Yoshida, Y.; Narita, F. Footstep Energy Harvesting with the Magnetostrictive Fiber Integrated Shoes. Materials 2019, 12, 2055. [Google Scholar] [CrossRef]
- Yang, Z.; Kurita, H.; Onodera, R.; Tayama, T.; Chiba, D.; Narita, F. Evaluation of Vibration Energy Harvesting Using a Magnetostrictive Iron–Cobalt/Nickel-Clad Plate. Smart Mater. Struct. 2018, 28, 034001. [Google Scholar] [CrossRef]
- Quattrocchi, A.; Montanini, R.; De Caro, S.; Panarello, S.; Scimone, T.; Foti, S.; Testa, A. A New Approach for Impedance Tracking of Piezoelectric Vibration Energy Harvesters Based on a Zeta Converter. Sensors 2020, 20, 5862. [Google Scholar] [CrossRef]
- IEEE. IEEE Standard on Piezoelectricity. In ANSI/IEEE Std 176-1987; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 1988. [Google Scholar]
- Wang, Z.; Kurita, H.; Nagaoka, H.; Narita, F. Potassium Sodium Niobate Lead-Free Piezoelectric Nanocomposite Generators Based on Carbon-Fiber-Reinforced Polymer Electrodes for Energy-Harvesting Structures. Compos. Sci. Technol. 2020, 199, 108331. [Google Scholar] [CrossRef]
- Rantz, R.; Roundy, S. Characterization of Real-world Vibration Sources and Application to Nonlinear Vibration Energy Harvesters. Energy Harvest. Syst. 2017, 4, 67–76. [Google Scholar] [CrossRef]
- Wang, J.; Sun, S.; Tang, L.; Hu, G.; Liang, J. On the Use of Metasurface for Vortex-Induced Vibration Suppression or Energy Harvesting. Energy Convers. Manag. 2021, 235, 113991. [Google Scholar] [CrossRef]
- Stamatellou, A.-M.; Kalfas, A. Piezoelectric Energy Harvesting Experiments under Combined Aerodynamic and Base Excitation. J. Intell. Mater. Syst. Struct. 2021, 32, 169–181. [Google Scholar] [CrossRef]
- Brenes, A.; Morel, A.; Juillard, J.; Lefeuvre, E.; Badel, A. Maximum Power Point of Piezoelectric Energy Harvesters: A Review of Optimality Condition for Electrical Tuning. Smart Mater. Struct. 2019, 29, 033001. [Google Scholar] [CrossRef]
- Richard, C.; Guyomar, D.; Audigier, D.; Bassaler, H. Enhanced Semi-Passive Damping Using Continuous Switching of a Piezoelectric Device on an Inductor. In Proceedings of the SPIE’s 7th Annual International Symposium on Smart Structures and Materials, Newport Beach, CA, USA, 6–9 March 2000; Volume 3989, pp. 288–300. [Google Scholar] [CrossRef]
- Bagheri, S.; Wu, N.; Filizadeh, S. Numerical Modeling and Analysis of Self-Powered Synchronous Switching Circuit for the Study of Transient Charging Behavior of a Vibration Energy Harvester. Smart Mater. Struct. 2019, 28, 105056. [Google Scholar] [CrossRef]
- Makihara, K.; Onoda, J.; Minesugi, K. Comprehensive Assessment of Semi-Active Vibration Suppression Including Energy Analysis. J. Vib. Acoust. 2006, 129, 84–93. [Google Scholar] [CrossRef]
- Viant, J.-N.; Quiquerez, L.; Lombard, P.; Lu, G.-N. An ASIC-Based Vibration Damping System. IEEE/ASME Trans. Mechatronics 2011, 18, 148–154. [Google Scholar] [CrossRef]
- Bao, B.; Guyomar, D.; Lallart, M. Vibration Reduction for Smart Periodic Structures via Periodic Piezoelectric Arrays with Nonlinear Interleaved-Switched Electronic Networks. Mech. Syst. Signal Process. 2017, 82, 230–259. [Google Scholar] [CrossRef]
- Chérif, A.; Richard, C.; Guyomar, D.; Belkhiat, S.; Meddad, M. Simulation of Multimodal Vibration Damping of a Plate Structure Using a Modal SSDI-Max Technique. J. Intell. Mater. Syst. Struct. 2012, 23, 675–689. [Google Scholar] [CrossRef]
- Asanuma, H. Selecting Nonlinear Piezoelectricity for Fully Autonomous Self-Sensing Synchronized Switch Damping on Inductor Technique. Mech. Syst. Signal Process. 2021, 159, 107846. [Google Scholar] [CrossRef]
- Zhang, F.; Li, L.; Fan, Y.; Liu, J. Dual-Connected Synchronized Switch Damping for Vibration Control of Bladed Disks in Aero-Engines. Appl. Sci. 2020, 10, 1478. [Google Scholar] [CrossRef]
- Kelley, C.R.; Kauffman, J.L. Adaptive Synchronized Switch Damping on an Inductor: A Self-Tuning Switching Law. Smart Mater. Struct. 2016, 26, 035032. [Google Scholar] [CrossRef]
- Ji, H.; Qiu, J.; Xia, P.; Guyomar, D. The Influence of Switching Phase and Frequency of Voltage on the Vibration Damping Effect in a Piezoelectric Actuator. Smart Mater. Struct. 2010, 20, 015008. [Google Scholar] [CrossRef]
- Guyomar, D.; Badel, A.; Lefeuvre, E.; Richard, C. Toward Energy Harvesting Using Active Materials and Conversion Improvement by Nonlinear Processing. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2005, 52, 584–595. [Google Scholar] [CrossRef]
- Hara, Y.; Saito, K.; Makihara, K. Compact, Digital and Self-Powered Piezoelectric Vibration Energy Harvester with Generation Control Using Voltage Measurement Circuit. Sens. Actuators A Phys. 2019, 299, 111609. [Google Scholar] [CrossRef]
- Hara, Y.; Yamamoto, Y.; Makihara, K. Self-Sensing State Estimation of Switch-Controlled Energy Harvesters. J. Intell. Mater. Syst. Struct. 2020, 31, 2326–2341. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Yoshimizu, K.; Makihara, K. Synthetic Assessment of Self-Powered Energy-Harvesting Including Robustness Evaluation. Mech. Eng. J. 2015, 2, 14. [Google Scholar] [CrossRef]
- Yoshimizu, K.; Yamamoto, Y.; Asahina, K.; Makihara, K. Strategy for Enhancing the Active Harvesting of Piezoelectric Energy. J. Intell. Mater. Syst. Struct. 2017, 28, 1059–1070. [Google Scholar] [CrossRef]
- Makihara, K.; Asahina, K. Analog Self-Powered Harvester Achieving Switching Pause Control to Increase Harvested Energy. Smart Mater. Struct. 2017, 26, 055007. [Google Scholar] [CrossRef]
- Liu, H.; Liang, J.; Ge, C. A Mechatronic Power Boosting Design for Piezoelectric Generators. Appl. Phys. Lett. 2015, 107, 141902. [Google Scholar] [CrossRef]
- Liu, W.; Qin, G.; Zhu, Q.; Hu, G. Synchronous Extraction Circuit with Self-Adaptive Peak-Detection Mechanical Switches Design for Piezoelectric Energy Harvesting. Appl. Energy 2018, 230, 1292–1303. [Google Scholar] [CrossRef]
- Liu, W.; Qin, G.; Zhu, Q.; Hu, G. Self-Adaptive Memory Foam Switches for Piezoelectric Synchronous Harvesting Circuits. Smart Mater. Struct. 2018, 27, 117003. [Google Scholar] [CrossRef]
- Giusa, F.; Giuffrida, A.; Trigona, C.; Andò, B.; Bulsara, A.R.; Baglio, S. “Random Mechanical Switching Harvesting on Inductor”: A Novel Approach to Collect and Store Energy from Weak Random Vibrations with Zero Voltage Threshold. Sens. Actuators A Phys. 2013, 198, 35–45. [Google Scholar] [CrossRef]
- Asanuma, H.; Sakamoto, K.; Komatsuzaki, T.; Iwata, Y. Comparative Study of Electrical and Switch-Skipping Mechanical Switch for Self-Powered SSHI in Medium Coupled Piezoelectric Vibration Energy Harvesters. Smart Mater. Struct. 2018, 27, 075025. [Google Scholar] [CrossRef]
- Lallart, M. Nonlinear Technique and Self-Powered Circuit for Efficient Piezoelectric Energy Harvesting under Unloaded Cases. Energy Convers. Manag. 2017, 133, 444–457. [Google Scholar] [CrossRef]
- Yoon, H.; Kim, M.; Park, C.-S.; Youn, B.D. Time-Varying Output Performances of Piezoelectric Vibration Energy Harvesting under Nonstationary Random Vibrations. Smart Mater. Struct. 2018, 27, 015004. [Google Scholar] [CrossRef]
- Adhikari, S.; Rastogi, A.; Bhattacharya, B. Piezoelectric Vortex Induced Vibration Energy Harvesting in a Random Flow Field. Smart Mater. Struct. 2019, 29, 035034. [Google Scholar] [CrossRef]
- Wang, Z.; Narita, F. Fabrication of Potassium Sodium Niobate Nano-Particle/Polymer Composites with Piezoelectric Stability and Their Application to Unsteady Wind Energy Harvesters. J. Appl. Phys. 2019, 126, 224501. [Google Scholar] [CrossRef]
- Zhao, D.; Li, H. Shaking Table Tests and Analyses of Semi-Active Fuzzy Control for Structural Seismic Reduction with a Piezoelectric Variable-Friction Damper. Smart Mater. Struct. 2010, 19, 105031. [Google Scholar] [CrossRef]
- Hara, Y.; Zhou, M.; Li, A.; Otsuka, K.; Makihara, K. Piezoelectric Energy Enhancement Strategy for Active Fuzzy Harvester with Time-Varying and Intermittent Switching. Smart Mater. Struct. 2021, 30, 015038. [Google Scholar] [CrossRef]
- Drezet, C.; Kacem, N.; Bouhaddi, N. Design of a Nonlinear Energy Harvester Based on High Static Low Dynamic Stiffness for Low Frequency Random Vibrations. Sens. Actuators A Phys. 2018, 283, 54–64. [Google Scholar] [CrossRef]
- Aridogan, U.; Basdogan, I.; Erturk, A. Random Vibration Energy Harvesting on Thin Plates using Multiple Piezopatches. J. Intell. Mater. Syst. Struct. 2016, 27, 2744–2756. [Google Scholar] [CrossRef]
- Tan, T.; Yan, Z.; Zou, Y.; Zhang, W. Optimal Dual-Functional Design for a Piezoelectric Autoparametric Vibration Absorber. Mech. Syst. Signal Process. 2019, 123, 513–532. [Google Scholar] [CrossRef]
- Aramaki, M.; Yoshimura, T.; Murakami, S.; Kanda, K.; Fujimura, N. Electromechanical Characteristics of Piezoelectric Vibration Energy Harvester with 2-Degree-of-Freedom System. Appl. Phys. Lett. 2019, 114, 133902. [Google Scholar] [CrossRef]
- Aldraihem, O.; Baz, A. Energy Harvester with a Dynamic Magnifier. J. Intell. Mater. Syst. Struct. 2011, 22, 521–530. [Google Scholar] [CrossRef]
- Mann, B.; Sims, N. Energy Harvesting from the Nonlinear Oscillations of Magnetic Levitation. J. Sound Vib. 2009, 319, 515–530. [Google Scholar] [CrossRef]
- Mann, B.; Owens, B. Investigations of a Nonlinear Energy Harvester with a Bistable Potential Well. J. Sound Vib. 2010, 329, 1215–1226. [Google Scholar] [CrossRef]
- Zergoune, Z.; Kacem, N.; Bouhaddi, N. On the Energy Localization in Weakly Coupled Oscillators for Electromagnetic Vibration Energy Harvesting. Smart Mater. Struct. 2019, 28, 07LT02. [Google Scholar] [CrossRef]
- Aouali, K.; Kacem, N.; Bouhaddi, N.; Mrabet, E.; Haddar, M. Efficient Broadband Vibration Energy Harvesting Based on Tuned Non-Linearity and Energy Localization. Smart Mater. Struct. 2020, 29, 10LT01. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hara, Y.; Otsuka, K.; Makihara, K. Adaptive and Robust Operation with Active Fuzzy Harvester under Nonstationary and Random Disturbance Conditions. Sensors 2021, 21, 3913. https://doi.org/10.3390/s21113913
Hara Y, Otsuka K, Makihara K. Adaptive and Robust Operation with Active Fuzzy Harvester under Nonstationary and Random Disturbance Conditions. Sensors. 2021; 21(11):3913. https://doi.org/10.3390/s21113913
Chicago/Turabian StyleHara, Yushin, Keisuke Otsuka, and Kanjuro Makihara. 2021. "Adaptive and Robust Operation with Active Fuzzy Harvester under Nonstationary and Random Disturbance Conditions" Sensors 21, no. 11: 3913. https://doi.org/10.3390/s21113913
APA StyleHara, Y., Otsuka, K., & Makihara, K. (2021). Adaptive and Robust Operation with Active Fuzzy Harvester under Nonstationary and Random Disturbance Conditions. Sensors, 21(11), 3913. https://doi.org/10.3390/s21113913





