Specific Loss Power of Co/Li/Zn-Mixed Ferrite Powders for Magnetic Hyperthermia
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Structural Properties
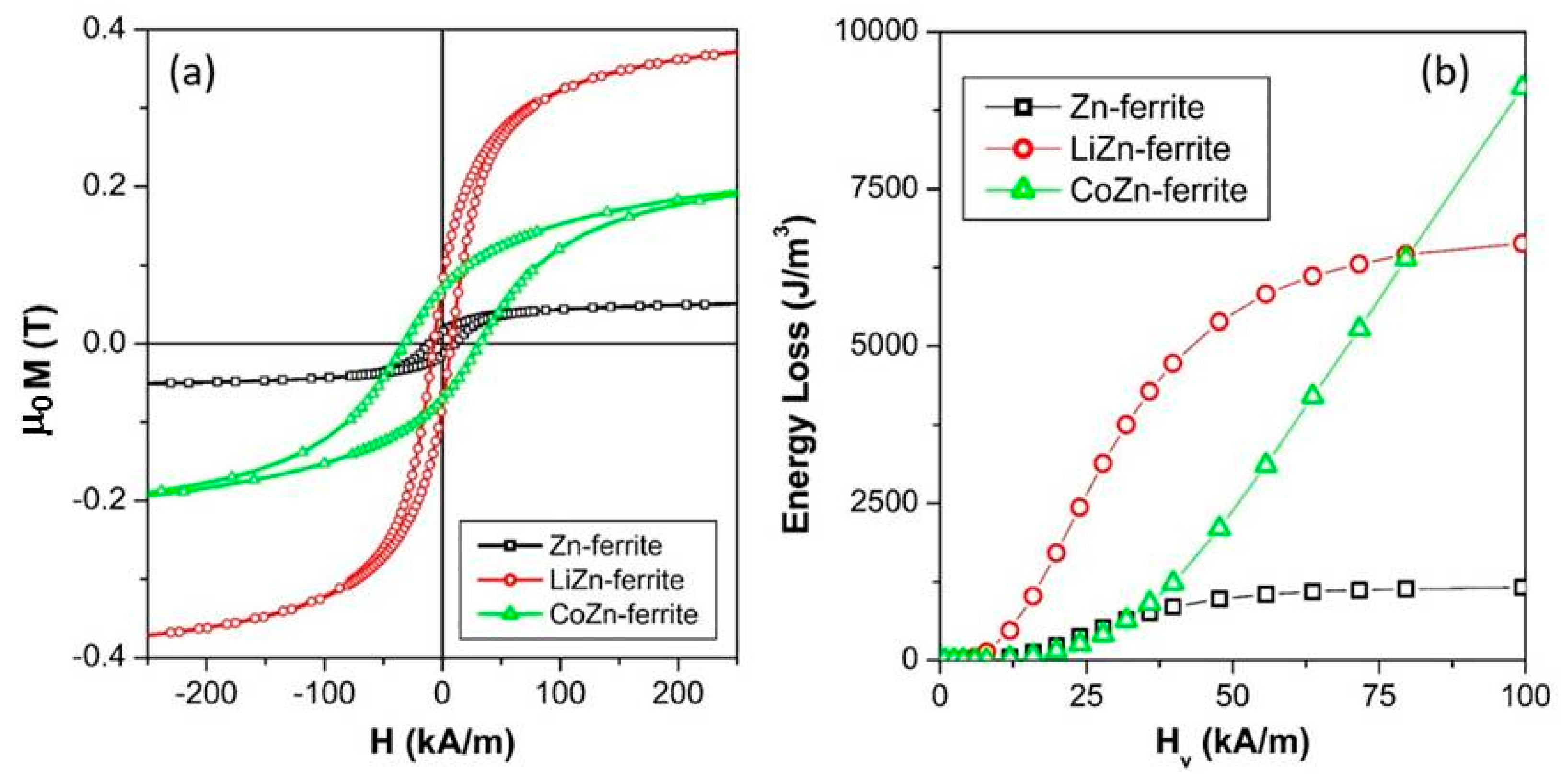
3.2. DC-Magnetic Properties
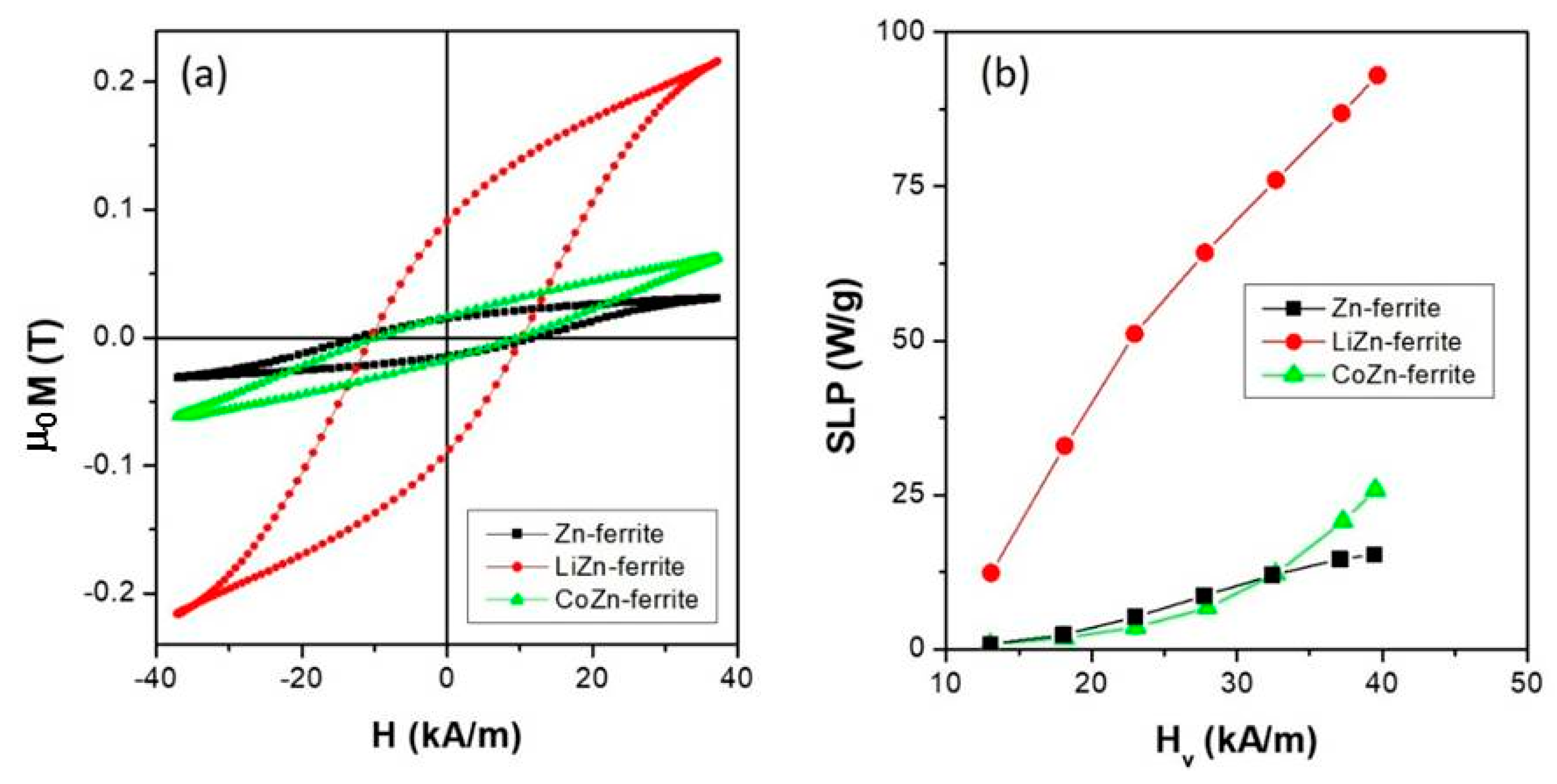
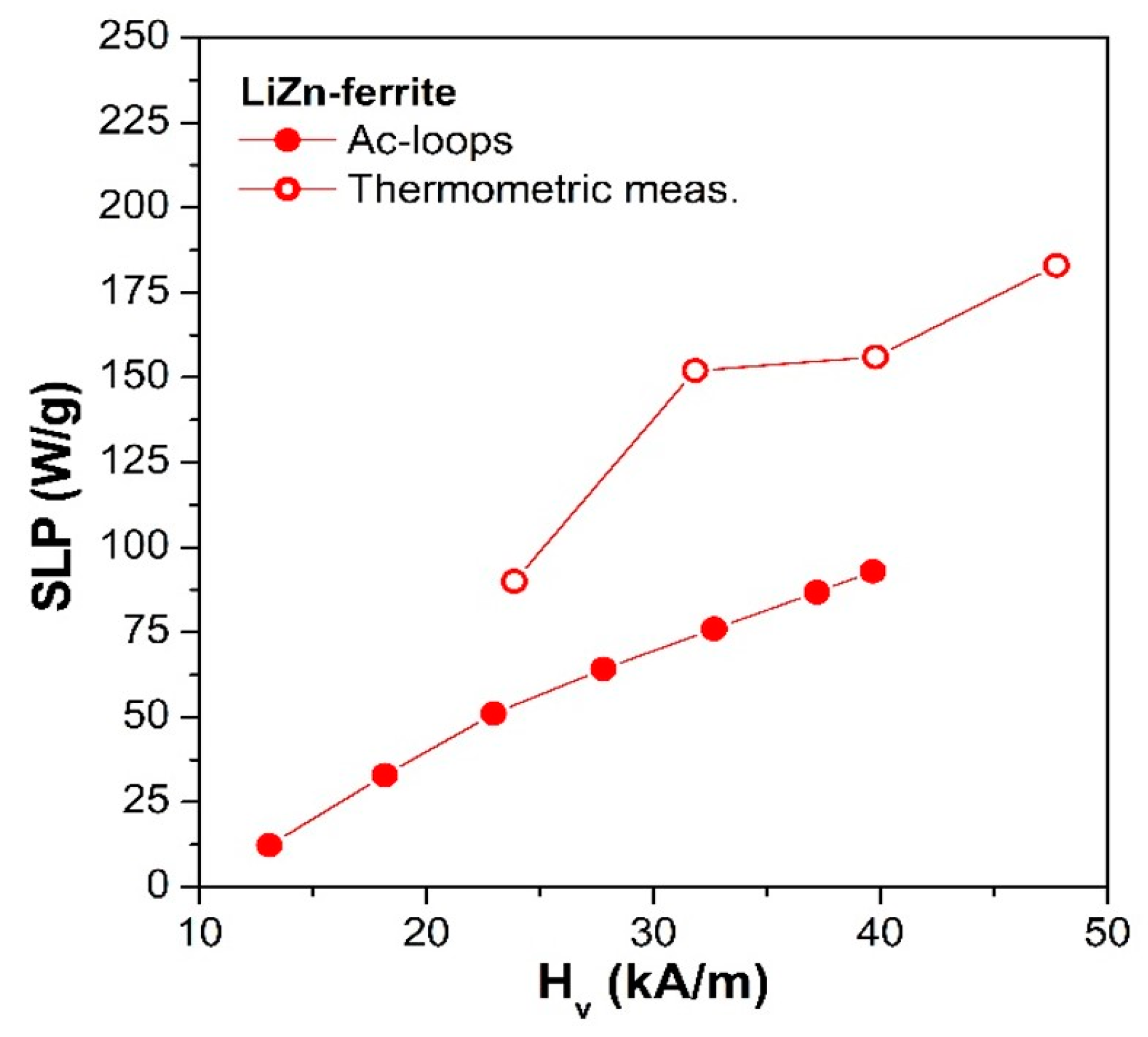
3.3. Ac-Measurements and SLP Evaluation
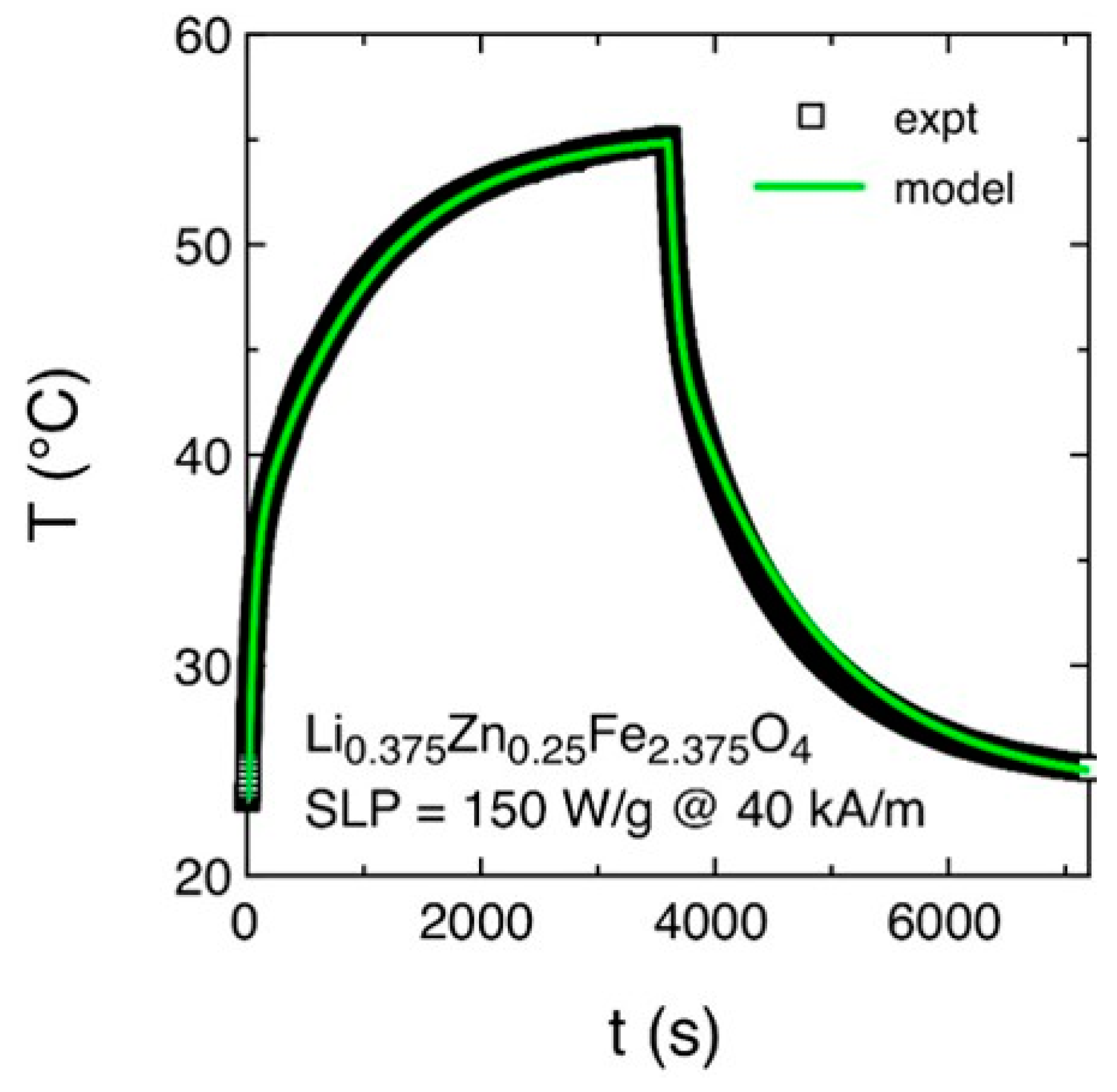
3.4. Thermometric Measurements and SLP Evaluation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Bhushan, B. Springer Handbook of Nanotechnology, 3rd ed.; Bhushan, B., Ed.; Springer: Heidelberg, Germany, 2010; ISBN 978-3-642-02524-2. [Google Scholar]
- Hussein, A.K. Applications of nanotechnology in renewable energies—A comprehensive overview and understanding. Renew. Sustain. Energy Rev. 2014, 42, 460–476. [Google Scholar] [CrossRef]
- Bio-Inspired Nanotechnology; Knecht, M.R., Walsh, T.R., Eds.; Springer: New York, NY, USA, 2014; ISBN 978-1-4614-9445-4. [Google Scholar]
- Sposito, A.J.; Kurdekar, A.; Zhao, J.; Hewlett, I. Application of nanotechnology in biosensors for enhancing pathogen detection. Wiley Interdiscip. Rev. Nanomed. Nanobiotechnol. 2018, 10, e1512. [Google Scholar] [CrossRef] [PubMed]
- Ye, W.; Xu, Y.; Zheng, L.; Zhang, Y.; Yang, M.; Sun, P. A nanoporous alumina membrane based electrochemical biosensor for histamine determination with biofunctionalized magnetic nanoparticles concentration and signal amplification. Sensors 2016, 16, 1767. [Google Scholar] [CrossRef] [PubMed]
- Rocha-Santos, T.A.P. Sensors and biosensors based on magnetic nanoparticles. TrAC Trends Anal. Chem. 2014, 62, 28–36. [Google Scholar] [CrossRef]
- Barrera, G.; Celegato, F.; Coisson, M.; Manzin, A.; Ferrarese Lupi, F.; Seguini, G.; Boarino, L.; Aprile, G.; Perego, M.; Tiberto, P. Magnetization switching in high-density magnetic nanodots by a fine-tune sputtering process on large area diblock copolymer mask. Nanoscale 2017, 9, 16981–16992. [Google Scholar] [CrossRef]
- Sattler, K.D. Handbook of Nanophysics. 3, Nanoparticles and Quantum Dots; CRC Press: Boca Raton, FL, USA, 2011; ISBN 9781420075441. [Google Scholar]
- Zeng, H.; Sun, S. Syntheses, Properties, and Potential Applications of Multicomponent Magnetic Nanoparticles. Adv. Funct. Mater. 2008, 18, 391–400. [Google Scholar] [CrossRef]
- Khanna, L.; Gupta, G.; Tripathi, S.K. Effect of size and silica coating on structural, magnetic as well as cytotoxicity properties of copper ferrite nanoparticles. Mater. Sci. Eng. C 2018, 97, 552–566. [Google Scholar] [CrossRef]
- Sun, C.; Lee, J.S.H.; Zhang, M. Magnetic nanoparticles in MR imaging and drug delivery. Adv. Drug Deliv. Rev. 2008, 60, 1252–1265. [Google Scholar] [CrossRef]
- Hedayatnasab, Z.; Abnisa, F.; Daud, W.M.A.W. Review on magnetic nanoparticles for magnetic nanofluid hyperthermia application. Mater. Des. 2017, 123, 174–196. [Google Scholar] [CrossRef]
- Thanh, N.T.K.T. Magnetic Nanoparticles from Fabrication to Clinical Applications; CRC Press: Boca Raton, FL, USA, 2012; Volume 54, ISBN 9781439869321. [Google Scholar]
- Amiri, M.; Salavati-Niasari, M.; Pardakhty, A.; Ahmadi, M.; Akbari, A. Caffeine: A novel green precursor for synthesis of magnetic CoFe2O4 nanoparticles and pH-sensitive magnetic alginate beads for drug delivery. Mater. Sci. Eng. C 2017, 76, 1085–1093. [Google Scholar] [CrossRef]
- Maksoud, M.I.A.A.; El-sayyad, G.S.; Ashour, A.H.; El-batal, A.I.; Abd-elmonem, M.S.; Hendawy, H.A.M.; Abdel-khalek, E.K.; Labib, S.; Abdeltwab, E.; El-okr, M.M. Synthesis and characterization of metals-substituted cobalt ferrite as antimicrobial agents and sensors for Anagrelide determination in biological samples. Mater. Sci. Eng. C 2018, 92, 644–656. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, R.O.; Baldi, G.; Doumett, S.; Garcia-Hevia, L.; Gallo, J.; Bañobre-López, M.; Dražić, G.; Calhelha, R.C.; Ferreira, I.C.F.R.; Lima, R.; et al. Multifunctional graphene-based magnetic nanocarriers for combined hyperthermia and dual stimuli-responsive drug delivery. Mater. Sci. Eng. C 2018, 93, 206–217. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Liu, X.; Liang, Q.; Liang, X.J.; Tian, J. Optimization and Design of Magnetic Ferrite Nanoparticles with Uniform Tumor Distribution for Highly Sensitive MRI/MPI Performance and Improved Magnetic Hyperthermia Therapy. Nano Lett. 2019, 19, 3618–3626. [Google Scholar] [CrossRef] [PubMed]
- Koh, I.; Josephson, L. Magnetic Nanoparticle Sensors. Sensors 2009, 9, 8130–8145. [Google Scholar] [CrossRef] [PubMed]
- Jaufenthaler, A.; Schier, P.; Middelmann, T.; Liebl, M.; Wiekhorst, F.; Baumgarten, D. Quantitative 2D magnetorelaxometry imaging of magnetic nanoparticles using optically pumped magnetometers. Sensors 2020, 20, 753. [Google Scholar] [CrossRef] [PubMed]
- Chieh, J.J.; Wei, W.C.; Liao, S.H.; Chen, H.H.; Lee, Y.F.; Lin, F.C.; Chiang, M.H.; Chiu, M.J.; Horng, H.E.; Yang, S.Y. Eight-channel AC magnetosusceptometer of magnetic nanoparticles for high-throughput and ultra-high-sensitivity immunoassay. Sensors 2018, 18, 1043. [Google Scholar] [CrossRef]
- Périgo, E.A.; Hemery, G.; Sandre, O.; Ortega, D.; Garaio, E.; Plazaola, F.; Teran, F.J. Fundamentals and advances in magnetic hyperthermia. Appl. Phys. Rev. 2015, 2, 041302. [Google Scholar] [CrossRef]
- Patil, R.M.; Thorat, N.D.; Shete, P.B.; Otari, S.V.; Tiwale, B.M.; Pawar, S.H. In vitro hyperthermia with improved colloidal stability and enhanced SAR of magnetic core/shell nanostructures. Mater. Sci. Eng. C 2016, 59, 702–709. [Google Scholar] [CrossRef]
- Aquino, V.R.R.; Vinícius-Araújo, M.; Shrivastava, N.; Sousa, M.H.; Coaquira, J.A.H.; Bakuzis, A.F. Role of the Fraction of Blocked Nanoparticles on the Hyperthermia Efficiency of Mn-Based Ferrites at Clinically Relevant Conditions. J. Phys. Chem. C 2019, 123, 27725–27734. [Google Scholar] [CrossRef]
- Maldonado-Camargo, L.; Torres-Díaz, I.; Chiu-Lam, A.; Hernández, M.; Rinaldi, C. Estimating the contribution of Brownian and Néel relaxation in a magnetic fluid through dynamic magnetic susceptibility measurements. J. Magn. Magn. Mater. 2016, 412, 223–233. [Google Scholar] [CrossRef]
- Nemati, Z.; Alonso, J.; Rodrigo, I.; Das, R.; Garaio, E.; García, J.Á.; Orue, I.; Phan, M.H.; Srikanth, H. Improving the Heating Efficiency of Iron Oxide Nanoparticles by Tuning Their Shape and Size. J. Phys. Chem. C 2018, 122, 2367–2381. [Google Scholar] [CrossRef]
- Bender, P.; Fock, J.; Frandsen, C.; Hansen, M.F.; Balceris, C.; Ludwig, F.; Posth, O.; Wetterskog, E.; Bogart, L.K.; Southern, P.; et al. Relating Magnetic Properties and High Hyperthermia Performance of Iron Oxide Nanoflowers. J. Phys. Chem. C 2018, 122, 3068–3077. [Google Scholar] [CrossRef]
- Atkinson, W.; Brezovich, I.; Chakraborty, D.P. Usable Frequencies in Hyperthermia with Thermal Seeds. IEEE Trans. Biomed. Eng. 1984, 31, 70–75. [Google Scholar] [CrossRef] [PubMed]
- Hergt, R.; Dutz, S. Magnetic particle hyperthermia—Biophysical limitations of a visionary tumour therapy. J. Magn. Magn. Mater. 2007, 311, 187–192. [Google Scholar] [CrossRef]
- Shaterabadi, Z.; Nabiyouni, G.; Soleymani, M. Physics responsible for heating efficiency and self-controlled temperature rise of magnetic nanoparticles in magnetic hyperthermia therapy. Prog. Biophys. Mol. Biol. 2018, 133, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Reddy, L.H.; Arias, J.L.; Nicolas, J.; Couvreur, P. Magnetic Nanoparticles: Design and Characterization, Toxicity and Biocompatibility, Pharmaceutical and Biomedical Applications. Chem. Rev. 2012, 112, 5818–5878. [Google Scholar] [CrossRef]
- Blanco-Andujar, C.; Walter, A.; Cotin, G.; Bordeianu, C.; Mertz, D.; Felder-Flesch, D.; Begin-Colin, S. Design of iron oxide-based nanoparticles for MRI and magnetic hyperthermia. Nanomedicine 2016, 11, 1889–1910. [Google Scholar] [CrossRef]
- Seehra, M. Magnetic Spinels: Synthesis, Properties and Applications; IntechOpen: London, UK, 2017. [Google Scholar]
- Smit, J.; Wijn, H.P.J. Ferrites; Cleaver-Hume Press Ltd: London, UK, 1959. [Google Scholar]
- He, S.; Zhang, H.; Liu, Y.; Sun, F.; Yu, X.; Li, X.; Zhang, L.; Wang, L.; Mao, K.; Wang, G.; et al. Maximizing Specific Loss Power for Magnetic Hyperthermia by Hard–Soft Mixed Ferrites. Small 2018, 14, 1800135. [Google Scholar] [CrossRef]
- Pilati, V.; Cabreira Gomes, R.; Gomide, G.; Coppola, P.; Silva, F.G.; Paula, F.L.O.; Perzynski, R.; Goya, G.F.; Aquino, R.; Depeyrot, J. Core/Shell Nanoparticles of Non-Stoichiometric Zn-Mn and Zn-Co Ferrites as Thermosensitive Heat Sources for Magnetic Fluid Hyperthermia. J. Phys. Chem. C 2018, 122, 3028–3038. [Google Scholar] [CrossRef]
- Sharifi Dehsari, H.; Asadi, K. Impact of Stoichiometry and Size on the Magnetic Properties of Cobalt Ferrite Nanoparticles. J. Phys. Chem. C 2018, 122, 29106–29121. [Google Scholar] [CrossRef]
- Demirci Dönmez, C.E.; Manna, P.K.; Nickel, R.; Aktürk, S.; Van Lierop, J. Comparative Heating Efficiency of Cobalt-, Manganese-, and Nickel-Ferrite Nanoparticles for a Hyperthermia Agent in Biomedicines. ACS Appl. Mater. Interfaces 2019, 11, 6858–6866. [Google Scholar] [CrossRef]
- Albino, M.; Fantechi, E.; Innocenti, C.; López-Ortega, A.; Bonanni, V.; Campo, G.; Pineider, F.; Gurioli, M.; Arosio, P.; Orlando, T.; et al. Role of Zn2+ Substitution on the Magnetic, Hyperthermic, and Relaxometric Properties of Cobalt Ferrite Nanoparticles. J. Phys. Chem. C 2019, 123, 6148–6157. [Google Scholar] [CrossRef]
- Amiri, S.; Shokrollahi, H. The role of cobalt ferrite magnetic nanoparticles in medical science. Mater. Sci. Eng. C 2013, 33, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Fantechi, E.; Innocenti, C.; Albino, M.; Lottini, E.; Sangregorio, C. Influence of cobalt doping on the hyperthermic efficiency of magnetite nanoparticles. J. Magn. Magn. Mater. 2015, 380, 365–371. [Google Scholar] [CrossRef]
- Joshi, H.M.; Lin, Y.P.; Aslam, M.; Prasad, P.V.; Schultz-Sikma, E.A.; Edelman, R.; Meade, T.; Dravid, V.P. Effects of shape and size of cobalt ferrite nanostructures on their MRI contrast and thermal activation. J. Phys. Chem. C 2009, 113, 17761–17767. [Google Scholar] [CrossRef]
- Mallick, A.; Mahapatra, A.S.; Mitra, A.; Greneche, J.M.; Ningthoujam, R.S.; Chakrabarti, P.K. Magnetic properties and bio-medical applications in hyperthermia of lithium zinc ferrite nanoparticles integrated with reduced graphene oxide. J. Appl. Phys. 2018, 123, 055103. [Google Scholar] [CrossRef]
- Lithium and Cell Physiology; Bach, P.O., Gallicchio, V.S., Eds.; Springer: New York, NY, USA, 1990; ISBN 978-1-4612-7967-9. [Google Scholar]
- Barrera, G.; Coisson, M.; Celegato, F.; Raghuvanshi, S.; Mazaleyrat, F.; Kane, S.N.; Tiberto, P. Cation distribution effect on static and dynamic magnetic properties of Co1-xZnxFe2O4ferrite powders. J. Magn. Magn. Mater. 2018, 456, 372–380. [Google Scholar] [CrossRef]
- Chakrabarty, S.; Dutta, A.; Pal, M. Enhanced magnetic properties of doped cobalt ferrite nanoparticles by virtue of cation distribution. J. Alloys Compd. 2015, 625, 216–223. [Google Scholar] [CrossRef]
- Mohamed, M.B.; Yehia, M. Cation distribution and magnetic properties of nanocrystalline gallium substituted cobalt ferrite. J. Alloys Compd. 2014, 615, 181–187. [Google Scholar] [CrossRef]
- Thanh, N.K.; Loan, T.T.; Duong, N.P.; Anh, L.N.; Nguyet, D.T.T.; Nam, N.H.; Soontaranon, S.; Klysubun, W.; Hien, T.D. Cation Distribution Assisted Tuning of Magnetization in Nanosized Magnesium Ferrite. Phys. Status Solidi Appl. Mater. Sci. 2018, 215, 1700397. [Google Scholar] [CrossRef]
- Tomitaka, A.; Hirukawa, A.; Yamada, T.; Morishita, S.; Takemura, Y. Biocompatibility of various ferrite nanoparticles evaluated by in vitro cytotoxicity assays using HeLa cells. J. Magn. Magn. Mater. 2009, 321, 1482–1484. [Google Scholar] [CrossRef]
- Oliveira, A.B.B.; De Moraes, F.R.; Candido, N.M.; Sampaio, I.; Paula, A.S.; De Vasconcellos, A.; Silva, T.C.; Miller, A.H.; Rahal, P.; Nery, J.G.; et al. Metabolic Effects of Cobalt Ferrite Nanoparticles on Cervical Carcinoma Cells and Nontumorigenic Keratinocytes. J. Proteome Res. 2016, 15, 4337–4348. [Google Scholar] [CrossRef] [PubMed]
- Giri, J.; Pradhan, P.; Somani, V.; Chelawat, H.; Chhatre, S.; Banerjee, R.; Bahadur, D. Synthesis and characterizations of water-based ferrofluids of substituted ferrites [Fe1−xBxFe2O4, B = Mn, Co (x = 0–1)] for biomedical applications. J. Magn. Magn. Mater. 2008, 320, 724–730. [Google Scholar] [CrossRef]
- Amiri, M.; Salavati-Niasari, M.; Akbari, A. Magnetic nanocarriers: Evolution of spinel ferrites for medical applications. Adv. Colloid Interface Sci. 2019, 265, 29–44. [Google Scholar] [CrossRef] [PubMed]
- Raghuvanshi, S.; Mazaleyrat, F.; Kane, S.N. Mg1-xZnxFe2O4nanoparticles: Interplay between cation distribution and magnetic properties. AIP Adv. 2018, 8, 047804. [Google Scholar] [CrossRef]
- Patton, C.E.; Edmondson, C.A.; Liu, Y.H. Magnetic properties of lithium zinc ferrite. J. Appl. Phys. 1982, 53, 2431–2433. [Google Scholar] [CrossRef]
- Lutterotti, L.; Scardi, P. Simultaneous structure and size-strain refinement by the Rietveld method. J. Appl. Crystallogr. 1990, 23, 246–252. [Google Scholar] [CrossRef]
- Weil, L.; Bertaut, F.; Bochirol, L.; Weil, L.; Bertaut, F.; Propri, L.B. Propriétés magnétiques et structure de la phase quadratique du ferrite de cuivre. J.Phys. Radium 1950, 11, 208–212. [Google Scholar] [CrossRef]
- Tanna, A.R.; Joshi, H.H. Computer Aided X-Ray Diffraction Intensity Analysis for Spinels: Hands-On Computing Experience. Int. J. Phys. Math. Sci. 2013, 7, 334–340. [Google Scholar]
- Wolska, E.; Riedel, E.; Wolski, W. The Evidence of Cd2+xFe1−x3+[Ni1−x2+Fe1+x3+]O4 Cation Distribution Based on X-Ray and Mössbauer Data. Phys. Status Solidi 1992, 132, K51–K56. [Google Scholar] [CrossRef]
- Červinka, L.; Šimša, Z. Distribution of copper ions in some copper-manganese ferrites. Czechoslov. J. Phys. 1970, 20, 470–474. [Google Scholar] [CrossRef]
- Cullity, B.D.; Graham, C.D. Introduction to Magnetic Materials; John Wiley & Sons: Hoboken, NJ, USA, 2009; ISBN 9780471477419. [Google Scholar]
- Coïsson, M.; Barrera, G.; Celegato, F.; Martino, L.; Kane, S.N.; Raghuvanshi, S.; Vinai, F.; Tiberto, P. Hysteresis losses and specific absorption rate measurements in magnetic nanoparticles for hyperthermia applications. Biochim. Biophys. Acta Gen. Subj. 2017, 1861, 1545–1558. [Google Scholar] [CrossRef] [PubMed]
- Kurlyandskaya, G.V.; Litvinova, L.S.; Safronov, A.P.; Schupletsova, V.V.; Tyukova, I.S.; Khaziakhmatova, O.G.; Slepchenko, G.B.; Yurova, K.A.; Cherempey, E.G.; Kulesh, N.A.; et al. Water-Based suspensions of iron oxide nanoparticles with electrostatic or steric stabilization by chitosan: Fabrication, characterization and biocompatibility. Sensors 2017, 17, 2605. [Google Scholar] [CrossRef] [PubMed]
- Ranjith Kumar, E.; Jayaprakash, R.; Kumar, S. The role of annealing temperature and bio template (egg white) on the structural, morphological and magnetic properties of manganese substituted MFe2O4(M = Zn, Cu, Ni, Co) nanoparticles. J. Magn. Magn. Mater. 2014, 351, 70–75. [Google Scholar] [CrossRef]
- Jadhav, S.A. Magnetic properties of Zn-substituted Li-Cu ferrites. J. Magn. Magn. Mater. 2001, 224, 167–172. [Google Scholar] [CrossRef]
- Patil, R.S.; Kakatkar, S.V.; Patil, S.A.; Sankpal, A.M.; Sawant, S.R. X-Ray and bulk magnetic studies on Li0.5ZnxTixFe2.5−2xO4. Mater. Chem. Phys. 1991, 28, 355–365. [Google Scholar] [CrossRef]
- Gore, S.K.; Jadhav, S.S.; Jadhav, V.V.; Patange, S.M.; Naushad, M.; Mane, R.S.; Kim, K.H. The structural and magnetic properties of dual phase cobalt ferrite. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef]
- Denton, A.R.; Ashcroft, N.W. Vegard’s law. Phys. Rev. A 1991, 43, 3161–3164. [Google Scholar] [CrossRef]
- Satalkar, M.; Kane, S.N.; Ghosh, A.; Ghodke, N.; Barrera, G.; Celegato, F.; Coisson, M.; Tiberto, P.; Vinai, F. Synthesis and soft magnetic properties of Zn0.8−xNixMg0.1Cu0.1Fe2O4 (x = 0.0–0.8) ferrites prepared by sol-gel auto-combustion method. J. Alloys Compd. 2015, 615, S313–S316. [Google Scholar] [CrossRef]
- Rathod, V.; Anupama, A.V.; Jali, V.M.; Hiremath, V.A.; Sahoo, B. Combustion synthesis, structure and magnetic properties of Li-Zn ferrite ceramic powders. Ceram. Int. 2017, 43, 14431–14440. [Google Scholar] [CrossRef]
- Patterson, A.L. The Scherrer Formula for X-Ray Particle Size Determination. Phys. Rev. 1939, 56, 978. [Google Scholar] [CrossRef]
- Randhawa, B.S.; Dosanjh, H.S.; Kumar, N. Synthesis of lithium ferrite by precursor and combustion methods: A comparative study. J. Radioanal. Nucl. Chem. 2007, 274, 581–591. [Google Scholar] [CrossRef]
- Murugesan, C.; Perumal, M.; Chandrasekaran, G. Structural, dielectric and magnetic properties of cobalt ferrite prepared using auto combustion and ceramic route. Phys. B Condens. Matter 2014, 448, 53–56. [Google Scholar] [CrossRef]
- Rathod, V.; Anupama, A.V.; Kumar, R.V.; Jali, V.M.; Sahoo, B. Correlated vibrations of the tetrahedral and octahedral complexes and splitting of the absorption bands in FTIR spectra of Li-Zn ferrites. Vib. Spectrosc. 2017, 92, 267–272. [Google Scholar] [CrossRef]
- Mathew, D.S.; Juang, R.S. An overview of the structure and magnetism of spinel ferrite nanoparticles and their synthesis in microemulsions. Chem. Eng. J. 2007, 129, 51–65. [Google Scholar] [CrossRef]
- Coey, J.M.D. Magnetism and Magnetic Materials; Cambridge University Press: Cambridge, UK, 2009; ISBN 9780521816144. [Google Scholar]
- Tachiki, M. Origin of the Magnetic Anisotropy Energy of Cobalt Ferrite. Prog. Theor. Phys. 1960, 23, 1055–1072. [Google Scholar] [CrossRef]
- Fairweather, A.; Roberts, F.F.; Welch, A.J.E. Ferrites. Reports Prog. Phys. 1952, 15, 306. [Google Scholar] [CrossRef]
- Murthy, N.S.S.; Natera, M.G.; Youssef, S.I.; Begum, R.J.; Srivastava, C.M. Yafet-kittel angles in zinc-nickel ferrites. Phys. Rev. 1969, 181, 969–977. [Google Scholar] [CrossRef]
- El-Sayed, H.M.; Ali, I.A.; Azzam, A.; Sattara, A.A. Influence of the magnetic dead layer thickness of Mg-Zn ferrites nanoparticle on their magnetic properties. J. Magn. Magn. Mater. 2017, 424, 226–232. [Google Scholar] [CrossRef]
- Sciancalepore, C.; Gualtieri, A.F.; Scardi, P.; Flor, A.; Allia, P.; Tiberto, P.; Barrera, G.; Messori, M.; Bondioli, F. Structural characterization and functional correlation of Fe3O4 nanocrystals obtained using 2-ethyl-1,3-hexanediol as innovative reactive solvent in non-hydrolytic sol-gel synthesis. Mater. Chem. Phys. 2018, 207, 337–349. [Google Scholar] [CrossRef]
- Reilly, J.P. Principles of Nerve and Heart Excitation by Time-varying Magnetic Fields. Ann. N. Y. Acad. Sci. 1992, 649, 96–117. [Google Scholar] [CrossRef] [PubMed]
- Oleson, J.R.; Cetas, T.C.; Corry, P.M. Hyperthermia by Magnetic Induction: Experimental and Theoretical Results for Coaxial Coil Pairs. Radiat. Res. 1983, 95, 175. [Google Scholar] [CrossRef] [PubMed]
- Beola, L.; Gutiérrez, L.; Grazú, V.; Asín, L. A Roadmap to the Standardization of In Vivo Magnetic Hyperthermia. Nanomater. Magn. Opt. Hyperth. Appl. 2019, 317–337. [Google Scholar]
- Garaio, E.; Sandre, O.; Collantes, J.M.; Garcia, J.A.; Mornet, S.; Plazaola, F. Specific absorption rate dependence on temperature in magnetic field hyperthermia measured by dynamic hysteresis losses (ac magnetometry). Nanotechnology 2015, 26, 015704. [Google Scholar] [CrossRef]
- Garaio, E.; Collantes, J.M.; Garcia, J.A.; Plazaola, F.; Mornet, S.; Couillaud, F.; Sandre, O. A wide-frequency range AC magnetometer to measure the specific absorption rate in nanoparticles for magnetic hyperthermia. J. Magn. Magn. Mater. 2014, 368, 432–437. [Google Scholar] [CrossRef]
- Guibert, C.; Fresnais, J.; Peyre, V.; Dupuis, V. Magnetic fluid hyperthermia probed by both calorimetric and dynamic hysteresis measurements. J. Magn. Magn. Mater. 2017, 421, 384–392. [Google Scholar] [CrossRef]
- O’Connell, J. Heating water: Rate correction due to Newtonian cooling. Phys. Teach. 1999, 37, 551–552. [Google Scholar] [CrossRef][Green Version]
- Dutz, S.; Hergt, R. Magnetic particle hyperthermia—A promising tumour therapy? Nanotechnology 2014, 25, 452001. [Google Scholar] [CrossRef]
- Ota, S.; Takemura, Y. Characterization of Néel and Brownian Relaxations Isolated from Complex Dynamics Influenced by Dipole Interactions in Magnetic Nanoparticles. J. Phys. Chem. C 2019, 123, 28859–28866. [Google Scholar] [CrossRef]
- Soukup, D.; Moise, S.; Céspedes, E.; Dobson, J.; Telling, N.D. In Situ Measurement of Magnetization Relaxation of Internalized Nanoparticles in Live Cells. ACS Nano 2015, 9, 231–240. [Google Scholar] [CrossRef]
- Di Corato, R.; Espinosa, A.; Lartigue, L.; Tharaud, M.; Chat, S.; Pellegrino, T.; Ménager, C.; Gazeau, F.; Wilhelm, C. Magnetic hyperthermia efficiency in the cellular environment fordifferent nanoparticle designs. Biomaterials 2014, 35, 6400–6411. [Google Scholar] [CrossRef] [PubMed]
- Kalambur, V.S.; Han, B.; Hammer, B.E.; Shield, T.W.; Bischof, J.C. In vitro characterization of movement, heating and visualization of magnetic nanoparticles for biomedical applications. Nanotechnology 2005, 16, 1221–1233. [Google Scholar] [CrossRef]
- Coral, D.F.; Mendoza Zélis, P.; Marciello, M.; Morales, M.D.P.; Craievich, A.; Sánchez, F.H.; Fernández Van Raap, M.B. Effect of Nanoclustering and Dipolar Interactions in Heat Generation for Magnetic Hyperthermia. Langmuir 2016, 32, 1201–1213. [Google Scholar] [CrossRef] [PubMed]
- Serantes, D.; Baldomir, D.; Martinez-Boubeta, C.; Simeonidis, K.; Angelakeris, M.; Natividad, E.; Castro, M.; Mediano, A.; Chen, D.X.; Sanchez, A.; et al. Influence of dipolar interactions on hyperthermia properties of ferromagnetic particles. J. Appl. Phys. 2010, 108, 073918. [Google Scholar] [CrossRef]
- Branquinho, L.C.; Carrião, M.S.; Costa, A.S.; Zufelato, N.; Sousa, M.H.; Miotto, R.; Ivkov, R.; Bakuzis, A.F. Effect of magnetic dipolar interactions on nanoparticle heating efficiency: Implications for cancer hyperthermia. Sci. Rep. 2013, 3, 20–22. [Google Scholar] [CrossRef]
- Dalal, M.; Ningthoujam, R.S.; Chakrabarti, P.K. Structural, magnetic, microwave and ac induction heating study of Li0.35Zn0.30Co0.05Fe2.3O4 integrated in multi-walled carbon nanotube matrix. AIP Conf. Proc. 2018, 1942, 3–7. [Google Scholar]
- Wang, L.; Yan, Y.; Wang, M.; Yang, H.; Zhou, Z.; Peng, C.; Yang, S. An integrated nanoplatform for theranostics via multifunctional core-shell ferrite nanocubes. J. Mater. Chem. B 2016, 4, 1908–1914. [Google Scholar] [CrossRef]
- Thorat, N.D.; Bohara, R.A.; Yadav, H.M.; Tofail, S.A.M. Multi-modal MR imaging and magnetic hyperthermia study of Gd doped Fe3O4 nanoparticles for integrative cancer therapy. RSC Adv. 2016, 6, 94967–94975. [Google Scholar] [CrossRef]
- Kim, D.H.; Lee, S.H.; Kim, K.N.; Kim, K.M.; Shim, I.B.; Lee, Y.K. Temperature change of various ferrite particles with alternating magnetic field for hyperthermic application. J. Magn. Magn. Mater. 2005, 293, 320–327. [Google Scholar] [CrossRef]
- Veverka, P.; Pollert, E.; Závěta, K.; Vasseur, S.; Duguet, E. Sr-hexaferrite/maghemite composite nanoparticles—Possible new mediators for magnetic hyperthermia. Nanotechnology 2008, 19, 215705. [Google Scholar] [CrossRef]
- Lee, J.H.; Jang, J.T.; Choi, J.S.; Moon, S.H.; Noh, S.H.; Kim, J.W.; Kim, J.G.; Kim, I.S.; Park, K.I.; Cheon, J. Exchange-coupled magnetic nanoparticles for efficient heat induction. Nat. Nanotechnol. 2011, 6, 418–422. [Google Scholar] [CrossRef] [PubMed]
- Hergt, R.; Hiergeist, R.; Zeisberger, M.; Schüler, D.; Heyen, U.; Hilger, I.; Kaiser, W.A. Magnetic properties of bacterial magnetosomes as potential diagnostic and therapeutic tools. J. Magn. Magn. Mater. 2005, 293, 80–86. [Google Scholar] [CrossRef]

| Sample | aexp (nm) | ρXRD (g/cm3) | <DXRD> (nm) | Cation Distribution |
|---|---|---|---|---|
| Co0.76Zn0.24Fe2O4 | 0.8391 | 5.3 | 32 | (Co0.00Zn0.10Fe0.90) [Co0.76Zn0.14Fe1.10]O4 |
| Li0.375Zn0.25Fe2.375O4 | 0.8365 | 4.9 | 38 | (Li0.05Zn0.10Fe0.85) [Li0.325Zn0.15Fe1.525]O4 |
| ZnFe2O4 | 0.8435 | 5.3 | 35 | (Zn0.09Fe0.91) [Zn0.91Fe1.09]O4 |
| Sample | μ0Ms | Hc | μ0Mr | μ0Msth | Area |
|---|---|---|---|---|---|
| (T) | (kA/m) | (T) | (T) | (J/m3) | |
| Co0.76Zn0.24Fe2O4 | 0.255 | 31.90 | 0.071 | 0.52 | 21709 |
| Li0.375Zn0.25Fe2.375O4 | 0.415 | 7.37 | 0.078 | 0.54 | 7826 |
| ZnFe2O4 | 0.066 | 10.65 | 0.015 | 0.14 | 1467 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barrera, G.; Coisson, M.; Celegato, F.; Martino, L.; Tiwari, P.; Verma, R.; Kane, S.N.; Mazaleyrat, F.; Tiberto, P. Specific Loss Power of Co/Li/Zn-Mixed Ferrite Powders for Magnetic Hyperthermia. Sensors 2020, 20, 2151. https://doi.org/10.3390/s20072151
Barrera G, Coisson M, Celegato F, Martino L, Tiwari P, Verma R, Kane SN, Mazaleyrat F, Tiberto P. Specific Loss Power of Co/Li/Zn-Mixed Ferrite Powders for Magnetic Hyperthermia. Sensors. 2020; 20(7):2151. https://doi.org/10.3390/s20072151
Chicago/Turabian StyleBarrera, Gabriele, Marco Coisson, Federica Celegato, Luca Martino, Priyanka Tiwari, Roshni Verma, Shashank N. Kane, Frédéric Mazaleyrat, and Paola Tiberto. 2020. "Specific Loss Power of Co/Li/Zn-Mixed Ferrite Powders for Magnetic Hyperthermia" Sensors 20, no. 7: 2151. https://doi.org/10.3390/s20072151
APA StyleBarrera, G., Coisson, M., Celegato, F., Martino, L., Tiwari, P., Verma, R., Kane, S. N., Mazaleyrat, F., & Tiberto, P. (2020). Specific Loss Power of Co/Li/Zn-Mixed Ferrite Powders for Magnetic Hyperthermia. Sensors, 20(7), 2151. https://doi.org/10.3390/s20072151






