Blood pressure (BP) always fluctuates due to factors such as stress, exercise, disease, and inherent physiological oscillations [
1]. However, the physiological variance of BP, which can rise up to 20 mmHg, has been neglected so far [
2]. Even though physiological uncertainty is larger than the margin of error of standard BP measurement protocols. The issue of accuracy, precision and uncertainty in the measurement of physiological parameters has been of constant concern for practitioners [
3]. Even though the standard for the expression of uncertainty in measurement [
4] states that it is applicable to a broad span of fields, in practice it has been applied only to measurements determined on the basis of a series of observations obtained under repeatable conditions, a situation which is rarely reproducible in physiological measurements. Recently cuff-less BP devices using the photoplethysmograph (PPG) sensors have recently been used to measure BP [
5,
6,
7]. Kachuee et al. [
5] proposed a method to estimate BP based on the PPG for continuous health-care monitoring. A continuous BP estimation method using machine learning was introduced by Chen et al. [
6]. Tjahjadi et al. [
7] a novel classification method for BP based on PPG signal using long short-term memory (LSTM). However, automated oscillometric blood pressure measurement methods [
8,
9] are more commonly and popularly used to measure BP for many patients at the home, office, and medical centers. These devices usually offer a single BP value. However, these devices are unlikely to provide values that are superior to those that may be obtained by repeated BP measurements [
10]. That is because individual BP measurements are inherently subject to sources of uncertainty sources that cause deviations of the measured value (i.e., estimate) from the true BP value (i.e., reference BP) [
11]. The sources of uncertainty can be separated into random errors and systematic errors [
11], which will be dealt with in more detail in the following section. If BP measurements are simultaneously influenced by many sources of uncertainty, the distribution function of these measurements converges towards Gaussian distribution as the number of uncertainties increases, regardless of the distribution function of parameters representing the source of uncertainty [
11]. Few researchers have tried to study uncertainty in physiological measurements [
12,
13] and there have been no attempts to include the characterization of the quality of the acquired signal and its compatibility with the employed estimation algorithms in a global figure of merit of confidence in the measurement accuracy. Thus, the confidence interval (CI) should be provided in such a way as to assess and express uncertainty in BP measurements where CI provides an estimated range of BP values, which possibly includes significant unknown sources [
11]. Based on some aggregated statistics, wide CIs can provide alerts to patients, medical staff, and families. Thus, measuring the CI of a blood pressure measurement is very important, but unfortunately, there has been very little study done to determine the CI for an oscillometric BP measurement. Indeed, in order to estimate the CI for each patient, we need many BP measurements. However, it is very difficult to measure BP multiple times for each patient using an oscillometry BP device since repeatable circumstances for reproducible BP measurements cannot be guaranteed [
14]. For this reason, it is necessary to calculate CI using a small number of measurements, and as a result, the bootstrap technique was proposed to obtain CI estimates from BP measurements using a small sample size [
14].
Soueidan et al. also proposed a new method to augment the noninvasive measurement by providing the mean systolic blood pressure (SBP) and diastolic blood pressure (DBP) with CIs [
15]. However, these methods did not satisfy the allowable bias specified by the standard protocol [
16]. To address this issue, Lee et al. recently introduced the deep neural network (DNN) estimator [
17] to estimate BP measurements. However, this method has many random and initialized parameters in the training procedure, such as weights and bias, which can cause unstable estimates such as large standard deviations of errors. To address the above challenge, Lee et al. also provided a method to obtain accurate BP estimates using the DNN ensemble estimator [
18]. Here, we introduce a novel methodology using an ensemble-based recursive methodology (EBRM) to measure uncertainty for oscillometric BP measurements. There are three stages to the methodology: the first is pre-learning to initialize good parameters using the bagging technique [
19], where the sample number of artificial features is augmented using the bagging technique to obtain effective ensemble parameters by training each estimator. After that, in the second stage, we fine-tune the parameters using the EBRM that is used to accurately estimate BPs and then measure the uncertainty for the SBP and DBP in the third stage. As far as we know, the proposed method is one of the first studies using the EBRM based on the DNN model to measure the uncertainty for the SBP and DBP. This paper is an expanded version of the paper [
14,
18] with the following contributions:
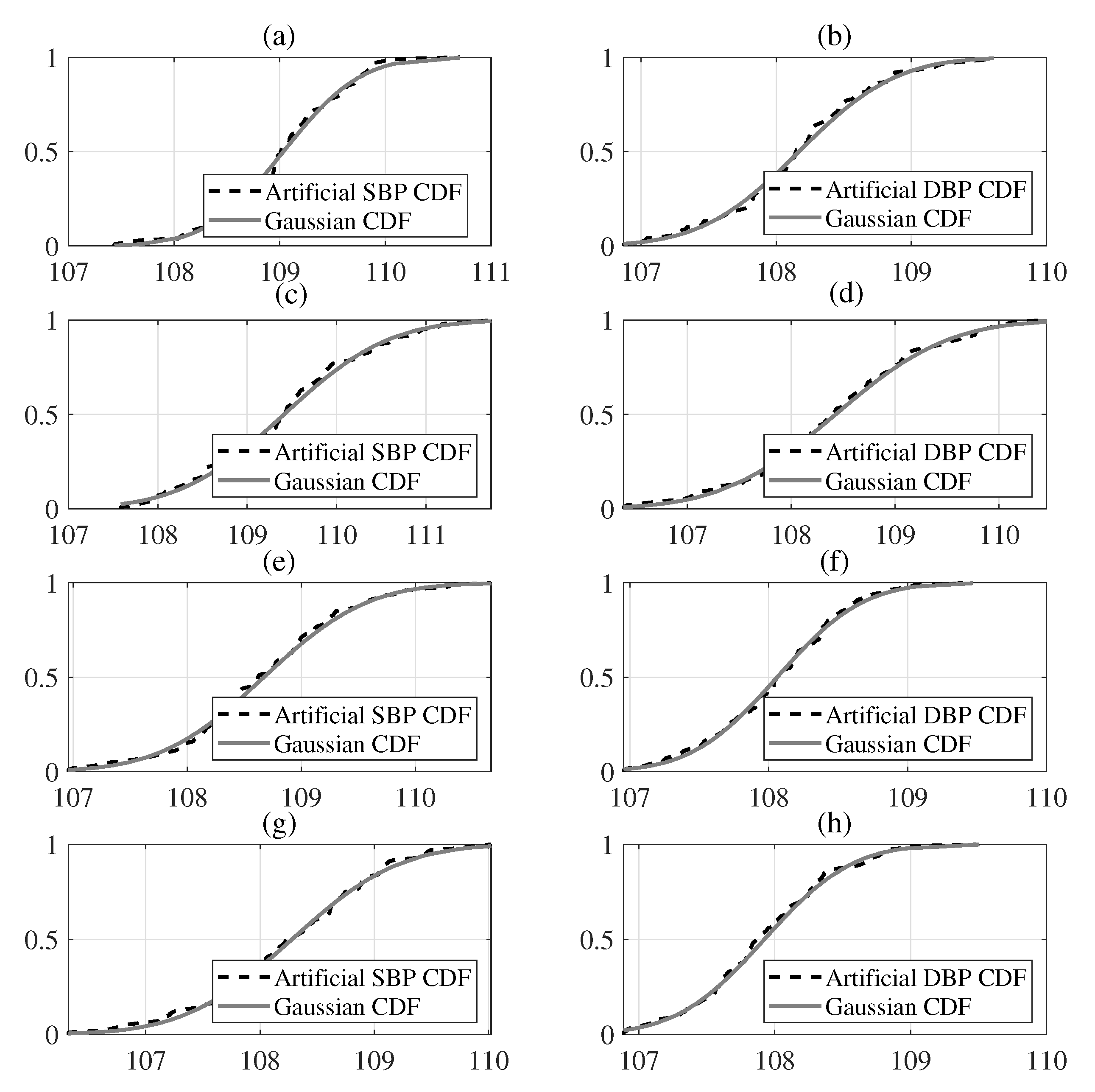
The introduced methodology is expressed as follows. First, we acquire the features from the oscillometric waveform (OMW) signals and envelopes after pre-signal processing on the BP signals. We then create the artificial features from the original features and evaluate the normality of the distribution of all the features. We then constitute the proposed EBRM through the pre-training and a fine-tuning [
17]. Based on the EBRM, we estimate the BP values (SBP and DBP) for the individual subjects. Subsequently, to measure the CIs, standard deviation of error, bias, standard uncertainty, and expanded uncertainty for the SBP and DBP. We then confirm the normality of the artificial BPs for individual subjects.