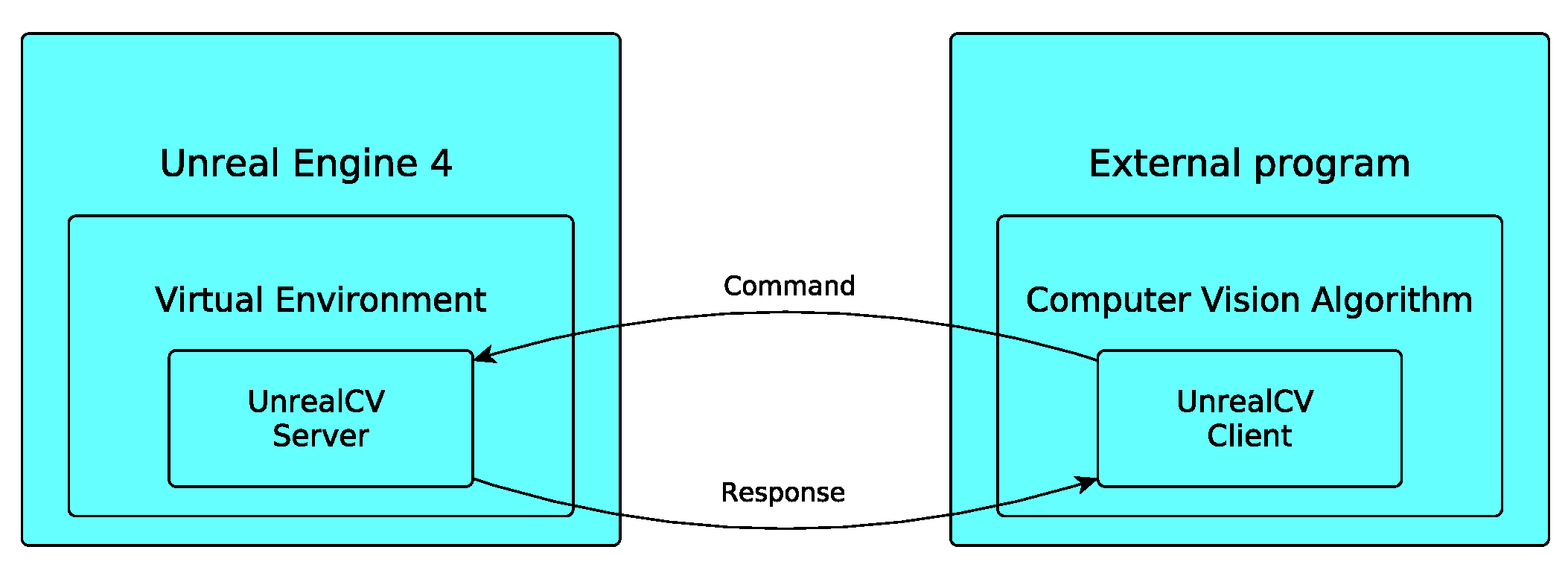
In this section, we introduce the projection models for the different cameras that are implemented in the proposed tool. We are going to explain the relationship between image–plane coordinates and the coordinates of the projection ray in the camera reference. We distinguish two types of camera models: central-projection camera models and non-central-projection camera models. Among the central projection cameras, we consider:
2.2.1. Central-Projection Cameras
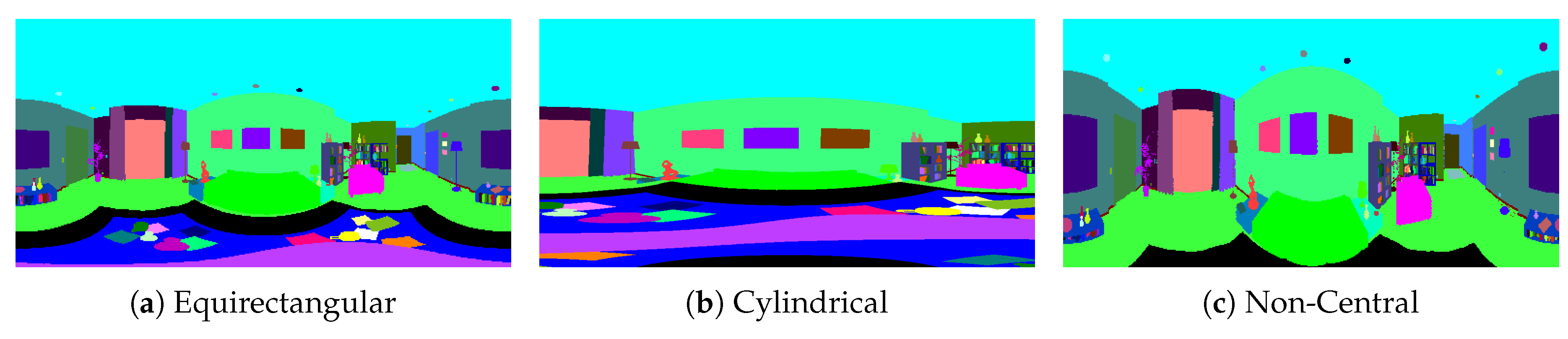
Central-projection cameras are characterized by having a unique optical center. That means that every ray coming from the environment goes through the optical center to the image. Among omnidirectional systems, panoramas are the most used in computer vision. Equirectangular panoramas are 360°-field-of-view images that show the whole environment around the camera. This kind of image is useful to obtain a complete projection of the environment from only one shot. However, this representation presents heavy distortions in the upper and lower part of the image. That is because the equirectangular panorama is based on spherical coordinates. If we take the center of the sphere as the optical center, we can define the ray that comes from the environment in spherical coordinates
. Moreover, since the image plane is an unfolded sphere, each pixel can be represented in the same spherical coordinates, giving a direct relationship between the image plane and the ray that comes from the environment. This relationship is described by:
where
are pixel coordinates and
the maximum value, i.e., the image resolution.
In the case of cylindrical panoramas, the environment is projected into the lateral surface of a cylinder. This panorama does not have a 360° practical field of view, since the perpendicular projection to the lateral surface of the environment cannot be projected. However, we can achieve up to 360° on the horizontal field of view,
, and theoretical 180° on the vertical field of view,
, that usually is reduced from 90° to 150° for real applications. We can describe the relationship between the ray that comes from the environment and the image plane as:
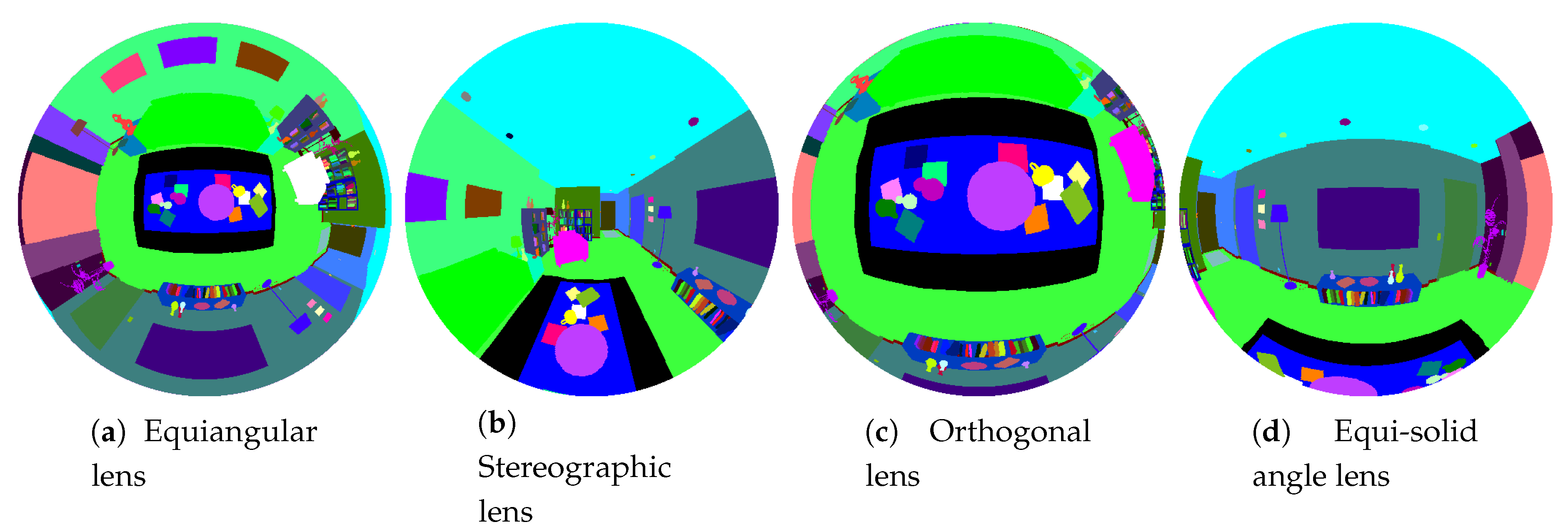
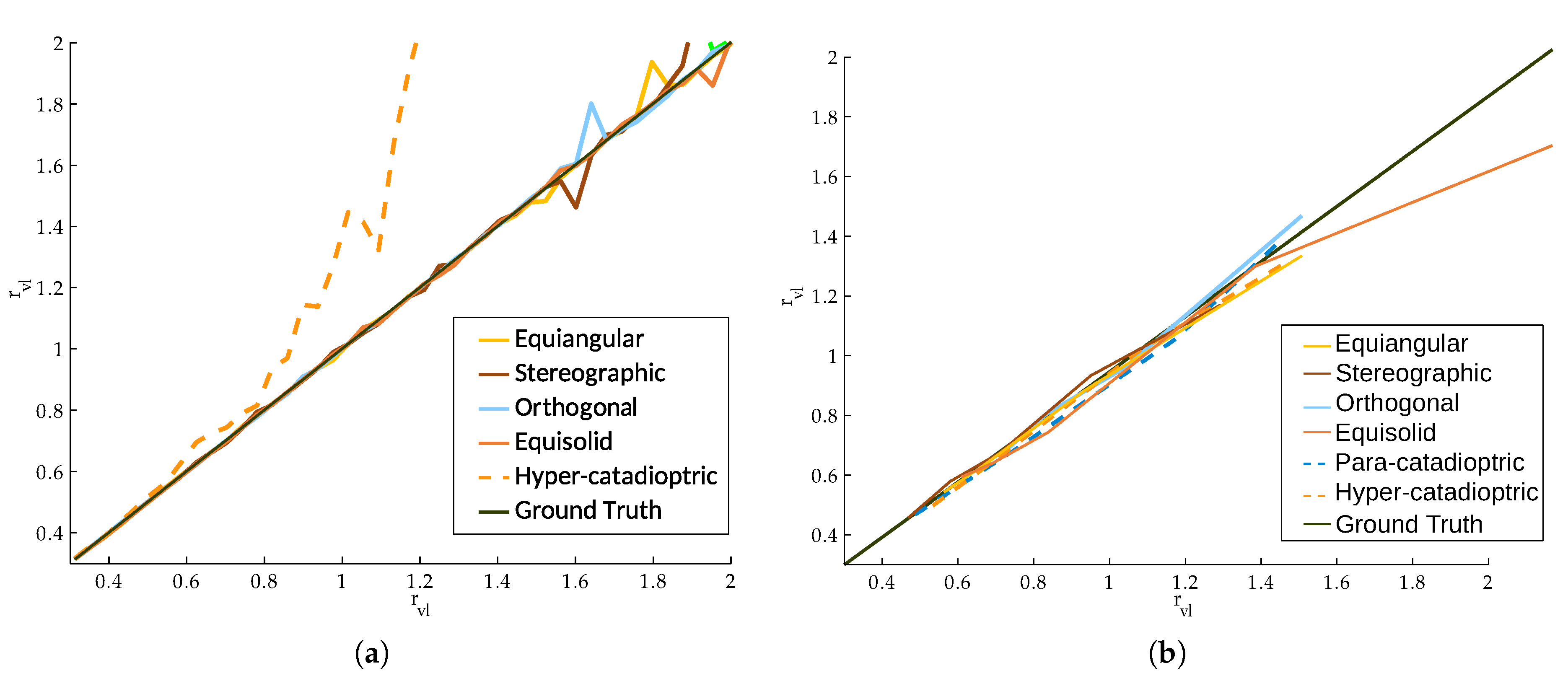
Next, we introduce the fish-eye cameras [
22]. The main characteristic of this kind of camera is the wide field of view. The projection model for this camera system has been obtained in [
34], where a unified model for revolution symmetry cameras is defined. This method consists of the projection of the environment rays into a unit radius sphere. The intersection between the sphere and the ray is projected into the image plane through a non-linear function
, which depends on the angle of the ray and the modeled fish-eye lens. In
Table 1 for the lenses implemented in this work is defined.
For catadioptric systems, we use the sphere model, presented in [
24]. As in fish-eye cameras, we have the intersection of the environment’s ray with the unit radius sphere. Then, through a non-linear function, we project the intersected point into a normalized plane. The non-linear function,
, depends on the mirror we are modeling. The final step of this model projects the point in the normalized plane into the image plane with the calibration matrix H
, defined as H
= K
R
M
, where K
is the calibration matrix of the perspective camera, R
is the rotation matrix of the catadioptric system and M
defines the behavior of the mirror (see Equation (
3)).
where
are the focal length of the camera, and
the coordinates of the optical center in the image, the parameters
and
represent the geometry of the mirror and are defined in
Table 2,
d is the distance between the camera and the mirror and
2p is the semi-latus rectum of the mirror.
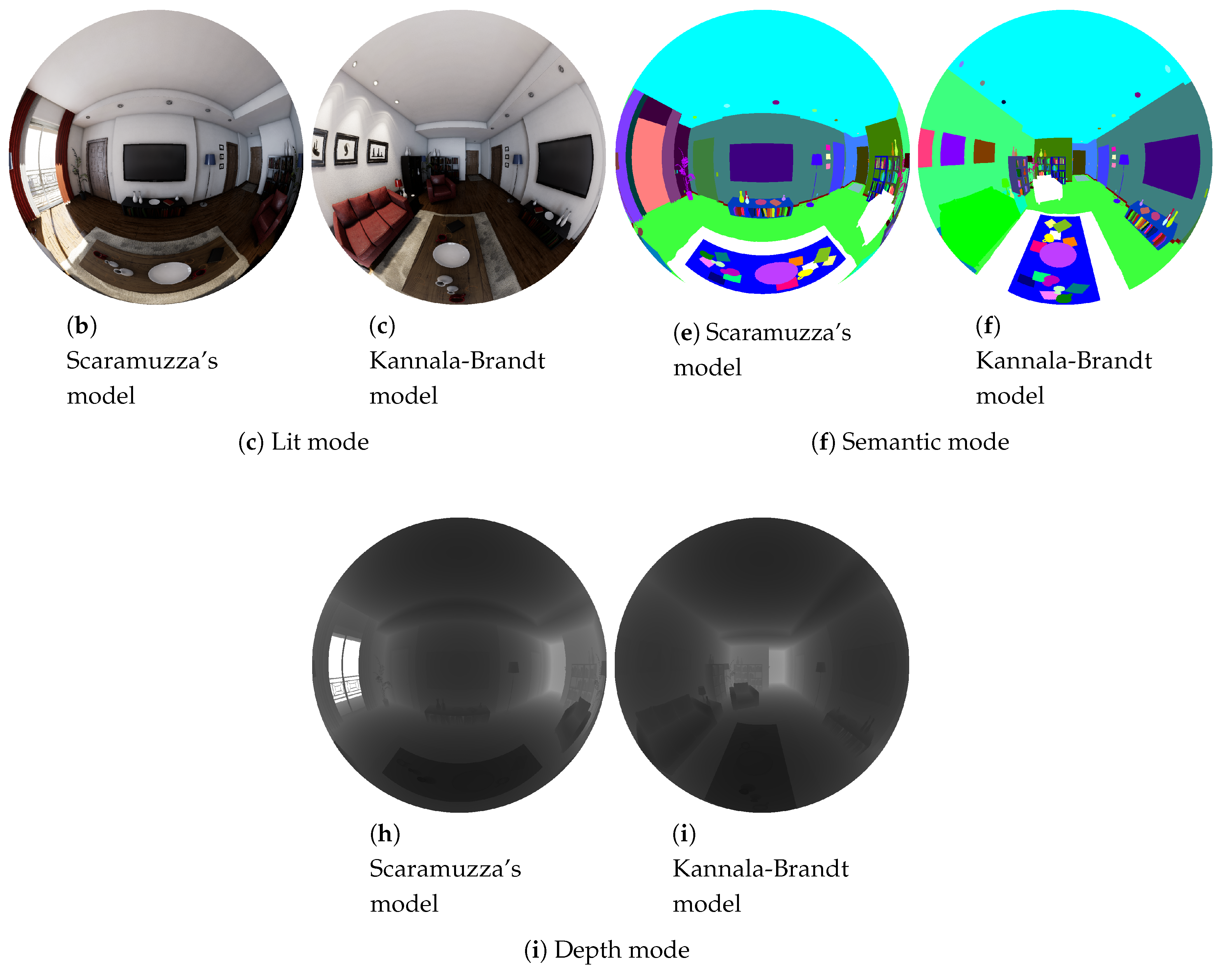
The last central-projection models presented in this work are the Scaramuzza and Kannala–Brandt models. Summarizing [
25,
26], these empiric models represent the projection of a 3D point into the image plane through non-lineal functions.
In the Scaramuzza model, the projection is represented by . The non-lineal function, , is defined by the image coordinates and a n-grade polynomial function , where is defined as the distance of the pixel to the optical center in the image plane, and are calibration parameters of the modeled camera.
In the Kannala–Brandt camera model, the forward projection model is represented as:
where
,
are the coordinates of the optical center and
is the non-linear function which is defined as
, where
and
are the parameters that characterize the modeled camera.
2.2.2. Non-Central-Projection Cameras
Central-projection cameras are characterized by the unique optical center. By contrast, in non-central-projection models, we do not have a single optical center for each image. For the definition of non-central-projection models, we use Plücker coordinates. In this work, we summarize the models; however, a full explanation of the models and Plücker coordinates is described in [
35].
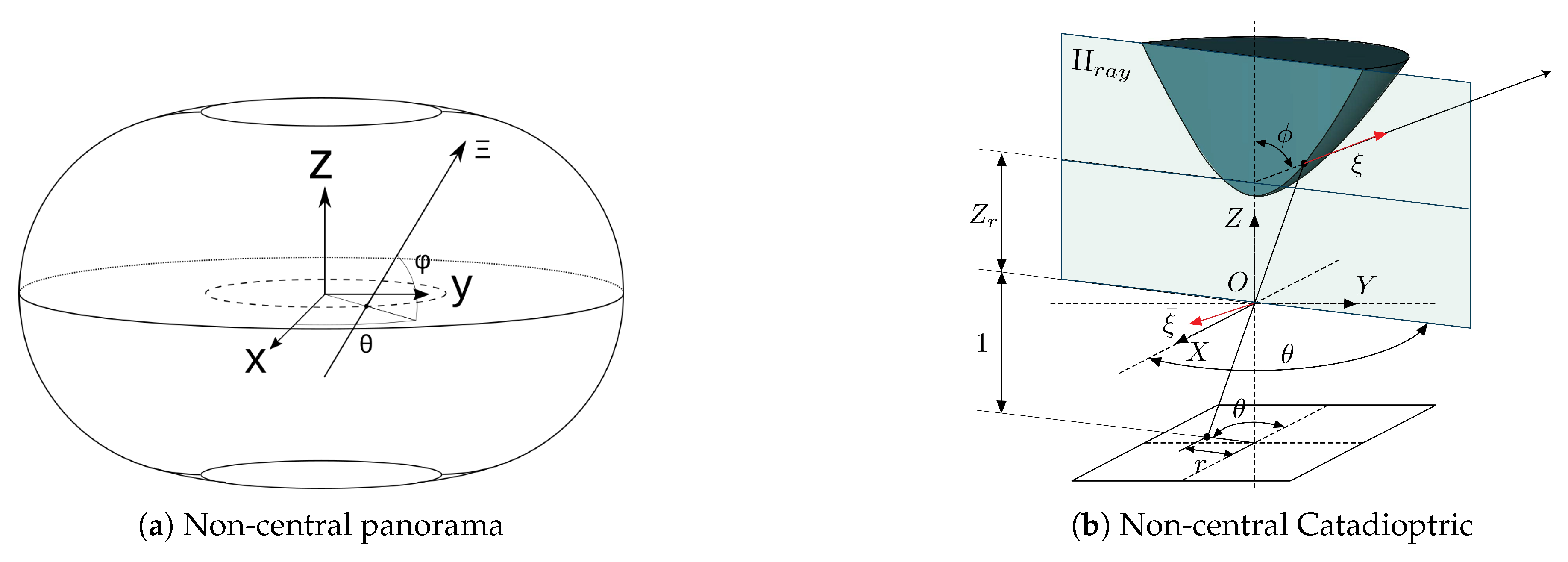
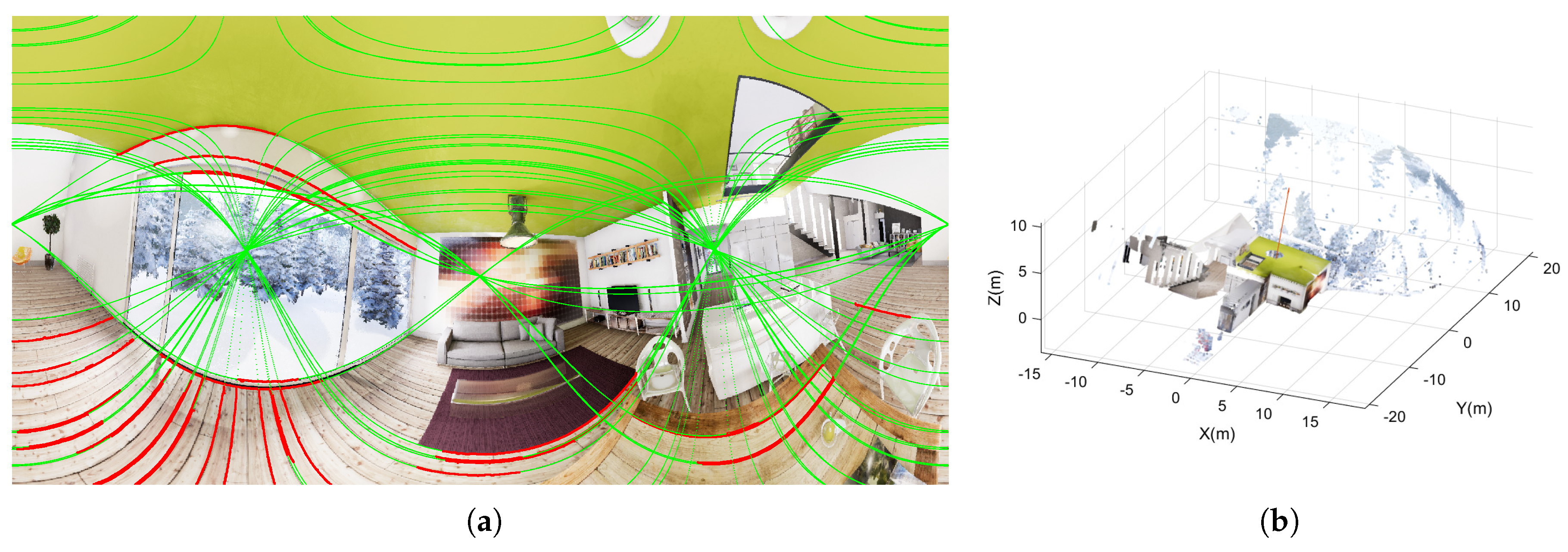
Non-central panoramas have similarities with equirectangular panoramas. The main difference with central panoramas is that each column of the non-central panorama shares a different optical center. Moreover, since central panoramas are the projection of the environment into a sphere, non-central panoramas are the projection into a semi-toroid, as can be seen in
Figure 4a. The optical center of the image is distributed in the trajectory of centers of the semi-toroid. This trajectory is defined as a circle, dashed line in
Figure 4a, whose center is the revolution axis. The definition of the rays that go to the environment from the non-central system is obtained in [
27], given as the result of Equation (
5). The parameter
is the radius of the circle of optical centers and
are spherical coordinates in the coordinate system.
Finally, spherical and conical catadioptric systems are also described by non-central-projection models. Just as with non-central panoramas, a full explanation of the model can be found on [
28,
29].
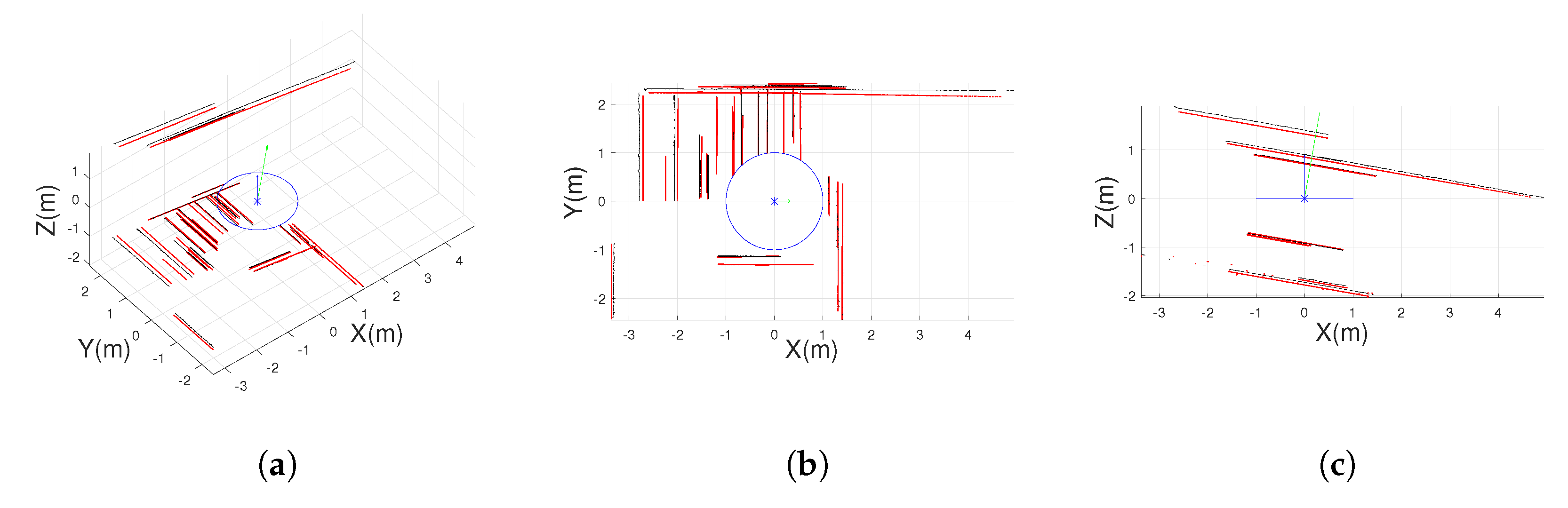
Even though the basis of non-central and central catadioptric systems is the same, we take a picture of a mirror from a perspective camera, the mathematical model is quite different. As in non-central panoramas, for spherical and conical mirror we also use the Plücker coordinates to define projection rays; see
Figure 4b. For conical catadioptric systems, we define
, where
and
are geometrical parameters and
, where
is the aperture angle of the cone. When these parameters are known, the 3D ray in Plücker coordinates is defined by:
For the spherical catadioptric system, we define the geometric parameters as
,
,
and
. Given the coordinates at a point of the image plane, the Equation (
7) defines the ray that reflects on the mirror:
where
;
;
and
.