Nondestructive Testing of the Miter Gates Using Various Measurement Methods
Abstract
1. Introduction
2. Materials and Methods
2.1. Observations Regarding Gates Operation
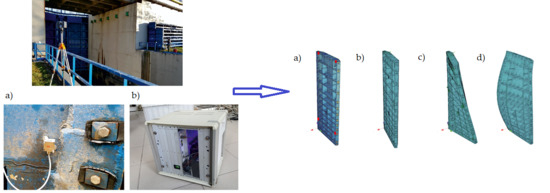
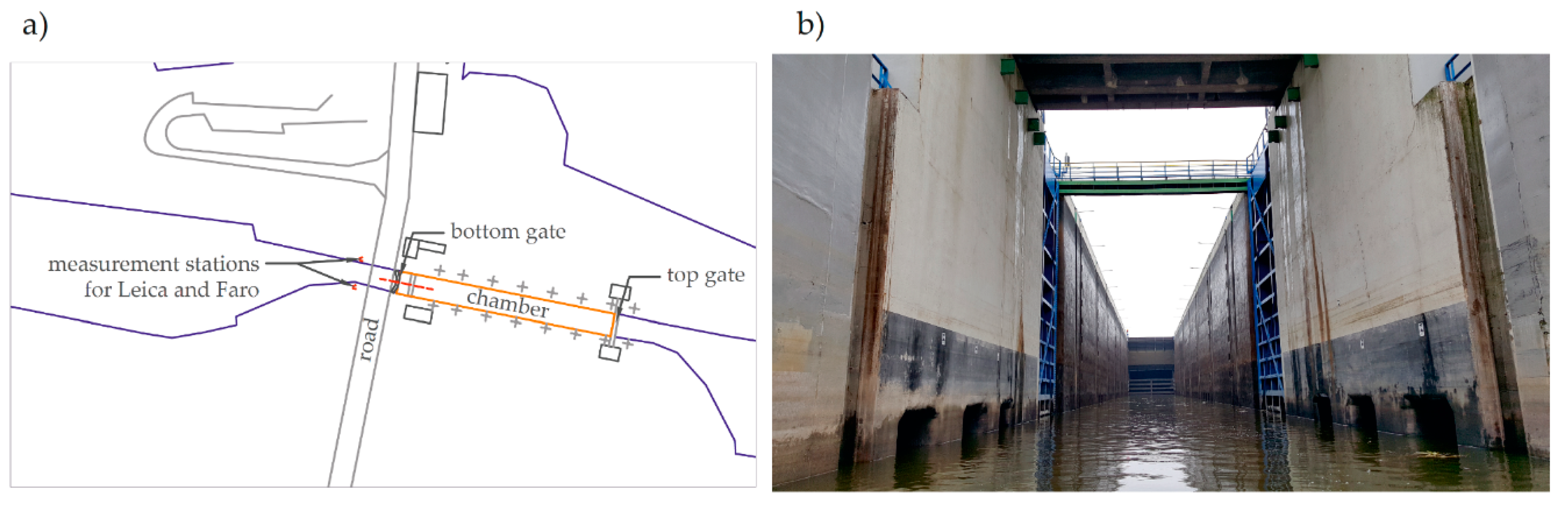
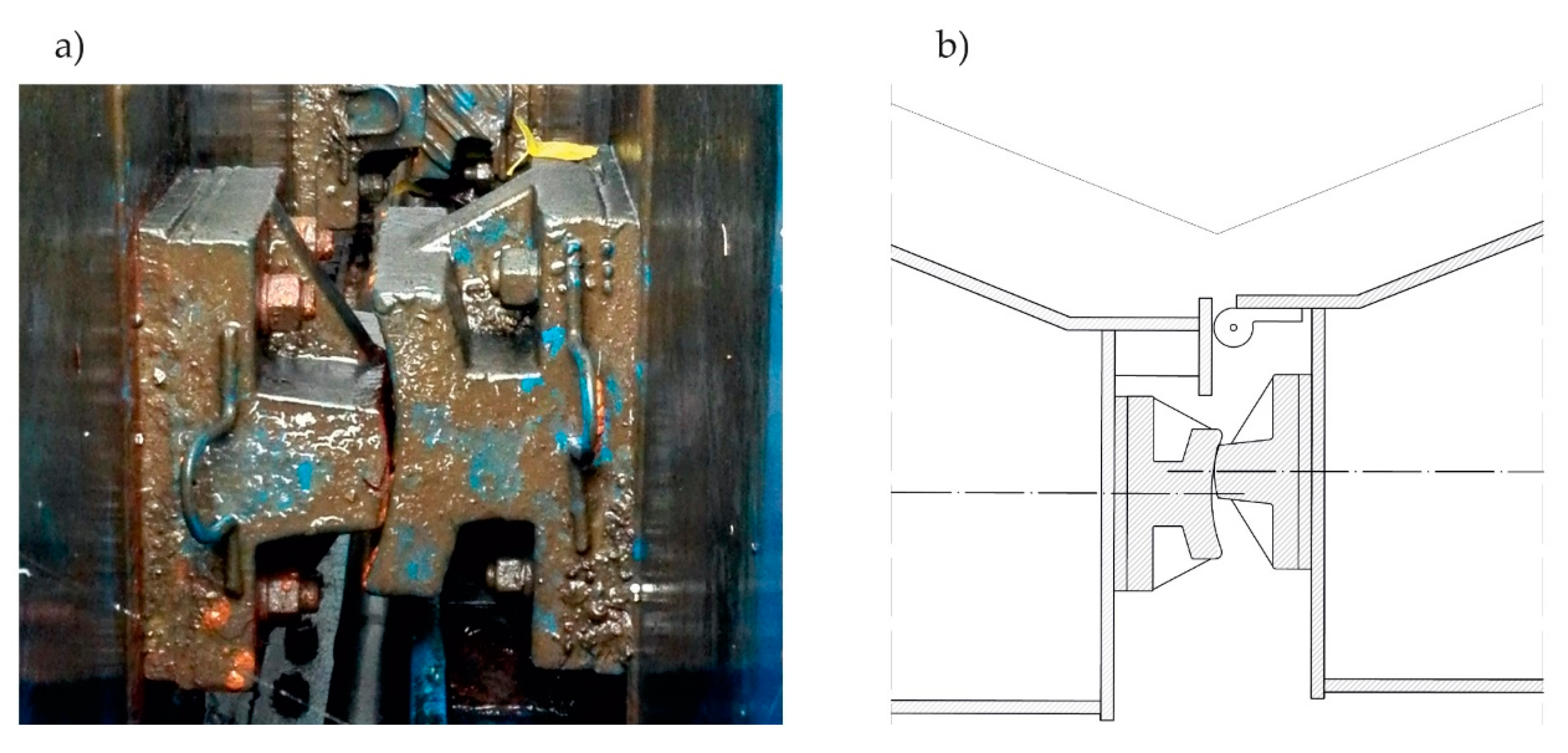
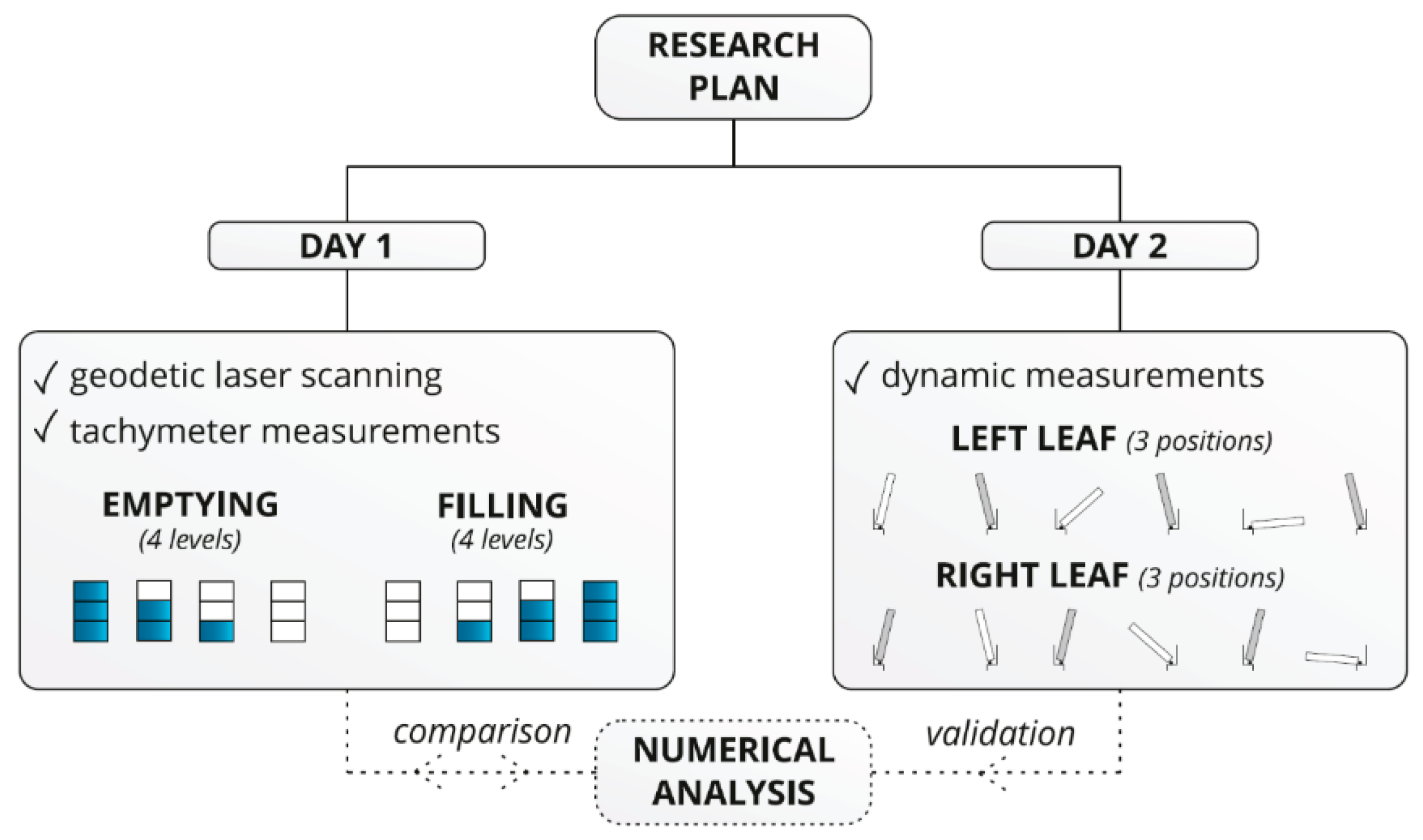
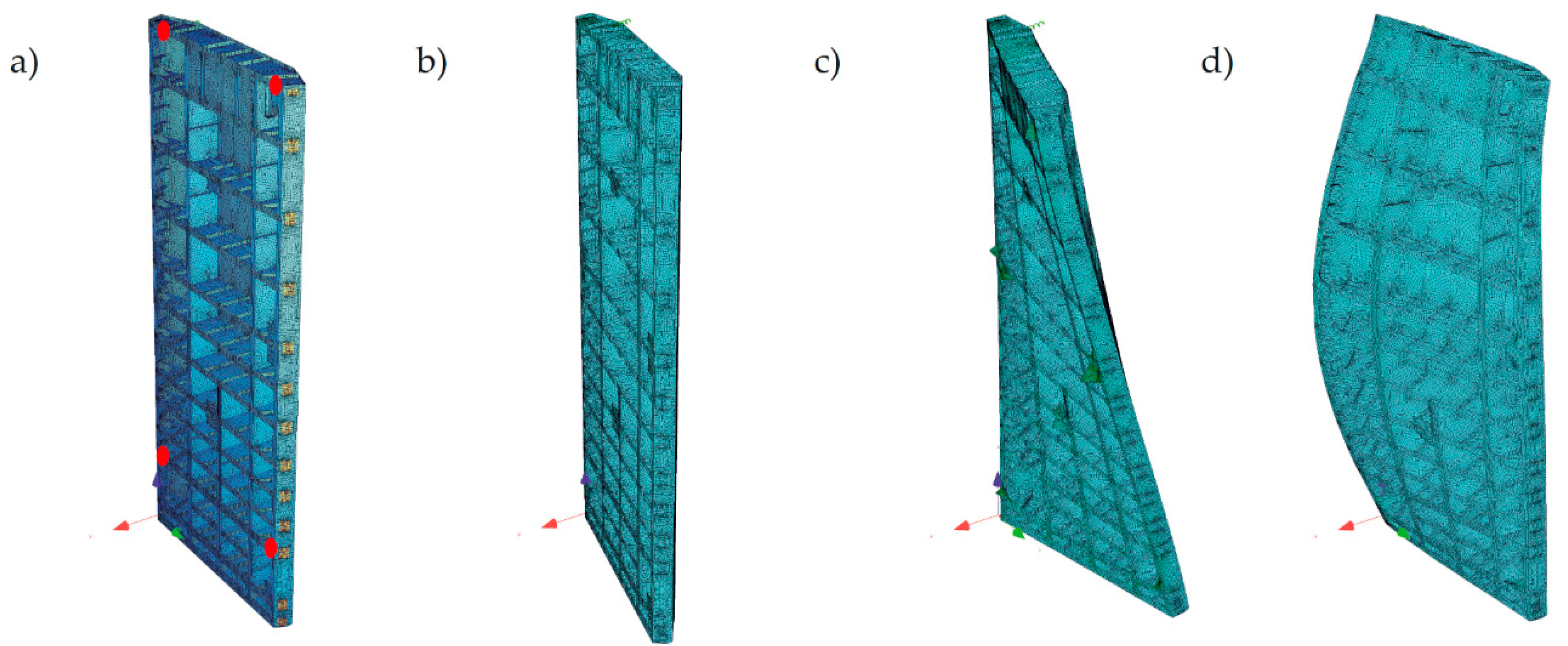
2.2. Measurements and Methods
- A, maximum top water level (57.30 m above sea level) and bottom water zero level (41.80 m above sea level);
- B.1, top water level 1/3 and bottom water level + 1 m;
- B.2, top water level increase from 1/3 to 2/3 and bottom water level + 1 m;
- B.3, top water level increase from 2/3 to 3/3 and bottom water level + 1 m.
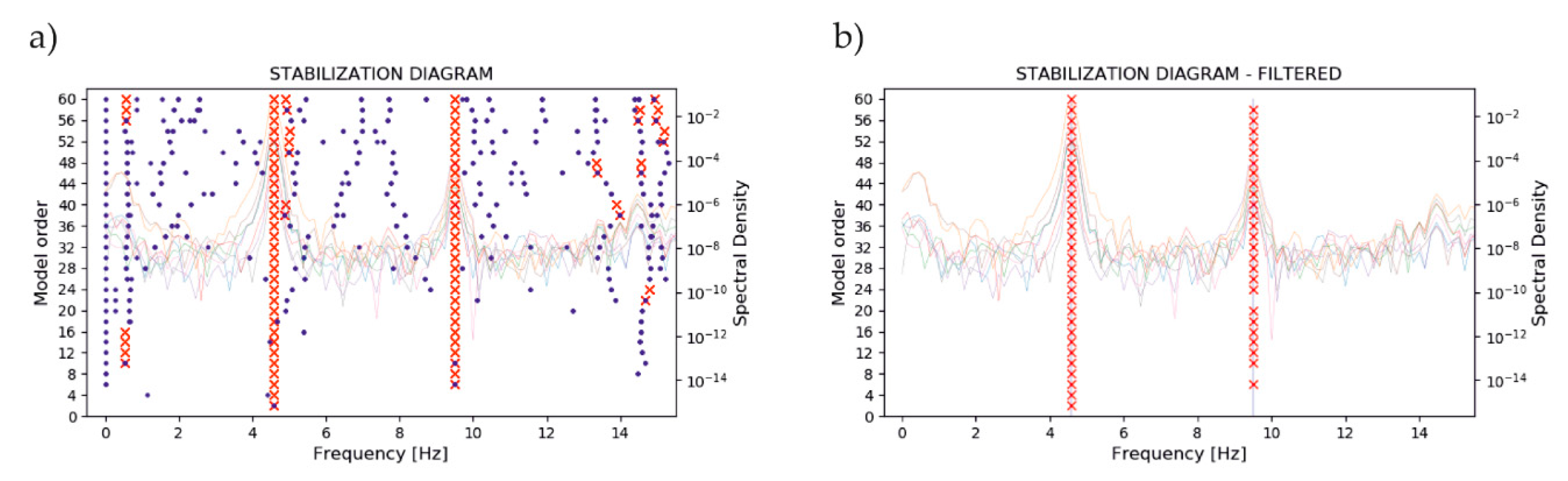
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Eick, B.; Treece, Z.R.; Spencer, B.F.; Smith, M.D.; Sweeney, S.C.; Alexander, Q.G.; Foltz, S.D. Automated damage detection in miter gates of navigation locks. Struct. Control. Heal. Monit. 2017, 25, e2053. [Google Scholar] [CrossRef]
- Eick, B.A.; Treece, Z.R.; Spencer, B.F., Jr.; Smith, M.D.; Sweeney, S.C.; Alexander, Q.G.; Foltz, S.D. Miter Gate Gap Detection Using Principal Component Analysis; ERDC-TR-18-2, US Army Engineer Research and Development Center: Vicksburg, MI, USA, 2018. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals; Elsevier: San Diego, CA, USA, 2005; ISBN 0-08-047277-X. [Google Scholar]
- Hartmann, F.; Katz, C. Structural Analysis with Finite Elements, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 978-3-540-49698-4. [Google Scholar]
- Zhu, L.; Lyu, L.; Zhang, X.; Wang, Y.; Guo, J.; Xiong, X. Bending Properties of Zigzag-Shaped 3D Woven Spacer Composites: Experiment and FEM Simulation. Materials 2019, 12, 1075. [Google Scholar] [CrossRef]
- Kawecki, B.; Podgórski, J. Numerical Analysis and Its Laboratory Verification in Bending Test of Glue Laminated Timber Pre-Cracked Beam. Materials 2019, 12, 955. [Google Scholar] [CrossRef]
- Rainieri, C.; Fabbrocino, G. Operational Modal Analysis of Civil. Engineering Structures: An. Introduction and Guide for Applications; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Brownjohn, J.M.W.; Moyo, P.; Omenzetter, P.; Lu, Y. Assessment of Highway Bridge Upgrading by Dynamic Testing and Finite-Element Model Updating. J. Bridg. Eng. 2003, 8, 162–172. [Google Scholar] [CrossRef]
- Degrauwe, D.; Reynders, E.; De Roeck, G.; Van den Broeck, P. Operational modal analysis and updating of a footbridge. In Proceedings of the 7th European Conference on Structural Dynamics, Southampton, UK, 7–9 July 2008. [Google Scholar]
- Zhang, L.; Huang, J. Dynamic interaction analysis of the high-speed maglev vehicle/guideway system based on a field measurement and model updating method. Eng. Struct. 2019, 180, 1–17. [Google Scholar] [CrossRef]
- Pavic, A.; Hartley, M.J.; Waldron, P. Updating of the Analytical Models of Two Footbridges Based on Modal Testing of Full-Scale Structures. In Proceedings of the International Seminar on Modal Analysis, Los Angeles, CA, USA, 28 October 1998. [Google Scholar]
- Salawu, O.S.; Williams, C. Bridge assessment using forced-vibration testing. J. Struct. Eng. 1995, 121, 161–173. [Google Scholar] [CrossRef]
- Salawu, O.S. Detection of structural damage through changes in frequency: A review. Eng. Struct. 1997, 19, 718–723. [Google Scholar] [CrossRef]
- Maadani, S.; Akbari, R.; Maalek, S. Monitoring the dynamic characteristics of an urban bridge before, during and after widening. Struct. Infrastruct. Eng. 2015, 11, 944–956. [Google Scholar] [CrossRef]
- Worden, K.; Friswell, M.I. Modal-Vibration-Based Damage Identification. In Encyclopedia of Structural Health Monitoring; Boller, C., Chang, F.-K., Fujino, Y., Eds.; John Wiley & Sons, Ltd.: Chichester, UK, 2008; ISBN 978-0-470-05822-0. [Google Scholar]
- Naito, H.; Bolander, J.E. Damage detection method for RC members using local vibration testing. Eng. Struct. 2019, 178, 361–374. [Google Scholar] [CrossRef]
- Kim, J.-T.; Ryu, Y.-S.; Cho, H.-M.; Stubbs, N. Damage identification in beam-type structures: Frequency-based method vs mode-shape-based method. Eng. Struct. 2003, 25, 57–67. [Google Scholar] [CrossRef]
- Brincker, R.; Andersen, P.; Cantieni, R. Identification and Level I Damage Detection of the Z24 Highway Bridge. Exp. Tech. 2001, 25, 51–57. [Google Scholar] [CrossRef]
- Shatilov, Y.Y.; Lyapin, A.A. Vibration-Based Damage Detection Techniques for Health Monitoring of Construction of a Multi-Storey Building. Mater. Sci. Forum 2018, 931, 178–183. [Google Scholar] [CrossRef]
- Fitzgerald, P.C.; Malekjafarian, A.; Bhowmik, B.; Prendergast, L.J.; Cahill, P.; Kim, C.-W.; Hazra, B.; Pakrashi, V.; OBrien, E.J. Scour Damage Detection and Structural Health Monitoring of a Laboratory-Scaled Bridge Using a Vibration Energy Harvesting Device. Sensors 2019, 19, 2572. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; He, X.; Jiao, Y. Damage Identification Algorithm of Hinged Joints for Simply Supported Slab Bridges Based on Modified Hinge Plate Method and Artificial Bee Colony Algorithms. Algorithms 2018, 11, 198. [Google Scholar] [CrossRef]
- Kang, F.; Li, J.; Xu, Q. Damage detection based on improved particle swarm optimization using vibration data. Appl. Soft Comput. 2012, 12, 2329–2335. [Google Scholar] [CrossRef]
- Zielińska, M.; Rucka, M. Non-Destructive Assessment of Masonry Pillars using Ultrasonic Tomography. Materials 2018, 11, 2543. [Google Scholar] [CrossRef]
- Rucka, M. Monitoring Steel Bolted Joints during a Monotonic Tensile Test Using Linear and Nonlinear Lamb Wave Methods: A Feasibility Study. Metals 2018, 8, 683. [Google Scholar] [CrossRef]
- Żółtowski, K.; Romaszkiewicz, T. Roof of PGE Arena-The Stadium Built for Euro 2012 in Gdansk. BAUINGENIEUR-GERMANY 2012, 87, 137–142. [Google Scholar]
- Żółtowski, K. Footbridges, numerical approach. In Footbridge Vibration Design; Caetano, E., Cunha, A., Hoorpah, W., Raoul, J., Eds.; CRC Press: Boca Raton, FL, USA, 2009; pp. 53–70. [Google Scholar]
- Żółtowski, K.; Binczyk, M.; Kalitowski, P. Footbridges. Dynamic Design–Selected problems. In Footbridge 2017 Berlin-Tell A Story; Technische Universität Berlin: Berlin, Germany, 2017; pp. 1–10. [Google Scholar]
- Zoltowski, K.; Wask, T. Cable stayed bridge over Vistula river in Plock. Dynamic analysis and site test. In Proceedings of the International Conference on Bridges, Dubrovnik, Croatia, 21–24 May 2006; Radic, J., Ed.; Structural Engineering Conferences and Croatian Society of Structural Engineers: Dubrovnik, Croatia, 2006. [Google Scholar]
- Miskiewicz, M.; Makowska, K. Displacement measurements during load testing of railway arch bridge. In Proceedings of the 17th International Multidisciplinary Scientific Geoconference, SGEM 2017 Conference Proceedings, Albena, Bulgaria, 29 June–5 July 2017. [Google Scholar] [CrossRef]
- Strach, M.; Makowska, K. Analyzing the Geometry of the Turnouts and Their Adjustment Basing on the Tacheometer Measurements. In Proceedings of the 2016 Baltic Geodetic Congress (BGC Geomatics), Gdansk, Poland, 2–4 June 2016; pp. 28–33. [Google Scholar]
- Filipiak-Kowszyk, D.; Janowski, A.; Kamiński, W.; Makowska, K.; Szulwic, J.; Wilde, K. The geodetic monitoring of the engineering structure–a practical solution of the problem in 3D space. Rep. Geod. Geoinformatics 2016, 102, 1–14. [Google Scholar] [CrossRef]
- Acosta, L.E.; De Lacy, M.C.; Ramos, M.I.; Cano, J.P.; Herrera, A.M.; Avilés, M.; Gil, A.J. Displacements Study of an Earth Fill Dam Based on High Precision Geodetic Monitoring and Numerical Modeling. Sensors 2018, 18, 1369. [Google Scholar] [CrossRef]
- Sekiya, H.; Kinomoto, T.; Miki, C. Determination Method of Bridge Rotation Angle Response Using MEMS IMU. Sensors 2016, 16, 1882. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Yan, L.; Huang, G.; Chen, C.; Wu, Z. Monitoring Building Deformation with InSAR: Experiments and Validation. Sensors 2016, 16, 2182. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Zhang, Z.; Liu, X.; Ma, S. Development of Laser Scanner for Full Cross-Sectional Deformation Monitoring of Underground Gateroads. Sensors 2017, 17, 1311. [Google Scholar] [CrossRef] [PubMed]
- Gui, R.; Xu, X.; Zhang, D.; Lin, H.; Pu, F.; He, L.; Cao, M. A Component Decomposition Model for 3D Laser Scanning Pavement Data Based on High-Pass Filtering and Sparse Analysis. Sensors 2018, 18, 2294. [Google Scholar] [CrossRef] [PubMed]
- Scaioni, M.; Marsella, M.; Crosetto, M.; Tornatore, V.; Wang, J. Geodetic and Remote-Sensing Sensors for Dam Deformation Monitoring. Sensors 2018, 18, 3682. [Google Scholar] [CrossRef]
- Ziolkowski, P.; Szulwic, J.; Miskiewicz, M. Deformation Analysis of a Composite Bridge during Proof Loading Using Point Cloud Processing. Sensors 2018, 18, 4332. [Google Scholar] [CrossRef]
- Ge, Y.; Tang, H.; Gong, X.; Zhao, B.; Lu, Y.; Chen, Y.; Lin, Z.; Chen, H.; Qiu, Y. Deformation Monitoring of Earth Fissure Hazards Using Terrestrial Laser Scanning. Sensors 2019, 19, 1463. [Google Scholar] [CrossRef]
- Schmitz, B.; Holst, C.; Medic, T.; Lichti, D.D.; Kuhlmann, H. How to Efficiently Determine the Range Precision of 3D Terrestrial Laser Scanners. Sensors 2019, 19, 1466. [Google Scholar] [CrossRef]
- Simm, A.; Wang, Q.; Huang, S.; Zhao, W. Laser based measurement for the monitoring of shaft misalignment. Measurement 2016, 87, 104–116. [Google Scholar] [CrossRef]
- Zheng, F.; Shao, L.; Racic, V.; Brownjohn, J. Measuring human-induced vibrations of civil engineering structures via vision-based motion tracking. Measurement 2016, 83, 44–56. [Google Scholar] [CrossRef]
- Burke, R.D.; Burke, K.A.; Chappell, E.C.; Gee, M.; Williams, R. A novel use of multivariate statistics to diagnose test-to-test variation in complex measurement systems. Measurement 2018, 130, 467–481. [Google Scholar] [CrossRef]
- Zhang, G.; Zappalá, D.; Crabtree, C.; Donaghy-Spargo, C.; Hogg, S. Duffy, A. Validation of a non-contact technique for torque measurements in wind turbines using an enhanced transient FSV approach. Measurement 2019. [Google Scholar] [CrossRef]
- Khalili, P.; Cawley, P. The choice of ultrasonic inspection method for the detection of corrosion at inaccessible locations. NDT E Int. 2018, 92, 80–92. [Google Scholar] [CrossRef]
- Safari, A.; Zhang, J.; Velichko, A.; Drinkwater, B.W. Assessment methodology for defect characterisation using ultrasonic arrays. NDT E Int. 2018, 94, 126–136. [Google Scholar] [CrossRef]
- Howard, R.; Cegla, F. Detectability of corrosion damage with circumferential guided waves in reflection and transmission. NDT E Int. 2017, 91, 108–119. [Google Scholar] [CrossRef]
- Howard, R.; Cegla, F.B. On the probability of detecting wall thinning defects with dispersive circumferential guided waves. NDT E Int. 2017, 86, 73–82. [Google Scholar] [CrossRef]
- Alvin, K.; Robertson, A.; Reich, G.; Park, K. Structural system identification: From reality to models. Comput. Struct. 2003, 81, 1149–1176. [Google Scholar] [CrossRef]
- Ewins, D.J. Modal Testing : Theory, Practice and Application, Mechanical Engineering Research studies/Engineering Dynamics Series 10; Research Studies Press: Baldock, UK, 2000; ISBN 978-0-86380-218-8. [Google Scholar]
- Pappa, R.S.; Juang, J.N. An Eigensystem Realization Algorithm (ERA) for modal parameter identification and model reduction. In Proceedings of the Workshop on Identification and Control of Flexible Space Struct, San Diego, CA, USA, 1 April 1985; Volume 3. [Google Scholar]
- Suzuki, H.; Juang, J.-N. An Eigensystem Realization Algorithm in Frequency Domain for modal parameter identification. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, Williamsburg, Virginia, 18–20 August 1986. [Google Scholar]
- De Schutter, B. Minimal state-space realization in linear system theory: An overview. J. Comput. Appl. Math. 2000, 121, 331–354. [Google Scholar] [CrossRef]
- Li, P.; Hu, S.; Li, H. Noise issues of modal identification using eigensystem realization algorithm. Procedia Eng. 2011, 14, 1681–1689. [Google Scholar] [CrossRef][Green Version]
- Caicedo, J.M. Practical guidelines for the natural excitation technique (NExT) and the eigensystem realization algorithm (ERA) for modal identification using ambient vibration. Exp. Tech. 2010, 35, 52–58. [Google Scholar] [CrossRef]
- Allemang, R.J. The Modal Assurance Criterion—Twenty Years of Use and Abuse. Sound Vib. 2003, 37, 14–23. [Google Scholar]
- Pappa, R.S.; Elliott, K.B.; Schenk, A. Consistent-mode indicator for the eigensystem realization algorithm. J. Guid. Control. Dyn. 1993, 16, 852–858. [Google Scholar] [CrossRef]
- Miskiewicz, M.; Lachowicz, J.; Tysiac, P.; Jaskuła, P.; Wilde, K. The application of non-destructive methods in the diagnostics of the approach pavement at the bridges. IOP Conf. Series: Mater. Sci. Eng. 2018, 356, 012023. [Google Scholar] [CrossRef]
- Commander, B.C.; Schulz, J.X.; Goble, G.G.; Chasten, C.P. Detection of Structural Damage on Miter Gates; US Army Corps Engineers: Vicksburg, MS, USA, 1994. [Google Scholar]

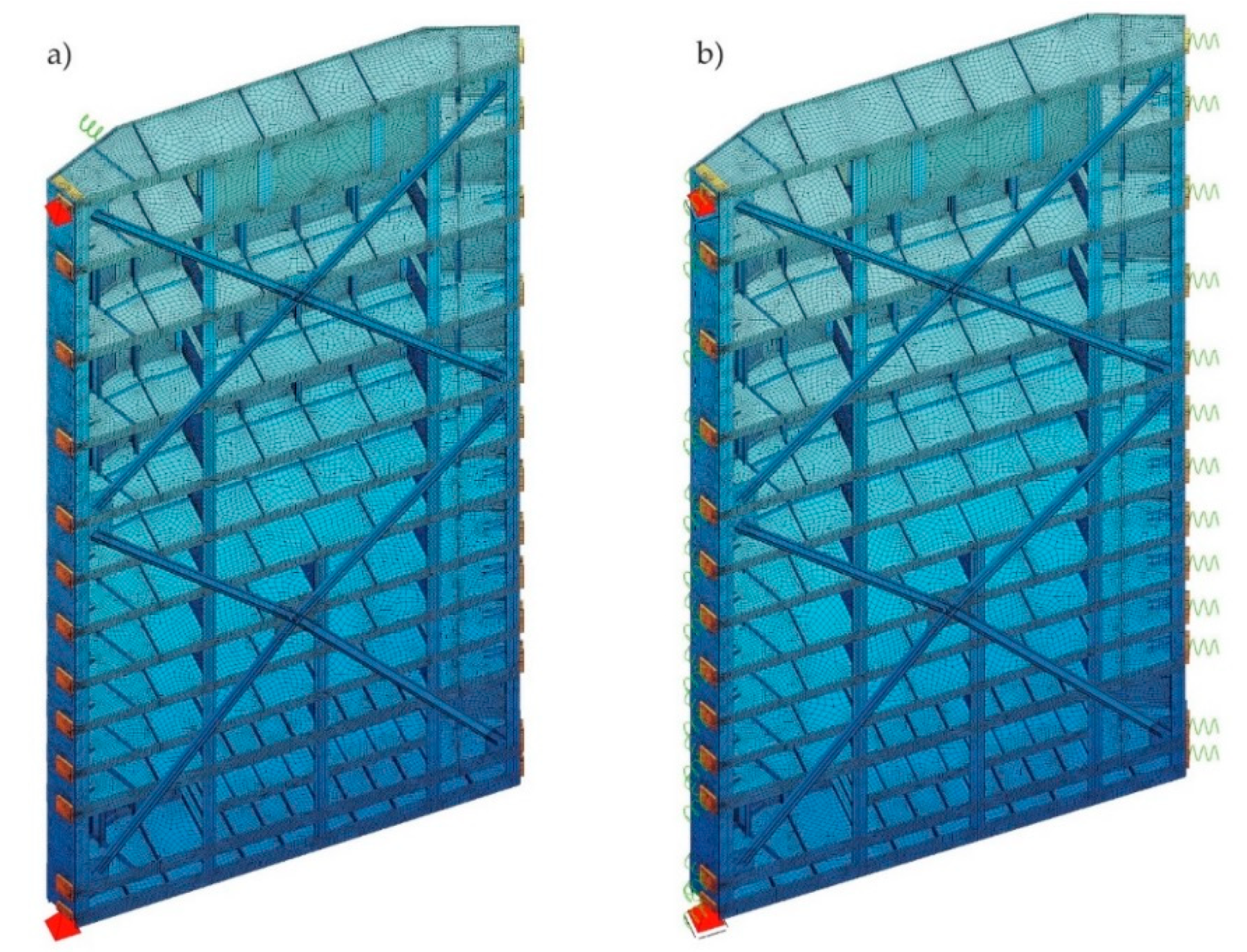
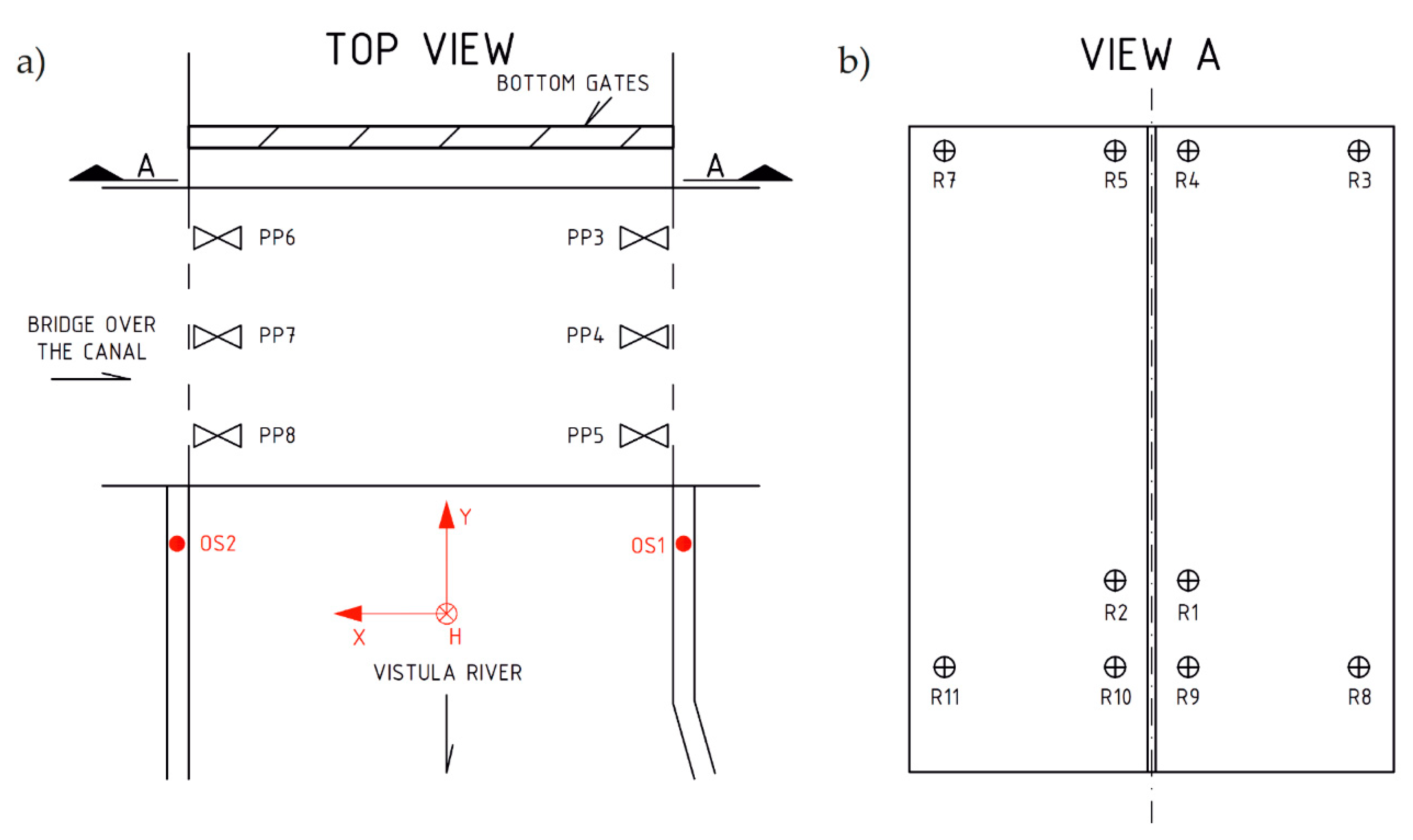



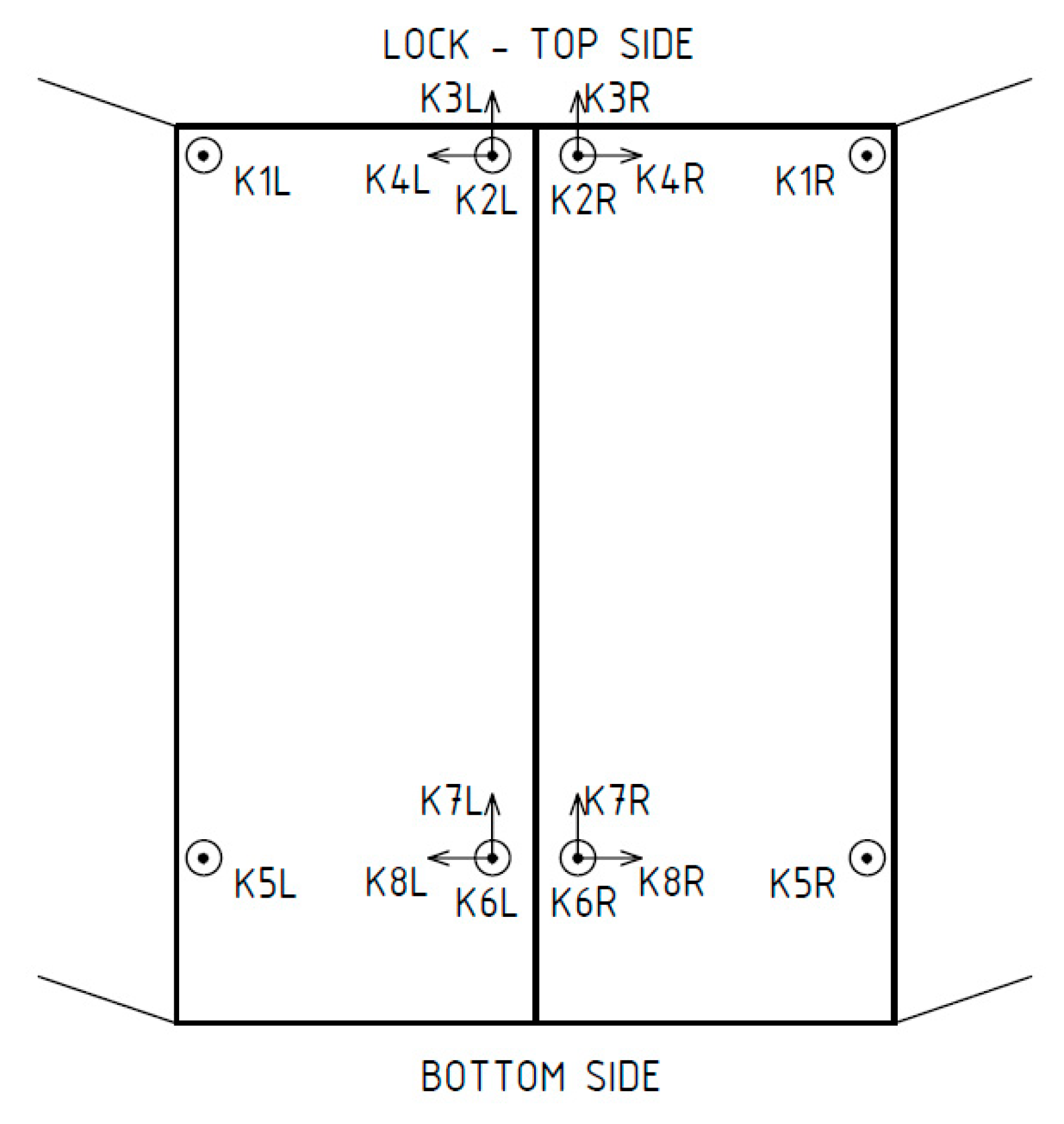
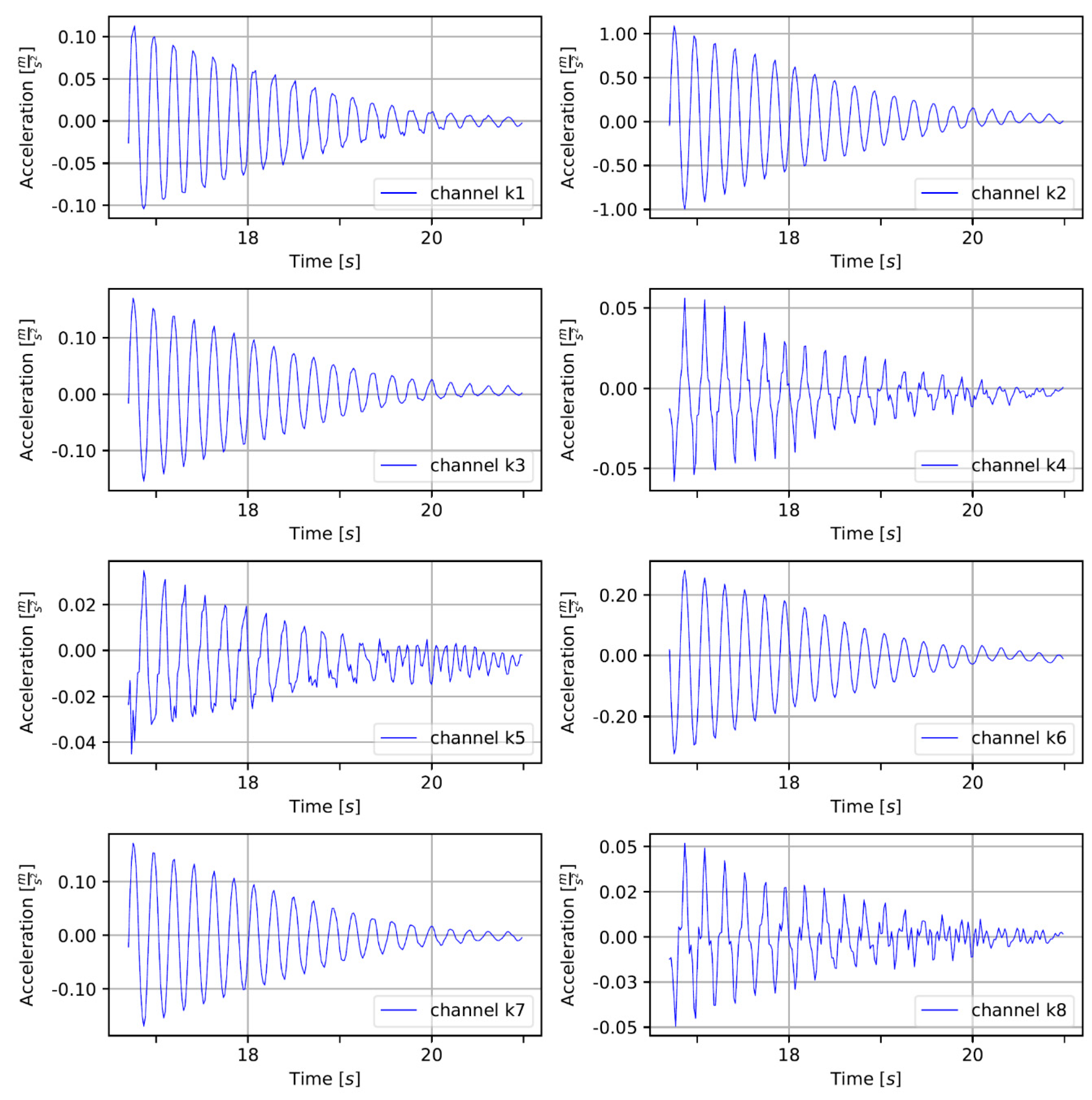
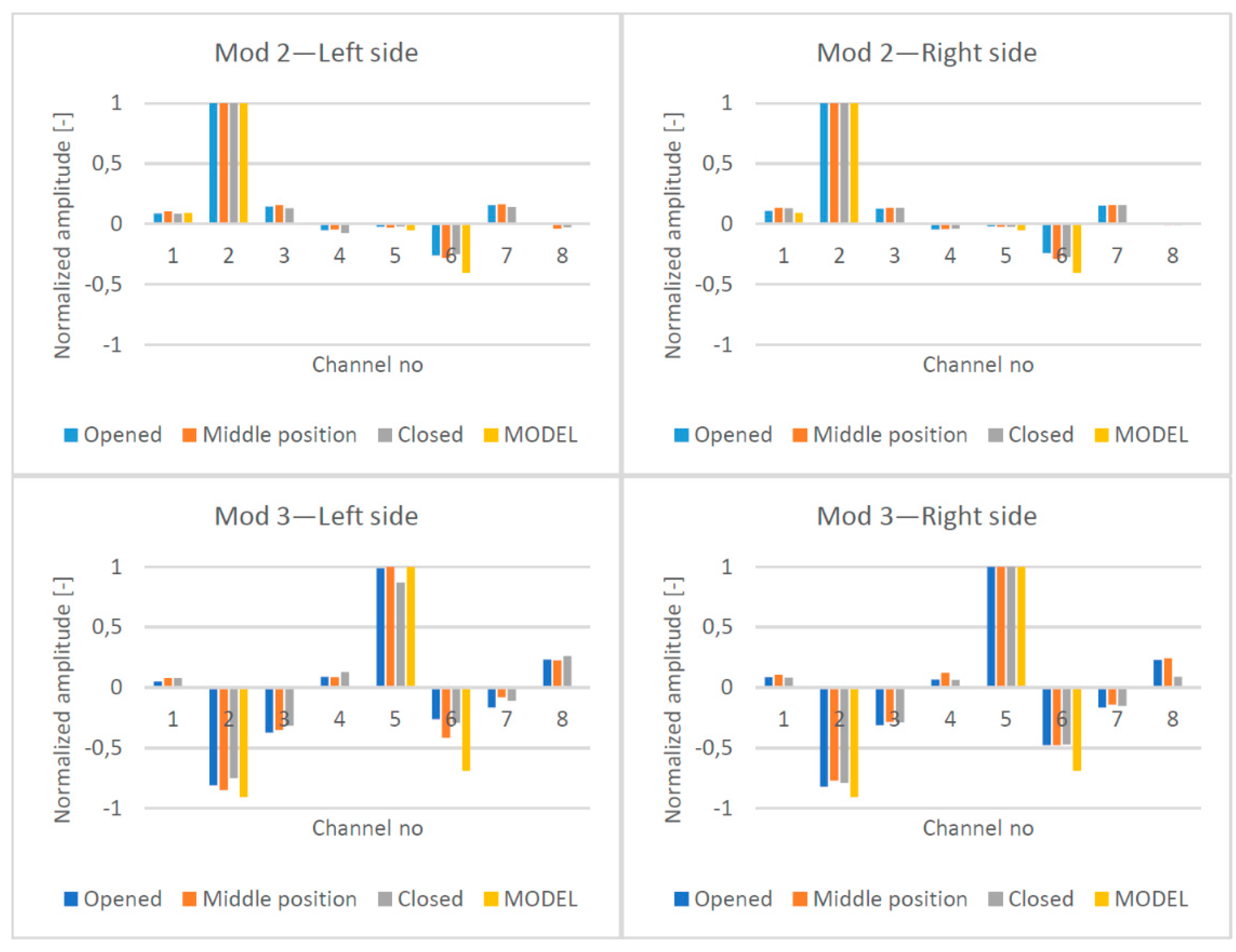
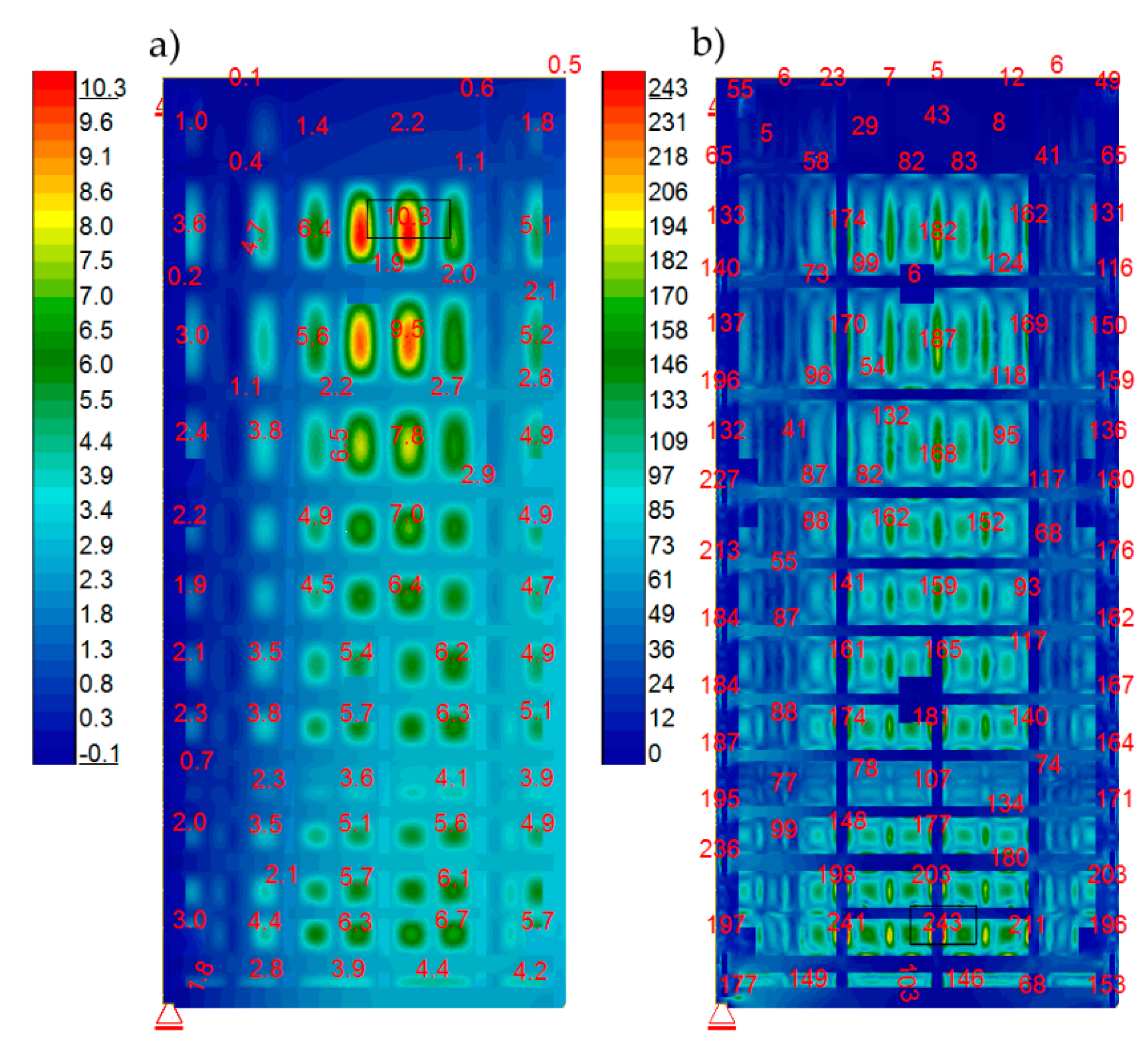
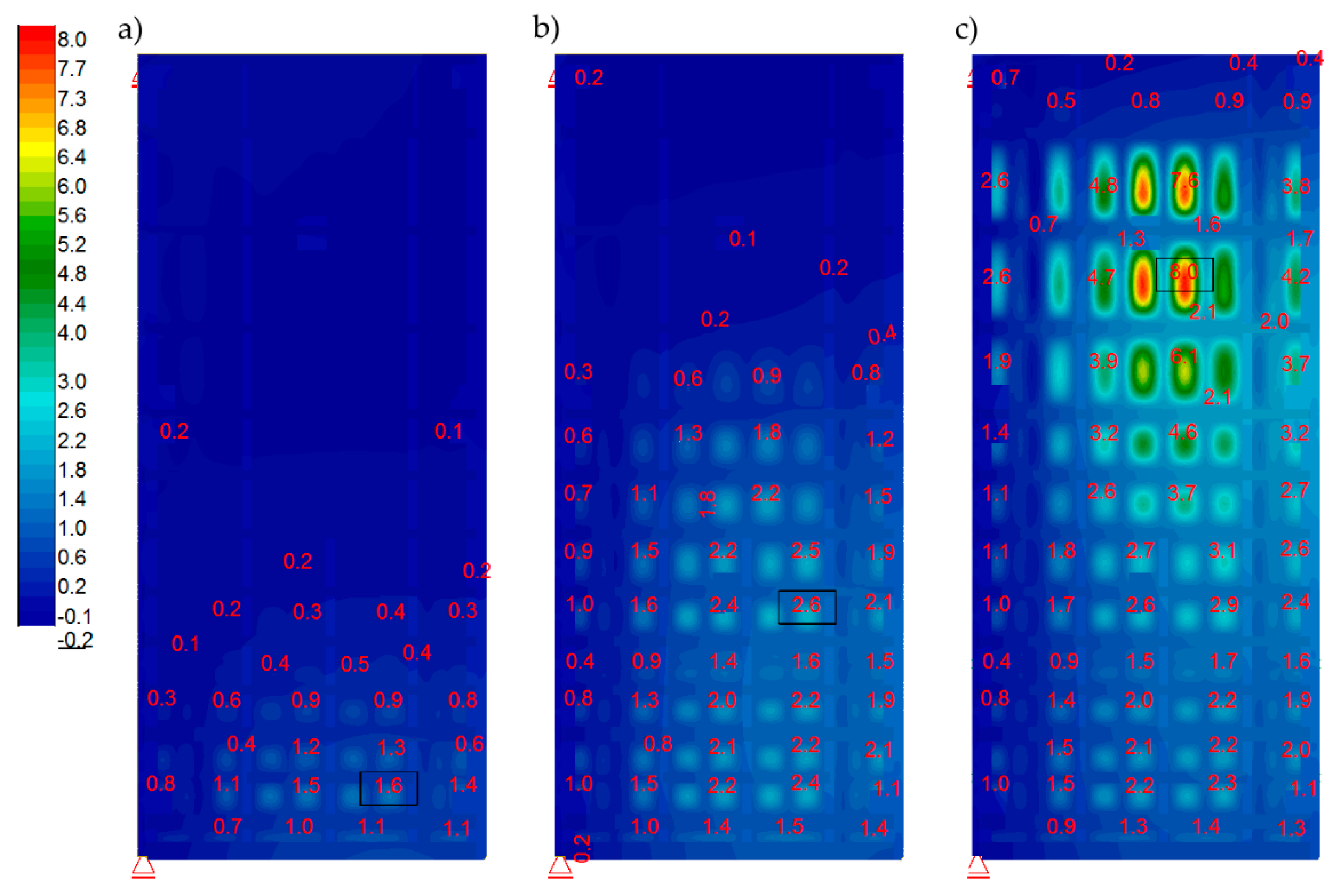
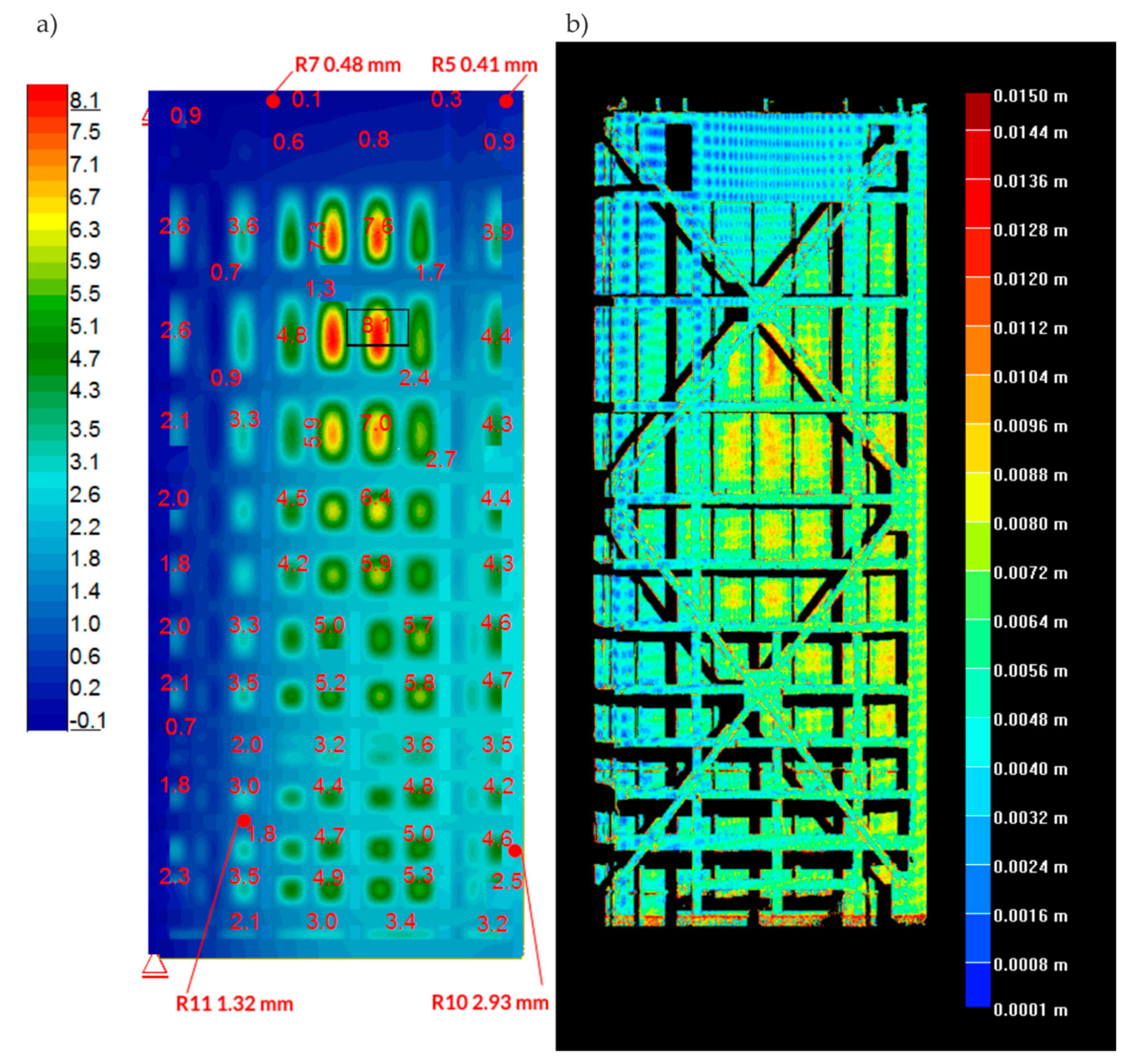

| Gates Leaf | Mod 2—Frequency (Hz) | Mod 3—Frequency (Hz) | ||||
|---|---|---|---|---|---|---|
| Opened | Mid | Closed | Opened | Mid | Closed | |
| Left | 4.698 | 4.657 | 4.671 | 9.260 | 9.255 | 9.317 |
| Right | 4.706 | 4.573 | 4.594 | 9.301 | 9.498 | 9.548 |
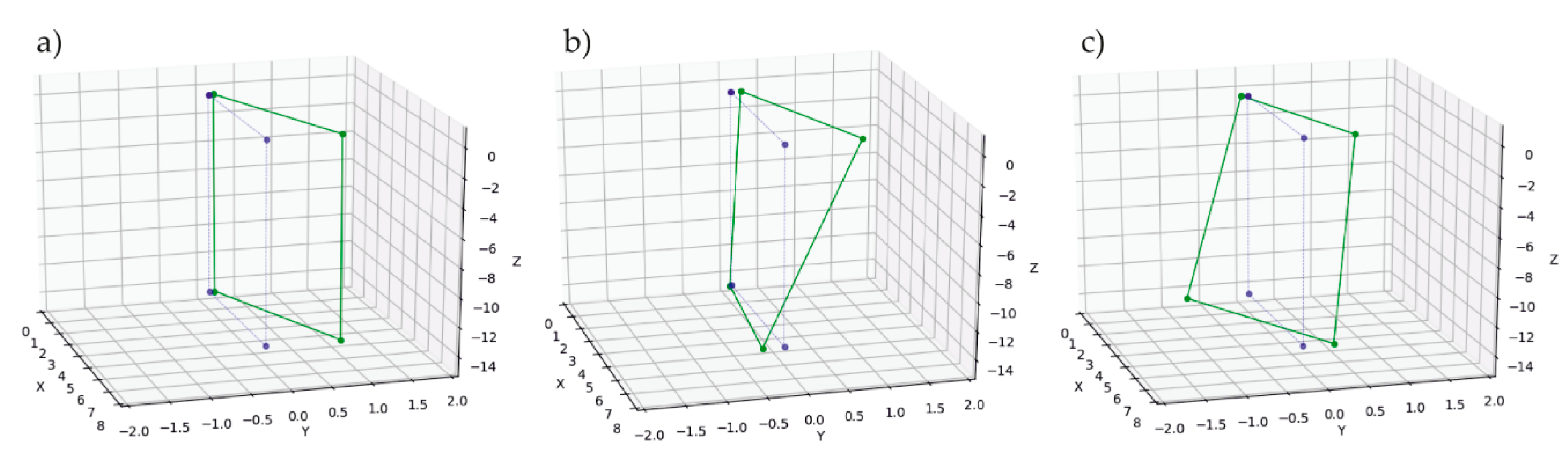
| NR. | dX (mm) | dY (mm) | dH (mm) |
|---|---|---|---|
| R1 | –0.6 | 5.2 | 1.1 |
| R2 | 0.6 | 5.6 | –0.1 |
| R3 | 1.3 | 0.2 | 0.3 |
| R4 | –0.2 | 4.0 | 0.2 |
| R5 | 1.2 | 5.0 | 0.3 |
| R6 | 0.3 | 1.1 | 0.4 |
| NR. | dX (mm) | dY (mm0 | dH (mm) |
|---|---|---|---|
| R1 | –1.5 | –4.2 | 0.6 |
| R2 | –2.5 | –4.4 | 0.5 |
| R3 | –2.9 | –0.7 | –0.3 |
| R4 | –2.3 | –2.4 | –0.1 |
| R5 | –2.1 | –3.2 | –0.4 |
| R6 | –1.4 | –0.3 | 0.0 |
| R7 | –1.8 | –2.8 | –0.6 |
| R8 | –1.4 | –4.0 | 0.6 |
| R9 | –2.5 | –4.2 | 0.4 |
| R10 | –1.2 | –0.8 | 0.2 |
| NR. | dYFEM (mm) | dYtachymeter (mm) | dYtachymeter / dYFEM (%) |
|---|---|---|---|
| R3 | −0.48 | −0.7 | 146% |
| R4 | −0.41 | −2.4 | 585% |
| R7 | −1.32 | −2.8 | 212% |
| R8 | −2.93 | −4.0 | 137% |
| R5 | −0.41 | −3.2 | 780% |
| R6 | −0.48 | −0.3 | 63% |
| R9 | −2.93 | −4.2 | 143% |
| R10 | −1.32 | −0.8 | 61% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Binczyk, M.; Kalitowski, P.; Szulwic, J.; Tysiac, P. Nondestructive Testing of the Miter Gates Using Various Measurement Methods. Sensors 2020, 20, 1749. https://doi.org/10.3390/s20061749
Binczyk M, Kalitowski P, Szulwic J, Tysiac P. Nondestructive Testing of the Miter Gates Using Various Measurement Methods. Sensors. 2020; 20(6):1749. https://doi.org/10.3390/s20061749
Chicago/Turabian StyleBinczyk, Mikolaj, Przemyslaw Kalitowski, Jakub Szulwic, and Pawel Tysiac. 2020. "Nondestructive Testing of the Miter Gates Using Various Measurement Methods" Sensors 20, no. 6: 1749. https://doi.org/10.3390/s20061749
APA StyleBinczyk, M., Kalitowski, P., Szulwic, J., & Tysiac, P. (2020). Nondestructive Testing of the Miter Gates Using Various Measurement Methods. Sensors, 20(6), 1749. https://doi.org/10.3390/s20061749