A Review on the Development of Tunable Graphene Nanoantennas for Terahertz Optoelectronic and Plasmonic Applications
Abstract
1. Introduction
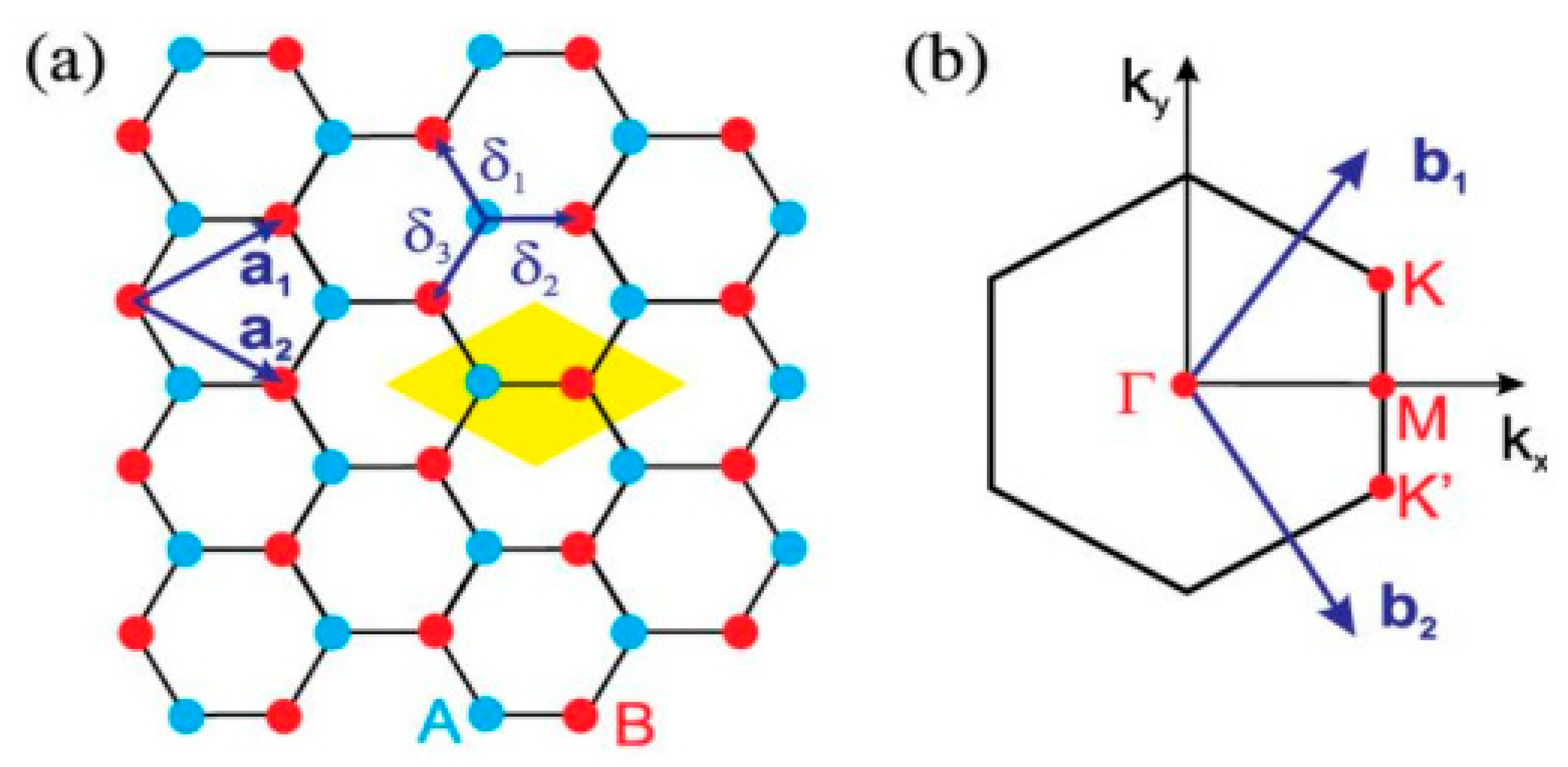
2. Structural Foundation and Modeling of Graphene
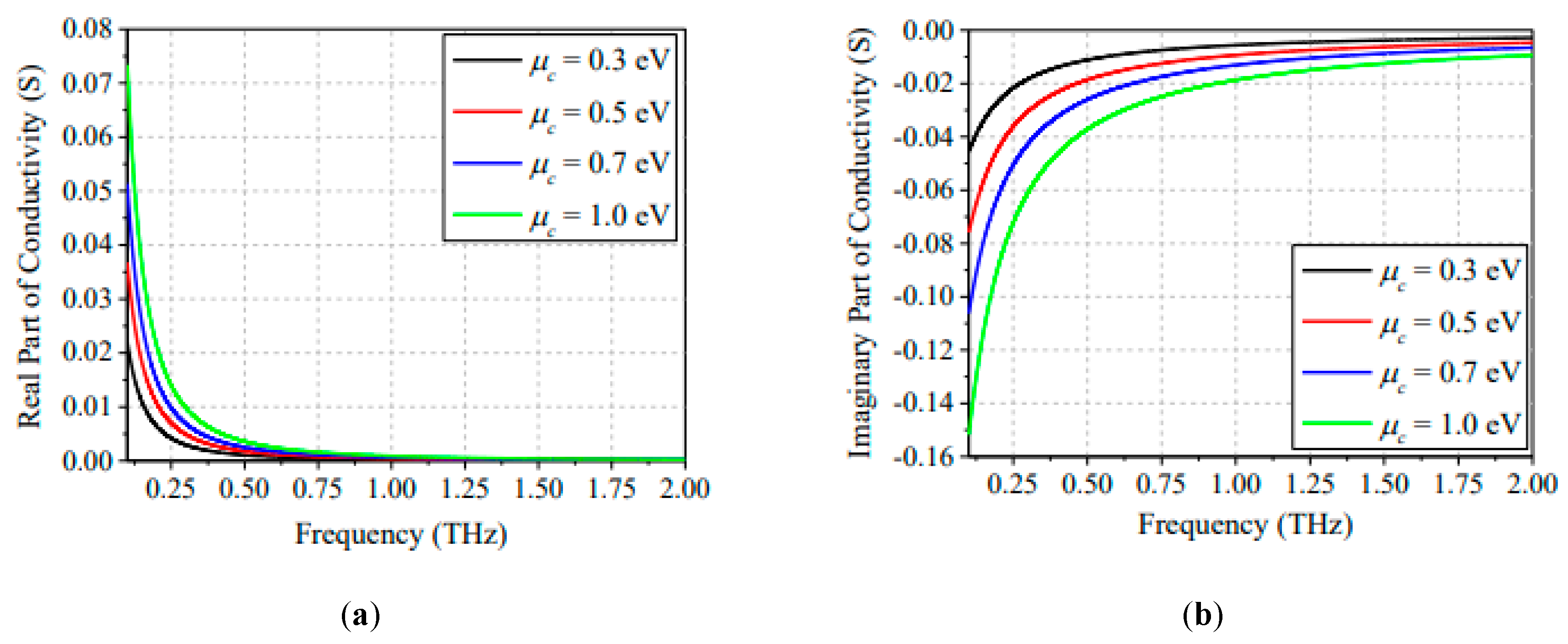
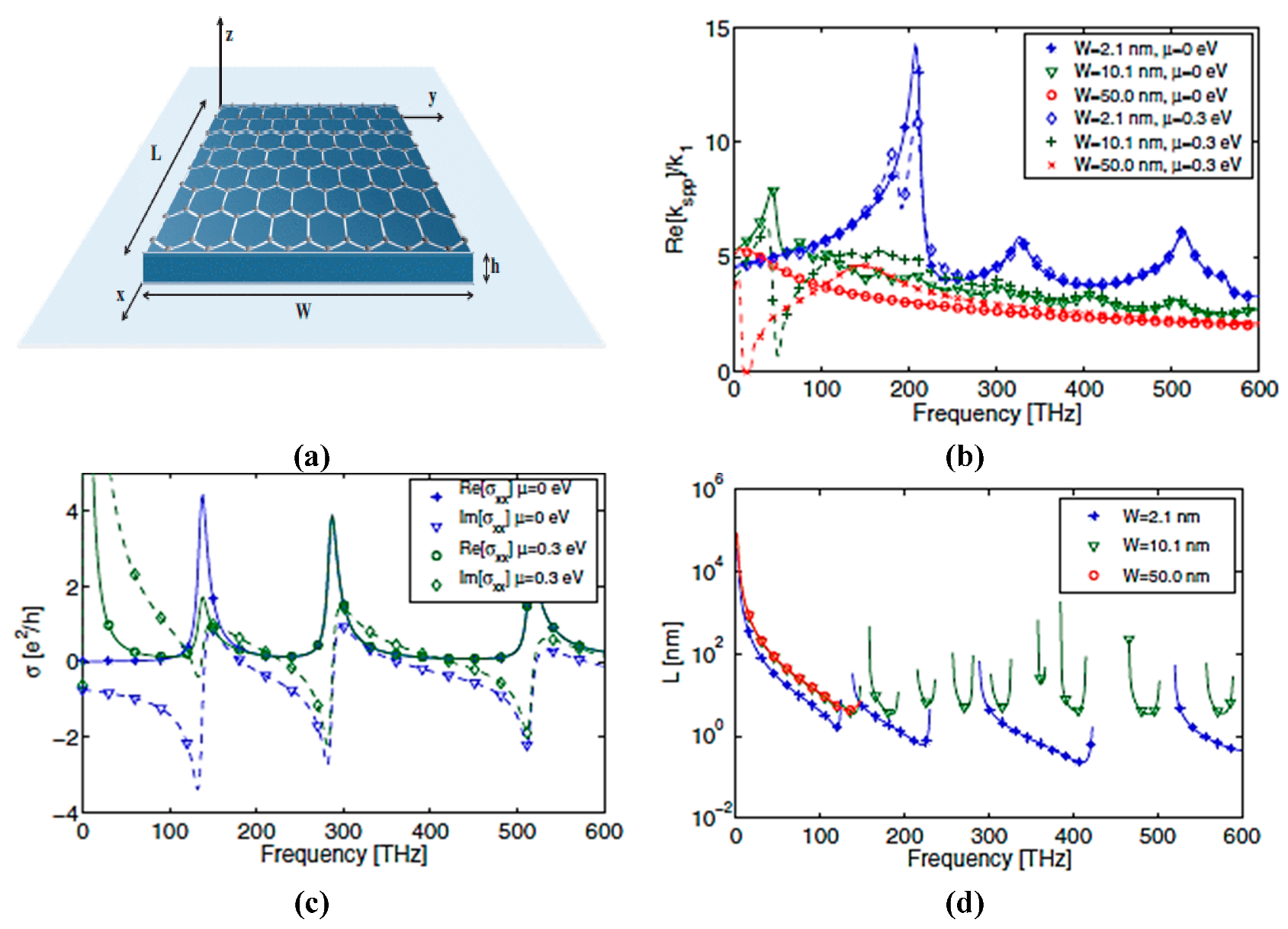
2.1. Surface Plasmon Resonance and Gate Tuning of Graphene Conductivity
2.2. Conductivity of Multi-Layer Stacked Graphene Sheets
2.3. Electromagnetic Interaction and Computational Modeling of Graphene Antenna Devices
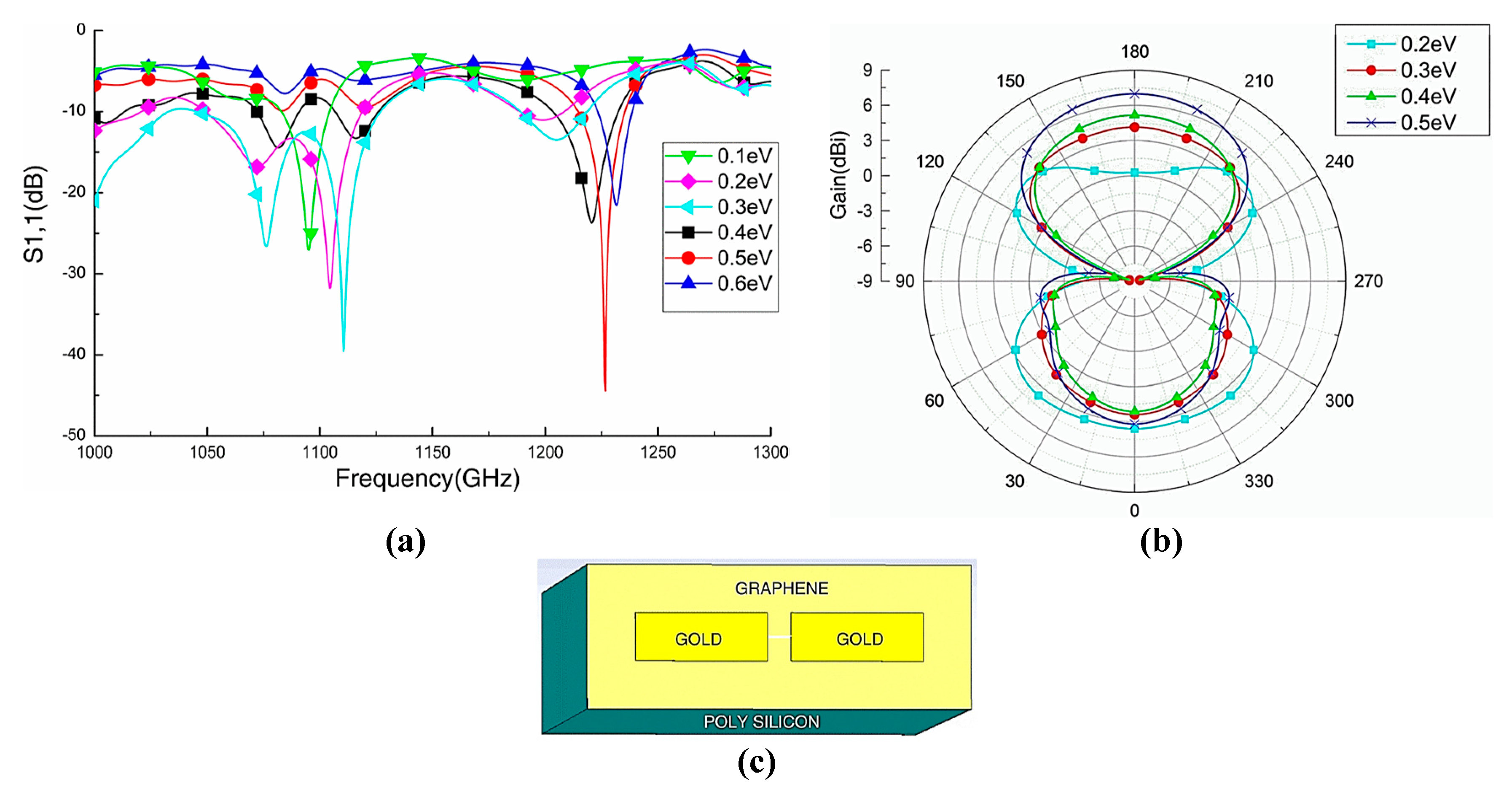
3. Graphene Resonant Terahertz Antennas
4. Tunable Hybrid Graphene–Metal Plasmonic Nanoantennas and Their Characteristics
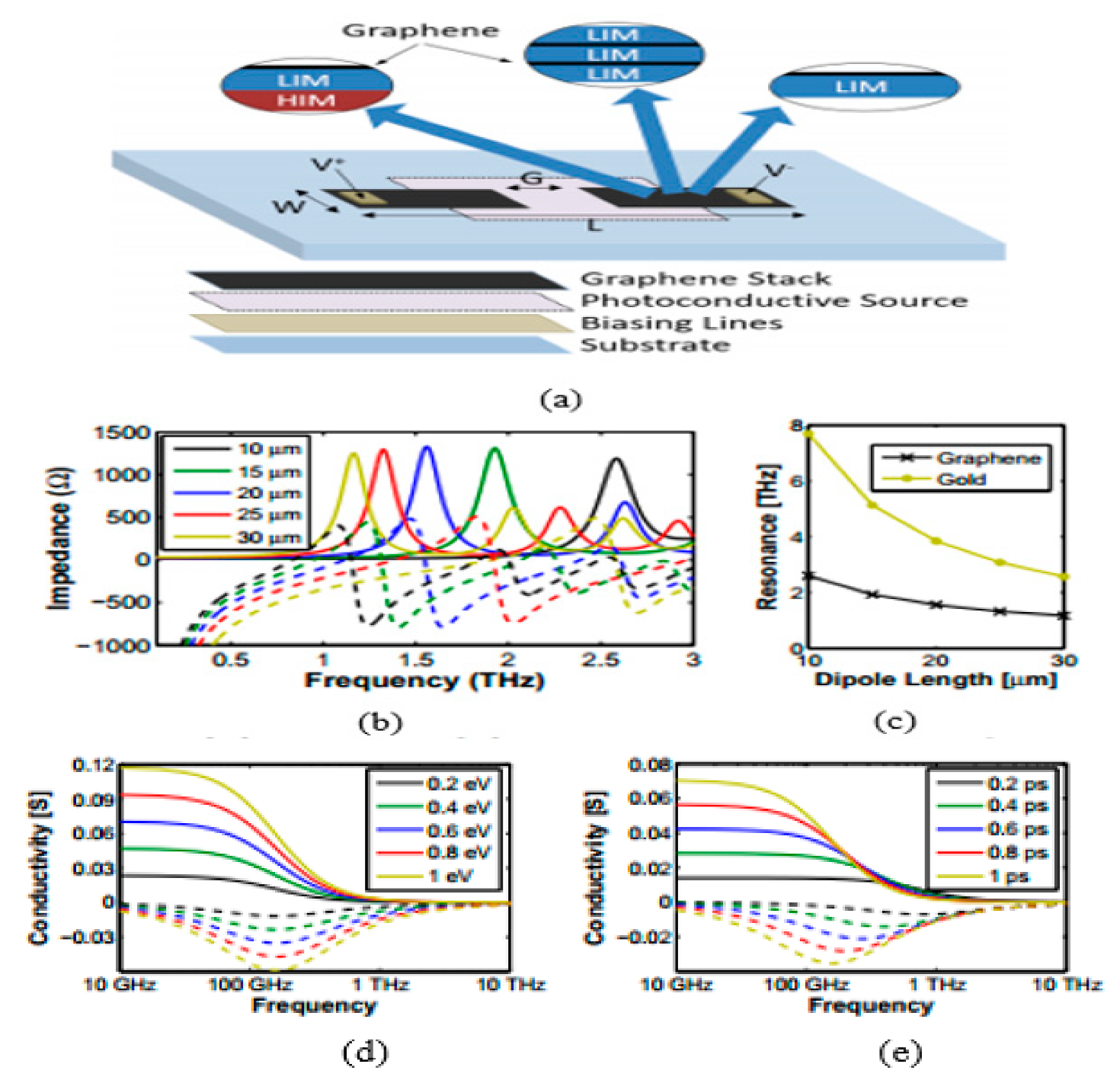
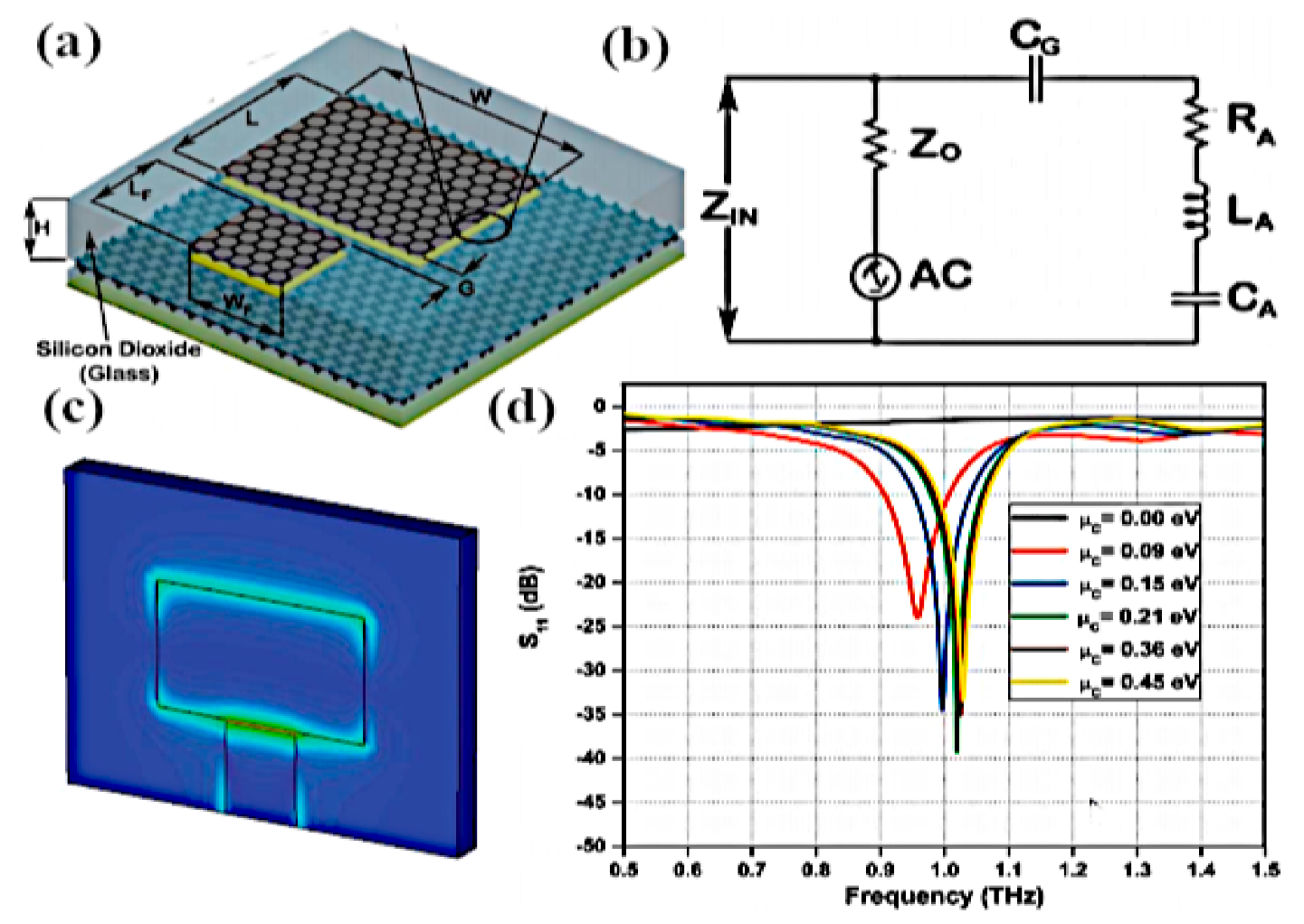
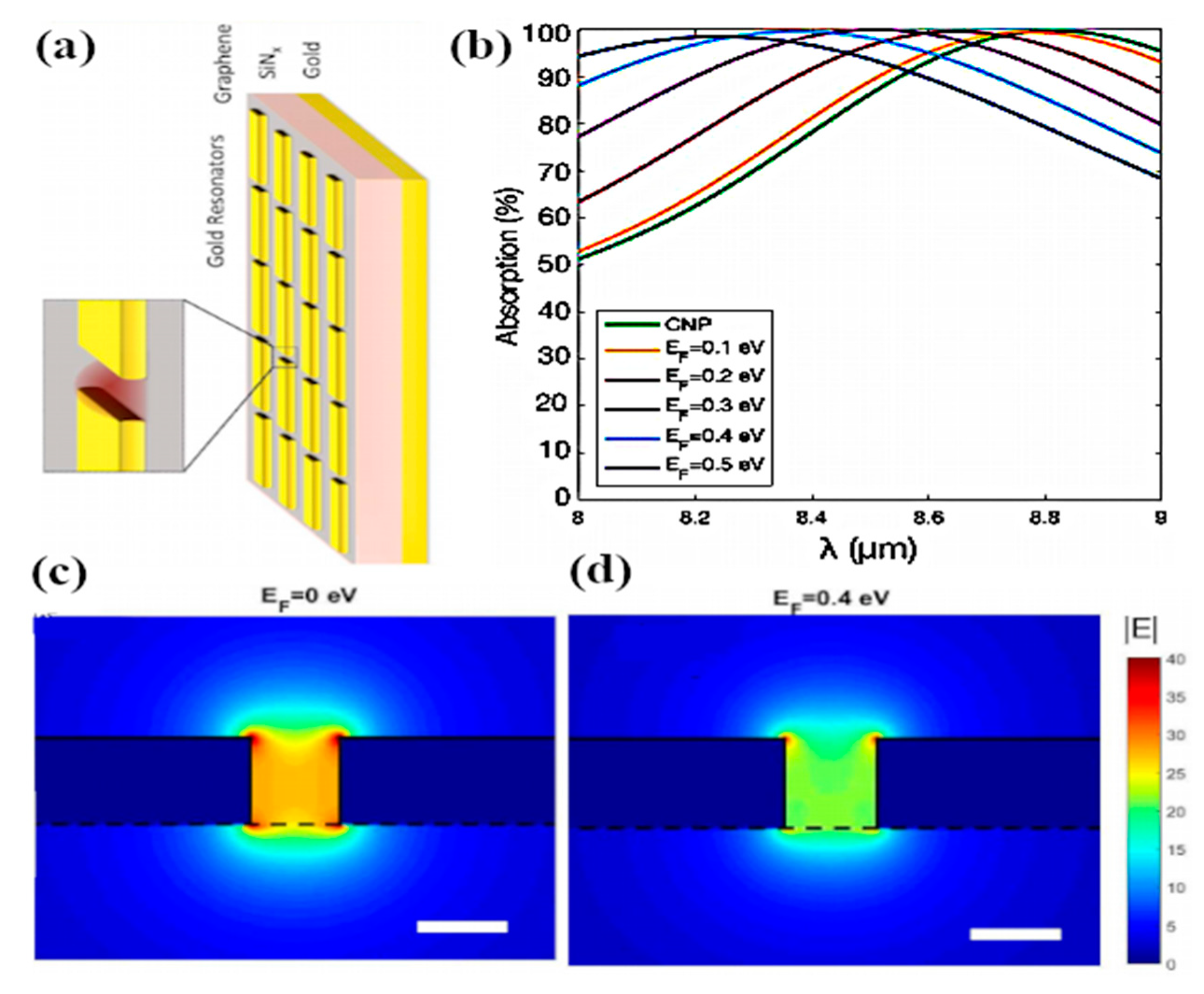
4.1. Tunable Absorption Handling in Graphene–Metal Antennas
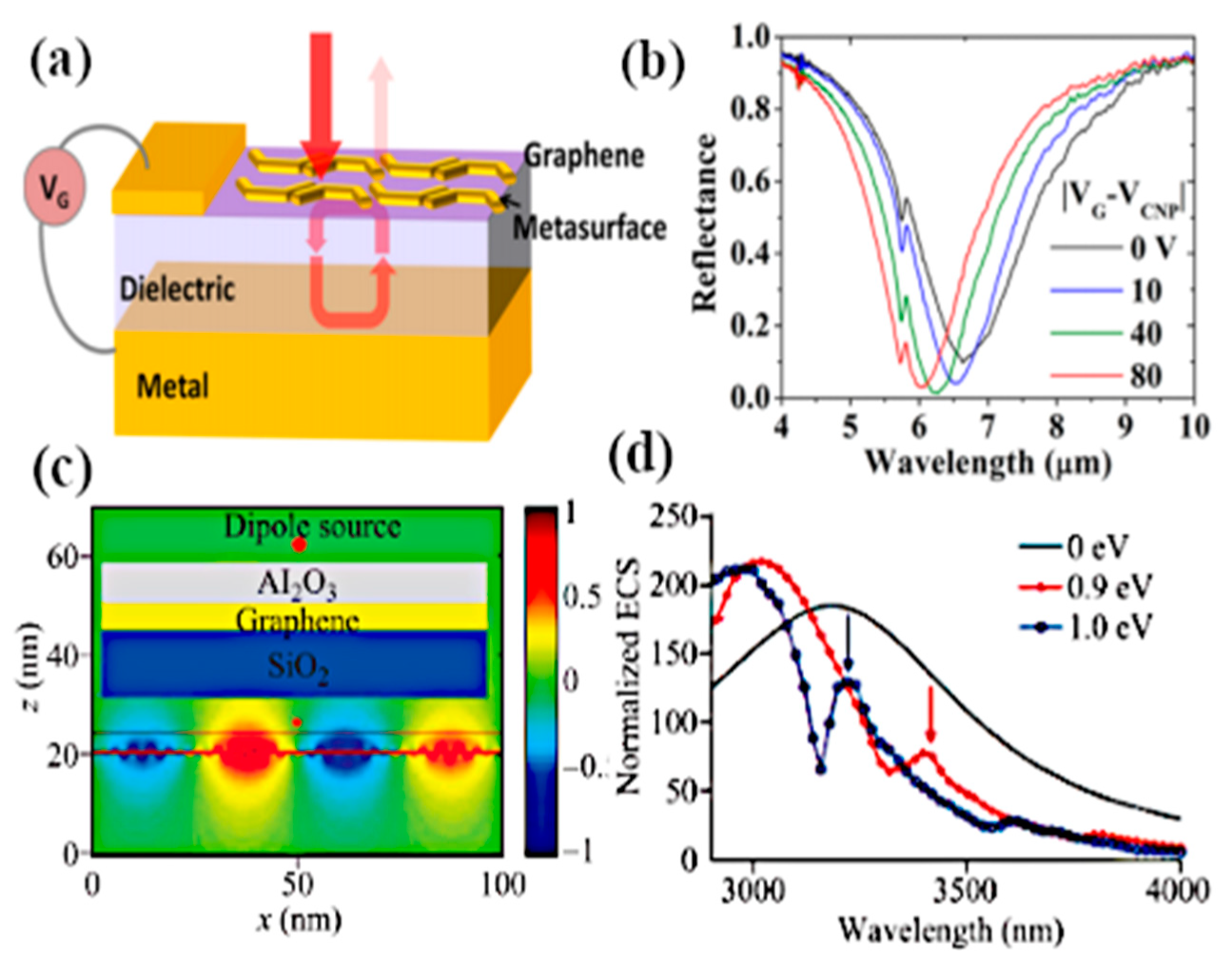
4.2. Modulation of Optical Features by Tuning Graphene Conductivity
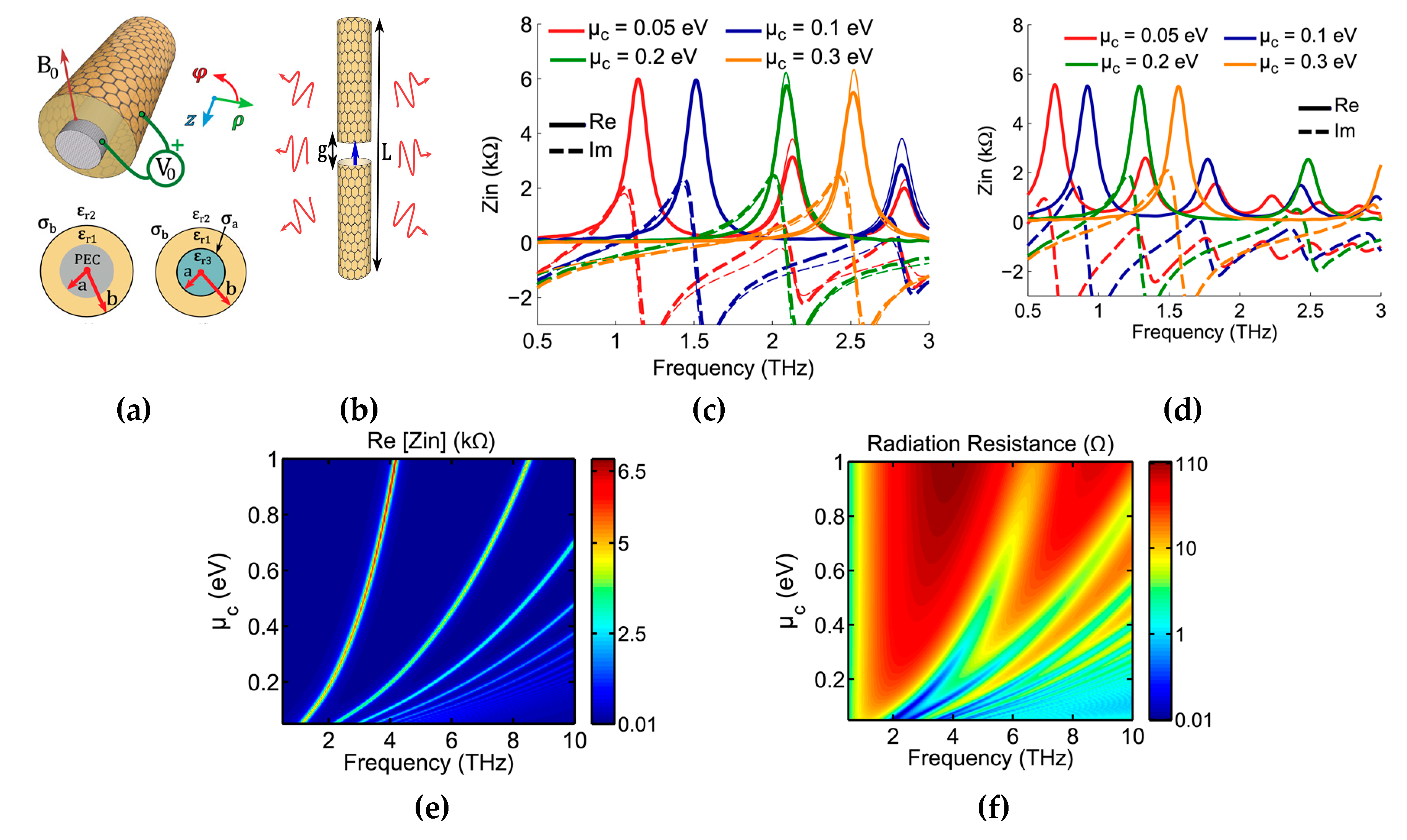
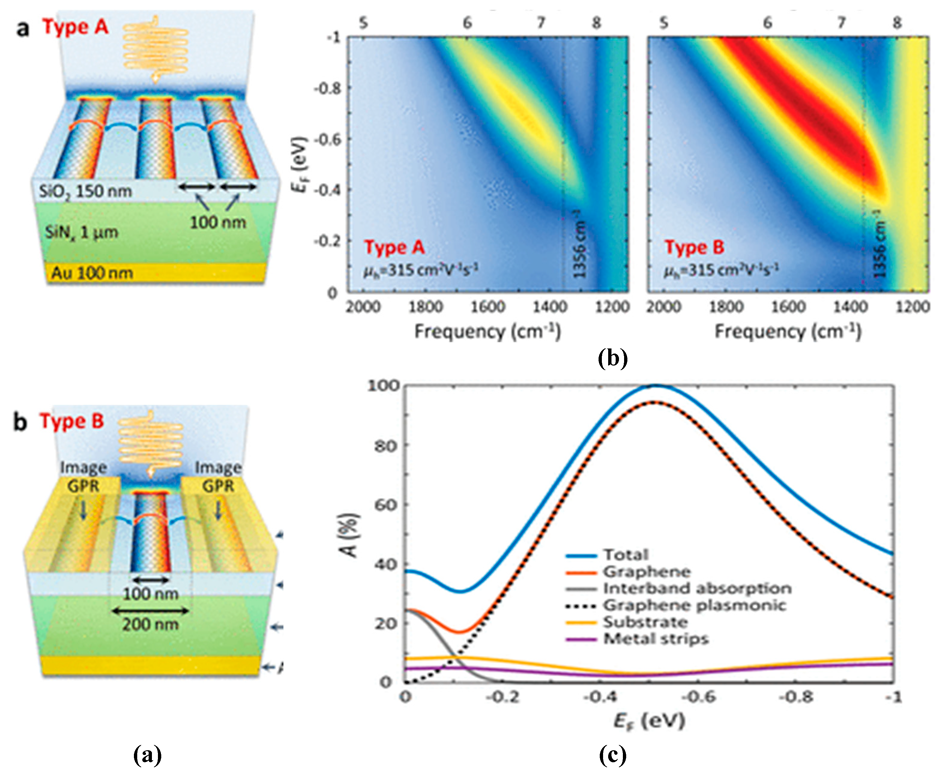
4.3. Effective Utilization of Graphene Plasmons
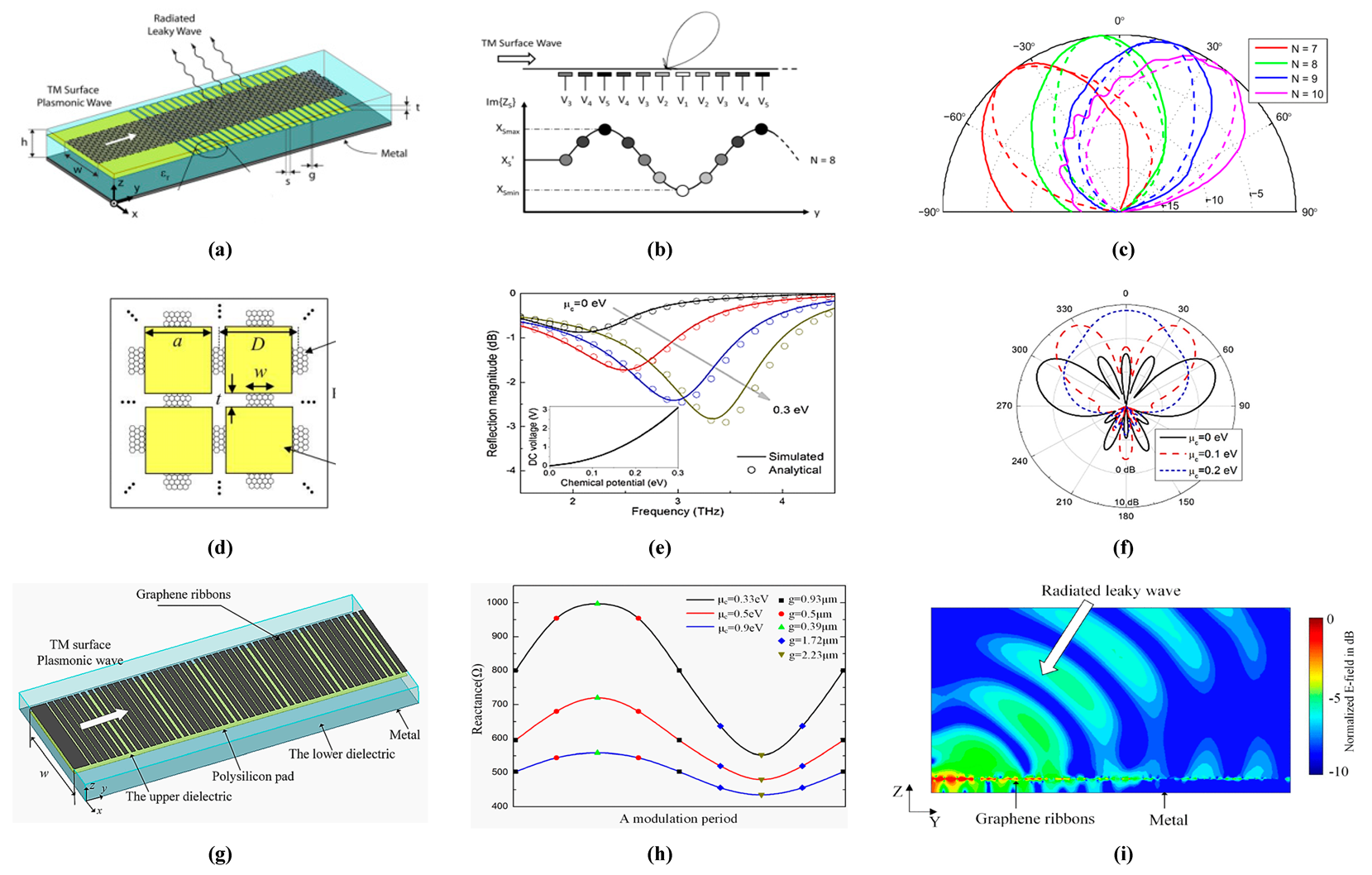
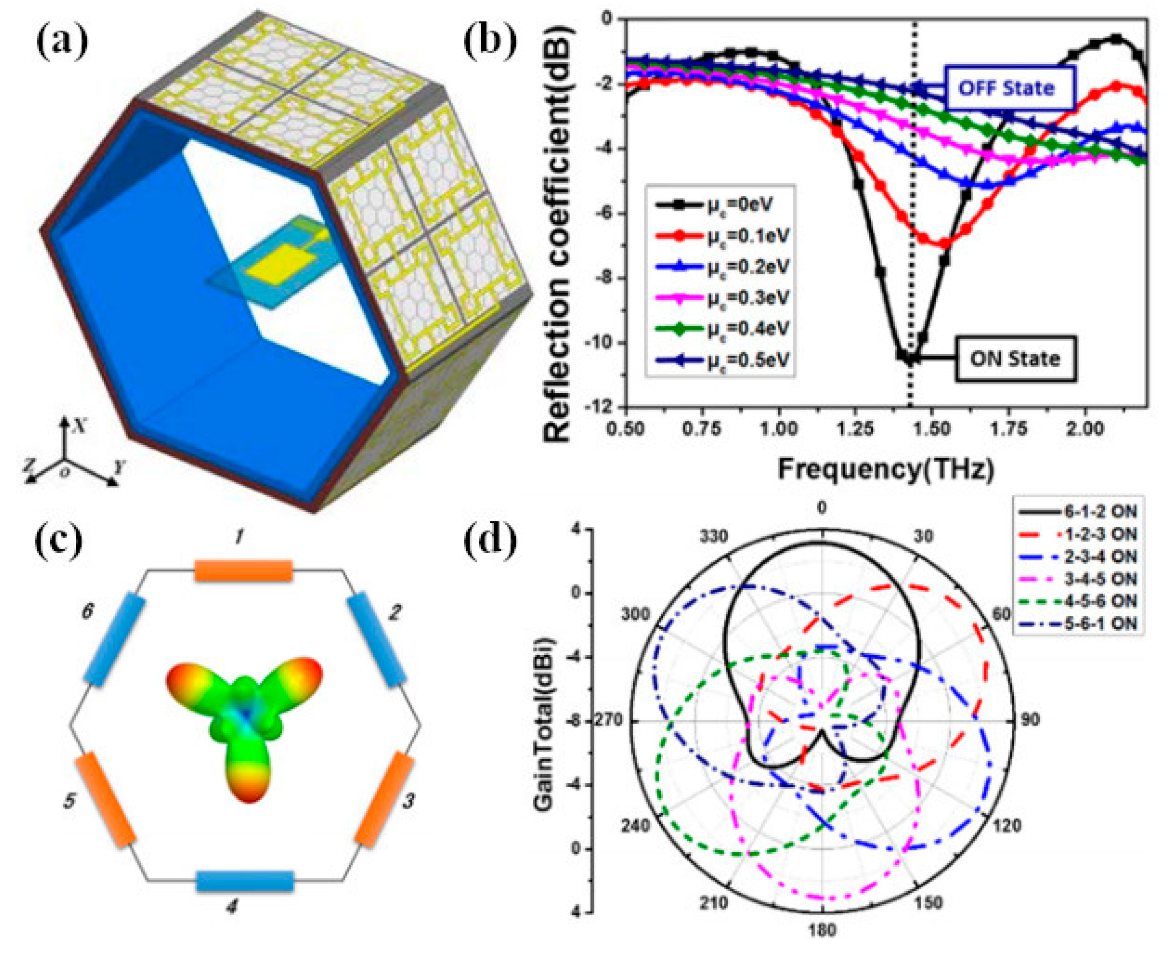
5. Graphene Leaky-Wave and Reflectarray Antennas for Frequency Tuning and Radiation Beam Scanning
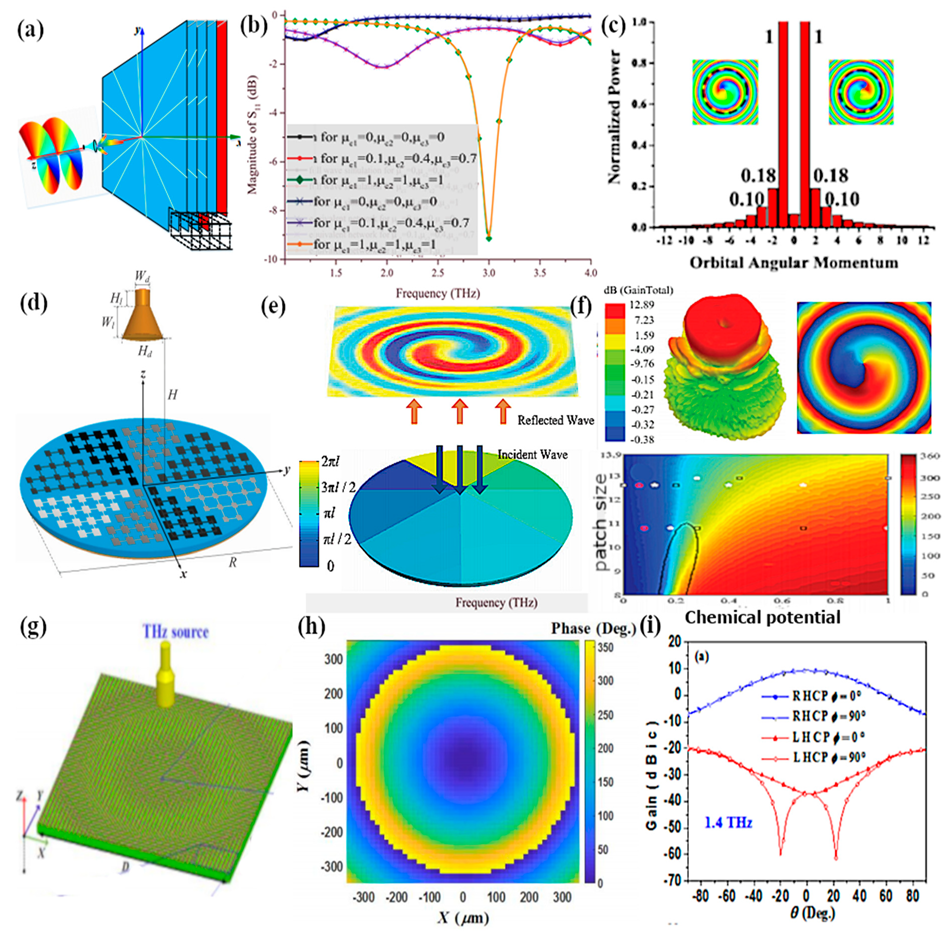
5.1. Graphene Reflectarrays for Vortex Beam Generation and Beam Scanning
5.2. Beam Steering Graphene Antennas and Phased Arrays
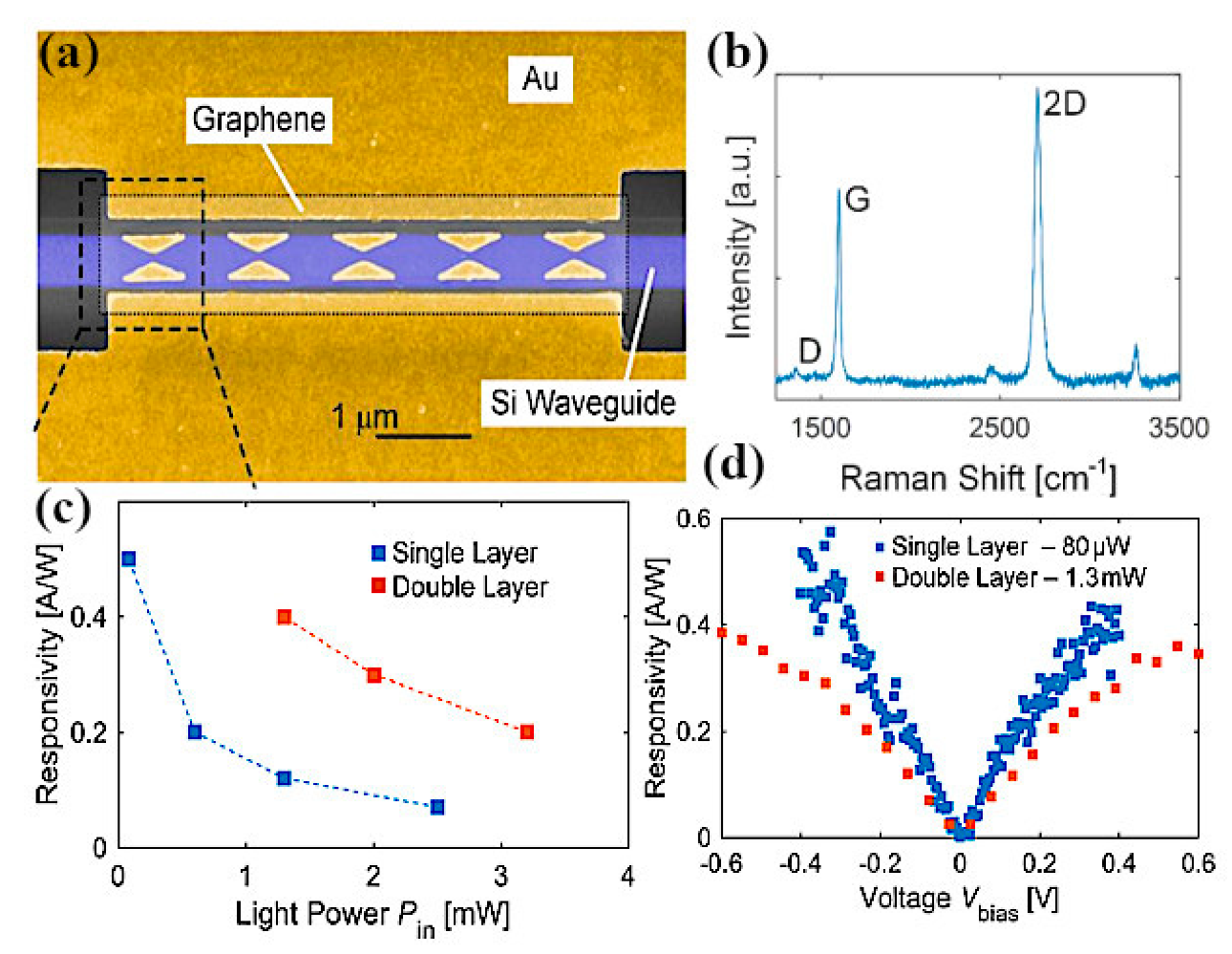
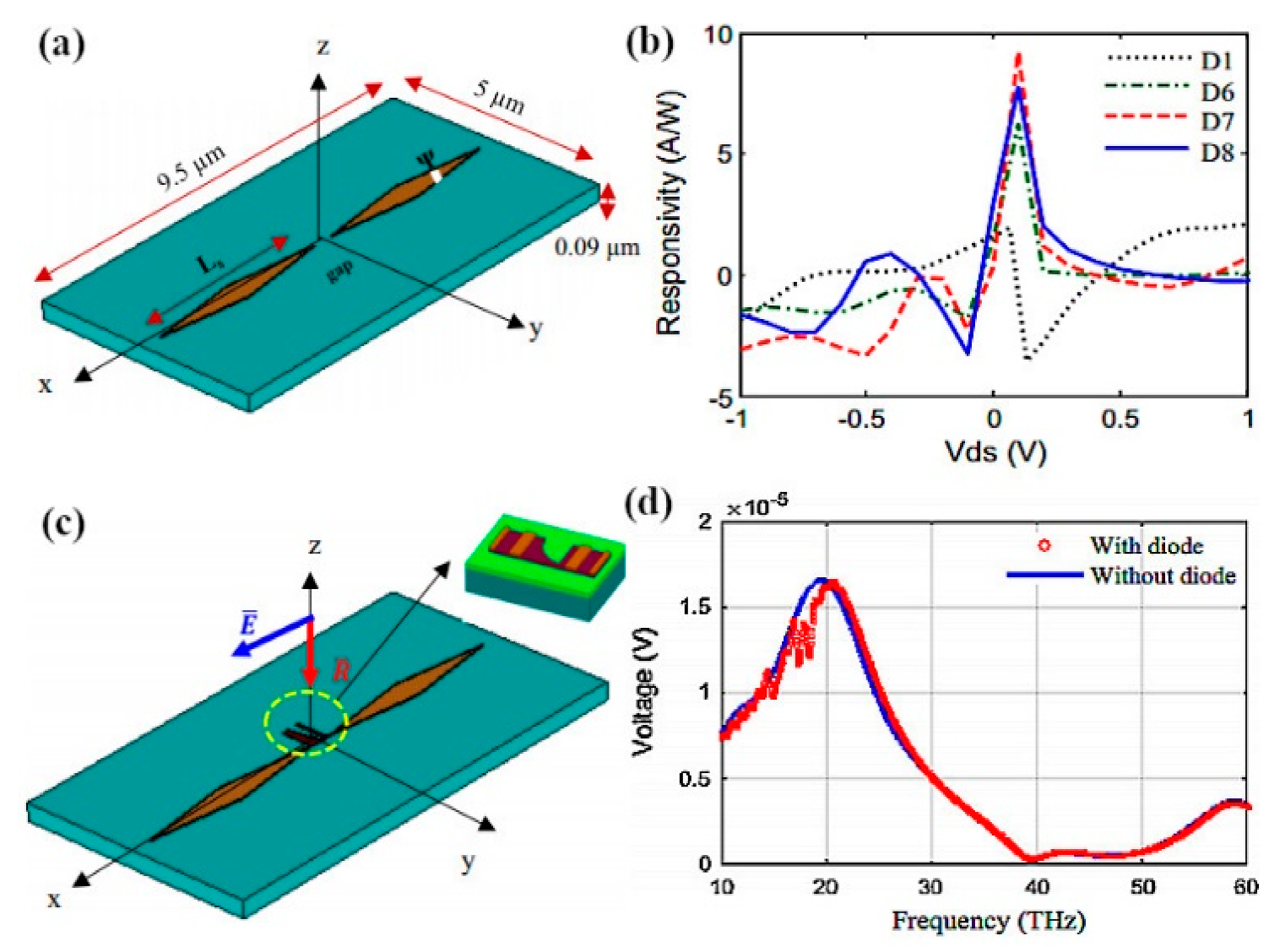
6. Graphene Antenna Enhanced Photodetectors
7. Graphene-Based Rectennas for Energy Harvesting Applications
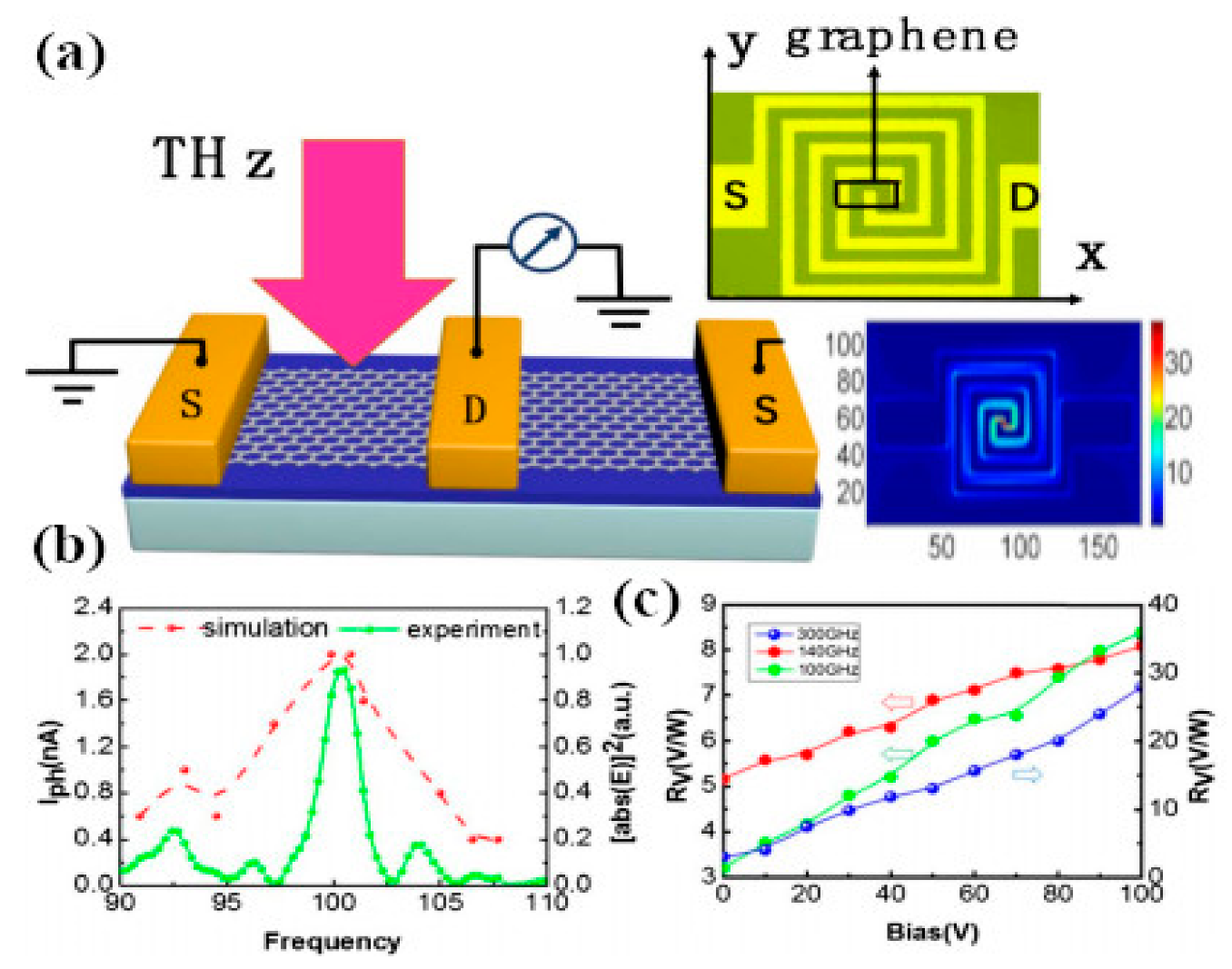
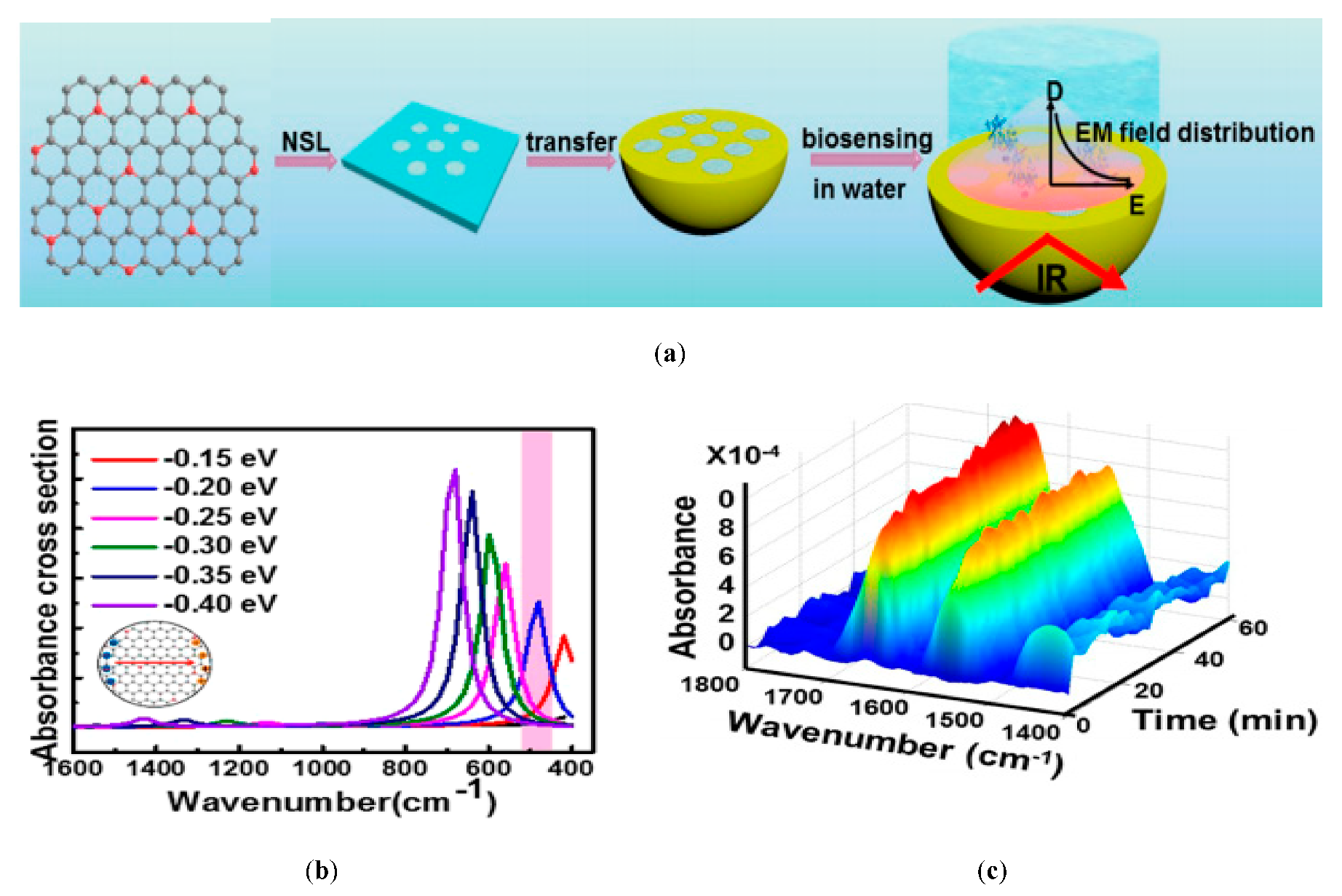
8. Graphene-Based Antennas for Plasmonic and Biosensing
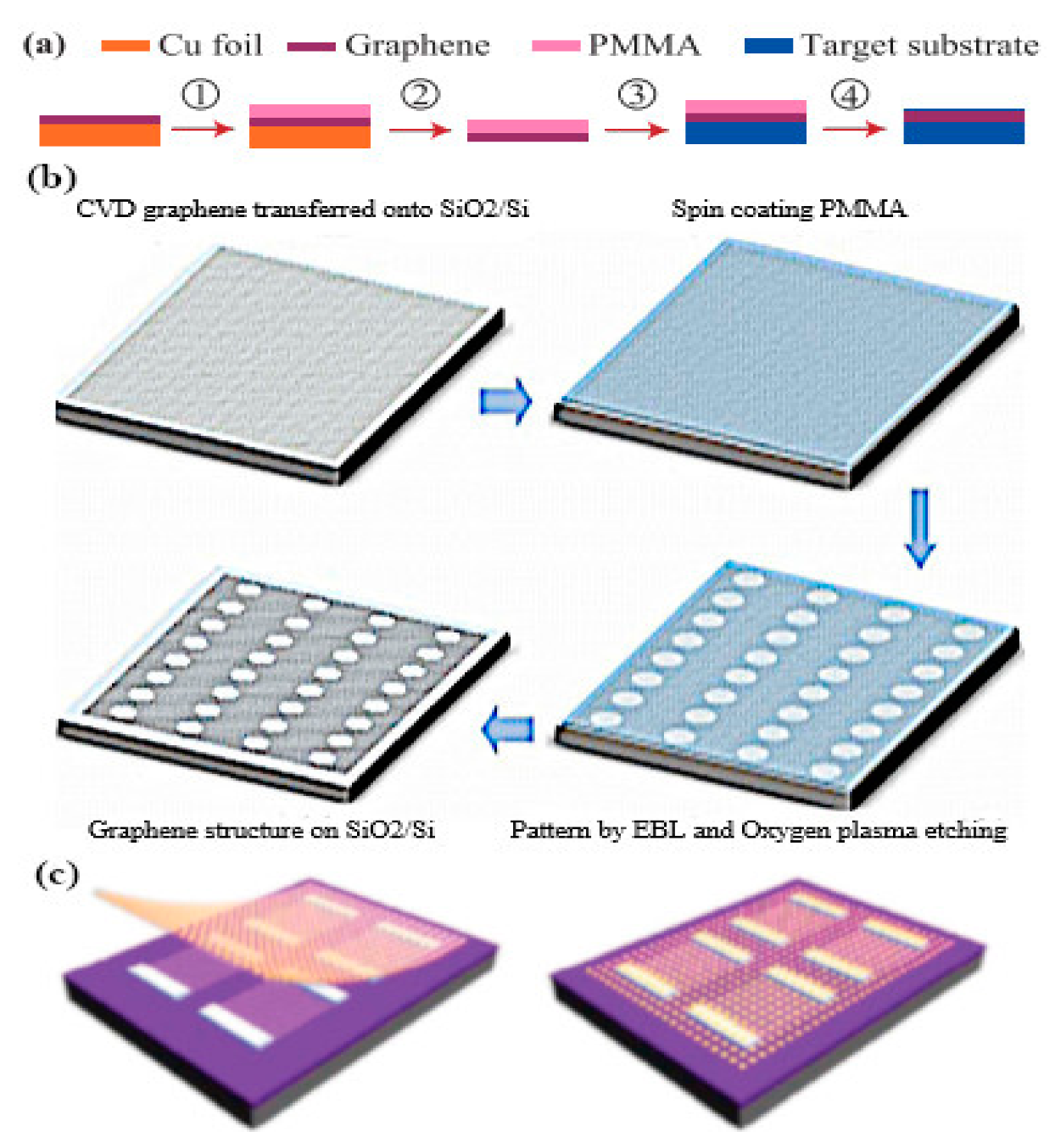
9. Synthesis of Graphene and the Fabrication of Graphene–Metal Plasmonic Nanoantennas
10. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stutzman, W.L.; Thiele, G.A. Antenna Theory and Design; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Liu, N.; Tang, M.L.; Hentschel, M.; Giessen, H.; Alivisatos, A.P. Nanoantenna-enhanced gas sensing in a single tailored nanofocus. Nat. Mater. 2011, 10, 631–636. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Langguth, L.; Weiss, T.; Kästel, J.; Fleischhauer, M.; Pfau, T.; Giessen, H. Plasmonic analogue of electromagnetically induced transparency at the Drude damping limit. Nat. Mater. 2009, 8, 758–762. [Google Scholar] [CrossRef] [PubMed]
- Aieta, F.; Genevet, P.; Kats, M.; Capasso, F. Aberrations of flat lenses and aplanatic metasurfaces. Opt. Express 2013, 21, 31530. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Chan, C.T.; Sheng, P. Transformation optics and metamaterials. Nat. Mater. 2010, 9, 387–396. [Google Scholar] [CrossRef] [PubMed]
- Ye, F.; Mihalache, D.; Hu, B.; Panoiu, N.C. Subwavelength vortical plasmonic lattice solitons. Opt. Lett. 2011, 36, 1179. [Google Scholar] [CrossRef] [PubMed]
- Xue, Y.; Ye, F.; Mihalache, D.; Panoiu, N.C.; Chen, X. Plasmonic lattice solitons beyond the coupled-mode theory. Laser Photonics Rev. 2014, 8, 52–57. [Google Scholar] [CrossRef]
- Lamminen, A.; Arapov, K.; De With, G.; Haque, S.; Sandberg, H.G.O.; Friedrich, H.; Ermolov, V. Graphene-Flakes Printed Wideband Elliptical Dipole Antenna for Low-Cost Wireless Communications Applications. IEEE Ant. and Wire. Prop. Lett. 2017, 16, 1883–1886. [Google Scholar] [CrossRef]
- Xu, Q.; Ma, T.; Danesh, M.; Shivananju, B.N.; Gan, S.; Song, J.; Qiu, C.-W.; Cheng, H.-M.; Ren, W.; Bao, Q. Effects of edge on graphene plasmons as revealed by infrared nanoimaging. Light-Sci. Appl. 2017, 6, e16204. [Google Scholar] [CrossRef]
- Kannegulla, A.; Shams, M.I.; Liu, L.B.; Cheng, L.-J. Photo-induced spatial modulation of THz waves: Opportunities and limitations. Opt. Express 2015, 23, 32098. [Google Scholar] [CrossRef]
- Bandurin, D.A.; Svintsov, D.; Gayduchenko, I.; Xu, S.G.; Principi, A.; Moskotin, M.; Tretyakov, I.; Yagodkin, D.; Zhukov, S.; Taniguchi, T.; et al. Resonant terahertz detection using graphene plasmons. Nat. Comm. 2018, 9, 4–11. [Google Scholar] [CrossRef]
- Zangeneh-Nejad, F.; Safian, R. Significant enhancement in the efficiency of photoconductive antennas using a hybrid graphene molybdenum disulphide structure. J. Nanophotonics 2016, 10, 036005. [Google Scholar] [CrossRef]
- Mehta, B.; Benkstein, K.D.; Semancik, S.; Zaghloul, M.E. Gas Sensing with Bare and Graphene-covered Optical Nano-Antenna Structures. Sci. Rep. 2016, 6, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Weiss, T.; Mesch, M.; Langguth, L.; Eigenthaler, U.; Hirscher, M.; Sönnichsen, C.; Giessen, H. Planar metamaterial analogue of electromagnetically induced transparency for plasmonic sensing. Nano Lett. 2010, 10, 1103–1107. [Google Scholar] [CrossRef] [PubMed]
- Manjavacas, A.; Nordlander, P.; García De Abajo, F.J. Plasmon blockade in nanostructured graphene. ACS Nano 2012, 6, 1724–1731. [Google Scholar] [CrossRef] [PubMed]
- Walasik, W.; Nazabal, V.; Chauvet, M.; Kartashov, Y.; Renversez, G. Low-power plasmon–soliton in realistic nonlinear planar structures. Opt. Lett. 2012, 37, 4579. [Google Scholar] [CrossRef]
- Conforti, M.; De Angelis, C.; Akylas, T.R. Energy localization and transport in binary waveguide arrays. Phys. Rev. A 2011, 83, 043822. [Google Scholar] [CrossRef]
- Bozhevolnyi, S.I.; Volkov, V.S.; Devaux, E.; Ebbesen, T.W. Channel plasmon-polariton guiding by subwavelength metal grooves. Phys. Rev. Lett. 2005, 95, 1–4. [Google Scholar] [CrossRef]
- Metzger, B.; Hentschel, M.; Schumacher, T.; Lippitz, M.; Ye, X.; Murray, C.B.; Knabe, B.; Buse, K.; Giessen, H. Doubling the Efficiency of Third Harmonic Generation by Positioning. Nano Lett. 2014, 14, 2467–2872. [Google Scholar] [CrossRef]
- Soukoulis, C.M.; Zhou, J.; Koschny, T.; Kafesaki, M.; Economou, E.N. The science of negative index materials. J. Phys. Condens. Matter 2008, 20, 304217. [Google Scholar] [CrossRef]
- Biagioni, P.; Huang, J.S.; Hecht, B. Nanoantennas for visible and infrared radiation. Rep. Prog. Phys. 2012, 75, 024402. [Google Scholar] [CrossRef]
- Kolomenski, A.; Kolomenskii, A.; Noel, J.; Peng, S.; Schuessler, H. Propagation length of surface plasmons in a metal film with roughness. Appl. Opt. 2009, 48, 5683. [Google Scholar] [CrossRef] [PubMed]
- Lindquist, N.C.; Nagpal, P.; McPeak, K.M.; Norris, D.J.; Oh, S.H. Engineering metallic nanostructures for plasmonics and nanophotonics. Rep. Prog. Phys. 2012, 75, 036501. [Google Scholar] [CrossRef] [PubMed]
- Tassin, P.; Koschny, T.; Kafesaki, M.; Soukoulis, C.M. A comparison of graphene, superconductors and metals as conductors for metamaterials and plasmonics. Nat. Photonics 2012, 6, 259–264. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric fild effct in atomically thin carbon fims. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Avouris, P. Graphene: Electronic and photonic properties and devices. Nano Lett. 2010, 10, 4285–4294. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
- Gómez-Díaz, J.S.; Perruisseau-Carrier, J.; Sharma, P.; Ionescu, A. Non-contact characterization of graphene surface impedance at micro and millimeter waves. J. Appl. Phys. 2012, 111, 114908. [Google Scholar] [CrossRef]
- Lovat, G. Equivalent circuit for electromagnetic interaction and transmission through graphene sheets. IEEE Trans. Electromagn. Compat. 2012, 54, 101–109. [Google Scholar] [CrossRef]
- Feo, O.D.; Kennedy, M.P.; Bernardo, M.D.; Mykolatis, G.; Bumeliene, S.; Cenys, A.; Lindberg, E.; Chou, H.C.; Chou, J.H.; Technol, M.O.; et al. A Broadband Array of Archimedean Spiral Antennas. Microw. Opt. Technol. Lett. 2013, 48, 195–200. [Google Scholar]
- Nagatsuma, T.; Ducournau, G.; Renaud, C.C. Advances in terahertz communications accelerated by photonics. Nat. Photonics 2016, 10, 371–379. [Google Scholar] [CrossRef]
- Yoon, H.J.; Jun, D.H.; Yang, J.H.; Zhou, Z.; Yang, S.S.; Cheng, M.M.C. Carbon dioxide gas sensor using a graphene sheet. Sensors Actuat. B-Chem. 2011, 157, 310–313. [Google Scholar] [CrossRef]
- Llatser, I.; Kremers, C.; Cabellos-Aparicio, A.; Jornet, J.M.; Alarcón, E.; Chigrin, D.N. Graphene-based nano-patch antenna for terahertz radiation. Photonics Nanostruct. - Fundam. Appl. 2012, 10, 353–358. [Google Scholar] [CrossRef]
- Martí, I.L.; Kremers, C.; Cabellos-Aparicio, A.; Jornet, J.M.; Alarcón, E.; Chigrin, D.N. Scattering of terahertz radiation on a graphene-based nano-antenna. In AIP Conference Proceedings; American Institute of Physics: New York, NY, USA, 2011; Volume 1398, pp. 144–146. [Google Scholar]
- Gomez-Diaz, J.S.; Perruisseau-Carrier, J. Graphene-based plasmonic switches at near infrared frequencies. 2013, 21, 15490–15504. Opt. Exp. 2013, 21, 15490–15504. [Google Scholar]
- Correas-Serrano, D.; Gomez-Diaz, J.S.; Sounas, D.L.; Hadad, Y.; Alvarez-Melcon, A.; Alu, A. Nonreciprocal Graphene Devices and Antennas Based on Spatiotemporal Modulation. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 1529–1533. [Google Scholar] [CrossRef]
- Correas-Serrano, D.; Gomez-Diaz, J.S.; Alvarez-Melcon, A. On the influence of spatial dispersion on the performance of graphene-based plasmonic devices. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 345–348. [Google Scholar] [CrossRef]
- Sounas, D.L.; Caloz, C. Edge surface modes in magnetically biased chemically doped graphene strips. Appl. Phys. Lett. 2011, 99, 2011–2014. [Google Scholar] [CrossRef]
- Estep, N.A.; Sounas, D.L.; Alù, A. Magnetless Microwave Circulators Based on Spatiotemporally Modulated Rings of Coupled Resonators. IEEE Trans. Microw. Theory Tech. 2016, 64, 502–518. [Google Scholar] [CrossRef]
- Perruisseau-Carrier, J.; Tamagnone, M.; Gomez-Diaz, J.S.; Carrasco, E. Graphene antennas: Can integration and reconfigurability compensate for the loss? In European Microwave Week 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 369–372. [Google Scholar]
- Fallahi, A.; Perruisseau-Carrier, J. Manipulation of giant Faraday rotation in graphene metasurfaces. Appl. Phys. Lett. 2012, 101, 1–5. [Google Scholar] [CrossRef]
- Hadad, Y.; Soric, J.C.; Alu, A. Breaking temporal symmetries for emission and absorption. Proc. Natl. Acad. Sci. USA 2016, 113, 3471–3475. [Google Scholar] [CrossRef]
- Woessner, A.; Lundeberg, M.B.; Gao, Y.; Principi, A.; Alonso-González, P.; Carrega, M.; Watanabe, K.; Taniguchi, T.; Vignale, G.; Polini, M.; et al. Highly confined low-loss plasmons in graphene-boron nitride heterostructures. Nat. Mater. 2015, 14, 421–425. [Google Scholar] [CrossRef]
- Tielrooij, K.J.; Piatkowski, L.; Massicotte, M.; Woessner, A.; Ma, Q.; Lee, Y.; Myhro, K.S.; Lau, C.N.; Jarillo-Herrero, P.; Van Hulst, N.F.; et al. Generation of photovoltage in graphene on a femtosecond timescale through efficient carrier heating. Nat. Nanotechnol. 2015, 10, 437–443. [Google Scholar] [CrossRef] [PubMed]
- Brar, V.W.; Jang, M.S.; Sherrott, M.; Kim, S.; Lopez, J.J.; Kim, L.B.; Choi, M.; Atwater, H. Hybrid surface-phonon-plasmon polariton modes in graphene/monolayer h-BN heterostructures. Nano Lett. 2014, 14, 3876–3880. [Google Scholar] [CrossRef] [PubMed]
- Phare, C.T.; Daniel Lee, Y.H.; Cardenas, J.; Lipson, M. Graphene electro-optic modulator with 30 GHz bandwidth. Nat. Photonics 2015, 9, 511–514. [Google Scholar] [CrossRef]
- Sensale-Rodriguez, B.; Yan, R.; Kelly, M.M.; Fang, T.; Tahy, K.; Hwang, W.S.; Jena, D.; Liu, L.; Xing, H.G. Broadband graphene terahertz modulators enabled by intraband transitions. Nat. Commun. 2012, 3, 780–787. [Google Scholar] [CrossRef] [PubMed]
- Vicarelli, L.; Vitiello, M.S.; Coquillat, D.; Lombardo, A.; Ferrari, A.C.; Knap, W.; Polini, M.; Pellegrini, V.; Tredicucci, A. Graphene field-effect transistors as room-temperature terahertz detectors. Nat. Mater. 2012, 11, 865–871. [Google Scholar] [CrossRef]
- Dean, C.R.; Young, A.F.; Meric, I.; Lee, C.; Wang, L.; Sorgenfrei, S.; Watanabe, K.; Taniguchi, T.; Kim, P.; Shepard, K.L.; et al. Boron nitride substrates for high-quality graphene electronics. Nat. Nanotechnol. 2010, 5, 722–726. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, Y.X.; Yu, H.H.; Zhang, H.J.; Yang, R.L.; Yang, B.C.; Liu, Z.Y.; Wang, J.Y. Broadband Black Phosphorus Optical Modulator in the Spectral Range from Visible to Mid-Infrared. Adv. Opt. Mater. 2015, 3, 1787–1792. [Google Scholar] [CrossRef]
- Sensale-Rodriguez, B.; Rafique, S.; Yan, R.; Zhu, M.; Protasenko, V.; Jena, D.; Liu, L.; Xing, H.G.; Liu, H.; Zhong, H.; et al. Terahertz imaging employing graphene modulator arrays " Terahertz Spectroscopy and Imaging for Defense and Security Applications. Opt. Commun 2007, 281, 1514–1527. [Google Scholar]
- Fo, Q.; Pan, L.; Chen, X.; Xu, Q.; Ouyang, C.; Zhang, X.; Tian, Z.; Gu, J.; Liu, L.; Han, J.; et al. Anisotropic Plasmonic Response of Black Phosphorus Nanostrips in Terahertz Metamaterials. IEEE Photonics J. 2018, 10, 1–9. [Google Scholar] [CrossRef]
- Lu, J.; Yang, J.; Carvalho, A.; Liu, H.; Lu, Y.; Sow, C.H. Light-Matter Interactions in Phosphorene. Acc. Chem. Res. 2016, 49, 1806–1815. [Google Scholar] [CrossRef]
- Nguyen, B.H.; Nguyen, V.H. Two-dimensional hexagonal semiconductors beyond graphene. Adv. Nat. Sci. Nanosci. Nanotechnol. 2016, 7, 1–18. [Google Scholar] [CrossRef]
- Morell, N.; Reserbat-Plantey, A.; Tsioutsios, I.; Schädler, K.G.; Dubin, F.; Koppens, F.H.L.; Bachtold, A. High Quality Factor Mechanical Resonators Based on WSe2 Monolayers. Nano Lett. 2016, 16, 5102–5108. [Google Scholar] [CrossRef] [PubMed]
- Correas-Serrano, D.; Gomez-Diaz, J.S.; Melcon, A.A.; Alù, A. Black phosphorus plasmonics: Anisotropic elliptical propagation and nonlocality-induced canalization. J. Opt. 2016, 18, 1–10. [Google Scholar] [CrossRef]
- Milovanović, S.P.; Peeters, F.M. Strained Graphene Structures: From Valleytronics to Pressure Sensing; NATO Science for Peace and Security Series A: Chemistry and Biology; Springer: Dordrecht, Netherlands, 2018; Volume 4, pp. 3–17. ISBN 978-94-024-1304-5. [Google Scholar]
- Sounas, D.L.; Caloz, C. Graphene-based non-reciprocal spatial isolator. In Proceedings of the 2011 IEEE International Symposium on Antennas and Propagation, Spokane, WA, USA, 3–8 July 2011; pp. 1597–1600. [Google Scholar]
- Novoselov, K.S.; Fal’Ko, V.I.; Colombo, L.; Gellert, P.R.; Schwab, M.G.; Kim, K. A roadmap for graphene. Nature 2012, 490, 192–200. [Google Scholar] [CrossRef] [PubMed]
- Svintsov, D.; Devizorova, Z.; Otsuji, T.; Ryzhii, V. Plasmons in tunnel-coupled graphene layers: Backward waves with quantum cascade gain. Phys. Rev. B 2016, 94, 115301. [Google Scholar] [CrossRef]
- Bagheri, S.; Mansouri, N.; Aghaie, E. Phosphorene: A new competitor for graphene. Int. J. Hydrog. Energy 2016, 41, 4085–4095. [Google Scholar] [CrossRef]
- Correas-Serrano, D.; Gomez-Diaz, J.S.; Perruisseau-Carrier, J.; Álvarez-Melcón, A. Spatially dispersive graphene single and parallel plate waveguides: Analysis and circuit model. IEEE Trans. Microw. Theory Tech. 2013, 61, 4333–4344. [Google Scholar] [CrossRef]
- Correas-Serrano, D.; Gomez-Diaz, J.S.; Perruisseau-Carrier, J.; Alvarez-Melcon, A. Graphene-based plasmonic tunable low-pass filters in the terahertz band. IEEE Trans. Nanotechnol. 2014, 13, 1145–1153. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, Z.; Hao, Z.; DiMarco, C.; Maturavongsadit, P.; Hao, Y.; Lu, M.; Stein, A.; Wang, Q.; Hone, J.; et al. Optical conductivity-based ultrasensitive mid-infrared biosensing on a hybrid metasurface. Light-Sci. Appl. 2018, 7, 1–11. [Google Scholar] [CrossRef]
- Nayyeri, V.; Soleimani, M.; Ramahi, O.M. Modeling Graphene in the finite-difference time-domain method using a surface boundary condition. IEEE Trans. Antennas Propag. 2013, 61, 4176–4182. [Google Scholar] [CrossRef]
- Shao, Y.; Yang, J.J.; Huang, M. A Review of Computational Electromagnetic Methods for Graphene Modeling. Int. J. Antennas Propag. 2016, 2016, 1–9. [Google Scholar] [CrossRef]
- Yao, Y.; Kats, M.A.; Genevet, P.; Yu, N.; Song, Y.; Kong, J.; Capasso, F. Broad electrical tuning of graphene-loaded optical antennas. In Proceedings of the Cleo: 2013, San Jose, CA, USA, 9–14 June 2013. [Google Scholar]
- Portela, G.; Dmitriev, V.; Oliveira, C.; Castro, W. Theoretical study of plasmonically induced transparency effect in arrays of graphene-based double disk resonators. J. Microw. Optoelectron. Electromagn. Appl. 2019, 18, 114–125. [Google Scholar] [CrossRef]
- Boubanga-Tombet, S.; Chan, S.; Watanabe, T.; Satou, A.; Ryzhii, V.; Otsuji, T. Ultrafast carrier dynamics and terahertz emission in optically pumped graphene at room temperature. Phys. Rev. B Condens. Matter 2012, 85, 3–8. [Google Scholar] [CrossRef]
- Sounas, D.L.; Caloz, C. Gyrotropy and nonreciprocity of graphene for microwave applications. IEEE Trans. Microw. Theory Tech. 2012, 60, 901–914. [Google Scholar] [CrossRef]
- Correas-Serrano, D.; Gomez-Diaz, J.S.; Tymchenko, M.; Alù, A. Nonlocal response of hyperbolic metasurfaces. Opt. Express 2015, 23, 29434. [Google Scholar] [CrossRef] [PubMed]
- De Abajo, F.J.G. Graphene plasmonics: Challenges and opportunities. ACS Photonics 2014, 1, 133–152. [Google Scholar]
- Tang, D.; Wang, Q.; Wang, Z.; Liu, Q.; Zhang, B.; He, D.; Wu, Z.; Mu, S. Highly sensitive wearable sensor based on a flexible multi-layer graphene film antenna. Sci. Bull. 2018, 63, 574–579. [Google Scholar] [CrossRef]
- Gomez-Diaz, J.S.; Moldovan, C.; Capdevila, S.; Romeu, J.; Bernard, L.S.; Magrez, A.; Ionescu, A.M.; Perruisseau-Carrier, J. Self-biased reconfigurable graphene stacks for terahertz plasmonics. Nat. Commun. 2015, 6, 1–8. [Google Scholar] [CrossRef]
- Koshino, M. Stacking-dependent optical absorption in multilayer graphene. New J. Phys. 2013, 15, 015010. [Google Scholar] [CrossRef]
- Falkovsky, L.A. Optical properties of graphene. J. Phys. Conf. Ser. 2008, 129, 012004. [Google Scholar] [CrossRef]
- Crassee, I.; Levallois, J.; Van Der Marel, D.; Walter, A.L.; Seyller, T.; Kuzmenko, A.B. Multicomponent magneto-optical conductivity of multilayer graphene on SiC. Phys. Rev. B 2011, 84, 1–8. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, J.; Liu, C.; Wu, Z.P.; He, D. Equivalent resonant circuit modeling of a graphene-based bowtie antenna. Electronics 2018, 7, 285. [Google Scholar] [CrossRef]
- Lin, S.; Ju, S.; Zhang, J.; Shi, G.; He, Y.; Jiang, D. Ultrathin flexible graphene films with high thermal conductivity and excellent EMI shielding performance using large-sized graphene oxide flakes. RSC Adv. 2019, 9, 1419–1427. [Google Scholar] [CrossRef]
- Wu, H.; Drzal, L.T. Graphene nanoplatelet paper as a light-weight composite with excellent electrical and thermal conductivity and good gas barrier properties. Carbon 2012, 50, 1135–1145. [Google Scholar] [CrossRef]
- Teng, C.; Xie, D.; Wang, J.; Yang, Z.; Ren, G.; Zhu, Y. Ultrahigh Conductive Graphene Paper Based on Ball-Milling Exfoliated Graphene. Adv. Funct. Mater. 2017, 27, 1700240. [Google Scholar] [CrossRef]
- Song, R.; Wang, Q.; Mao, B.; Wang, Z.; Tang, D.; Zhang, B.; Zhang, J.; Liu, C.; He, D.; Wu, Z.; et al. Flexible graphite films with high conductivity for radio-frequency antennas. Carbon 2018, 130, 164–169. [Google Scholar] [CrossRef]
- Zhou, W.; Liu, C.; Song, R.; Zeng, X.; Li, B.W.; Xia, W.; Zhang, J.; Huang, G.L.; Wu, Z.P.; He, D. Flexible radiofrequency filters based on highly conductive graphene assembly films. Appl. Phys. Lett. 2019, 114, 1–6. [Google Scholar] [CrossRef]
- Wang, S.Y.; Zhang, T.; Yin, W.Y.; Zhou, L. Interaction of electromagnetic waves with multilayer bi-anisotropic graphene structure. In Proceedings of the 2013 USNC-URSI Radio Science Meeting (Joint with AP-S Symposium), Lake Buena Vista, FL, USA, 7–13 July 2013; p. 53. [Google Scholar]
- Yee, K.S. Solution of Initial and Boundary Value Problems. IEEE Trans. Antennas Propag. 1966, 14, 169–200. [Google Scholar]
- Yu, X.; Sarris, C.D. A perfectly matched layer for subcell FDTD and applications to the modeling of graphene structures. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 1080–1083. [Google Scholar]
- De Oliveira, R.M.; Rodrigues, N.R.; Dmitriev, V. FDTD Formulation for Graphene Modeling Based on Piecewise Linear Recursive Convolution and Thin Material Sheets Techniques. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 767–770. [Google Scholar] [CrossRef]
- Feizi, M.; Nayyeri, V.; Ramahi, O.M. Modeling Magnetized Graphene in the Finite-Difference Time-Domain Method Using an Anisotropic Surface Boundary Condition. IEEE Trans. Antennas Propag. 2018, 66, 233–241. [Google Scholar] [CrossRef]
- Gutiérrez, Y.; Giangregorio, M.M.; Brown, A.S.; Moreno, F.; Losurdo, M. Understanding Electromagnetic Interactions and Electron Transfer in Ga Nanoparticle–Graphene–Metal Substrate Sandwich Systems. Appl. Sci. 2019, 9, 4085. [Google Scholar] [CrossRef]
- Brar, V.W.; Jang, M.S.; Sherrott, M.; Lopez, J.J.; Atwater, H.A. Highly confined tunable mid-infrared plasmonics in graphene nanoresonators. Nano Lett. 2013, 13, 2541–2547. [Google Scholar] [CrossRef] [PubMed]
- Tamagnone, M.; Gómez-Díaz, J.S.; Mosig, J.R.; Perruisseau-Carrier, J. Reconfigurable terahertz plasmonic antenna concept using a graphene stack. Appl. Phys. Lett. 2012, 101, 11–14. [Google Scholar] [CrossRef]
- Li, P.; Jiang, L.J. Modeling of magnetized graphene from microwave to thz range by DGTD with a scalar RBC and an ADE. IEEE Trans. Antennas Propag. 2015, 63, 4458–4467. [Google Scholar] [CrossRef]
- Li, P.; Jiang, L.J.; Bağci, H. A Resistive Boundary Condition Enhanced DGTD Scheme for the Transient Analysis of Graphene. IEEE Trans. Antennas Propag. 2015, 63, 3065–3076. [Google Scholar] [CrossRef]
- Wang, P.; Shi, Y.; Tian, C.Y.; Li, L. Analysis of Graphene-Based Devices Using Wave Equation Based Discontinuous Galerkin Time-Domain Method. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 2169–2173. [Google Scholar] [CrossRef]
- Nikitin, A.Y.; Garcia-Vidal, F.J.; Martin-Moreno, L. Analytical expressions for the electromagnetic dyadic green’s function in graphene and thin layers. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 4600611. [Google Scholar] [CrossRef]
- Araneo, R.; Burghignoli, P.; Lovat, G.; Hanson, G.W. Modal Propagation and Crosstalk Analysis in Coupled Graphene Nanoribbons. IEEE Trans. Electromagn. Compat. 2015, 57, 726–733. [Google Scholar] [CrossRef]
- Burghignoli, P.; Araneo, R.; Lovat, G.; Hanson, G. Space-domain method of moments for graphene nanoribbons. In Proceedings of the 8th European Conference on Antennas and Propagation, (EuCAP2014), The Hague, Netherlands, 6–11 April 2014; pp. 666–669. [Google Scholar]
- Hatefi Ardakani, H.; Mehrdadian, A.; Forooraghi, K. Analysis of Graphene-Based Microstrip Structures. IEEE Access 2017, 5, 20887–20897. [Google Scholar] [CrossRef]
- Cao, Y.S.; Jiang, L.J.; Ruehli, A.E. An Equivalent Circuit Model for Graphene-Based Terahertz Antenna Using the PEEC Method. IEEE Trans. Antennas Propag. 2016, 64, 1385–1393. [Google Scholar] [CrossRef]
- Tamagnone, M.; Perruisseau-Carrier, J. Predicting input impedance and efficiency of graphene reconfigurable dipoles using a simple circuit model. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 313–316. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, J.; Liu, C.; Wu, Z.P. Input impedance and efficiency analysis of graphene-based plasmonic nanoantenna using theory of characteristic modes. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 2031–2035. [Google Scholar] [CrossRef]
- Abadal, S.; Hosseininejad, S.E.; Cabellos-Aparicio, A.; Alarcón, E. Graphene-based terahertz antennas for area-constrained applications. In Proceedings of the 2017 40th International Conference on Telecommunications and Signal Processing, TSP 2017, Barcelona, Spain, 5–7 July 2017; pp. 817–820. [Google Scholar]
- Hosseininejad, S.E.; Rouhi, K.; Neshat, M.; Faraji-Dana, R.; Cabellos-Aparicio, A.; Abadal, S.; Alarcón, E. Reprogrammable Graphene-based Metasurface Mirror with Adaptive Focal Point for THz Imaging. Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Bala, R.; Marwaha, A. Investigation of graphene based miniaturized terahertz antenna for novel substrate materials. Eng. Sci. Technol. Int. J. 2016, 19, 531–537. [Google Scholar] [CrossRef]
- Zakrajsek, L.; Einarsson, E.; Thawdar, N.; Medley, M.; Jornet, J.M. Design of graphene-based plasmonic nano-antenna arrays in the presence of mutual coupling. In Proceedings of the 2017 11th European Conference on Antennas and Propagation, EUCAP 2017, Paris, France, 19–24 March 2017; pp. 1381–1385. [Google Scholar]
- Jornet, J.M.; Akyildiz, I.F. Graphene-based plasmonic nano-antenna for terahertz band communication in nanonetworks. IEEE J. Sel. Areas Commun. 2013, 31, 685–694. [Google Scholar] [CrossRef]
- Shapoval, O.V.; Gomez-Diaz, J.S.; Perruisseau-Carrier, J.; Mosig, J.R.; Nosich, A.I. Integral equation analysis of plane wave scattering by coplanar graphene-strip gratings in the thz range. IEEE Trans. Terahertz Sci. Technol. 2013, 3, 666–674. [Google Scholar] [CrossRef]
- Kaipa, C.S.R.; Yakovlev, A.B.; Hanson, G.W.; Padooru, Y.R.; Medina, F.; Mesa, F. Enhanced transmission with a graphene-dielectric microstructure at low-terahertz frequencies. Phys. Rev. B 2012, 85, 4–9. [Google Scholar] [CrossRef]
- Tamagnone, M.; Gómez-Díaz, J.S.; Mosig, J.R.; Perruisseau-Carrier, J. Analysis and design of terahertz antennas based on plasmonic resonant graphene sheets. J. Appl. Phys. 2012, 112, 114915. [Google Scholar] [CrossRef]
- Qin, X.; Chen, J.; Xie, C.; Xu, N.; Shi, J. A tunable THz dipole antenna based on graphene. In Proceedings of the 2016 IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications, IMWS-AMP 2016, Chengdu, China, 20–22 July 2016; pp. 1–3. [Google Scholar]
- Inum, R.; Rana, M.M.; Shushama, K.N. Performance analysis of graphene based nano dipole antenna on stacked substrate. In Proceedings of the ICECTE 2016—2nd International Conference on Electrical, Computer and Telecommunication Engineering, Rajshahi, Bangladesh, 8–10 December 2016; pp. 6–10. [Google Scholar]
- Goyal, R.; Vishwakarma, D.K. Design of a graphene-based patch antenna on glass substrate for high-speed terahertz communications. Microw. Opt. Technol. Lett. 2018, 60, 1594–1600. [Google Scholar] [CrossRef]
- Correas-Serrano, D.; Gomez-Diaz, J.S.; Alu, A.; Alvarez-Melcon, A. Electrically and Magnetically Biased Graphene-Based Cylindrical Waveguides: Analysis and Applications as Reconfigurable Antennas. IEEE Trans. Terahertz Sci. Technol. 2015, 5, 951–960. [Google Scholar] [CrossRef]
- Correas-Serrano, D.; Alvarez-Melcon, A.; Gomez-Diaz, J.S.; Alu, A. Surface plasmon modes in self-biased coupled graphene-coated wires. In Proceedings of the 2015 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, Vancouver, BC, Canada, 19–24 July 2015; pp. 1638–1639. [Google Scholar]
- Zhu, B.; Ren, G.; Gao, Y.; Yang, Y.; Lian, Y.; Jian, S. Graphene-coated tapered nanowire infrared probe: A comparison with metal-coated probes. Opt. Express 2014, 22, 24096. [Google Scholar] [CrossRef] [PubMed]
- Correas-Serrano, D.; Gomez-Diaz, J.S.; Alvarez-Melcon, A. Surface plasmons in graphene cylindrical waveguides. In Proceedings of the 2014 IEEE Antennas and Propagation Society International Symposium (APSURSI), Memphis, TN, USA, 6–11 July 2014; pp. 896–897. [Google Scholar]
- Soto Lamata, I.; Alonso-González, P.; Hillenbrand, R.; Nikitin, A.Y. Plasmons in cylindrical 2D materials as a platform for nanophotonic circuits. ACS Photonics 2015, 2, 280–286. [Google Scholar] [CrossRef]
- Jornet, J.M.; Cabellos, A. On the feeding mechanisms for graphene-based THz plasmonic nano-antennas. In Proceedings of the IEEE-NANO 2015—15th International Conference on Nanotechnology, Rome, Italy, 27–30 July 2015; pp. 168–171. [Google Scholar]
- Tamagnone, M.; Mosig, J.R. Theoretical Limits on the Efficiency of Reconfigurable and Nonreciprocal Graphene Antennas. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 1549–1552. [Google Scholar] [CrossRef]
- Cabellos-Aparicio, A.; Llatser, I.; Alarcón, E.; Hsu, A.; Palacios, T. Use of Terahertz Photoconductive Sources to Characterize Tunable Graphene RF Plasmonic Antennas. IEEE Trans. Nanotechnol. 2015, 14, 390–396. [Google Scholar] [CrossRef]
- Filter, R.; Farhat, M.; Steglich, M.; Alaee, R.; Rockstuhl, C.; Lederer, F. Tunable graphene antennas for selective enhancement of THz-emission. Opt. Express 2013, 21, 3737. [Google Scholar] [CrossRef]
- Chen, P.Y.; Alù, A. A terahertz photomixer based on plasmonic nanoantennas coupled to a graphene emitter. Nanotechnology 2013, 24, 455202. [Google Scholar] [CrossRef]
- Chen, P.Y.; Farhat, M. Modulatable optical radiators and metasurfaces based on quantum nanoantennas. Phys. Rev. B 2015, 91, 1–8. [Google Scholar] [CrossRef]
- Miscuglio, M.; Spirito, D.; Zaccaria, R.P.; Krahne, R. Shape Approaches for Enhancing Plasmon Propagation in Graphene. ACS Photonics 2016, 3, 2170–2175. [Google Scholar] [CrossRef]
- Hong, Q.; Luo, J.; Wen, C.; Zhang, J.; Zhu, Z.; Qin, S.; Yuan, X. Hybrid metal-graphene plasmonic sensor for multi-spectral sensing in both near- and mid-infrared ranges. Opt. Express 2019, 27, 35914. [Google Scholar] [CrossRef]
- Dai, S.; Ma, Q.; Liu, M.K.; Andersen, T.; Fei, Z.; Goldflam, M.D.; Wagner, M.; Watanabe, K.; Taniguchi, T.; Thiemens, M.; et al. Graphene on hexagonal boron nitride as a tunable hyperbolic metamaterial. Nat. Nanotechnol. 2015, 10, 682–686. [Google Scholar] [CrossRef] [PubMed]
- Rosolen, G.; Maes, B. Patterned graphene edges for tailored reflection of plasmonic modes. Opt. Lett. 2015, 40, 2727. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, C.; Beams, R.; Goodfellow, K.M.; Wicks, G.W.; Novotny, L.; Vamivakas, A.N. Optical antenna enhanced graphene photodetector. Appl. Phys. Lett. 2014, 105, 4–7. [Google Scholar] [CrossRef]
- Brar, V.W.; Sherrott, M.C.; Jang, M.S.; Kim, S.; Kim, L.; Choi, M.; Sweatlock, L.A.; Atwater, H.A. Electronic modulation of infrared radiation in graphene plasmonic resonators. Nat. Commun. 2015, 6, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Gilbertson, A.M.; Francescato, Y.; Roschuk, T.; Shautsova, V.; Chen, Y.; Sidiropoulos, T.P.H.; Hong, M.; Giannini, V.; Maier, S.A.; Cohen, L.F.; et al. Plasmon-induced optical anisotropy in hybrid graphene-metal nanoparticle systems. Nano Lett. 2015, 15, 3458–3464. [Google Scholar] [CrossRef] [PubMed]
- Waters, R.F.; Hobson, P.A.; MacDonald, K.F.; Zheludev, N.I. Optically switchable photonic metasurfaces. Appl. Phys. Lett. 2015. [Google Scholar] [CrossRef]
- Ahmadivand, A.; Karabiyik, M.; Pala, N. Plasmonic photodetectors. Photodet. Mater. Devices Appl. 2015, 24, 157–193. [Google Scholar]
- Qin, Y.; Xiong, X.Y.Z.; Sha, W.E.I.; Jiang, L.J. Electrically tunable polarizer based on graphene-loaded plasmonic cross antenna. J. Phys. Condens. Matter 2018, 30, 144007. [Google Scholar] [CrossRef]
- Dash, S.; Patnaik, A.; Kaushik, B.K. Performance enhancement of graphene plasmonic nanoantennas for THz communication. IET Microw. Antennas Propag. 2018, 13, 71–75. [Google Scholar] [CrossRef]
- Yao, Y.; Kats, M.A.; Genevet, P.; Yu, N.; Song, Y.; Kong, J.; Capasso, F. Broad electrical tuning of graphene-loaded plasmonic antennas. Nano Lett. 2013, 13, 1257–1264. [Google Scholar] [CrossRef]
- Wu, P.C.; Pala, R.A.; Kafaie Shirmanesh, G.; Cheng, W.H.; Sokhoyan, R.; Grajower, M.; Alam, M.Z.; Lee, D.; Atwater, H.A. Dynamic beam steering with all-dielectric electro-optic III–V multiple-quantum-well metasurfaces. Nat. Commun 2019, 10, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Xia, H.; Pan, Q.; Hu, J.; Yin, W. Design of a novel graphene terahertz antenna at 500GHz with reconfigurable radiation pattern. In Proceedings of the 2015 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, Vancouver, BC, Canada, 19–24 July 2015; pp. 1462–1463. [Google Scholar]
- Hosseininejad, S.E.; Komjani, N. Waveguide-Fed Tunable Terahertz Antenna Based on Hybrid Graphene-Metal Structure. IEEE Trans. Antennas Propag. 2016, 64, 3787–3793. [Google Scholar] [CrossRef]
- Dong, Z.; Sun, C.; Si, J.; Deng, X. A tunable plasmonic nano-antenna based on metal-graphene double-nanorods. Laser Phys. Lett. 2018, 15, 056202. [Google Scholar] [CrossRef]
- Mehta, B.; Zaghloul, M.E. Tuning the scattering response of the optical nano antennas using graphene. IEEE Photonics J. 2014, 6, 1–8. [Google Scholar] [CrossRef]
- Zhou, T.; Cheng, Z.; Zhang, H. Miniaturized tunable terahertz antenna based on graphene. Microw. Opt. Technol. Lett. 2014, 56, 1792–1794. [Google Scholar] [CrossRef]
- Emani, N.K.; Chung, T.-F.; Ni, X.; Kildishev, A.; Chen, Y.P.; Boltasseva, A. Electrically Tunable Plasmonic Resonances with Graphene. In Proceedings of the Conference on Lasers and Electro.-Optics, San Jose, CA, USA, 6–11 May 2012. [Google Scholar] [CrossRef]
- Casanova, F.; Hueso, L.E.; Velez, S.; Centeno, A.; Koppens, F.; Pesquera, A.; Navickaite, G.; Alonso-Gonzalez, P.; Golmar, F.; Chen, J.; et al. Controlling graphene plasmons with resonant metal antennas and spatial conductivity patterns. Science 2014, 344, 1369–1373. [Google Scholar]
- Sherrott, M.C.; Hon, P.W.C.; Fountaine, K.T.; Garcia, J.C.; Ponti, S.M.; Brar, V.W.; Sweatlock, L.A.; Atwater, H.A. Experimental Demonstration of >230° Phase Modulation in Gate-Tunable Graphene-Gold Reconfigurable Mid-Infrared Metasurfaces. Nano Lett. 2017, 17, 3027–3034. [Google Scholar] [CrossRef]
- Yasir, M.; Savi, P.; Bistarelli, S.; Cataldo, A.; Bozzi, M.; Perregrini, L.; Bellucci, S. A Planar Antenna with Voltage-Controlled Frequency Tuning Based on Few-Layer Graphene. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2380–2383. [Google Scholar] [CrossRef]
- Dragoman, M.; Neculoiu, D.; Bunea, A.C.; Deligeorgis, G.; Aldrigo, M.; Vasilache, D.; Dinescu, A.; Konstantinidis, G.; Mencarelli, D.; Pierantoni, L.; et al. A tunable microwave slot antenna based on graphene. Appl. Phys. Lett. 2015, 106, 153101. [Google Scholar] [CrossRef]
- Singh, V.; Bosman, S.J.; Schneider, B.H.; Blanter, Y.M.; Castellanos-Gomez, A.; Steele, G.A. Optomechanical coupling between a multilayer graphene mechanical resonator and a superconducting microwave cavity. Nat. Nanotechnol. 2014, 9, 820–824. [Google Scholar] [CrossRef]
- Zak, A.; Andersson, M.A.; Bauer, M.; Matukas, J.; Lisauskas, A.; Roskos, H.G.; Stake, J. Antenna-integrated 0.6 THz FET direct detectors based on CVD graphene. Nano Lett. 2014, 14, 5834–5838. [Google Scholar] [CrossRef] [PubMed]
- Emadi, R.; Safian, R.; Nezhad, A.Z.; Barani, N. Design of photoconductive antenna using spatially dispersive graphene strips. In Proceedings of the 2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, San Diego, CA, USA, 9–14 July 2017; pp. 2585–2586. [Google Scholar]
- Alvarez, C.N.; Cheung, R.; Thompson, J.S. Performance Analysis of Hybrid Metal-Graphene Frequency Reconfigurable Antennas in the Microwave Regime. IEEE Trans. Antennas Propag. 2017, 65, 1558–1569. [Google Scholar] [CrossRef]
- Dong, Y.; Liu, P.; Yu, D.; Li, G.; Tao, F. Dual-Band Reconfigurable Terahertz Patch Antenna with Graphene-Stack-Based Backing Cavity. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 1541–1544. [Google Scholar] [CrossRef]
- Dash, S.; Patnaik, A. Dual band reconfigurable plasmonic antenna using bilayer graphene. In Proceedings of the 2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, San Diego, CA, USA, 9–14 July 2017; pp. 921–922. [Google Scholar]
- Zhang, B.; Zhang, J.; Zhang, B.; Liu, C.; Wu, Z. Investigation on reconfigurable THz bowtie antenna based on graphene. In Proceedings of the 2015 IEEE 4th Asia-Pacific Conference on Antennas and Propagation, APCAP 2015, Kuta, Indonesia, 30 June–3 July 2015; pp. 146–147. [Google Scholar]
- Liu, H.; Sun, S.; Wu, L.; Bai, P. Optical Near-Field Enhancement with Graphene Bowtie Antennas. Plasmonics 2014, 9, 845–850. [Google Scholar] [CrossRef]
- Liu, P.; Cai, W.; Wang, L.; Zhang, X.; Xu, J. Tunable terahertz optical antennas based on graphene ring structures. Appl. Phys. Lett. 2012, 100, 153111. [Google Scholar] [CrossRef]
- Lin, Y.M.; Jenkins, K.A.; Alberto, V.G.; Small, J.P.; Farmer, D.B.; Avouris, P. Circular beam-reconfigurable antenna base on graphene-metal hybrid. Electron. Lett. 2016, 52, 494–496. [Google Scholar]
- Song, J.; Wu, X.; Huang, C.; Yang, J.; Ji, C.; Zhang, C.; Luo, X. Broadband and Tunable RCS Reduction using High-order Reflections and Salisbury-type Absorption Mechanisms. Sci. Rep. 2019, 9, 9036. [Google Scholar] [CrossRef]
- Yang, J.; Kong, F.; Li, K. Broad Tunable Nanoantenna Based on Graphene Log-Periodic Toothed Structure. Plasmonics 2017, 11, 981–986. [Google Scholar] [CrossRef]
- Halas, N.J.; Fang, Z.; Liu, Z.; Nordlander, P.; Zhu, X.; García de Abajo, F.J.; Ajayan, P.M.; Schlather, A.E.; Wang, Y. Active Tunable Absorption Enhancement with Graphene Nanodisk Arrays. Nano Lett. 2013, 14, 299–304. [Google Scholar]
- Fang, Z.; Wang, Y.; Liu, Z.; Schlather, A.; Ajayan, P.M.; Koppens, F.H.L.; Nordlander, P.; Halas, N.J. Plasmon-induced doping of graphene. ACS Nano 2012, 6, 10222–10228. [Google Scholar] [CrossRef]
- Wu, J. Tunable ultranarrow spectrum selective absorption in a graphene monolayer at terahertz frequency. J. Phys. D Appl. Phys. 2016, 49, 215108. [Google Scholar] [CrossRef]
- Xiong, F.; Zhang, J.; Zhu, Z.; Yuan, X.; Qin, S. Ultrabroadband, More than One Order Absorption Enhancement in Graphene with Plasmonic Light Trapping. Sci. Rep. 2015, 5, 1–8. [Google Scholar] [CrossRef]
- Yu, A. Tunable strong THz absorption assisted by graphene-dielectric stacking structure. Superlattices Microstruct. 2018, 122, 461–470. [Google Scholar] [CrossRef]
- Mackenzie, B.R.; Myers, R.A.; Scotia, N. Tuning control of broadband terahertz absorption using designed graphene multilayers. J. Opt. 2019, 21, 075101. [Google Scholar]
- Matthaiakakis, N.; Yan, X.; Mizuta, H.; Charlton, M.D.B. Tuneable strong optical absorption in a graphene-insulator-metal hybrid plasmonic device. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Jang, M.S.; Brar, V.W.; Mauser, K.W.; Kim, L.; Atwater, H.A. Electronically Tunable Perfect Absorption in Graphene. Nano Lett. 2018, 18, 971–979. [Google Scholar] [CrossRef] [PubMed]
- Sikdar, D.; Zhu, W.; Cheng, W.; Premaratne, M. Substrate-Mediated Broadband Tunability in Plasmonic Resonances of Metal Nanoantennas on Finite High-Permittivity Dielectric Substrate. Plasmonics 2015, 10, 1663–1673. [Google Scholar] [CrossRef]
- Locatelli, A.; Town, G.E.; De Angelis, C. Graphene-based terahertz waveguide modulators. IEEE Trans. Terahertz Sci. Technol. 2015, 5, 351–357. [Google Scholar] [CrossRef]
- Yu, R.; Pruneri, V.; Garciá De Abajo, F.J. Active modulation of visible light with graphene-loaded ultrathin metal plasmonic antennas. Sci. Rep. 2016, 6, 1–7. [Google Scholar]
- Li, Z.; Yu, N. Modulation of mid-infrared light using graphene-metal plasmonic antennas. Appl. Phys. Lett. 2013, 102, 131108. [Google Scholar] [CrossRef]
- Kong, J.; Song, Y.; Shankar, R.; Loncar, M.; Yao, Y.; Capasso, F.; Kats, M.A. Wide Wavelength Tuning of Optical Antennas on Graphene with Nanosecond Response Time. Nano Lett. 2013, 14, 214–219. [Google Scholar]
- Yi, N.; Liu, Z.; Sun, S.; Song, Q.; Xiao, S. Mid-infrared tunable magnetic response in graphene-based diabolo nanoantennas. Carbon 2015, 94, 501–506. [Google Scholar] [CrossRef]
- Liang, G.; Hu, X.; Yu, X.; Shen, Y.; Li, L.H.; Davies, A.G.; Linfield, E.H.; Liang, H.K.; Zhang, Y.; Yu, S.F.; et al. Integrated Terahertz Graphene Modulator with 100% Modulation Depth. ACS Photonics 2015, 2, 1559–1566. [Google Scholar] [CrossRef]
- Lei, L.; Sun, Y.; Xiao, D.; Ouyang, Z.; Liu, Q.; Tao, K. Coupled Resonance Enhanced Modulation for a Graphene-Loaded Metamaterial Absorber. Nanoscale Res. Lett. 2019, 14, 32. [Google Scholar]
- Han, C.; Parrott, E.P.J.; Humbert, G.; Crunteanu, A.; Pickwell-Macpherson, E. Broadband modulation of terahertz waves through electrically driven hybrid bowtie antenna-VO 2 devices. Sci. Rep. 2017, 7, 1–9. [Google Scholar]
- Yao, Y.; Shankar, R.; Kats, M.A.; Song, Y.; Kong, J.; Loncar, M.; Capasso, F. Electrically tunable metasurface perfect absorbers for ultrathin mid-infrared optical modulators. Nano Lett. 2014, 14, 6526–6532. [Google Scholar] [CrossRef] [PubMed]
- Hosseinbeig, A.; Pirooj, A.; Zarrabi, F.B. A reconfigurable subwavelength plasmonic fano nano-antenna based on split ring resonator. J. Magn. Magn. Mater. 2017, 423, 203–207. [Google Scholar] [CrossRef]
- Wu, Y.; Qu, M.; Jiao, L.; Liu, Y.; Ghassemlooy, Z. Graphene-based Yagi-Uda antenna with reconfigurable radiation patterns. Aip Adv. 2016, 6, 065308. [Google Scholar] [CrossRef]
- Seyedsharbaty, M.M.; Sadeghzadeh, R.A. Antenna gain enhancement by using metamaterial radome at THz band with reconfigurable characteristics based on graphene load. Opt. Quantum Electron. 2017, 49, 1–13. [Google Scholar] [CrossRef]
- He, X.; Gao, P.; Shi, W. A further comparison of graphene and thin metal layers for plasmonics. Nanoscale 2016, 8, 10388–10397. [Google Scholar] [CrossRef]
- Jadidi, M.M.; Sushkov, A.B.; Myers-Ward, R.L.; Boyd, A.K.; Daniels, K.M.; Gaskill, D.K.; Fuhrer, M.S.; Drew, H.D.; Murphy, T.E. Tunable Terahertz Hybrid Metal-Graphene Plasmons. Nano Lett. 2015, 15, 7099–7104. [Google Scholar] [CrossRef]
- Zhao, X.; Yuan, C.; Zhu, L.; Yao, J. Graphene-based tunable terahertz plasmon-induced transparency metamaterial. Nanoscale 2016, 8, 15273–15280. [Google Scholar] [CrossRef] [PubMed]
- Bao, Y.; Zu, S.; Zhang, Y.; Fang, Z. Active Control of Graphene-Based Unidirectional Surface Plasmon Launcher. ACS Photonics 2015, 2, 1135–1140. [Google Scholar] [CrossRef]
- Kim, S.; Jang, M.S.; Brar, V.W.; Tolstova, Y.; Mauser, K.W.; Atwater, H.A. Electronically tunable extraordinary optical transmission in graphene plasmonic ribbons coupled to subwavelength metallic slit arrays. Nat. Commun. 2016, 7, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Alonso-González, P.; Nikitin, A.Y.; Golmar, F.; Centeno, A.; Pesquera, A.; Vélez, S.; Chen, J.; Navickaite, G.; Koppens, F.; Zurutuza, A.; et al. Controlling graphene plasmons with resonant metal antennas and spatial conductivity patterns. Science 2014, 344, 1369–1373. [Google Scholar] [CrossRef] [PubMed]
- Hutchings, L.M.; Andrews, F.N. Isolation of Brucella suis from boar’s semen. J. Bacteriol. 1945, 50, 715. [Google Scholar] [PubMed]
- Gomez-Diaz, J.S.; Cañete-Rebenaque, D.; Alvarez-Melcon, A. A simple CRLH LWA circuit condition for constant radiation rate. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 29–32. [Google Scholar] [CrossRef][Green Version]
- Gomez-Diaz, J.S.; Álvarez-Melcon, A.; Bertuch, T. A modal-based iterative circuit model for the analysis of CRLH leaky-wave antennas comprising periodically loaded PPW. IEEE Trans. Antennas Propag. 2011, 59, 1101–1112. [Google Scholar] [CrossRef]
- Mahmoud, S.F.; Antar, Y.M.M. Leaky wave antennas: Theory and design. Natl. Radio Sci. Conf. NrscProc. 2013, 2013-Janua, 1–8. [Google Scholar]
- Guzmán-Quirós, R.; Gómez-Tornero, J.L.; Weily, A.R.; Guo, Y.J. Electronically steerable 1-d fabry-perot leaky-wave antenna employing a tunable high impedance surface. IEEE Trans. Antennas Propag. 2012, 60, 5046–5055. [Google Scholar] [CrossRef]
- Guglielmi, M.; Jackson, D.R. Broadside Radiation from Periodic Leaky-Wave Antennas. IEEE Trans. Antennas Propag. 2000, 41, 31–37. [Google Scholar] [CrossRef]
- Burghignoli, P.; Lovat, G.; Capolino, F.; Jackson, D.R.; Wilton, D.R. Directive leaky-wave radiation from a dipole source in a wire-medium slab. IEEE Trans. Antennas Propag. 2014, 56, 1329–1339. [Google Scholar] [CrossRef][Green Version]
- Ren, X.; Sha, W.E.I.; Choy, W.C.H. Tuning optical responses of metallic dipole nanoantenna using graphene. Opt. Express 2013, 21, 31824. [Google Scholar] [CrossRef] [PubMed]
- Hadad, Y.; Sounas, D.L.; Alu, A. Space-time gradient metasurfaces. Phys. Rev. B 2015, 92, 1–6. [Google Scholar] [CrossRef]
- Olinert, A.A.; Hesselt, A. Guided Waves on Sinusoidally-modulated Reactance Surfaces. IEEE Trans. Antennas Propag. 1957, 153–160. [Google Scholar]
- Grbic, A.; Eleftheriades, G.V. Leaky CPW-based slot antenna arrays for millimeter-wave applications. IEEE Trans. Antennas Propag. 2012, 50, 1494–1504. [Google Scholar] [CrossRef]
- Ettorre, M.; Rudloph, S.; Grbic, A. Generation of Propagating Bessel Beams Using Leaky-wave Modes. IEEE Trans. Antennas Propag. 2012, 60, 3605–3613. [Google Scholar] [CrossRef]
- Patel, A.M.; Grbic, A. A printed leaky-wave antenna based on a sinusoidally-modulated reactance surface. IEEE Trans. Antennas Propag. 2011, 59, 2087–2096. [Google Scholar] [CrossRef]
- Fuscaldo, W. Rigorous Evaluation of Losses in Uniform Leaky-Wave Antennas. IEEE Trans. Antennas Propag. 2019, 68, 1. [Google Scholar] [CrossRef]
- Esquius-Morote, M.; Gómez-Dı, J.S.; Perruisseau-Carrier, J. Sinusoidally-Modulated Graphene Leaky-Wave Antenna for Electronic Beamscanning at THz. IEEE Trans. Terahertz Sci. Technol. 2014, 4, 116–122. [Google Scholar] [CrossRef]
- Gómez-Díaz, J.S.; Esquius-Morote, M.; Perruisseau-Carrier, J. Plane wave excitation-detection of non-resonant plasmons along finite-width graphene strips. Opt. Express 2013, 21, 24856. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Díaz-Rubio, A.; Asadchy, V.S.; Ptitcyn, G.; Generalov, A.A.; Ala-Laurinaho, J.; Tretyakov, S.A. Extreme Asymmetry in Metasurfaces via Evanescent Fields Engineering: Angular-Asymmetric Absorption. Phys. Rev. Lett. 2018, 121, 256802. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; He, M.; Wu, C.; Zhang, C. Radiation-pattern-reconfigurable graphene leaky-wave antenna at terahertz band based on dielectric grating structure. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 1771–1775. [Google Scholar] [CrossRef]
- Moreno, G.; Bernety, H.M.; Yakovlev, A.B. Reduction of mutual coupling between strip dipole antennas at terahertz frequencies with an elliptically shaped graphene monolayer. In Proceedings of the 2016 IEEE Antennas and Propagation Society International Symposium, APSURSI 2016, Fajardo, Puerto Rico, 26 June–1 July 2016; pp. 887–888. [Google Scholar]
- Cheng, Y.; Wu, L.S.; Tang, M.; Zhang, Y.P.; Mao, J.F. A Sinusoidally-Modulated Leaky-Wave Antenna with Gapped Graphene Ribbons. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 3000–3004. [Google Scholar] [CrossRef]
- Ettorre, M.; Grbic, A. Generation of Propagating Bessel Beams Using Leaky-Wave Modes: Experimental Validation. IEEE Trans. Antennas Propag. 2012, 60, 2645–2653. [Google Scholar] [CrossRef]
- Chu, D.A.; Hon, P.W.C.; Itoh, T.; Williams, B.S. Feasibility of graphene CRLH metamaterial waveguides and leaky wave antennas. J. Appl. Phys. 2016, 120, 013103. [Google Scholar] [CrossRef]
- Gomez-Tornero, J.L.; Quesada-Pereira, F.D.; Alvarez-Melcon, A. Analysis and design of periodic leaky-wave antennas for the millimeter waveband in hybrid waveguide-planar technology. IEEE Trans. Antennas Propag. 2005, 53, 2834–2842. [Google Scholar] [CrossRef]
- Huang, Y.; Wu, L.S.; Tang, M.; Mao, J. Design of a Beam Reconfigurable THz Antenna with Graphene-Based Switchable High-Impedance Surface. IEEE Trans. Nanotechnol. 2012, 11, 836–842. [Google Scholar] [CrossRef]
- Minatti, G.; Caminita, F.; Casaletti, M.; MacI, S. Spiral leaky-wave antennas based on modulated surface impedance. IEEE Trans. Antennas Propag. 2011, 59, 4436–4444. [Google Scholar] [CrossRef]
- Fuscaldo, W.; Burghignoli, P.; Baccarelli, P.; Galli, A. A Reconfigurable Substrate-Superstrate Graphene-Based Leaky-Wave THz Antenna. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 1545–1548. [Google Scholar] [CrossRef]
- Fuscaldo, W.; Burghignoli, P.; Baccarelli, P.; Galli, A. A graphene-loaded substrate-superstrate leaky-wave THz antenna. In Proceedings of the 2016 10th European Conference on Antennas and Propagation, EuCAP 2016, Davos, Switzerland, 10–15 April 2016; pp. 1–3. [Google Scholar]
- Fuscaldo, W.; Tofani, S.; Burghignoli, P.; Baccarelli, P.; Notargiacomo, A.; Cibella, S.; Pea, M.; Carelli, P.; Mishra, N.; Coletti, C.; et al. Graphene-Based Fabry-Perot Cavity Leaky-Wave Antennas: Towards an Experimental Validation. In Proceedings of the 2018 48th European Microwave Conference, EuMC 2018, Madrid, Spain, 23–27 September 2018; pp. 276–279. [Google Scholar]
- Fuscaldo, W.; Burghignoli, P.; Baccarelli, P.; Galli, A. Graphene fabry-perot cavity leaky-wave antennas: Plasmonic versus nonplasmonic solutions. IEEE Trans. Antennas Propag. 2017, 65, 1651–1660. [Google Scholar] [CrossRef]
- Correas-Serrano, D.; Gomez-Diaz, J.S. Nonreciprocal Graphene-Based Leaky-Wave Antennas: Theory and Applications. 2nd URSI Atlantic Radio Sci. Meet. 2018, 21, 95616. [Google Scholar]
- Estep, N.A.; Sounas, D.L.; Soric, J.; Alù, A. Magnetic-free non-reciprocity and isolation based on parametrically modulated coupled-resonator loops. Nat. Phys. 2014, 10, 923–927. [Google Scholar] [CrossRef]
- Yu, H.; Yao, Y.; Qu, S.; Yu, J.; Chen, X. Design of graphene based reflectarray antenna. In Proceedings of the 2015 8th UK, Europe, China Millimeter Waves and THz Technology Workshop, UCMMT 2015, Cardiff, UK, 14–15 September 2015; pp. 1–4. [Google Scholar]
- Dreyer, P.; Gomez Diaz, J.S.; Perruisseau-Carrier, J. Design of a reflectarray element integrated in a Solar Cell panel. In Proceedings of the 2013 IEEE Antennas and Propagation Society International Symposium (APSURSI), Orlando, FL, USA, 7–13 July 2013; pp. 1558–1559. [Google Scholar]
- Encinar, J.A.; Arrebola, M.; De La Fuente, L.F.; Toso, G. A transmit-receive reflectarray antenna for direct broadcast satellite applications. IEEE Trans. Antennas Propag. 2011, 59, 3255–3264. [Google Scholar] [CrossRef]
- Legay, H.; Pinte, B.; Charrier, M.; Ziaep, A.; Girard, E.; Gillard, R. A steerable reflectarray antenna. In Proceedings of the IEEE International Symposium on Phased Array Systems and Technology, Boston, MA, USA, 14–17 October; 2003; pp. 494–499. [Google Scholar]
- Sun, S.; He, Q.; Xiao, S.; Xu, Q.; Li, X.; Zhou, L. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves. Nat. Mater. 2012, 11, 426–431. [Google Scholar] [CrossRef]
- Estakhri, N.M.; Alù, A. Wave-front transformation with gradient metasurfaces. Phys. Rev. X 2016, 6, 1–17. [Google Scholar]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.P.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef]
- Zheludev, N.I.; Kivshar, Y.S. From metamaterials to metadevices. Nat. Mater. 2012, 11, 917–924. [Google Scholar] [CrossRef]
- Perruisseau-carrier, J.; Skrivervik, A.K. Monolithic MEMS-Based Reflectarray Cell Digitally Reconfigurable Over a 360° Phase Range. IEEE Antennas Wirel. Propag. Lett. 2008, 7, 138–141. [Google Scholar]
- Carrasco, E.; Barba, M.; Encinar, J.A. Reflectarray element based on aperture-coupled patches with slots and lines of variable length. IEEE Trans. Antennas Propag. 2007, 55, 820–825. [Google Scholar] [CrossRef]
- Hum, S.V.; McFeetors, G.; Okoniewski, M. Integrated MEMS reflectarray elements. In Proceedings of the 2006 First European Conference on Antennas and Propagation, Nice, France, 6–10 November 2006; pp. 1–6. [Google Scholar]
- Bliokh, K.Y.; Shadrivov, I.V.; Kivshar, Y.S. Goos–Hänchen and Imbert–Fedorov shifts of polarized vortex beams. Opt. Lett. 2009, 34, 389. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Chen, S.; Kang, M.; Li, J.; Pun, E.Y.-B.; Zhang, S. Spin-enabled plasmonic metasurfaces for manipulating orbital angular momentum of light. Nano Lett. 2013, 13, 4148–4151. [Google Scholar] [CrossRef]
- Carrasco, E.; Perruisseau-Carrier, J. Reflectarray antenna at terahertz using graphene. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 253–256. [Google Scholar] [CrossRef]
- Taravati, S.; Caloz, C. Mixer-Duplexer-Antenna Leaky-Wave System Based on Periodic Space-Time Modulation. IEEE Trans. Antennas Propag. 2017, 65, 442–452. [Google Scholar] [CrossRef]
- Carrasco, E.; Tamagnone, M.; Perruisseau-Carrier, J. Tunable graphene reflective cells for THz reflectarrays and generalized law of reflection. Appl. Phys. Lett. 2013, 102, 104103. [Google Scholar] [CrossRef]
- Mosallaei, A.; Forouzmand, H. Tunable two dimensional optical beam steering with reconfigurable indium tin oxide plasmonic reflectarray metasurface. J. Opt. 2016, 18, 125003. [Google Scholar]
- Wu, B.; Hu, Y.; Zhao, Y.T.; Lu, W.B.; Zhang, W. Large angle beam steering THz antenna using active frequency selective surface based on hybrid graphene-gold structure. Opt. Express 2018, 26, 15353. [Google Scholar] [CrossRef]
- McMorran, B.J.; Agrawal, A.; Anderson, I.M.; Herzing, A.A.; Lezec, H.J.; McClelland, J.J.; Unguris, J. Electron vortex beams with high quanta of orbital angular momentum. Science 2011, 331, 192–195. [Google Scholar] [CrossRef]
- Mehmood, M.Q.; Mei, S.; Hussain, S.; Huang, K.; Siew, S.Y.; Zhang, L.; Zhang, T.; Ling, X.; Liu, H.; Teng, J.; et al. Visible-Frequency Metasurface for Structuring and Spatially Multiplexing Optical Vortices. Adv. Mater. 2016, 28, 2533–2539. [Google Scholar] [CrossRef]
- Tamburini, F.; Sponselli, A.; Bianchini, A.; Mari, E.; Thidé, B.; Romanato, F. Encoding many channels on the same frequency through radio vorticity: First experimental test. New J. Phys. 2012, 14, 033001. [Google Scholar] [CrossRef]
- Gonçalves, P.A.D.; Stenger, N.; Cox, J.D.; Mortensen, N.A.; Xiao, S. Strong Light–Matter Interactions Enabled by Polaritons in Atomically Thin Materials. Adv. Opt. Mater. 2020, 1901473, 1–25. [Google Scholar] [CrossRef]
- Meng, Z.K.; Shi, Y.; Wei, W.Y.; Zhang, Y.; Li, L. Graphene-based metamaterial transmitarray antenna design for the generation of tunable orbital angular momentum vortex electromagnetic waves. Opt. Mater. Express 2019, 9, 3709. [Google Scholar] [CrossRef]
- Li, C.C.; Wu, L.S.; Yin, W.Y. A dual-polarized and reconfigurable reflectarray for generation of vortex radio waves. Aip Adv. 2018, 8, 055331. [Google Scholar] [CrossRef]
- Zhu, B.; Ren, G.; Gao, Y.; Wu, B.; Lian, Y.; Jian, S. Creation of Graphene Plasmons Vortex via Cross Shape Nanoantennas Under Linearly Polarized Incidence. Plasmonics 2017, 12, 1–6. [Google Scholar] [CrossRef]
- Deng, L.; Zhang, Y.; Zhu, J.; Zhang, C. Wide-band circularly polarized reflectarray using graphene-based Pancharatnam-Berry phase unit-cells for terahertz communication. Materials 2018, 11, 956. [Google Scholar] [CrossRef] [PubMed]
- Deng, L.; Wu, Y.; Zhang, C.; Hong, W.; Peng, B.; Zhu, J.; Li, S. Manipulating of Different-Polarized Reflected Waves with Graphene-based Plasmonic Metasurfaces in Terahertz Regime. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef]
- You, B.; Zhou, L.; Wu, L.S.; Mao, J.F. Reconfigurable graphene reflectarray with switchable focus. In Proceedings of the 2016 IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications, IMWS-AMP 2016, Chengdu, China, 20–22 July 2016; pp. 1–3. [Google Scholar]
- Carrasco, E.; Tamagnone, M.; Mosig, J.R.; Low, T.; Perruisseau-Carrier, J. Gate-controlled mid-infrared light bending with aperiodic graphene nanoribbons array. Nanotechnology 2015, 26, 134002. [Google Scholar] [CrossRef]
- Wong, J.; Selvanayagam, M.; Eleftheriades, G.V. A thin printed metasurface for microwave refraction. In Proceedings of the 2014 IEEE MTT-S International Microwave Symposium (IMS2014), Tampa, FL, USA, 1–6 June 2014; pp. 8–11. [Google Scholar]
- Monticone, F.; Estakhri, N.M.; Alù, A. Full control of nanoscale optical transmission with a composite metascreen. Phys. Rev. Lett. 2013, 110, 1–5. [Google Scholar] [CrossRef]
- Sa’Don, S.N.H.; Jamaluddin, M.H.; Kamarudin, M.R.; Ahmad, F.; Yamada, Y.; Kamardin, K.; Idris, I.H. Analysis of graphene antenna properties for 5G applications. Sensors 2019, 19, 4835. [Google Scholar] [CrossRef]
- Artemenko, A.A.; Ssorin, V.N.; Maslennikov, R.O.; Mozharovskiy, A.V. Lens antenna with electronic beam steering capabilities. U.S. Patent 14/593,552, 30 April 2015. [Google Scholar]
- Chen, P.Y.; Farhat, M.; Askarpour, A.N.; Tymchenko, M.; Alú, A. Infrared beam-steering using acoustically modulated surface plasmons over a graphene monolayer. J. Opt. 2014, 16, 094008. [Google Scholar] [CrossRef]
- Zangeneh-Nejad, F.; Safian, R. A tunable high-impedance THz antenna array. In Proceedings of the ICEE 2015—Proceedings of the 23rd Iranian Conference on Electrical Engineering, Tehran, Iran, 10–14 May 2015; Volume 10, pp. 402–405. [Google Scholar]
- Varshney, A.K.; Pathak, N.P.; Sircar, D. Beam Steering THz Antenna Array using Graphene-based Phase Shifter. In Proceedings of the 2018 IEEE Indian Conference on Antennas and Propogation (InCAP), Hyderabad, India, 16–19 December 2018; pp. 1–4. [Google Scholar]
- Wang, C.; Yao, Y.; Yu, J.; Chen, X. 3d beam reconfigurable THz antenna with graphene-based high-impedance surface. Electronics 2019, 8, 1291. [Google Scholar] [CrossRef]
- Orazbayev, B.; Beruete, M.; Khromova, I. Graphene-dielectric metamaterial for beam steering. In Proceedings of the 2016 10th International Congress on Advanced Electromagnetic Materials in Microwaves and Optics, METAMATERIALS, Chania, Greece, 19–22 September 2016; pp. 253–255. [Google Scholar]
- Chang, Z.; You, B.; Wu, L.S.; Tang, M.; Zhang, Y.P.; Mao, J.F. A Reconfigurable Graphene Reflectarray for Generation of Vortex THz Waves. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 1537–1540. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, Y. Generation of Wideband Tunable Orbital Angular Momentum Vortex Waves Using Graphene Metamaterial Reflectarray. IEEE Access 2017, 6, 5341–5347. [Google Scholar] [CrossRef]
- Huang, X.; Leng, T.; Zhu, M.; Zhang, X.; Chen, J.; Chang, K.; Aqeeli, M.; Geim, A.K.; Novoselov, K.S.; Hu, Z. Highly Flexible and Conductive Printed Graphene for Wireless Wearable Communications Applications. Sci. Rep. 2015, 5, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Tredicucci, A.; Vitiello, M.S. Device concepts for graphene-based terahertz photonics. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 130–138. [Google Scholar] [CrossRef]
- Lundeberg, M.B.; Gao, Y.; Woessner, A.; Tan, C.; Alonso-González, P.; Watanabe, K.; Taniguchi, T.; Hone, J.; Hillenbrand, R.; Koppens, F.H.L. Thermoelectric detection and imaging of propagating graphene plasmons. Nat. Mater. 2017, 16, 204–207. [Google Scholar] [CrossRef]
- Thampy, A.S.; Darak, M.S.; Dhamodharan, S.K. Analysis of graphene based optically transparent patch antenna for terahertz communications. Phys. E Low-Dimens. Syst. Nanostruct. 2015, 66, 67–73. [Google Scholar] [CrossRef]
- Bala, R.; Marwaha, A. Development of computational model for tunable characteristics of graphene based triangular patch antenna in THz regime. J. Comput. Electron. 2016, 15, 222–227. [Google Scholar] [CrossRef]
- Kopyt, P.; Salski, B.; Olszewska-Placha, M.; Janczak, D.; Sloma, M.; Kurkus, T.; Jakubowska, M.; Gwarek, W. Graphene-Based Dipole Antenna for a UHF RFID Tag. IEEE Trans. Antennas Propag. 2016, 64, 2862–2868. [Google Scholar] [CrossRef]
- Naghdehforushha, S.A.; Moradi, G. High directivity plasmonic graphene-based patch array antennas with tunable THz band communications. Optik 2018, 168, 440–445. [Google Scholar] [CrossRef]
- Feenstra, R.M.; Jena, D.; Gu, G. Single-particle tunneling in doped graphene-insulator-graphene junctions. J. Appl. Phys. 2012, 111, 043711. [Google Scholar] [CrossRef]
- Fallahazad, B.; Lee, K.; Kang, S.; Xue, J.; Larentis, S.; Corbet, C.; Kim, K.; Movva, H.C.P.; Taniguchi, T.; Watanabe, K.; et al. Gate-tunable resonant tunneling in double bilayer graphene heterostructures. Nano Lett. 2015, 15, 428–433. [Google Scholar] [CrossRef] [PubMed]
- Pitanti, A.; Coquillat, D.; Ercolani, D.; Sorba, L.; Teppe, F.; Knap, W.; De Simoni, G.; Beltram, F.; Tredicucci, A.; Vitiello, M.S. Terahetz detection by heterostructed InAs/InSb nanowire based field effect transistors. Appl. Phys. Lett. 2012, 101, 141103. [Google Scholar] [CrossRef]
- Zhang, N.; Song, R.; Hu, M.; Shan, G.; Wang, C.; Yang, J. A Low-Loss Design of Bandpass Filter at the Terahertz Band. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 573–575. [Google Scholar] [CrossRef]
- Sensale-Rodriguez, B. Graphene-insulator-graphene active plasmonic terahertz devices. Appl. Phys. Lett. 2013, 103, 123109. [Google Scholar] [CrossRef]
- Anand, S.; Kumar, D.S.; Wu, R.J.; Chavali, M. Graphene nanoribbon based terahertz antenna on polyimide substrate. Optik 2014, 125, 5546–5549. [Google Scholar] [CrossRef]
- Cakmakyapan, S.; Lu, P.K.; Navabi, A.; Jarrahi, M. Gold-patched graphene nano-stripes for high-responsivity and ultrafast photodetection from the visible to infrared regime. Light Sci. Appl. 2018, 7, 2047–7538. [Google Scholar] [CrossRef]
- Fang, Z.; Liu, Z.; Wang, Y.; Ajayan, P.M.; Nordlander, P.; Halas, N.J. Graphene-antenna sandwich photodetector. Nano Lett. 2012, 12, 3808–3813. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, W.; Gong, T.; Su, Y.; Zhang, H.; He, Y.; Liu, Z.; Yu, B. Ultra-sensitive near-infrared graphene photodetectors with nanopillar antennas. Nanoscale 2017, 9, 17459–17464. [Google Scholar] [CrossRef]
- Castilla, S.; Terrés, B.; Autore, M.; Viti, L.; Li, J.; Nikitin, A.Y.; Vangelidis, I.; Watanabe, K.; Taniguchi, T.; Lidorikis, E.; et al. Fast and Sensitive Terahertz Detection Using an Antenna-Integrated Graphene pn Junction. Nano Lett. 2019, 19, 2765–2773. [Google Scholar] [CrossRef]
- Ma, P.; Salamin, Y.; Baeuerle, B.; Josten, A.; Heni, W.; Emboras, A.; Leuthold, J. Plasmonically Enhanced Graphene Photodetector Featuring 100 Gbit/s Data Reception, High Responsivity, and Compact Size. ACS Photonics 2019, 6, 154–161. [Google Scholar] [CrossRef]
- Song, Y.; Shankar, R.; Capasso, F.; Yao, Y.; Loncar, M.; Rauter, P.; Kong, J. High-Responsivity Mid-Infrared Graphene Detectors with Antenna-Enhanced Photocarrier Generation and Collection. Nano Lett. 2014, 14, 3749–3754. [Google Scholar]
- Degl’Innocenti, R.; Xiao, L.; Jessop, D.S.; Kindness, S.J.; Ren, Y.; Lin, H.; Zeitler, J.A.; Alexander-Webber, J.A.; Joyce, H.J.; Braeuninger-Weimer, P.; et al. Fast Room-Temperature Detection of Terahertz Quantum Cascade Lasers with Graphene-Loaded Bow-Tie Plasmonic Antenna Arrays. ACS Photonics 2016, 3, 1747–1753. [Google Scholar] [CrossRef]
- Guo, W.; Wang, L.; Chen, X.; Liu, C.; Tang, W.; Guo, C.; Wang, J.; Lu, W. Graphene-based broadband terahertz detector integrated with a square-spiral antenna. Opt. Lett. 2018, 43, 1647. [Google Scholar] [CrossRef] [PubMed]
- Lau, D.; Song, N.; Hall, C.; Jiang, Y.; Lim, S.; Perez-Wurfl, I.; Ouyang, Z.; Lennon, A. Hybrid solar energy harvesting and storage devices: The promises and challenges. Mater. Today Energy 2019, 13, 22–44. [Google Scholar] [CrossRef]
- Nouri-Novin, S.; Sadatgol, M.; Zarrabi, F.B.; Bazgir, M. A hollow rectangular plasmonic absorber for nano biosensing applications. Optik 2019, 176, 14–23. [Google Scholar] [CrossRef]
- Zarrabi, F.B.; Naser-Moghadasi, M.; Heydari, S.; Maleki, M.; Arezomand, A.S. Cross-slot nano-antenna with graphene coat for bio-sensing application. Opt. Commun. 2016, 371, 34–39. [Google Scholar] [CrossRef]
- Moghadasi, M.N.; Sadeghzadeh, R.A.; Toolabi, M.; Jahangiri, P.; Zarrabi, F.B. Fractal cross aperture nano-antenna with graphene coat for bio-sensing application. Microelectron. Eng. 2016, 162, 1–5. [Google Scholar] [CrossRef]
- Zarrabi, F.B.; Mohaghegh, M.; Bazgir, M.; Arezoomand, A.S. Graphene-Gold Nano-ring antenna for Dual-resonance optical application. Opt. Mater. 2016, 51, 98–103. [Google Scholar] [CrossRef]
- Vakil, A.; Bajwa, H. Energy harvesting using Graphene based antenna for UV spectrum. In Proceedings of the 2014 IEEE Long Island Systems, Applications and Technology Conference, LISAT 2014, Farmingdale, NY, USA, 2 May 2014; pp. 1–4. [Google Scholar]
- Shanawani, M.; Masotti, D.; Costanzo, A. THz Rectennas and Their Design Rules. Electronics 2017, 6, 99. [Google Scholar] [CrossRef]
- Andersson, M.A.; Vorobiev, A.; Stake, J.; Ozcelikkale, A.; Johansson, M.; Engstorm, U. Feasibility of Ambient RF Energy Harvesting for Self-Sustainable M2M Communications Using Transparent and Flexible Graphene Antennas. IEEE Access 2016, 4, 5850–5857. [Google Scholar] [CrossRef]
- Zhu, Z.; Joshi, S.; Pelz, B.; Moddel, G. Overview of optical rectennas for solar energy harvesting. Proc. SPIE 2013. [Google Scholar] [CrossRef]
- Pandesh, S.; Maleki, M.; Zarrabi, F.B. The sub-wavelength plasmonic nano-antenna based on cross structure. Optik 2016, 127, 3770–3774. [Google Scholar] [CrossRef]
- Kang, L.; Wang, C.; Guo, X.; Ni, X.; Liu, Z.; Werner, D.H. Nonlinear Chiral Meta-Mirrors: Enabling Technology for Ultrafast Switching of Light Polarization. Nano Lett. 2020, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Dragoman, M.; Aldrigo, M. Graphene rectenna for efficient energy harvesting at terahertz frequencies. Appl. Phys. Lett. 2016, 109, 113105. [Google Scholar] [CrossRef]
- Sabaawi, A.M.A.; Tsimenidis, C.C.; Sharif, B.S. Infra-red nano-antennas for solar energy collection. In Proceedings of the LAPC 2011—2011 Loughborough Antennas and Propagation Conference, Loughborough, UK, 14–15 November 2011; pp. 1–4. [Google Scholar]
- Masotti, D.; Costanzo, A.; Fantuzzi, M.; Mastri, F.; Aldrigo, M.; Dragoman, M. Graphene-based nano-rectenna in the far infrared frequency band. In Proceedings 44th European Microwave Conference. Rome, Italy, 6–9 October 2014; pp. 1202–1205. [Google Scholar]
- Zhu, Z.; Joshi, S.; Moddel, G. High performance room temperature rectenna IR detectors using graphene geometric diodes. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 70–78. [Google Scholar]
- Ionin, A.A.; Kinyaevskiy, I.O.; Klimachev, Y.M.; Kotkov, A.A.; Sagitova, A.M. THz sources based on frequency conversion of multi-line molecular lasers in nonlinear crystals and on optically pumped molecular lasers. EPJ Web Conf. 2018, 195, 03004. [Google Scholar] [CrossRef][Green Version]
- Jang, J.A.; Kim, H.S.; Cho, H.B. Smart roadside system for driver assistance and safety warnings: Framework and applications. Sensors 2011, 11, 7420–7436. [Google Scholar] [CrossRef]
- Rong, Z.; Leeson, M.S.; Higgins, M.D.; Lu, Y. Nano-rectenna powered body-centric nano-networks in the terahertz band. Healthc. Technol. Lett. 2018, 5, 113–117. [Google Scholar] [CrossRef]
- Zainud-Deen, S.H.; Malhat, H.A.; El-Araby, H.A. Energy harvesting enhancement of nanoantenna coupled to geometrie diode using transmitarray. In Proceedings of the 2017 Japan-Africa Conference on Electronics, Communications and Computers (JAC-ECC), JAC-ECC 2017, Alexandria, Egypt, 18–20 December 2017; pp. 152–155. [Google Scholar]
- El-Araby, H.A.; Malhat, H.A.; Zainud-Deen, S.H. Performance of nanoantenna-coupled geometric diode with infrared radiation. In Proceedings of the 34th National Radio Science Conference (NRSC), Alexandria, Egypt, 13–16 March 2017; pp. 15–21. [Google Scholar]
- El-Araby, H.A.; Malhat, H.A.E.A.; Zainud-Deen, S.H. Nanoantenna with Geometric Diode for Energy Harvesting. Wirel. Pers. Commun. 2018, 99, 941–952. [Google Scholar] [CrossRef]
- Reed, J.C.; Zhu, H.; Zhu, A.Y.; Li, C.; Cubukcu, E. Graphene-enabled silver nanoantenna sensors. Nano Lett. 2012, 12, 4090–4094. [Google Scholar] [CrossRef] [PubMed]
- Amin, M.; Farhat, M.; Baǧci, H. A dynamically reconfigurable Fano metamaterial through graphene tuning for switching and sensing applications. Sci. Rep. 2013, 3, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Mittendorff, M.; Winnerl, S.; Kamann, J.; Eroms, J.; Weiss, D.; Schneider, H.; Helm, M. Ultrafast graphene-based broadband THz detector. Appl. Phys. Lett. 2013, 103, 021113. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, T.; Zeng, B.; Zhang, H.; Lv, H.; Huang, X.; Zhang, W.; Azad, A.K. A graphene based tunable terahertz sensor with double Fano resonances. Nanoscale 2015, 7, 12682–12688. [Google Scholar] [CrossRef]
- Zangeneh-Nejad, F.; Safian, R. Hybrid graphene-molybdenum disulphide based ring resonator for label-free sensing. Opt. Commun. 2016, 371, 9–14. [Google Scholar] [CrossRef]
- Zangeneh-Nejad, F.; Safian, R. A Graphene-Based THz Ring Resonator for Label-Free Sensing. IEEE Sens. J. 2016, 16, 4338–4344. [Google Scholar] [CrossRef]
- Rodrigo, D.; Limaj, O.; Janner, D.; Etezadi, D.; García De Abajo, F.J.; Pruneri, V.; Altug, H. Mid-infrared plasmonic biosensing with graphene. Sci. Rep. Appl. Phys. 2015, 349, 165–168. [Google Scholar] [CrossRef]
- Zheng, B.; Yang, X.; Li, J.; Shi, C.F.; Wang, Z.L.; Xia, X.H. Graphene Plasmon-Enhanced IR Biosensing for in Situ Detection of Aqueous-Phase Molecules with an Attenuated Total Reflection Mode. Anal. Chem. 2018, 90, 10786–10794. [Google Scholar] [CrossRef]
- Afapour, Z.O.V.; Ajati, Y.A.H.; Ajati, M.O.H. Graphene-based mid-infrared biosensor. J. Opt. Soc. Am. B 2017, 34, 2586–2592. [Google Scholar] [CrossRef]
- Park, J.; Kim, J.; Kim, K.; Kim, S.Y.; Cheong, W.H.; Park, K.; Song, J.H.; Namgoong, G.; Kim, J.J.; Heo, J.; et al. Wearable, wireless gas sensors using highly stretchable and transparent structures of nanowires and graphene. Nanoscale 2016, 8, 10591–10597. [Google Scholar] [CrossRef]
- Leng, T.; Huang, X.; Chang, K.; Chen, J.; Abdalla, M.A.; Hu, Z. Graphene Nanoflakes Printed Flexible Meandered-Line Dipole Antenna on Paper Substrate for Low-Cost RFID and Sensing Applications. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 1565–1568. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, R.; Liao, L.; Zhou, H.; Bai, J.; Liu, G.; Liu, L.; Huang, Y.; Duan, X. Plasmon resonance enhanced multicolour photodetection by graphene. Nat. Commun. 2011, 2, 577–579. [Google Scholar] [CrossRef] [PubMed]
- Tong, J.; Muthee, M.; Chen, S.Y.; Yngvesson, S.K.; Yan, J. Antenna Enhanced Graphene THz Emitter and Detector. Nano Lett. 2015, 15, 5295–5301. [Google Scholar] [CrossRef] [PubMed]
- Choi, G.; Hong, S.J.; Bahk, Y.-M. Graphene-assisted biosensing based on terahertz nanoslot antennas. Sci. Rep. 2019, 9, 9749. [Google Scholar] [CrossRef]
- Taliercio, T.; Biagioni, P. Semiconductor infrared plasmonics. Nanophotonics 2019, 8, 949–990. [Google Scholar] [CrossRef]
- Zhao, Q.; Guclu, C.; Huang, Y.; Capolino, F.; Boyraz, O. Experimental Demonstration of Directive Si3N4 Optical Leaky Wave Antennas with Semiconductor Perturbations. J. Lightwave Technol. 2016, 34, 4864–4871. [Google Scholar] [CrossRef]
- Zhao, Y.; Du, J.; Ruan, Z.; Shen, L.; Li, S.; Wang, J. Design and Fabrication of 2 μm Metasurface-based Orbital Angular Momentum (OAM) Mode Generator Employing Reflective Optical Antenna Array. In Proceedings of the 2017 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 14–19 May 2017. [Google Scholar]
- Hashiguchi, H.; Baba, T.; Arai, H. An Optical Leaky Wave Antenna Excited by Parabolic Reflector. In Proceedings of the 2018 International Symposium on Antennas and Propagation (ISAP), Busan, Korea, 23–26 October 2018; pp. 1–2. [Google Scholar]
- Liu, H.; Si, G.; Lv, J. Functional plasmonic nanoantennae as optical filters. Micro Nano Lett. 2015, 10, 5–8. [Google Scholar]
- Hashiguchi, H.; Baba, T.; Arai, H. High Gain Optical Leaky Wave Antenna by Photonic Bandgap Reflector. In Proceedings of the 2018 IEEE International Workshop on Electromagnetics: Applications and Student Innovation Competition, iWEM 2018, Nagoya, Japan, 29–31 August 2018; Volume 35, pp. 1–2. [Google Scholar]
- Liu, P.Q.; Luxmoore, I.J.; Mikhailov, S.A.; Savostianova, N.A.; Valmorra, F.; Faist, J.; Nash, G.R. Highly tunable hybrid metamaterials employing split-ring resonators strongly coupled to graphene surface plasmons. Nat. Commun. 2015, 6, 1–7. [Google Scholar] [CrossRef]
- Moreno-Bárcenas, A.; Perez-Robles, J.F.; Vorobiev, Y.V.; Ornelas-Soto, N.; Mexicano, A.; García, A.G. Graphene synthesis using a CVD reactor and a discontinuous feed of gas precursor at atmospheric pressure. J. Nanomater. 2018, 2018. [Google Scholar] [CrossRef]
- El Fatimy, A.; Myers-Ward, R.L.; Boyd, A.K.; Daniels, K.M.; Gaskill, D.K.; Barbara, P. Epitaxial graphene quantum dots for high-performance terahertz bolometers. Nat. Nanotechnol. 2016, 11, 335–338. [Google Scholar] [CrossRef]
- Degl’innocenti, R.; Jessop, D.S.; Sol, C.W.O.; Xiao, L.; Kindness, S.J.; Lin, H.; Zeitler, J.A.; Braeuninger-Weimer, P.; Hofmann, S.; Ren, Y.; et al. Fast Modulation of Terahertz Quantum Cascade Lasers Using Graphene Loaded Plasmonic Antennas. ACS Photonics 2016, 3, 464–470. [Google Scholar] [CrossRef]
- Cakmakyapan, S.; Sahin, L.; Pierini, F.; Ozbay, E. Resonance tuning and broadening of bowtie nanoantennas on graphene. Photonics Nanostruct. Fundam. Appl. 2014, 12, 199–204. [Google Scholar] [CrossRef]
- Huang, C.H.; Su, C.Y.; Okada, T.; Li, L.J.; Ho, K.I.; Li, P.W.; Chen, I.H.; Chou, C.; Lai, C.S.; Samukawa, S. Ultra-low-edge-defect graphene nanoribbons patterned by neutral beam. Carbon 2013, 61, 229–235. [Google Scholar] [CrossRef]
- Kalita, D. Graphene Produced by Chemical Vapor Deposition: From Control and Understanding of Atomic Scale Defects to Production of Macroscale Functional Devices. Ph.D. Thesis, Université Grenoble Alpes, Grenoble, France, 2015. [Google Scholar]
- Burford, N.M.; Evans, M.J.; El-Shenawee, M. Fabrication and Characterization of Plasmonic Thin-Film Terahertz Photoconductive Antenna. In Proceedings of the 2018 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, Boston, MA, USA, 8–13 July 2018; pp. 803–804. [Google Scholar]
- He, H.; Akbari, M.; Ukkonen, L.; Virkki, J. Fabrication and Evaluation of 3D-Printed Heat and Photonic Cured Graphene RFID Tags on Veneer. In Proceedings of the 2017 International Applied Computational Electromagnetics Society Symposium (ACES), Suzhou, China, 1–4 August 2017; pp. 3–4. [Google Scholar]
- Yang, M.C.; Yue, C.; Liao, C.T.; Chen, C.A.; Lee, Y.H.; Lee, M.C. Fabrication of large-area optical antenna arrays for studying spontaneous emission enhancement of 2D transition metal dichalcogenide. In Proceedings of the 2017 International Conference on Optical MEMS and Nanophotonics (OMN), Santa Fe, NM, USA, 13–17 august 2017; pp. 4–5. [Google Scholar]
- Liu, C.; Schauff, J.; Lee, S.; Cho, J.-H. Fabrication of Nanopillar-Based Split Ring Resonators for Displacement Current Mediated Resonances in Terahertz Metamaterials. J. Vis. Exp. 2017, 3–9. [Google Scholar] [CrossRef] [PubMed]
- Papasimakis, N.; Thongrattanasiri, S.; Zheludev, N.I.; García De Abajo, F.J. The magnetic response of graphene split-ring metamaterials. Light-Sci. Appli. 2013, 2, 23–26. [Google Scholar] [CrossRef]
- Wang, R.; Raju, S.; Chan, M.; Jiang, L.J. Low Frequency Behavior of Cvd Graphene From Dc To 40 Ghz. Prog. Electromagn. Res. C 2017, 71, 1–7. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, G.; Yuan, W.; Wen, Z.; Li, M.; Zhang, Z.; Sun, Y.; Ruan, D. The Fabrication of Large-Area, Uniform Graphene Nanomeshes for High-Speed, Room-Temperature Direct Terahertz Detection. Nanoscale Res. Lett. 2018, 13, 190. [Google Scholar]
- Zhu, Z.; Joshi, S.; Grover, S.; Moddel, G. Graphene geometric diodes for terahertz rectennas. J. Phys. D: Appl. Phys. 2013, 46, 185101. [Google Scholar] [CrossRef]
- Zakrajsek, L.; Einarsson, E.; Thawdar, N.; Medley, M.; Jornet, J.M. Lithographically Defined Plasmonic Graphene Antennas for Terahertz-Band Communication. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 1553–1556. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, Z.; Hao, Y.; Hone, J.; Yu, N.; Lin, Q.; York, N. Tunable Mid-Infrared Biosensors Based on Graphene Metasurfaces. In Proceedings of the 2017 19th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Kaohsiung, Taiwan, 18–22 June 2017; pp. 1340–1343. [Google Scholar]
- Dragoman, M.; Muller, A.A.; Dragoman, D.; Coccetti, F.; Plana, R. Terahertz antenna based on graphene. J. Appl. Phys. 2010, 107, 1–4. [Google Scholar] [CrossRef]
- Hong, J.Y.; Jang, J. Micropatterning of graphene sheets: Recent advances in techniques and applications. J. Mater. Chem. 2012, 22, 8179–8191. [Google Scholar] [CrossRef]
- Gadalla, M.N.; Abdel-Rahman, M.; Shamim, A. Design, Optimization and Fabrication of a 28.3 THz Nano-Rectenna for Infrared Detection and Rectification. Sci. Rep. 2014, 4, 1–9. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, W.-S.; Hu, J.; Zhang, T. A Novel Tunable Antenna At Thz Frequencies Using Graphene-Based Artificial Magnetic Conductor (Amc). Prog. Electromagn. Res. Lett. 2014, 41, 29–38. [Google Scholar] [CrossRef]
- Shin, K.Y.; Hong, J.Y.; Jang, J. Micropatterning of graphene sheets by inkjet printing and its wideband dipole-antenna application. Adv. Mater. 2011, 23, 2113–2118. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Akbari, M.; Sydanheimo, L.; Ukkonen, L.; Virkki, J. 3D-printed graphene and stretchable antennas for wearable RFID applications. In Proceedings of the 2017 International Symposium on Antennas and Propagation, ISAP 2017, Phuket, Thailand, 30 October–2 November 2017; pp. 1–2. [Google Scholar]
- Akbari, M.; Khan, M.W.A.; Hasani, M.; Bjorninen, T.; Sydanheimo, L.; Ukkonen, L. Fabrication and Characterization of Graphene Antenna for Low-Cost and Environmentally Friendly RFID Tags. IEEE Antennas Wirel Propag. Lett. 2016, 15, 1569–1572. [Google Scholar] [CrossRef]
| Contribution/Study | Design and Resonant Frequency (THz) | Substrate Material | Bandwidth (THz) | Tunability Range (THz) |
|---|---|---|---|---|
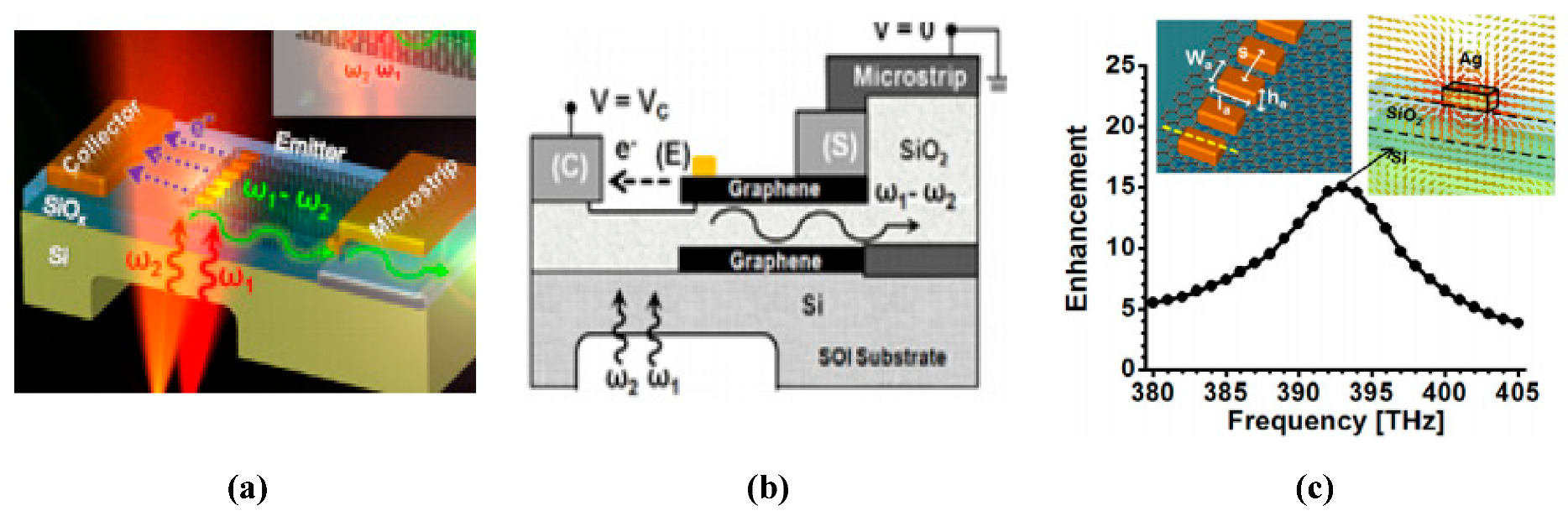
| Graphene-based nanoantenna-enhanced photomixer for wideband-tunable terahertz frequency generation, 2013 [122] | Graphene nanoemitter for planar emission @ 392 | SiO2/Si | 25 | 380–400 |
| Lateral confinement of SPP in graphene nanoribbons antenna, 2013 [106] | GNR on flat metallic surface @ 120 | SiO2 | 50 | 100–600 |
| Graphene cylindrical waveguides as reconfigurable antennas, 2015 [113] | GCW-based dipole antenna @ 1.5 | SiO2 | 0.3 | 1–3 |
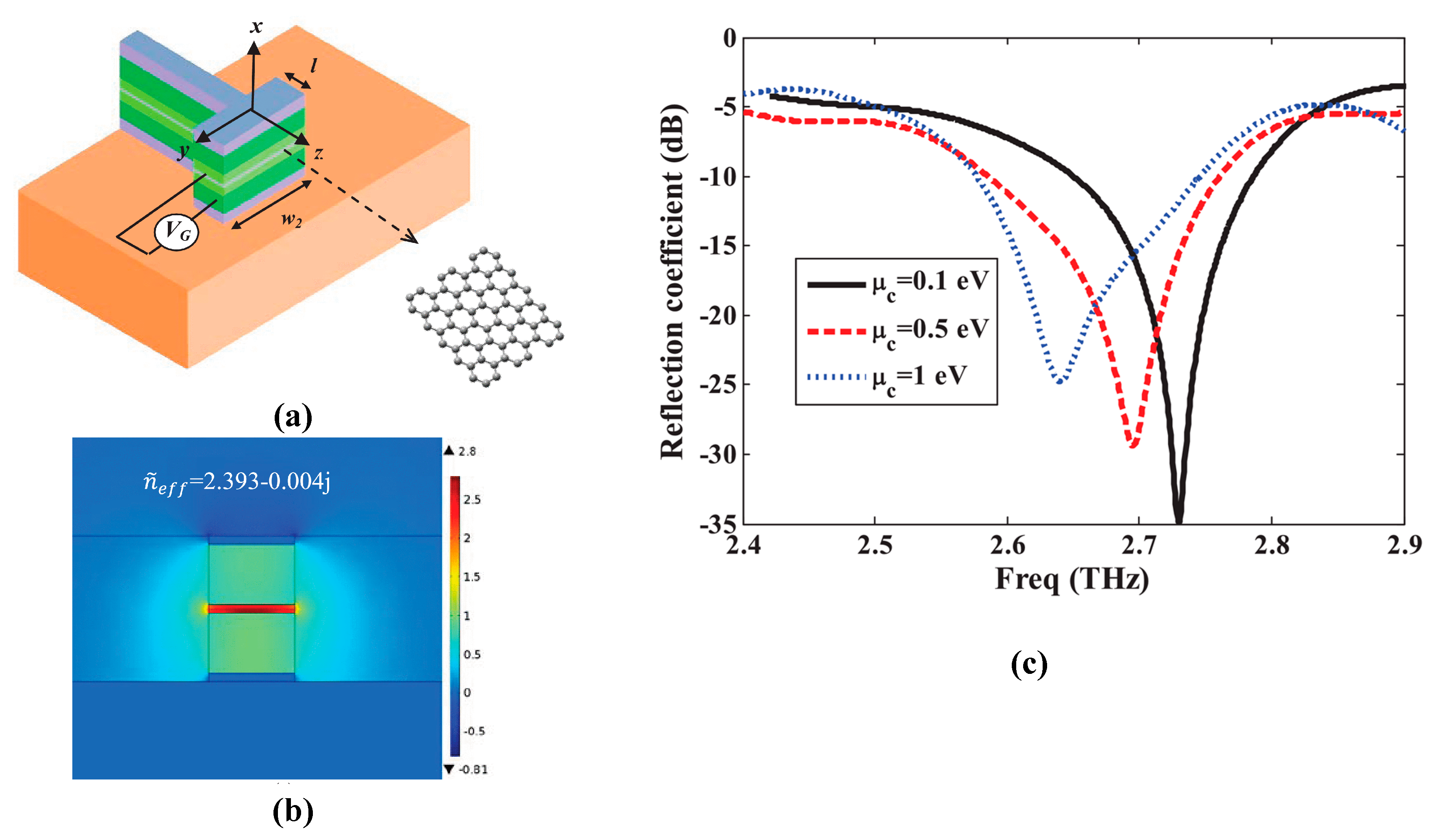
| Waveguide fed tunable graphene–metal antenna for sensing, 2016 [138] | Staked graphene patch with waveguide fed @ 2.73 | Si/SiO2 substrate with Ag | 0.8 | 2.63–2.73 |
| Efficiency improvement of graphene stack antenna with LIM and high index material layers, 2017 [102] | Graphene-based stack dipole antenna @ 1.2 | LIM and HIM Stacks | 0.6 | 0.5–3 |
| Reduction of mutual coupling of graphene antenna arrays, 2017 [105] | Graphene antenna array @ 1 | SiO2 | 8 | 1–8 |
| Tuning of radiation characteristics, 2017 [112] | Graphene patch antenna @ 0.97 | SiO2 | 1 | 0.97–1.09 |
| Electrically tunable polarizer with graphene cross antenna, 2018 [133] | Graphene loaded cross shape dipole antenna array @ 50 | SiO2 | 67 | 33–100 |
| Contribution/Study | Geometry and Wavelength | Results and Measurement |
|---|---|---|
| Control of graphene plasmons, 2014 [185] | Metallic dipole wrapped in graphene sheet @ 11.06 µm | Enhancement factor f2 = 3 |
| Tuning of scattering response of nanoantenna, 2014 [140] | Graphene dipole @ 500 nm | Multi-layer graphene results in better scattering |
| Magnetic tunable responses of graphene, 2015 [172] | Graphene diabolo with Au reflector @ 7 µm | Intensity modulation 1460%, tuning range 63.1% |
| Active modulation of visible light with graphene, 2016 [169] | Graphene with silver rod array @ 749 nm | Reflection (>600%) and modulation depth 36% |
| Beam steering and far-field light propagation modulation, 2017 [144] | Graphene metasurface with Au resonators @ 8.4 µm | 98% absorption at Ef = 0.25 eV with better beam intensity |
| Tunable metasurface for metallic biosensor antenna, 2017 [184] | Rectangular Au arrays with graphene @ 7142 nm | Enhancement factor from 13 to 20, at a rate of ~0.07/cm−1 |
| Broadband modulation of terahertz waves, 2017 [175] | Bowie arrays on top of VO2 film @ 199 µm | Maximum intensity 1407 J/m3 |
| LSPR of nanorods with graphene for bio-sensing, 2018 [139] | Meta-graphene double-nanorods @ 10 µm | Extinction cross section 20 µm2, directivity 24 dB |
| Contribution/Study | Geometry and Frequency | Phase Tuning and Beam Scanning |
|---|---|---|
| Tuning beam steering with HIS, 2015 [179] | Leaky-wave graphene antenna @ 3.2 THz | 60° scanning angle, reflection phase 135° |
| Dispersion and radiation properties, 2016 [211] | Substrate–superstrate graphene LWA @ 0.92 THz | Beamwidth 0° to 45°, Chemical potential tuning 0 eV to 1 eV |
| Efficiency improvement of reconfigurable LWA, 2017 [214] | Graphene FPCAs with metasurface @ 1 THz | 30° and 45° beam scanning, 70% efficiency |
| Dynamic reconfiguration of vertex modes, 2016 [255] | Graphene reflectarray with circular sectors @ 1.6 THz | Beamwidth 24.6°, efficiency 67%, reflection phase 360° |
| Sinusoidal modulation for beam scanning, 2017 [205] | Leaky-wave antenna with gapped graphene @ 2 THz | 45° beam scanning, 77% radiation efficiency |
| Generation of OAM vortex waves, 2017 [256] | Graphene metamaterial reflectarray @ 1.8–2.8 THz | 360° phase range, reflection magnitude -2.5 dB |
| Pancharatnam–Berry phase principle, 2018 [242] | Reflectarray using graphene @ 1.52 THz | Tunable phase range of 360°, beamwidth 120° |
| Contribution/Study | Geometry and Method | Measurements |
|---|---|---|
| Low-cost graphene antenna fabrication, 2015 [342] | Microstrip graphene antenna @ 890 MHz, ink-printed graphene | Conductivity 1.25 × 104, sheet resistance 1.9 ± 0.1 |
| Fabrication of graphene antenna, 2016 [334] | Graphene hexagon antenna fabrication on SiO2 @ 0.1–10 THz | CVD and focused ion beam lithography method |
| I–V characteristics of a graphene rectenna, 2017 [297] | Graphene geometric diode coupled with nanoantenna @ 20.5 THz | Voltage 1.6 × 10−5 V, responsivity 1.646 A/W |
| Energy harvesting enhancement, 2017 [296] | Nanoantenna coupled to graphene diode @ 19.4 THz | Received voltage 97.6 µm, gain 20 dBi |
| Ultra-sensitive near-infrared photodetection, 2017 [273] | Metallic nanopillar antennas with graphene @ 0.6–1.2 µm | Photoresponsivity 7 A/m at 8 µm, absorption 70 % at 8 µm |
| Highly-responsive ultrafast photodetection, 2018 [270] | Gold-patch graphene nano-strips @ 0.8 µm, 20 µm | Responsivity 0.6 A/M, 11.5 A/M, output power -80 dBm |
| Nano-rectenna for body-centric networks, 2018 [295] | Insulator-coated carbon nanotube cathode with bowtie nanoantenna | Capacitor charge time 2.2 s, capacitance 100 mF-cm-2 |
| Graphene geometric diode IR harvesting, 2018 [297] | Nanoantenna coupled with geometric diode @ 20.5 THz | Current 15 mA, responsivity 9 A/W |
| graphene-plasmons IR biosensor, 2018 [307] | boron-doped graphene nanodisk array @ 400-800 (cm-1) | Absorbance 8× 10-4 at -0.4 eV, maximum detection 0.5 nM |
| Meta biosensor, 2018 [308] | Slotted metametrial @ 16-22 THz | Transmittance 0.2 at 18 THz |
| CVD graphene synthesis, 2018 [320] | CVD precursors H2, CH4, and pure copper, pressure 760 °C | Raman shift 2680 cm−1 |
| Fabrication of large-area graphene, 2018 [332] | Circular and rectangular graphene nanomesh, EBL method | Photoconductive effect 10 mA/W, bandgap 0.23 eV |
| Fabrication of graphene-assisted biosensor nano slot antennas, 2019 [312] | Monolayer graphene growth through CVD and focused ion beam lithography | D peak 1350 cm−1, 630 E-field enhancement |
| Plasmonically enhanced photodetector, 2019 [274] | Graphene waveguide with bowtie antenna @ 1480–1620 nm | Responsivity 0.5 A/m, photoresponse speed 110 GHz |
| Fast and sensitive terahertz detection, 2019 [273] | Antenna integrated graphene p–n junction @ 1.8–4.25 THz | Speed 30 ns, noise equivalent power 80 pW/ |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullah, Z.; Witjaksono, G.; Nawi, I.; Tansu, N.; Irfan Khattak, M.; Junaid, M. A Review on the Development of Tunable Graphene Nanoantennas for Terahertz Optoelectronic and Plasmonic Applications. Sensors 2020, 20, 1401. https://doi.org/10.3390/s20051401
Ullah Z, Witjaksono G, Nawi I, Tansu N, Irfan Khattak M, Junaid M. A Review on the Development of Tunable Graphene Nanoantennas for Terahertz Optoelectronic and Plasmonic Applications. Sensors. 2020; 20(5):1401. https://doi.org/10.3390/s20051401
Chicago/Turabian StyleUllah, Zaka, Gunawan Witjaksono, Illani Nawi, Nelson Tansu, Muhammad Irfan Khattak, and Muhammad Junaid. 2020. "A Review on the Development of Tunable Graphene Nanoantennas for Terahertz Optoelectronic and Plasmonic Applications" Sensors 20, no. 5: 1401. https://doi.org/10.3390/s20051401
APA StyleUllah, Z., Witjaksono, G., Nawi, I., Tansu, N., Irfan Khattak, M., & Junaid, M. (2020). A Review on the Development of Tunable Graphene Nanoantennas for Terahertz Optoelectronic and Plasmonic Applications. Sensors, 20(5), 1401. https://doi.org/10.3390/s20051401







