1. Introduction
Measuring wind velocity near the Earth’s surface is critical to understanding the surface-atmosphere interactions driving the dynamic state of the atmospheric boundary layer (ABL). How the ABL evolves with space and time impacts public health and safety [
1,
2,
3,
4,
5,
6], transport of air pollutants, pollen and spores [
7,
8,
9,
10], wind power supply to smart grid systems [
11,
12,
13,
14,
15], forecast of local weather [
3,
4,
5,
6,
16], air traffic control at airports [
17,
18,
19,
20], the spread and management of wildfires [
21,
22,
23,
24], and emissions mitigation of greenhouse gases [
25,
26,
27,
28,
29]. Therefore, accurately characterizing the dynamic state of the ABL over micro- and mesoscale domains is important [
3,
16,
30,
31]. However, observations of wind velocity at high spatial resolution are difficult to attain due to the cost and limited mobility of conventional atmospheric sensing technology.
Early work to address the existing gap of atmospheric wind measurements and atmospheric parameters such as atmospheric pressure, air temperature, and relative humidity (PTH) involved fixed-wing aircraft for their predictable dynamics, payload capacity, and flight endurance. Approaches to measuring wind with fixed wing aircraft consist of direct and indirect measurements of wind velocity. Direct methods have combined inertial and air-relative velocity measurements from GPS and a Pitot tube or multi-hole air data system to infer wind velocity using the wind triangle relationship [
32,
33]. Indirect methods, on the other hand, have exploited GPS and IMU measurements along with vehicle dynamic models to estimate wind velocity employing state estimation algorithms [
34,
35]. A comprehensive review of established direct and indirect methods for inferring wind with fixed-wing aircraft is presented in [
36]. However, despite the advantages of operating fixed wing aircraft over open space, safely maneuvering in urban and complex environments to measure wind speed and PTH variables remains a challenge.
More recently, multirotor UAS have become popular for direct and indirect measurements of atmospheric wind and PTH variables within the ABL. Multirotor UAS are mobile, portable, low cost, and easy to operate over complex and urban environments where it is prohibitively difficult for conventional atmospheric sensors or fixed-wind aircraft. Direct methods involve measuring wind velocity from an on-board flow sensor, which include various types of anemometers [
37,
38,
39,
40,
41] and air data systems integrated with Pitot tubes or multi-hole probes [
42,
43]. The choice of sensor for wind sensing depends on size and power requirement of the sensor, as well as the airframe configuration and payload capacity of the multirotor UAS. Indirect methods, on the other hand, estimate wind velocity from wind induced perturbations to the aircraft motion and do not require an onboard airflow sensor. Conventional model-based approaches to wind estimation have involved kinematic [
44,
45], point mass [
1,
39,
46,
47,
48], and rigid body models [
1,
49] of control-augmented quadrotor dynamics, which characterize how a quadrotor responds to disturbances under feedback stabilization. A comparison of all three vehicle motion models has demonstrated that both the accuracy and bandwidth of wind estimates increases with model fidelity [
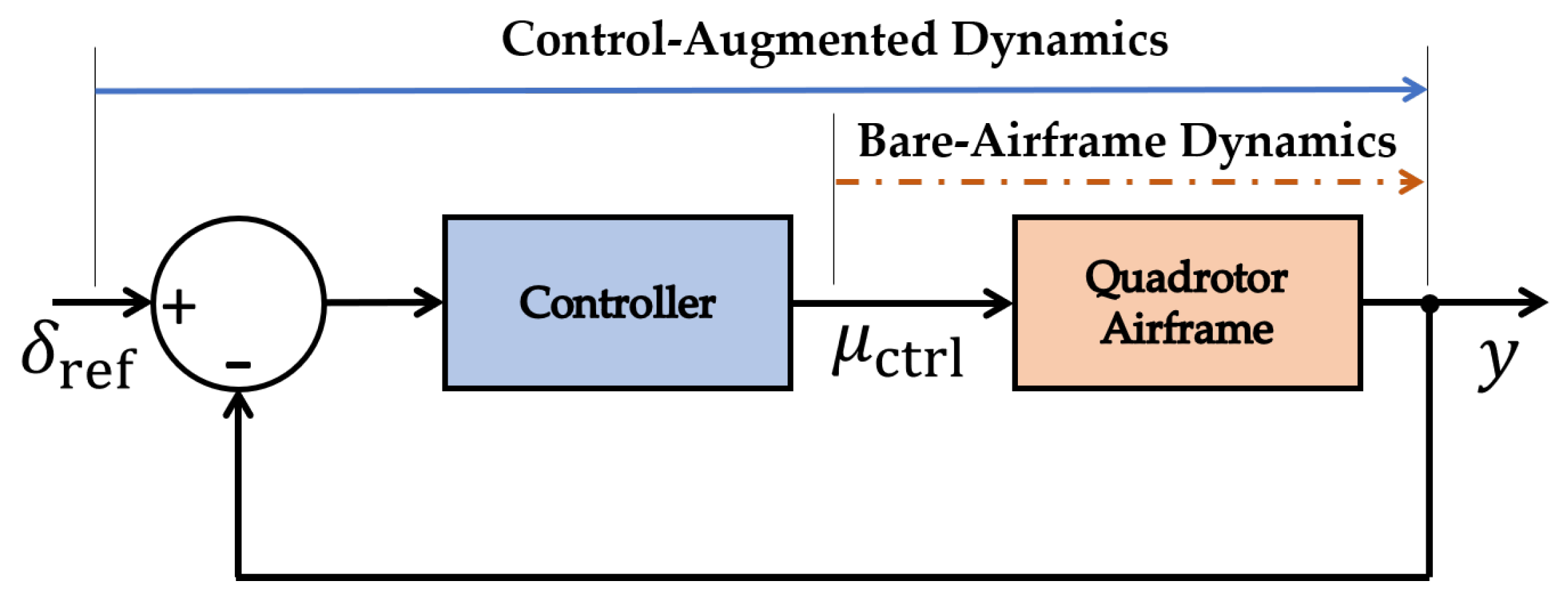
1], which has made model-based wind sensing inside the ABL more useful and reliable. Especially in scenarios where direct measurements are impossible, i.e., when the aircraft is very small or when the aircraft is intended for some other purpose and is not equipped to measure the wind.
To date, model-based wind estimation approaches accounting for vehicle dynamics have mostly incorporated models appropriate for
hovering flight [
1,
46,
47,
48,
49,
50]. Measuring wind velocity only while hovering limits the efficiency of multirotor aircraft to sample the lower atmosphere. The limited effectiveness of stationary sampling is largely due to the endurance of multirotor aircraft, which is typically less than 20 min. Many applications of multirotor UAS wind sensing require atmospheric sampling over horizontal and vertical distances. Therefore, there is a need to develop wind estimation algorithms that allow for movement of the multirotor UAS while accurately measuring wind velocity inside the ABL.
This paper presents the validation of a model-based method for estimating vertical profiles of the horizontal wind velocity employing wind measurements from a sonic anemometer and SoDAR (Sound Detection And Ranging) wind profilers. The model-based method that is validated, referred as the
dynamic rigid body wind profiling method or
DRBWindPro method, is the extension presented in [
2] of the wind sensing algorithm described in [
1] to infer wind velocity using a dynamic rigid body model for hovering flight. The extension of the wind sensing algorithm incorporates dynamic rigid body models characterized from system identification for equilibrium flight conditions corresponding to steady ascent rates ranging from 0 to 2 m/s. The models from system identification were used to estimate the wind velocity in the vicinity of ground-based in situ and remote atmospheric sensors. Quadrotor wind estimates and wind measurements from ground-based atmospheric sensors were then compared to determine the accuracy of the DRBWindPro method.
The organization of this paper is as follows.
Section 2 introduces materials and methods used for model-based wind estimation. This section includes the formulation of aircraft dynamics, system identification of aircraft models, and the design of a state observer for wind estimation. The ground-based wind measurement methods are described in
Section 3. In
Section 4, results from system identification experiments and comparison of multirotor wind velocity measurements with ground-based measurements are presented.
Section 5 presents a thorough discussion of results from system identification and from comparing multirotor and ground-based wind measurements. Finally, a summary of findings and future work to extend the utility of multirotor UAS for wind sensing are presented in
Section 6.
5. Discussion
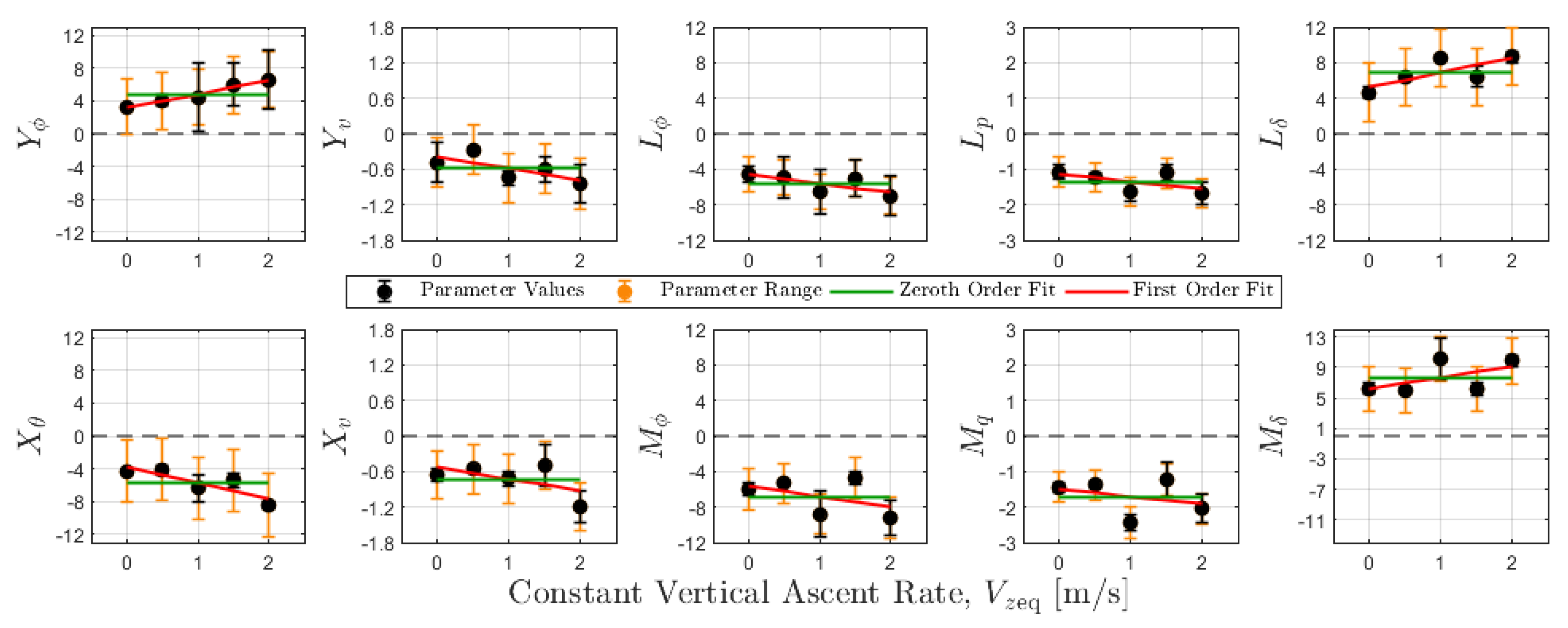
Five models were identified to characterize the control-augmented rigid body dynamics of a quadrotor for wind estimation in hovering and steady vertical-ascent flight. An observability analysis confirmed that it is possible to estimate wind velocity using all five models. However, model parameter estimates were found to fluctuate significantly at higher ascent rates, which can greatly impact wind estimation error based on the sensitivity analysis presented in
Appendix C. Parameter fluctuations, as mentioned in
Section 4.1.2, may be the product of ambient flow and vehicle interactions at specific flight regimes or related to limitations with system identification experiments. Hence, more in-depth studies are required to understand the nature of parameter fluctuations at higher rates.
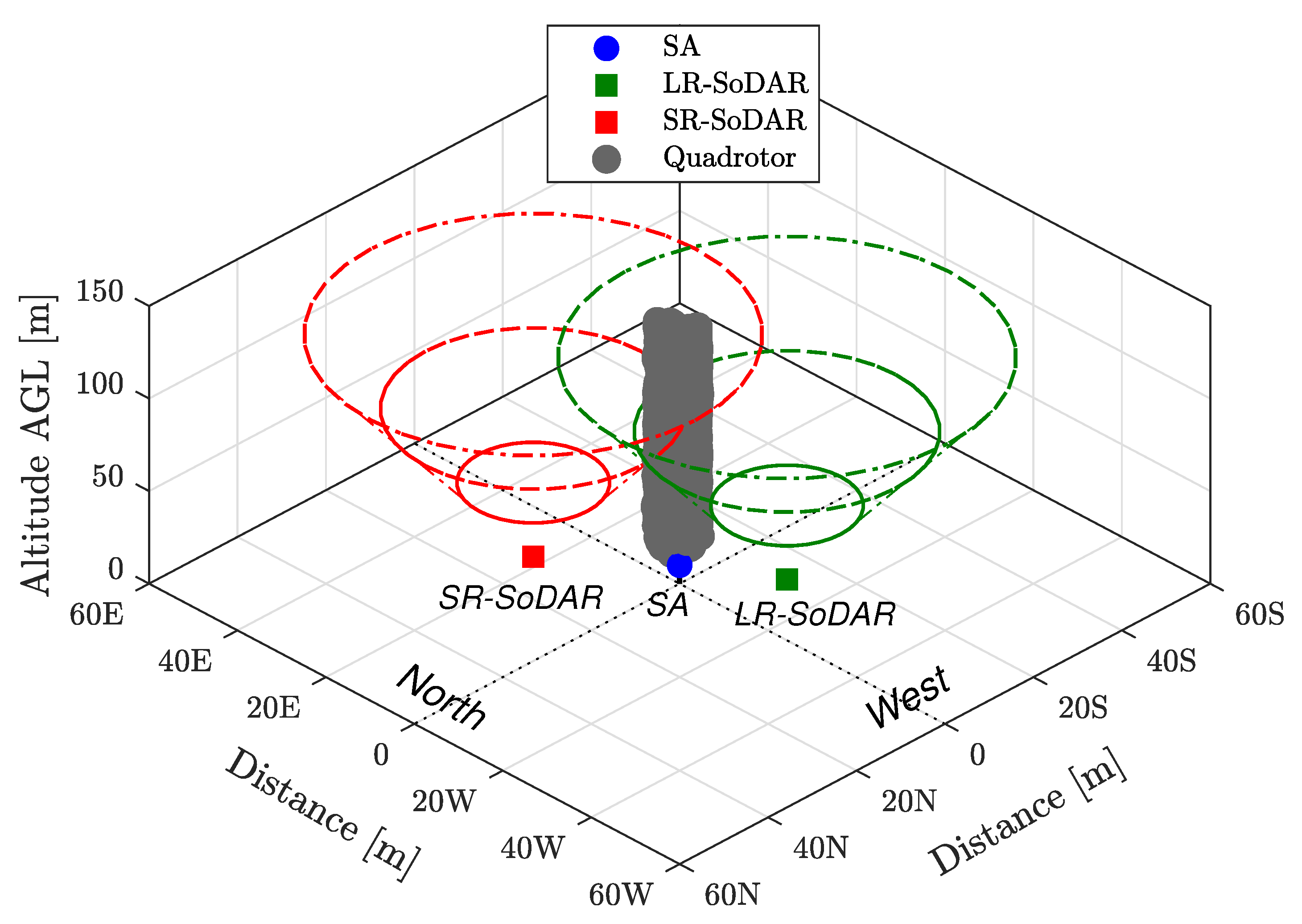
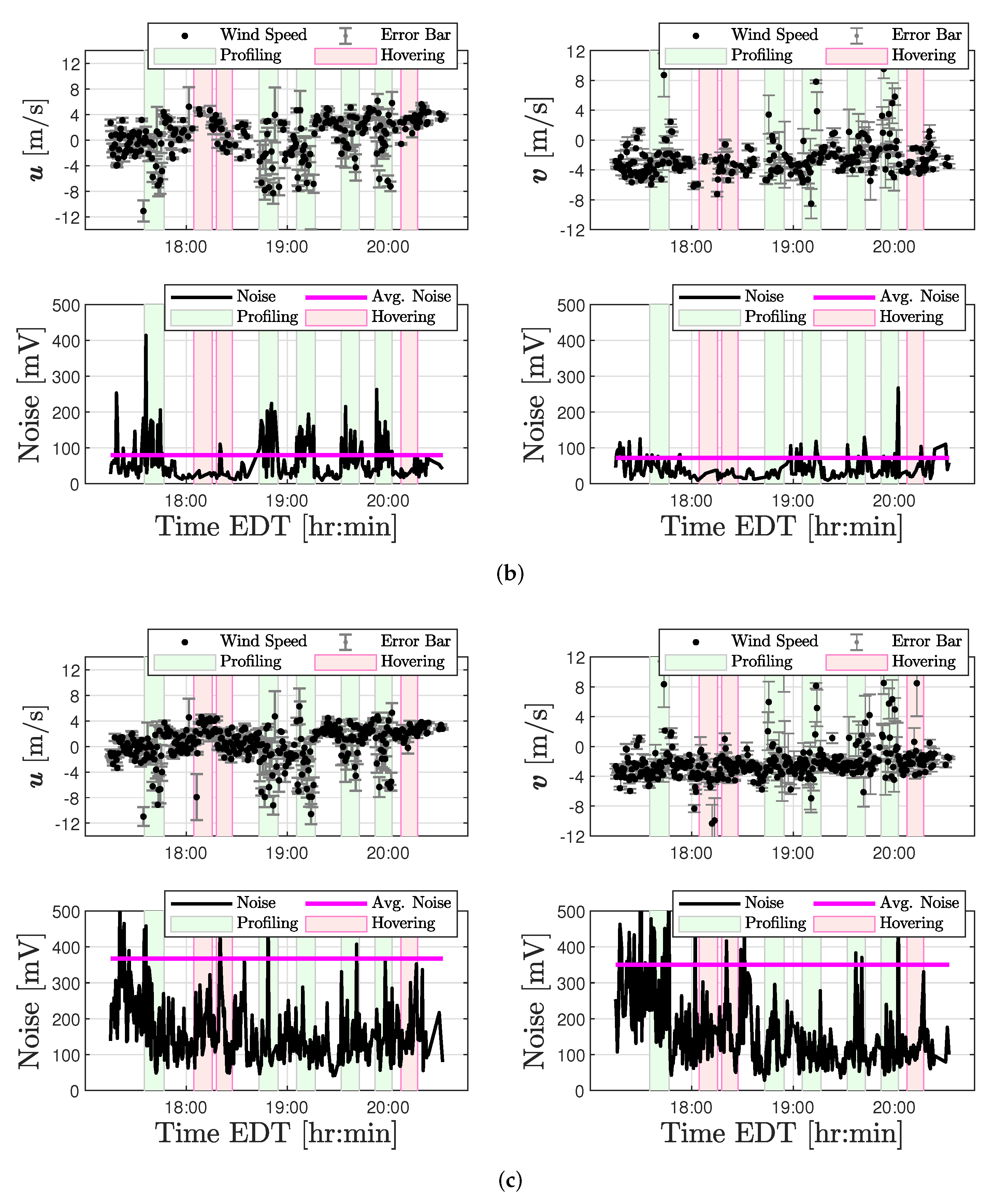
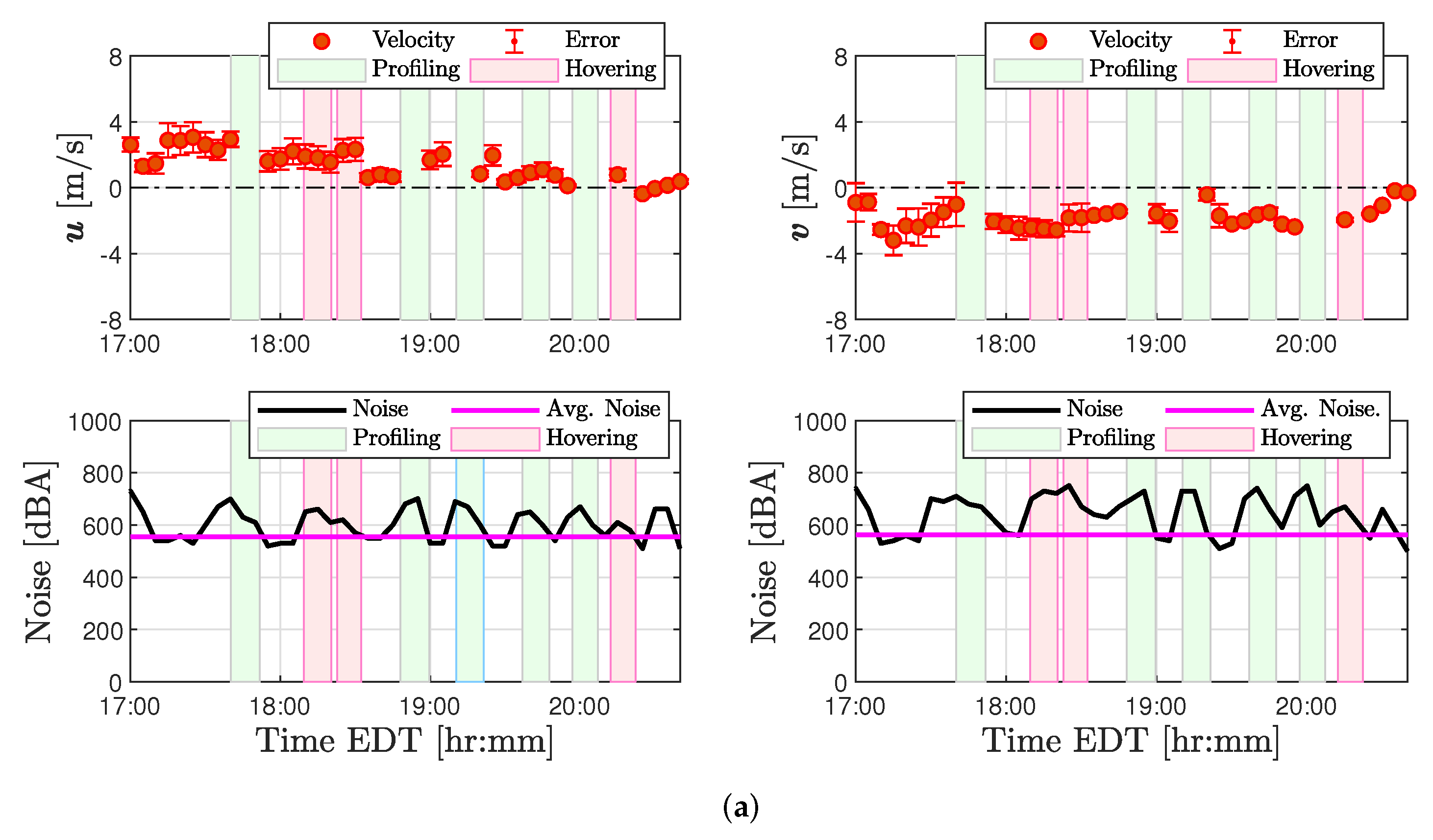
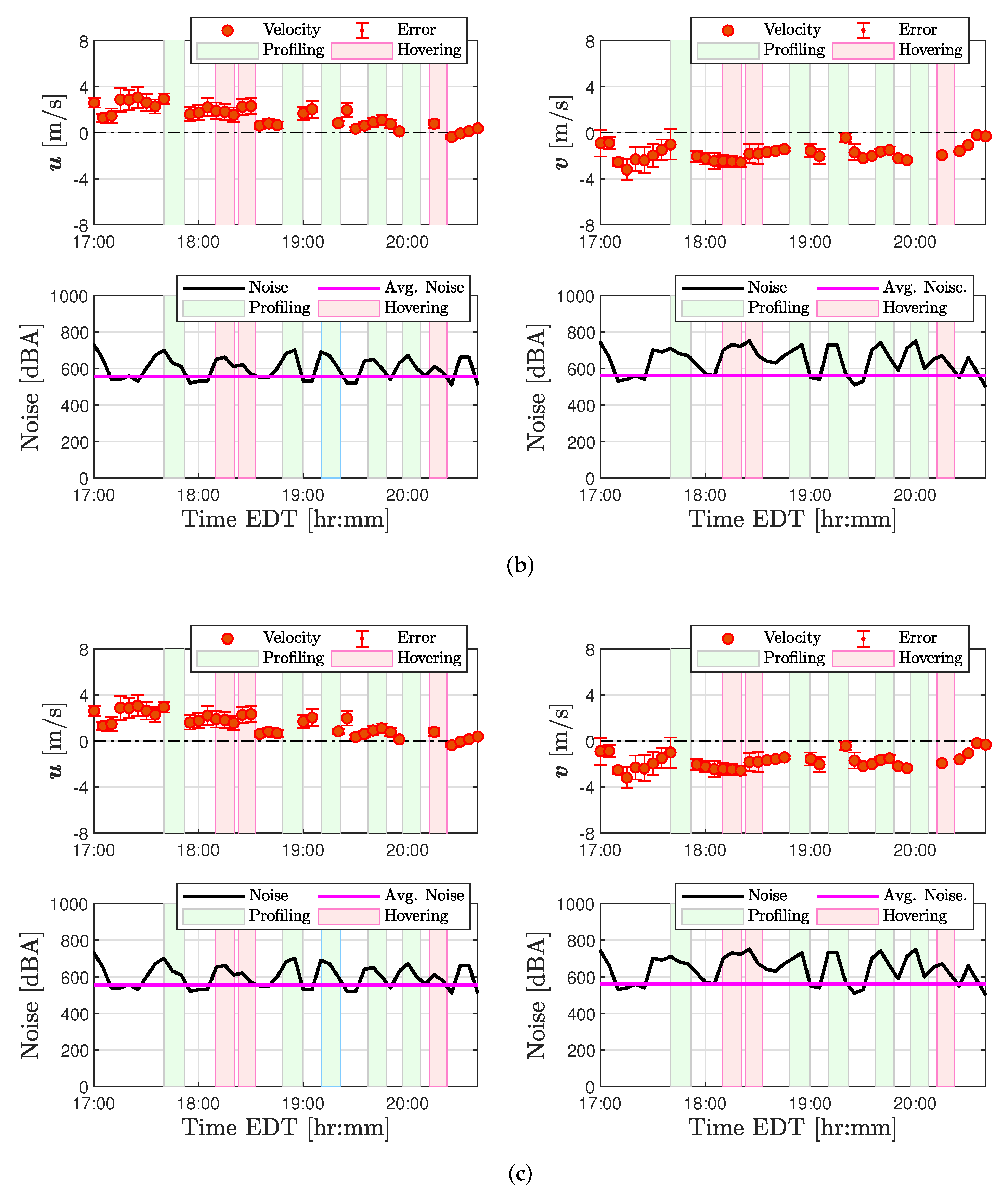
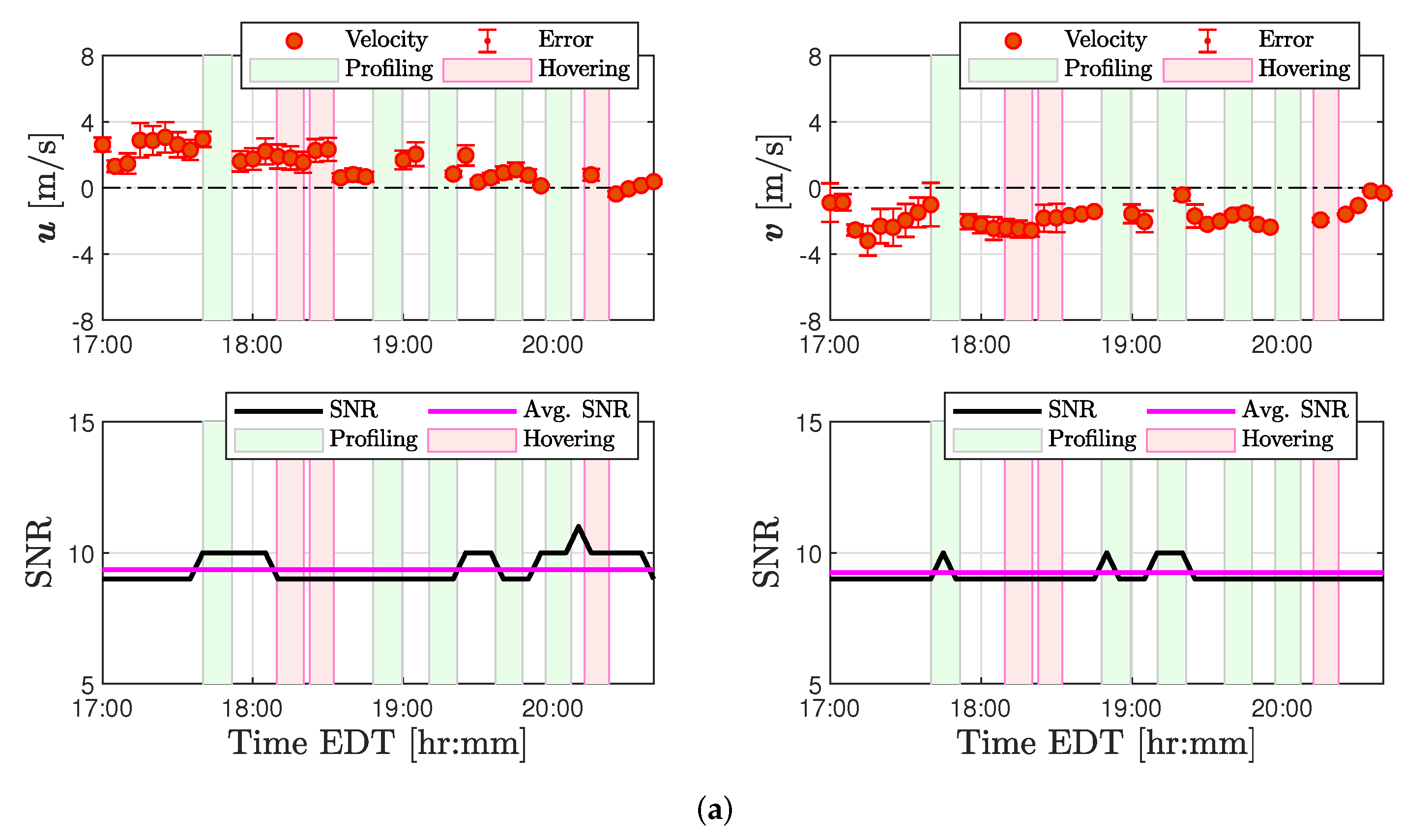
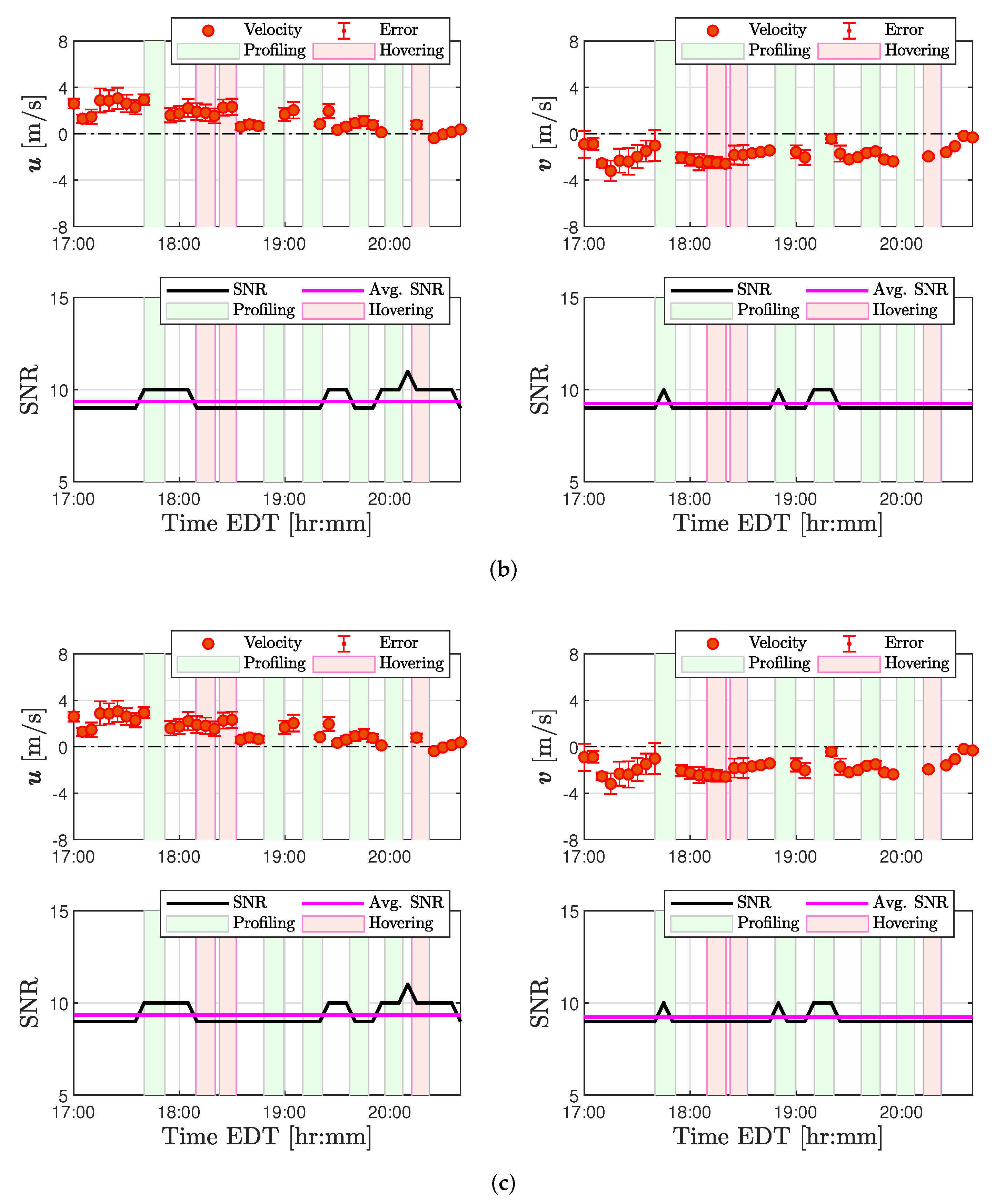
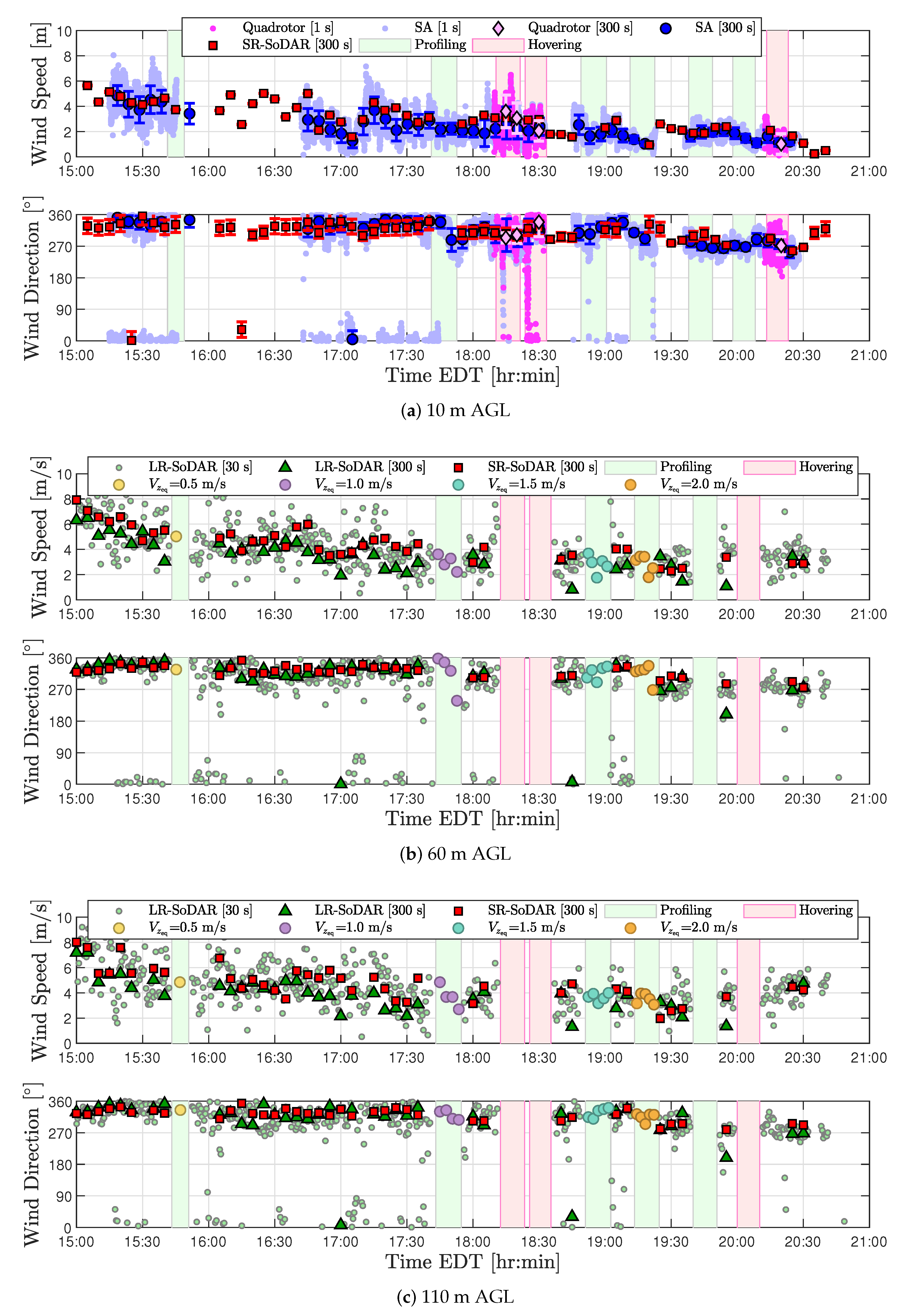
Anomalies were also detected in SoDAR wind measurements coinciding with periods of quadrotor operations. A two-part evaluation was performed to determine the nature of factors corrupting SoDAR observations. Examination of GPS position coordinates demonstrated the quadrotor to ascend through the sampling volume of SoDARs at approximately 60 m AGL. An assessment described in
Appendix A of both the noise intensity and signal-to-noise ratio recorded by each SoDAR revealed a correlation between corrupted measurements and flight operations that strengthened with altitude. For this reason, it has been determined that quadrotor operations can significantly impact SoDAR observations when operating within the SoDAR’s sampling volume. Therefore, experiments involving SoDAR and multirotor operations in close proximity will have to mitigate for quadrotor noise.
A separate quadrotor with a small sonic anemometer on board was also considered as an alternative to validate model-based wind estimates. However, due to a hardware malfunction, the quadrotor-based wind sensor was not used in validation experiments. Other commercially available options employing indirect black-box methods for wind sensing, like the ones built into DJI multirotor aircraft, were not considered to validate model-based wind estimation. These alternatives are largely proprietary, do not offer wind data storage, and lack accuracy specifications for wind measurements. Thus, validation experiments were conducted for hovering and steady vertical-ascent flight wind estimates employing anemometer and SoDAR measurements only.
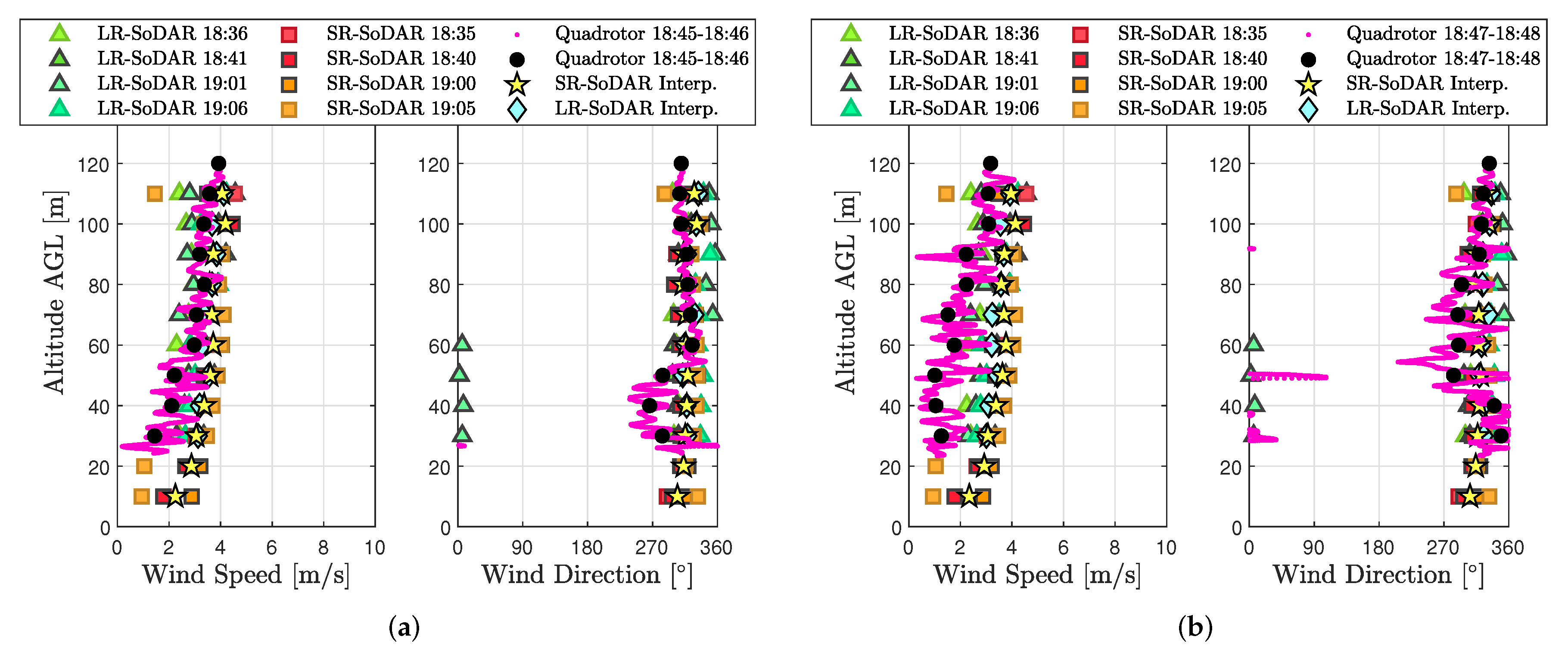
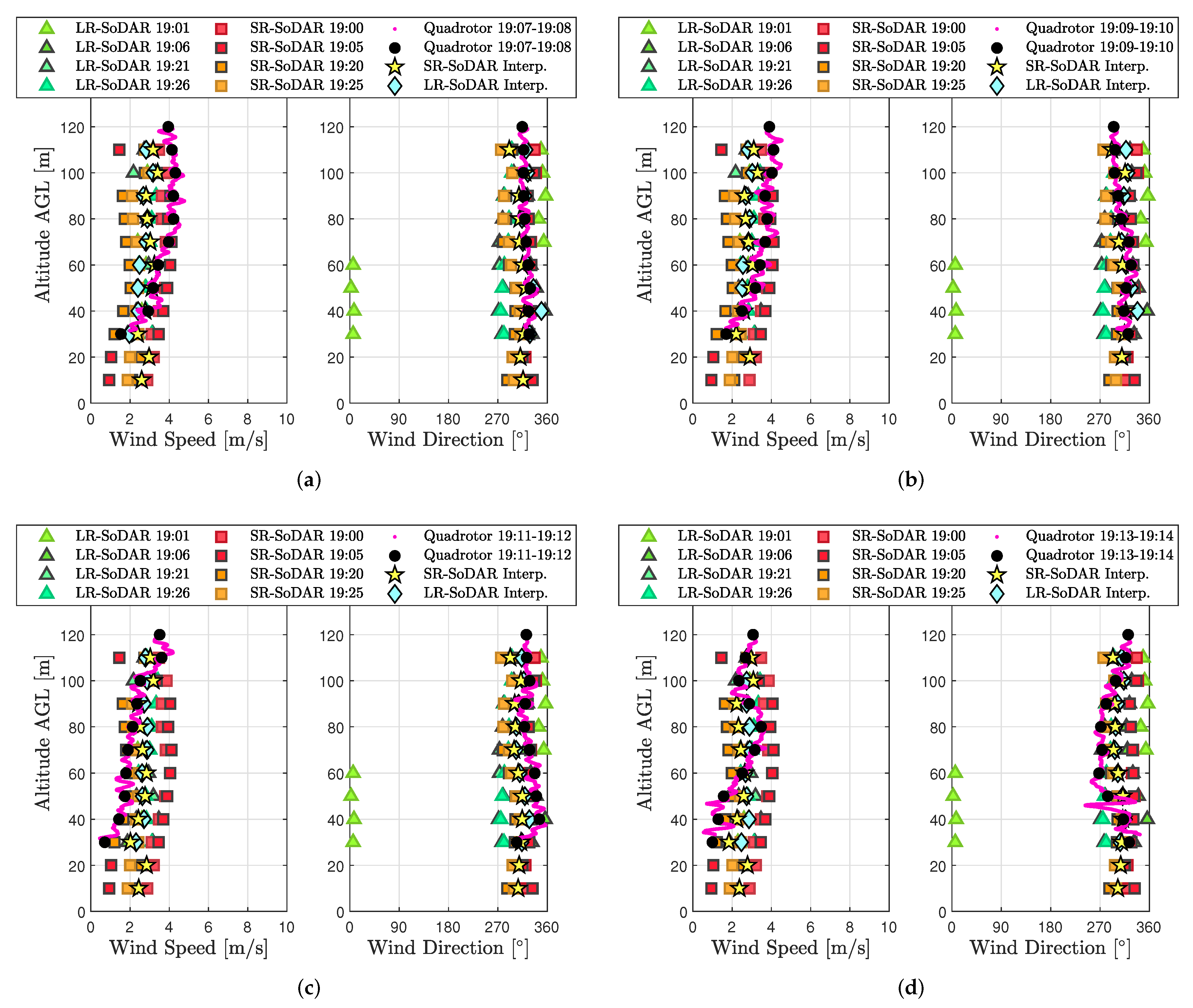
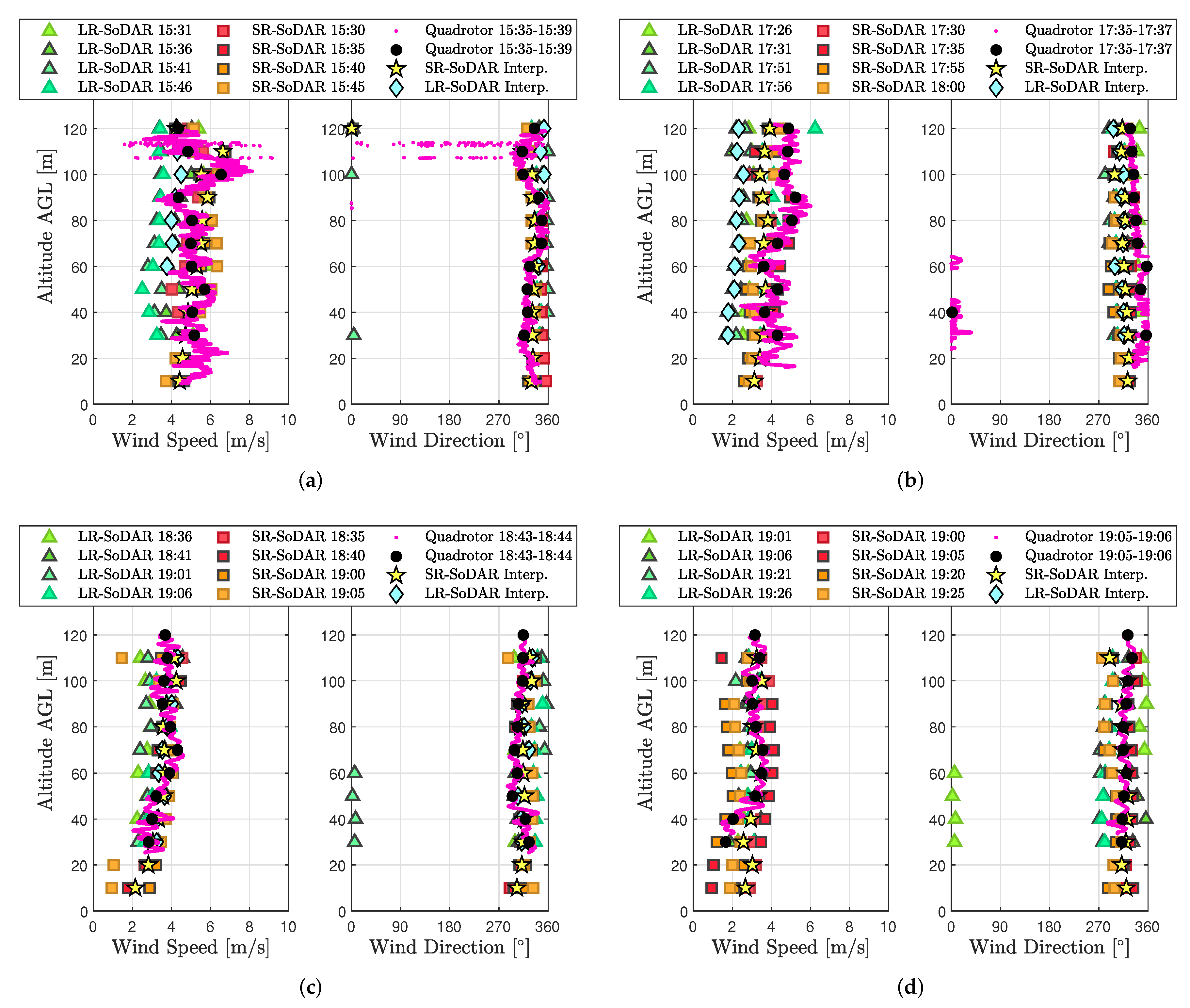
In spite of challenges with validation experiments, a considerable number of wind estimates were validated successfully. Wind estimates from the quadrotor hovering at 10 m AGL demonstrated good agreement between sonic anemometer and SoDAR measurements across all three flights. These results were found to be comparable to rigid-body model wind estimates reported in [
1]. Thus, the rigid-body model wind estimation algorithms we use for measuring wind in hovering flight performs well across different quadrotor platforms. Quadrotor wind profile estimates, on the other hand, were validated using SoDAR observations from 10 to 120 AGL. Comparison results for periods of low wind variability demonstrate quadrotor wind profile estimates in close agreement with SoDAR wind speed and wind direction observations. This outcome provides impetus for additional comparisons to assess more closely the accuracy of model-based wind profiling inside the ABL.
Future work will involve improving validation experiments for a more thorough performance assessment of quadrotor wind profile estimates. Field experiments for wind estimate validation will require increasing the spatial separation between SoDARs to ensure quadrotor operations do not interfere with wind field measurements. Validation of model-based wind estimates will also incorporate in situ measurements from a sonic anemometer on board a separate quadrotor. Lastly, because coincident measurements are not feasible, validation experiments will have to take place when atmospheric conditions are relatively homogeneous and stationary, and significant uniformity of the wind field sampled by atmospheric sensors is expected.
6. Conclusions
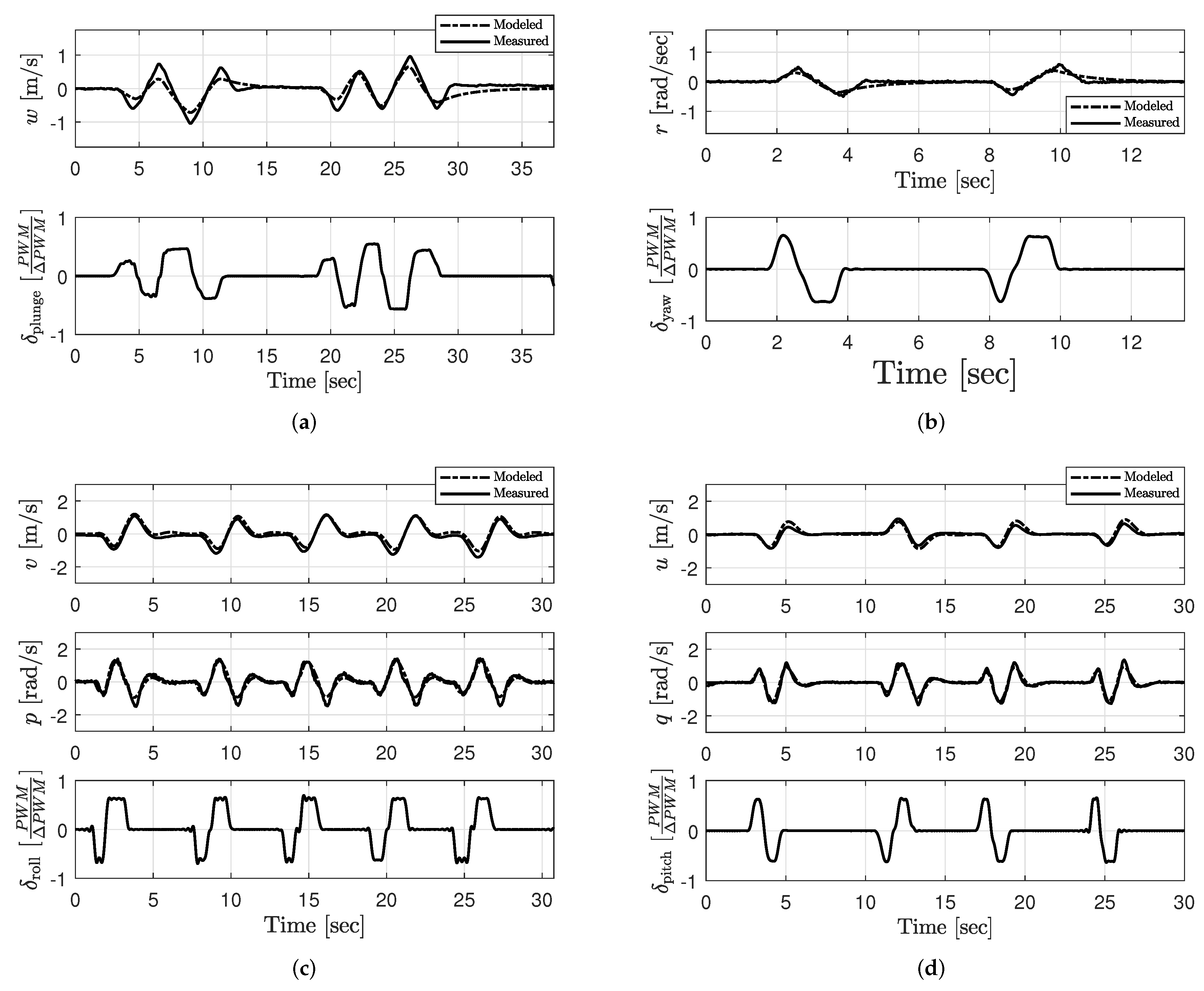
An off-the-shelf quadrotor can be used to obtain model-based wind velocity estimates as long as the motion data logged on board the autopilot is accessible to the user. However, the accuracy of wind velocity estimates depends on how well the motion model characterizes the dynamics of the quadrotor for its operating condition. This paper extends a model based framework exploiting the rigid body dynamics of a quadrotor for hovering-flight wind estimation to estimate wind velocity along a vertical path in the lower atmosphere. The extension involved characterizing rigid body models for equilibrium flight conditions corresponding to each of five steady-ascending rates: m/s. Each quadrotor model was characterized employing stepwise regression and output error parameter estimation. An observability analysis confirmed the feasibility of estimating wind velocity using the identified model structures. Trends in parameter estimates also suggest that slower ascent rates may result in more accurate wind estimates. Significant variations in parameter estimates for higher ascent rates can be the outcome of limitations generating manually the rich and precisely timed excitation signals needed for model identification. Further studies are required to investigate this possibility in depth.
Field experiments were conducted to validate quadrotor wind estimates using in-situ and remote-sensing atmospheric sensors. Results from validation experiments demonstrated quadrotor wind estimates in hovering flight to be within within small error of sonic anemometer and SoDAR wind observations. Quadrotor wind profile estimates, on the other hand, were difficult to validate comprehensively because quadrotor operations affect the reliability of SoDAR wind measurements. However, in instances when atmospheric conditions were relatively invariant prior to and after quadrotor operations, quadrotor wind estimates demonstrated very good agreement with wind speed and wind direction from SoDAR measurements. Overall, this study demonstrates the feasibility of model-based vertical wind profiling using multirotor UAS in the lower atmosphere.