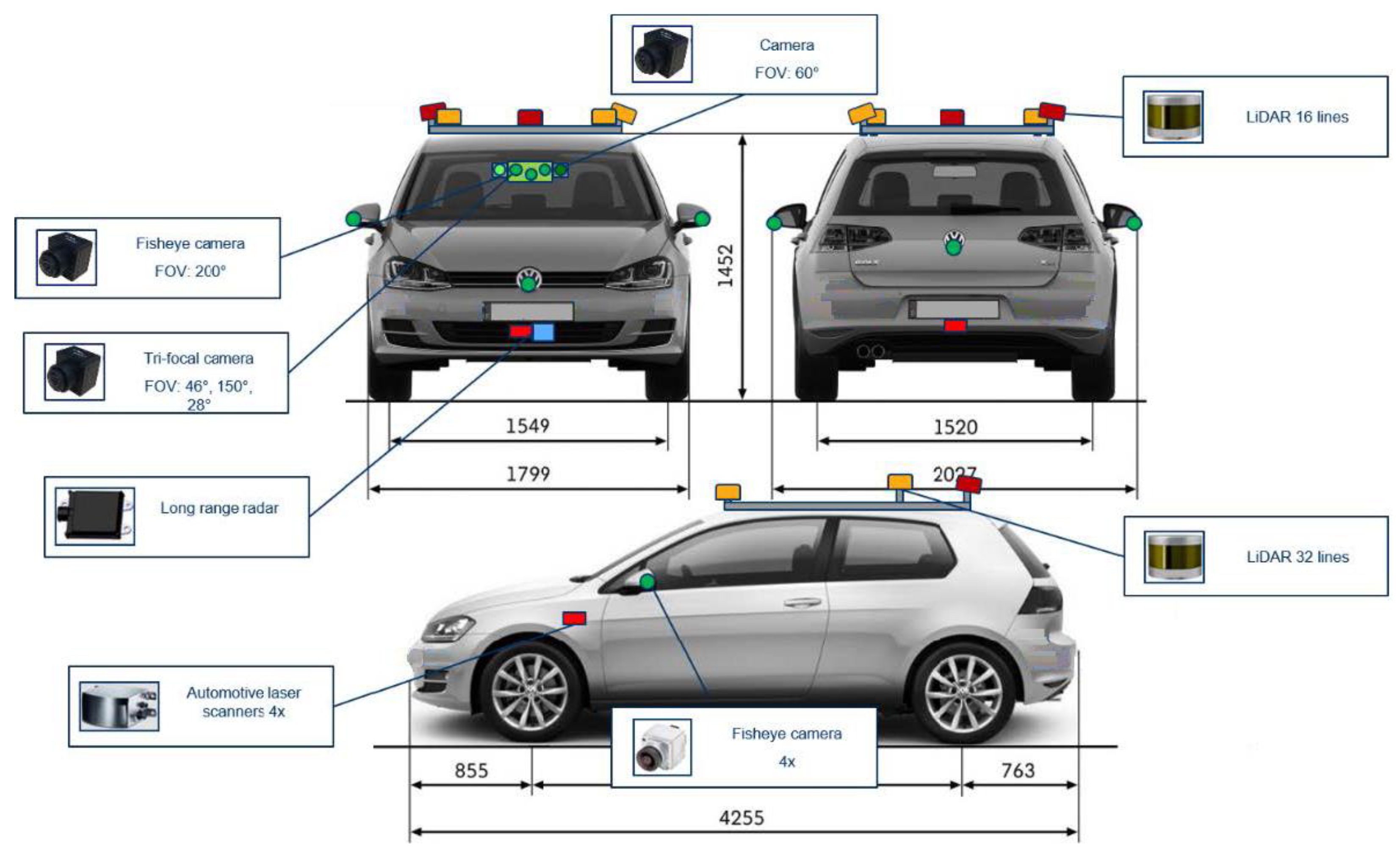
Figure 1.
Position of sensors on the ego vehicle.
Figure 1.
Position of sensors on the ego vehicle.
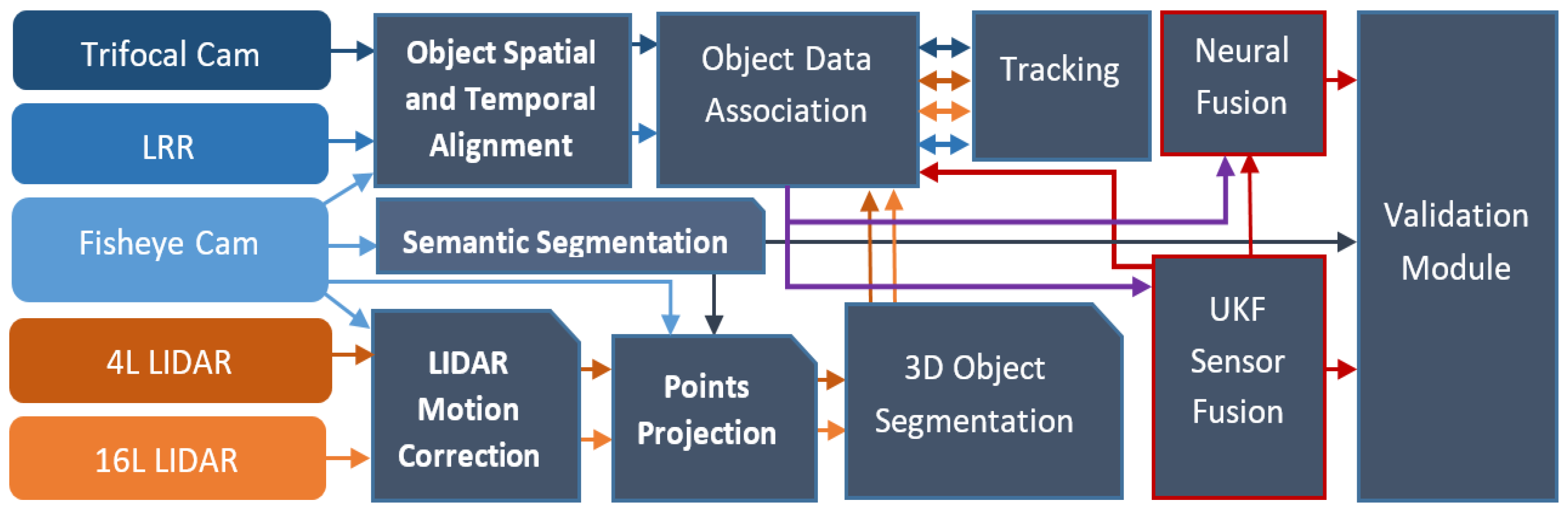
Figure 2.
Processing pipeline used in the self-driving car solution. The flow of data from each sensor to the modules is depicted using the sensor or module color assigned.
Figure 2.
Processing pipeline used in the self-driving car solution. The flow of data from each sensor to the modules is depicted using the sensor or module color assigned.
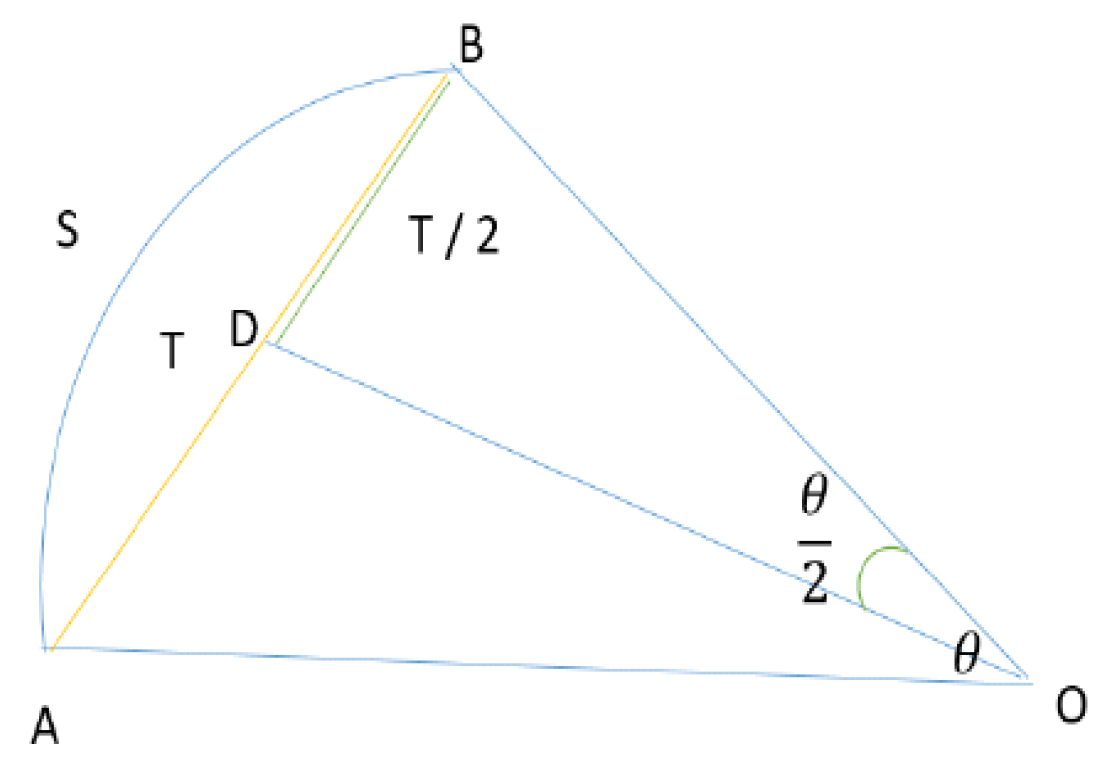
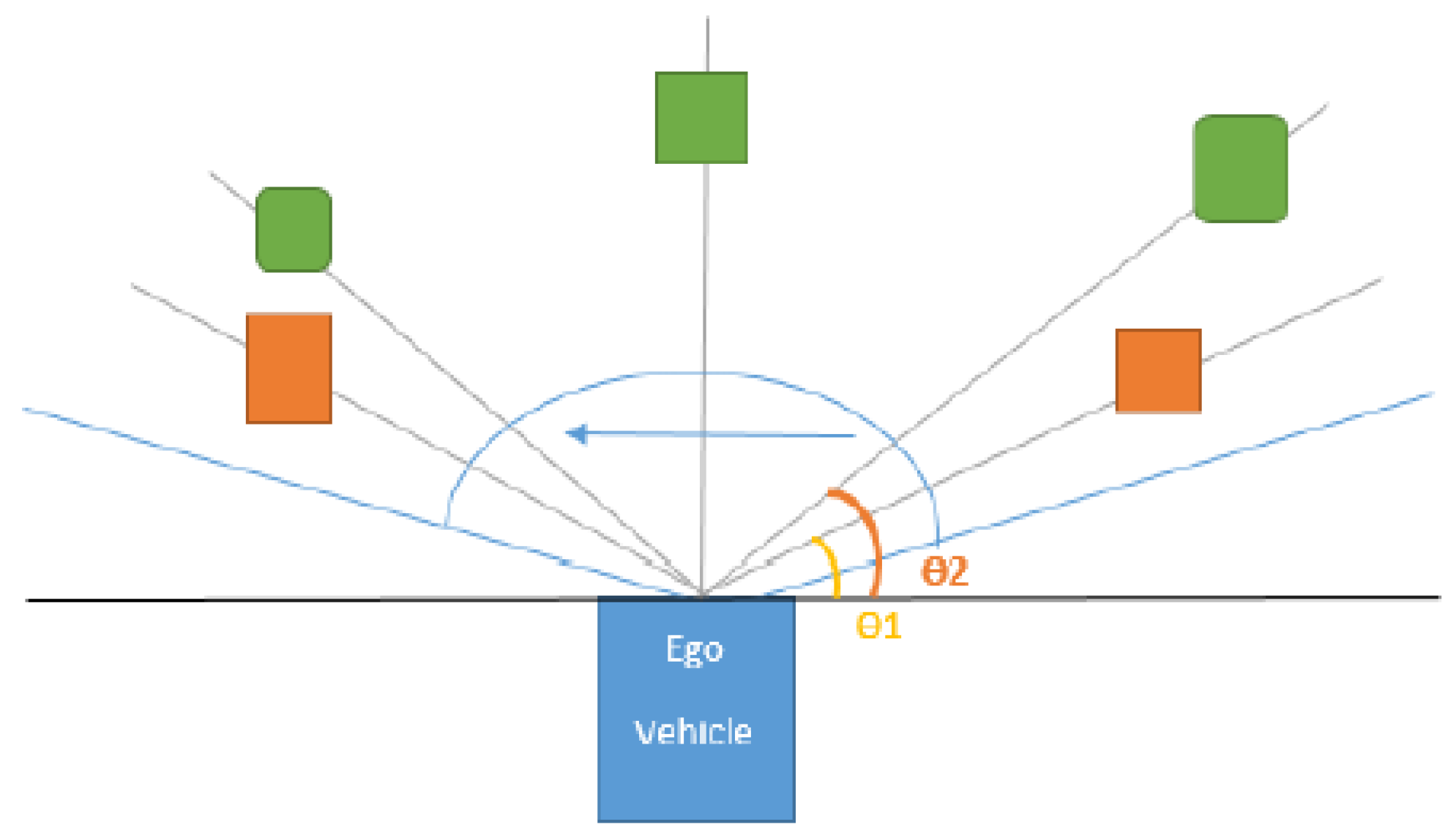
Figure 3.
Notations (on the figure) depicting ego vehicle movement from point A to point B.
Figure 3.
Notations (on the figure) depicting ego vehicle movement from point A to point B.
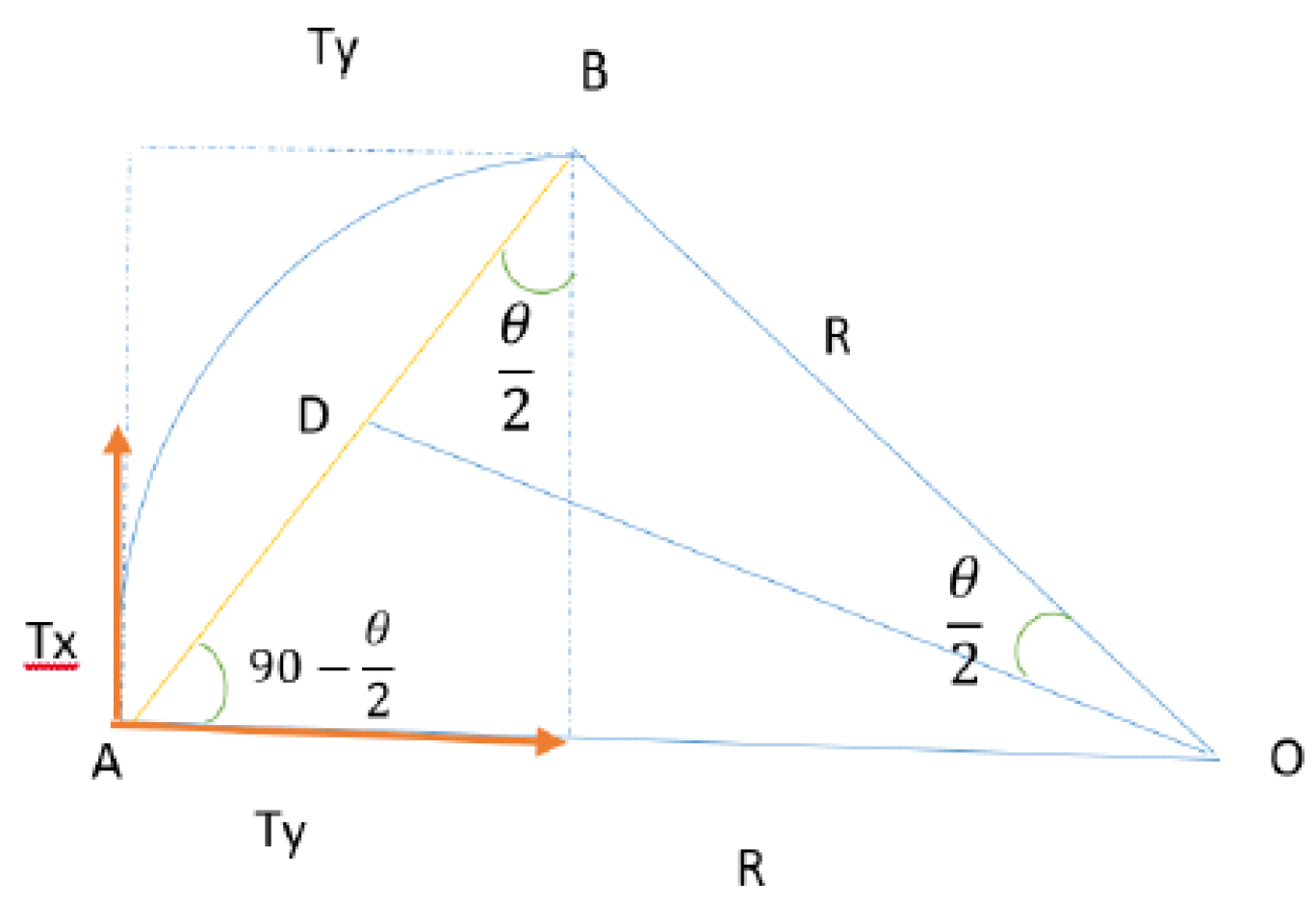
Figure 4.
Tx and Ty movement components.
Figure 4.
Tx and Ty movement components.
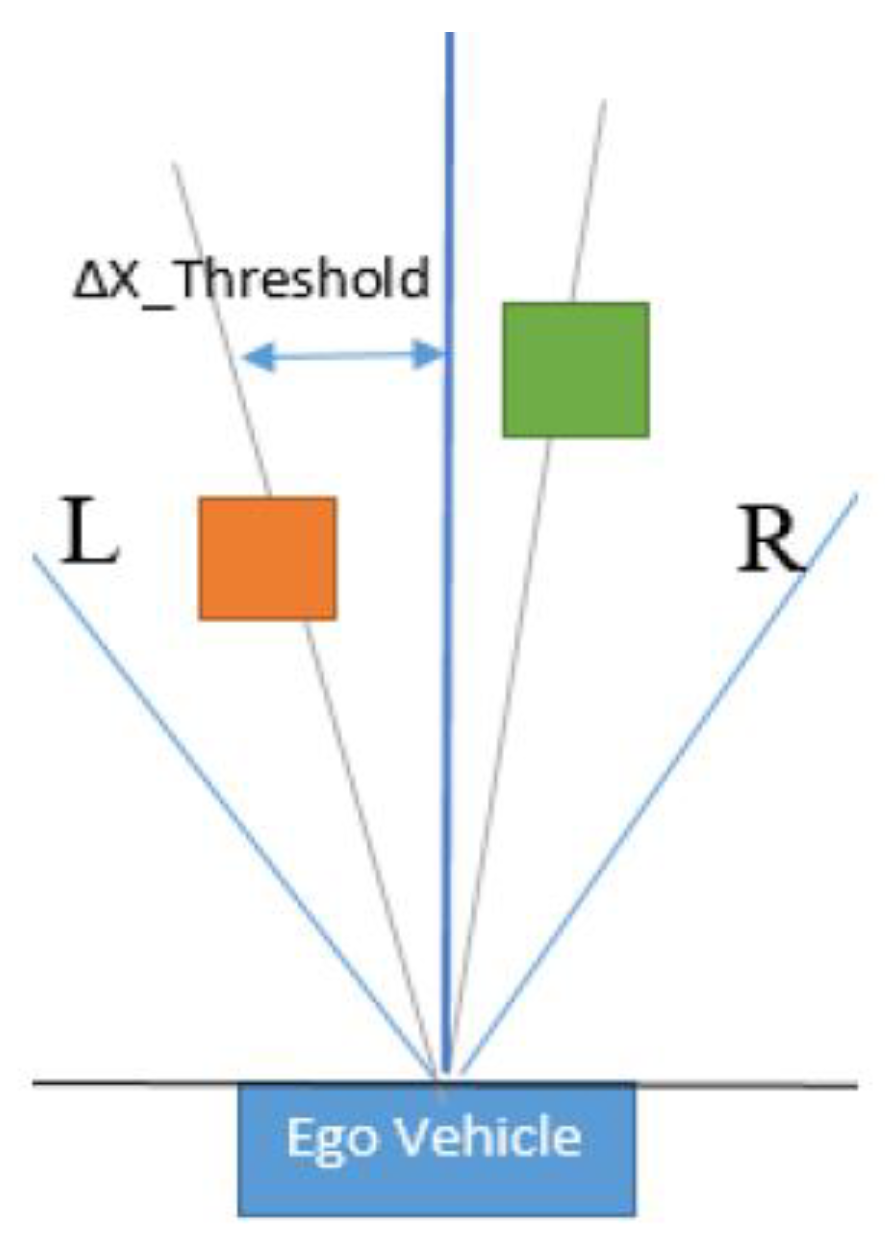
Figure 5.
Corresponding objects in the left half (orange) and the right half (green) spaces.
Figure 5.
Corresponding objects in the left half (orange) and the right half (green) spaces.
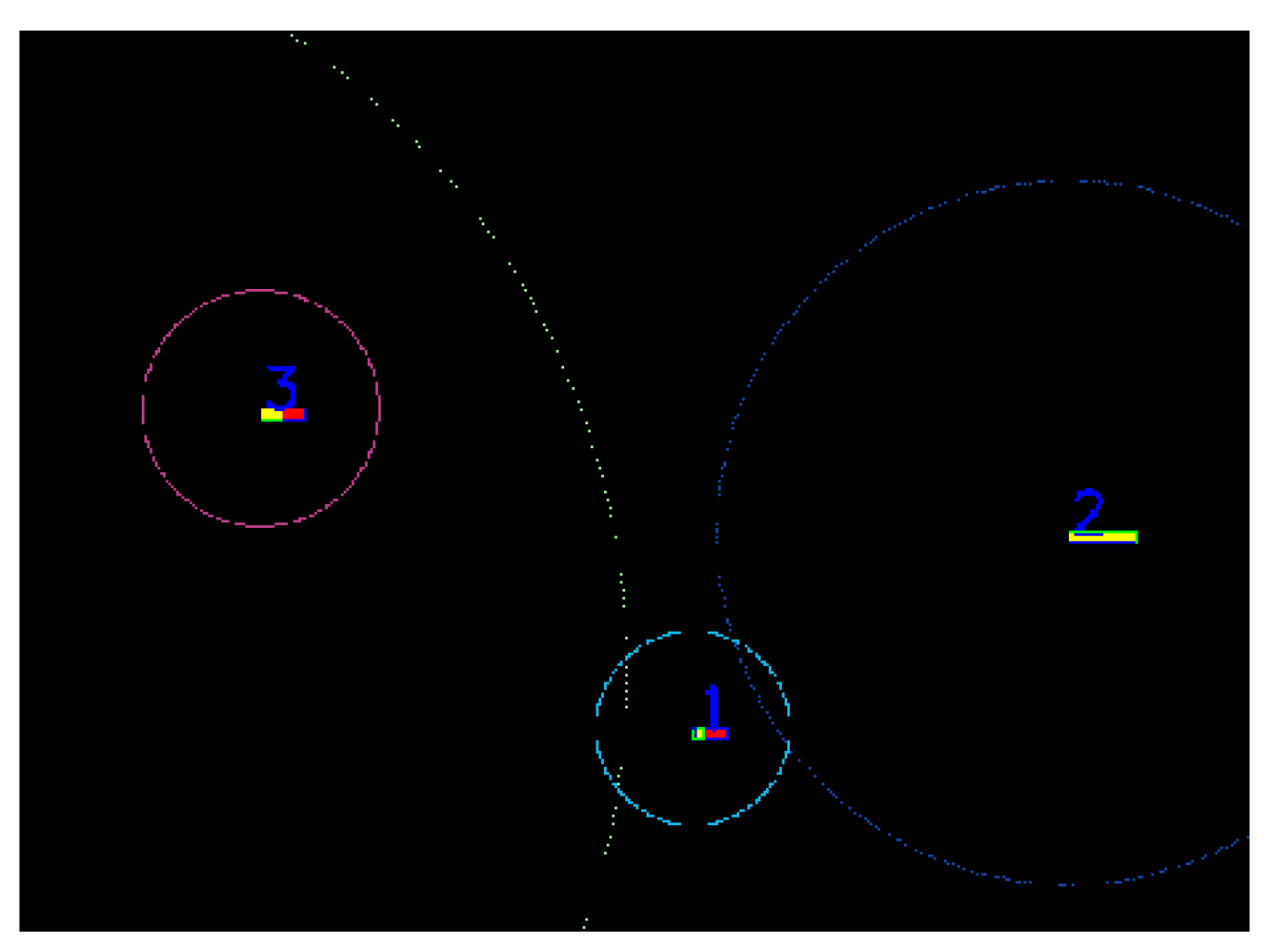
Figure 6.
2D sweeping polar rays for object association are depicted in a light blue color. In orange, we illustrate motion-corrected trifocal objects, and in green, the target objects.
Figure 6.
2D sweeping polar rays for object association are depicted in a light blue color. In orange, we illustrate motion-corrected trifocal objects, and in green, the target objects.
Figure 7.
Results of LIDAR object to trifocal object association. On the left-hand side, the color image of the recorded scene is displayed. On the right-hand side, the processed sensory data containing trifocal and LIDAR objects are shown.
Figure 7.
Results of LIDAR object to trifocal object association. On the left-hand side, the color image of the recorded scene is displayed. On the right-hand side, the processed sensory data containing trifocal and LIDAR objects are shown.
Figure 8.
Correspondence of the trifocal camera objects and LIDAR and RADAR sensor measurements. On the left-hand side, the color image captured by the camera is shown. On the right-hand image, the data association of objects from different sensors is illustrated.
Figure 8.
Correspondence of the trifocal camera objects and LIDAR and RADAR sensor measurements. On the left-hand side, the color image captured by the camera is shown. On the right-hand image, the data association of objects from different sensors is illustrated.
Figure 9.
First step of the data association algorithm. In this image, three detected objects and their tracks along with their covariance ellipses are shown.
Figure 9.
First step of the data association algorithm. In this image, three detected objects and their tracks along with their covariance ellipses are shown.
Figure 10.
Semantic class of each 3D point. On the left-hand side, we observe the assigned semantic class of each projected 3D LIDAR point. In the right image, the semantic class image with 50% transparency is overlapped over the color image.
Figure 10.
Semantic class of each 3D point. On the left-hand side, we observe the assigned semantic class of each projected 3D LIDAR point. In the right image, the semantic class image with 50% transparency is overlapped over the color image.
Figure 11.
Tracking of dynamic and static objects. In the top-left corner, the birds-eye view 3D image of the scene can be observed. In the top-right corner, the 3D object detections are projected over the color image in blue. In the bottom-right image, the tracks corresponding to the detections are shown in red. In the bottom-left image, the traces of the tracked objects are shown in the same color for the same object instance.
Figure 11.
Tracking of dynamic and static objects. In the top-left corner, the birds-eye view 3D image of the scene can be observed. In the top-right corner, the 3D object detections are projected over the color image in blue. In the bottom-right image, the tracks corresponding to the detections are shown in red. In the bottom-left image, the traces of the tracked objects are shown in the same color for the same object instance.
Figure 12.
Tracking of static objects. In the left image, the 3D top-view scene containing measurements and tracks with their relative motion vectors is shown. In the top-right and bottom-right images, the measurements and tracks are projected onto the RGB image in blue and red, respectively.
Figure 12.
Tracking of static objects. In the left image, the 3D top-view scene containing measurements and tracks with their relative motion vectors is shown. In the top-right and bottom-right images, the measurements and tracks are projected onto the RGB image in blue and red, respectively.
Figure 13.
Graphical depiction of the tracking module with two motion models.
Figure 13.
Graphical depiction of the tracking module with two motion models.
Figure 14.
Associations between measurements coming from different sensors and their fusion. On the left-hand side, we observe the RGB image. On the right-hand side, we observe the data associations among sensors as well as the super-sensor object depicted in white.
Figure 14.
Associations between measurements coming from different sensors and their fusion. On the left-hand side, we observe the RGB image. On the right-hand side, we observe the data associations among sensors as well as the super-sensor object depicted in white.
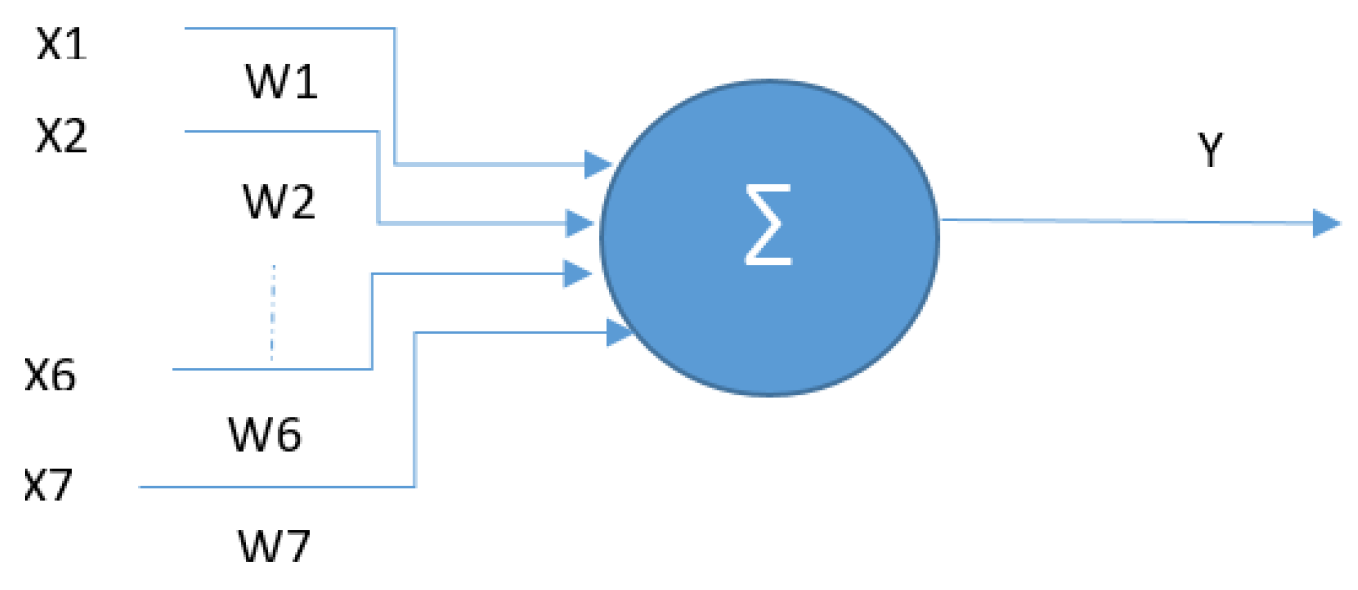
Figure 15.
Single-layer perceptron model, with 7 inputs, 1 processing unit and 1 output.
Figure 15.
Single-layer perceptron model, with 7 inputs, 1 processing unit and 1 output.
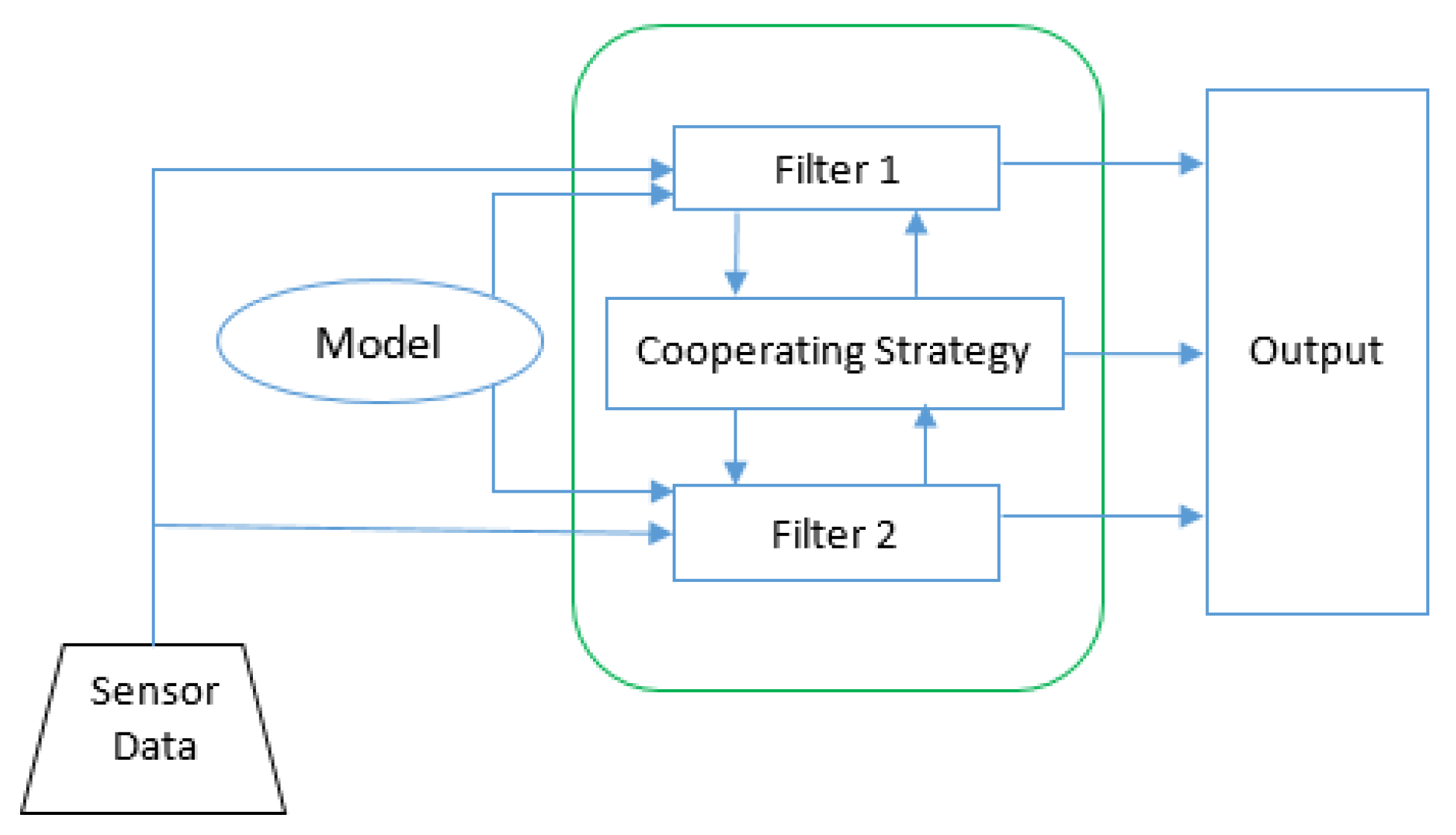
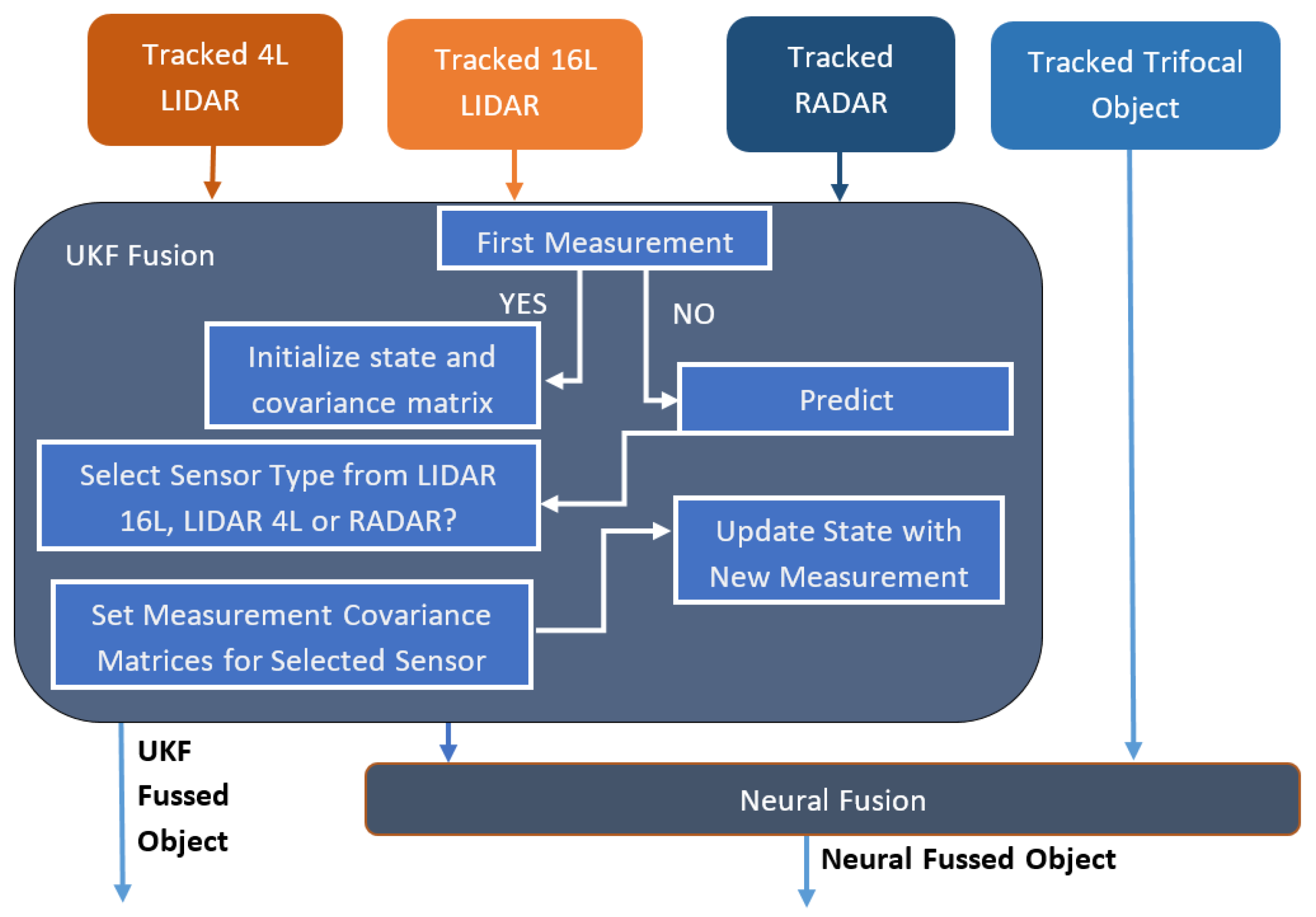
Figure 16.
UKF (Unscented Kalman Filter) and neural fusion architecture.
Figure 16.
UKF (Unscented Kalman Filter) and neural fusion architecture.
Figure 17.
The result of the UKF and neural fusion depicted in white and purple.
Figure 17.
The result of the UKF and neural fusion depicted in white and purple.
Figure 18.
Example of mismatch in the validation procedure. On the left-hand side, we observe the projected fused object on the RGB image with the semantic class UNKNOWN. In the right image, the same object is projected onto the semantic class image in a region with the dominant class car. The class mismatch is represented using red color.
Figure 18.
Example of mismatch in the validation procedure. On the left-hand side, we observe the projected fused object on the RGB image with the semantic class UNKNOWN. In the right image, the same object is projected onto the semantic class image in a region with the dominant class car. The class mismatch is represented using red color.
Figure 19.
Example of successful validation. In the left image, the super-sensor object is projected onto the RGB image. In the right image, the same object is projected onto the semantic segmentation image. The semantic classes’ match is represented using green color.
Figure 19.
Example of successful validation. In the left image, the super-sensor object is projected onto the RGB image. In the right image, the same object is projected onto the semantic segmentation image. The semantic classes’ match is represented using green color.
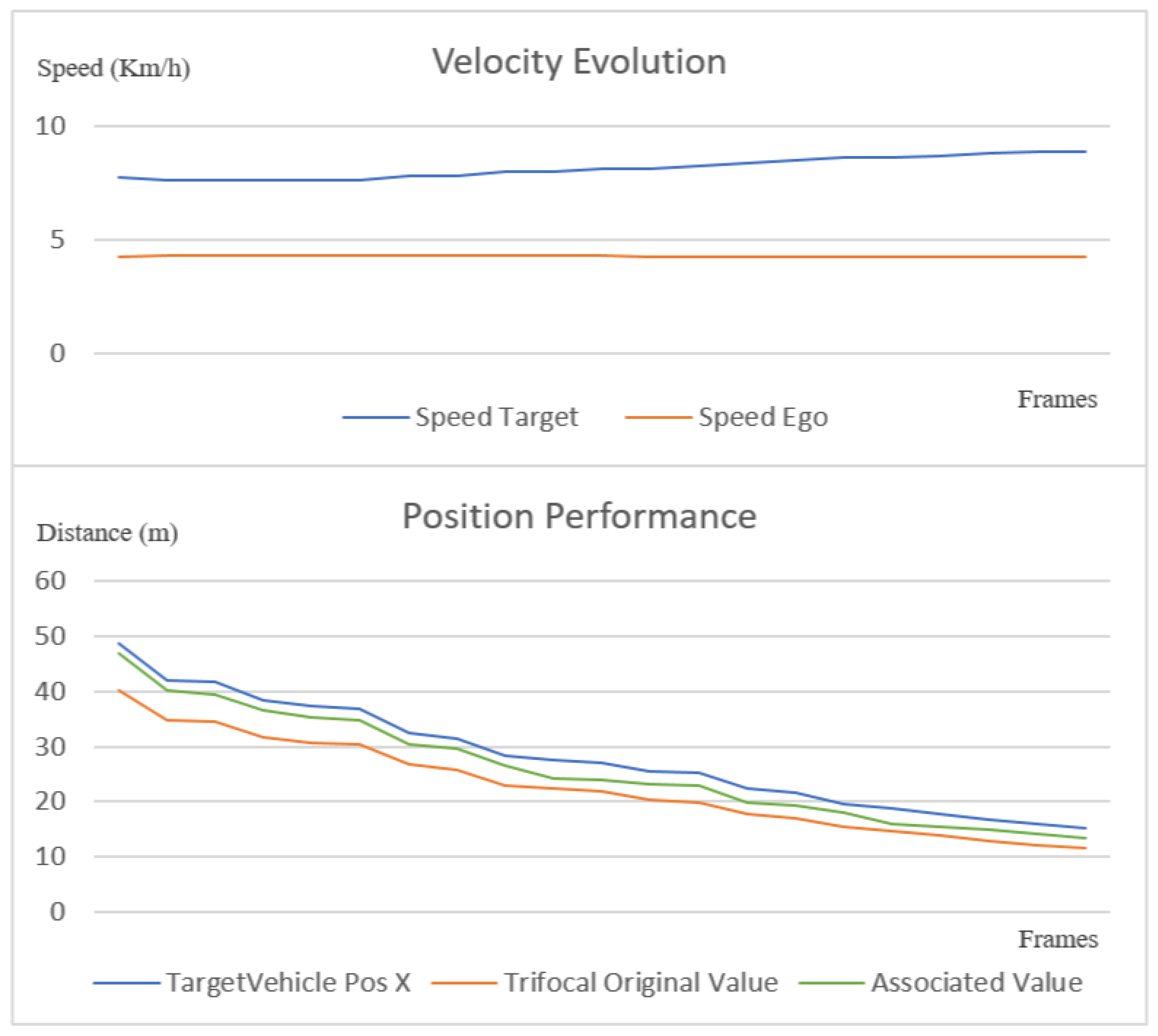
Figure 20.
Speed chart (top) and position chart (bottom) of a trifocal object association scenario.
Figure 20.
Speed chart (top) and position chart (bottom) of a trifocal object association scenario.
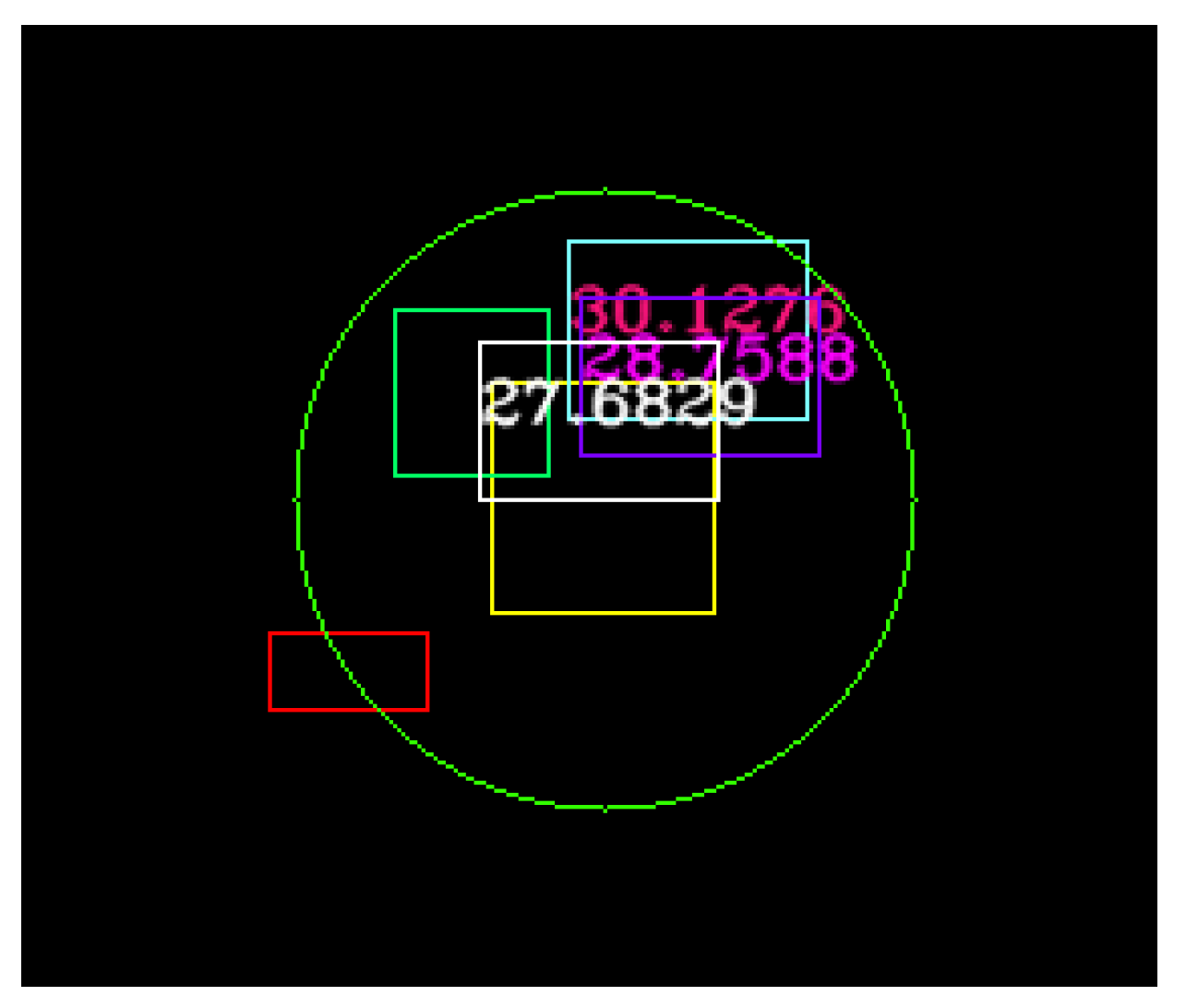
Figure 21.
Another scenario that demonstrates the performance of the object association.
Figure 21.
Another scenario that demonstrates the performance of the object association.
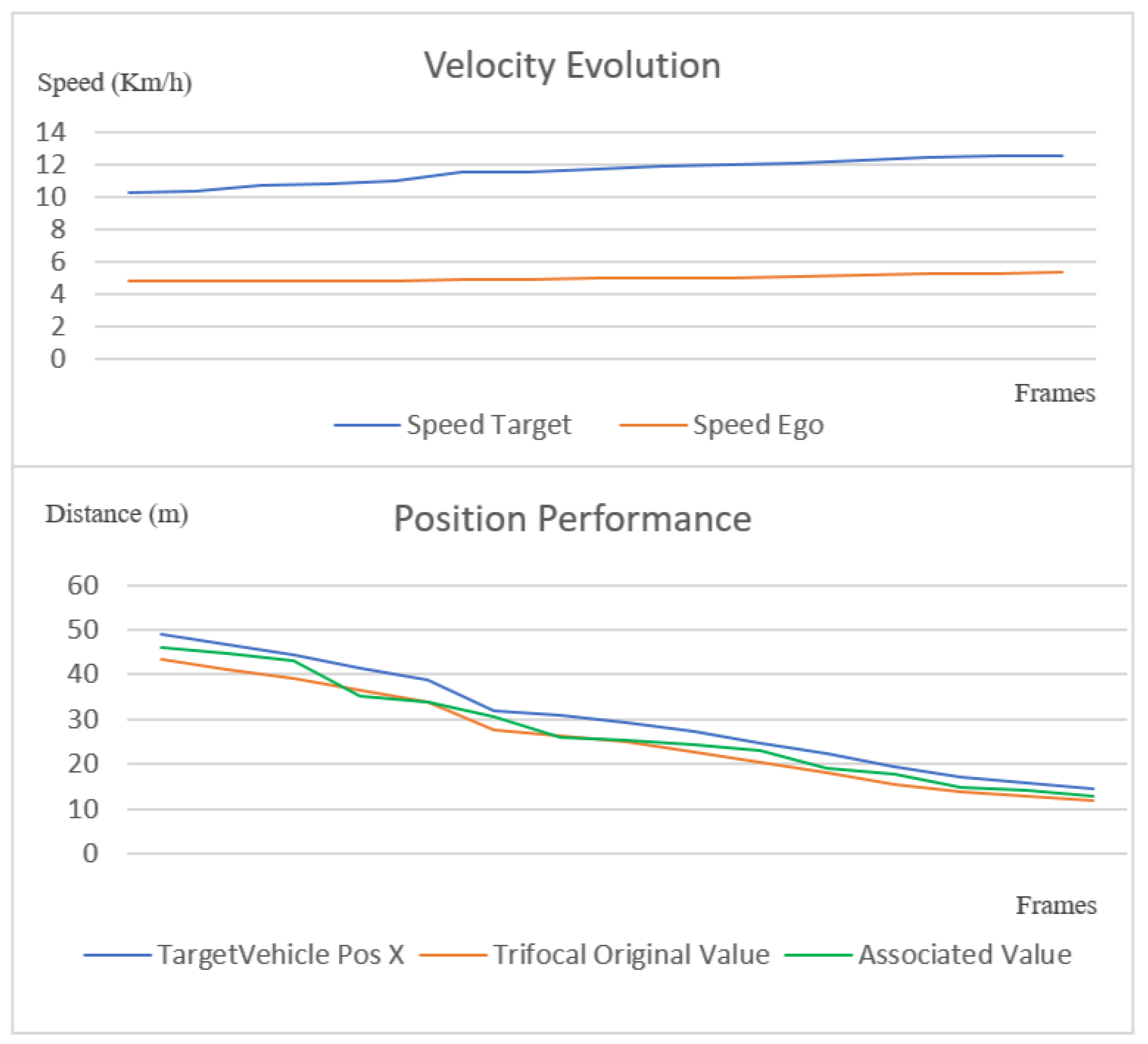
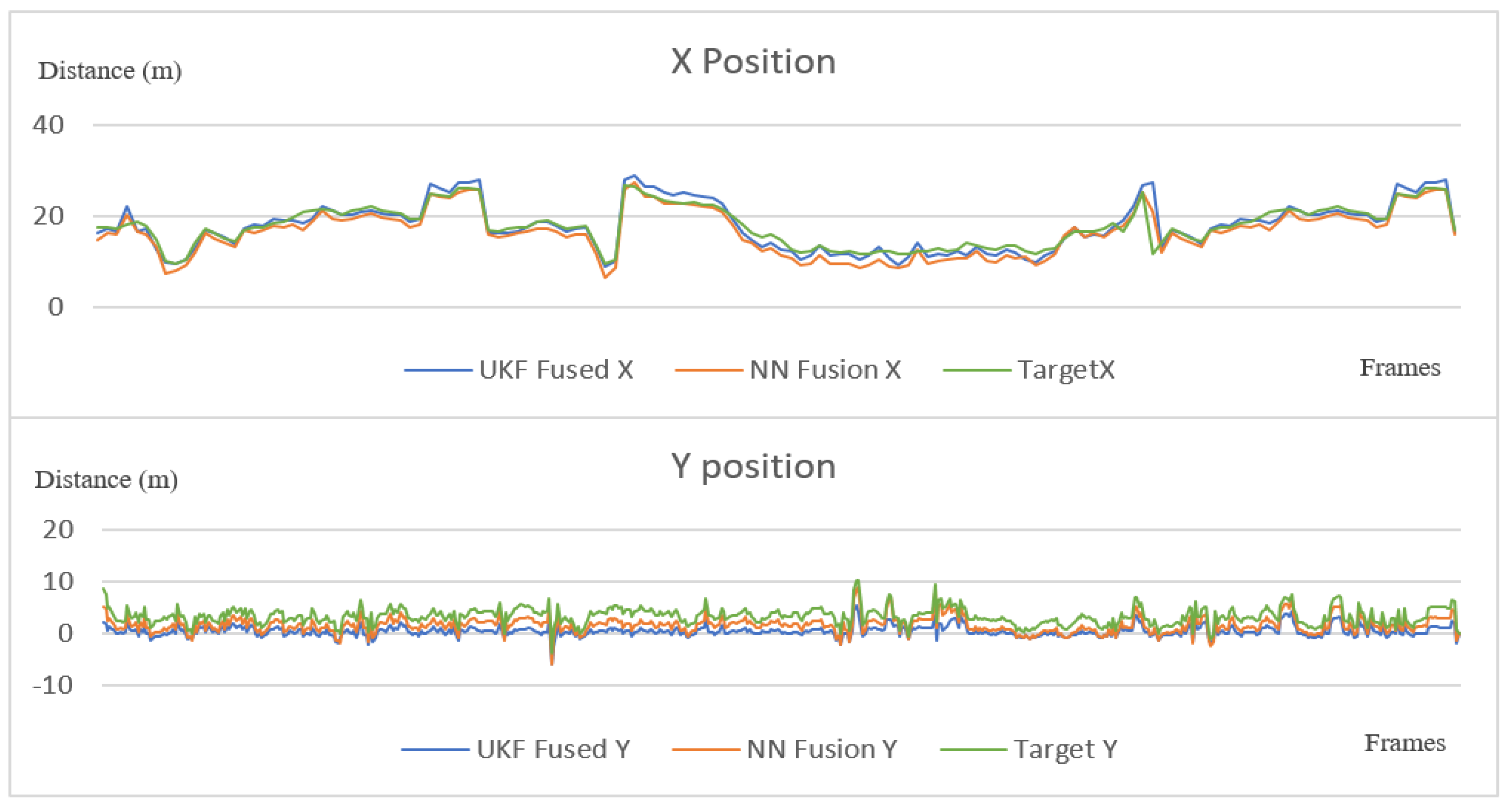
Figure 22.
Position performance on the x and y axes of the proposed sensor fusion methods and the target vehicle.
Figure 22.
Position performance on the x and y axes of the proposed sensor fusion methods and the target vehicle.
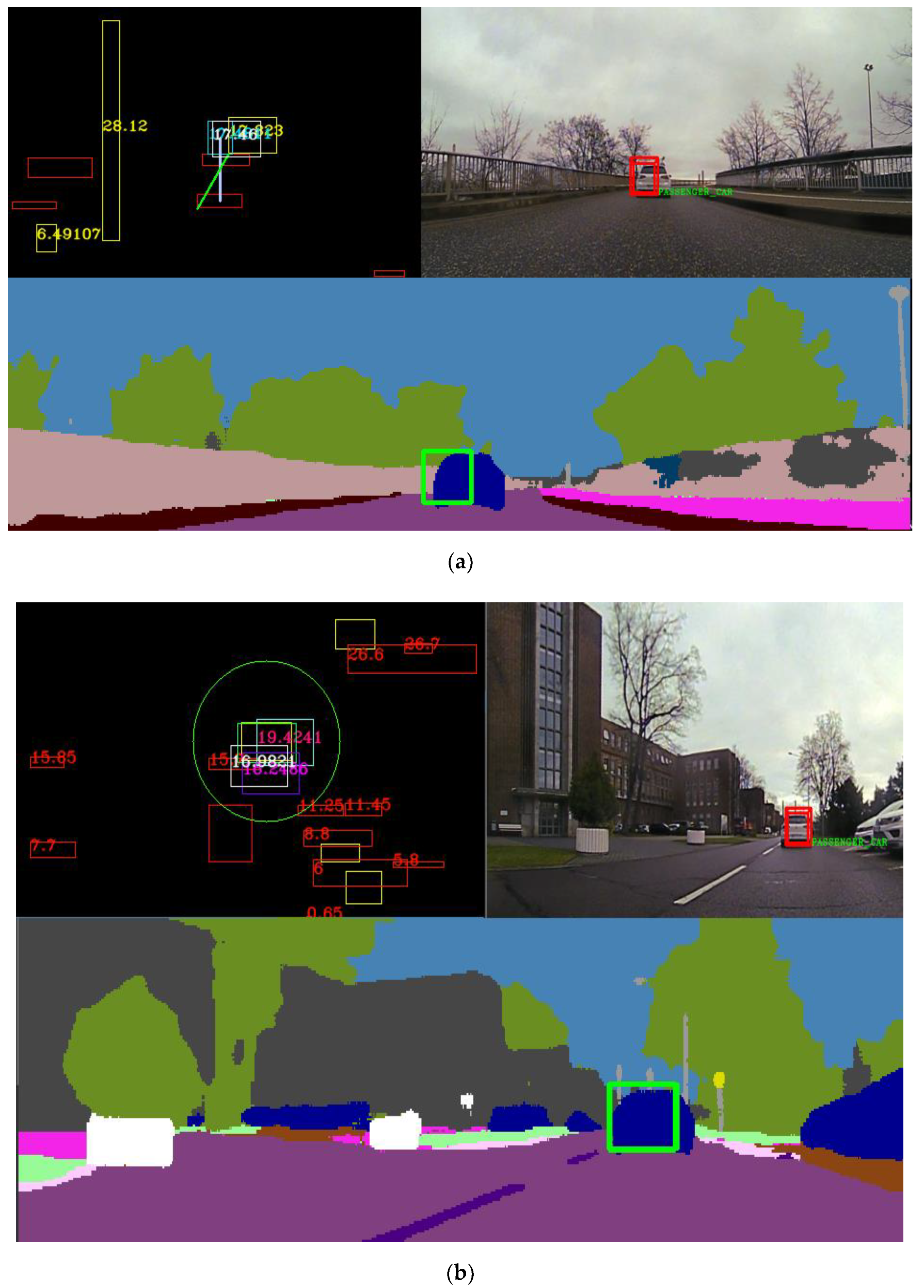
Figure 23.
(a) In the top left picture, we illustrate the birds-eye view virtual image of the scene, where all objects are projected. In the top-right figure, we show the RGB image and the validated and stabilized super-sensor object projected on it. In the bottom image, the semantic segmentation image is depicted, and the validated super-sensor object is displayed with a green rectangle. In this scenario, only the UKF fusion was enabled. (b) The presented algorithm is depicted running in a heavy clutter scenario. The top-left figure is the birds-eye view virtual image. The top-right figure is the RGB image with the validated super-sensor object projected onto it. The bottom image displays the validated fused object projected onto the semantic segmentation image. In this scenario, both the UKF and neural fusion methods were enabled.
Figure 23.
(a) In the top left picture, we illustrate the birds-eye view virtual image of the scene, where all objects are projected. In the top-right figure, we show the RGB image and the validated and stabilized super-sensor object projected on it. In the bottom image, the semantic segmentation image is depicted, and the validated super-sensor object is displayed with a green rectangle. In this scenario, only the UKF fusion was enabled. (b) The presented algorithm is depicted running in a heavy clutter scenario. The top-left figure is the birds-eye view virtual image. The top-right figure is the RGB image with the validated super-sensor object projected onto it. The bottom image displays the validated fused object projected onto the semantic segmentation image. In this scenario, both the UKF and neural fusion methods were enabled.
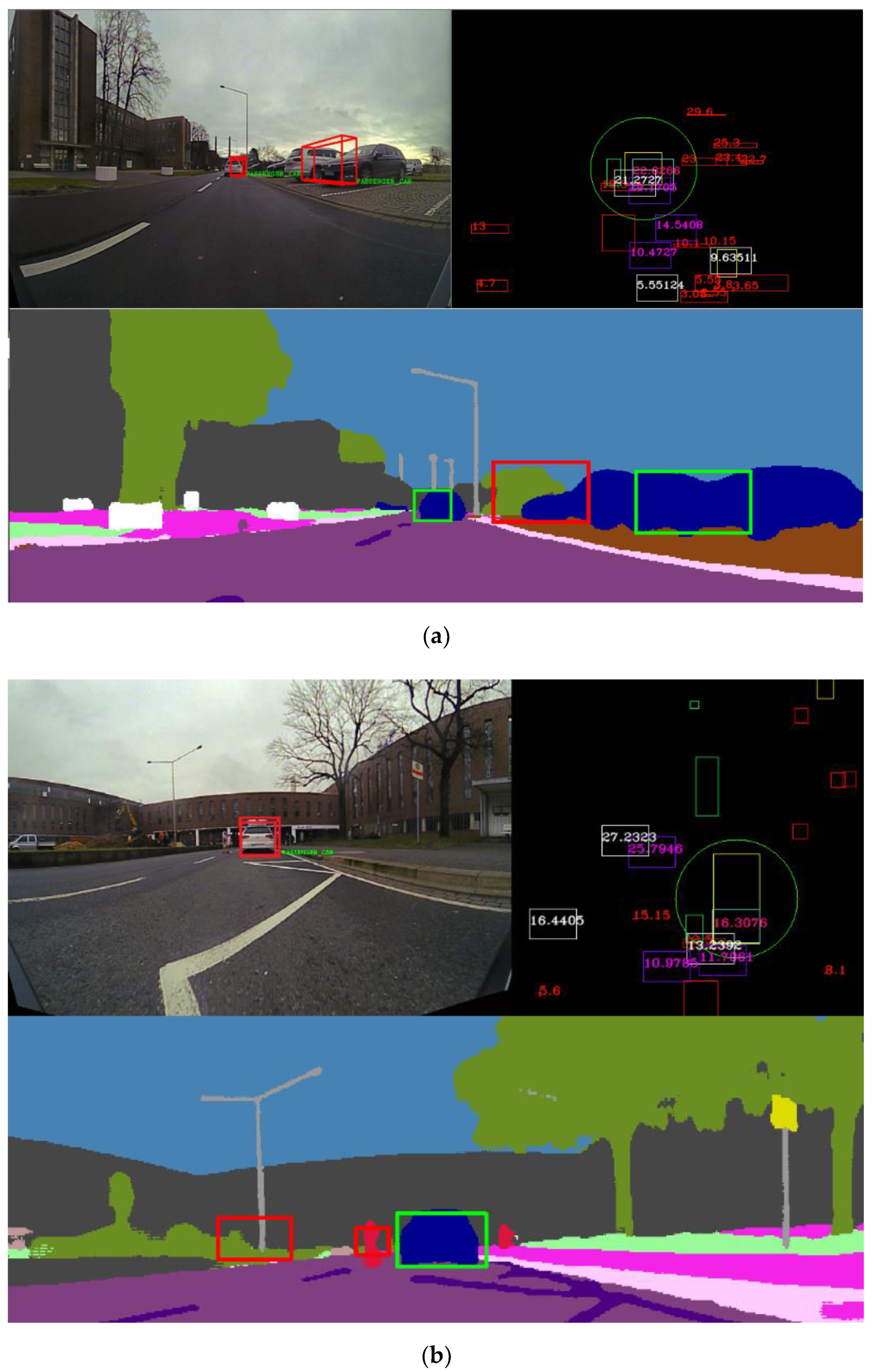
Figure 24.
(a) In the top-right image, we observe the birds-eye view virtual scene of the real-world scenario, where all objects are projected. We note the presence of multiple super-sensor objects. In the bottom figure, the fused objects are projected onto the semantic segmentation image, and if the object is validated, a green rectangle is drawn; otherwise, the rectangle drawn has red color. In the top-left image, only the validated super-sensor objects are projected onto the RGB image. (b) Another scene where we note the presence of multiple super-sensor objects. In the top right, the birds-eye view image is depicted. The bottom image shows the semantic image with the validated super-sensor objects drawn in green and objects that are not validated drawn in red. The top-left image illustrates the RGB image, where the super-sensor objects are displayed.
Figure 24.
(a) In the top-right image, we observe the birds-eye view virtual scene of the real-world scenario, where all objects are projected. We note the presence of multiple super-sensor objects. In the bottom figure, the fused objects are projected onto the semantic segmentation image, and if the object is validated, a green rectangle is drawn; otherwise, the rectangle drawn has red color. In the top-left image, only the validated super-sensor objects are projected onto the RGB image. (b) Another scene where we note the presence of multiple super-sensor objects. In the top right, the birds-eye view image is depicted. The bottom image shows the semantic image with the validated super-sensor objects drawn in green and objects that are not validated drawn in red. The top-left image illustrates the RGB image, where the super-sensor objects are displayed.
Table 1.
GPS characteristics. The column numbers represent the following: I. Standard, II. Positioning, III. Position Accuracy, IV. Velocity Accuracy, V. Roll/pitch Accuracy (1σ), VI. Heading Accuracy (1σ)2, VII. Track angle Accuracy (1σ)3, VIII. Slip Angle Accuracy (1σ)4 IX. Axis, X. Earth Axis (Direction), XI. Ego Vehicle Axis (Direction).
Table 1.
GPS characteristics. The column numbers represent the following: I. Standard, II. Positioning, III. Position Accuracy, IV. Velocity Accuracy, V. Roll/pitch Accuracy (1σ), VI. Heading Accuracy (1σ)2, VII. Track angle Accuracy (1σ)3, VIII. Slip Angle Accuracy (1σ)4 IX. Axis, X. Earth Axis (Direction), XI. Ego Vehicle Axis (Direction).
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI |
|---|
| RT3003 | L1, L2 | 0.01 m | 0.05 Km/h | 0.03° | 0.1° | 0.07° | 0.15° | X, Y, Z | North, East, Down | Forward, Right, Down |
Table 2.
16 L LIDAR characteristics.
Table 2.
16 L LIDAR characteristics.
| Feature |
|---|
| Time of flight distance measurement with calibrated reflective |
| 16 channels |
| Measurement range up to 100 m |
| Accuracy +/−3 cm |
| Dual returns |
| Field of view (vertical): 30° (+15° to −15°) |
| Angular resolution (vertical): 2° |
| Field of view (horizontal/azimuth): 360° |
| Angular resolution (horizontal/azimuth): 0.1°–0.4° |
| Rotation rate: 5–20 Hz |
Table 3.
4 L LIDAR characteristics.
Table 3.
4 L LIDAR characteristics.
| Feature |
|---|
| Time of flight distance measurement with calibrated reflective |
| 4 channels |
| Measurement range up to 327 m |
| Accuracy +/−3 cm |
| Dual returns |
| Field of view (vertical): 3.2° |
| Angular resolution (vertical): 4 Layers @ 0.8° |
| Field of view (horizontal/azimuth): 145° |
| Angular resolution (horizontal/azimuth): 0.25° |
| Rotation rate: 12.5 Hz |
Table 4.
RADAR characteristics.
Table 4.
RADAR characteristics.
| Feature |
|---|
| Operation Frequency 77 Ghz |
| Distance Measurement 0.25–250 m |
| Accuracy for distance measurement +/−2 m |
| Speed Measurement −400 + 200 kph |
| Sensitivity 0.1 kph |
Table 5.
Trifocal camera characteristics.
Table 5.
Trifocal camera characteristics.
| Feature |
|---|
| 3 Cameras with FOV: 34, 46, 150 degrees |
The sensor provides data for the following functions:Road infrastructure detection Object classification (cars, trucks, pedestrians etc.) 3D terrain perception (curb stones, generic road boundaries) Free space grid construction
|
| Resolution: 1280 × 960, Bits per pixel 12 |
| Upgrade Rate 33 ms |
| Color Grayscale |
Table 6.
Overall evaluation results.
Table 6.
Overall evaluation results.
| Method | MOTA | MOTP | IDSW (Sum) | Running Time |
|---|
| Proposed | 86.12% | 91.01% | 75 | 0.3 ms |
| GNN | 31.88% | 77.68% | 511 | 0.05 ms |
Table 7.
Comparison with solutions from the KITTI benchmark.
Table 7.
Comparison with solutions from the KITTI benchmark.
| No. | Solution Name | MOTA | MOTP | Running Time |
|---|
| 1 | Proposed Multi-Object Tracker | 77.05% | 81.65% | 0.35 s |
| 2 | MDP [51] | 76.59% | 82.10% | 0.9 s |
| 3 | CIWT [52] | 75.39% | 79.25% | 0.3 s |
| 4 | DCO-X [53] | 68.11% | 78.85% | 0.9 s |
Table 8.
Different fusion position samples.
Table 8.
Different fusion position samples.
| Fused Object UKF | Fused Object NN | GPS Ground Truth |
|---|
| X (m) | Y (m) | X (m) | Y (m) | X (m) | Y (m) |
| 15.46 | 0.94 | 14.87 | 1.1 | 16.01 | 1.3 |
| 17.04 | 1.57 | 16.95 | 1.87 | 16.71 | 1.44 |
| 24.37 | 0.85 | 24.36 | 1.62 | 25.29 | 1.56 |
| 15.16 | 1.04 | 15.24 | 0.9 | 18.01 | 1.03 |
| 9.79 | 1.00 | 8.1 | 0.71 | 10.03 | 1.4 |