Mechanical Flexibility of DNA: A Quintessential Tool for DNA Nanotechnology
Abstract
1. Introduction
2. DNA-Springs as Regulators
2.1. Allosteric Regulation of Enzyme Activity
- (i)
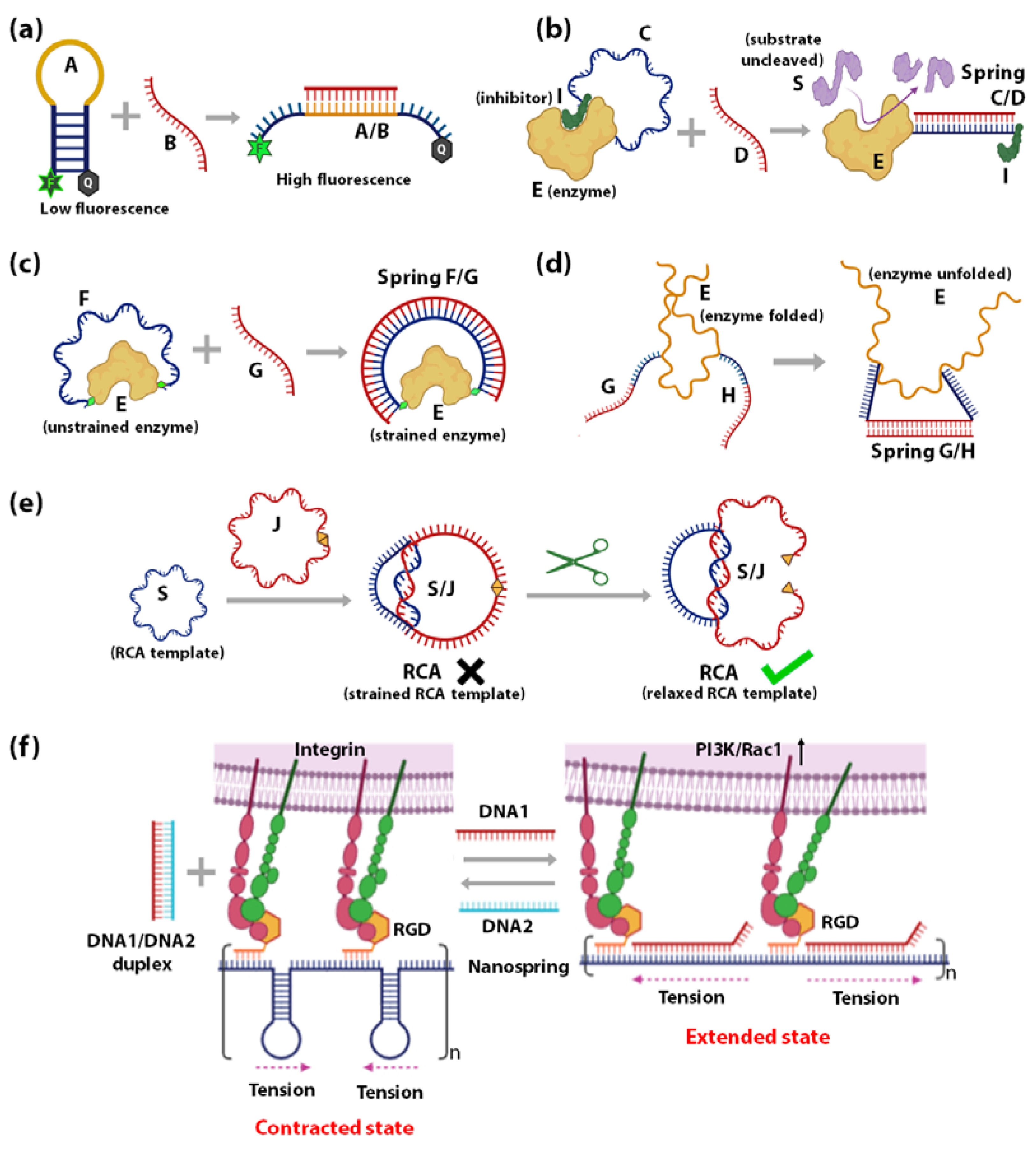
- Influencing the accessibility of regulatory molecules: The first strategy using DNA springs to regulate enzymes is by controlling the accessibility of enzyme regulatory factors, e.g., inhibitors. Ghadiri et al., reported the allosteric regulation of a protein enzyme Cereus Neutral Protease 5 (CNP) by a DNA spring using this strategy (Figure 2b) [117]. In this study, the two ends of DNA strand C (blue) were conjugated to CNP (shown as E) and its inhibitor (shown as I). The flexible nature of ssDNA C allows the inhibitor I to remain bound to the enzyme E until the complementary ssDNA D (red) hybridizes to strand C. The rigid dsDNA duplex C/D causes the dissociation of the inhibitor from the enzyme and keeps it away. CNP’s catalytic activity recovers noticeably upon the unbinding of the inhibitor I caused by the binding of strand B.
- (ii)
- Mechanical force regulation of enzymes: The second strategy uses DNA springs to exert force on enzymes to modulate their mechanochemistry. Choi et al., demonstrated this concept in 2005 (Figure 2c) [115] by covalently attaching two ends of a flexible 60-nucleotide ssDNA strand F (blue) to the two lobes of a maltose-binding protein (MBP). MBP retains its high binding affinity to maltose when F remains in the ssDNA state, as it does not apply external force to the MBP. However, when a complementary strand G binds to F, an external force up to 10 pN is applied on the MBP from the stiffness of the F/G duplex. This mechanical stress makes it energetically unfavourable for MBP to undergo the conformational changes required for maltose binding. As the length of strand G increases above 30 bases, the mechanical stress exerted on MBP increases, leading to further diminished maltose-binding affinity. Through this mechanism, regulation of MBP-maltose affinity was achieved through the external forces generated by a DNA spring. A similar concept was applied to achieve reversible allosteric regulation of enzyme guanylate kinase (GK) [109] and cAMP-dependent Protein Kinase A (PKA) [110]. The binding of GK to its substrates adenosine triphosphate (ATP) and guanosine monophosphate (GMP) requires a conformational change, which was reversibly inhibited by mechanical tension applied through a dsDNA spring. On the other hand, PKA was activated by the mechanical tension applied through a dsDNA spring, such that it demonstrated activity even in the absence of cyclic adenosine monophosphate (cAMP), the co-factor typically required for its activation. In 2007, Silverman et al., extended the application of DNA springs to the allosteric regulation of ribozymes (Figure 2d) [118]. Here, the hammerhead ribozyme’s mechanical control was attained by attaching two complementary ssDNA G and H to two different portions of the ribozyme. When G and H hybridize, they pull apart their corresponding attachment points, causing the tertiary structure of ribozyme E to unfold and lose function.
- (iii)
- Mechanical force regulation of substrates: The third strategy is to exert strain on the substrate such that it affects the efficiency of the enzyme. Based on this strategy, a circular ssDNA was used as a topological constraint to regulate the Rolling Circle Amplification (RCA) activity of Φ29 DNA Polymerase enzyme [119]. This was illustrated by Liu et al., where a circular RCA ssDNA template (shown as S, blue) was mechanically strained by a strong linking duplex formed with another circular ssDNA (shown as J, red) as in the case of DNA catenanes (Figure 2e). The strained template cannot undergo RCA until the spring/constraint is cleaved, and the strain is released. This system has been employed to demonstrate specific target-triggered RCA for detecting a specific E. coli strain with detection limits of 10 cells/mL.
2.2. Regulation of Live Cells
3. Mechanical Rigidity-Facilitated DNA Sensors
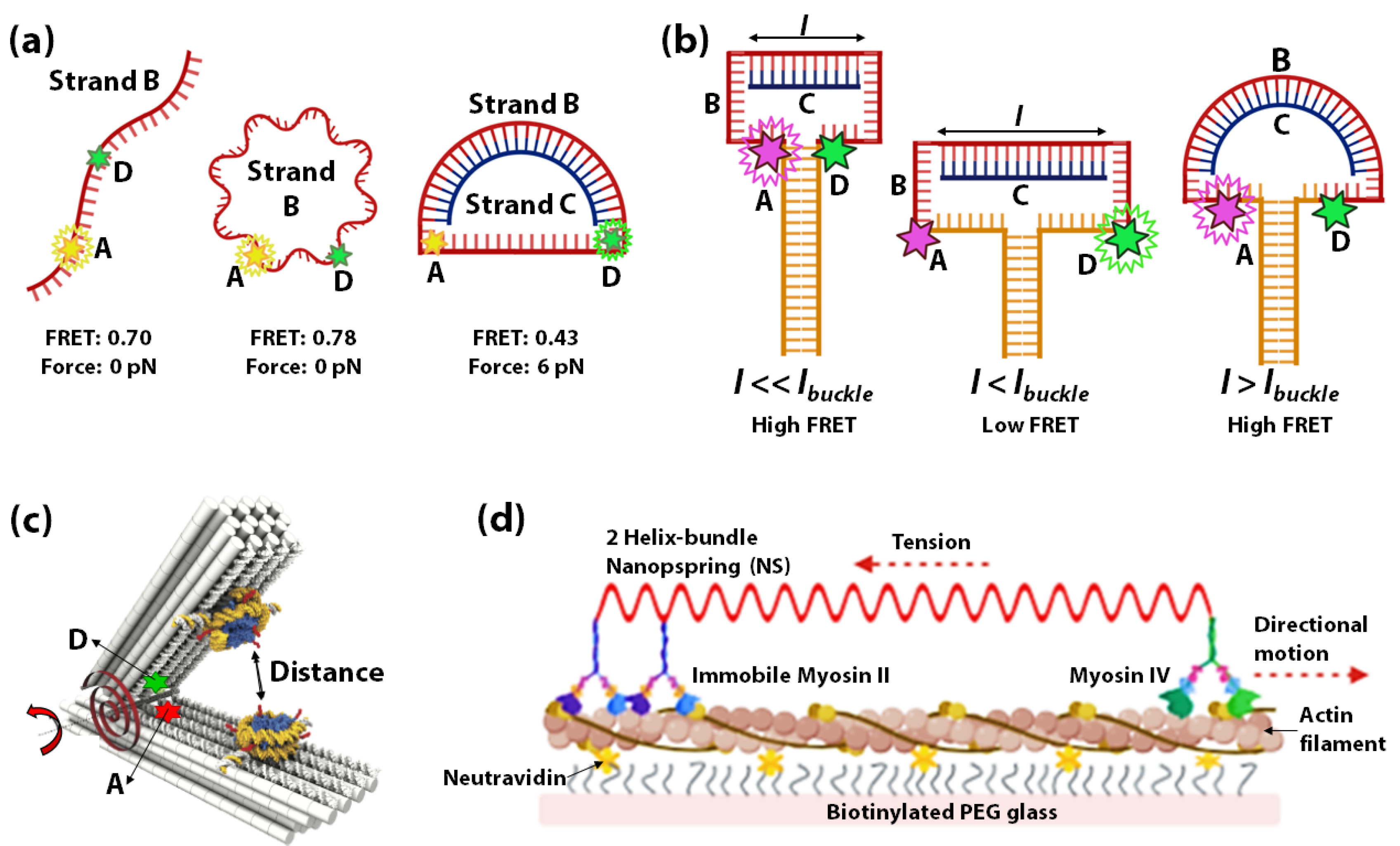
3.1. DNA Springs as Force-Sensors
3.2. pH-Sensitive DNA Spring
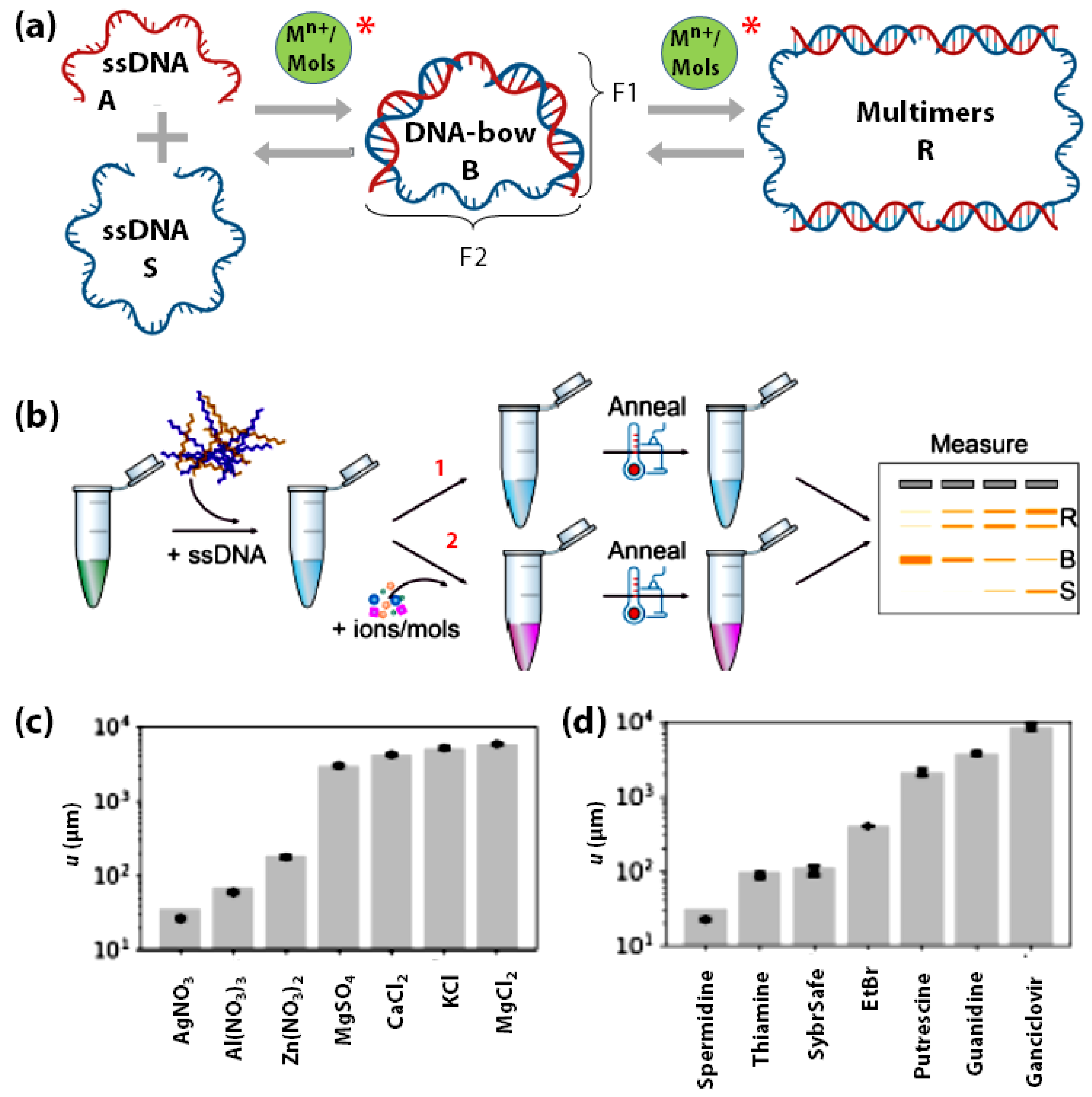
3.3. DNA-Bows as Metal Ion/Small-Molecule Sensors
3.4. DNA Stiffness Assisted Temperature and Osmolarity Sensing
3.5. DNA Bending Assisted Protein Sensing
4. DNA-Flexibility: A Game-Changer for DNA Nanostructures
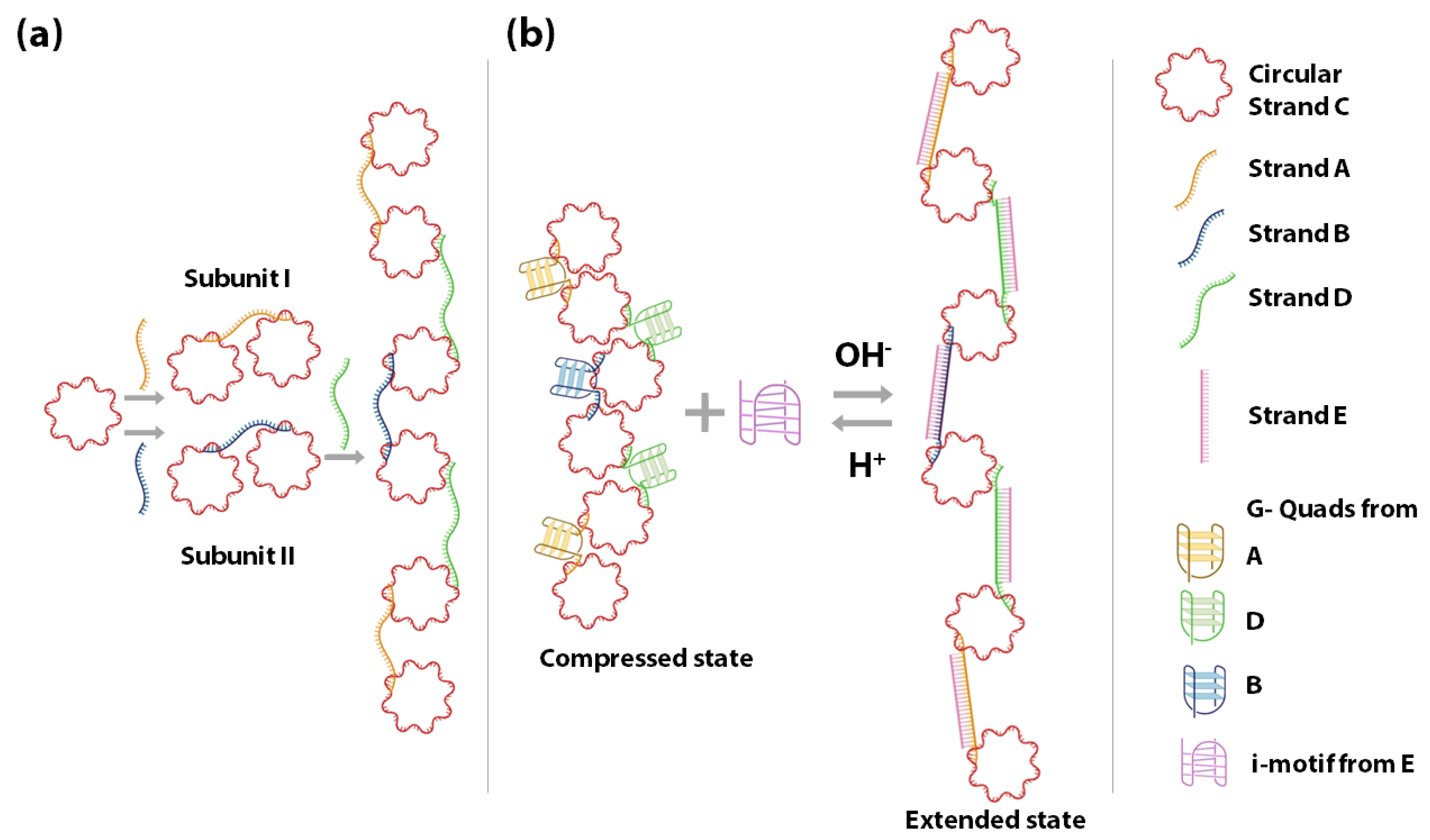
4.1. Circular DNA as the Basis of Origami
4.2. Mechanical Flexibility of DNA Can Tune the Efficiency of DNA-Based Nanomachines
5. Summary and Future Directions
Author Contributions
Funding
Conflicts of Interest
References
- Seeman, N.C. DNA Nanotechnology at 40. Nano Lett. 2020, 20, 1477–1478. [Google Scholar] [CrossRef]
- Peters, J.P.; Maher, L.J. DNA Curvature and Flexibility in Vitro and in Vivo. Q. Rev. Biophys. 2010, 43, 23–63. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.T.; Yang, H.; Chu, J.W. Structure-Mechanics Statistical Learning Unravels the Linkage between Local Rigidity and Global Flexibility in Nucleic Acids. Chem. Sci. 2020, 11, 4969–4979. [Google Scholar] [CrossRef]
- Vologodskii, A.; Frank-Kamenetskii, M.D. Strong Bending of the DNA Double Helix. Nucleic Acids Res. 2013, 41, 6785–6792. [Google Scholar] [CrossRef]
- Drozdetski, A.V.; Anandakrishnan, R.; Onufriev, A. Estimating Persistence Length of DNA from Molecular Dynamics Simulations. Biophys. J. 2015, 108, 233a. [Google Scholar] [CrossRef][Green Version]
- Beveridge, D.L. Molecular Dynamics Simulations of DNA Curvature and Flexibility: Helix Phasing and Premelting. Biopolymers 2020, 73, 380–403. [Google Scholar] [CrossRef] [PubMed]
- Curuksu, J.; Zacharias, M.; Lavery, R.; Zakrzewska, K. Local and Global Effects of Strong DNA Bending Induced during Molecular Dynamics Simulations. Nucleic Acids Res. 2009, 37, 3766–3773. [Google Scholar] [CrossRef]
- Brinkers, S.; Dietrich, H.R.C.; De Groote, F.H.; Young, I.T.; Rieger, B. The Persistence Length of Double Stranded DNA Determined Using Dark Field Tethered Particle Motion. J. Chem. Phys. 2009, 130. [Google Scholar] [CrossRef]
- Wang, H.; Milstein, J.N. Simulation Assisted Analysis of the Intrinsic Stiffness for Short DNA Molecules Imaged with Scanning Atomic Force Microscopy. PLoS ONE 2015, 10, 1–11. [Google Scholar] [CrossRef][Green Version]
- Olson, W.K.; Zhurkin, V.B. Modeling DNA Deformations. Curr. Opin. Struct. Biol. 2000, 10, 286–297. [Google Scholar] [CrossRef]
- Strauss, J.K.; Maher, L.J. DNA Bending by Asymmetric Phosphate Neutralization. Science 1994, 266, 1829–1834. [Google Scholar] [CrossRef] [PubMed]
- Strutz, K. Intrinsic Curvature of Plasmid DNAs Analyzed by Polyacrylamide Gel Electrophoresis. Electrophoresis 1996, 17, 989–995. [Google Scholar] [CrossRef] [PubMed]
- Crothers, D.M.; Drak, J. Global Features of DNA Structure by Comparative Gel Electrophoresis. Methods Enzymol. Acad. Press 1992, 212, 46–71. [Google Scholar] [CrossRef]
- Hellman, L.M.; Fried, M.G. Electrophoretic Mobility Shift Assays. Nat. Methods 2005, 2, 557–558. [Google Scholar] [CrossRef]
- Jost, J.P.; Saluz, H.P. (Eds.) A Laboratory Guide to In Vitro Studies of Protein-DNA Interactions; Birkhäuser: Basel, Switzerland, 1991; Volume 5, pp. 245–257. [Google Scholar] [CrossRef]
- Harrington, R.E. Studies of DNA Bending and Flexibility Using Gel Electrophoresis. Electrophoresis 1993, 14, 732–746. [Google Scholar] [CrossRef]
- Freeland, J.; Khadka, P.; Wang, Y. Mechanical-Energy-Based Amplifiers for Probing Interactions of DNA with Metal Ions. Phys. Rev. E 2018, 98, 62403. [Google Scholar] [CrossRef]
- Freeland, J.; Zhang, L.; Wang, S.-T.; Ruiz, M.; Wang, Y. Bent DNA Bows as Amplifiers and Biosensors for Detecting DNA-Interacting Salts and Molecules. bioRxiv 2020. [Google Scholar] [CrossRef]
- Vafabakhsh, R.; Ha, T. Extreme Bendability of DNA Less than 100 Base Pairs Long Revealed by Single-Molecule Cyclization. Science 2012, 337, 1097–1101. [Google Scholar] [CrossRef]
- Jeong, J.; Kim, H.D. Determinants of Cyclization-Decyclization Kinetics of Short DNA with Sticky Ends. bioRxiv 2018. [Google Scholar] [CrossRef]
- Du, Q.; Vologodskaia, M.; Kuhn, H.; Frank-Kamenetskii, M.; Vologodskii, A. Gapped DNA and Cyclization of Short DNA Fragments. Biophys. J. 2005, 88, 4137–4145. [Google Scholar] [CrossRef]
- Le, T.T.; Kim, H.D. Studying DNA Looping by Single-Molecule FRET. J. Vis. Exp. 2014, 88, e51667. [Google Scholar] [CrossRef] [PubMed]
- Ngo, T.T.M.; Yoo, J.; Dai, Q.; Zhang, Q.; He, C.; Aksimentiev, A.; Ha, T. Effects of Cytosine Modifications on DNA Flexibility and Nucleosome Mechanical Stability. Nat. Commun. 2016, 7, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Dlakic, M.; Harrington, R.E. Bending and Torsional Flexibility of G/C-Rich Sequences as Determined by Cyclization Assays. J. Biol. Chem. 1995, 270, 29945–29952. [Google Scholar] [CrossRef] [PubMed]
- Shore, D.; Langowski, J.; Baldwin, R.L. DNA Flexibility Studied by Covalent Closure of Short Fragments into Circles. Proc. Natl. Acad. Sci. USA 1981, 78, 4833–4837. [Google Scholar] [CrossRef]
- Yan, J.; Marko, J.F. Localized Single-Stranded Bubble Mechanism for Cyclization of Short Double Helix DNA. Phys. Rev. Lett. 2004, 93, 3–6. [Google Scholar] [CrossRef]
- Cherstvy, A.G. DNA Cyclization: Suppression or Enhancement by Electrostatic Repulsions? J. Phys. Chem. B 2011, 115, 4286–4294. [Google Scholar] [CrossRef]
- Cloutier, T.E.; Widom, J. DNA Twisting Flexibility and the Formation of Sharply Looped Protein–DNA Complexes. Proc. Natl. Acad. Sci. USA 2005, 102, 3645LP–3650. [Google Scholar] [CrossRef]
- Crothers, D.M.; Drak, J.; Kahn, J.D.; Levene, S.D. DNA Bending, Flexibility, and Helical Repeat by Cyclization Kinetics. Methods Enzymol. 1992, 212, 3–29. [Google Scholar] [CrossRef] [PubMed]
- Cloutier, T.E.; Widom, J. Spontaneous Sharp Bending of Double-Stranded DNA. Mol. Cell 2004, 14, 355–362. [Google Scholar] [CrossRef]
- Du, Q.; Smith, C.; Shiffeldrim, N.; Vologodskaia, M.; Vologodskii, A. Cyclization of Short DNA Fragments and Bending Fluctuations of the Double Helix. Proc. Natl. Acad. Sci. USA 2005, 102, 5397LP–5402. [Google Scholar] [CrossRef]
- Driessen, R.P.C.; Sitters, G.; Laurens, N.; Moolenaar, G.F.; Wuite, G.J.L.; Goosen, N.; Dame, R.T. Effect of Temperature on the Intrinsic Flexibility of DNA and Its Interaction with Architectural Proteins. Biochemistry 2014, 53, 6430–6438. [Google Scholar] [CrossRef] [PubMed]
- Song, D.; Mousley, B.; Gambino, S.; Helou, E.; Loparo, J.; Price, A.C. Tethered Particle Motion with Single DNA Molecules. Am. J. Phys. 2015, 83, 418–426. [Google Scholar] [CrossRef]
- Kovari, D.T.; Yan, Y.; Finzi, L.; Dunlap, D. Tethered Particle Motion: An Easy Technique for Probing DNA Topology and Interactions with Transcription Factors. Methods Mol. Biol. 2018, 1665, 317–340. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.D.; Yin, H.; Landick, R.; Gelles, J.; Block, S.M. Stretching DNA with Optical Tweezers. Biophys. J. 1997, 72, 1335–1346. [Google Scholar] [CrossRef]
- Gross, P.; Laurens, N.; Oddershede, L.B.; Bockelmann, U.; Peterman, E.J.G.; Wuite, G.J.L. Quantifying How DNA Stretches, Melts and Changes Twist under Tension. Nat. Phys. 2011, 7, 731–736. [Google Scholar] [CrossRef]
- Bockelmann, U.; Thomen, P.; Essevaz-Roulet, B.; Viasnoff, V.; Heslot, F. Unzipping DNA with Optical Tweezers: High Sequence Sensitivity and Force Flips. Biophys. J. 2002, 82, 1537–1553. [Google Scholar] [CrossRef]
- van Mameren, J.; Wozniak, A.; Ragona, S. Single-Molecule DNA Stretching Using Optical Tweezers. Micros. Today 2009, 17, 42–43. [Google Scholar] [CrossRef]
- Epstein, C.S.; Mann, A.J. Measurement of the DNA Spring Constant Using Optical Tweezers. Phys. Rev. E. 2003, 67, 051906. [Google Scholar]
- Kang, J.; Jung, J.; Kim, S.K. Flexibility of Single-Stranded DNA Measured by Single-Molecule FRET. Biophys. Chem. 2014, 195, 49–52. [Google Scholar] [CrossRef]
- Murphy, M.C.; Rasnik, I.; Cheng, W.; Lohman, T.M.; Ha, T. Probing Single-Stranded DNA Conformational Flexibility Using Fluorescence Spectroscopy. Biophys. J. 2004, 86, 2530–2537. [Google Scholar] [CrossRef]
- Dragan, A.I.; Privalov, P.L. Use of Fluorescence Resonance Energy Transfer (FRET) in Studying Protein-Induced DNA Bending. Methods Enzymol. 2008, 450, 185–199. [Google Scholar] [CrossRef] [PubMed]
- Williams, S.L.; Parkhurst, L.K.; Parkhurst, L.J. Changes in DNA Bending and Flexing Due to Tethered Cations Detected by Fluorescence Resonance Energy Transfer. Nucleic Acids Res. 2006, 34, 1028–1035. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Woźniak, A.K.; Schröder, G.F.; Grubmüller, H.; Seidela, C.A.M.; Oesterhelt, F. Single-Molecule FRET Measures Bends and Kinks in DNA. Proc. Natl. Acad. Sci. USA 2008, 105, 18337–18342. [Google Scholar] [CrossRef]
- Tóth, K.; Sauermann, V.; Langowski, J. DNA Curvature in Solution Measured by Fluorescence Resonance Energy Transfer. Biochemistry 1998, 37, 8173–8179. [Google Scholar] [CrossRef] [PubMed]
- Le, T.T.; Kim, H.D. Probing the Elastic Limit of DNA Bending. Nucleic Acids Res. 2014, 42, 10786–10794. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, S.V.; Sugimura, S.; Vivas, P.; Crothers, D.M.; Ansari, A. Direct Observation of DNA Bending/Unbending Kinetics in Complex with DNA-Bending Protein IHF. Proc. Natl. Acad. Sci. USA 2006, 103, 18515LP–18520. [Google Scholar] [CrossRef] [PubMed]
- Maaloum, M.; Muller, P.; Harlepp, S. DNA-Intercalator Interactions: Structural and Physical Analysis Using Atomic Force Microscopy in Solution. Soft Matter 2013, 9, 11233–11240. [Google Scholar] [CrossRef]
- Hansma, H.G.; Laney, D.E.; Bezanilla, M.; Sinsheimer, R.L.; Hansma, P.K. Applications for Atomic Force Microscopy of DNA. Biophys. J. 1995, 68, 1672–1677. [Google Scholar] [CrossRef]
- Mazur, A.K.; Maaloum, M. Atomic Force Microscopy Study of DNA Flexibility on Short Length Scales: Smooth Bending versus Kinking. Nucleic Acids Res. 2014, 42, 14006–14012. [Google Scholar] [CrossRef]
- Beckwitt, E.C.; Kong, M.; Van Houten, B. Studying Protein-DNA Interactions Using Atomic Force Microscopy. Semin. Cell Dev. Biol. 2018, 73, 220–230. [Google Scholar] [CrossRef]
- Hansma, H. Surface Biology of DNA by Atomic Force Microscopy. Annu. Rev. Phys. Chem. 2001, 52, 71–92. [Google Scholar] [CrossRef] [PubMed]
- Faas, F.G.A.; Rieger, B.; van Vliet, L.J.; Cherny, D.I. DNA Deformations near Charged Surfaces: Electron and Atomic Force Microscopy Views. Biophys. J. 2009, 97, 1148–1157. [Google Scholar] [CrossRef] [PubMed]
- Kahn, J.D. DNA, Flexibly Flexible. Biophys. J. 2014, 107, 282–284. [Google Scholar] [CrossRef][Green Version]
- Camunas-Soler, J.; Ribezzi-Crivellari, M.; Ritort, F. Elastic Properties of Nucleic Acids by Single-Molecule Force Spectroscopy. Annu. Rev. Biophys. 2016, 45, 65–84. [Google Scholar] [CrossRef] [PubMed]
- Demurtas, D.; Amzallag, A.; Rawdon, E.J.; Maddocks, J.H.; Dubochet, J.; Stasiak, A. Bending Modes of DNA Directly Addressed by Cryo-Electron Microscopy of DNA Minicircles. Nucleic Acids Res. 2009, 37, 2882–2893. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Lukoyanova, N.; Miah, S.; Lucas, J.; Vaughan, C.K. Insights into Centromere DNA Bending Revealed by the Cryo-EM Structure of the Core Centromere Binding Factor 3 with Ndc10. Cell Rep. 2018, 24, 744–754. [Google Scholar] [CrossRef]
- Bednar, J.; Furrer, P.; Katritch, V.; Stasiak, A.; Dubochet, J.; Stasiak, A. Determination of DNA Persistence Length by Cryo-Electron Microscopy. Separation of the Static and Dynamic Contributions to the Apparent Persistence Length of DNA. J. Mol. Biol. 1995, 254, 579–594. [Google Scholar] [CrossRef]
- Bai, X.C.; Martin, T.G.; Scheres, S.H.W.; Dietz, H. Cryo-EM Structure of a 3D DNA-Origami Object. Proc. Natl. Acad. Sci. USA 2012, 109, 20012–20017. [Google Scholar] [CrossRef]
- Dunlop, D. Scanning Tunneling Microscopy of DNA. IEEE Eng. Med. Biol. Mag. 1996, 15, 46–50. [Google Scholar] [CrossRef]
- Marilley, M.; Pasero, P.; Humbert, A.; Granjeaud, S.; Dayez, M.; Pierrisnard, R.; Jordan, B. Scanning Tunneling Microscopy Study of a DNA Fragment of Known Size and Sequence. Microsc. Microanal. Microstruct. 1994, 5, 47–56. [Google Scholar] [CrossRef]
- Müller, T.; Gilson, E.; Schmidt, R.; Giraldo, R.; Sogo, J.; Gross, H.; Gasser, S. Imaging the Asymmetrical DNA Bend Induced by Repressor Activator Protein 1 with Scanning Tunneling Microscopy. J. Struct. Biol. 1994, 113, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Subirana, J.A. A Crystallographic Approach to DNA Bending: Prediction of Nusleosome Formation by DNA Triple Repeats and: Other Repetitive Sequences. FEBS Lett. 1997, 417, 352–354. [Google Scholar] [CrossRef]
- Kornyshev, A.A.; Lee, D.J.; Wynveen, A.; Leikin, S. Signatures of DNA Flexibility, Interactions and Sequence-Related Structural Variations in Classical X-Ray Diffraction Patterns. Nucleic Acids Res. 2011, 39, 7289–7299. [Google Scholar] [CrossRef] [PubMed]
- Mathew-Fenn, R.S.; Das, R.; Harbury, P.A.B. Remeasuring the Double Helix. Science 2008, 322, 446–449. [Google Scholar] [CrossRef]
- Mastroianni, A.J.; Sivak, D.A.; Geissler, P.L.; Alivisatos, A.P. Probing the Conformational Distributions of Subpersistence Length DNA. Biophys. J. 2009, 97, 1408–1417. [Google Scholar] [CrossRef]
- Vermeulen, A.; Zhou, H.; Pardi, A. Determining DNA Global Structure and DNA Bending by Application of NMR Residual Dipolar Couplings. J. Am. Chem. Soc. 2000, 122, 9638–9647. [Google Scholar] [CrossRef]
- Ben Imeddourene, A.; Xu, X.; Zargarian, L.; Oguey, C.; Foloppe, N.; Mauffret, O.; Hartmann, B. The Intrinsic Mechanics of B-DNA in Solution Characterized by NMR. Nucleic Acids Res. 2016, 44, 3432–3447. [Google Scholar] [CrossRef]
- Wu, Z.; Maderia, M.; Barchi, J.J.; Marquez, V.E.; Bax, A. Changes in DNA Bending Induced by Restricting Nucleotide Ring Pucker Studied by Weak Alignment NMR Spectroscopy. Proc. Natl. Acad. Sci. USA 2005, 102, 24–28. [Google Scholar] [CrossRef]
- Campagne, S.; Gervais, V.; Milon, A. Nuclear Magnetic Resonance Analysis of Protein—DNA Interactions. J. R. Soc. Interface 2011, 8, 1065–1078. [Google Scholar] [CrossRef]
- Nathan, D.; Crothers, D.M. Bending and Flexibility of Methylated and Unmethylated EcoRI DNA. J. Mol. Biol. 2002, 316, 7–17. [Google Scholar] [CrossRef]
- Renzoni, D.; Esposito, D.; Pfuhl, M.; Hinton, J.C.D.; Higgins, C.F.; Driscoll, P.C.; Ladbury, J.E. Structural Characterization of the N-Terminal Oligomerization Domain of the Bacterial Chromatin-Structuring Protein, H-NS1 1Edited by A. R. Fersht. J. Mol. Biol. 2001, 306, 1127–1137. [Google Scholar] [CrossRef] [PubMed]
- Meints, G.A.; Drobny, G.P. Dynamic Impact of Methylation at the M. HhaI Target Site: A Solid-State Deuterium NMR Study. Biochemistry 2001, 40, 12436–12443. [Google Scholar] [CrossRef]
- Hagerman, P.J. Investigation of the Flexibility of DNA Using Transient Electric Birefringence. Biopolymers 1981, 20, 1503–1535. [Google Scholar] [CrossRef] [PubMed]
- Mills, J.B.; Hagerman, P.J. Origin of the Intrinsic Rigidity of DNA. Nucleic Acids Res. 2004, 32, 4055–4059. [Google Scholar] [CrossRef] [PubMed]
- Cohen, A.E.; Moemer, W.E. Method for Trapping and Manipulating Nanoscale Objects in Solution. Appl. Phys. Lett. 2005, 86, 1–3. [Google Scholar] [CrossRef]
- Dekker, J.; Rippe, K.; Dekker, M.; Kleckner, N. Capturing Chromosome Conformation. Science 2002, 295, 1306LP–1311. [Google Scholar] [CrossRef]
- Göndör, A.; Rougier, C.; Ohlsson, R. High-Resolution Circular Chromosome Conformation Capture Assay. Nat. Protoc. 2008, 3, 303–313. [Google Scholar] [CrossRef]
- Lieberman-Aiden, E.; van Berkum, N.L.; Williams, L.; Imakaev, M.; Ragoczy, T.; Telling, A.; Amit, I.; Lajoie, B.R.; Sabo, P.J.; Dorschner, M.O.; et al. Comprehensive Mapping of Long-Range Interactions Reveals Folding Principles of the Human Genome. Science 2009, 326, 289LP–293. [Google Scholar] [CrossRef]
- Zhou, G.-L.; Xin, L.; Song, W.; Di, L.-J.; Liu, G.; Wu, X.-S.; Liu, D.-P.; Liang, C.-C. Active Chromatin Hub of the Mouse Alpha-Globin Locus Forms in a Transcription Factory of Clustered Housekeeping Genes. Mol. Cell. Biol. 2006, 26, 5096–5105. [Google Scholar] [CrossRef]
- Becker, N.A.; Kahn, J.D.; James Maher, L. Bacterial Repression Loops Require Enhanced DNA Flexibility. J. Mol. Biol. 2005, 349, 716–730. [Google Scholar] [CrossRef]
- Becker, N.A.; Kahn, J.D.; Maher, L.J., 3rd. Effects of Nucleoid Proteins on DNA Repression Loop Formation in Escherichia coli. Nucleic Acids Res. 2007, 35, 3988–4000. [Google Scholar] [CrossRef] [PubMed]
- Müller, J.; Oehler, S.; Müller-Hill, B. Repression of Lac Promoter as a Function of Distance, Phase and Quality of an Auxiliary Lac Operator. J. Mol. Biol. 1996, 257, 21–29. [Google Scholar] [CrossRef] [PubMed]
- Oehler, S.; Eismann, E.R.; Krämer, H.; Müller-Hill, B. The Three Operators of the Lac Operon Cooperate in Repression. EMBO J. 1990, 9, 973–979. [Google Scholar] [CrossRef] [PubMed]
- Oehler, S.; Müller-Hill, B. High Local Concentration: A Fundamental Strategy of Life. J. Mol. Biol. 2010, 395, 242–253. [Google Scholar] [CrossRef]
- Becker, N.A.; Kahn, J.D.; Maher, L.J., 3rd. Eukaryotic HMGB Proteins as Replacements for HU in E. coli Repression Loop Formation. Nucleic Acids Res. 2008, 36, 4009–4021. [Google Scholar] [CrossRef]
- Bellomy, G.R.; Mossing, M.C.; Record, M.T.J. Physical Properties of DNA in Vivo as Probed by the Length Dependence of the Lac Operator Looping Process. Biochemistry 1988, 27, 3900–3906. [Google Scholar] [CrossRef]
- Garcia, H.G.; Grayson, P.; Han, L.; Inamdar, M.; Kondev, J.; Nelson, P.C.; Phillips, R.; Widom, J.; Wiggins, P.A. Biological Consequences of Tightly Bent DNA: The Other Life of a Macromolecular Celebrity. Biopolymers 2007, 85, 115–130. [Google Scholar] [CrossRef]
- Zhang, Y.; McEwen, A.E.; Crothers, D.M.; Levene, S.D. Statistical-Mechanical Theory of DNA Looping. Biophys. J. 2006, 90, 1903–1912. [Google Scholar] [CrossRef]
- Zhang, Y.; McEwen, A.E.; Crothers, D.M.; Levene, S.D. Analysis of In-Vivo LacR-Mediated Gene Repression Based on the Mechanics of DNA Looping. PLoS ONE 2006, 1. [Google Scholar] [CrossRef]
- Krämer, H.; Niemöller, M.; Amouyal, M.; Revet, B.; von Wilcken-Bergmann, B.; Müller-Hill, B. Lac Repressor Forms Loops with Linear DNA Carrying Two Suitably Spaced Lac Operators. EMBO J. 1987, 6, 1481–1491. [Google Scholar] [CrossRef]
- Law, S.M.; Bellomy, G.R.; Schlax, P.J.; Record, M.T.J. In Vivo Thermodynamic Analysis of Repression with and without Looping in Lac Constructs. Estimates of Free and Local Lac Repressor Concentrations and of Physical Properties of a Region of Supercoiled Plasmid DNA in Vivo. J. Mol. Biol. 1993, 230, 161–173. [Google Scholar] [CrossRef] [PubMed]
- Mossing, M.C.; Record, M.T.J. Upstream Operators Enhance Repression of the Lac Promoter. Science 1986, 233, 889–892. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.B.; Cui, Y.; Bustamante, C. Overstretching B-DNA: The Elastic Response of Individual Double-Stranded and Single-Stranded DNA Molecules. Science 1996, 271, 795–799. [Google Scholar] [CrossRef]
- Williams, L.D.; Maher, L.J. 3rd. Electrostatic Mechanisms of DNA Deformation. Annu. Rev. Biophys. Biomol. Struct. 2000, 29, 497–521. [Google Scholar] [CrossRef] [PubMed]
- Range, K.; Mayaan, E.; Maher, L.J.; York, D.M. The Contribution of Phosphate-Phosphate Repulsions to the Free Energy of DNA Bending. Nucleic Acids Res. 2005, 33, 1257–1268. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Strauss, J.K.; Roberts, C.; Nelson, M.G.; Switzer, C.; Maher, L.J. DNA Bending by Hexamethylene-Tethered Ammonium Ions. Proc. Natl. Acad. Sci. USA 1996, 93, 9515–9520. [Google Scholar] [CrossRef]
- Manning, G.S.; Ebralidse, K.K.; Mirzabekov, A.D.; Rich, A. An Estimate of the Extent of Folding of Nucleosomal DNA by Laterally Asymmetric Neutralization of Phosphate Groups. J. Biomol. Struct. Dyn. 1989, 6, 877–889. [Google Scholar] [CrossRef]
- Strauss-Soukup, J.K.; Vaghefi, M.M.; Hogrefe, R.I.; Maher, L.J. Effects of Neutralization Pattern and Stereochemistry on DNA Bending by Methylphosphonate Substitutions. Biochemistry 1997, 36, 8692–8698. [Google Scholar] [CrossRef]
- Kim, Y.J.; Kim, D.N. Structural Basis for Elastic Mechanical Properties of the DNA Double Helix. PLoS ONE 2016, 11, 1–11. [Google Scholar] [CrossRef]
- Gore, J.; Bryant, Z.; Nöllmann, M.; Le, M.U.; Cozzarelli, N.R.; Bustamante, C. DNA Overwinds When Stretched. Nature 2006, 442, 836–839. [Google Scholar] [CrossRef]
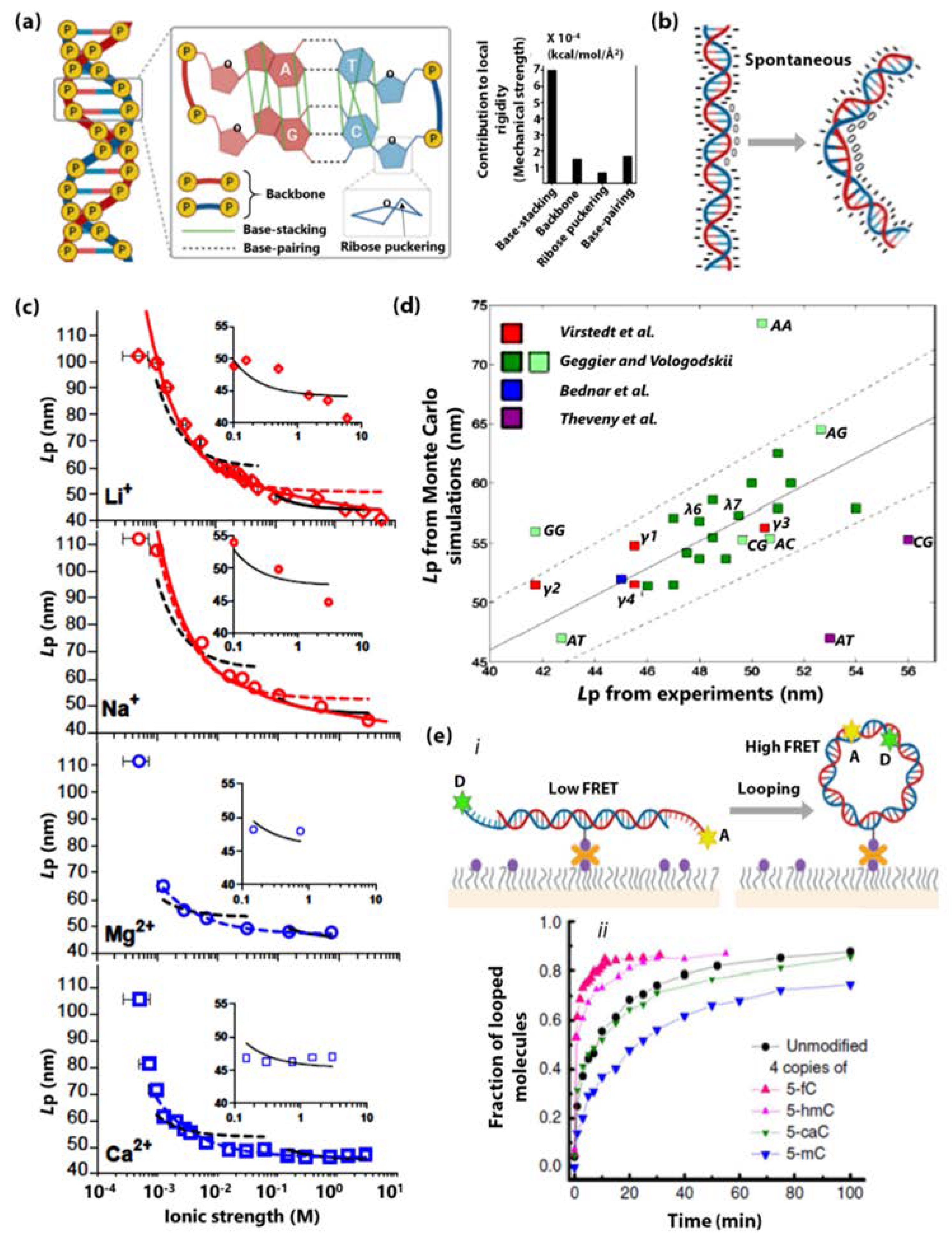
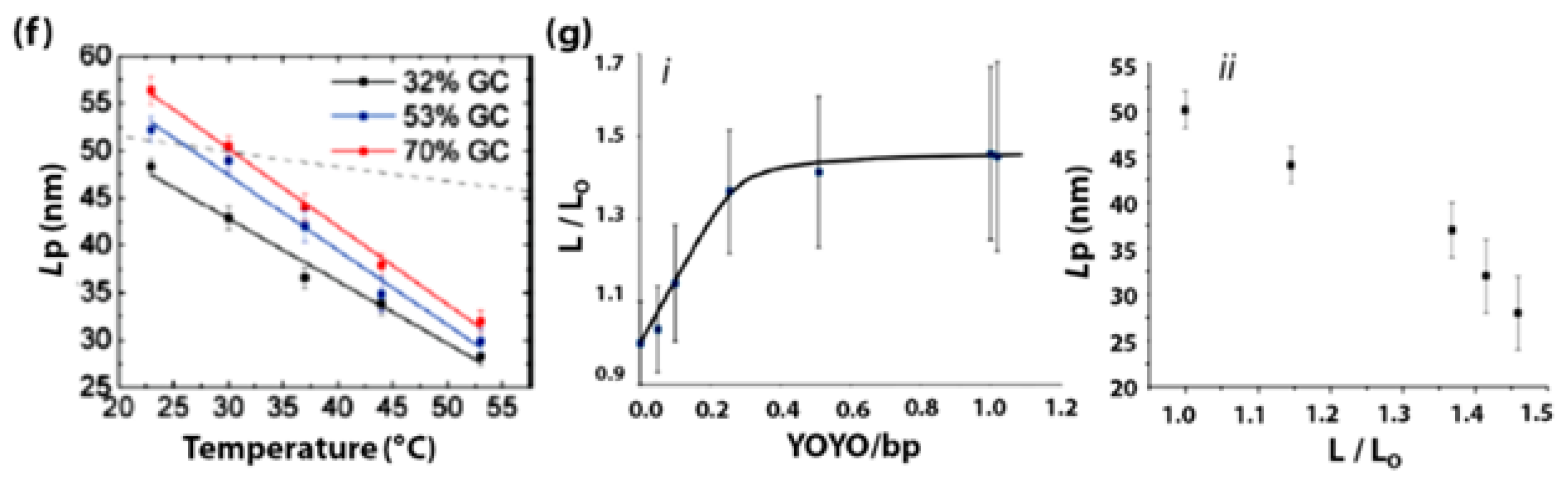
- Guilbaud, S.; Salomé, L.; Destainville, N.; Manghi, M.; Tardin, C. Dependence of DNA Persistence Length on Ionic Strength and Ion Type. Phys. Rev. Lett. 2019, 122, 81–91. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, J.S.; Glowacki, J.; Grandchamp, A.E.; Manning, R.S.; Maddocks, J.H. Sequence-Dependent Persistence Lengths of DNA. J. Chem. Theory Comput. 2017, 13, 1539–1555. [Google Scholar] [CrossRef] [PubMed]
- Severin, P.M.D.; Zou, X.; Gaub, H.E.; Schulten, K. Cytosine Methylation Alters DNA Mechanical Properties. Nucleic Acids Res. 2011, 39, 8740–8751. [Google Scholar] [CrossRef] [PubMed]
- Carson, S.; Wilson, J.; Aksimentiev, A.; Weigele, P.R.; Wanunu, M. Hydroxymethyluracil Modifications Enhance the Flexibility and Hydrophilicity of Double-Stranded DNA. Nucleic Acids Res. 2015, 44, 2085–2092. [Google Scholar] [CrossRef] [PubMed]
- Destainville, N.; Manghi, M.; Palmeri, J. Microscopic Mechanism for Experimentally Observed Anomalous Elasticity of DNA in Two Dimensions. Biophys. J. 2009, 96, 4464–4469. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Forties, R.A.; Bundschuh, R.; Poirier, M.G. The Flexibility of Locally Melted DNA. Nucleic Acids Res. 2009, 37, 4580–4586. [Google Scholar] [CrossRef]
- Yuan, C.; Rhoades, E.; Lou, X.W.; Archer, L.A. Spontaneous Sharp Bending of DNA: Role of Melting Bubbles. Nucleic Acids Res. 2006, 34, 4554–4560. [Google Scholar] [CrossRef][Green Version]
- Choi, B.; Zocchi, G.; Wu, Y.; Chan, S.; Jeanne Perry, L.; Perry, L. Allosteric Control through Mechanical Tension. Phys. Rev. Lett. 2005, 95, 78102. [Google Scholar] [CrossRef]
- Choi, B.; Zocchi, G. Mimicking CAMP-Dependent Allosteric Control of Protein Kinase A through Mechanical Tension. J. Am. Chem. Soc. 2006, 128, 8541–8548. [Google Scholar] [CrossRef]
- Tseng, C.-Y. UCLA Mechanical Control of Enzymes Using DNA Molecular Springs. Ph.D. Thesis, UCLA, Los Angeles, CA, USA, 2013. Available online: https://escholarship.org/uc/item/49d611tc (accessed on 27 September 2018).
- Zocchi, G. Controlling Proteins Through Molecular Springs. Annu. Rev. Biophys. 2009, 38, 75–88. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, A.; Qu, H.; Zocchi, G. Protein–DNA Chimeras: Synthesis of Two-Arm Chimeras and Non-Mechanical Effects of the DNA Spring. J. Phys. Condens. Matter 2009, 21, 335103. [Google Scholar] [CrossRef] [PubMed]
- Tseng, C.Y.; Zocchi, G. Equilibrium Softening of an Enzyme Explored with the DNA Spring. Appl. Phys. Lett. 2014, 104. [Google Scholar] [CrossRef]
- Choi, B.; Zocchi, G.; Canale, S.; Wu, Y.; Chan, S.; Perry, L.J. Artificial Allosteric Control of Maltose Binding Protein. Phys. Rev. Lett. 2005, 94, 7–10. [Google Scholar] [CrossRef] [PubMed]
- Tyagi, S.; Kramer, F.R. Molecular Beacon Probes That Fluoresce on Hybridiztion. Nat. Publ. Gr. 1996, 14, 303–308. [Google Scholar]
- Saghatelian, A.; Guckian, K.M.; Thayer, D.A.; Ghadiri, M.R. DNA Detection and Signal Amplification via an Engineered Allosteric Enzyme. J. Am. Chem. Soc. 2003, 125, 344–345. [Google Scholar] [CrossRef]
- Zelin, E.; Silverman, S.K. Allosteric Control of Ribozyme Catalysis by Using DNA Constraints. ChemBioChem 2007, 8, 1907–1911. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, Q.; Li, Z.; Gu, J.; Brennan, J.D.; Li, Y. Programming a Topologically Constrained DNA Nanostructure into a Sensor. Nat. Commun. 2016, 7, 1–7. [Google Scholar] [CrossRef]
- Zhang, K.; Deng, R.; Sun, Y.; Zhang, L.; Li, J. Reversible Control of Cell Membrane Receptor Function Using DNA Nano-Spring Multivalent Ligands. Chem. Sci. 2017, 8, 7098–7105. [Google Scholar] [CrossRef]
- Wang, X.; Ha, T. Defining Single Molecular Forces Required to Activate Integrin and Notch Signaling. Science 2013, 340, 991–994. [Google Scholar] [CrossRef]
- Wang, X.; Rahil, Z.; Li, I.T.S.; Chowdhury, F.; Leckband, D.E.; Chemla, Y.R.; Ha, T. Constructing Modular and Universal Single Molecule Tension Sensor Using Protein G to Study Mechano-Sensitive Receptors. Sci. Rep. 2016, 6, 1–10. [Google Scholar] [CrossRef]
- Chowdhury, F.; Li, I.T.S.; Leslie, B.J.; Doğanay, S.; Singh, R.; Wang, X.; Seong, J.; Lee, S.H.; Park, S.; Wang, N.; et al. Single Molecular Force across Single Integrins Dictates Cell Spreading. Integr. Biol. 2015, 7, 1265–1271. [Google Scholar] [CrossRef]
- Chowdhury, F.; Li, I.T.S.; Ngo, T.T.M.; Leslie, B.J.; Kim, B.C.; Sokoloski, J.E.; Weiland, E.; Wang, X.; Chemla, Y.R.; Lohman, T.M.; et al. Defining Single Molecular Forces Required for Notch Activation Using Nano Yoyo. Nano Lett. 2016, 16, 3892–3897. [Google Scholar] [CrossRef] [PubMed]
- Li, I.T.S.; Ha, T.; Chemla, Y.R. Mapping Cell Surface Adhesion by Rotation Tracking and Adhesion Footprinting. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef]
- Yasunaga, A.; Murad, Y.; Li, I.T.S. Quantifying Molecular Tension-Classifications, Interpretations and Limitations of Force Sensors. Phys. Biol. 2019, 17, 011001. [Google Scholar] [CrossRef]
- Murad, Y.; Li, I.T.S. Quantifying Molecular Forces with Serially Connected Force Sensors. Biophys. J. 2019, 116, 1282–1291. [Google Scholar] [CrossRef] [PubMed]
- Grome, M.W.; Zhang, Z.; Lin, C. Stiffness and Membrane Anchor Density Modulate DNA-Nanospring-Induced Vesicle Tubulation. ACS Appl. Mater. Interfaces 2019, 11, 22987–22992. [Google Scholar] [CrossRef] [PubMed]
- Shroff, H.; Reinhard, B.M.; Siu, M.; Agarwal, H.; Spakowitz, A.; Liphardt, J. Biocompatible Force Sensor with Optical Readout and Dimensions of 6 Nm 3. Nano Lett. 2005, 5, 1509–1514. [Google Scholar] [CrossRef] [PubMed]
- Fields, A.P.; Meyer, E.A.; Cohen, A.E. Euler Buckling and Nonlinear Kinking of Double-Stranded DNA. Nucleic Acids Res. 2013, 41, 9881–9890. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Marras, A.E.; Su, H.J.; Castro, C.E. DNA Origami Compliant Nanostructures with Tunable Mechanical Properties. ACS Nano 2014, 8, 27–34. [Google Scholar] [CrossRef]
- Funke, J.J.; Ketterer, P.; Lieleg, C.; Schunter, S.; Korber, P.; Dietz, H. Uncovering the Forces between Nucleosomes Using DNA Origami. Sci. Adv. 2016, 2. [Google Scholar] [CrossRef]
- Iwaki, M.; Wickham, S.F.; Ikezaki, K.; Yanagida, T.; Shih, W.M. A Programmable DNA Origami Nanospring That Reveals Force-Induced Adjacent Binding of Myosin VI Heads. Nat. Commun. 2016, 7, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.; Sachs, F. Orientation-Based FRET Sensor for Real-Time Imaging of Cellular Forces. J. Cell Sci. 2012, 125, 743–750. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.; Sachs, F. Visualizing Dynamic Cytoplasmic Forces with a Compliance-Matched FRET Sensor. J. Cell Sci. 2011, 124, 261–269. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.; Suchyna, T.M.; Lazakovitch, E.; Gronostajski, R.M.; Sachs, F. Real Time FRET Based Detection of Mechanical Stress in Cytoskeletal and Extracellular Matrix Proteins. Cell. Mol. Bioeng. 2011, 4, 148–159. [Google Scholar] [CrossRef]
- Guo, J.; Wang, Y.; Sachs, F.; Meng, F. Actin Stress in Cell Reprogramming. Proc. Natl. Acad. Sci. USA 2014, 111, E5252–E5261. [Google Scholar] [CrossRef]
- Wang, C.; Huang, Z.; Lin, Y.; Ren, J.; Qu, X. Artificial DNA Nano-Spring Powered by Protons. Adv. Mater. 2010, 22, 2792–2798. [Google Scholar] [CrossRef]
- Lipfert, J.; Doniach, S.; Das, R.; Herschlag, D. Understanding Nucleic Acid-Ion Interactions. Annu. Rev. Biochem. 2014, 83, 813–841. [Google Scholar] [CrossRef]
- Bui, V.C.; Nguyen, T.H. DNA Aggregation Induced by Mg2+ Ions under Different Conditions. J. Mol. Recognit. 2018, 31, 1–5. [Google Scholar] [CrossRef]
- Kim, K.-J.; Choi, S.; Sang Cho, Y.; Yang, S.-J.; Cho, Y.-S.; Kim, K.K. Magnesium Ions Enhance Infiltration of Osteoblasts in Scaffolds via Increasing Cell Motility. J. Mater. Sci. Mater. Med. 2017, 28, 96. [Google Scholar] [CrossRef]
- Draper, D.E.; Grilley, D.; Soto, A.M. Ions and RNA Folding. Annu. Rev. Biophys. Biomol. Struct. 2005, 34, 221–243. [Google Scholar] [CrossRef]
- Yang, L.; Arora, K.; Beard, W.A.; Wilson, S.H.; Schlick, T. Critical Role of Magnesium Ions in DNA Polymerase Beta’s Closing and Active Site Assembly. J. Am. Chem. Soc. 2004, 126, 8441–8453. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, I.; Tainer, J.A.; McCammon, J.A. Unraveling the Three-Metal-Ion Catalytic Mechanism of the DNA Repair Enzyme Endonuclease IV. Proc. Natl. Acad. Sci. USA 2007, 104, 1465–1470. [Google Scholar] [CrossRef] [PubMed]
- Hartwig, A. Role of Magnesium in Genomic Stability. Mutat. Res. 2001, 475, 113–121. [Google Scholar] [CrossRef]
- Fei, B.-L.; Xu, W.-S.; Tao, H.-W.; Li, W.; Zhang, Y.; Long, J.-Y.; Liu, Q.-B.; Xia, B.; Sun, W.-Y. Effects of Copper Ions on DNA Binding and Cytotoxic Activity of a Chiral Salicylidene Schiff Base. J. Photochem. Photobiol. B. 2014, 132, 36–44. [Google Scholar] [CrossRef]
- Tchounwou, P.B.; Yedjou, C.G.; Patlolla, A.K.; Sutton, D.J. Heavy Metal Toxicity and the Environment. Exp. Suppl. 2012, 101, 133–164. [Google Scholar] [CrossRef]
- Hartwig, A.; Asmuss, M.; Ehleben, I.; Herzer, U.; Kostelac, D.; Pelzer, A.; Schwerdtle, T.; Bürkle, A. Interference by Toxic Metal Ions with DNA Repair Processes and Cell Cycle Control: Molecular Mechanisms. Environ. Health Perspect. 2002, 110, 797–799. [Google Scholar] [CrossRef]
- Asmuss, M.; Mullenders, L.H.; Hartwig, A. Interference by Toxic Metal Compounds with Isolated Zinc Finger DNA Repair Proteins. Toxicol. Lett. 2000, 112–113, 227–231. [Google Scholar] [CrossRef]
- Anastassopoulou, J.; Theophanides, T. Magnesium-DNA Interactions and the Possible Relation of Magnesium to Carcinogenesis. Irradiation and Free Radicals. Crit. Rev. Oncol. Hematol. 2002, 42, 79–91. [Google Scholar] [CrossRef]
- Sigel, A.; Sigel, H.; Sigel, R.K.O. Metal. Ions in Toxicology: Effects, Interactions, Interdependencies. Met. Ions Life Sci. 2011, 8, vii–viii. [Google Scholar]
- Liang, L.; Shen, J.-W.; Wang, Q. Molecular Dynamics Study on DNA Nanotubes as Drug Delivery Vehicle for Anticancer Drugs. Colloids Surf. B. Biointerfaces 2017, 153, 168–173. [Google Scholar] [CrossRef]
- Palchaudhuri, R.; Hergenrother, P.J. DNA as a Target for Anticancer Compounds: Methods to Determine the Mode of Binding and the Mechanism of Action. Curr. Opin. Biotechnol. 2007, 18, 497–503. [Google Scholar] [CrossRef] [PubMed]
- Hurley, L.H. DNA and Its Associated Processes as Targets for Cancer Therapy. Nat. Rev. Cancer 2002, 2, 188–200. [Google Scholar] [CrossRef] [PubMed]
- Agudelo, D.; Bourassa, P.; Bérubé, G.; Tajmir-Riahi, H.-A. Intercalation of Antitumor Drug Doxorubicin and Its Analogue by DNA Duplex: Structural Features and Biological Implications. Int. J. Biol. Macromol. 2014, 66, 144–150. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Saran, R.; Liu, J. Metal Sensing by DNA. Chem. Rev. 2017, 117, 8272–8325. [Google Scholar] [CrossRef]
- Qu, H.; Tseng, C.Y.; Wang, Y.; Levine, A.J.; Zocchi, G. The Elastic Energy of Sharply Bent Nicked DNA. EPL 2010, 90, 1–5. [Google Scholar] [CrossRef]
- Qu, H.; Wang, Y.; Tseng, C.Y.; Zocchi, G. Critical Torque for Kink Formation in Double-Stranded DNA. Phys. Rev. X 2011, 1, 1–11. [Google Scholar] [CrossRef]
- Qu, H.; Zocchi, G. The Complete Bending Energy Function for Nicked DNA. EPL Europhys. Lett. 2011, 94, 18003. [Google Scholar] [CrossRef]
- Ussery, D.W.; Hinton, J.C.D.; Jorji, B.J.A.M.; Granum, P.E.; Seirafi, A.; Stephen, R.J.; Tupper, A.E.; Berridge, G.; Sidebotham, J.M.; Higgins, C.F. The Chromatin-Associated Protein H-NS. Biochimie 1994, 76, 968–980. [Google Scholar] [CrossRef]
- Williams, R.M.; Rimsky, S. Molecular Aspects of the E. Coli Nucleoid Protein, H-NS: A Central Controller of Gene Regulatory Networks. FEMS Microbiol. Lett. 1997, 156, 175–185. [Google Scholar] [CrossRef]
- Tupper, A.E.; Owen-Hughes, T.A.; Ussery, D.W.; Santos, D.S.; Ferguson, D.J.; Sidebotham, J.M.; Hinton, J.C.; Higgins, C.F. The Chromatin-Associated Protein H-NS Alters DNA Topology in Vitro. EMBO J. 1994, 13, 258–268. [Google Scholar] [CrossRef]
- Hommais, F.; Evelyne, K.; Laurent-Winter, C.; Soutourina, O.; Malpertuy, A.; Le Caer, J.-P.; Danchin, A.; Bertin, P. Large-Scale Monitoring of Pleiotropic Regulation of Gene Expression by the Prokaryotic Nucleoid-Associated Protein, H-NS. Mol. Microbiol. 2001, 40, 20–36. [Google Scholar] [CrossRef] [PubMed]
- Caramel, A.; Schnetz, K. Lac and Lambda Repressors Relieve Silencing of the Escherichia Coli Bgl Promoter. Activation by Alteration of a Repressing Nucleoprotein Complex. J. Mol. Biol. 1998, 284, 875–883. [Google Scholar] [CrossRef] [PubMed]
- Bustamante, V.H.; Santana, F.J.; Calva, E.; Puente, J.L. Transcriptional Regulation of Type III Secretion Genes in Enteropathogenic Escherichia Coli: Ler Antagonizes H-NS-Dependent Repression. Mol. Microbiol. 2001, 39, 664–678. [Google Scholar] [CrossRef]
- Rimsky, S.; Zuber, F.; Buckle, M.; Buc, H. A Molecular Mechanism for the Repression of Transcription by the H-NS Protein. Mol. Microbiol. 2001, 42, 1311–1323. [Google Scholar] [CrossRef] [PubMed]
- Falconi, M.; Colonna, B.; Prosseda, G.; Micheli, G.; Gualerzi, C.O. Thermoregulation of Shigella and Escherichia Coli EIEC Pathogenicity. A Temperature-Dependent Structural Transition of DNA Modulates Accessibility of VirF Promoter to Transcriptional Repressor H-NS. EMBO J. 1998, 17, 7033–7043. [Google Scholar] [CrossRef]
- Friedberg, D.; Umanski, T.; Fang, Y.; Rosenshine, I. Hierarchy in the Expression of the Locus of Enterocyte Effacement Genes of Enteropathogenic Escherichia Coli. Mol. Microbiol. 1999, 34, 941–952. [Google Scholar] [CrossRef]
- Göransson, M.; Sondén, B.; Nilsson, P.; Dagberg, B.; Foreman, K.; Emanuelsson, K.; Uhlin, B.E. Transcriptional Silencing and Thermoregulation of Gene Expression in Escherichia Coli. Nature 1990, 344, 682–685. [Google Scholar] [CrossRef]
- McLeod, S.M.; Johnson, R.C. Control of Transcription by Nucleoid Proteins. Curr. Opin. Microbiol. 2001, 4, 152–159. [Google Scholar] [CrossRef]
- Atlung, T.; Ingmer, H. H-NS: A Modulator of Environmentally Regulated Gene Expression. Mol. Microbiol. 1997, 24, 7–17. [Google Scholar] [CrossRef]
- Thei Dame, R.; Wyman, C.; Goosen, N. Structural Basis for Preferential Binding of H-NS to Curved DNA. Biochimie 2001, 83, 231–234. [Google Scholar] [CrossRef]
- Smyth, C.P.; Lundbäck, T.; Renzoni, D.; Siligardi, G.; Beavil, R.; Layton, M.; Sidebotham, J.M.; Hinton, J.C.; Driscoll, P.C.; Higgins, C.F.; et al. Oligomerization of the Chromatin-Structuring Protein H-NS. Mol. Microbiol. 2000, 36, 962–972. [Google Scholar] [CrossRef] [PubMed]
- Spurio, R.; Falconi, M.; Brandi, A.; Pon, C.L.; Gualerzi, C.O. The Oligomeric Structure of Nucleoid Protein H-NS Is Necessary for Recognition of Intrinsically Curved DNA and for DNA Bending. EMBO J. 1997, 16, 1795–1805. [Google Scholar] [CrossRef] [PubMed]
- Dame, R.T.; Wyman, C.; Goosen, N. H-NS Mediated Compaction of DNA Visualised by Atomic Force Microscopy. Nucleic Acids Res. 2000, 28, 3504–3510. [Google Scholar] [CrossRef]
- Spassky, A.; Rimsky, S.; Garreau, H.; Buc, H. H1a, an E. Coli DNA-Binding Protein Which Accumulates in Stationary Phase, Strongly Compacts DNA in Vitro. Nucleic Acids Res. 1984, 12, 5321–5340. [Google Scholar] [CrossRef] [PubMed]
- Ali, B.M.J.; Amit, R.; Braslavsky, I.; Oppenheim, A.B.; Gileadi, O.; Stavans, J. Compaction of Single DNA Molecules Induced by Binding of Integration Host Factor (IHF). Proc. Natl. Acad. Sci. USA 2001, 98, 10658LP–10663. [Google Scholar] [CrossRef] [PubMed]
- Strick, T.R.; Allemand, J.-F.; Bensimon, D.; Bensimon, A.; Croquette, V. The Elasticity of a Single Supercoiled DNA Molecule. Science 1996, 271, 1835LP–1837. [Google Scholar] [CrossRef] [PubMed]
- Amit, R.; Oppenheim, A.B.; Stavans, J. Increased Bending Rigidity of Single DNA Molecules by H-NS, a Temperature and Osmolarity Sensor. Biophys. J. 2003, 84, 2467–2473. [Google Scholar] [CrossRef]
- Arold, S.T.; Leonard, P.G.; Parkinson, G.N.; Ladbury, J.E. H-NS Forms a Superhelical Protein Scaffold for DNA Condensation. Proc. Natl. Acad. Sci. USA 2010, 107, 15728LP–15732. [Google Scholar] [CrossRef]
- Anuchin, A.M.; Goncharenko, A.V.; Demidenok, O.I.; Kaprelyants, A.S. Histone-like Proteins of Bacteria (Review). Appl. Biochem. Microbiol. 2011, 47, 580. [Google Scholar] [CrossRef]
- Branden, C.I.; Tooze, J. Introduction to Protein Structure; Garland Science: New York, NY, USA, 2012. [Google Scholar]
- Robertson, G.; Hirst, M.; Bainbridge, M.; Bilenky, M.; Zhao, Y.; Zeng, T.; Euskirchen, G.; Bernier, B.; Varhol, R.; Delaney, A.; et al. Genome-Wide Profiles of STAT1 DNA Association Using Chromatin Immunoprecipitation and Massively Parallel Sequencing. Nat. Methods 2007, 4, 651–657. [Google Scholar] [CrossRef]
- Wu, H.-M.; Crothers, D.M. The Locus of Sequence-Directed and Protein-Induced DNA Bending. Nature 1984, 308, 509–513. [Google Scholar] [CrossRef] [PubMed]
- Kotlarz, D.; Fritsch, A.; Buc, H. Variations of Intramolecular Ligation Rates Allow the Detection of Protein-Induced Bends in DNA. EMBO J. 1986, 5, 799–803. [Google Scholar] [CrossRef] [PubMed]
- Finzi, L.; Dunlap, D.D. Single-Molecule Approaches to Probe the Structure, Kinetics, and Thermodynamics of Nucleoprotein Complexes That Regulate Transcription. J. Biol. Chem. 2010, 285, 18973–18978. [Google Scholar] [CrossRef] [PubMed]
- Lymperopoulos, K.; Crawford, R.; Torella, J.P.; Heilemann, M.; Hwang, L.C.; Holden, S.J.; Kapanidis, A.N. Single-Molecule DNA Biosensors for Protein and Ligand Detection. Angew. Chem.—Int. Ed. 2010, 49, 1316–1320. [Google Scholar] [CrossRef] [PubMed]
- Kapanidis, A.N.; Laurence, T.A.; Lee, N.K.; Margeat, E.; Kong, X.; Weiss, S. Alternating-Laser Excitation of Single Molecules. Acc. Chem. Res. 2005, 38, 523–533. [Google Scholar] [CrossRef]
- Shen, W.; Bruist, M.F.; Goodman, S.D.; Seeman, N.C. A Protein-Driven DNA Device That Measures the Excess Binding Energy of Proteins That Distort DNA. Angew. Chem.—Int. Ed. 2004, 43, 4750–4752. [Google Scholar] [CrossRef]
- Stryer, L.; Haugland, R.P. Energy Transfer: A Spectroscopic Ruler. Proc. Natl. Acad. Sci. USA 1967, 58, 719–726. [Google Scholar] [CrossRef]
- Crawford, R.; Kelly, D.J.; Kapanidis, A.N. A Protein Biosensor That Relies on Bending of Single DNA Molecules. Chem. Phys. Chem. 2012, 13, 918–922. [Google Scholar] [CrossRef]
- van der Vliet, P.C. Bending of DNA by Transcription Factors. BioEssays 1993, 15, 25–32. [Google Scholar] [CrossRef]
- Tang, G.Q.; Deshpande, A.P.; Patel, S.S. Transcription Factor-Dependent DNA Bending Governs Promoter Recognition by the Mitochondrial RNA Polymerase. J. Biol. Chem. 2011, 286, 38805–38813. [Google Scholar] [CrossRef]
- Dornberger, U.; Hillisch, A.; Gollmick, F.A.; Fritzsche, H.; Diekmann, S. Solution Structure of a Five-Adenine Bulge Loop within a DNA Duplex. Biochemistry 1999, 38, 12860–12868. [Google Scholar] [CrossRef] [PubMed]
- Hong, F.; Zhang, F.; Liu, Y.; Yan, H. DNA Origami: Scaffolds for Creating Higher Order Structures. Chem. Rev. 2017, 117. [Google Scholar] [CrossRef] [PubMed]
- Yoo, J.; Aksimentiev, A. In Situ Structure and Dynamics of DNA Origami Determined through Molecular Dynamics Simulations. Proc. Natl. Acad. Sci. USA 2013, 110, 20099–20104. [Google Scholar] [CrossRef] [PubMed]
- Pan, K.; Kim, D.N.; Zhang, F.; Adendorff, M.R.; Yan, H.; Bathe, M. Lattice-Free Prediction of Three-Dimensional Structure of Programmed DNA Assemblies. Nat. Commun. 2014, 5, 1–7. [Google Scholar] [CrossRef]
- Kim, D.N.; Kilchherr, F.; Dietz, H.; Bathe, M. Quantitative Prediction of 3D Solution Shape and Flexibility of Nucleic Acid Nanostructures. Nucleic Acids Res. 2012, 40, 2862–2868. [Google Scholar] [CrossRef]
- Douglas, S.M.; Marblestone, A.H.; Teerapittayanon, S.; Vazquez, A.; Church, G.M.; Shih, W.M. Rapid Prototyping of 3D DNA-Origami Shapes with CaDNAno. Nucleic Acids Res. 2009, 37, 5001–5006. [Google Scholar] [CrossRef]
- Zhang, Y.; Crothers, D.M. High-Throughput Approach for Detection of DNA Bending and Flexibility Based on Cyclization. Proc. Natl. Acad. Sci. USA 2003, 100, 3161–3166. [Google Scholar] [CrossRef]
- Alexandrov, L.B.; Bishop, A.R.; Rasmussen, K.O.; Alexandrov, B.S. The Role of Structural Parameters in DNA Cyclization. BMC Bioinformatics 2016, 17, 1–10. [Google Scholar] [CrossRef]
- Gubu, A.; Wang, J.; Jin, H.; Tang, X. Synthesis and “DNA Interlocks” Formation of Small Circular Oligodeoxynucleotides. ACS Appl. Mater. Interfaces 2020, 12, 12584–12590. [Google Scholar] [CrossRef]
- Schmidt, T.L.; Heckel, A. Construction of a Structurally Defined Double-Stranded DNA Catenane. Nano Lett. 2011, 11, 1739–1742. [Google Scholar] [CrossRef] [PubMed]
- Mao, C.; Sun, W.; Seeman, N.C. Assembly of Borromean Rings from DNA. Nature 1997, 386, 137–138. [Google Scholar] [CrossRef] [PubMed]
- Ackermann, D.; Schmidt, T.L.; Hannam, J.S.; Purohit, C.S.; Heckel, A.; Famulok, M. A Double-Stranded DNA Rotaxane. Nat. Nanotechnol. 2010, 5, 436–442. [Google Scholar] [CrossRef]
- Li, J.; Mohammed-Elsabagh, M.; Paczkowski, F.; Li, Y. Circular Nucleic Acids: Discovery, Functions and Applications. Chem. Bio. Chem. 2020, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Seeman, N.C. From Genes to Machines: DNA Nanomechanical Devices. Trends Biochem. Sci. 2005, 30, 119–125. [Google Scholar] [CrossRef]
- Krishnan, Y.; Simmel, F.C. Nucleic Acid Based Molecular Devices. Angew. Chem. Int. Ed. Engl. 2011, 50, 3124–3156. [Google Scholar] [CrossRef]
- Ramezani, H.; Dietz, H. Building Machines with DNA Molecules. Nat. Rev. Genet. 2020, 21, 5–26. [Google Scholar] [CrossRef]
- Wang, F.; Willner, B.; Willner, I. DNA-Based Machines. Top. Curr. Chem. 2014, 354, 279–338. [Google Scholar] [CrossRef]
- Khara, D.C.; Schreck, J.S.; Tomov, T.E.; Berger, Y.; Ouldridge, T.E.; Doye, J.P.K.; Nir, E. DNA Bipedal Motor Walking Dynamics: An Experimental and Theoretical Study of the Dependency on Step Size. Nucleic Acids Res. 2017, 46, 1553–1561. [Google Scholar] [CrossRef]
- Park, S.; Song, J.; Kim, J.S. In Silico Construction of a Flexibility-Based DNA Brownian Ratchet for Directional Nanoparticle Delivery. Sci. Adv. 2019, 5, eaav4943. [Google Scholar] [CrossRef]
- Tomov, T.E.; Tsukanov, R.; Liber, M.; Masoud, R.; Plavner, N.; Nir, E. Rational Design of DNA Motors: Fuel Optimization through Single-Molecule Fluorescence. J. Am. Chem. Soc. 2013, 135, 11935–11941. [Google Scholar] [CrossRef] [PubMed]
- Tomov, T.E.; Tsukanov, R.; Glick, Y.; Berger, Y.; Liber, M.; Avrahami, D.; Gerber, D.; Nir, E. DNA Bipedal Motor Achieves a Large Number of Steps Due to Operation Using Microfluidics-Based Interface. ACS Nano 2017, 11, 4002–4008. [Google Scholar] [CrossRef] [PubMed]
- Liber, M.; Tomov, T.E.; Tsukanov, R.; Berger, Y.; Nir, E. A Bipedal DNA Motor That Travels Back and Forth between Two DNA Origami Tiles. Small 2015, 11, 568–575. [Google Scholar] [CrossRef] [PubMed]
- Geggier, S.; Vologodskii, A. Sequence Dependence of DNA Bending Rigidity. Proc. Natl. Acad. Sci. USA 2010, 107, 15421LP–15426. [Google Scholar] [CrossRef] [PubMed]
- Chuang, H.-M.; Reifenberger, J.G.; Cao, H.; Dorfman, K.D. Sequence-Dependent Persistence Length of Long DNA. Phys. Rev. Lett. 2017, 119, 227802. [Google Scholar] [CrossRef]
- Suzuki, Y.; Kawamata, I.; Mizuno, K.; Murata, S. Large Deformation of a DNA-Origami Nanoarm Induced by the Cumulative Actuation of Tension-Adjustable Modules. Angew. Chem. Int. Ed. 2020, 59, 6230–6234. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saran, R.; Wang, Y.; Li, I.T.S. Mechanical Flexibility of DNA: A Quintessential Tool for DNA Nanotechnology. Sensors 2020, 20, 7019. https://doi.org/10.3390/s20247019
Saran R, Wang Y, Li ITS. Mechanical Flexibility of DNA: A Quintessential Tool for DNA Nanotechnology. Sensors. 2020; 20(24):7019. https://doi.org/10.3390/s20247019
Chicago/Turabian StyleSaran, Runjhun, Yong Wang, and Isaac T. S. Li. 2020. "Mechanical Flexibility of DNA: A Quintessential Tool for DNA Nanotechnology" Sensors 20, no. 24: 7019. https://doi.org/10.3390/s20247019
APA StyleSaran, R., Wang, Y., & Li, I. T. S. (2020). Mechanical Flexibility of DNA: A Quintessential Tool for DNA Nanotechnology. Sensors, 20(24), 7019. https://doi.org/10.3390/s20247019