Quantification of Arm Swing during Walking in Healthy Adults and Parkinson’s Disease Patients: Wearable Sensor-Based Algorithm Development and Validation
Abstract
1. Introduction
2. Materials and Methods
2.1. Subjects and Data Collection
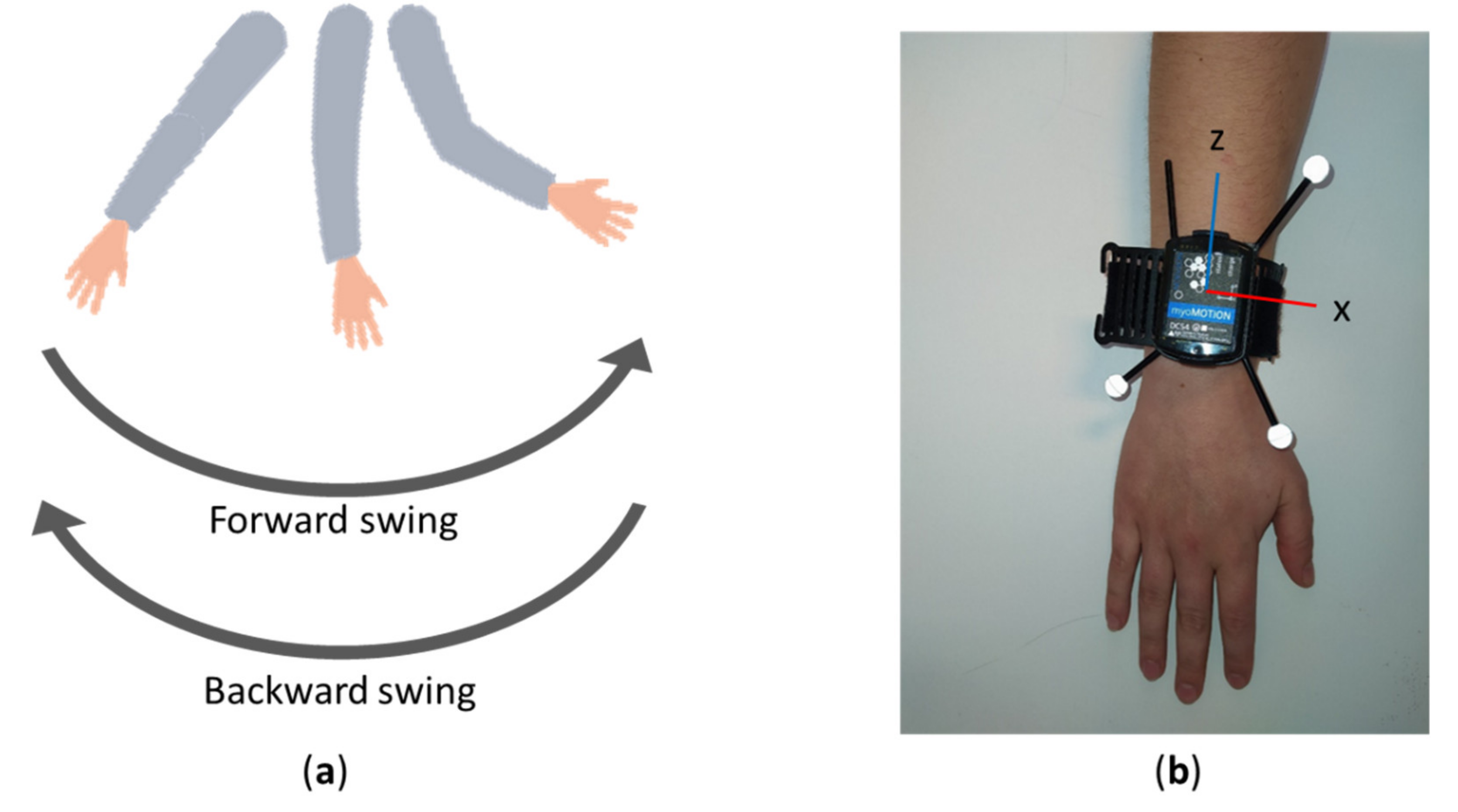
2.2. Definition of Arm Swing during Locomotion
2.3. Equipment
2.4. Data Processing
2.4.1. Inertial Measurement Unit Data
2.4.2. Optical Data
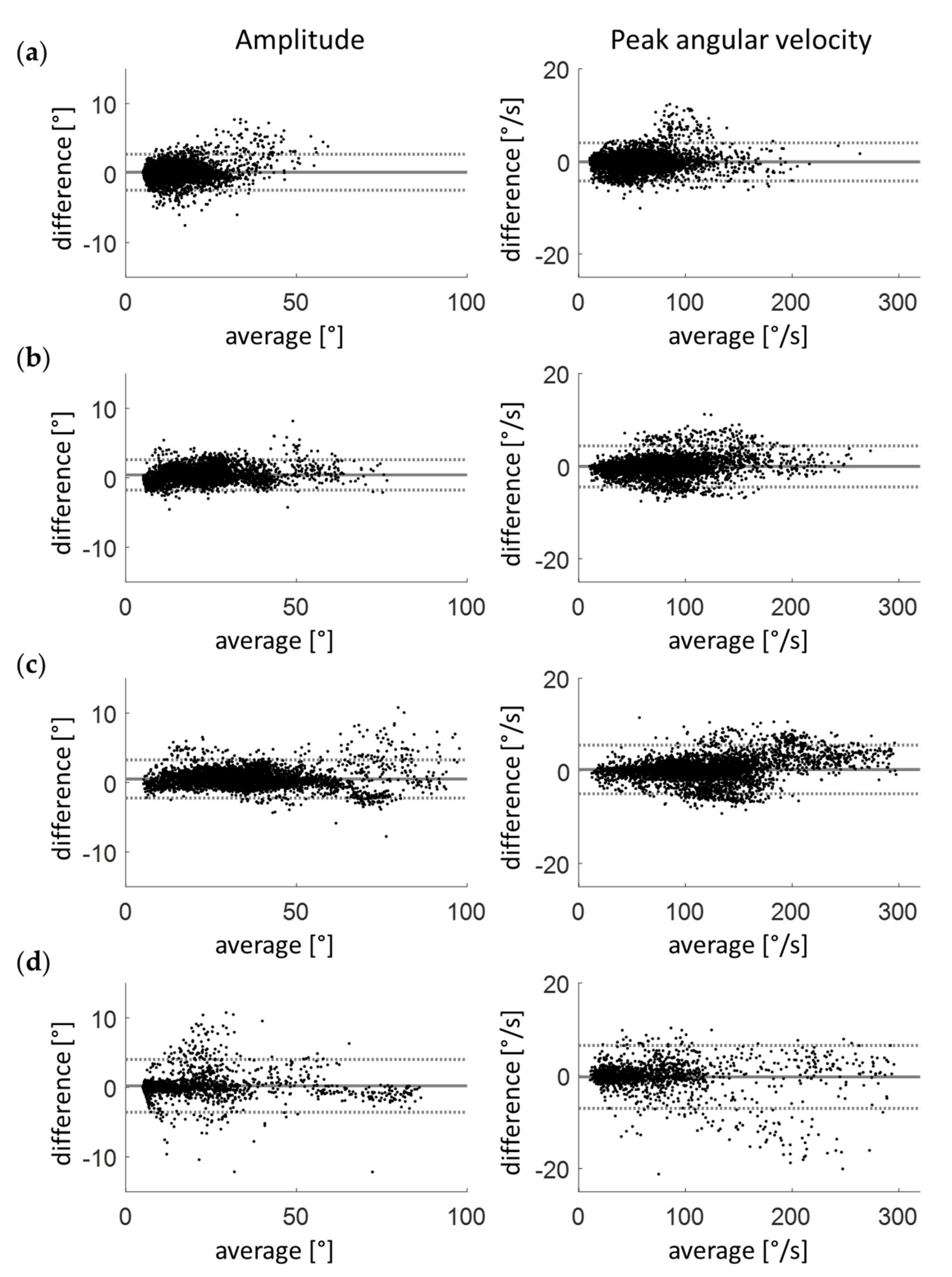
2.5. Statistical Analysis
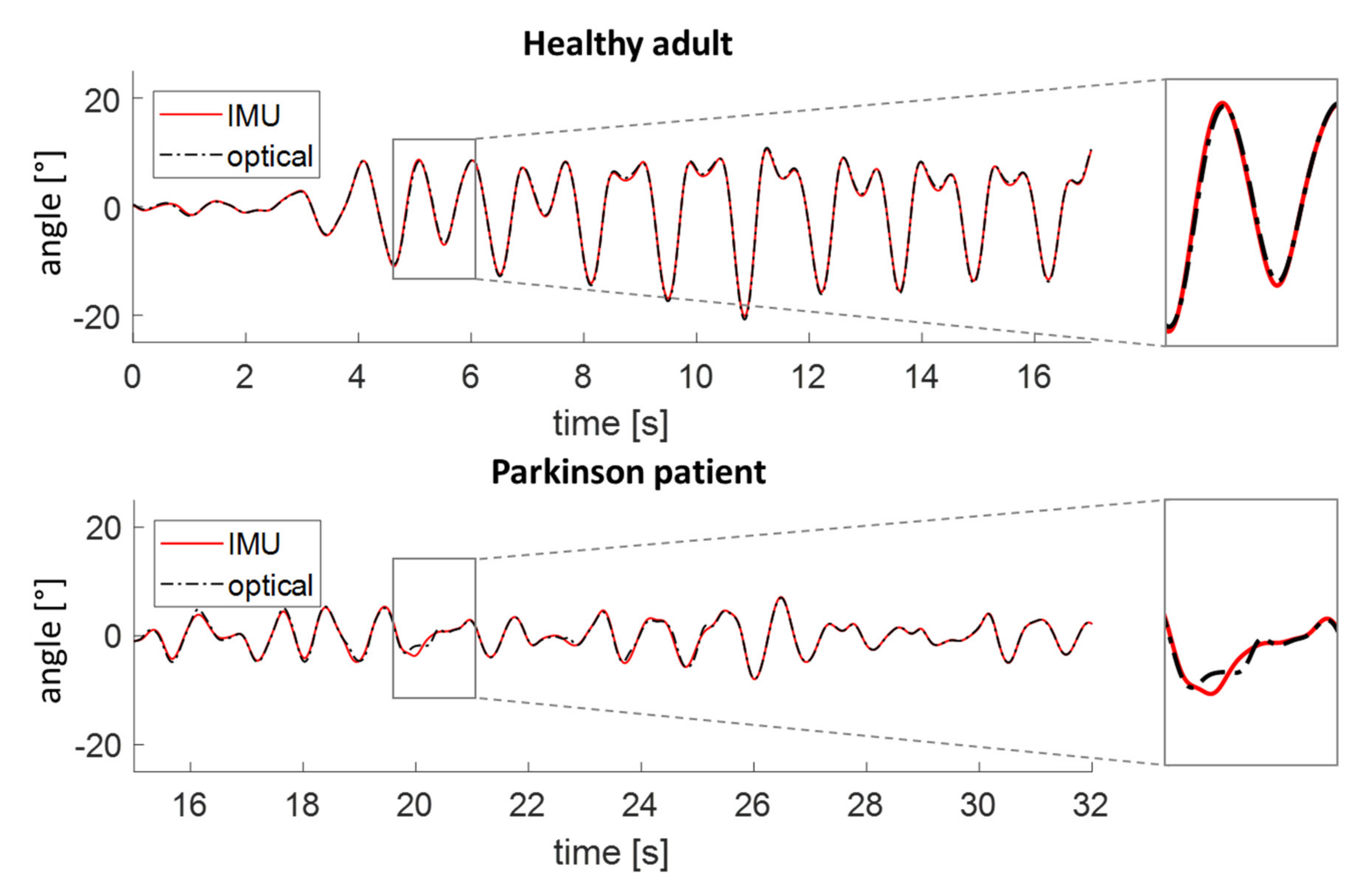
3. Results
3.1. Healthy Adults
3.2. Patients with Parkinson’s Disease
3.3. Clinical Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Meyns, P.; Bruijn, S.M.; Duysens, J. The how and why of arm swing during human walking. Gait Posture 2013, 38, 555–562. [Google Scholar] [CrossRef] [PubMed]
- Goudriaan, M.; Jonkers, I.; van Dieen, J.H.; Bruijn, S.M. Arm swing in human walking: What is their drive? Gait Posture 2014, 40, 321–326. [Google Scholar] [CrossRef] [PubMed]
- Mirelman, A.; Bernad-Elazari, H.; Nobel, T.; Thaler, A.; Peruzzi, A.; Plotnik, M.; Giladi, N.; Hausdorff, J.M. Effects of Aging on Arm Swing during Gait: The Role of Gait Speed and Dual Tasking. PLoS ONE 2015, 10, e0136043. [Google Scholar] [CrossRef] [PubMed]
- Plate, A.; Sedunko, D.; Pelykh, O.; Schlick, C.; Ilmberger, J.R.; Bötzel, K. Normative data for arm swing asymmetry: How (a)symmetrical are we? Gait Posture 2015, 41, 13–18. [Google Scholar] [CrossRef]
- Punt, M.; Bruijn, S.M.; Wittink, H.; van Dieën, J.H. Effect of arm swing strategy on local dynamic stability of human gait. Gait Posture 2015, 41, 504–509. [Google Scholar] [CrossRef]
- Johansson, G.M.; Frykberg, G.E.; Grip, H.; Broström, E.W.; Häger, C.K. Assessment of arm movements during gait in stroke—The Arm Posture Score. Gait Posture 2014, 40, 549–555. [Google Scholar] [CrossRef]
- Huang, X.; Mahoney, J.M.; Lewis, M.M.; Guangwei, D.; Piazza, S.J.; Cusumano, J.P. Both coordination and symmetry of arm swing are reduced in Parkinson’s disease. Gait Posture 2012, 35, 373–377. [Google Scholar] [CrossRef]
- Roggendorf, J.; Chen, S.; Baudrexel, S.; van de Loo, S.; Seifried, C.; Hilker, R. Arm swing asymmetry in Parkinson’s disease measured with ultrasound based motion analysis during treadmill gait. Gait Posture 2012, 35, 116–120. [Google Scholar] [CrossRef]
- Lewek, M.D.; Poole, R.; Johnson, J.; Halawa, O.; Huang, X. Arm Swing Magnitude and Asymmetry During Gait in the Early Stages of Parkinson’s Disease. Gait Posture 2010, 31, 256–260. [Google Scholar] [CrossRef]
- Rovini, E.; Maremmani, C.; Cavallo, F. How wearable sensors can support parkinson’s disease diagnosis and treatment: A systematic review. Front. Neurosci. 2017, 11, 555. [Google Scholar] [CrossRef]
- Mirelman, A.; Bernad-Elazari, H.; Thaler, A.; Giladi-Yacobi, E.; Gurevich, T.; Gana-Weisz, M.; Saunders-Pullman, R.; Raymond, D.; Doan, N.; Bressman, S.; et al. Arm Swing as a Potential New Prodromal Marker of Parkinson’s Disease. Mov. Disord. 2016, 31, 1527–1534. [Google Scholar] [CrossRef] [PubMed]
- Sterling, N.W.; Cusumano, J.P.; Shaham, N.; Piazza, S.J.; Liu, G.; Kong, L.; Du, G.; Lewis, M.M.; Huang, X. Dopaminergic modulation of arm swing during gait among Parkinson’s disease patients. J. Parkinsons Dis. 2015, 5, 141–150. [Google Scholar] [CrossRef] [PubMed]
- Curtze, C.; Nutt, J.G.; Carlson-Kuhta, P.; Mancini, M.; Horak, F.B. Levodopa Is a Double-Edged Sword for Balance and Gait in People With Parkinson’s Disease. Mov. Disord. 2015, 30, 1361–1370. [Google Scholar] [CrossRef]
- Brognara, L.; Palumbo, P.; Grimm, B.; Palmerini, L. Assessing Gait in Parkinson’s Disease Using Wearable Motion Sensors: A Systematic Review. Diseases 2019, 7, 18. [Google Scholar] [CrossRef]
- Vizcarra, J.A.; Sánchez-Ferro, Á.; Maetzler, W.; Marsili, L.; Zavala, L.; Lang, A.E.; Martinez-Martin, P.; Mestre, T.A.; Reilmann, R.; Hausdorff, J.M.; et al. The Parkinson’s disease e-diary: Developing a clinical and research tool for the digital age. Mov. Disord. 2019, 34, 676–681. [Google Scholar] [CrossRef]
- Maetzler, W.; Domingos, J.; Srulijes, K.; Ferreira, J.J.; Bloem, B.R. Quantitative wearable sensors for objective assessment of Parkinson’s disease. Mov. Disord. 2013, 28, 1628–1637. [Google Scholar] [CrossRef] [PubMed]
- Warmerdam, E.; Hausdorff, J.M.; Atrsaei, A.; Zhou, Y.; Mirelman, A.; Aminian, K.; Espay, A.J.; Hansen, C.; Evers, L.J.W.; Keller, A.; et al. Long-term unsupervised mobility assessment in movement disorders. Lancet Neurol. 2020, 19, 462–470. [Google Scholar] [CrossRef]
- Gibb, W.R.G.; Lees, A.J. The relevance of the Lewy body to the pathogenesis of idiopathic Parkinson’s disease. J. Neurol. Neurosurg. Psychiatry 1988, 51, 745–752. [Google Scholar] [CrossRef]
- Moe-Nilssen, R.; Helbostad, J.L. Estimation of gait cycle characteristics by trunk accelerometry. J. Biomech. 2004, 37, 121–126. [Google Scholar] [CrossRef]
- Killeen, T.; Elshehabi, M.; Filli, L.; Hobert, M.A.; Hansen, C.; Rieger, D.; Brockmann, K.; Nussbaum, S.; Zörner, B.; Bolliger, M.; et al. Arm swing asymmetry in overground walking. Sci. Rep. 2018, 8, 1–10. [Google Scholar] [CrossRef]
- Gløersen, Ø.; Federolf, P. Predicting missing marker trajectories in human motion data using marker intercorrelations. PLoS ONE 2016, 11, e0152616. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 327, 307–310. [Google Scholar] [CrossRef]
- Salarian, A.; Russmann, H.; Vingerhoets, F.J.G.; Dehollain, C.; Blanc, Y.; Burkhard, P.R.; Aminian, K. Gait assessment in Parkinson’s disease: Toward an ambulatory system for long-term monitoring. IEEE Trans. Biomed. Eng. 2004, 51, 1434–1443. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.; Lebel, K.; Bogard, S.; Goubault, E.; Boissy, P.; Clinicians, Q.P.N. Using Inertial Sensors to Automatically Detect and Segment Activities of Daily Living in People with Parkinson’s Disease. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 26, 197–204. [Google Scholar] [CrossRef] [PubMed]
- Ospina, B.M.; Chaparro, J.A.V.; Paredes, J.D.A.; Pino, Y.J.C.; Navarro, A.; Orozco, J.L. Objective arm swing analysis in early-stage Parkinson’s disease using an RGB-D Camera (Kinect®). J. Parkinsons Dis. 2018, 8, 563–570. [Google Scholar] [CrossRef] [PubMed]
- Sveinbjornsdottir, S. The clinical symptoms of Parkinson’s disease. J. Neurochem. 2016, 139, 318–324. [Google Scholar] [CrossRef]
- Mirelman, A.; Bonato, P.; Camicioli, R.; Ellis, T.D.; Giladi, N.; Hamilton, J.L.; Hass, C.J.; Hausdorff, J.M.; Pelosin, E.; Almeida, Q.J. Gait impairments in Parkinson’s disease. Lancet Neurol. 2019, 18, 697–708. [Google Scholar] [CrossRef]
- Del Din, S.; Elshehabi, M.; Galna, B.; Hobert, M.A.; Warmerdam, E.; Suenkel, U.; Brockmann, K.; Metzger, F.; Hansen, C.; Berg, D.; et al. Gait analysis with wearables predicts conversion to parkinson disease. Ann. Neurol. 2019, 86, 357–367. [Google Scholar] [CrossRef]
- Pham, M.H.; Elshehabi, M.; Haertner, L.; Heger, T.; Hobert, M.A.; Faber, G.S.; Salkovic, D.; Ferreira, J.J.; Berg, D.; Sanchez-Ferro, Á.; et al. Algorithm for Turning Detection and Analysis Validated under Home-Like Conditions in Patients with Parkinson’s Disease and Older Adults using a 6 Degree-of-Freedom Inertial Measurement Unit at the Lower Back. Front. Neurol. 2017, 8, 135. [Google Scholar] [CrossRef]
- El-Gohary, M.; Pearson, S.; McNames, J.; Mancini, M.; Horak, F.; Mellone, S.; Chiari, L. Continuous monitoring of turning in patients with movement disability. Sensors 2014, 14, 356–369. [Google Scholar] [CrossRef]
- Kubo, M.; Wagenaar, R.C.; Saltzman, E.; Holt, K.G. Biomechanical mechanism for transitions in phase and frequency of arm and leg swing during walking. Biol. Cybern. 2004, 91, 91–98. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wagenaar, R.C.; Van Emmerik, R.E.A. Resonant frequencies of arms and legs identify different walking patterns. J. Biomech. 2000, 33, 853–861. [Google Scholar] [CrossRef]
- Chockalingam, N.; Chatterley, F.; Greenhalgh, A.; Dangerfield, P. Postural differences in the shoulder girdle during normal locomotion in treadmill vs. over ground walking. Stud. Health Technol. Inform. 2006, 123, 404–408. [Google Scholar] [PubMed]

| Healthy Adults | PD Patients | |
|---|---|---|
| n (male) | 15 (9) | 13 (5) |
| Age [years] | 31 ± 9 | 71 ± 9 |
| Body mass index [kg/m2] | 23.4 ± 2.7 | 28.5 ± 5.9 |
| Hoehn and Yahr stage (1–5) | NA | 2.8 ± 0.7 |
| Healthy Adults 2 km/h | Healthy Adults 3 km/h | Healthy Adults 4 km/h | PwP Preferred | ||
|---|---|---|---|---|---|
| Angle RMSe [°] | 0.83 | 0.91 | 0.72 | 1.18 | |
| Angular velocity RMSe [°/s] | 0.03 | 0.03 | 0.03 | 0.16 | |
| No. of swings | 3885 | 3788 | 4103 | 1762 | |
| Amplitude [°] | Systematic error | 0.1 | 0.4 | 0.5 | 0.2 |
| Random error | 2.6 | 2.2 | 2.7 | 3.8 | |
| Absolute error | 0.9 | 0.9 | 1.1 | 1.1 | |
| Peak angular velocity [°/s] | Systematic error | −0.1 | −0.1 | 0.3 | −0.3 |
| Random error | 4.2 | 4.4 | 5.3 | 6.8 | |
| Absolute error | 1.4 | 1.6 | 1.9 | 2.0 | |
| Healthy Adults (2 km/h) | Healthy Adults (3 km/h) | Healthy Adults (4 km/h) | PwP (Preferred) | |
|---|---|---|---|---|
| Amplitude [°] | 16 | 23 * | 36 * | 17 |
| Peak angular velocity [°/s] | 57 | 84 * | 122 * | 60 |
| Forward peak angular velocity [°/s] | 59 | 87 * | 124 * | 60 |
| Backward peak angular velocity [°/s] | 55 | 80 * | 120 * | 59 |
| Percentage of walk with swinging motion in an arm [%] | 93 * | 99 * | 99 * | 78 |
| Frequency [Hz] | 0.9 | 0.9 | 0.9 | 0.9 |
| Regularity (0–1) | 0.8 | 0.9 * | 0.9 * | 0.7 |
| Percentage of walk with swinging motion in both arms simultaneously [%] | 90 * | 97 * | 98 * | 64 |
| Absolute amplitude asymmetry index [%] | 20 | 17 | 20 | 36 |
| Absolute peak angular velocity asymmetry index [%] | 19 | 18 | 21 | 33 |
| Coordination (0–1) | 0.7 | 0.8 | 0.8 | 0.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Warmerdam, E.; Romijnders, R.; Welzel, J.; Hansen, C.; Schmidt, G.; Maetzler, W. Quantification of Arm Swing during Walking in Healthy Adults and Parkinson’s Disease Patients: Wearable Sensor-Based Algorithm Development and Validation. Sensors 2020, 20, 5963. https://doi.org/10.3390/s20205963
Warmerdam E, Romijnders R, Welzel J, Hansen C, Schmidt G, Maetzler W. Quantification of Arm Swing during Walking in Healthy Adults and Parkinson’s Disease Patients: Wearable Sensor-Based Algorithm Development and Validation. Sensors. 2020; 20(20):5963. https://doi.org/10.3390/s20205963
Chicago/Turabian StyleWarmerdam, Elke, Robbin Romijnders, Julius Welzel, Clint Hansen, Gerhard Schmidt, and Walter Maetzler. 2020. "Quantification of Arm Swing during Walking in Healthy Adults and Parkinson’s Disease Patients: Wearable Sensor-Based Algorithm Development and Validation" Sensors 20, no. 20: 5963. https://doi.org/10.3390/s20205963
APA StyleWarmerdam, E., Romijnders, R., Welzel, J., Hansen, C., Schmidt, G., & Maetzler, W. (2020). Quantification of Arm Swing during Walking in Healthy Adults and Parkinson’s Disease Patients: Wearable Sensor-Based Algorithm Development and Validation. Sensors, 20(20), 5963. https://doi.org/10.3390/s20205963







